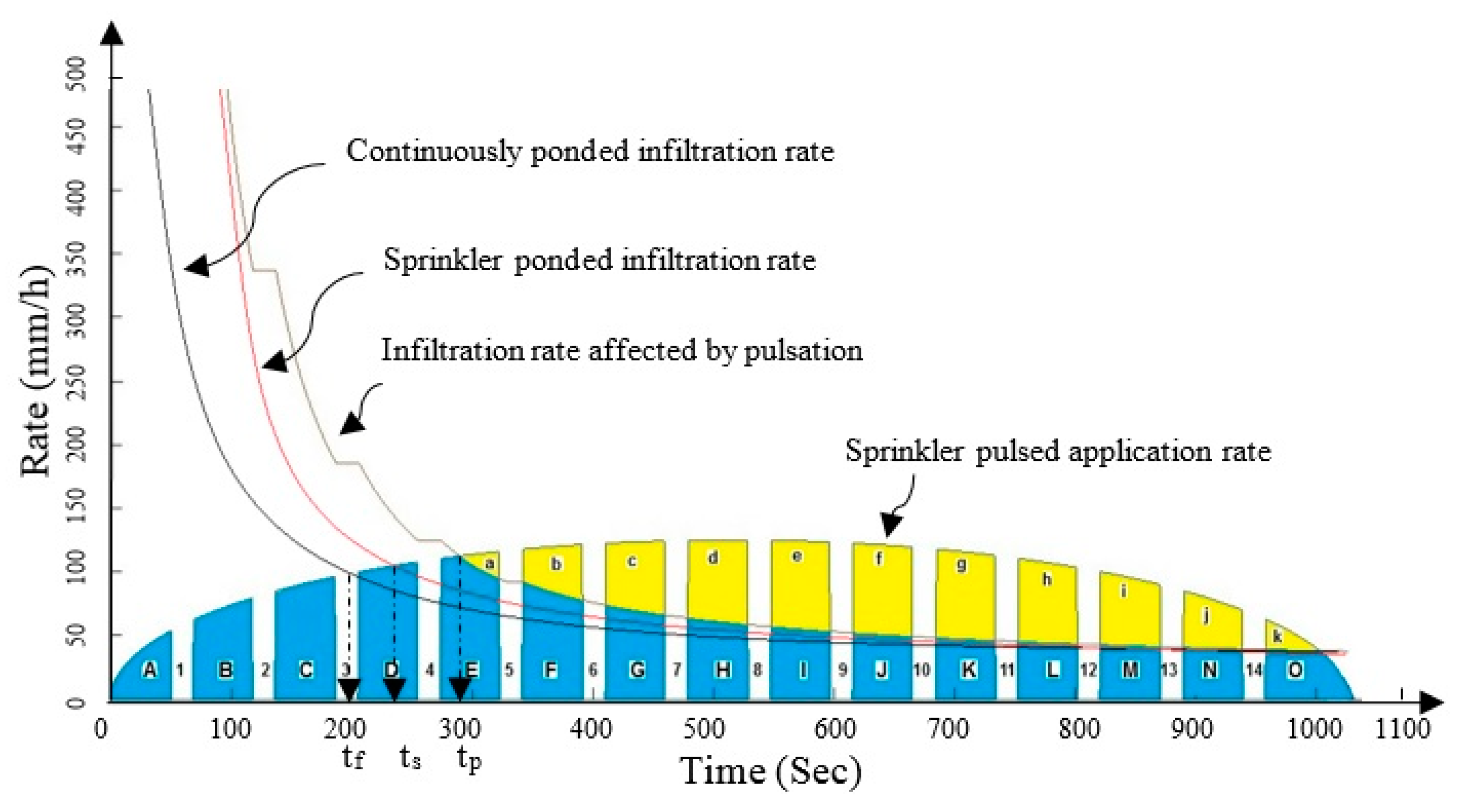
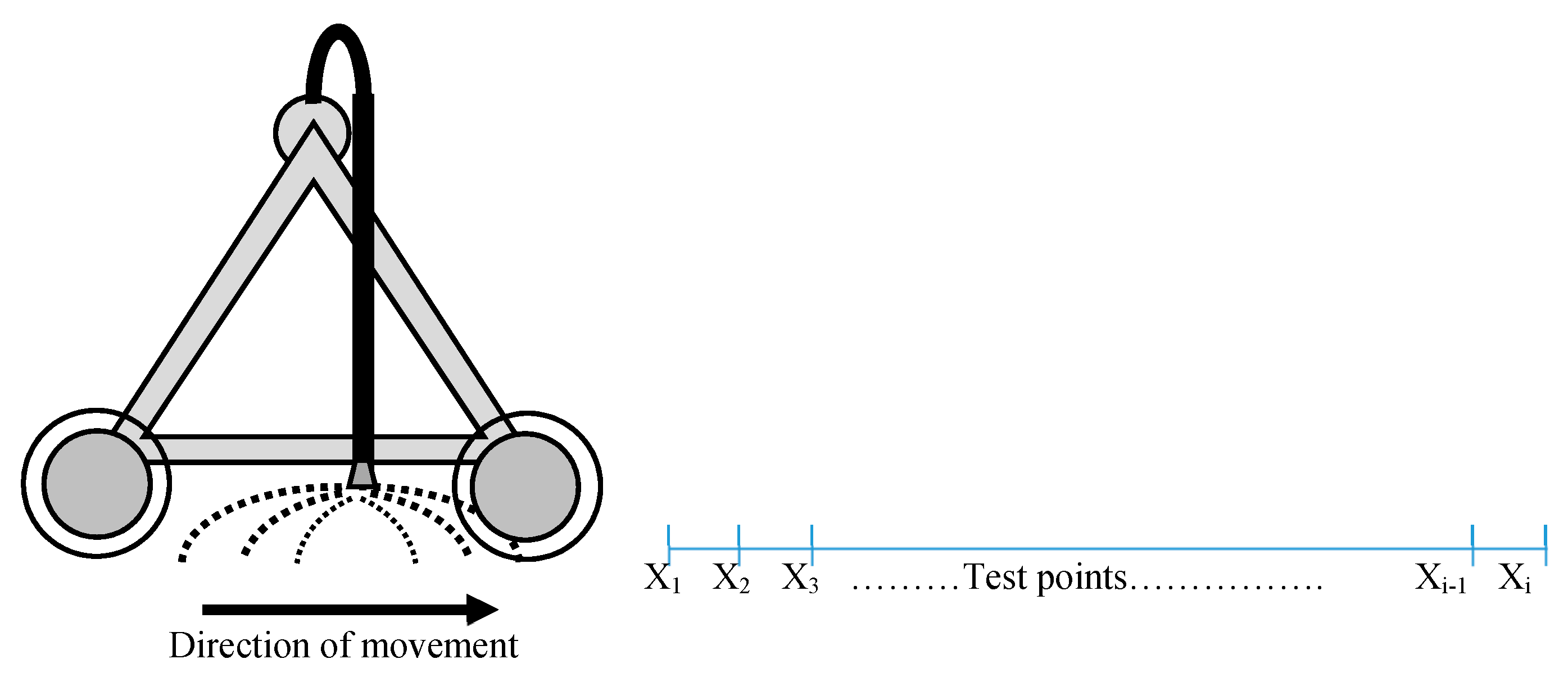1. Introduction
Many factors put pressure on freshwater resources, such as climate change (global warming), pollution, and population increase [
1]. These pressures lead to an increase in the demand for fresh water, while the availability of it is decreasing [
1]. Since agriculture is the primary sector that consumes water worldwide, and mostly for irrigation, it will be the sector most affected by water scarcity. In recent years, self-propelled sprinkler irrigation machines irrigated more than 12.5 million hectares worldwide [
2], and they have become widely used to replace other conventional irrigation methods such as flood irrigation and some other types of sprinkler irrigation [
2,
3,
4,
5]. Also, the self-propelled sprinkler systems are suitable for almost all crops and all types of topography and they have a high level of automation. Furthermore, the application efficiency for the self-propelled sprinkler systems is the highest among all the other types of sprinkler systems, and applying water on a regular and consistent basis is the most significant advantage of these machines [
6]. Also, the self-propelled sprinkler can irrigate large fields efficiently with low labour costs, and it can be adapted to many different soils and the changing terrain [
7].
The purpose of the sprinkler irrigation system is to distribute water evenly on the farm to supplement a soil moisture deficiency that is not replenished by rainfall [
8]. If the irrigation water is not uniformly applied within the field, then the underwatered areas will result in reduced crop yields and the overwatered regions will result in the reduction or loss of crop yields [
9], possibly due to plants suffering anoxia in soil water saturation conditions [
9], besides increased pumping costs. Therefore, irrigation uniformity becomes very important because it is observed that it has a direct function on the crop yield [
8]. Improper irrigation applications lead to crop water stress and low yield [
10,
11]. On the other hand, excessive irrigation can lead to pollution due to loss of plant nutrients through deep percolation, runoff, and soil erosion as well as oxygen stress [
12,
13,
14]. Therefore, the greatest effort in the design and management of irrigation systems should be focused towards dealing with problems related to reducing water losses, minimizing overwatering, and increasing irrigation uniformity.
Nowadays, the low-pressure sprinkler has been widely used to replace high-pressure impact sprinklers in self-propelled sprinkler systems due to its low operating cost and high efficiency [
15]. The low-pressure sprinklers that operate closer to or below the crop canopy are more water-efficient than high-pressure sprinklers [
16,
17]. The efficiency enhancement is believed to result from reduced water loss through evaporation and wind drift [
15]. The operating pressure is related directly to the wetting diameter of the sprinklers and will affect the instantaneous application rate [
18]. High-pressure sprinklers have a wider wetting diameter compared to low-pressure sprinklers [
19]. Therefore, to apply a certain water depth to a specific soil using the high-pressure sprinkler, the applied water will spread out on a wide area due to the wide wetting diameter and hence resulting in a low instantaneous application rate [
17]. If the low-pressure sprinkler is used to apply the same water depth, the same amount of water would spread out on a smaller area, resulting in a higher instantaneous application rate [
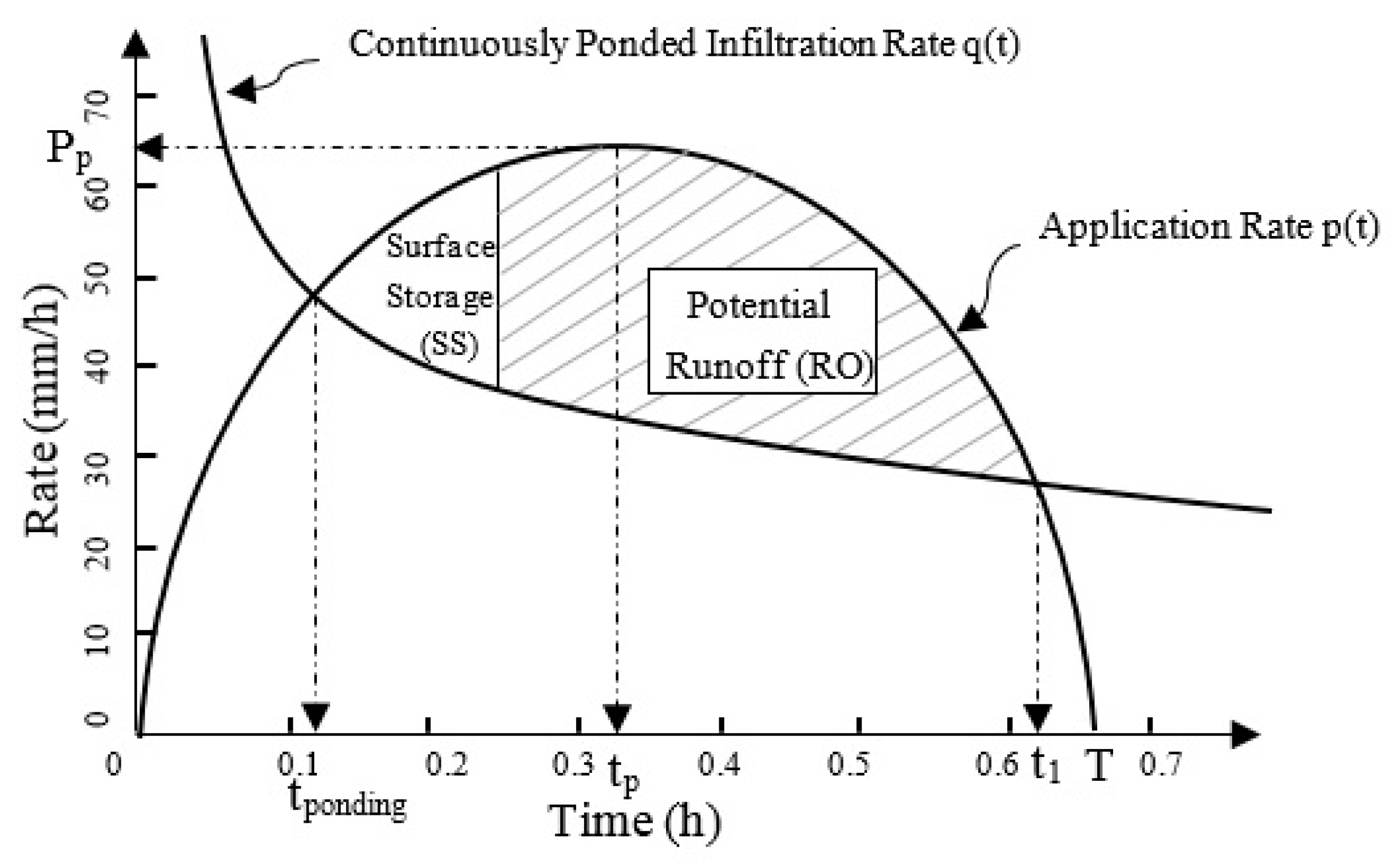
19]. For any sprinkler irrigation system, the surface runoff occurs when the water application rate exceeds the soil infiltration rate and the soil surface storage capacity [
20,
21]. The low-pressure sprinklers have a small wetting diameter, which results in a high instantaneous application rate and causes surface runoff on most of the soil types except soils with high intake rates [
22,
23]. Since the low-pressure sprinkler system has a high instantaneous application rate, the potential for increased surface runoff is higher [
24].
Most researchers have reported that self-propelled sprinkler systems have the problem of surface runoff [
25]. The magnitude of the runoff depends on several factors, such as irrigation machine characteristics, soil type, crop type, cultivation practices, and topography [
26,
27]. Ben-Hur, Plaut [
28] and Letey, Vaux [
10] suggested that crop yield can be affected by runoff in three ways: (1) The loss of runoff from the cultivated field is a loss of the water targeted for crop production; (2) the runoff will increase soil erosion and lead to a loss in fertiliser and nutrients that are washed out of the field; (3) the runoff water that accumulates in the low areas within the field will cause a poor distribution of water, reduce the water efficiency, and it can cause waterlogging that leads to either crop loss or a reduction in the crop yield. Kincaid, Heermann [
22] concluded that 22% of the applied water was lost under high-pressure centre pivot sprinkler systems spraying a field with silty loam soil. Addink [
23] noted that the runoff was 65% under a low-pressure sprinkler machine, while it was 22% under a high-pressure sprinkler system when irrigating a field with very fine sandy soil. Addink [
23] and Kincaid, Heermann [
22] reported that no runoff happened under both low-pressure and high-pressure sprinkler systems when irrigating a field with sandy soil.
Many studies have attempted to reduce surface runoff losses under the linear move sprinkler system by increasing soil infiltration rate and surface storage capacity through applying specific tillage practices or adding some materials to the soil surface [
28,
29,
30,
31,
32,
33,
34]. These practices can decrease runoff volume to some extent, but they will not eliminate it. Other studies have focused on reducing either machine speed or sprinkler discharge rate to minimise surface runoff using different techniques [
4,
18,
26,
35,
36,
37,
38]. However, the use of these methods often leads to a reduction in the applied depth for each pass of the irrigation machine, and the amount of the resulting runoff is not certainly at the lowest possible value. Also, some of these methods can affect the distribution uniformity and result in nonuniform water distribution, especially for low irrigation depths [
39,
40].
The efficiency of self-propelled sprinkler irrigation systems can be increased by decreasing runoff losses through matching the applied water volume and application rate to specific soil characteristics [
39]. One of the methods used to increase the efficiency of self-propelled irrigation systems was to apply variable amounts of water along their lateral span and in the direction of movement to accommodate variable soil or crop conditions [
40]. Variable-rate irrigation (VRI) technology has been used in precision irrigation. However, it is not a basic component in precision irrigation, but one of many other tools that might be suitable in the implementation of precision irrigation systems [
41]. The potential for water saving by using precision or variable-rate irrigation can be achieved by: (1) not watering empty (uncultivated) areas inside the field; (2) decreasing irrigation to an amount suitable for specific problems, such as surface runoff, and matching the soil infiltration rate or different crop needs; and (3) fully optimizing and maximizing the economic value of the irrigation water [
41].
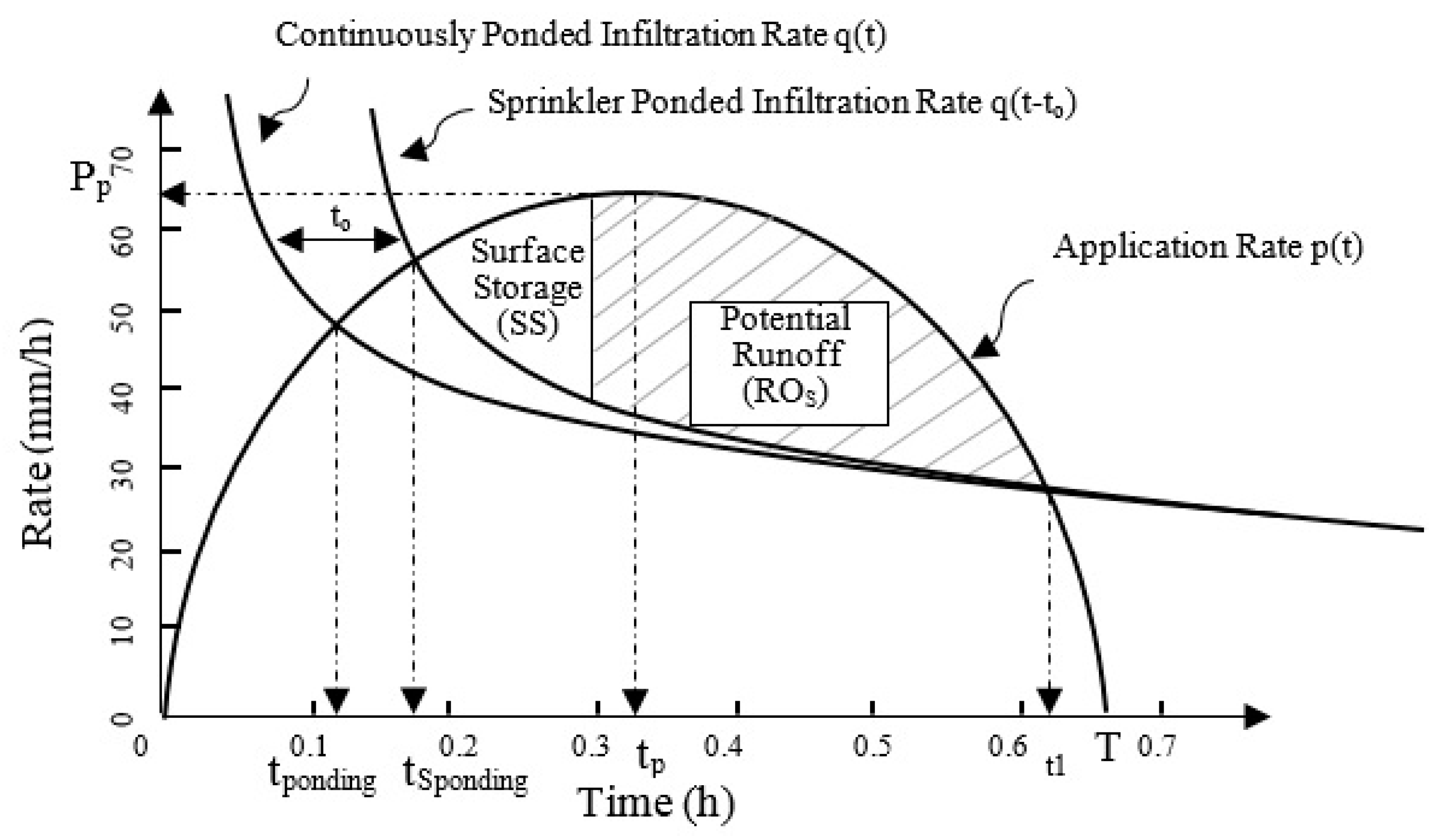
For self-propelled irrigation systems, a variable rate has been achieved by: varying the ground speed of the system [
26,
38], changing the sprinkler nozzle bore by pulsing a retractable concentric pin in the nozzle bore over predefined duty cycles [
42,
43], or changing the ON time of individual or banks of nozzles of the sprinkler system [
44]. Most researchers achieved variable water application by pulsing (opening) an individual or bank of solenoid valves for a part of the predetermined irrigation cycle (60 s or longer), to be compatible with a desired application rate [
45,
46]. The pulse modulation (on–off cycling of sprinkler valves) has become the most common industry standard technique used to control variable application rates [
47]. Most research has used pulse modulation VRI to apply variable irrigation depths and hold the water from untargeted areas inside the field to overcome spatial differences in the water needs due to crop or soil variations [
48]. However, there is very little research that has aimed to reduce surface runoff explicitly using the VRI technique, especially for the low-pressure sprinkler systems.
For VRI systems, application uniformity can be affected by sprinkler spacing, operating pressure, irrigation system component conditions, climatic conditions [
49,
50], and sprinkler height above the soil surface [
51]. Some studies have reported a uniformity issue with VRI, especially with low application depths. Han et al. [
52] measured the coefficient of uniformity (CU) under a linear move system supplied with VRI using the pulsing technique. The CU values for the variable application depths of 6, 13, 19, and 25 mm were 79.5%, 91.7%, 94.8%, and 94%, respectively. Their results showed that the uniformity decreased when applying lower depths. O’Shaughnessy et al. [
48] performed uniformity tests (coefficient of uniformity (CU) and low quarter distribution uniformity (DU
lq)) in the direction of travel of a centre pivot irrigation system by applying variable application depths using VRI with a pulsing technique. The mean values of CU and DU
lq were between 86.3% to 89.5% and 76.3% to 82.9%, respectively, after applying irrigation depths in a range of 100%, 80%, 70%, 50%, and 30% from a 25-mm irrigation depth. The study highlighted a uniformity issue for the low pulsing rate, where the CU was decreased to 70% when applying a 30% pulsing rate (or depth = 7.6 mm) compared with pulsing rates >50%. Also, the DU
lq was significantly decreased for the 30% pulsing rate compared with the higher pulsing rates.
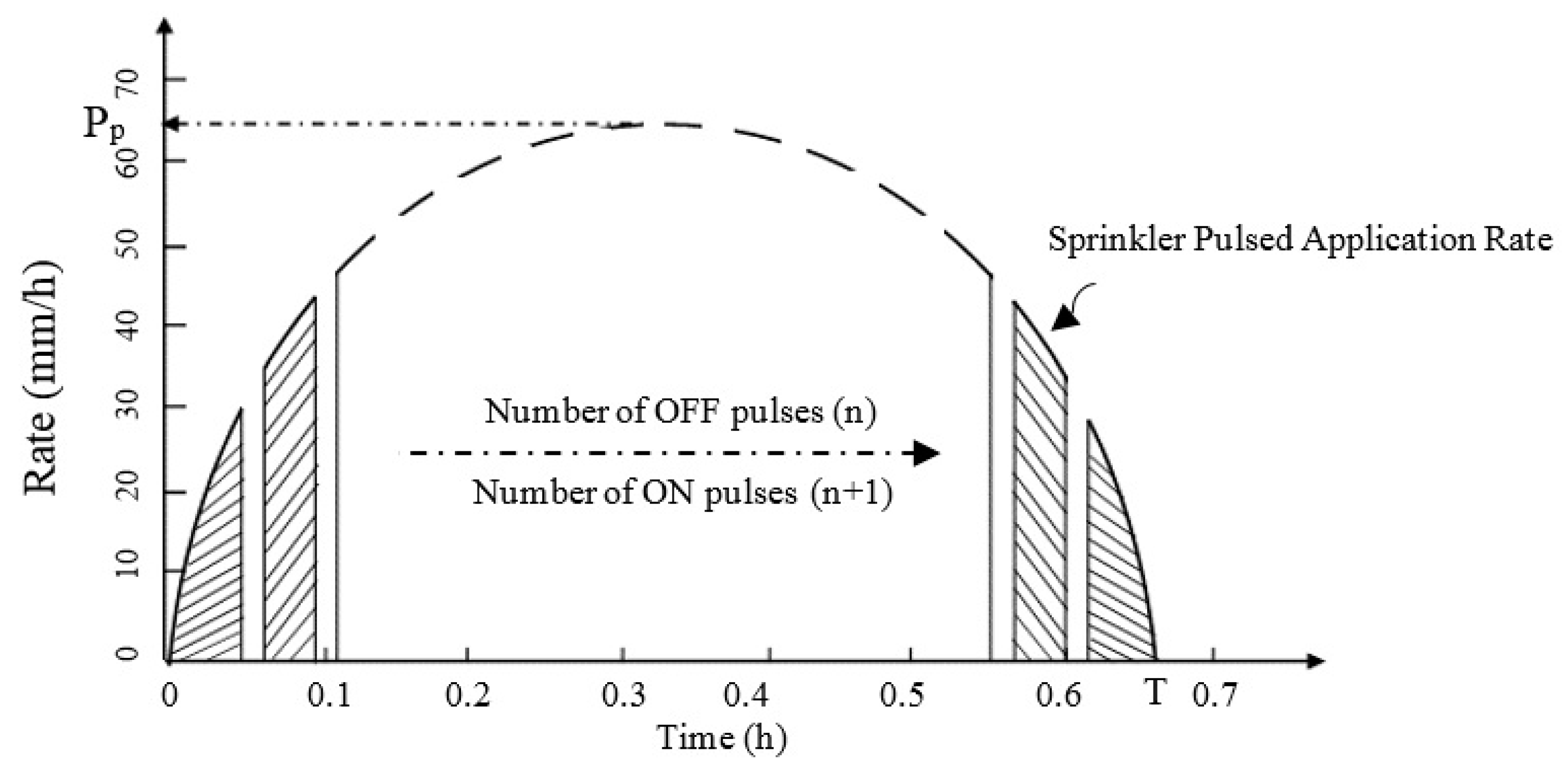
Pulse modulation has become the industry standard [
47]. However, most of the existing solenoids, pressure regulators, and valves can cycle between 250,000–300,000 times before breakdown [
47]. Therefore, pulsing frequency (number of pulses) has become another major issue for the VRI technique when applying different targeted depths or application rates. However, considering lowering the number of pulses while applying variable irrigation depths has not been thoroughly investigated.
This research aims to develop a variable pulsed irrigation algorithm (VPIA) which is able to reduce surface runoff while delivering the highest irrigation depth under the linear move sprinkler irrigation system supplied with a Low Elevation Spray Application LESA using the ON–OFF pulsing technique. Also, it aims to assure a high distribution uniformity in the direction of movement with the lowest number of pulses to ensure the sustainability of the sprinklers’ mechanical parts.
4. Simulation Results
To examine the performance of the proposed algorithm, we simulated the soil infiltration rate and the machine application rate before and after pulsing using a code written in MATLAB software. The MATLAB code was written to apply the VPIA on the selected sprinkler system described in
Table 2 to irrigate a field of sandy loam soil. The code consists of four steps: In the first step, for each speed of the irrigation machine, the surface runoff potential will be checked according to the sprinkler ponded infiltration rate that corresponds to the application rate of the specified speed. The results of the runoff for each speed will be stored in a table called the runoff potential table (RPT). The second step comprises the calculation of the RST, which contains the best solutions of the number of pulses and the ON and OFF widths for the speeds at which the runoff exceeds the allowable threshold which is listed in the RPT. In the third step, for each result listed in the RST, a distribution uniformity and runoff check are performed for the successive test points, and then the UCT is created. The final step is to select the best solution among all the solutions that resulted from the previous two tables according to the selection criteria. The results of each step will be stored in Excel spreadsheets for easy access to be retrieved for further calculations.
Since the irrigation machine has a range of speeds, the algorithm will be applied for the speeds at which the runoff exceeds the allowable threshold. The runoff threshold is set to 1% from the applied depth in our algorithm. Therefore, the runoff losses (ROs) along with the supplied irrigation depth (dg) and the infiltration depth (I) for the speed range of the irrigation machine used were calculated and listed in the runoff potential table (RPT) as shown in
Table 3.
From the RPT, it seems that the runoff starts when applying an irrigation depth of ≥20 mm. Therefore, the VPIA will be applied to all the speeds that have resulted in an amount of runoff that exceeds the threshold of 1% from the applied depth. Working on the first speed of 25 m/h to apply a 20 mm irrigation depth, the generated runoff was (1.55 mm > threshold (0.2 mm)), and the total time (T) that the machine needed to irrigate any single point of the soil was (T = 733 s). Therefore, the application rate will be pulsed within this time using several pulsing cases, starting with the first pulsing case (Case 1), in which the application rate will be pulsed with 2 OFF pulses and 3 ON pulses. In each case, a wide range of steps with different pulse widths will be tested, where the time of the OFF pulses will start from (T
OFF = 2 s) as a first step, and the steps will continue by increasing the time of the OFF pulses by one second for each next step until the runoff is equal to zero, considering that all these calculations are made for the first test point (X
1) by applying the new intermittent application rate. Also, the amount of surface storage capacity (SS = 5 mm) is considered when calculating the surface runoff and the actual infiltration depth. The results of these calculations are presented in
Table 4, where the applied depth was 20 mm and the infiltrated depth before pulsing was 18.45 mm with 1.55 mm of runoff, considering a surface storage capacity of 5 mm.
From
Table 4, it is shown that for Case 1, it took 28 steps to get zero runoff, with T
OFF = 29 sec, T
ON = 225 sec, and infiltrated depth I
1 = 18.128 mm as a solution for zero runoff for this case. In our algorithm, we suggested that the maximum allowed number of OFF pulses is 50 pulses, which the user can change to match the sprinkler and nozzle specifications. Therefore, the same calculations were repeated for the other 48 cases, and the results of all the solutions that give zero runoff were listed in the RST. The RST is shown in
Table 5, where the applied depth was 20 mm and the infiltrated depth before pulsing was 18.45 mm with 1.55 mm of runoff, taking into account a surface storage capacity of 5 mm.
The solutions listed in
Table 5 represent the best solutions for different pulse numbers that gives zero runoff for the first test point (X
1). Since the time shift between the successive test points will cause a reshaping and shifting in the new pulsed application rate, it will result in variations in the runoff and infiltration depth values for each test point. Therefore, the next stage in the algorithm is to check the runoff and the distribution uniformity when applying the new pulsed application rate for each of these solutions to the successive test points in the direction of movement.
Since the pulsing will affect the application pattern, hypothetical test points must be used to check the runoff losses and the distribution uniformity for the successive points in the direction of movement. The number of the test points and the distance between them depends on the sprinkler wetting diameter and the aimed level of accuracy for the calculations. According to the sprinkler wetting diameter (5.2 m) of the system used, 22 test points (X
1- X
22) are suggested to be used and placed in one line in the direction of movement. These points were spaced 0.25 meters apart along the line, as shown in
Figure 6, except the last point was placed at 0.2 m distance from the previous point to match the width of the wetting diameter.
Starting with the first solution of Case 1 that is listed in
Table 5 (number of OFF pulses = 2, T
OFF = 29 s, T
ON = 225 s), the runoff and infiltration depths were calculated for all other 21 test points after applying the new and shifted pulsed application rate. The new results were arranged in another table, as shown in
Table 6. The average of runoffs and depths for the test points along with the standard deviation of the depths were also be calculated and listed in the same table (
Table 6). The same calculation procedure was repeated for all the cases listed in
Table 5, and the results were arranged and listed in the UCT as shown in
Table 7.
The final stage of the VPIA is to apply the selection criteria to choose one unique solution among the solutions listed in the UCT (
Table 7) for the selected speed of 25 m/h. By applying the first criterion, the following cases were excluded because they have an average runoff higher than 0.2 mm: Case 1, Case 2, and Case 3. From the remaining cases, the following cases were excluded because they did not satisfy the uniformity distribution criterion: Case 4 and Case 6. According to the infiltrated depth, the cases that were left after applying the previous two criterions were ordered in descending order along with their corresponding pulse number and width. Since Case 32 has the highest infiltration depth of 18.230 mm, it will be the first case in the new list. To apply the third criterion, the new infiltration depth threshold was set at 1% lower than the highest depth of 18.230 mm, which becomes 18.048 mm. Therefore, all cases that have an infiltration depth lower than 18.048 mm were excluded. The remaining cases with their corresponding details are listed in
Table 8. All the solutions listed in
Table 8 are good solutions that give low runoff and uniform depth along the direction of movement. However, we must select only one solution among these solutions. Therefore, to select a unique solution among all the listed solutions in
Table 8, the fourth criterion was applied by selecting the case with lowest pulse number, which was Case 5 with the following factors: number of OFF pulses: 6 pulses, T
ON = 96.14 sec, T
OFF = 10 sec. Therefore, for the selected speed of 25 m/h, when applying Case 5 factors to generate the pulsed application rate, the new average runoff decreased from 1.55 mm to 0.144 mm, while the new average delivered infiltration depth decreased from 18.45 mm to 18.20 mm.
The VPIA will be applied to all other speeds that generate a runoff higher than the threshold values.
Table 9 shows the best solutions for these speeds after applying the VPIA.
5. Discussion
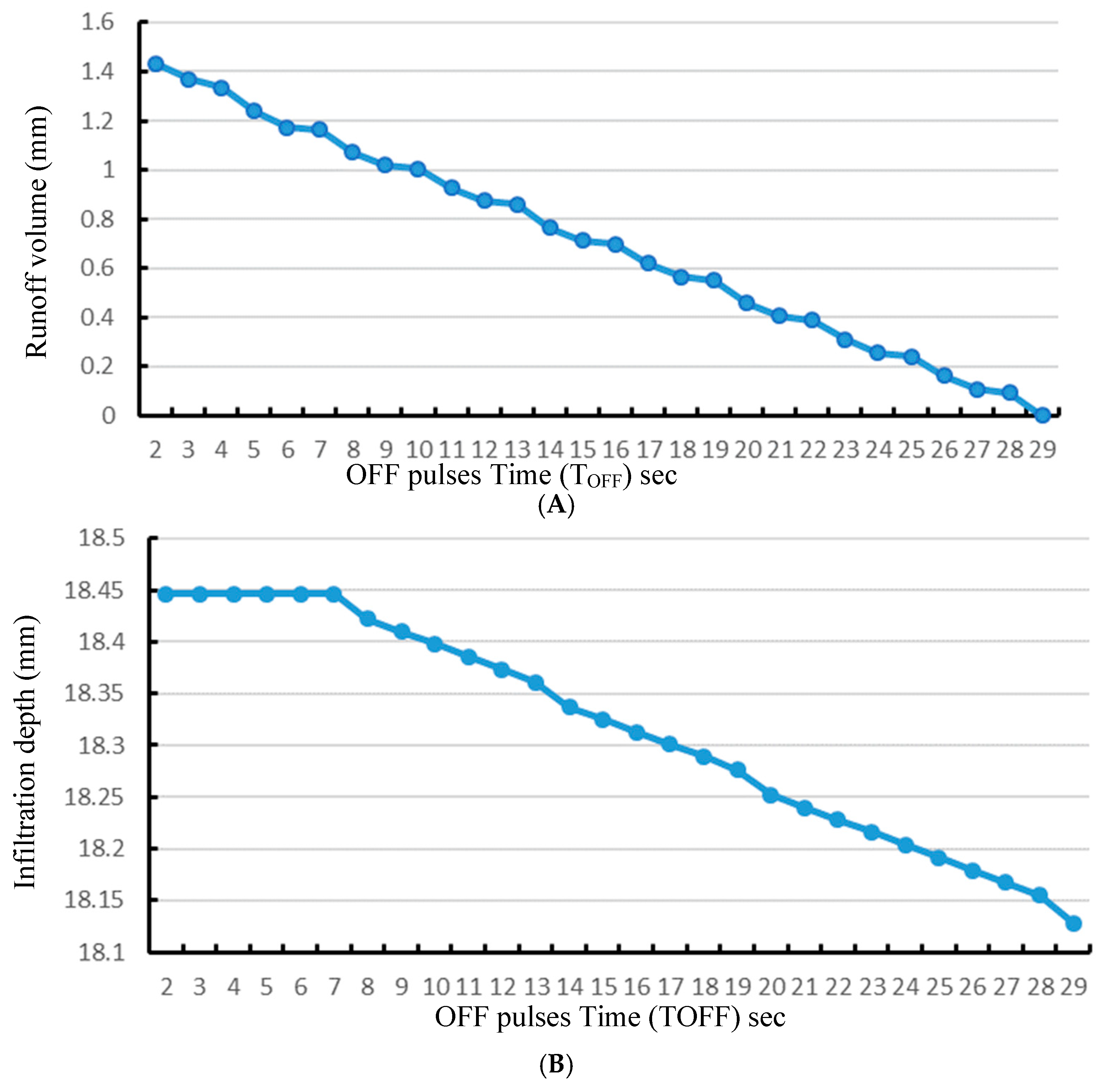
According to the VPIA, the runoff reduction is controlled by the number and the width of the OFF pulses within the total time (T). Regarding the results listed in
Table 4 for the first test point,
Figure 7A shows that for the specified case (Case 1) with a fixed number of OFF pulses (2 OFF pulses), the runoff was reduced by gradually increasing the width of the OFF pulses until it reached a zero value. However, the infiltration depth for the same point will decrease because of increasing the width of the OFF pulses, as shown in
Figure 7B. From these results, we conclude that the OFF pulses’ width had two impacts: first, it decreased the amount of the applied water, and second, it gave more time for the accumulated water to infiltrate into the soil. Therefore, increasing the width of the OFF pulses will positively decrease the runoff volume, but on the other hand, will reduce the infiltrated depth.
For the first case, the number and width of the OFF pulses that make the runoff for the first test point equal zero was selected as the best solution for this case. Since the application rate pattern was altered by the pulse effect, successive test points in the direction of movement received a quantity and pattern of water that differs from the first test point. This may lead to an uneven distribution of water in the direction of movement and increase the possibility of runoff for these points. Therefore, to check the uniformity and the runoff potential for the selected case, the infiltration depth and the runoff must be calculated for each test point by using the same calculation procedure that was applied on the first test point, considering the changes in the application rate pattern for every test point.
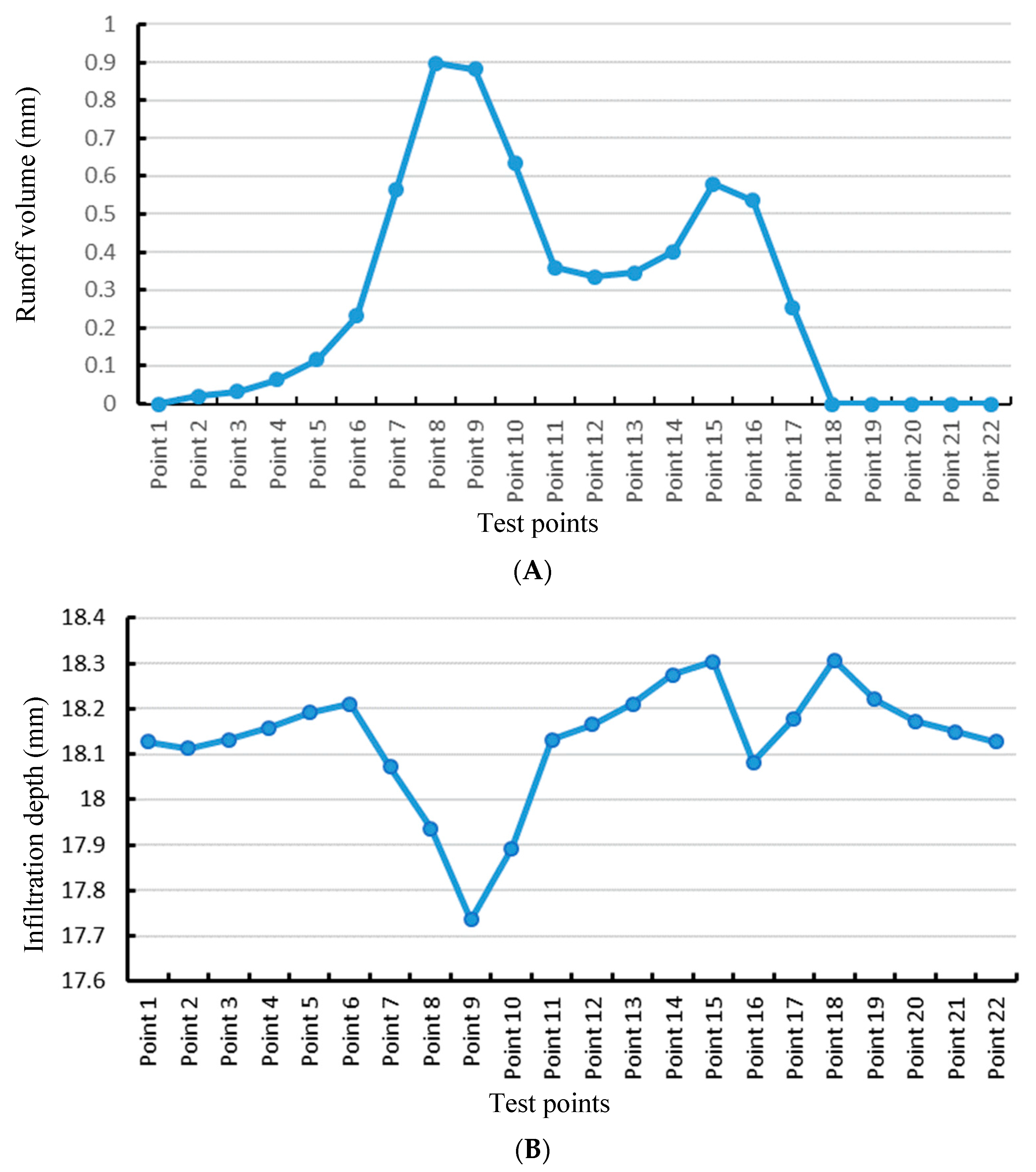
Figure 8A shows the runoff potentials when applying the pulsed application rate (resulting from the first test point in Case 1) to the successive test points using the results listed in
Table 6, while the infiltration depths for the successive test points after applying the same pulsed application rate is shown in
Figure 8B. From
Figure 8A, it is obvious that the Case 1 solution was not a good solution as it w caused an undesirable amount of runoff (>0.2 mm) for several of the successive test points, even if it gave zero runoff for some of the others. Also, this solution led to unequal distribution of water for the successive test points, as shown in
Figure 8B. Therefore, we must try other case solutions by increasing the number of the OFF pulses and repeating the same procedures. Finally, we must choose one from all the solutions that satisfy the selection criteria.
The final solutions for the different machine speeds listed in
Table 9 show that our proposed algorithm has reduced the amount of runoff by 90.7%, 94.65%, 96.98%, and 96.94% for the applied depths of 20 mm, 25 mm, 30 mm, and 35 mm, respectively. Also,
Table 9 can be considered as a look-up table (i.e., for every machine speed, the computer will directly select the solution that gives the best results from this table).
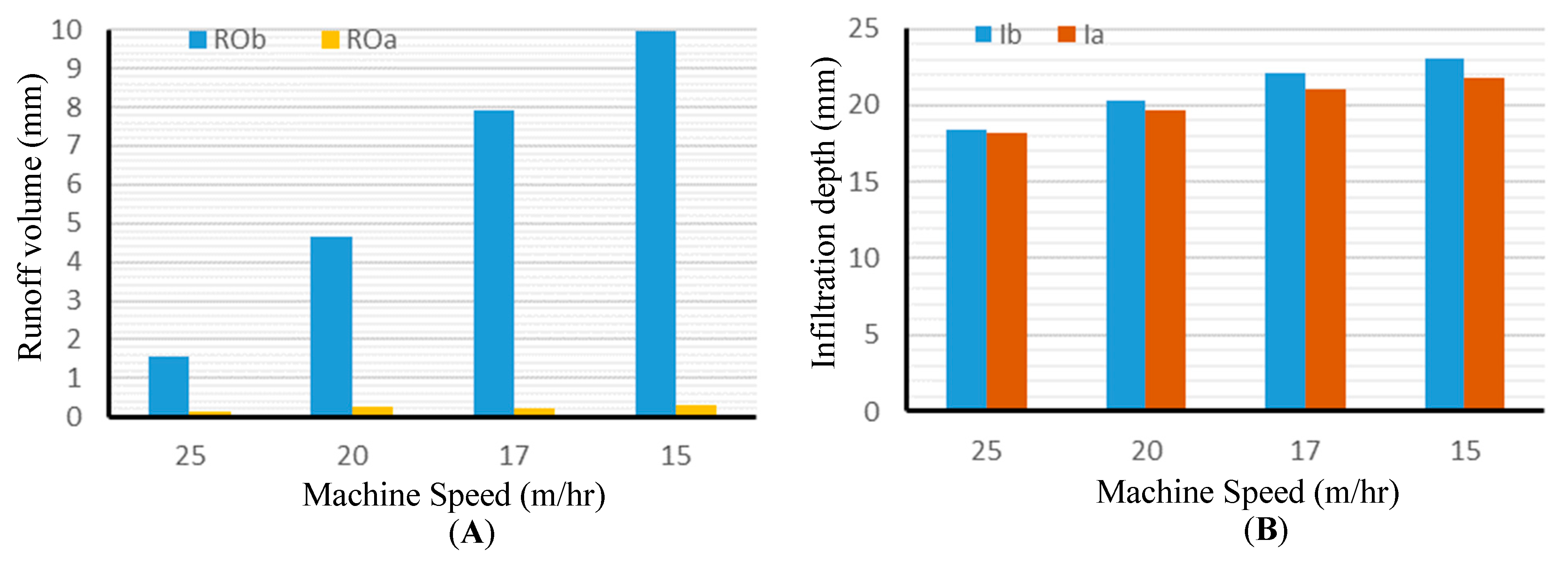
Figure 9A shows a comparison between the runoff before pulsing (ROb) and after pulsing (ROa) for different machine speeds. Although the delivered average irrigation depth using the VPIA was slightly decreased compared with the normal continuous application rate, the VPIA achieved the delivery of an acceptably high irrigation depth with very low runoff losses.
Figure 9B shows a comparison between the average infiltration depth before pulsing (Ib) and after pulsing (Ia) for different machine speeds. The results also show that the proposed VPIA maintains a uniform distribution of water in the direction of movement. The uniformity of water distribution and the runoff have a direct impact on the crop growth, crop yield, and soil and water resource sustainability. Therefore, the VPIA allows the irrigator or the farmer to specify the threshold for the acceptable runoff and the level of uniformity according to their experiences about the impact of these factors on the crop growth and resource sustainability.