Next Article in Journal
Comprehensive Evaluation of the ‘Shixia’ Longan Quality under Postharvest Ambient Storage: The Volatile Compounds Played a Critical Part
Previous Article in Journal
Identification and Characterization of a Virulent Meloidogyne incognita Population Breaking Tomato Mi-1-Mediated Resistance in Indiana
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Horticulturae
Volume 10
Issue 6
10.3390/horticulturae10060584
horticulturae-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Pollen- and Weather-Based Machine Learning Models for Estimating Regional Olive Production

by
Ana Galveias
1,
Célia Antunes
1,
Ana Rodrigues Costa
1 and
Helder Fraga
2,*
1
Department of Medical and Health Sciences, School of Health and Human Development & Institute of Earth Sciences & Centro Académico Clinico, C-TRAIL, University of Évora, Rua Romao Ramalho, 59, 7000-671 Évora, Portugal
2
Centre for the Research and Technology of Agro-Environmental and Biological Sciences (CITAB), Institute for Innovation, Capacity Building, and Sustainability of Agri-Food Production (Inov4Agro), University of Trás-os-Montes e Alto Douro (UTAD), P.O. Box 1013, 5000-801 Vila Real, Portugal
*
Author to whom correspondence should be addressed.
Horticulturae 2024, 10(6), 584; https://doi.org/10.3390/horticulturae10060584
Submission received: 10 May 2024 / Revised: 23 May 2024 / Accepted: 28 May 2024 / Published: 3 June 2024
Browse Figures
Versions Notes

Abstract

:
The olive tree is one of the most common type of cultivation in the Mediterranean area, having high economic and social importance. The Alentejo region, Portugal, is an area with a high presence of olive groves, which in 2022 accounted for 201,474 hectares. The aim of this study was to assess the relationship between olive pollen, weather data, and olive tree production, between the years 2002 and 2022. Pollen data were obtained from an urban station located in Évora, in the Alentejo region, and were used to calculate several metrics, such as the Pollen Season Duration (PSD), Seasonal Pollen Index (SPIn), peak value, and weekly pollen accumulation values. Monthly minimum, maximum, and mean temperature and precipitation sums were obtained from the E-OBS observational dataset. Considering the relationship between pollen/weather and olive production, mutual information and correlation analyses were conducted. Subsequently, several machine learning algorithms were trained using pollen and weather datasets, and we obtained suitable forecast models for olive tree production after cross-validation. The results showed high variability in pollen concentrations in Évora over the years. Complex associations were found, with certain weeks of pollen accumulation showing significant mutual information with olive production, particularly during June. The analyzed linear correlation coefficients remained generally low, underscoring the challenge of predicting olive production based on linear relationships. Among the machine learning algorithms employed to predict olive production, Decision Trees, Extreme Gradient Boosting, and Gradient Boosting Regressor were the most robust performers (r2 > 0.70), while linear models displayed a subpar performance (r2 < 0.5), emphasizing the complexity of this approach. These models highlight the roles of maximum and minimum temperatures during March and May and pollen accumulation during the second half of June. The developed models may be used as decision-support tools by growers and stakeholders to further enhance the sustainability of the thriving olive sector in southern Portugal.

1. Introduction

The olive tree Olea europeae, subsp. europeae var. europeae, is a species represented in 95% of the Mediterranean region with high social, historical, and economic importance [1]. The culture of the olive grove is believed to have originated about 6000 years ago in the Middle Eastern area [2]. Cultivation of olive groves occurs in 40 countries (2022 data) [3] and occupies about 12.5 million hectares on the Earth’s surface, with the olive considered the most cultivated fruit tree. In 2023, in Portugal, 379,565 hectares were accounted for, an increase of 40,054 hectares since 1986. In the Alentejo region alone, 201,298 hectares were identified, which is equivalent to more than 50% of Portugal’s total [4,5]. In fact, with the construction of the Alqueva dam infrastructure, olive grove cultivation has become even more pronounced [6,7]. Trás-os-Montes is the second region in which olive grove planting is accentuated (81,475 ha—22%). Less than 1% of the olive-growing area is found in the region of Entre o Douro e Minho [8,9]. As it is a crop characterized by high pollen production, high productivity, and a long flowering period, its expansion in the number of hectares has been particularly evident [10]. The olive tree is a dicotyledonous angiosperm, of the Oleaceae family, the same family to which the ash, privet, and lilac belong. From a physiological point of view, the olive tree adapts perfectly to all types of soils, resisting, for example, poorly drained or very calcareous soils. The most prevalent and at the same time limiting factors, when we refer to fruit production, are water and luminosity in the hottest months [11].
The selection of olive cultivars, carried out by growers over time, has led to a change in the pollination process, i.e., the olive tree is an entomophilous species that evolves into an anemophilous species with high pollen and flower production [12], where pollen spreading is conducted by the wind. In this pollination process, the existence of large amounts of pollen helps reproduction and fertilization [13,14]. The olive tree, as in other fruit trees, has a biennial reproductive or vegetative cycle, that is, years with high and low pollen production [15]. Cyclical behavior, completed after 2 years, is strongly determined by the flowering load—since in the second year, the buds develop into inflorescences [1,16]—and is a characteristic observed in all cultivatable varieties of olive trees. This phenomenon can occur in one individual tree or in parts of a single tree. One of the possible causes for the occurrence of this phenomenon is the production of endogenous hormone levels, which can promote or inhibit flowering and consequently contribute to the variability of the Seasonal Pollen Index [17]. Flowering in fruit trees can be inhibited by gibberellins and promoted by cytokines [18], and the balance between these two hormones can correlate with flowering [19]. However, gibberellins are hormones that play a very important role in plants at the physiological level, and they have already been described as substances that contribute to the development of buds and induction of flowers [20]. This is an andromonoecious species, that is, one where hermaphrodite and functional male flowers occur in the same individual [21]. Olive pollen is colporate and tricolporate with a reticulated exine [22,23]. The monitoring and performance of aerobiological studies with olive pollen have shown not only a high importance in terms of the risk to public health with the development of allergic disease [24,25] but also for ecological [26] and agricultural studies [27,28,29,30].
In agricultural studies, harvest forecasting in agricultural crops throughout the year has become essential at all levels of production. Until the end of the 20th century, harvest forecasting was usually carried out through observation by a plot farmer. From this observation, it was possible to extrapolate the total production of a region [31]. However, this method had disadvantages since estimates of crop yields made by a single individual observing a field were very subjective. It was also costly, as there would have to be many sampling points, and on top of that, the older estimates had a huge error that could only be corrected in the next harvest. Other methods include the use of crop growth monitoring system models or prediction models based on satellite measurements [32]. However, due to the disadvantages of the methods described above, in 1980, a methodology was developed that used aerosolized pollen as a bioindicator in production forecasting [33]. Airborne pollen counts are an indicator of pollen production by a plant, and their use in creating long-term pollen time series has been proven by several studies to be an effective technique [34]. This relationship between pollen emission and fruit production has been demonstrated for many other crops, such as Vitis vinifera [35] and Quercus ilex [36]. However, although pollen is important from the point of view of forecasting production, it cannot be the only factor considered since there are other external factors that can condition production both in terms of quality and quantity, such as atmospheric and physiological conditions arising from lack of water and extreme temperatures, as well as the occurrence of phytopathological problems [26,29,34,37]. Hence, forecasting olive production remains of key importance, particularly under the predicted climate change challenges for this sector [38,39].
Several studies have shown the significance of using pollen to model olive production/yield, providing valuable insights into predicting olive production [40]. As an example, [41] focused on developing pollen-based models for forecasting Mediterranean olive production, highlighting the importance of understanding the reproductive biology of olive trees for improved crop management. Ref. [42], in northern Portugal, developed a bioclimatic model, integrating pollen and weather data to quantitatively forecast the olive yield. Ref. [40] emphasized the positive correlation between annual pollen production and olive yield, indicating the potential for pollen-based forecasting of fruit production. These studies collectively underscore the value of pollen data in enhancing the accuracy of olive yield predictions and optimizing agricultural practices. Nonetheless, most of these studies take advantage of the linear relationship between pollen and olive tree parameters, which is only possible in certain conditions, i.e., if the pollen traps are placed directly on the olive groves [41]. The European Aeroallergen Network (EAN) database is a network of pollen stations scattered throughout Europe (including Portugal), which provides a database of several sources of pollen, such as from olive trees. Many of these stations are located in urban areas, not located directly in olive orchards. To the authors’ knowledge, data from these stations have never been used to develop suitable models, possibly due to the difficulty in establishing effective relationships.
Given the high interest in the use of pollen data in harvest forecasting, specifically of olive trees, the current study aimed to investigate the possibility of modeling regional olive production based on pollen counts acquired from stations not located within olive groves, along with using weather data, thus filling a research gap. The objectives of the current study were four-fold: (i) to analyze a long-term series of olive pollen data obtained from an urban station; (ii) to assess linear relationships between the pollen series and regional olive production; (iii) to train (linear and non-linear) machine learning models using pollen and weather data to forecast olive production; and (iv) to attempt to understand the most important factors that influence regional olive yields. Hence, the current study attempted to improve our knowledge of how to make an olive production forecast from pollen emissions and weather variables, aiming to optimize all technical and human resources associated with harvesting.

2. Materials and Methods

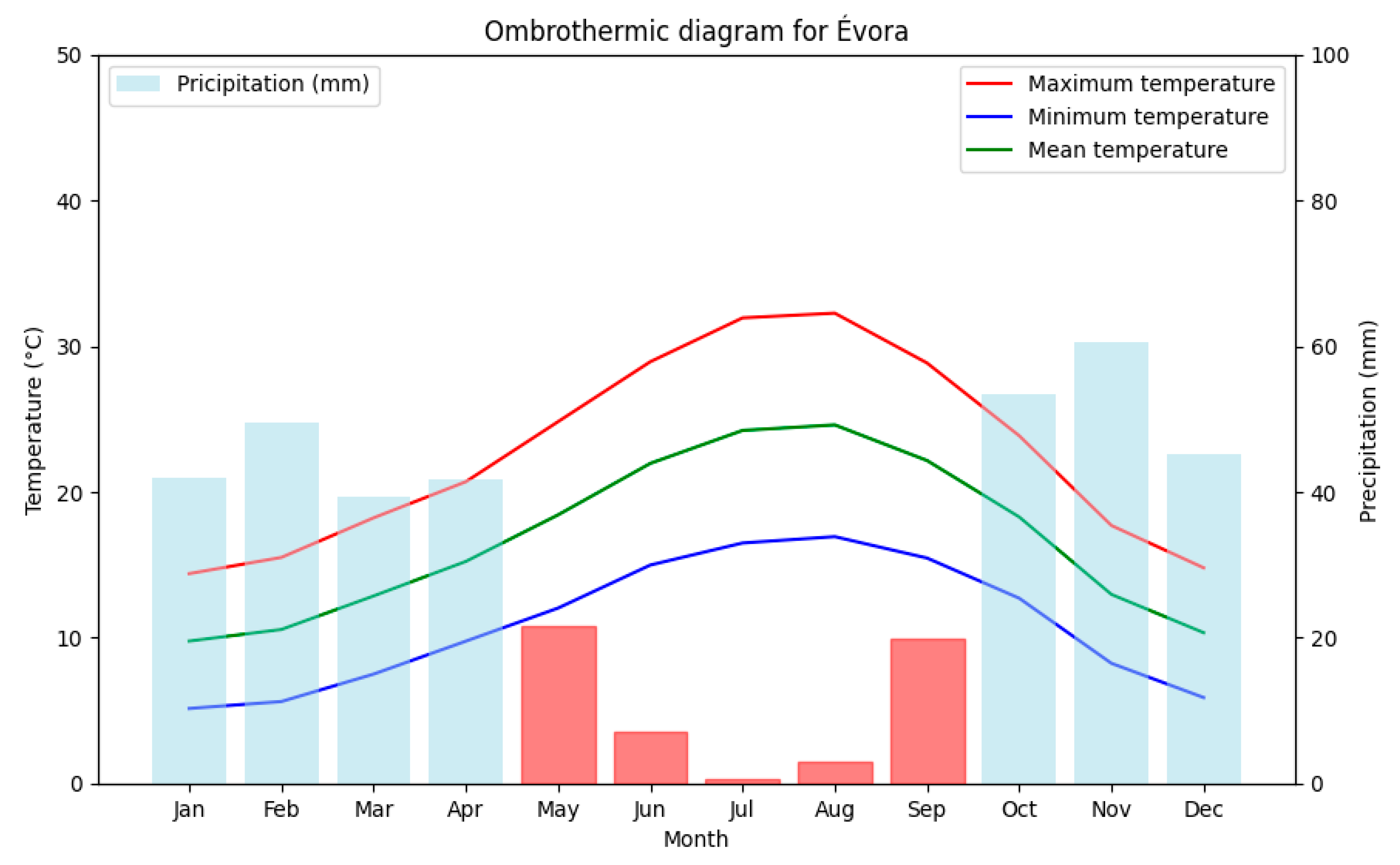
2.1. Study Area

This research was conducted in the city of Évora, situated in the south of Portugal (Figure 1) and characterized by a temperate climate with warm and dry summers, which can be described as a hot-summer Mediterranean climate (Köppen Climate Classification—Csa).
The annual mean air temperature in Évora is 16.8 °C, with the highest monthly temperature occurring in August, with 32.3 °C, and the lowest in January, with 5.1 °C (Figure 2). The annual precipitation is approximately 400 mm and the summer precipitation is only 10 mm (Figure 2). According to an ombrothermic diagram (Figure 2), the dry season starts in May and ends in September (where precipitation values are lower than 2× the temperature), and it only accounts for 50 mm of rainfall.
The cultivation of olive groves is predominant in the Alentejo region (Figure 1) and specifically in the region south of Évora, where a greater number of hectares are concentrated [6]. The pollen monitoring station is located in the Évora Atmospheric Sciences Observatory (EVASO) of the Institute of Earth Sciences (ICT) at the University of Évora (38°34′ N, 7°54′ W, 293 m asl), which is in an urban area; however, on its periphery, there are many olive groves (Figure 1).

2.2. Aerobiological Data

The airborne olive pollen was collected with a volumetric trap of the Hirst type [43], located at the Évora Atmospheric Sciences Observatory (EVASO) of the Institute of Earth Sciences, University of Évora, at approximately 10 m above ground level. The station belongs to the EAN network. The data were collected from 2002 to 2022, except in the years 2007, 2015, and 2016, for which records are unavailable. The sampled air passing through the inlet hole (2 × 14 mm) impacts a tape placed in a sampling drum driven by a clock that rotates at an angular velocity of 2 mm/h for 7 days. After the end of the 7 days of sampling, the double-sided tape is removed from the drum and cut into segments of 48 mm in size, where each one corresponds to one day of sampling. After all the slides are prepared, each slide is analyzed under an optical microscope, at a magnification of 40×, to count and identify the pollen. The pollen results are expressed in pollen per cubic meter of air (Pollen/m3). The main pollen season of the olive tree was calculated by the logistic method, developed by [44] and modified by [45]. This method is based on the fitting of a non-linear logistic regression model to the accumulated daily curve for each type of pollen [44]. Parameters such as start_date, end_date, Pollen Season Duration (PSD), Seasonal Pollen Index (SPIn), peak value and date, and a weekly pollen accumulation time series were determined based on asymptotes when pollen amounts were stabilized at the beginning and end of the accumulated curve (Table 1).

2.3. Climatic Data

The climatic data utilized in this study were sourced from the E-OBS observational interpolated/gridded dataset, version 29.0e [46]. This ensemble dataset is constructed through a conditional simulation procedure and is produced by the European Climate Assessment & Dataset (E-OBS). The data were retrieved from the Copernicus Climate Service (CCS). Despite some documented limitations [47], the E-OBS dataset offers uninterrupted and homogeneous gridded fields of daily minimum (TN), maximum (TX), and mean (TM) temperatures, as well as the daily precipitation (RR) across Europe, dating back to 1950. These data are provided at a spatial resolution of approximately 10 km. To facilitate analysis, climatic data corresponding to the Évora station grid-box were extracted. Subsequently, the monthly means of TN, TX, and TM, as well as the monthly sums of RR, were computed from the extracted dataset. This robust dataset and subsequent computations provide a comprehensive understanding of the climatic conditions in the study area, aiding in the investigation of their influence on the target variables under consideration.

2.4. Machine Learning Models

In this study, we selected several regression machine learning algorithms to model the relationship between predictor variables (weekly pollen accumulation and monthly temperatures and precipitation) and olive production. Each algorithm offers unique characteristics suited for different types of datasets and predictive tasks (Table 2). We categorized each algorithm into 1 of 3 distinct categories—linear algorithms, boosting algorithms, or bagging algorithms—or they were categorized under “Others” [48].
Linear models were chosen for their ability to capture linear relationships between predictor variables and olive production, as well as to address issues such as multicollinearity and outliers. In this category, we selected linear regression (LR), which is a fundamental algorithm used for modeling the linear relationship between predictor variables and the target variable [49]. Ridge regression (RD) is a regularization technique that adds a penalty term to the linear regression cost function to shrink the coefficients, effectively reducing model complexity and mitigating multicollinearity issues [50]. Lasso regression (LR), similar to ridge regression, adds a penalty term to the linear regression, but employs L1 regularization, which encourages sparsity by driving some coefficients to zero, thus performing feature selection [51]. ElasticNet regression (EN) combines the penalties of ridge and lasso regression (L1 and L2 regularization) to address both multicollinearity and feature selection simultaneously [52]. Finally, Huber regression (HR) is a robust regression technique that minimizes the sum of absolute differences (L1 loss) between the observed and predicted values, thereby reducing the impact of outliers on the model [53].
Boosting algorithms sequentially build a strong learner by combining several weak learners. In this category, we employed Gradient Boosting Regression (GBR), AdaBoost Regression (ABR), and XGBoost Regression (XGB). GBR constructs an ensemble of weak learners (typically decision trees) sequentially, with each new model fitting the residual errors of the previous model, reducing bias and improving predictive performance [54]. ABR iteratively trains weak learners (e.g., decision trees) on subsets of the data, focusing on instances that were misclassified by previous models, to improve overall accuracy [55]. XGB is an optimized implementation of gradient boosting, introducing enhancements such as parallelization, tree pruning, and regularization for faster training and improved performance [56].
Bagging algorithms utilize bootstrap resampling to create multiple models and aggregate their predictions. In our study, we utilized Random Forest Regression (RF) and Extra Trees Regression (ET). RF constructs multiple decision trees during training and averages their predictions, enhancing accuracy and robustness [57]. ET builds multiple decision trees using random subsets of features and random thresholds to split nodes, improving model diversity and generalization [58].
Lastly, we explored other regression techniques to capture various aspects of the relationship between predictor variables and olive production, such as K-Nearest Neighbors Regression (KNN) and Decision Tree Regression (DT). KNN predicts the target variable of a new data point by averaging the target values of its nearest neighbors in the feature space, suitable for capturing non-linear relationships [59]. DT partitions the feature space into disjoint regions and fits a simple model (e.g., constant value) within each region, providing interpretability and capturing complex non-linear relationships [60].
These diverse regression techniques were selected to explore different modeling strategies and capture various aspects of the relationship between predictor variables and olive production. To evaluate model performance and errors, we employed standard metrics such as the Coefficient of Determination (r2), MAPE (Mean Absolute Percentage Error), and the Maximum Percentage Error (MAXP) [61]. Although other algorithms were also selected, such as neural networks and SVN, their performance was very low, and they were not included in this study. These two models usually require large amounts of training data, which potentially explains their low performance.

2.5. Feature Selection and Model Training

As potential predictors (features), weekly pollen accumulation and monthly temperatures and precipitation were considered (Table 3). In order to isolate potential outliers, we only considered features from a certain temporal resolution. For example, for pollen accumulation, we used weekly data relating to the historical seasonal pollen from the 1st week of April (91) until the 2nd week of July (195). Regarding weather data, we used monthly data from January to May. To assess the best possible combinations of features for model training, the bestFeatures v1.0 python package was used [62]. This script uses a cross-validation scheme when running each model for each combination of features in order to evaluate the performance of each algorithm. Specifically, a k-fold cross-validation technique with 5 folds is used, meaning each algorithm is effectively evaluated multiple times with the split dataset. Each split divides the data into training and testing, with the test dataset being withheld from the algorithm. This cross-validation technique helped us to avoid model overfitting and obtain a more accurate estimate of the model performance. Additionally, hyperparameter tunning was applied for each algorithm. Grid search techniques were employed to find the optimal combination of hyperparameters that maximized the model performance [63]. Hence, the bestFeatures script accurately provides the best combination of features for each model.

3. Results

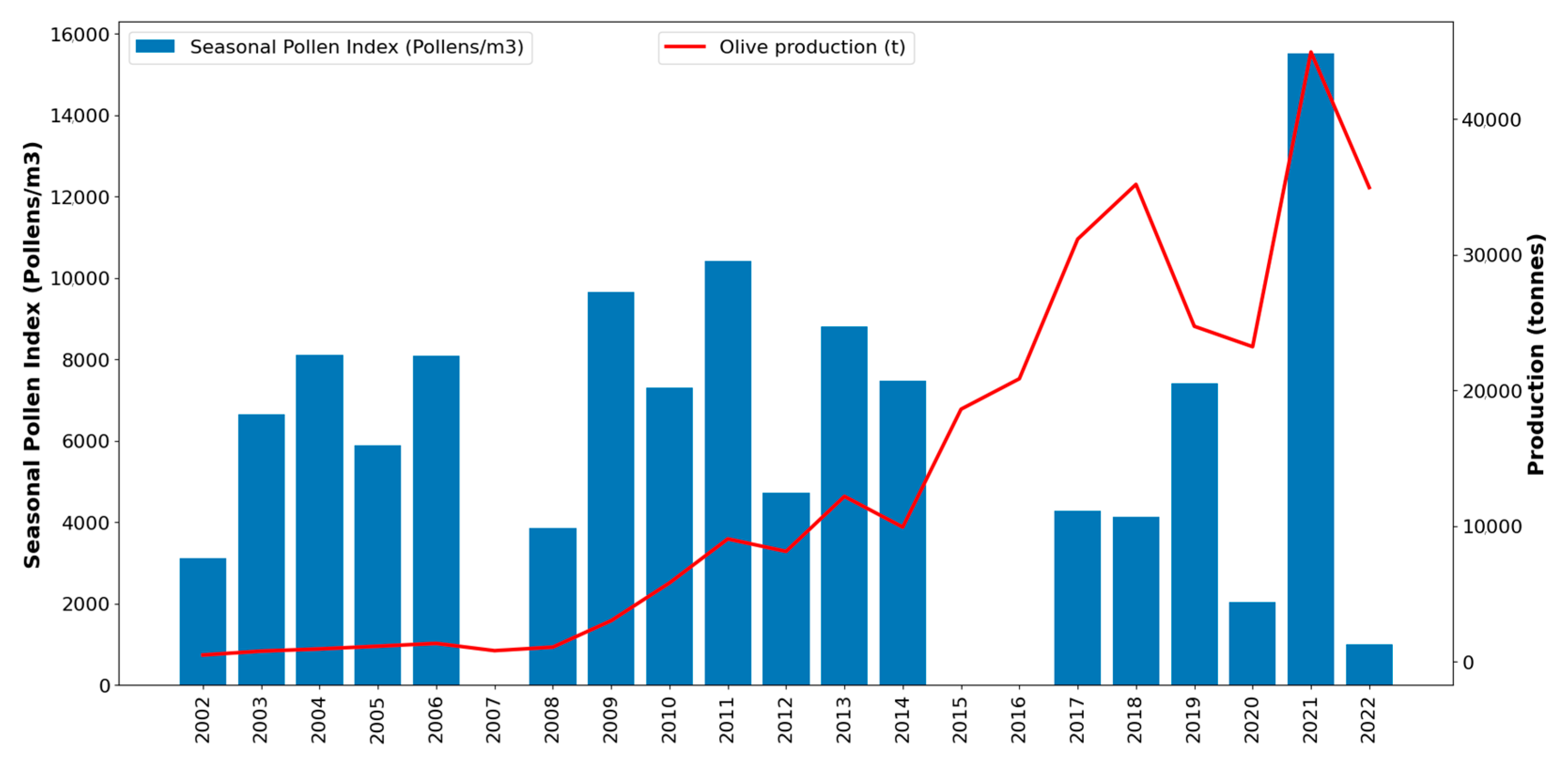
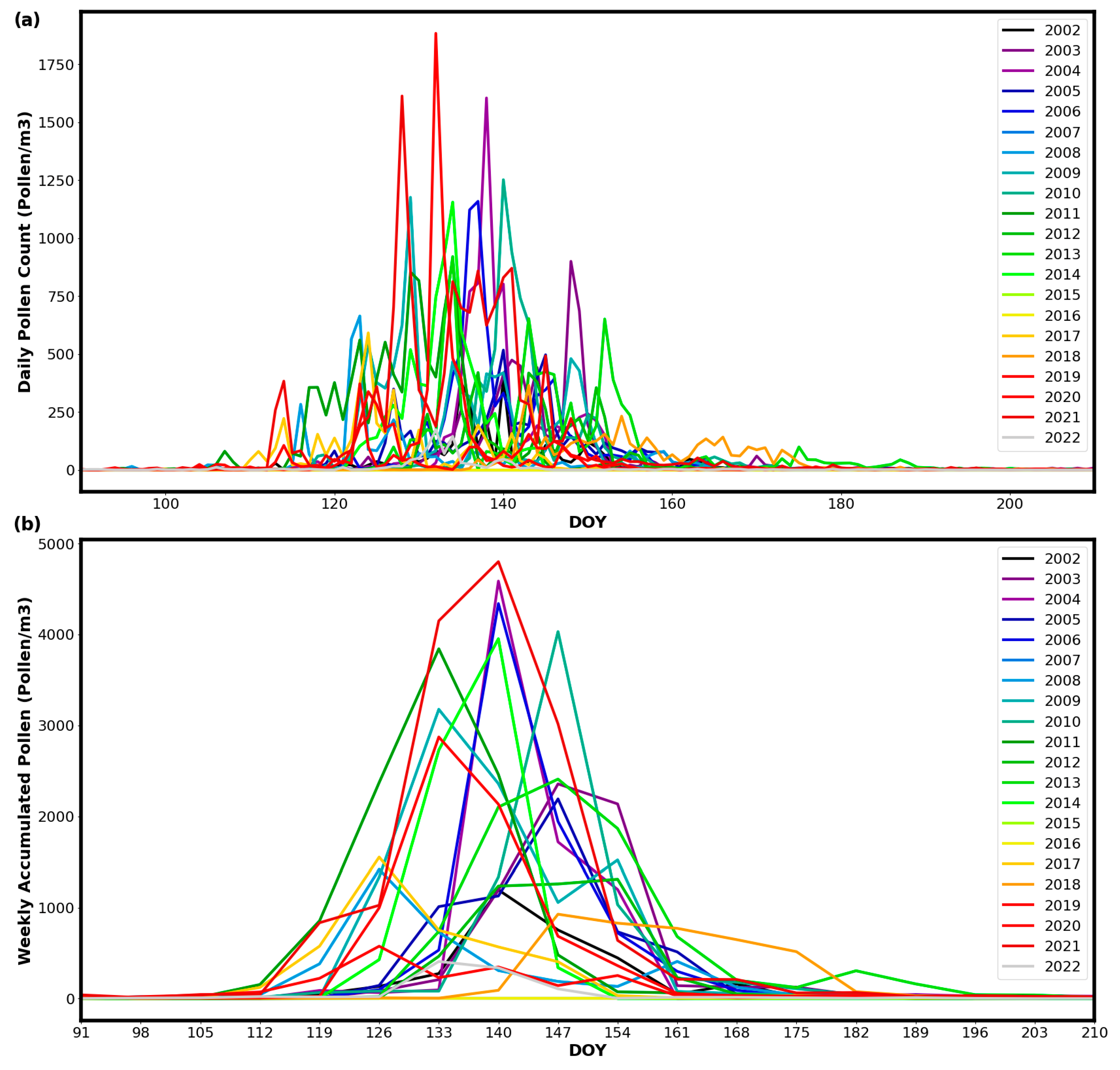
3.1. Characterization of Olea Pollen Season between the Years 2002 and 2022

The characteristics of the Olea pollen season in the period of 2002–2022 were analyzed and are presented in Table 1 and Figure 3 and Figure 4. Olea pollen was detected in large concentrations in the atmosphere of the city of Évora, where its specific pollination period occurs in the month of May. In most of the years under study, the beginning of the pollen season occurred between the end of April and the beginning of May; however, there were years in which the beginning occurred earlier, as is the cases of 2008 (14 April) and 2017 (17 April). The year 2020 registered an earlier start to the season, on 11 April. Regarding the duration of the pollen season, on average, the duration was 35 ± 11 days; however, it was observed that the year 2008 had a duration of 51 days, followed by the year 2020 with 58 days. We found that in 2010 the pollen season was relatively shorter, with only 20 days. Regarding the SPIn, the average among all the years under study was 6067 ± 3168 pollen/m3; however, there was only one year in which 10,000 pollen/m3 was exceeded, in 2021 (13,718 pollen/m3). We found that 2020 and 2022 had the lowest pollen indexes, with only 1896 and 869 pollen/m3, respectively. In Figure 3, it can be observed that Olea SPIn has an alternate bearing behavior, that is, there are high years followed by low years. The peak of the maximum concentration occurred in the month of May for all years, obtaining an average of 893 ± 496 pollen/m3. The year 2019 had the highest peak maximum concentration (1884 pollen/m3), followed by 2021 with 1613 pollen/m3 and 2004 with 1604 pollen/m3. Meanwhile, in the year 2022, only a 174 pollen/m3 maximum concentration was reached in the entire season. In 7 of the 18 years under study, the peak maximum concentration was lower than the average for all years (Table 1).

3.2. Relationship between Pollen/Weather and Olive Production

A preliminary analysis was performed to investigate the relationship between pollen/weather and olive production. Two metrics were computed: mutual information and correlations. Mutual information quantifies the degree of dependence or association between two variables and serves as a crucial metric in comprehending the relationship between features and a target variable, particularly in predictive modeling contexts [64]. In this scenario, the features encompass meteorological data such as maximum temperature (TX), minimum temperature (TN), and precipitation (RR), alongside pollen weeks (dates), while the target variable is olive production. Therefore, the mutual information values provided indicate the strength of association between each feature and the target variable. A higher mutual information value suggests a stronger relationship, signifying that the feature contains valuable information for predicting olive production.
It is imperative to note that while some features exhibit discernible relationships with olive production, the overall mutual information values are generally low, highlighting the complexity inherent in predicting olive production. This suggests that multiple factors may result in a non-linear relationship with olive production.
Among the features considered, accumulated pollen demonstrates varying degrees of mutual information with olive production (Figure 5a). For instance, the third and fourth weeks of June (168 and 175, respectively) have the highest mutual information values, indicating a potential relationship with olive production. Other weeks, such as the thirrd and fourth weeks of May (140 and 147, respectively), also exhibit significant mutual information values, albeit comparatively lower. Similarly, meteorological features such as maximum temperature (TX), minimum temperature (TN), and precipitation (RR) for certain months showcase their respective mutual information values. For example, the maximum temperatures in May (TX_05) and precipitation in February (RR_02) possess relatively higher mutual information values, suggesting stronger associations with olive production during those periods.
Correlation analysis is another valuable method for understanding the relationships between features and a target variable (Figure 5b). Correlation coefficients close to 1 indicate a strong positive linear relationship, whereas values near −1 suggest a strong negative linear relationship. Values around 0 imply little to no linear relationship. Herein, the correlations show relatively low values, which further indicates the low collinearity with olive production. Nonetheless, the maximum temperature in January (TX_01) exhibits the highest positive correlation coefficient (0.34), indicating a positive relationship with olive production. This suggests that high temperatures in January positively influence olive production. Other features such as the minimum and mean temperatures in May (TN_05 and TM_05) and precipitation in February (RR_02) demonstrate negative correlation coefficients, implying a negative relationship with olive production. For instance, high temperatures in May could adversely affect olive production. Regarding the pollen accumulation during specific weeks, these also display low degrees of correlation with olive production, indicating no linear relationship. Weeks like the third (168) and fourth weeks of June (175) show positive correlations, despite higher mutual information (cf. above), while others like the third (140) and fourth weeks of May (147) display higher negative correlations, although still relatively weak. It is important to note that while correlation analysis provides valuable insights into linear relationships, other non-linear factors may be at play.

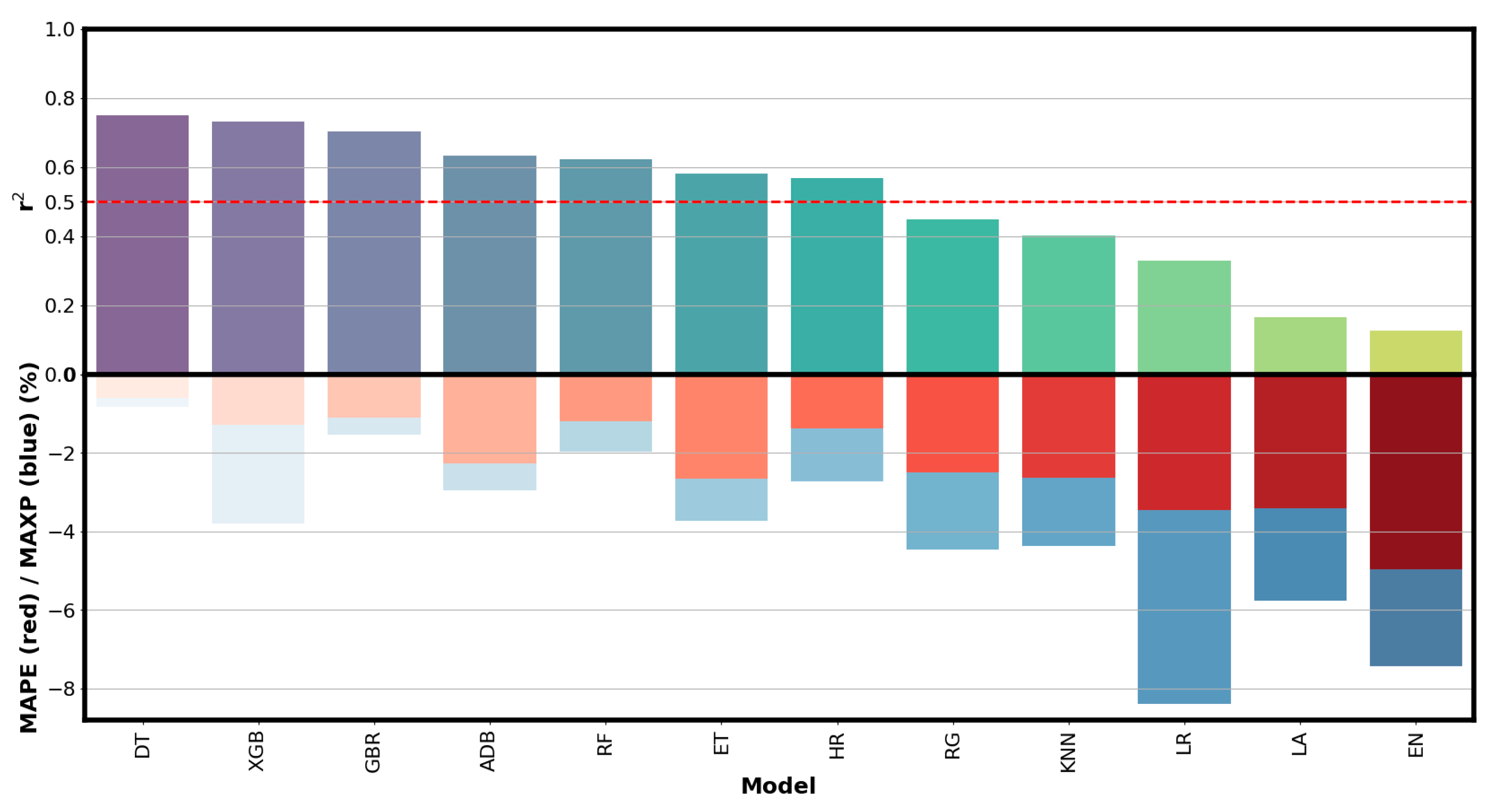
3.3. Model Performance

Figure 6 shows the performance (r2—Coefficient of Determination) and errors (MAPE—Mean Absolute Percentage Error and MAPX—Maximum Percentage Error) for all trained models. Among the array of regression machine learning algorithms employed in this study, the DT model emerged as the most robust performer, boasting the lowest MAPE/MAXP and the highest r2 value. Such results signify DT’s predictive accuracy and its adeptness in elucidating the underlying relationships between predictor variables and the target variable. Conversely, the EN model exhibited subpar performance, displaying the highest errors and the lowest performance among the models scrutinized. However, in effect, all of the linear models used show low performance levels, with r2 values lower than 0.5. This underscores the ineffectiveness of these models in capturing intricate patterns within the data and in accommodating the inherent complexity of the dataset. All bagging and boosting algorithms demonstrated notable performance levels. Regarding the bagging algorithms, the RF model demonstrated a good performance, characterized by relatively low MAPE/MAXP and relatively high R2 values, indicative of its ability to mitigate overfitting and capture nuanced relationships within the data. Still, the ET model showcased less favorable outcomes, suggesting potential limitations in its ability to generalize well to unseen data. Similarly, within the boosting category, models such as GBR displayed a strong predictive performance, while models like ADB exhibited inferior results, suggesting potential challenges in effectively leveraging the boosting methodology to improve predictive accuracy.

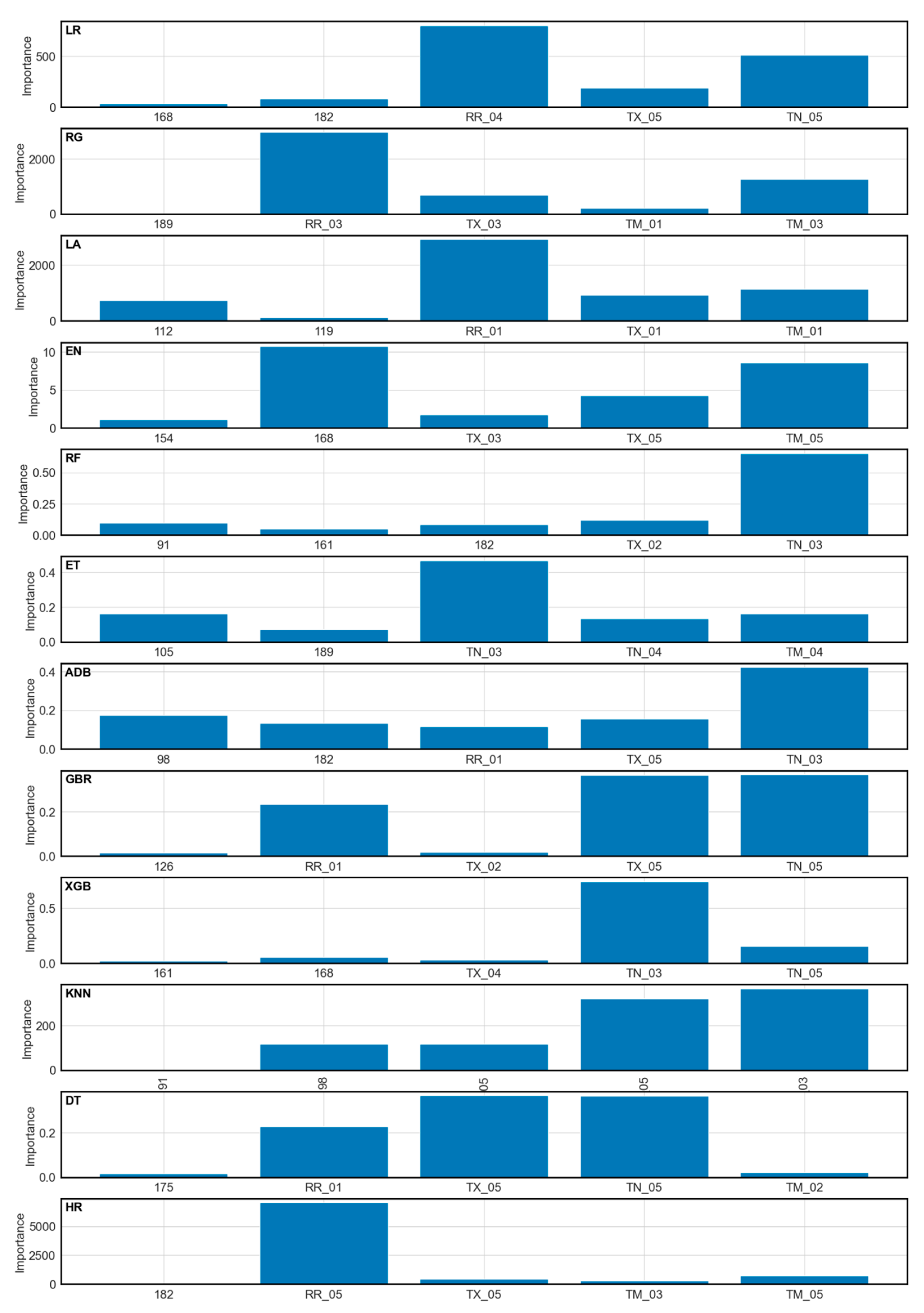
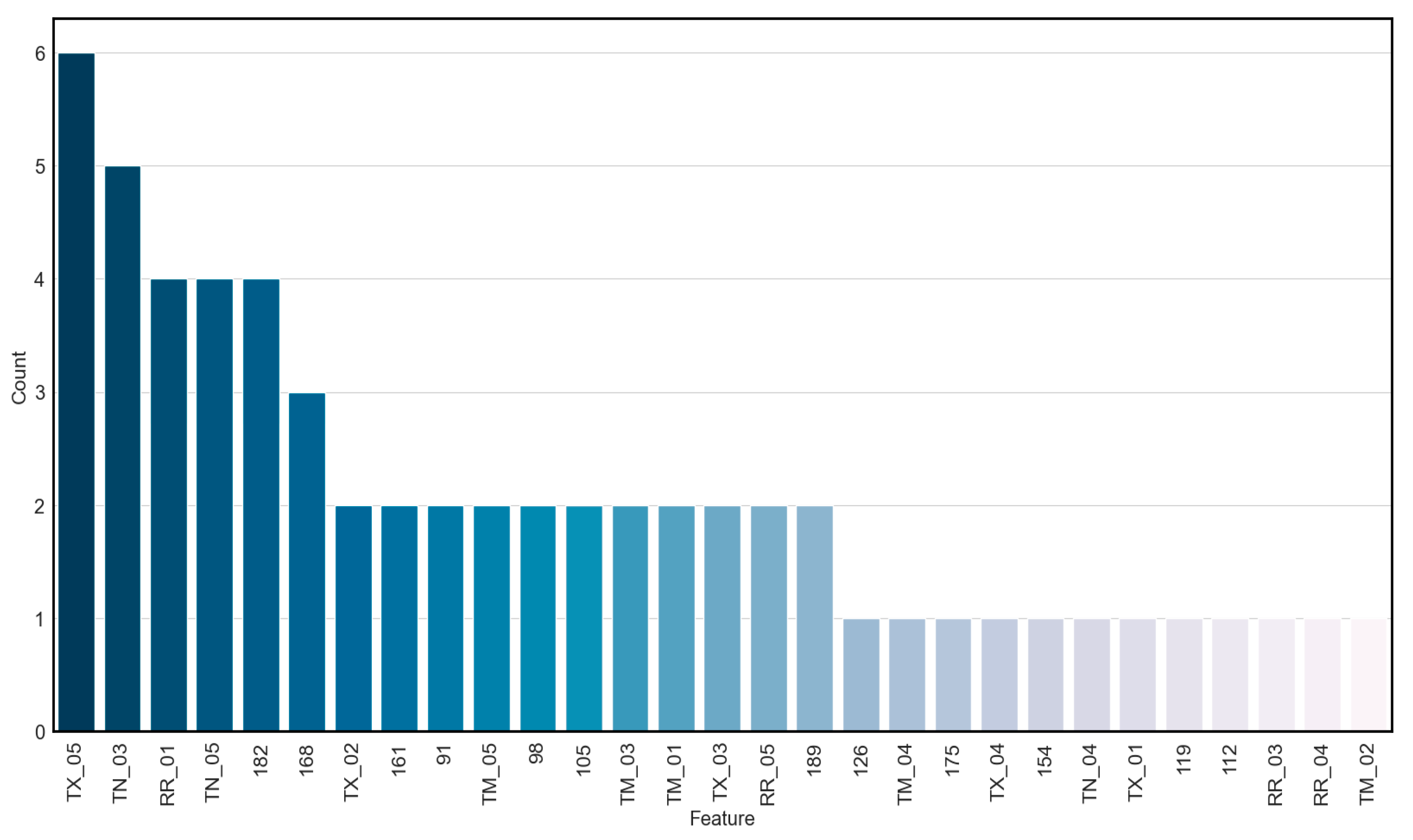
3.4. Feature Importance

Figure 7 shows the feature importance values for each model, providing valuable insights into the relative significance of individual features in predicting the target variable across different regression machine learning algorithms. Overall, all models give more importance to climatic variables than to pollen accumulation. In the DT model, which shows the highest performance (Figure 5), strong importance is given to May’s weather characteristics, with TX_05 and TN_05 demonstrating notable importance, combined with January’s precipitation (RR_01). Other models, such as the GBR model, completely agree with DT, while also giving strong importance to May’s climatic conditions (TX_05 and TN_05), with features such as RR_01 particularly high-importance values, indicating their crucial role in predicting the target variable.
In the ADB model, strong predictive importance is given to March’s minimum temperature (TN_03), along with the pollen counts at the beginning of the season. As such, there are some features with consistently high importance across multiple models, such as March and May’s temperatures (TX_05 and TN_03), underscoring their universal relevance and robust predictive power across diverse regression algorithms. In effect, Figure 8 presents the frequencies of occurrence of certain features in the feature importance levels across all models, indicating their collective importance in predicting the target variable. Understanding the frequency of feature occurrence in feature importance levels can provide insights into the relative importance levels and consistencies of features in predicting the target variable, guiding feature selection and model interpretation efforts in predictive modeling tasks. Among these features, TX_05 appears most frequently, occurring in the feature importance results of six models, followed by TN_03 and RR_01, each appearing in five models. Features such as TN_05 and pollen accumulation during the second half of June (DOY 168 and DOY 182) occur in four models, suggesting their consistent relevance in multiple predictive models. On the other hand, some features only appear once or twice in the feature importance results, indicating potentially lower importance or less consistent predictive power across models.

4. Discussion

Given the acknowledged significance of pollen in fruit production across various crops, including olives, as evidenced by prior research [65], it is logical to explore whether urban pollen station data may be used to effectively predict regional olive production. While the existing literature emphasizes the importance of direct pollen collection within olive groves, indicating a strong correlation, the potential utility of urban pollen data remains underexplored. Urban pollen stations, due to their distance from olive groves, may provide data that do not linearly correlate with olive tree parameters, and understanding the specific relationship between pollen and the fruit load in olive trees may become difficult. However, by employing cutting-edge machine learning algorithms, this study aimed to bridge this gap and ascertain the viability of urban pollen data as a predictor of olive production on a regional scale. Additionally, weather variables, such as monthly mean temperatures and monthly precipitation, were also included in this modeling approach [26,29,34,37].
The results collected in this study on the relationship between the olive season, fruit production, and meteorological variables are consistent with those of several studies present in the literature [31,44,66,67]. The Alentejo region, as seen in Figure 1, has the largest area of olive grove cultivation when related to other regions of Portugal [5]. The number of hectares of olive groves has grown exponentially, a fact proven by the significant difference between olive groves’ area in 2002 (146,266 ha) compared to that in 2022 (201,474 ha), constituting an increase of 37% (equivalent of 55,208 ha) in the number of hectares in the study area [5]. However, this significant increase in the olive grove area did not translate immediately into increased pollen concentrations in the air (Figure 3), probably due to the ages and sizes of the plants. Considering the period between the years 2002 and 2022, it can be observed that from year to year, there was a lot of variability in terms of pollen concentrations detected; however, when observing the pollen seasons in the period under analysis, the main pollen season usually occurred between the end of April and the beginning of May, and the month of May was when the maximum concentration of this crop occurred. These observations corroborated by other authors, specifically for the Iberian Peninsula area [68]. There are different factors that can contribute to the observed variation, such as meteorological parameters, associated with the increase or decrease in pollen concentration during the pollination season [69,70], along with the biennial reproductive cycle of the plant itself [17].
In addition to these two factors, there are already reports of differences in pollen concentrations in different olive cultivars [40]. Consequently, and since the pollen index is the sum of pollen concentrations over the main season, this represents an aerobiological variability directly related to flower production [12] and can be considered an important indicator of productivity [26]. Correlation analysis to investigate the relationship between pollen, climatic conditions, and yield reflects a common approach in the literature to understand the interactions between the three variables [69,70]. Finding that certain meteorological variables, such as temperature, show a significant association with fruit production is in line with what has already been observed by other authors who have highlighted the direct influence of meteorological conditions on productivity [71].
When examining the relationship between pollen/weather and olive production, mutual information and correlation analyses were conducted. The results indicate complex associations, with certain weeks of pollen accumulation showing significant mutual information with olive production. Linear correlation coefficients generally remain low, underscoring the challenge of predicting olive production based on linear relationships. Regarding model performance, among the machine learning algorithms employed to predict olive production, DT, XGB, and GBR were the most robust performers (r2 > 0.7), while linear models displayed a subpar performance, emphasizing the complexity of this approach. Bagging and boosting algorithms demonstrated varying degrees of success, with RF and GBR models performing well, although with differences in predictive accuracy. Feature importance analysis provided valuable insights into the relative significance of climatic variables versus pollen accumulation in predicting olive production. March and May temperature conditions consistently emerged as influential predictors across different models, highlighting their crucial role in forecasting olive production. Features such as the maximum temperature in May appeared frequently in the feature importance results of different high-performing models, indicating their universal relevance and robust predictive power.
Comparisons of the performance levels of the different models in predicting fruit production in olive trees reflect an increasingly common approach in precision agriculture, where predictive models are used to optimize production [72]. The results presented in this study using machine learning algorithms were analyzed to establish non-linear relationships between pollen concentrations and olive production, an innovative approach compared to other studies in the literature where linear regression models were used to try to establish an association between the two variables, pollen and yield [31,44,66,67]. Beyond that, the use of machine learning algorithms allows for the identification of complex, non-linear relationships that may not be captured by traditional linear regression models. This capability opens up new avenues for precision agriculture, enabling farmers to make more informed decisions and optimize production in response to changing environmental conditions. Furthermore, our approach uses pollen data from an urban station, which until now has not been performed. This novel approach not only expands the scope of previous research but also underscores the importance of considering diverse sources of data in agricultural studies. By incorporating pollen data from an urban station, this study not only provides insights into the relationship between pollen concentrations and olive production but also highlights the potential impact of urban environments on agricultural processes. Understanding these dynamics is crucial for developing resilient and sustainable agricultural practices, particularly in regions where urbanization is rapidly encroaching on agricultural land.

5. Conclusions

The present study advances our understanding of using urban pollen station data, combined with weather data and powerful ML algorithms, to predict regional olive pro-duction. The pollen season in Évora occurs mainly in the month of May, with high variability in relation to the yearly intensity and duration of the pollen season. Non-linear ML algorithms have shown better performance when compared to linear models. Algorithms such as DT, XGB, and GBR have shown promising results in detecting complex relationships or associations between the variables under study (r2 > 0.7). In the analysis of climatic conditions, the temperatures in the months of March and May, in particular, were identified as useful in the prediction of fruit production. Furthermore, pollen accumulation during the second half of June showed potential associations with olive production. The developed models may be used as decision-support tools by growers and stakeholders to further enhance the sustainability of the thriving olive sector in southern Portugal. Future research endeavors should focus on further validating these models across diverse environmental conditions and integrating them into practical agricultural management systems. In effect, several urban pollen stations are located throughout Europe but are not yet used for yield forecasting purposes. Analyzing these vast datasets could provide a more comprehensive understanding of how these factors influence olive production dynamics, possibly enabling the development of a multicriteria yield-forecasting system for olive trees in southern Europe.

Author Contributions

Conceptualization, A.G., C.A., A.R.C. and H.F.; data curation, A.G. and H.F.; formal analysis, A.G. and H.F.; funding acquisition, C.A., A.R.C. and H.F.; investigation, A.G. and H.F.; methodology, A.G. and H.F.; project administration, C.A. and H.F.; resources, A.G., C.A., A.R.C. and H.F.; software, A.G. and H.F.; supervision, C.A., A.R.C. and H.F.; validation, A.G., C.A., A.R.C. and H.F.; visualization, A.G. and H.F.; writing—original draft, A.G. and H.F.; writing—review and editing, A.G., C.A., A.R.C., and H.F. All authors have read and agreed to the published version of the manuscript.

Funding

This work was co-funded by Portuguese funds through FCT—Fundação para a Ciência e Tecnologia, I.P. (projects UIBD/04683/2020 and UIDP/04683/2020). The authors gratefully acknowledge the University of Évora for the instrumentation used in this work. Helder Fraga thanks the Portuguese Foundation for Science and Technology (FCT), for project UIDB/04033/2020 (https://doi.org/10.54499/UIDB/04033/2020), project LA/P/0126/2020 (https://doi.org/10.54499/LA/P/0126/2020), project 2022.04553.PTDC (https://doi.org/10.54499/2022.04553.PTDC), and project 2022.02317.CEECIND (https://doi.org/10.54499/2022.02317.CEECIND/CP1749/CT0002).

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors on request.

Acknowledgments

This work was co-funded by Portuguese funds through FCT- Fundação para a Ciência e Tecnologia, I.P. (projects UIBD/04683/2020 and UIDP/04683/2020). The authors gratefully acknowledge the University of Évora for the instrumentation used in this work. Helder Fraga thanks the Portuguese Foundation for Science and Technology (FCT), for project UIDB/04033/2020 (https://doi.org/10.54499/UIDB/04033/2020), project LA/P/0126/2020 (https://doi.org/10.54499/LA/P/0126/2020), project 2022.04553.PTDC (https://doi.org/10.54499/2022.04553.PTDC), and project 2022.02317.CEECIND (https://doi.org/10.54499/2022.02317.CEECIND/CP1749/CT0002). We would like to thank researcher Eciclê Duarte (https://orcid.org/0000-0002-2785-6648 and Ciência ID: 0016-A931-B667) from the Institute of Earth Sciences, School of Sciences and Technology & IIFA of the University of Évora for contributing a map of Portugal with photopoints of the main olive-growing areas.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Diego, B.; Rallo, L. Olive Cultivars in Spain. HortTechnology 2000, 10, 107–110. [Google Scholar] [CrossRef]
  2. Langgut, D.; Cheddadi, R.; Carrión, J.S.; Cavanagh, M.; Colombaroli, D.; Eastwood, W.J.; Greenberg, R.; Litt, T.; Mercuri, A.M.; Miebach, A.; et al. The Origin and Spread of Olive Cultivation in the Mediterranean Basin: The Fossil Pollen Evidence. Holocene 2019, 29, 902–922. [Google Scholar] [CrossRef]
  3. FAOSTAT. Available online: https://www.fao.org/faostat/en/#data/QCL/visualize (accessed on 5 February 2024).
  4. PORDATA—Ambiente de Consulta. Available online: https://www.pordata.pt/db/portugal/ambiente+de+consulta/tabela (accessed on 5 February 2024).
  5. Portal Do INE. Available online: https://www.ine.pt/xportal/xmain?xpgid=ine_main&xpid=INE (accessed on 20 February 2024).
  6. EDIA, S.A. Empresa de Desenvolvimento e Infra-estruturas do Alqueva, S.A. Available online: https://www.edia.pt/pt/ (accessed on 9 February 2024).
  7. Fraga, H.; Pinto, J.G.; Santos, J.A. Olive Tree Irrigation as a Climate Change Adaptation Measure in Alentejo, Portugal. Agric. Water Manag. 2020, 237, 106193. [Google Scholar] [CrossRef]
  8. Ges, A. Sustentabilidade dos Olivais em Portugal: Desafios e Respostas; Princípia Editora: Parede, Portugal, 2022; 174p. [Google Scholar]
  9. Barros, A.; Cordeiro, A.M.; Inês, C.S.F.; Serra, C.; Sá, C.; Lourenço, E.; Calouro, F.; Pavão, F.A.; Herculano, H. Azeites de Portugal: Guia 2018; Enigma Editores: Lisbon, Portugal, 2018; 96p. [Google Scholar]
  10. Oh, J.-W. Pollen Allergy in a Changing Planetary Environment. Allergy Asthma Immunol. Res. 2022, 14, 168–181. [Google Scholar] [CrossRef] [PubMed]
  11. Łysiak, G.P.; Szot, I. The Use of Temperature Based Indices for Estimation of Fruit Production Conditions and Risks in Temperate Climates. Agriculture 2023, 13, 960. [Google Scholar] [CrossRef]
  12. Rojo, J.; Rapp, A.; Lara, B.; Fernández-González, F.; Pérez-Badia, R. Effect of Land Uses and Wind Direction on the Contribution of Local Sources to Airborne Pollen. Sci. Total Environ. 2015, 538, 672–682. [Google Scholar] [CrossRef] [PubMed]
  13. Abrol, D.P. Pollination Biology: Biodiversity Conservation and Agricultural Production; Springer: New York, NY, USA, 2011; p. 792. [Google Scholar]
  14. Cruden, R. Pollen Grains: Why so Many? Plant Syst. Evol. 2000, 222, 143–165. [Google Scholar] [CrossRef]
  15. Crane, J.; Nelson, M.M. Effects of Crop Load, Girdling, and Auxin Application on Alternate Bearing of the Pistachio1. J. Amer. Soc. Hort. Sci. 1972, 97, 337–339. [Google Scholar] [CrossRef]
  16. CuevaS, J.; Rallo, L.; Rapoport, H. Initial Fruit Set at High Temperature in Olive, Olea europaea L. J. Hortic. Sci. 1994, 69, 665–672. [Google Scholar] [CrossRef]
  17. Al-Shdiefat, S.; Qrunfleh, M. Alternate Bearing of the Olive) Olea europaea L.) as Related to Endogenous Hormonal Content. Jordan. J. Agric. Sci. 2008, 4, 12. [Google Scholar]
  18. Benlloch-González, M.; Sánchez-Lucas, R.; Benlloch, M.; Ricardo, F.-E. An Approach to Global Warming Effects on Flowering and Fruit Set of Olive Trees Growing under Field Conditions. Sci. Hortic. 2018, 240, 405–410. [Google Scholar] [CrossRef]
  19. Marcelle, R. The Flowering Process and Its Control. Acta Hortic. 1984, 149, 65–70. [Google Scholar] [CrossRef]
  20. Castro-Camba, R.; Sánchez, C.; Vidal, N.; Vielba, J.M. Plant Development and Crop Yield: The Role of Gibberellins. Plants 2022, 11, 2650. [Google Scholar] [CrossRef] [PubMed]
  21. Trigo, M.M.; Jato, V.; Fernández, D.; Galán, C. Atlas Aeropalinológico de España; Secretariado de Publicaciones de la Universidad de Leon: Leon, Spain, 2008; ISBN 978-84-9773-403-5. [Google Scholar]
  22. del Carmen Fernández, M.; Romero-García, A.T.; Rodríguez-García, M.I. Aperture Structure, Development and Function in Lycopersicum Esculentum Miller (Solanaceae) Pollen Grain. Rev. Palaeobot. Palynol. 1992, 72, 41–48. [Google Scholar] [CrossRef]
  23. Pacini, E.; Juniper, B.E. The Ultrastructure of Pollen-Grain Development in the Olive (Olea europaea). 2. Secretion by the Tapetal Cells. New Phytol. 1979, 83, 165–174. [Google Scholar] [CrossRef]
  24. Dominguez-Vilches, E.; Infante, F.; Galán, C.; Pasadas, F.; Torre, F. Variations in the Concentration of Airborne Olea Pollen and Associated Pollinosis in Cordoba (Spain): A Study of the 10-Year Period 1982–1991. J. Investig. Allergol. Clin. Immunol. Off. Organ Int. Assoc. Asthmology (INTERASMA) Soc. Latinoam. Alerg. Inmunol. 1993, 3, 121–129. [Google Scholar]
  25. Florido, J.F.; Delgado, P.G.; de San Pedro, B.S.; Quiralte, J.; de Saavedra, J.M.; Peralta, V.; Valenzuela, L.R. High Levels of Olea europaea Pollen and Relation with Clinical Findings. Int. Arch. Allergy Immunol. 1999, 119, 133–137. [Google Scholar] [CrossRef] [PubMed]
  26. Orlandi, F.; Garcia-Mozo, H.; Ben Dhiab, A.; Galán, C.; Msallem, M.; Fornaciari, M. Olive Tree Phenology and Climate Variations in the Mediterranean Area over the Last Two Decades. Theor. Appl. Climatol. 2013, 115, 207–218. [Google Scholar] [CrossRef]
  27. Aguilera, F.; Fornaciari, M.; Ruiz-Valenzuela, L.; Galán, C.; Msallem, M.; Dhiab, A.B.; la Guardia, C.D.; Del Mar Trigo, M.; Bonofiglio, T.; Orlandi, F. Phenological Models to Predict the Main Flowering Phases of Olive (Olea europaea L.) along a Latitudinal and Longitudinal Gradient across the Mediterranean Region. Int. J. Biometeorol. 2015, 59, 629–641. [Google Scholar] [CrossRef]
  28. Galán, C.; Vázquez, L.; García-Mozo, H.; Domínguez, E. Forecasting Olive (Olea europaea) Crop Yield Based on Pollen Emission. Field Crops Res. 2004, 86, 43–51. [Google Scholar] [CrossRef]
  29. Galán, C.; Garcia-Mozo, H.; Vazquez, L.; Valenzuela, L.; Guardia, C.; Dominguez-Vilches, E. Modeling Olive Crop Yield in Andalusia, Spain. Agron. J. 2008, 100, 98–104. [Google Scholar] [CrossRef]
  30. Ribeiro, H.; Cunha, M.; Calado, L.; Abreu, I. Pollen Morphology and Quality of Twenty Olive (Olea europaea L.) Cultivars Grown in Portugal. Acta Hortic. 2012, 949, 259–264. [Google Scholar] [CrossRef]
  31. Minero, F.J.G.; Candau, P.; Morales, J.; Tomas, C. Forecasting Olive Crop Production Based on Ten Consecutive Years of Monitoring Airborne Pollen in Andalusia (Southern Spain). Agric. Ecosyst. Environ. 1998, 69, 201–215. [Google Scholar] [CrossRef]
  32. Bastiaanssen, W.G.M.; Ali, S. A New Crop Yield Forecasting Model Based on Satellite Measurements Applied across the Indus Basin, Pakistan. Agric. Ecosyst. Environ. 2003, 94, 321–340. [Google Scholar] [CrossRef]
  33. Cour, P.; Van Campo, M. Previsions de Recoltes a Partir de l’analyse Du Contenu Pollinique de l’atmosphere [Intensite de La Pollinisation]. Comptes Rendus Hebd. Des Seances De L’academie Des Sciences. Ser. D 1980, 290, 1043–1046. [Google Scholar]
  34. Aguilera, F.; Ruiz-Valenzuela, L. Forecasting Olive Crop Yields Based on Long-Term Aerobiological Data Series and Bioclimatic Conditions for the Southern Iberian Peninsula. Span. J. Agric. Res. 2014, 12, 215–224. [Google Scholar] [CrossRef]
  35. Cunha, J.; Teixeira Santos, M.; Carneiro, L.C.; Fevereiro, P.; Eiras-Dias, J.E. Portuguese Traditional Grapevine Cultivars and Wild Vines (Vitis vinifera L.) Share Morphological and Genetic Traits. Genet. Resour. Crop Evol. 2009, 56, 975–989. [Google Scholar] [CrossRef]
  36. Garcia-Mozo, H.; Dominguez-Vilches, E.; Galan, C. A Model to Account for Variations in Holm-Oak (Quercus Ilex Subsp. Ballota) Acorn Production in Southern Spain. Ann. Agric. Environ. Med. 2012, 19, 403–408. [Google Scholar]
  37. Oteros, J.; García-Mozo, H.; Hervás, C.; Galán, C. Biometeorological and Autoregressive Indices for Predicting Olive Pollen Intensity. Int. J. Biometeorol. 2013, 57, 307–316. [Google Scholar] [CrossRef]
  38. Fraga, H.; Guimarães, N.; Freitas, T.R.; Malheiro, A.C.; Santos, J.A. Future Scenarios for Olive Tree and Grapevine Potential Yields in the World Heritage Côa Region, Portugal. Agronomy 2022, 12, 350. [Google Scholar] [CrossRef]
  39. Fraga, H.; Pinto, J.G.; Viola, F.; Santos, J.A. Climate Change Projections for Olive Yields in the Mediterranean Basin. Int. J. Climatol. 2020, 40, 769–781. [Google Scholar] [CrossRef]
  40. Rojas Gómez, M.D.L.M.; Moral, J.; López-Orozco, R.; Cabello, D.; Oteros, J.; Diego, B.; Galán, C.; Díez, C. Pollen Production in Olive Cultivars and Its Interannual Variability. Ann. Bot. 2023, 132, 1145–1158. [Google Scholar] [CrossRef] [PubMed]
  41. Oteros, J.; Orlandi, F.; García-Mozo, H.; Aguilera, F.; Dhiab, A.; Bonofiglio, T.; Abichou, M.; Ruiz-Valenzuela, L.; Trigo, M.; Díaz de La Guardia, C.; et al. Better Prediction of Mediterranean Olive Production Using Pollen-Based Models. Agron. Sustain. Dev. 2014, 34, 685–694. [Google Scholar] [CrossRef]
  42. Ribeiro, H.; Cunha, M.; Abreu, I. Quantitative Forecasting of Olive Yield in Northern Portugal Using a Bioclimatic Model. Aerobiologia 2008, 24, 141–150. [Google Scholar] [CrossRef]
  43. Hirst, J.M. An Automatic Volumetric Spore Trap. Ann. Appl. Biol. 1952, 39, 257–265. [Google Scholar] [CrossRef]
  44. Ribeiro, H.; Cunha, M.; Abreu, I. Definition of Main Pollen Season Using a Logistic Model. Ann. Agric. Environ. Med. 2007, 14, 259–264. [Google Scholar]
  45. Cunha, M.; Ribeiro, H.; Costa, P.; Abreu, I. A Comparative Study of Vineyard Phenology and Pollen Metrics Extracted from Airborne Pollen Time Series. Aerobiologia 2015, 31, 45–56. [Google Scholar] [CrossRef]
  46. Cornes, R.C.; Van Der Schrier, G.; Van Den Besselaar, E.J.M.; Jones, P.D. An Ensemble Version of the E-OBS Temperature and Precipitation Data Sets. JGR Atmos. 2018, 123, 9391–9409. [Google Scholar] [CrossRef]
  47. Hofstra, N.; Haylock, M.; New, M.; Jones, P.D. Testing E-OBS European High-Resolution Gridded Data Set of Daily Precipitation and Surface Temperature. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
  48. Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer Series in Statistics; Springer: New York, NY, USA, 2013; ISBN 978-0-387-21606-5. [Google Scholar]
  49. Edwards, V.P.M.; Edwards, A.L. An Introduction to Linear Regression and Correlation; Books in Psychology; W. H. Freeman: New York, NY, USA, 1976; ISBN 978-0-7167-0562-8. [Google Scholar]
  50. Hilt, D.E.; Seegrist, D.W.; United States. Forest Service; Northeastern Forest Experiment Station (Radnor, Pa.). In Ridge, a Computer Program for Calculating Ridge Regression Estimates; Dept. of Agriculture, Forest Service, Northeastern Forest Experiment Station: Upper Darby, PA, USA, 1977; Volume 236. [Google Scholar]
  51. Tibshirani, R. Regression Shrinkage and Selection via the Lasso. J. R. Stat. Society. Ser. B (Methodol.) 1996, 58, 267–288. [Google Scholar] [CrossRef]
  52. Zou, H.; Hastie, T. Regularization and Variable Selection Via the Elastic Net. J. R. Stat. Soc. Ser. B Stat. Methodol. 2005, 67, 301–320. [Google Scholar] [CrossRef]
  53. Peter, J. Huber Robust Estimation of a Location Parameter. Ann. Math. Stat. 1964, 35, 73–101. [Google Scholar] [CrossRef]
  54. Jerome, H. Friedman Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
  55. Solomatine, D.P.; Shrestha, D.L. AdaBoost.RT: A Boosting Algorithm for Regression Problems. In Proceedings of the 2004 IEEE International Joint Conference on Neural Networks (IEEE Cat. No.04CH37541), Budapest, Hungary, 25–29 July 2004; Volume 2, pp. 1163–1168. [Google Scholar]
  56. Chen, T.; Guestrin, C. Xgboost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
  57. Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
  58. John, V.; Liu, Z.; Guo, C.; Mita, S.; Kidono, K. Real-Time Lane Estimation Using Deep Features and Extra Trees Regression; Springer: Berlin/Heidelberg, Germany, 2016; pp. 721–733. [Google Scholar]
  59. Fix, E.; Hodges, J.L. Discriminatory Analysis: Nonparametric Discrimination: Consistency Properties; USAF School of Aviation Medicine: Berkeley, CA, USA, 1951. [Google Scholar]
  60. Studer, M.; Ritschard, G.; Gabadinho, A.; Nicolas, S. Müller Discrepancy Analysis of State Sequences. Sociol. Methods Res. 2011, 40, 471–510. [Google Scholar] [CrossRef]
  61. Webb, R.L.; Tadlock, J. Mostly Harmless Statistics; Lulu.com: Morrisville, NC, USA, 2021; ISBN 978-1-71639-891-9. [Google Scholar]
  62. Fraga, H.; Guimarães, N.; Santos, J. Vintage Port Prediction and Climate Change Scenarios. OENO One 2023, 57. [Google Scholar] [CrossRef]
  63. Murphy, K. Machine Learning: A Probabilistic Perspective; MIT Press: Cambridge, MA, USA, 2012; Volume 58. [Google Scholar]
  64. Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley: Hoboken, NJ, USA, 2012; ISBN 978-1-118-58577-1. [Google Scholar]
  65. Ribeiro, H.; Abreu, I.; Cunha, M. Olive Crop-Yield Forecasting Based on Airborne Pollen in a Region Where the Olive Groves Acreage and Crop System Changed Drastically. Aerobiologia 2017, 33, 473–480. [Google Scholar] [CrossRef]
  66. Orlandi, F.; Romano, B.; Fornaciari, M. Relationship between Pollen Emission and Fruit Production in Olive (Olea europaea L.). Grana 2005, 44, 98–103. [Google Scholar] [CrossRef]
  67. Ben Dhiab, A.; Ben Mimoun, M.; Oteros, J.; Garcia-Mozo, H.; Domínguez-Vilches, E.; Galán, C.; Abichou, M. Modeling olive-crop forecasting in Tunisia. Theor. Appl. Climatol. 2017, 128, 541–549. [Google Scholar] [CrossRef]
  68. Linares, J.C.; Tíscar, P.A. Climate Change Impacts and Vulnerability of the Southern Populations of Pinus nigra Subsp. Salzmannii. Tree Physiol. 2010, 30, 795–806. [Google Scholar] [CrossRef]
  69. Alba, F.; De La Guardia, C.D.; Comtois, P. The Effect of Meteorological Parameters on Diurnal Patterns of Airborne Olive Pollen Concentration. Grana 2000, 39, 200–208. [Google Scholar] [CrossRef]
  70. Vázquez, L.M.; Galán, C.; Domínguez-Vilches, E. Influence of Meteorological Parameters on Olea Pollen Concentrations in Córdoba (South-Western Spain). Int. J. Biometeorol. 2003, 48, 83–90. [Google Scholar] [CrossRef] [PubMed]
  71. Hatfield, J.L.; Boote, K.J.; Kimball, B.A.; Ziska, L.H.; Izaurralde, R.C.; Ort, D.; Thomson, A.M.; Wolfe, D. Climate Impacts on Agriculture: Implications for Crop Production. Agron. J. 2011, 103, 351–370. [Google Scholar] [CrossRef]
  72. Perez-Ruiz, M.; Martínez-Guanter, J.; Upadhyaya, S.K. Chapter 15—High-Precision GNSS for Agricultural Operations. In GPS and GNSS Technology in Geosciences; Petropoulos, G.P., Srivastava, P.K., Eds.; Elsevier: Amsterdam, The Netherlands, 2021; pp. 299–335. ISBN 978-0-12-818617-6. [Google Scholar]
Horticulturae 10 00584 g001
Figure 1. Map of Portugal with photopoints of the main olive-growing areas according to the 6th National Forest Inventory (2015) (Instituto da s Florestas (ICNF), 2024).
Figure 1. Map of Portugal with photopoints of the main olive-growing areas according to the 6th National Forest Inventory (2015) (Instituto da s Florestas (ICNF), 2024).
Horticulturae 10 00584 g001
Horticulturae 10 00584 g002
Figure 2. Ombrothermic diagram for Évora, calculated using the E-OBS dataset from 2002 to 2022, representing monthly minimum, maximum, and mean air temperatures and the monthly precipitation sum. The red-colored bars represent the dry season months.
Figure 2. Ombrothermic diagram for Évora, calculated using the E-OBS dataset from 2002 to 2022, representing monthly minimum, maximum, and mean air temperatures and the monthly precipitation sum. The red-colored bars represent the dry season months.
Horticulturae 10 00584 g002
Horticulturae 10 00584 g003
Figure 3. Seasonal Pollen Index (SPIn Pollens/m3) recorded at the Évora station between 2002 and 2022, along with the regional olive production (t) for the same period. In the years 2007, 2015, and 2016, records were not available.
Figure 3. Seasonal Pollen Index (SPIn Pollens/m3) recorded at the Évora station between 2002 and 2022, along with the regional olive production (t) for the same period. In the years 2007, 2015, and 2016, records were not available.
Horticulturae 10 00584 g003
Horticulturae 10 00584 g004
Figure 4. Pollen concentration daily (a) and weekly (b) for each year.
Figure 4. Pollen concentration daily (a) and weekly (b) for each year.
Horticulturae 10 00584 g004
Horticulturae 10 00584 g005
Figure 5. (a) Information on each feature of olive production. (b) Correlation of each feature with olive production.
Figure 5. (a) Information on each feature of olive production. (b) Correlation of each feature with olive production.
Horticulturae 10 00584 g005
Horticulturae 10 00584 g006
Figure 6. Metrics for each model: top—Coefficient of Determination (r2); bottom—Mean Absolute Percentage Error (MAPE; in red color) and Maximum Percentage Error (MAXP; in blue color), both represented in negative percentages.
Figure 6. Metrics for each model: top—Coefficient of Determination (r2); bottom—Mean Absolute Percentage Error (MAPE; in red color) and Maximum Percentage Error (MAXP; in blue color), both represented in negative percentages.
Horticulturae 10 00584 g006
Horticulturae 10 00584 g007
Figure 7. Feature importance of all models used in the current study. For linear models, the features used are based on the individual predictors and coefficients.
Figure 7. Feature importance of all models used in the current study. For linear models, the features used are based on the individual predictors and coefficients.
Horticulturae 10 00584 g007
Horticulturae 10 00584 g008
Figure 8. Number of times each feature appears in the feature importance of all models.
Figure 8. Number of times each feature appears in the feature importance of all models.
Horticulturae 10 00584 g008
Table 1. Characterization of the Olea pollen seasons between 2002 and 2022. In the years 2007, 2015, and 2016, records were not available.
Table 1. Characterization of the Olea pollen seasons between 2002 and 2022. In the years 2007, 2015, and 2016, records were not available.
YearStart DateStart DOYEnd DateEnd DOYPSD
(Days)		Peak DatePeak DOYPeak Value
(Pollen/m3)		SPIn,
(Pollen/m3)
200202/0512305/061573520/051413962789
200310/0513106/061582828/051499005933
200406/0512705/061573118/0513916058201
200503/0512408/061603720/051415175567
200607/0512830/051512417/0513811597340
200814/0410503/061555103/051246643246
200926/0411701/061533709/0513011769435
201012/0513331/051522020/0514112526255
201124/0411522/051432914/051359069737
201207/0512808/061603317/051384204489
201302/0512315/061674514/051359208009
201404/0512524/051452114/0513511557483
201717/0410825/051463904/051255913967
201811/0513228/061804923/051443653855
201901/0512224/051452412/0513318846420
202011/0410207/061595803/051243721896
202126/0411701/061533708/05129161313,718
202201/0512224/051452412/05133174869
Avg30/0412103/061553514/051358936067
Table 2. List of the machine learning models used in the current study.
Table 2. List of the machine learning models used in the current study.
GroupAlgorithmsAcronym
LinearLinear RegressionLR
Ridge RegressionRG
Lasso RegressionLA
ElasticNet RegressionEN
Huber RegressionHR
BaggingRandom Forest RegressionRF
Extra Trees RegressionET
BoostingGradient Boosting RegressionGBR
AdaBoost RegressionADB
XGBoost RegressionXGB
OtherNearest Neighbors RegressionKNN
Decision Tree RegressionDT
Table 3. Feature acronyms and descriptions.
Table 3. Feature acronyms and descriptions.
FeatureDescription
91Pollen Accumulation—DOY 91–97 (1st week of April)
98Pollen Accumulation—DOY 98–104 (2nd week of April)
105Pollen Accumulation—DOY 105–111 (3rd week of April)
112Pollen Accumulation—DOY 112–118 (4th week of April)
119Pollen Accumulation—DOY 119–125 (1st week of May)
126Pollen Accumulation—DOY 126–132 (2nd week of May)
133Pollen Accumulation—DOY 133–139 (3rd week of May)
140Pollen Accumulation—DOY 140–146 (4th week of May)
147Pollen Accumulation—DOY 147–153 (1st week of June)
154Pollen Accumulation—DOY 154–160 (2nd week of June)
161Pollen Accumulation—DOY 161–167 (3rd week of June)
168Pollen Accumulation—DOY 168–174 (4th week of June)
175Pollen Accumulation—DOY 175–181 (5th week of June)
182Pollen Accumulation—DOY 182–188 (1st week of July)
189Pollen Accumulation—DOY 189–195 (2nd week of July)
TX_01Maximum Temperature—January
TN_01Minimum Temperature—January
TM_01Mean Temperature—January
RR_01Precipitation—January
TX_02Maximum Temperature—February
TN_02Minimum Temperature—February
TM_02Mean Temperature—February
RR_02Precipitation—February
TX_03Maximum Temperature—March
TN_03Minimum Temperature—March
TM_03Mean Temperature—March
RR_03Precipitation—March
TX_04Maximum Temperature—April
TN_04Minimum Temperature—April
TM_04Mean Temperature—April
RR_04Precipitation—April
TX_05Maximum Temperature—May
TN_05Minimum Temperature—May
TM_05Mean Temperature—May
RR_05Precipitation—May
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Galveias, A.; Antunes, C.; Costa, A.R.; Fraga, H. Pollen- and Weather-Based Machine Learning Models for Estimating Regional Olive Production. Horticulturae 2024, 10, 584. https://doi.org/10.3390/horticulturae10060584

AMA Style

Galveias A, Antunes C, Costa AR, Fraga H. Pollen- and Weather-Based Machine Learning Models for Estimating Regional Olive Production. Horticulturae. 2024; 10(6):584. https://doi.org/10.3390/horticulturae10060584

Chicago/Turabian Style

Galveias, Ana, Célia Antunes, Ana Rodrigues Costa, and Helder Fraga. 2024. "Pollen- and Weather-Based Machine Learning Models for Estimating Regional Olive Production" Horticulturae 10, no. 6: 584. https://doi.org/10.3390/horticulturae10060584

APA Style

Galveias, A., Antunes, C., Costa, A. R., & Fraga, H. (2024). Pollen- and Weather-Based Machine Learning Models for Estimating Regional Olive Production. Horticulturae, 10(6), 584. https://doi.org/10.3390/horticulturae10060584

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop