A Computational Model of the Respiratory CPG for the Artificial Control of Breathing
Abstract
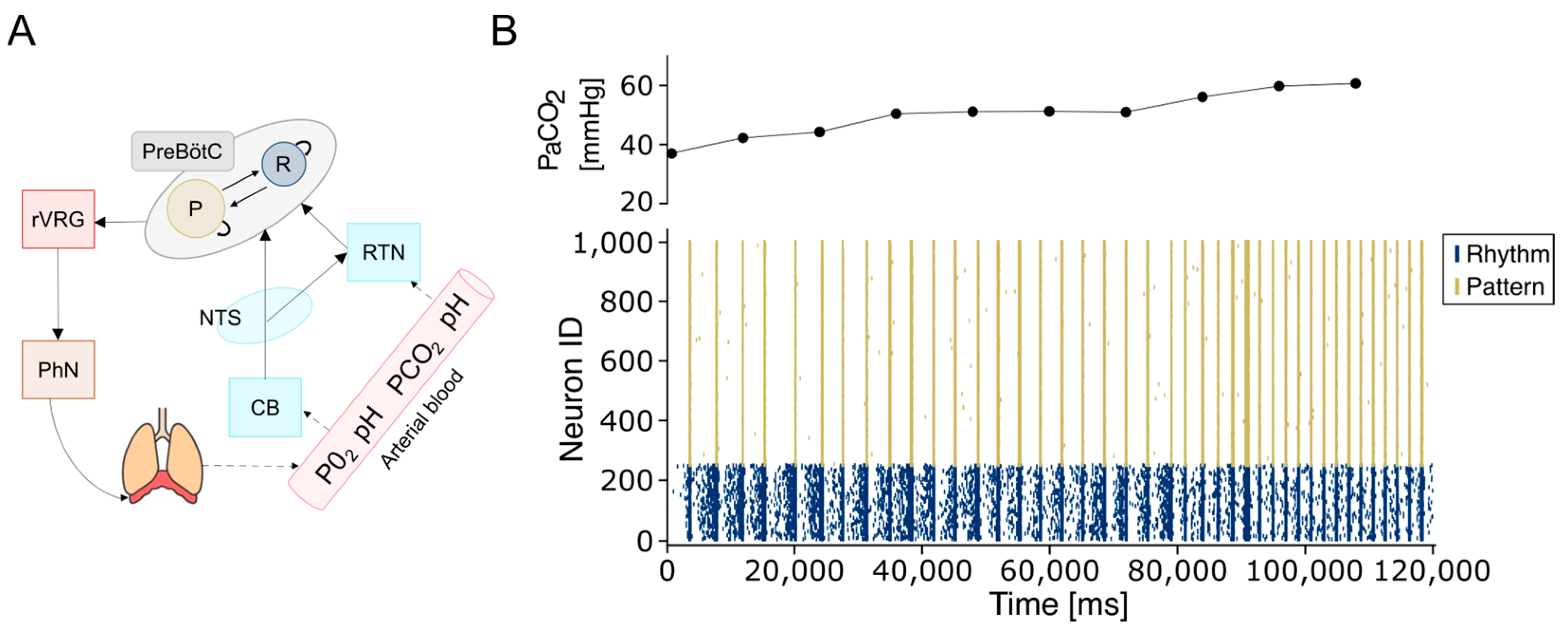
1. Introduction
2. Materials and Methods
2.1. The E-GLIF Neuron Model
2.2. The Synapse Model
- Synaptic weights within the rhythm population (rr) were set to 9.4.
- Connections from the rhythm to the pattern population (rp) were assigned a weight of 1.0.
- Connections from the pattern to the rhythm population (pr) were set to 0.1.
- Synapses within the pattern-generating population (pp) had a weight of 0.5.
- Static synapses from the spike generators—ideally representing the RTN—projecting to the rhythm population were set to a weight of 2.9.
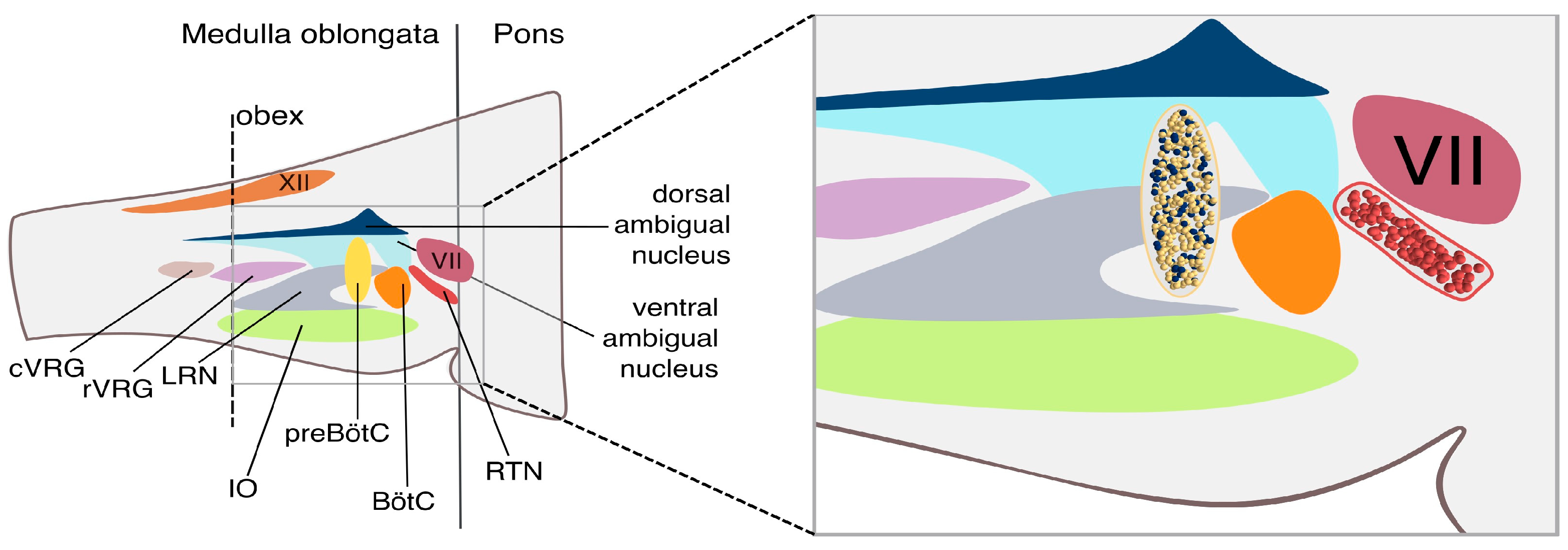
2.3. The Network Model
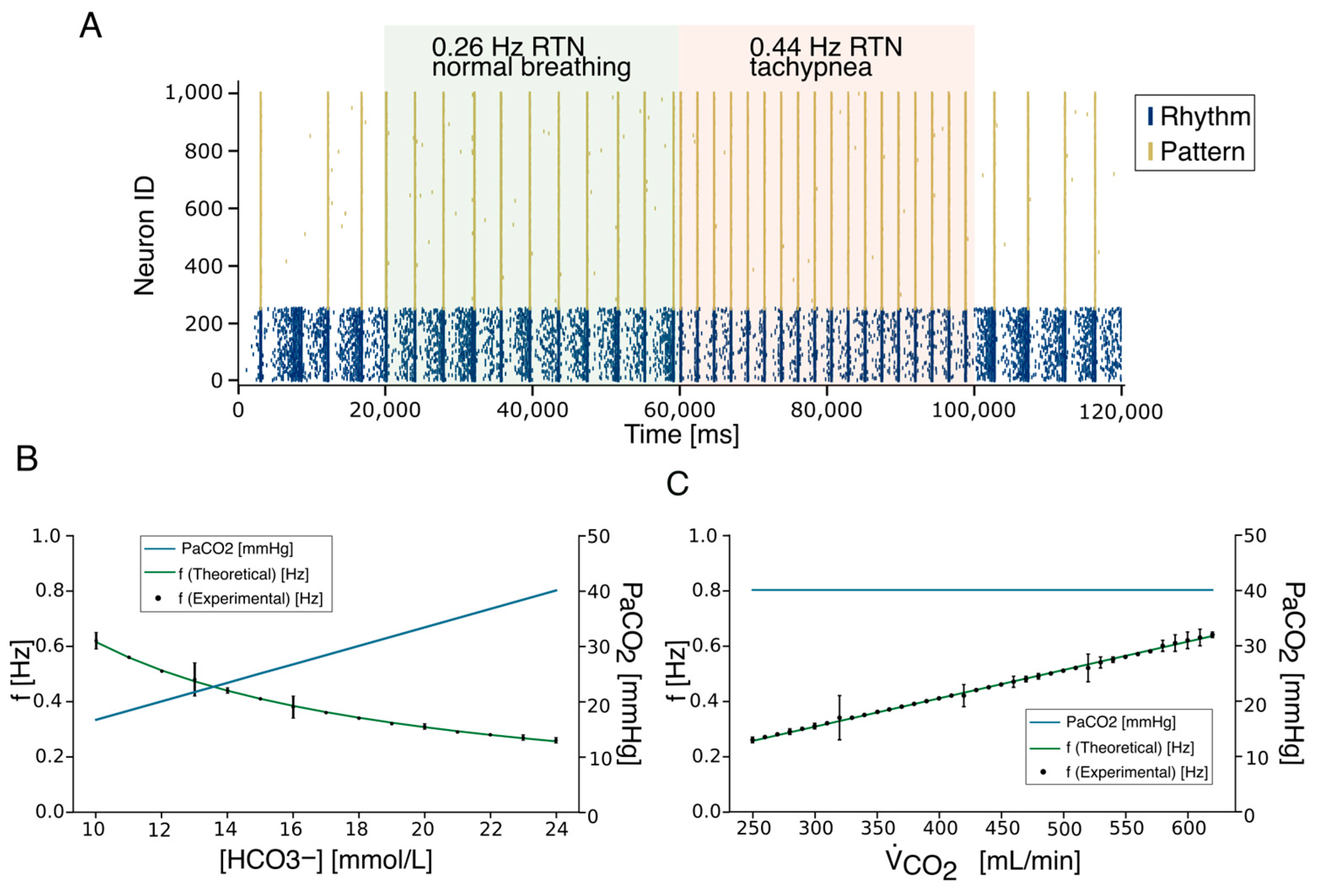
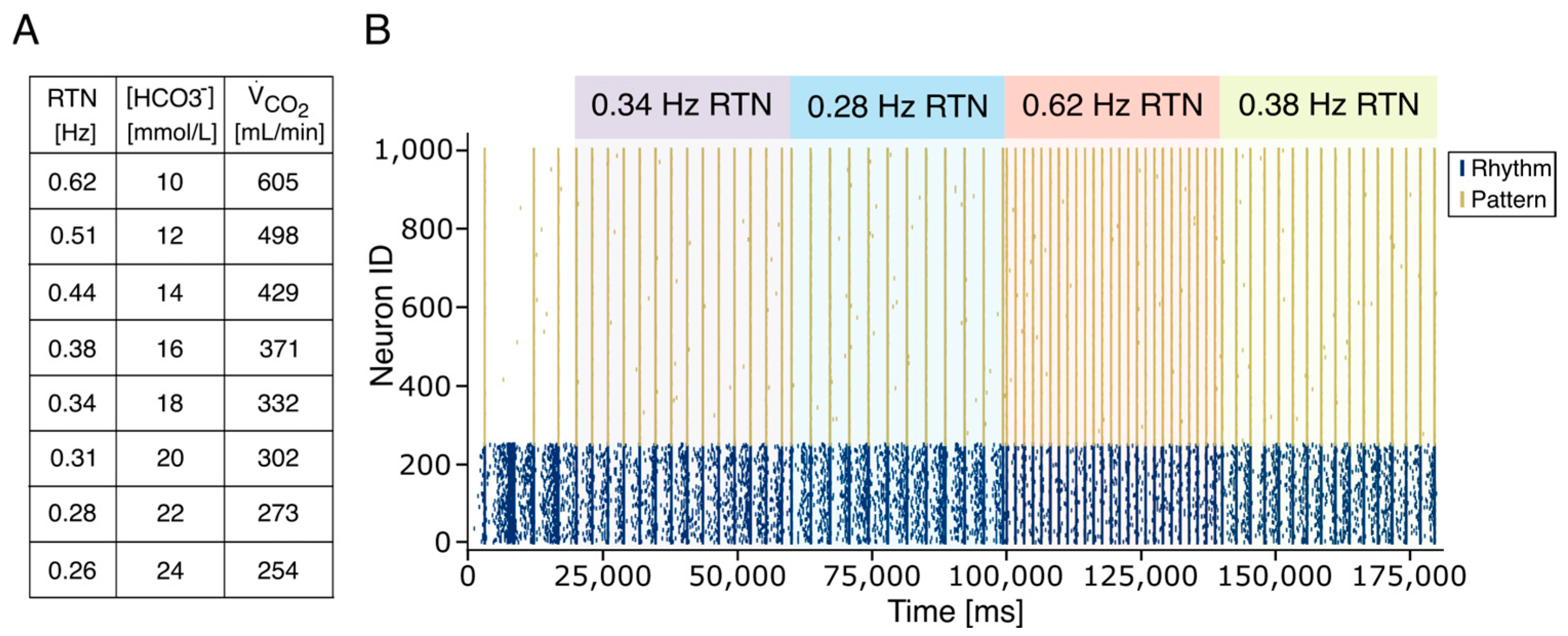
2.4. The Respiratory Rate Model
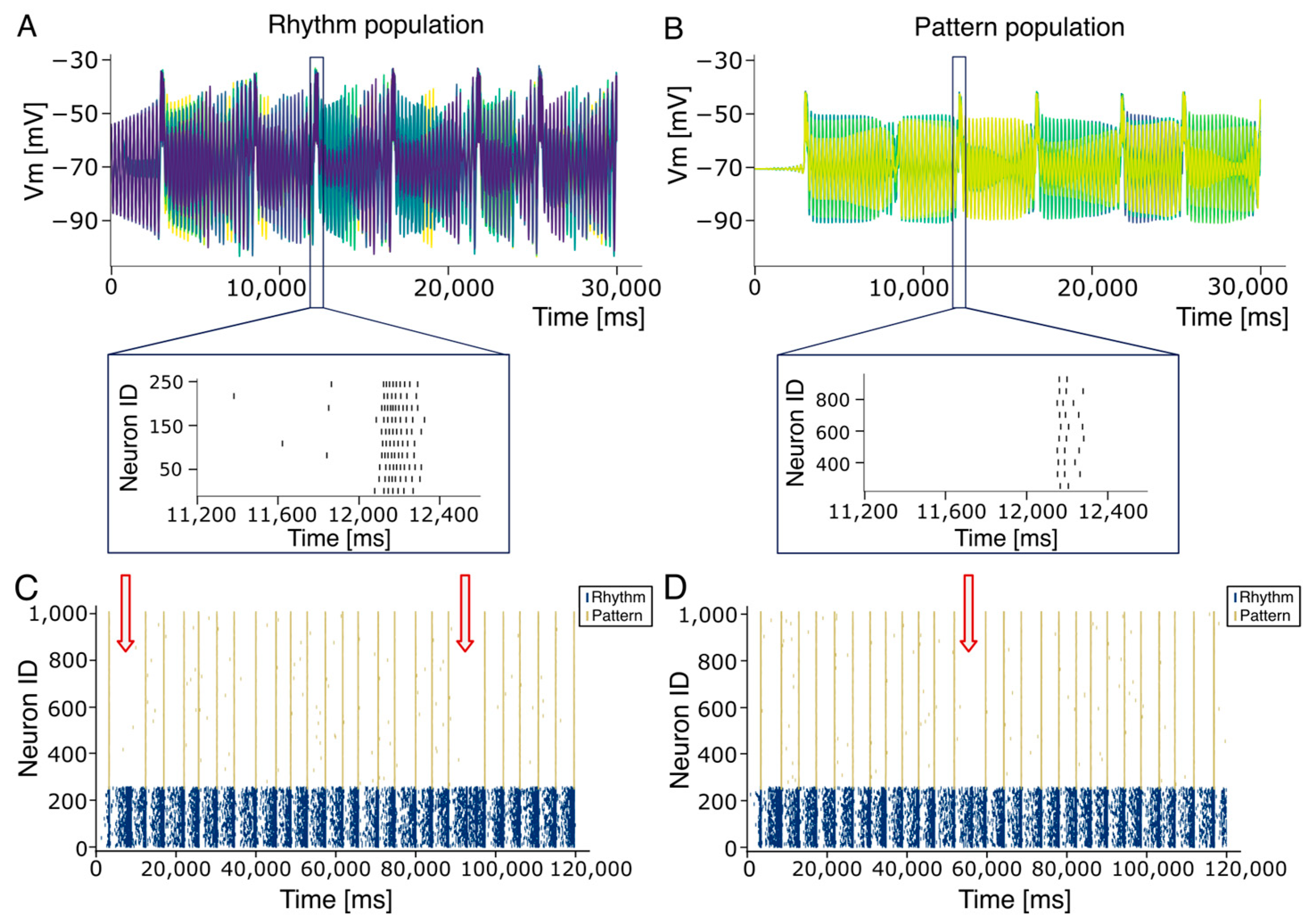
2.5. Burstlet–Burst Analysis
2.6. Interburst Variability
2.7. Network Performance
2.8. Real-Time Application for Artificial Breathing
2.9. Statistical Analysis
2.10. Data and Code Availability
3. Results
4. Discussion
4.1. Modeling the Respiratory CPG
4.2. Closed-Loop Control of Artificial Respiration
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Marder, E.; Bucher, D. Central pattern generators and the control of rhythmic movements. Curr. Biol. 2001, 11, R986–R996. [Google Scholar] [CrossRef]
- Ramirez, J.M. The human pre-botzinger complex identified. Brain 2011, 134, 8–10. [Google Scholar] [CrossRef] [PubMed]
- Huff, A.; Karlen-Amarante, M.; Pitts, T.; Ramirez, J.M. Optogenetic stimulation of pre–botzinger complex reveals novel circuit interactions in swallowing–breathing coordination. Proc. Nat. Acad. Sci. USA 2022, 119, e2121095119. [Google Scholar] [CrossRef]
- Shannon, R.; Baekey, D.; Morris, K.; Li, Z.; Lindsey, B. Functional connectivity among ventrolateral medullary respiratory neurones and responses during fictive cough in the cat. J. Physiol. 2000, 525, 207–224. [Google Scholar] [CrossRef] [PubMed]
- Marchenko, V.; Koizumi, H.; Mosher, B.; Koshiya, N.; Tariq, M.F.; Bezdudnaya, T.G.; Zhang, R.; Molkov, Y.I.; Rybak, I.A.; Smith, J.C. Perturbations of respiratory rhythm and pattern by disrupting synaptic inhibition within pre-botzinger and botzinger complexes. eNeuro 2016, 3. [Google Scholar] [CrossRef]
- Richerson, G.B. Response to CO2 of neurons in the rostral ventral medulla in vitro. J. Neurophysiol. 1995, 73, 933–944. [Google Scholar] [CrossRef] [PubMed]
- Krohn, F.; Novello, M.; van der Giessen, R.S.; De Zeeuw, C.I.; Pel, J.J.; Bosman, L.W. The integrated brain network that controls respiration. eLife 2023, 12, e83654. [Google Scholar] [CrossRef]
- Schwarzacher, S.W.; Rub, U.; Deller, T. Neuroanatomical characteristics of the human pre-botzinger complex and its involvement in neurodegenerative brainstem diseases. Brain 2011, 134, 24–35. [Google Scholar] [CrossRef]
- Sherman, D.; Worrell, J.W.; Cui, Y.; Feldman, J.L. Optogenetic perturbation of prebotzinger complex inhibitory neurons modulates respiratory pattern. Nat. Neurosci. 2015, 18, 408–414. [Google Scholar] [CrossRef]
- Smith, J.C.; Ellenberger, H.H.; Ballanyi, K.; Richter, D.W.; Feldman, J.L. Pre-botzinger complex: A brainstem region that may generate respiratory rhythm in mammals. Science 1991, 254, 726–729. [Google Scholar] [CrossRef]
- Gray, P.A.; Janczewski, W.A.; Mellen, N.; McCrimmon, D.R.; Feldman, J.L. Normal breathing requires prebotzinger complex neurokinin-1 receptor-expressing neurons. Nat. Neurosci. 2001, 4, 927–930. [Google Scholar] [CrossRef]
- Feldman, J.L.; Kam, K. Facing the challenge of mammalian neural microcircuits: Taking a few breaths may help. J. Physiol. 2015, 593, 3–23. [Google Scholar] [CrossRef] [PubMed]
- Del Negro, C.A.; Morgado-Valle, C.; Feldman, J.L. Respiratory rhythm: An emergent network property? Neuron 2002, 34, 821–830. [Google Scholar] [CrossRef]
- Cui, Y.; Kam, K.; Sherman, D.; Janczewski, W.A.; Zheng, Y.; Feldman, J.L. Defining prebotzinger complex rhythm-and pattern generating neural microcircuits in vivo. Neuron 2016, 91, 602–614. [Google Scholar] [CrossRef]
- Ashhad, S.; Feldman, J.L. Emergent elements of inspiratory rhythmogenesis: Network synchronization and synchrony propagation. Neuron 2020, 106, 482–497. [Google Scholar] [CrossRef] [PubMed]
- Picardo, M.C.D.; Weragalaarachchi, K.T.; Akins, V.T.; Del Negro, C.A. Physiological and morphological properties of dbx1-derived respiratory neurons in the pre-botzinger complex of neonatal mice. J. Physiol. 2013, 591, 2687–2703. [Google Scholar] [CrossRef] [PubMed]
- Lindsey, B.G.; Rybak, B.G.; Smith, J.C. Computational models and emergent properties of respiratory neural networks. Compr. Physiol. 2012, 2, 1619. [Google Scholar] [CrossRef]
- Chou, G.M.; Bush, N.E.; Phillips, R.S.; Baertsch, N.A.; Harris, K.D. Modeling effects of variable prebotzinger complex network topology and cellular properties on opioid-induced respiratory depression and recovery. eNeuro 2024, 11. [Google Scholar] [CrossRef]
- Phillips, R.S.; Baertsch, N.A. Interdependence of cellular and network properties in respiratory rhythm generation. Proc. Natl. Acad. Sci. USA 2024, 121, e2318757121. [Google Scholar] [CrossRef]
- Phillips, R.S.; Rubin, J.E. Putting the theory into ‘burstlet theory’ with a biophysical model of burstlets and bursts in the respiratory prebotzinger complex. eLife 2022, 11, e75713. [Google Scholar] [CrossRef]
- Bacak, B.J.; Kim, T.; Smith, J.C.; Rubin, J.E.; Rybak, I.A. Mixed mode oscillations and population bursting in the pre-botzinger complex. eLife 2016, 5, e13403. [Google Scholar] [CrossRef]
- Ashhad, S.; Slepukhin, V.M.; Feldman, J.L.; Levine, A.J. Microcircuit synchronization and heavy-tailed synaptic weight distribution augment prebotzinger complex bursting dynamics. J. Neurosci. 2023, 43, 240–260. [Google Scholar] [CrossRef]
- Butera, R.J., Jr.; Rinzel, J.; Smith, J.C. Models of respiratory rhythm generation in the pre-botzinger complex. i. bursting pacemaker neurons. J. Neurophysiol. 1999, 82, 382–397. [Google Scholar] [CrossRef]
- Del Negro, C.A.; Koshiya, N.; Butera, R.J., Jr.; Smith, J.C. Persistent sodium current, membrane properties and bursting behavior of pre-botzinger complex inspiratory neurons in vitro. J. Neurophysiol. 2002, 88, 2242–2250. [Google Scholar] [CrossRef]
- Mironov, S.L. Metabotropic glutamate receptors activate dendritic calcium waves and trpm channels which drive rhythmic respiratory patterns in mice. J. Physiol. 2008, 586, 2277–2291. [Google Scholar] [CrossRef] [PubMed]
- Kam, K.; Worrell, J.W.; Janczewski, W.A.; Cui, Y.; Feldman, J.L. Distinct inspiratory rhythm and pattern generating mechanisms in the prebotzinger complex. J. Neurosci. 2013, 33, 9235–9245. [Google Scholar] [CrossRef]
- Kallurkar, P.S.; Grover, C.; Picardo, M.C.D.; Del Negro, C.A. Evaluating the burstlet theory of inspiratory rhythm and pattern generation. eNeuro 2020, 7. [Google Scholar] [CrossRef] [PubMed]
- Rybak, I.A.; Molkov, Y.I.; Jasinski, P.E.; Shevtsova, N.A.; Smith, J.C. Rhythmic bursting in the pre-botzinger complex: Mechanisms and models. Progress Brain Res. 2014, 209, 1–23. [Google Scholar] [CrossRef]
- Jones, S.E.; Stanic, D.; Dutschmann, M. Dorsal and ventral aspects’ of the most caudal medullary reticular formation have differential roles in modulation and formation of the respiratory motor pattern in rat. Brain Struct. Funct. 2016, 221, 4353–4368. [Google Scholar] [CrossRef]
- Bianchi, A.; Grelot, L.; Iscoe, S.; Remmers, J. Electrophysiological’ properties of rostral medullary respiratory neurones in the cat: An intracellular study. J. Physiol. 1988, 407, 293–310. [Google Scholar] [CrossRef]
- Ott, M.M.; Nuding, S.C.; Segers, L.S.; O’Connor, R.; Morris, K.F.; Lindsey, B.G. Central chemoreceptor modulation of breathing via multipath tuning in medullary ventrolateral respiratory column circuits. J. Neurophysiol. 2012, 107, 603–617. [Google Scholar] [CrossRef]
- Smith, J.C.; Abdala, A.P.; Borgmann, A.; Rybak, I.A.; Paton, J.F. Brainstem respiratory networks: Building blocks and microcircuits. Trends Neurosci. 2013, 36, 152–162. [Google Scholar] [CrossRef]
- Moreira, T.S.; Sobrinho, C.R.; Falquetto, B.; Oliveira, L.M.; Lima, J.D.; Mulkey, D.K.; Takakura, A.C. The retrotrapezoid nucleus and the neuromodulation of breathing. J. Neurophysiol. 2021, 125, 699–719. [Google Scholar] [CrossRef]
- Pena, F.; Parkis, M.A.; Tryba, A.K.; Ramirez, J.-M. Differential contribution of pacemaker properties to the generation of respiratory rhythms during normoxia and hypoxia. Neuron 2004, 43, 105–117. [Google Scholar] [CrossRef]
- Kawai, A.; Onimaru, H.; Homma, I. Mechanisms of CO2/h+ chemoreception by respiratory rhythm generator neurons in the medulla from newborn rats in vitro. J. Physiol. 2006, 572, 525–537. [Google Scholar] [CrossRef]
- Guyenet, P.G.; Bayliss, D.A.; Stornetta, R.L.; Ludwig, M.-G.; Kumar, N.N.; Shi, Y.; Burke, P.G.; Kanbar, R.; Basting, T.M.; Holloway, B.B.; et al. Proton detection and breathing regulation by the retrotrapezoid nucleus J. Physiol. 2016, 594, 1529–1551. [Google Scholar] [CrossRef] [PubMed]
- Marhong, J.D.; Telesnicki, T.; Munshi, L.; Del Sorbo, L.; Detsky, M.; Fan, E. Mechanical ventilation during extracorporeal membrane oxygenation. an international survey. Ann. Am. Thorac. Soc. 2014, 11, 956–961. [Google Scholar] [CrossRef]
- Zhang, Z.; Gu, W.-J.; Chen, M.K.; Ni, H. Mechanical ventilation during extracorporeal membrane oxygenation in patients with acute severe respiratory failure. Can. Respir. J. 2017, 2017, 1783857. [Google Scholar] [CrossRef] [PubMed]
- Rehder, K.J.; Alibrahim, O.S. Mechanical ventilation during ecmo: Best practices Respir. Care 2023, 68, 838–845. [Google Scholar] [CrossRef] [PubMed]
- Perricone, F.; Tartarini, L.; De Toni, L.; Rovati, L.; Mapelli, J.; Gandolfi, D. The road toward a physiological control of artificial respiration: The role of bio-inspired neuronal networks. Front. Neurosci. 2025, 19, 1638547. [Google Scholar] [CrossRef]
- Cattini, S.; Accorsi, L.; Truzzi, S.; Ferrari, A.; Rovati, L. A preliminary investigation of the robustness of a measuring instrument for blood-pCO2 measurement during ECC. In Proceedings of the 2021 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Glasgow, UK, 17–20 May 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Cattini, S.; Accorsi, L.; Truzzi, S.; Rovati, L. On the development of an instrument for in-line and real-time monitoring of blood-pH in extracorporeal-circulation. IEEE Trans. Instrum. Meas. 2020, 69, 5640–5648. [Google Scholar] [CrossRef]
- Guglielmini, S.; Wiggli, E.; Scholkmann, F.; Wolf, M. Hemodynamics and vascular oxygenation measured at the forehead during changes in respiration: A SPA-fNIRS study. Respir. Physiol. Neurobiol. 2025, 331, 104364. [Google Scholar] [CrossRef] [PubMed]
- Hariharan, S.; Karnan, H.; Maheswari, D.U. Automated mechanical ventilator design and analysis using neural network. Sci. Rep. 2025, 15, 3212. [Google Scholar] [CrossRef] [PubMed]
- Avital, N.; Shulkin, N.; Malka, D. Automatic Calculation of Average Power in Electroencephalography Signals for Enhanced Detection of Brain Activity and Behavioral Patterns. Biosensors 2025, 15, 314. [Google Scholar] [CrossRef] [PubMed]
- Rabinovitch, A.; Baruch, E.B.; Siton, M.; Avital, N.; Yeari, M.; Malka, D. Efficient Detection of Mind Wandering During Reading Aloud Using Blinks, Pitch Frequency, and Reading Rate. AI 2025, 6, 83. [Google Scholar] [CrossRef]
- Edelman, B.J.; Zhang, S.; Schalk, G.; Brunner, P.; Muller-Putz, G.; Guan, C.; He, B. Non-Invasive Brain-Computer Interfaces: State of the Art and Trends. IEEE Rev. Biomed. Eng. 2025, 18, 26–49. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Geminiani, A.; Casellato, C.; Locatelli, F.; Prestori, F.; Pedrocchi, A.; D’Angelo, E. Complex dynamics in simplified neuronal models: Reproducing golgi cell electroresponsiveness. Front Neuroinform. 2018, 12, 88. [Google Scholar] [CrossRef]
- Linssen, C.; Babu, P.N.; Eppler, J.M.; Koll, L.; Rumpe, B.; Morrison, A.D. NESTML: A generic modeling language and code generation tool for the simulation of spiking neural networks with advanced plasticity rules. Front Neuroinform. 2025, 19, 1544143. [Google Scholar] [CrossRef]
- Pozzorini, C.; Mensi, S.; Hagens, O.; Naud, R.; Koch, C.; Gerstner, W. Automated high-throughput characterization of single neurons by means of simplified spiking models. PLoS Comput. Biol. 2015, 11, e1004275. [Google Scholar] [CrossRef]
- Mihalas, S.; Niebur, E. A generalized linear integrate-and-fire neural model produces diverse spiking behaviors. Neural Comput. 2009, 21, 704–718. [Google Scholar] [CrossRef]
- Gewaltig, M.O.; Diesmann, M. Nest (neural simulation tool). Scholarpedia 2007, 2, 1430. [Google Scholar] [CrossRef]
- Eppler, J.M.; Helias, M.; Muller, E.; Diesmann, M.; Gewaltig, M.-O. Pynest: A convenient interface to the nest simulator. Front. Neuroinform. 2009, 2, 363. [Google Scholar] [CrossRef]
- Guyton, A.C.; Hall, J.E. Textbook of Medical Physiology, 11th ed.; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Guyenet, P.G.; Stornetta, R.L.; Bayliss, D.A. Retrotrapezoid nucleus and central chemoreception. J. Physiol. 2008, 586, 2043–2048. [Google Scholar] [CrossRef]
- Vieth, M.; Rahimi, A.; Gorgan Mohammadi, A.; Triesch, J.; Ganjtabesh, M. Accelerating spiking neural network simulations with PymoNNto and PymoNNtorch. Front. Neuroinform. 2024, 18, 1331220. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Michaelis, C.; Lehr, A.B.; Oed, W.; Tetzlaff, C. Brian2Loihi: An emulator for the neuromorphic chip Loihi using the spiking neural network simulator Brian. Front. Neuroinform. 2022, 16, 1015624. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Richter, O.; Wu, C.; Whatley, A.M.; Köstinger, G.; Nielsen, C.; Qiao, N.; Indiveri, G. DYNAP-SE2: A scalable multi-core dynamic neuromorphic asynchronous spiking neural network processor. Neuromorphic Comput. Eng. 2024, 4, 014003. [Google Scholar] [CrossRef]
- Lutes, N.A.; Sriram Siddhardh Nadendla, V.; Krishnamurthy, K. Few-shot transfer learning for individualized braking intent detection on neuromorphic hardware. J. Neural Eng. 2025, 22, 016041. [Google Scholar] [CrossRef] [PubMed]
- Florini, D.; Gandolfi, D.; Mapelli, J.; Benatti, L.; Pavan, P.; Puglisi, F.M. A Hybrid CMOS-Memristor Spiking Neural Network Supporting Multiple Learning Rules. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 5117–5129. [Google Scholar] [CrossRef]
- Benatti, L.; Zanotti, T.; Gandolfi, D.; Mapelli, J.; Puglisi, F.M. Biologically Plausible Information Propagation in a CMOS Integrate-and-Fire Artificial Neuron Circuit with Memristive Synapses. Nano Futures 2023, 7, 025003. [Google Scholar] [CrossRef]
- Cattini, S.; Truzzi, S.; Accorsi, L.; Rovati, L. A measuring instrument for in-line and real-time measurement of blood-pco 2 in extracorporeal-circulation. IEEE Trans. Instrum. Meas. 2020, 70, 4000809. [Google Scholar] [CrossRef]
- Duffin, J.; Mohan, R.M.; Vasiliou, P.; Stephenson, R.; Mahamed, S. A model of the chemoreflex control of breathing in humans: Model parameters measurement. Respir. Physiol. 2020, 120, 13–26. [Google Scholar] [CrossRef] [PubMed]
- Rekling, J.C.; Shao, X.M.; Feldman, J.L. Electrical coupling and excitatory synaptic transmission between rhythmogenic respiratory neurons in the prebotzinger complex. J. Neurosci. 2000, 20, RC113. [Google Scholar] [CrossRef]
- Carroll, M.S.; Ramirez, J.-M. Cycle-by-cycle assembly of respiratory network activity is dynamic and stochastic. J. Neurophysiol. 2013, 109, 296–305. [Google Scholar] [CrossRef]
- Ashhad, S.; Kam, K.; Del Negro, C.A.; Feldman, J.L. Breathing rhythm and pattern and their influence on emotion. Annu. Rev. Neurosci. 2022, 45, 223–247. [Google Scholar] [CrossRef]
- Mulkey, D.K.; Stornetta, R.L.; Weston, M.C.; Simmons, J.R.; Parker, A.; Bayliss, D.A.; Guyenet, P.G. Respiratory control by ventral surface chemoreceptor neurons in rats. Nat. Neurosci. 2005, 7, 1360–1369. [Google Scholar] [CrossRef]
- Souza, G.M.; Kanbar, R.; Stornetta, D.S.; Abbott, S.B.; Stornetta, R.L.; Guyenet, P.G. Breathing regulation and blood gas homeostasis after near complete lesions of the retrotrapezoid nucleus in adult rats. J. Physiol. 2018, 596, 2521–2545. [Google Scholar] [CrossRef]
- Guyenet, P.G.; Mulkey, D.K.; Stornetta, R.L.; Bayliss, D.A. Regulation of ventral surface chemoreceptors by the central respiratory pattern generator. J. Neurosci. 2005, 25, 8938–8947. [Google Scholar] [CrossRef]
- Shao, X.M.; Feldman, J.L. Mechanisms underlying regulation of respiratory pattern by nicotine in preBötzinger complex. J. Neurophysiol. 2001, 85, 2461–2467. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Burgraff, N.J.; Phillips, R.S.; Severs, L.J.; Bush, N.E.; Baertsch, N.A.; Ramirez, J.M. Inspiratory rhythm generation is stabilized by Ih. J. Neurophysiol. 2022, 128, 181–196. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Yuan, G.; Drost, N.A.; McIvor, R.A. Respiratory rate and breathing pattern. McMaster Univ. Med. J. 2013, 10, 23–25. [Google Scholar]
- Gandolfi, D.; Boiani, G.M.; Bigiani, A.; Mapelli, J. Modeling neurotransmission: Computational tools to investigate neurological disorders. Int. J. Mol. Sci. 2021, 22, 4565. [Google Scholar] [CrossRef] [PubMed]
- Gandolfi, D.; Mapelli, J.; Solinas, S.; De Schepper, R.; Geminiani, A.; Casellato, C.; D’Angelo, E.; Migliore, M. A realistic morphoanatomical connection strategy for modelling full-scale point-neuron microcircuits. Sci. Rep. 2022, 12, 13864. [Google Scholar] [CrossRef]
- Mapelli, J.; Gandolfi, D.; Giuliani, E.; Casali, S.; Congi, L.; Barbieri, A.; D’Angelo, E.; Bigiani, A. The effects of the general anesthetic sevoflurane on neurotransmission: An experimental and computational study. Sci. Rep. 2021, 11, 4335. [Google Scholar] [CrossRef]
- Gandolfi, D.; Mapelli, J.; Solinas, S.M.; Triebkorn, P.; D’Angelo, E.; Jirsa, V.; Migliore, M. Full-scale scaffold model of the human hippocampus ca1 area. Nat. Comput. Sci. 2023, 3, 264–276. [Google Scholar] [CrossRef] [PubMed]
- Mapelli, J.; Gandolfi, D.; Giuliani, D.; Prencipe, F.P.; Pellati, F.; Barbieri, A.; D’Angelo, E.; Bigiani, A. The effect of desflurane on neuronal communication at a central synapse. PLoS ONE 2015, 10, e0123534. [Google Scholar] [CrossRef]
- Del Negro, C.A.; Funk, G.D.; Feldman, J.L. Breathing matters. Nat. Rev. Neurosci. 2018, 19, 351–367. [Google Scholar] [CrossRef] [PubMed]
- Rubin, J.E.; Hayes, J.A.; Mendenhall, J.L.; Del Negro, C.A. Calcium-activated nonspecific cation current and synaptic depression promote network-dependent burst oscillations. Proc. Natl. Acad. Sci. USA 2009, 106, 2939–2944. [Google Scholar] [CrossRef]
- Phillips, R.S.; John, T.T.; Koizumi, H.; Molkov, Y.I.; Smith, J.C. Biophysical mechanisms in the mammalian respiratory oscillator reexamined with a new data-driven computational model. eLife 2019, 8, e41555. [Google Scholar] [CrossRef]
- Kam, K.; Worrell, J.W.; Ventalon, C.; Emiliani, V.; Feldman, J.L. Emergence of population bursts from simultaneous activation of small subsets of prebotzinger complex inspiratory neurons. J. Neurosci. 2013, 33, 3332–3338. [Google Scholar] [CrossRef]
- Janczewski, W.A.; Tashima, A.; Hsu, P.; Cui, Y.; Feldman, J.L. Role of inhibition in respiratory pattern generation. J. Neurosci. 2013, 33, 5454–5465. [Google Scholar] [CrossRef]
- Ghali, M.G.Z. Respiratory rhythm generation and pattern formation: Oscillators and network mechanisms. J. Integr. Neurosci. 2019, 18, 481–517. [Google Scholar] [CrossRef]
- Baertsch, N.A.; Baertsch, H.C.; Ramirez, J.M. The interdependence of excitation and inhibition for the control of dynamic breathing rhythms. Nat. Commun. 2018, 9, 843. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Harris, K.D.; Dashevskiy, T.; Mendoza, J.; Garcia, A.J., 3rd; Ramirez, J.M.; Shea-Brown, E. Different roles for inhibition in the rhythm-generating respiratory network. J. Neurophysiol. 2017, 118, 2070–2088. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Pouille, F.; Scanziani, M. Enforcement of temporal fidelity in pyramidal cells by somatic feed-forward inhibition. Science 2001, 293, 1159–1163. [Google Scholar] [CrossRef] [PubMed]
- Mapelli, J.; Gandolfi, D.; D’Angelo, E. Combinatorial responses controlled by synaptic inhibition in the cerebellum granular layer. J. Neurophysiol. 2010, 103, 250–261. [Google Scholar] [CrossRef] [PubMed]
- D’Angelo, E.; Solinas, S.; Mapelli, J.; Gandolfi, D.; Mapelli, L.; Prestori, F. The cerebellar golgi cell and spatiotemporal organization of granular layer activity. Front. Neural Circuits 2013, 7, 93. [Google Scholar] [CrossRef] [PubMed]
- Mapelli, J.; Gandolfi, D.; D’Angelo, E. High-pass filtering and dynamic gain regulation enhance vertical bursts transmission along the mossy fiber pathway of cerebellum. Front. Cell. Neurosci. 2010, 4, 926. [Google Scholar] [CrossRef]
- Jager, P.; Ye, A.; Yu, X.; Zagoraiou, L.; Prekop, H.-T.; Partanen, J.; Jessell, T.M.; Wisden, W.; Brickley, S.G.; Delogu, A. Tectal-derived interneurons contribute to phasic and tonic inhibition in the visual thalamus. Nat. Commun. 2016, 7, 13579. [Google Scholar] [CrossRef]
- Headley, D.B.; Latimer, B.; Aberbach, A.; Nair, S.S. Spatially targeted inhibitory rhythms differentially affect neuronal integration. eLife 2024, 13, RP95562. [Google Scholar] [CrossRef]
- Gandolfi, D.; Benatti, L.; Zanotti, T.; Boiani, G.M.; Bigiani, A.; Puglisi, F.M.; Mapelli, J. Information transfer in neuronal circuits: From biological neurons to neuromorphic electronics. Intell. Comput. 2024, 3, 0059. [Google Scholar] [CrossRef]
- Molkov, Y.I.; Rubin, J.E.; Rybak, I.A.; Smith, J.C. Computational models of the neural control of breathing. Wiley Interdiscip. Rev. Syst. Biol. Med. 2017, 9, e1371. [Google Scholar] [CrossRef]
- Levy, J.; Facchinetti, P.; Jan, C.; Achour, M.; Bouvier, C.; Brunet, J.-F.; Delzescaux, T.; Giuliano, F. Tridimensional mapping of phox2b expressing neurons in the brainstem of adult macaca fascicularis and identification of the retrotrapezoid nucleus. J. Comp. Neurol. 2019, 527, 2875–2884. [Google Scholar] [CrossRef]
- Lavezzi, A.M.; Weese-Mayer, D.E.; Margaret, Y.Y.; Jennings, L.J.; Corna, M.F.; Casale, V.; Oneda, R.; Matturri, L. Developmental alterations of the respiratory human retrotrapezoid nucleus in sudden unexplained fetal and infant death. Auton. Neurosci. 2012, 170, 12–19. [Google Scholar] [CrossRef]
- Rudzinski, E.; Kapur, R.P. Phox2b immunolocalization of the candidate human retrotrapezoid nucleus. Pediatr. Dev. Pathol. 2010, 13, 291–299. [Google Scholar] [CrossRef]
- Levy, J.; Droz-Bartholet, F.; Achour, M.; Facchinetti, P.; Parratte, B.; Giuliano, F. Parafacial neurons in the human brainstem express specific markers for neurons of the retrotrapezoid nucleus. J. Comp. Neurol. 2021, 529, 3313–3320. [Google Scholar] [CrossRef] [PubMed]
- Ruffault, P.-L.; D’Autreaux, F.; Hayes, J.A.; Nomaksteinsky, M.; Autran, S.; Fujiyama, T.; Hoshino, M.; Hagglund, M.; Kiehn, O.; Brunet, J.-F.; et al. The retrotrapezoid nucleus neurons expressing atoh1 and phox2b are essential for the respiratory response to CO2. eLife 2015, 4, e07051. [Google Scholar] [CrossRef]
- Abbott, S.B.; Stornetta, R.L.; Fortuna, M.G.; Depuy, S.D.; West, G.H.; Harris, T.E.; Guyenet, P.G. Photostimulation of retrotrapezoid nucleus phox2b-expressing neurons in vivo produces long-lasting activation of breathing in rats. J. Neurosci. 2009, 29, 5806–5819. [Google Scholar] [CrossRef] [PubMed]
- Pham, T.; Heunks, L.; Bellani, G.; Madotto, F.; Aragao, I.; Beduneau, G.; Goligher, E.C.; Grasselli, G.; Laake, J.H.; Mancebo, J.; et al. Weaning from mechanical ventilation in intensive care units across 50 countries (WEAN SAFE): A multicentre, prospective, observational cohort study. Lancet Respir. Med. 2023, 11, 465–476. [Google Scholar] [CrossRef] [PubMed]
- Siu, R.; Abbas, J.J.; Fuller, D.D.; Gomes, J.; Renaud, S.; Jung, R. Autonomous control of ventilation through closed-loop adaptive respiratory pacing. Sci. Rep. 2020, 10, 21903. [Google Scholar] [CrossRef]
- Zbrzeski, A.; Bornat, Y.; Hillen, B.; Siu, R.; Abbas, J.; Jung, R.; Renaud, S. Bio-Inspired Controller on an FPGA Applied to Closed-Loop Diaphragmatic Stimulation. Front. Neurosci. 2016, 10, 275. [Google Scholar] [CrossRef]
- Donati, E.; Corradi, F.; Stefanini, C.; Indiveri, G. A spiking implementation of the lamprey’s Central Pattern Generator in neuromorphic VLSI. In Proceedings of the 2014 IEEE Biomedical Circuits and Systems Conference (BioCAS), Lausanne, Switzerland, 22–24 October 2014; pp. 512–515. [Google Scholar] [CrossRef]
- Gutierrez-Galan, D.; Dominguez-Morales, J.P.; Perez-Peña, F.; Jimenez-Fernandez, A.; Linares-Barranco, A. Neuropod: A real-time neuromorphic spiking CPG applied to robotics. Neurocomputing 2020, 381, 10–19. [Google Scholar] [CrossRef]
- Dupeyroux, J.; Hagenaars, J.J.; Paredes-Vallés, F.; de Croon, G.C.H.E. Neuromorphic control for optic-flow-based landing of MAVs using the Loihi processor. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 96–102. [Google Scholar] [CrossRef]
- Krause, R.; van Bavel, J.J.A.; Wu, C.; Vos, M.A.; Nogaret, A.; Indiveri, G. Robust neuromorphic coupled oscillators for adaptive pacemakers. Sci. Rep. 2021, 11, 18073. [Google Scholar] [CrossRef] [PubMed]
- Donati, E.; Krause, R.; Indiveri, G. Neuromorphic Pattern Generation Circuits for Bioelectronic Medicine. In Proceedings of the 10th International IEEE/EMBS Conference on Neural Engineering (NER), Virtual Event, 4–6 May 2021; pp. 1117–1120. [Google Scholar] [CrossRef]
- Abu-Hassan, K.; Taylor, J.D.; Morris, P.G.; Donati, E.; Bortolotto, Z.A.; Indiveri, G.; Paton, J.F.R.; Nogaret, A. Optimal solid state neurons. Nat. Commun. 2019, 10, 5309. [Google Scholar] [CrossRef] [PubMed]
- Dutta, S.; Kumar, V.; Shukla, A.; Mohapatra, N.R.; Ganguly, U. Leaky Integrate and Fire Neuron by Charge-Discharge Dynamics in Floating-Body MOSFET. Sci. Rep. 2017, 7, 8257. [Google Scholar] [CrossRef]
- Heidarpour, M.; Ahmadi, A.; Rashidzadeh, R. A CORDIC Based Digital Hardware For Adaptive Exponential Integrate and Fire Neuron. IEEE Trans. Circuits Syst. I Regul. Pap. 2016, 63, 1986–1996. [Google Scholar] [CrossRef]

| Vm (mV) | τm | λ0 (ms−1) | K2 (ms−1) | Kadap (MH−1) | K2 (ms−1) | A2 (pA) | tref (ms) | |
|---|---|---|---|---|---|---|---|---|
| Rhythm | −60 | 1.7 | 0.0001 | 0.0331 | 0.53 | 0.007 | 5.0 | 2.0 |
| Pattern | −70.6 | 0.9 | 0.0001 | 0.0333 | 0.53 | 0.007 | 5.0 | 2.0 |
| Target | |||
|---|---|---|---|
| Rhythm | Pattern | ||
| Source | Rhythm | (13%, 9.4) | (30%, 1.0) |
| Pattern | (30%, 0.1) | (2%, 0.5) | |
| RTN | (17%, 2.9) | none | |
| Parameter | Physiological Value | —Variation [250–620] mL/min | [HCO3−] Variation [10–24] mmol/L |
|---|---|---|---|
| pH | 7.4 | 7.4 | 7.4 |
| [HCO3−] (mmol/L) | 24 | 24 | [10–24] |
| PaCO2 (mmHg) | 40.1 | 40.1 | [16.71–40.1] |
| mL/min) | 250 | [250–620] | 250 |
| (L/min) | 5.38 | [5.38–13.3] | [12.91–5.38] |
| VA (L) | 0.35 | 0.35 | 0.35 |
| Bpm (1/min) | 15.4 | [15.4–38.1] | [36.9–15.4] |
| Interval (ms) | 3903 | [3903–1574] | [1626–3903] |
| RTN frequency (Hz) | 0.26 | [0.26–0.64] | [0.61–0.26] |
| Experimental Data | Model Output | PaCO2 Range | |
|---|---|---|---|
| Respiratory Rate | (12–35) bpm | (13–40) bpm | all data |
| Chemoreflex slope (ΔRR/ΔPaCO2) | 0.7 bpm/mmHg | 0.7 bpm/mmHg | (44.3–52.2) bpm/mmHg |
| Chemoreflex slope (ΔRR/ΔPaCO2) | 1.5 bpm/mmHg | 1.5 bpm/mmHg | (52.2–61) bpm/mmHg |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Toni, L.; Perricone, F.; Tartarini, L.; Boiani, G.M.; Cattini, S.; Rovati, L.; Rodarie, D.; D’Angelo, E.; Mapelli, J.; Gandolfi, D. A Computational Model of the Respiratory CPG for the Artificial Control of Breathing. Bioengineering 2025, 12, 1163. https://doi.org/10.3390/bioengineering12111163
De Toni L, Perricone F, Tartarini L, Boiani GM, Cattini S, Rovati L, Rodarie D, D’Angelo E, Mapelli J, Gandolfi D. A Computational Model of the Respiratory CPG for the Artificial Control of Breathing. Bioengineering. 2025; 12(11):1163. https://doi.org/10.3390/bioengineering12111163
Chicago/Turabian StyleDe Toni, Lorenzo, Federica Perricone, Lorenzo Tartarini, Giulia Maria Boiani, Stefano Cattini, Luigi Rovati, Dimitri Rodarie, Egidio D’Angelo, Jonathan Mapelli, and Daniela Gandolfi. 2025. "A Computational Model of the Respiratory CPG for the Artificial Control of Breathing" Bioengineering 12, no. 11: 1163. https://doi.org/10.3390/bioengineering12111163
APA StyleDe Toni, L., Perricone, F., Tartarini, L., Boiani, G. M., Cattini, S., Rovati, L., Rodarie, D., D’Angelo, E., Mapelli, J., & Gandolfi, D. (2025). A Computational Model of the Respiratory CPG for the Artificial Control of Breathing. Bioengineering, 12(11), 1163. https://doi.org/10.3390/bioengineering12111163









