A New Breast Cancer Discovery Strategy: A Combined Outlier Rejection Technique and an Ensemble Classification Method
Abstract
:1. Introduction
2. Related Works
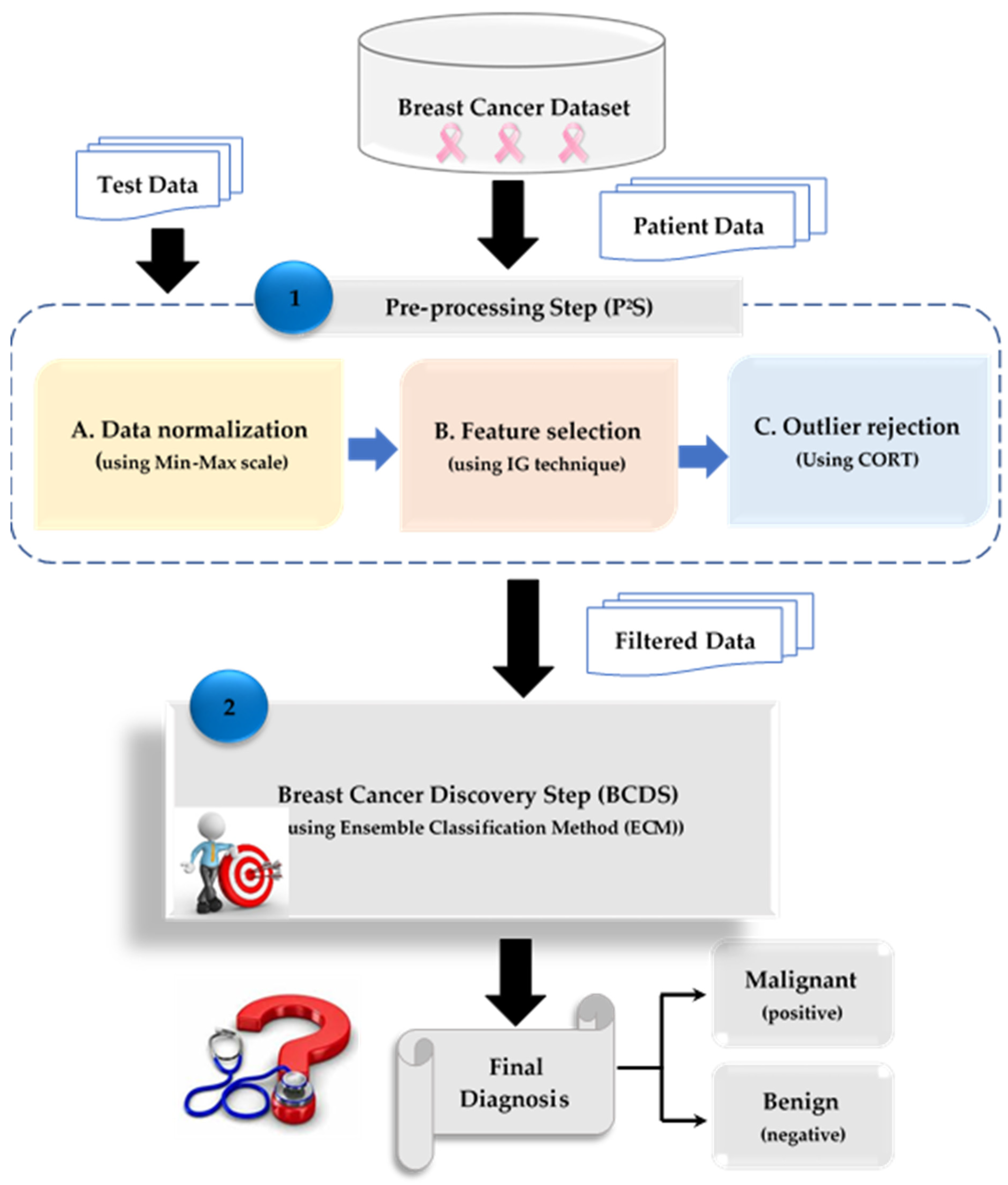
3. The Proposed Breast Cancer Discovery (BCD) Strategy
3.1. The Proposed Combined Outlier Rejection Technique (CORT)
- Initialization stage
- Exploration stage
- Exploration to exploitation
- Exploitation stage
| Algorithm 1: Combined Outlier Rejection Technique (CORT) |
| Input: ; input training dataset of ‘’ items expressed by in which each item is expressed as an ordered set of features; , ; Testing dataset. Input target classes expressed by the set : Maximum iterations, : population size; Output: Optimal Solution Steps: //Implement Quick Rejection Phase (QRP)// 1. eliminate outliers using standard deviation method to obtain valid training data, . //Implement Accurate Rejection Phase (ARP)// 2. Generate the initial position for hawks X 3. Evaluate the fitness of initial position 4. Set fitness value of 5. 6. 7. Update escape energy via (3) 8. if (|G| 1) then 9. Update the position via (1) 10. Determine the likelihood via sigmoid transfer function 11. Update new position of the hawk using (21) 12. if (|G| 1) then 13. if (|G| ≥ 0.5 and ) then 14. Update position via (4) 15. Determine the likelihood via sigmoid transfer function 16. Update new position of the hawk using (21) 17. else if (|G| 0.5 and ≥ ) then 18. Update position via (7) 19. Determine the likelihood via sigmoid transfer function 20. Update new position of the hawk using (21) 21. else if (|G| ≥ 0.5 and ) then 22. Update position via (12) 23. Determine the likelihood via sigmoid transfer function 24. Update new position of the hawk using (21) 25. else if (|G| 0.5 and ) then 26. Update position via (13) 27. Determine the likelihood via sigmoid transfer function 28. Update new position of the hawk using (21) 29. Compute the fitness of the updated population and then update the value 30. End for 31. End t 32. Select the optimal solution |
3.2. Breast Cancer Discovery Step (BCDS)
4. Experimental Results
4.1. Description of the BCD Dataset
4.2. Testing the Combined Outlier Rejection Technique (CORT)
4.3. Testing the Breast Cancer Discovery (BCD) Strategy
5. Discussion
6. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sung, H.; Ferlay, J.; Siegel, R.L.; Laversanne, M.; Soerjomataram, I.; Jemal, A.; Bray, F. Global cancer statistics 2020: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J. Clin. 2021, 71, 209–249. [Google Scholar] [CrossRef] [PubMed]
- The American Cancer Society. Breast Cancer Statistics|How Common Is Breast Cancer? Available online: https://www.cancer.org/cancer/types/breast-cancer/about/how-common-is-breast-cancer.html (accessed on 2 December 2023).
- Patil, S.; Kirange, D.; Nemade, V. Predictive modelling of brain tumor detection using deep learning. J. Crit. Rev. 2020, 7, 1805–1813. [Google Scholar]
- Barrios, C.H. Global challenges in breast cancer detection and treatment. Breast 2022, 62, 53–56. [Google Scholar] [CrossRef] [PubMed]
- Derevianko, A.; Pizzoli, S.F.M.; Pesapane, F.; Rotili, A.; Monzani, D.; Grasso, R.; Cassano, E.; Pravettoni, G. The Use of Artificial Intelligence (AI) in the Radiology Field: What Is the State of Doctor–Patient Communication in Cancer Diagnosis? Cancers 2023, 15, 470. [Google Scholar] [CrossRef] [PubMed]
- Alnaggar OA, M.F.; Jagadale, B.N.; Saif MA, N.; Ghaleb, O.A.; Ahmed, A.A.; Aqlan HA, A.; Al-Ariki HD, E. Efficient artificial intelligence approaches for medical image processing in healthcare: Comprehensive review, taxonomy, and analysis. Artif. Intell. Rev. 2024, 57, 221. [Google Scholar] [CrossRef]
- Ahn, J.S.; Shin, S.; Yang, S.A.; Park, E.K.; Kim, K.H.; Cho, S.I.; Ock, C.Y.; Kim, S. Artificial Intelligence in Breast Cancer Diagnosis and Personalized Medicine. J. Breast Cancer 2023, 26, 405–435. [Google Scholar] [CrossRef]
- Van Nijnatten TJ, A.; Payne, N.R.; Hickman, S.E.; Ashrafian, H.; Gilbert, F.J. Overview of trials on artificial intelligence algorithms in breast cancer screening—A roadmap for international evaluation and implementation. Eur. J. Radiol. 2023, 167, 111087. [Google Scholar] [CrossRef]
- Ali, S.H. An Innovative COVID-19 Patient Recognition Framework. Mansoura Eng. J. 2024, 49, 18. [Google Scholar] [CrossRef]
- Sarker, I.H. Machine Learning: Algorithms, Real-World Applications and Research Directions. SN Comput. Sci. 2021, 2, 160. [Google Scholar] [CrossRef]
- Abuassba, A.O.M.; Dezheng, Z.; Ali, H.; Zhang, F.; Ali, K. Classification with ensembles and case study on functional magnetic resonance imaging. Digit. Commun. Netw. 2022, 8, 80–86. [Google Scholar] [CrossRef]
- Feng, W.; Gou, J.; Fan, Z.; Chen, X. An ensemble machine learning approach for classification tasks using feature generation. Connect. Sci. 2023, 35, 2231168. [Google Scholar] [CrossRef]
- Silva Araújo, V.J.; Guimarães, A.J.; de Campos Souza, P.V.; Rezende, T.S.; Araújo, V.S. Using Resistin, Glucose, Age and BMI and Pruning Fuzzy Neural Network for the Construction of Expert Systems in the Prediction of Breast Cancer. Mach. Learn. Knowl. Extr. 2019, 1, 466–482. [Google Scholar] [CrossRef]
- Khashei, M.; Bakhtiarvand, N. A novel discrete learning-based intelligent methodology for breast cancer classification purposes. Artif. Intell. Med. 2023, 139, 102492. [Google Scholar] [CrossRef]
- Wei, Y.Z.; Zhang, D.; Gao, M.Y.; Tian, Y.H.; He, Y.; Huang, B.L.; Zheng, C.Y. Breast Cancer Prediction Based on Machine Learning. J. Softw. Eng. Appl. 2023, 16, 348–360. [Google Scholar] [CrossRef]
- Nafea, A.A.; Mahdawi, M.A.; Ali, K.M.; Ibrahim, M.S.; AL-Ani, M.M. A Hybrid Method of 1D-CNN and Machine Learning Algorithms for Breast Cancer Detection. Baghdad Sci. J. 2024, 21, 3333. [Google Scholar] [CrossRef]
- Uddin, K.M.M.; Biswas, N.; Rikta, S.T.; Dey, S.K. Machine learning-based diagnosis of breast cancer utilizing feature optimization technique. Comput. Methods Programs Biomed. Update 2023, 3, 100098. [Google Scholar] [CrossRef]
- Singh, L.K.; Khanna, M.; Singh, R. Artificial intelligence based medical decision support system for early and accurate breast cancer prediction. Adv. Eng. Softw. 2023, 175, 103338. [Google Scholar] [CrossRef]
- Chomatek, L.; Duraj, A. Efficient genetic algorithm for breast cancer diagnosis. In Proceedings of the International Conference on Information Technologies in Biomedicine, ITIB 2018: Advances in Intelligent Systems and Computing; Springer: Cham, Switzerland, 2019; Volume 762, pp. 64–76. [Google Scholar]
- Yusuf, A.; Dimab, R.M.; Aina, S.K. Optimized Breast Cancer Classification using Feature Selection and Outliers Detection. J. Niger. Soc. Phys. Sci. 2021, 3, 298–307. [Google Scholar] [CrossRef]
- Jensch, A.; Lopes, M.; Vinga, S.; Radde, N. ROSIE: RObust Sparse ensemble for outlIEr detection and gene selection in cancer omics data. Stat. Methods Med. Res. 2022, 31, 947–958. [Google Scholar] [CrossRef]
- Mohamed, T.I.; Ezugwu, A.E.; Fonou-Dombeu, J.V.; Ikotun, A.M.; Mohammed, M. A bio-inspired convolution neural network architecture for automatic breast cancer detection and classification using RNA-Seq gene expression data. Sci. Rep. 2023, 13, 14644. [Google Scholar] [CrossRef]
- Lopes, M.B.; Veríssimo, A.; Carrasquinha, E.; Casimiro, S.; Beerenwinkel, N.; Vinga, S. Ensemble outlier detection and gene selection in triple-negative breast cancer data. BMC Bioinform. 2018, 19, 168. [Google Scholar] [CrossRef] [PubMed]
- Pudjihartono, N.; Fadason, T.; Kempa-Liehr, A.W.; O’Sullivan, J.M. A Review of Feature Selection Methods for Machine Learning-Based Disease Risk Prediction. Front. Bioinform. 2022, 2, 927312. [Google Scholar] [CrossRef] [PubMed]
- Marques, H.O.; Swersky, L.; Sander, J.; Campello, R.J.; Zimek, A. On the evaluation of outlier detection and one-class classification: A comparative study of algorithms, model selection, and ensembles. Data Min. Knowl. Discov. 2023, 37, 1473–1517. [Google Scholar] [CrossRef]
- Ali, S.H. A New Intrusion Detection Strategy Based on Combined Feature Selection Methodology and Machine Learning Technique. MEJ Mansoura Eng. J. 2021, 46, 5. [Google Scholar] [CrossRef]
- Huang, S.; Cai, N.; Pacheco, P.P.; Narrandes, S.; Wang, Y.; Xu, W. Applications of Support Vector Machine (SVM) Learning in Cancer Genomics. Cancer Genom. Proteom. 2018, 15, 41–51. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Saleh, A.I.; Desouky, A.I.; Ali, S.H. Promoting the performance of vertical recommendation systems by applying new classification techniques. Knowl.-Based Syst. 2015, 75, 192–223. [Google Scholar] [CrossRef]
- Smiti, A. A critical overview of outlier detection methods. Comput. Sci. Rev. 2020, 38, 100306. [Google Scholar] [CrossRef]
- Abdel-Salam, M.; Askr, H.; Hassanien, A.E. Adaptive chaotic dynamic learning-based gazelle optimization algorithm for feature selection problems. Expert Syst. Appl. 2024, 256, 124882. [Google Scholar] [CrossRef]
- Rabie, A.H.; Ali, S.H.; Saleh, A.I.; Ali, H.A. A new outlier rejection methodology for supporting load forecasting in smart grids based on big data. Cluster Comput. 2020, 23, 509–535. [Google Scholar] [CrossRef]
- Lahmar, I.; Zaier, A.; Yahia, M.; Boaullegue, R. A Novel Improved Binary Harris Hawks Optimization for High dimensionality Feature Selection. Pattern Recognit. Lett. 2023, 171, 170–176. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Thaher, T.; Heidari, A.A.; Mafarja, M.; Dong, J.S.; Mirjalili, S. Binary Harris Hawks Optimizer for High-Dimensional, Low Sample Size Feature Selection. In Evolutionary Machine Learning Techniques: Algorithms for Intelligent Systems; Mirjalili, S., Faris, H., Aljarah, I., Eds.; Springer: Singapore, 2020. [Google Scholar] [CrossRef]
- Wolberg, W. Breast Cancer Wisconsin (Original) [Dataset]. UCI Machine Learning Repository. 1990. Available online: https://archive.ics.uci.edu/dataset/15/breast+cancer+wisconsin+original (accessed on 1 July 2024).
- Mangasarian, O.L.; Setiono, R.; Wolberg, W.H. Pattern recognition via linear programming: Theory and application to medical diagnosis. In Large-Scale Numerical Optimization; Coleman, T.F., Li, Y.Y., Eds.; SIAM Publications: Philadelphia, PA, USA, 1990; pp. 22–30. [Google Scholar]
- Street, W.N.; Wolberg, W.H.; Mangasarian, O.L. Nuclear feature extraction for breast tumor diagnosis. In Proceedings of the SPIE, San Jose, CA, USA, 11–16 July 1993; pp. 861–870. [Google Scholar] [CrossRef]

| Strategy | Description | Benefits | Drawbacks |
|---|---|---|---|
| [13] 2019 | A mixed architecture that combines fuzzy systems, neural networks, and pruning technique concepts was presented. The goal of this work was to develop an integrated approach that can forecast breast cancer with high accuracy while also producing a specialized system that can identify sick individuals by using fuzzy rules to pull knowledge from the database. |
| Using an integrated method might be computationally demanding, especially when working with very large datasets. |
| [14] 2023 | The proposed discrete learning classification system has the potential to significantly improve medical decision-making accuracy compared to conventional direction-based continuous techniques. |
|
|
| [15] 2023 | This research highlighted the potential of machine learning to detect and diagnose breast cancer early, leading to better results for patients and healthcare. |
|
|
| [16] 2024 | This work presented a method to identify breast cancer instances as benign or malignant by leveraging machine learning techniques and 1D CNN feature extraction in order to improve accuracy. |
|
|
| [17] 2023 | Breast cancer detection uses machine learning algorithms including Support Vector Machine, Naïve Bayes, K-Nearest Neighbors, and AdaBoost. This study included eleven machine learning classifiers to find the most appropriate technique for breast cancer prediction. |
|
|
| [18] 2023 | The goal of this research was to enable radiologists to utilize machine learning and soft computing techniques to more rapidly and reliably identify and categorize breast cancer. |
|
|
| Outlier Detection Method | Explanation |
|---|---|
| MGA [19] 2019 | This study proposed a set of objectives that make it possible to efficiently identify outliers with the use of a multi-objective genetic algorithm. |
| OCFS [20] 2021 | This study investigated the effects of outliers and feature elimination on the Wisconsin Diagnostic Breast Cancer Dataset, which was investigated via seven distinct algorithms for machine learning in an effort to tackle these problems. The findings demonstrated that the classifiers using AdaBoost, Random Forest, and Logistic Regression eliminated outliers from the dataset with the highest accuracy. |
| ROSIE [21] 2022 | This study suggested robust sparse ensemble for outlier detection (ROSIE), an ensemble classification technique that incorporates three basic and resilient algorithms for outlier detection and feature selection. It also includes a bootstrap-based validity test. ROSIE was used to identify outliers via the rank product test, which considered outlier ranks from all three approaches. The significant characteristics were those that were consistently selected by each technique. |
| AAIC [22] 2023 | The detection of breast cancer using gene expression data was made possible by a combination approach that blends the CNN design with the Ebola optimization technique. Array–Array Intensity Correlation was one of the pre-processing techniques used to exclude outliers. |
| EODA [23] 2018 | The feasibility of outlier identification was demonstrated using ensemble hypotheses based on genetic expression and clinical parameters for outlier patients. |
| Measure | Equation | Description |
|---|---|---|
| Precision (P) | The proportion of correct positive predictions. | |
| Recall (R) | The proportion of instances with positive labels that were also projected to be positive. | |
| Accuracy (A) | The proportion of predictions that are correct. | |
| Error (E) | The proportion of predictions that are incorrect. | |
| F1-measure | The weighted harmonic mean of precision and recall. |
| Technique | Accuracy (%) | Precision (%) | Recall (%) | Error (%) | F1-Measuer (%) | Run Time (s) |
|---|---|---|---|---|---|---|
| MGA [19] | 77 | 76.4 | 76 | 23 | 76.199 | 14 |
| OCFS [20] | 88 | 87.5 | 87.3 | 12 | 87.399 | 12 |
| ROSIE [21] | 90 | 89.6 | 89.4 | 10 | 89.499 | 9 |
| AAIC [22] | 91 | 90.3 | 90 | 9 | 90.149 | 7.3 |
| EODA [23] | 93 | 92.6 | 92.4 | 7 | 92.499 | 6.7 |
| Proposed CORT | 95 | 94.4 | 94.2 | 5 | 94.299 | 5 |
| Technique | Accuracy (%) | Precision (%) | Recall (%) | Error (%) | F1-Measure (%) | Run Time (s) |
|---|---|---|---|---|---|---|
| [13] | 80 | 79.6 | 79.3 | 20 | 79.449 | 12 |
| [14] | 93 | 92.5 | 92.4 | 7 | 92.449 | 9 |
| [15] | 95.5 | 94.2 | 94.1 | 4.5 | 94.149 | 7.8 |
| [16] | 97 | 96.1 | 95.8 | 3 | 95.949 | 6 |
| [17] | 97.7 | 96.6 | 96.3 | 2.3 | 96.449 | 5.4 |
| [18] | 98 | 97.4 | 97.2 | 2 | 97.299 | 4.3 |
| Proposed BCD strategy | 98.7 | 98.4 | 98 | 1.3 | 98.199 | 3 |
| Benefits | Drawbacks | ||
|---|---|---|---|
| Characteristic | Overview | Characteristic | Overview |
| Reliability | BCD is a reliable strategy since it can determine patients considering a variety of nuclear features. | Size of dataset | Although BCD uses the 699 examples from the WBCD dataset to illustrate different contemporary strategies, additional cases should be evaluated in order to yield more precise conclusions. |
| Quickness | BCD is a rapid deterministic strategy because an ECM can make choices based on accurate data that are free of outliers. | Complexity | BCD is a complex strategy because it comprises two layers, each containing several steps that are implemented consecutively. |
| Number of features | BCD has the capacity to handle a very large number of features and choose the optimal subset of them before using an ECM to recognize patients with certainty. | Multi-label classification | BCD is an assessment strategy that uses binary classification to divide instances into benign and malignant classes. As a result, multi-label data in the dataset should be used to test BCD. |
| Efficacy | BCD is a useful strategy because it can make quick, precise determinations. | ||
| Accuracy and precision | BCD can precisely diagnose breast cancer patients by utilizing an ECM after removing outliers and superfluous information from the data. | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, S.H.; Shehata, M. A New Breast Cancer Discovery Strategy: A Combined Outlier Rejection Technique and an Ensemble Classification Method. Bioengineering 2024, 11, 1148. https://doi.org/10.3390/bioengineering11111148
Ali SH, Shehata M. A New Breast Cancer Discovery Strategy: A Combined Outlier Rejection Technique and an Ensemble Classification Method. Bioengineering. 2024; 11(11):1148. https://doi.org/10.3390/bioengineering11111148
Chicago/Turabian StyleAli, Shereen H., and Mohamed Shehata. 2024. "A New Breast Cancer Discovery Strategy: A Combined Outlier Rejection Technique and an Ensemble Classification Method" Bioengineering 11, no. 11: 1148. https://doi.org/10.3390/bioengineering11111148
APA StyleAli, S. H., & Shehata, M. (2024). A New Breast Cancer Discovery Strategy: A Combined Outlier Rejection Technique and an Ensemble Classification Method. Bioengineering, 11(11), 1148. https://doi.org/10.3390/bioengineering11111148









