Preprocessing and Denoising Techniques for Electrocardiography and Magnetocardiography: A Review
Abstract
1. Introduction
2. Relationship Between MCG and ECG Signal
3. Noises in ECG Signal
4. Pre-Processing in ECG Signal
4.1. BW Removal in ECG Signal
4.2. EMG/MA Removal in ECG Signal
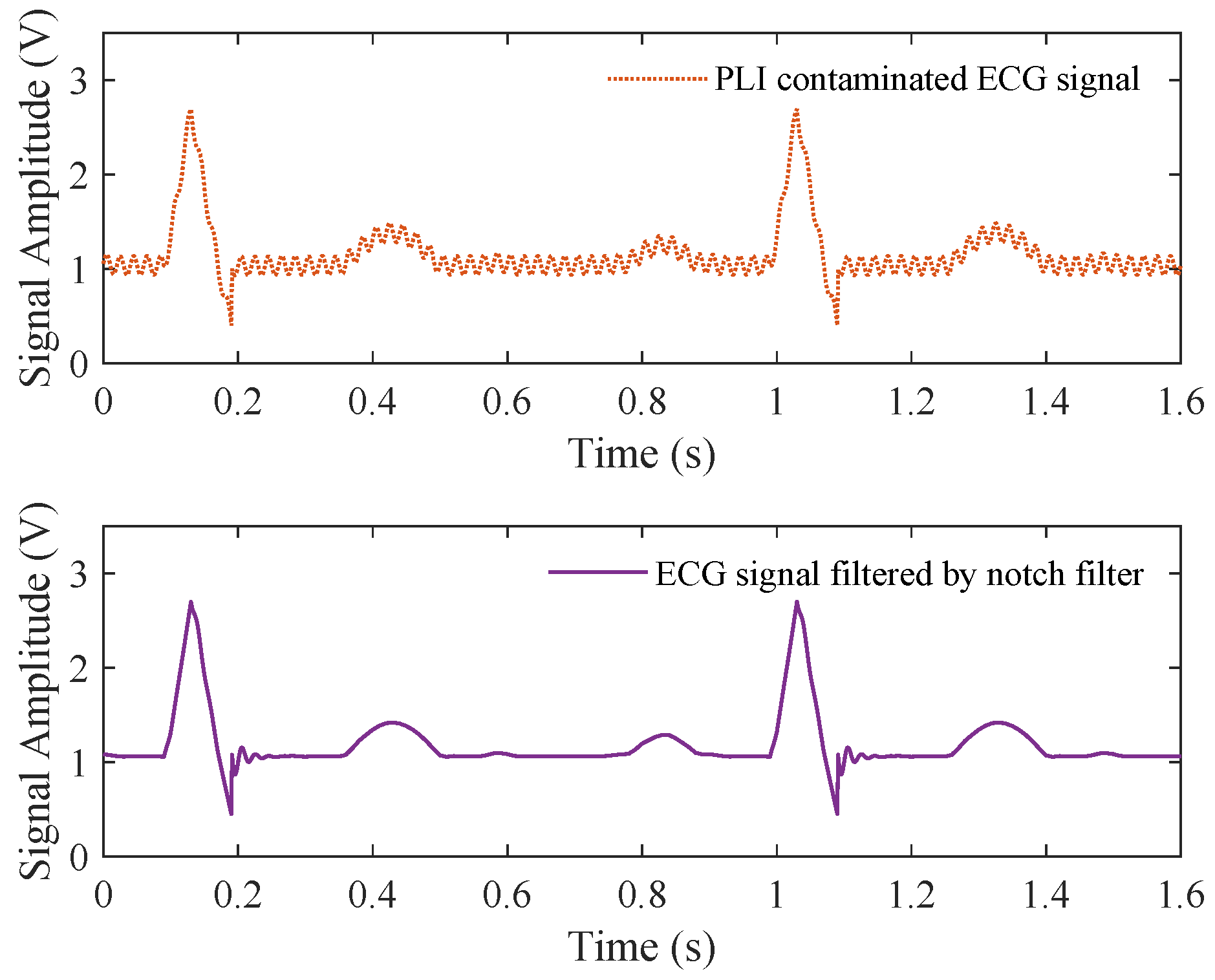
4.3. PLI Removal in ECG Signal
4.4. Composite Noise Removal in ECG
| Methods | Database | Record | Evaluation Parameters |
|---|---|---|---|
| Schrodinger equation followed by a new wavelet [38] | MIT-BIH and experimental data | 105, 234 | = 20 dB (avg.) MSE = 0.014 (avg.) PRD = 0.014 (avg.) |
| Variable frequency complex demodulation (VFCDM) algorithm [59] | MIT-BIH and Wearable Armnand ECG Data and NSTDB | 100, 101, 103, 105, 106, 115, 215 and 230 | = 7.5015 dB, PRD = 7.44%, WEDD = 6.52% (for 15 dB I/P SNR) |
| Variable-frequency complex demodulation (VFCDM) algorithm [134] | Experimental data | - | Emax = 19.01%, Eavg = 7.88%, WEDD = 4.70% |
| Singular spectrum analysis and digital filtering [22] | MIT-BIH, NSTDB, PTBDB | - | = 41.96 dB, PRD = 5.71%, WEDD = 2.99% (for MIT-BIH) |
| Periodic non-local means filter [92] | MIT-BIH, Real noisy ECG signals | 103, 105, 106, 109, 115, 121, 201, 203, 209, 231 and 233 | = 8.855 dB, MSE = 0.0010, PRD > 10% (for 10 dB I/P SNR) |
| Bandpass filter and group sparsity and singular spectrum analysis [154] | Simulate ECG data | s20011, s20031, s20041, s20051, s20061, s20071, s20081, s20091 and s20101 | = 10 dB (for 10 dB I/P SNR) |
| Adaptive dual-threshold filter and discrete wavelet transform [104] | MIT-BIH | 100, 101, 103, 105, 115, 122, 124 and 231 | = 7.143 dB, RMSE = 0.0042 (for 5 dB I/P SNR) |
| Discrete wavelet transform and non-local means (NLM) estimation [143] | MIT-BIH | 100, 103, 105, 106, 115, 215 | = 8.064 dB (for 10 dB I/P SNR), MSE = 0.0037, PRD = 5.5% |
| Dual-tree wavelet transform [71] | Simulated ECG data | 203, 109, 119, 111 and 108 | SNR = 30.493 dB (for 5 dB I/P SNR for record 108) |
| Biorthogonal wavelet transform and adaptive slope prediction-based threshold [72] | MIT-BIH, PTB, ST | 80 + 365 records | SNR = 32.6568 dB, MSE = 0.0003 |
| Biorthogonal wavelet transform and wavelet-Wiener filter thresholding [139] | QT database | 46 records | Avg. SNR = 4.2568 dB, MSE = 0.008, Avg. PRD = 12.14% (10 dB) Avg. SNR = 4.5594 dB, Avg. MSE = 0.0023, Avg. PRD = 11.19% (5 dB) |
| Local means (LM) method [137] | MIT-BIH, ST | 100, 103, 104, 105, 106, 115, 215 | Avg. = 10 dB, Avg. MSE = 0.0003, Avg. PRD < 12% (10 dB I/P SNR) Avg. = 10 dB, Avg. MSE = 0.0003, Avg. PRD ≈ 15% (for 10 dB I/P SNR) |
| Riemann–Liouville fractional integral filtering and Savitzky–Golay filtering and empirical mode decomposition [76] | MIT-BIH | 115 | SNR = 7.5288 dB, MSE = 0.0027 |
| EMD and non-local means [149] | MIT-BIH | 215, 115, 106, 105, 104, 103, 100 | Avg. > 8 dB, Avg. MSE = 0.000472, Avg. PRD < 20% (for 10 dB I/P SNR) |
| EMD and adaptive switching mean filter (ASMF) [98] | MIT-BIH | 100, 101, 103, 105, 115, 200, 215, and 230 | > 8 dB, MSE ≈ 0.002, PRD < 15% (for 10 dB I/P SNR) |
| Eigenvalue decomposition of the Hankel matrix [77] | MIT-BIH | 100, 101, 103, 105, 108, 109, 111, 112, 113, 115, 116, 117, 118, 121, 122, 123, 210, and 212 | = 12.89 dB, PRD ≈ 20% (for 5 dB I/P SNR and record 100) |
| Methods | Database | Record | Evaluation Parameters |
|---|---|---|---|
| Dual-tree complex wavelet transform and non-negative garrotte threshold function [141] | MIT-BIH | all 48 records | SNR = 58.23 dB, MSE = 0.0000000963, PRD = 0.001 (for record 100) |
| Cooperative filtering of similar segments and Savitzky–Golay and polynomial fitting [138] | MIT-BIH | 100, 101, 103, 104, 105, 106, 113, 115, 200, 215, 230 and 231 | ≥ 8 dB, MSE = 0.0010, PRD = 23.87% (for 5 dB I/P SNR and record 100) |
| Running denoising autoencoder [78] | Simulated ECG signals | - | ≈ 20 dB, MSE < 0.00005 (for 5 dB I/P SNR) |
| Non-local wavelet transform domain filtering [142] | MIT-BIH, PTB | 100, 103, 104, 105, 106, 115 and 215, s0032, s0207, s0508, s0510, s0430, s0035, s0354, s0370, s0003, s0012, s0432, s0390 | ≈ 6 dB, PRD ≈ 12%, MSE < 0.003 (for 20 dB I/P SNR and record 103), = 19.18 dB, PRD = 19.1%, MSE = 0.001 (for record s0032) |
| DAE using the fully convolutional network (FCN) [158] | MIT-BIH | all 48 records | Avg. > 8 dB, Avg. RMSE = 0.063, Avg.PRD = 19.68% (for −1 dB I/P SNR) |
| Stationary wavelet total variation algorithm [102] | MIT-BIT | 100, 103, 105, 113, 115, 117, 119, 122, 200, 215, 213, 230, 231 and 234 | SNR = 25.44 dB, RMSE = 0.3940, PRD = 40% (for 5 dB I/P SNR at record 231) |
| Fractional Stockwell transform (FrST) [79] | MIT-BIT, ST | 100, 101, 102, 103, 113, 201, 207, 217, 231, e0103, e0104, e0105 and e0106 | = 19.0699 dB, RMSE = 0.0807, PRD ≈ 8% (for 15 dB I/P SNR and record 100), = 24.6292 dB, RMSE = 0.0469 (for 15 dB I/P SNR and record e0103) |
| Ensemble empirical mode decomposition and genetic-algorithm-based thresholding technique [148] | MIT-BIH | - | > 5 dB, MSE < 0.05, PRD < 20% (for 10 dB I/P SNR) |
| Real-time accurate thresholding method and discrete wavelet transform [58] | MIT-BIH | 233 | = 6.0286 dB, RMSE = 0.2705 |
| Particle swarm optimization and wavelet transform [117] | MIT-BIH | 100 | SNR = 14.5189 dB, MSE = 0.143, RMSE = 0.1103, PRD = 20.1725% (for 5 dB I/P SNR) |
| U-Net [73] | PTB-XL, CPSC2018 | Manually label | SNR = 20.60 dB, RMSE = 0.0111 (for 20 dB I/P SNR) |
| Transformer encoder [163] | QT database | - | SNR = 13.60 dB, RMSE = 0.06, PRD = 22.85% (for 0–6 dB I/P SNR) |
| Sparse coding and Kalman filter [145] | QT database | - | = 18.6 dB, MAE = 0.026, (for −5 dB I/P SNR) |
| Bidirectional gated recurrent units [74] | Experimental data collected using wearable sensors | - | = 18.9 dB, RMSE = 0.029, PRD = 6.4% |
| Transformer and convolutional network [160] | MIT-BIH | all 48 records | = 8.49 dB, MSE = 0.035, (for 0 dB I/P SNR) |
5. Noises in MCG Signal
6. Pre-Processing in MCG Signal
| Methods | MCG Acquiring Device | Noise Source | Evaluation Parameters |
|---|---|---|---|
| Variational mode decomposition (VMD) and whale optimization algorithm (WOA) [178] | Simulated MCG signal and actual MCG signals collected by SQUID gradiometers | Baseline drift noise, industrial frequency noise, and Gaussian white noise | = 11.7892 dB, PRD = 0.5841, CC = 0.7218 (for 0 dB I/P SNR) |
| Independent component analysis (ICA) and ensemble empirical mode decomposition (EEMD) [191] | Actual MCG signals collected by a 37- channel SQUID | High-frequency baseline drifts, low-frequency baseline drift, breathing artifact, 50 Hz PLI, high-frequency random noise, etc. | ≈ 11.7892 dB |
| Convolutional neural network (CNN) [181] | Simulated MCG signal | noise | RMSE ≈ 0.03 (avg.) |
| Fourier wavelet denoising and sparse representation [180] | Simulated noise | High-frequency noise, power frequency noise, and low-frequency noise | SNR = 10.5521 dB, MSE = 0.0199 (for high-frequency noise) SNR = 17.5935 dB, MSE = 0.0035 (for power frequency noise) SNR = 10.4488 dB, MSE = 0.0232 (for low-frequency noise) |
| Correlation-based beat-by-beat approach and principal component analysis (PCA) [25] | Actual MCG signals collected by a 37- channel SQUID | Subjects with implanted devices | = 30 dB |
| Signal space separation (SSS) and projection operation [179] | Actual MCG signals collected by 48-channel tunneling magnetoresistance (TMR) sensors | Environmental magnetic sensor noise | Reduces the environmental magnetic noise by −73 dB and the sensor noise by about −23 dB |
| Independent component analysis (ICA) and EMD [26] | Actual MCG signals collected by an SERF atomic magnetometer array | Environmental noise, baseline drift, respiratory interference, and power line noise | Obvious characteristics of P wave, QRS wave, and T wave |
7. Performance Evaluation
8. Discussion and Challenges
9. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AWGN | Additive White Gaussian Noise: A type of noise with a constant intensity across all frequencies. |
| CC | Correlation Coefficient: A measure of how strongly two variables are related. |
| CNN | Convolutional Neural Network: A type of deep learning model often used for image and signal processing. |
| CVD | Cardiovascular Disease: Diseases that affect the heart and blood vessels. |
| DAEs | Denoising Autoencoders: Neural networks used to remove noise from signals or images. |
| ECG | Electrocardiography: A test that measures the electrical activity of the heart. |
| EKF | Extended Kalman Filter: A method used to estimate the state of a system when there is noise. |
| EMs | Electrode Motion Artifacts: Noise caused by electrode movement during measurements. |
| EMD | Empirical Mode Decomposition: A technique used to break down signals into simpler components. |
| EMG | Electromyogram: A test that measures the electrical activity in muscles. |
| GAN | Generative Adversarial Network: A model where two neural networks work together to generate realistic data. |
| ICA | Independent Component Analysis: A method used to separate mixed signals into independent sources. |
| IMF | Intrinsic Mode Function: Basic components of a signal derived through EMD. |
| MFMs | Magnetic Field Maps: Visual representations of magnetic fields. |
| MCG | Magnetocardiography: A test that records the magnetic fields generated by the heart. |
| MAs | Muscle Artifacts: Noise from muscle activity that interferes with signal measurements. |
| MSE | Mean Squared Error: A metric that measures the average squared difference between actual and predicted values. |
| NLM | Non-Local Means: A method for reducing noise by averaging similar data points. |
| OPM | Optically Pumped Magnetometer: A device used to measure small magnetic fields. |
| PCD | Pseudocurrent Density: A representation of current flow patterns based on magnetic data. |
| PCA | Principal Component Analysis: A technique used to reduce the dimensions of data by finding important patterns. |
| PLI | Power Line Interference: Noise from electrical power systems in signal recordings. |
| PRD | Percentage Root-Mean-Square Difference: A measure of the difference between two signals. |
| RSM | Residual Signal Method: A way to isolate and analyze noise in signals. |
| SNR | Signal-to-Noise Ratio: A measure of signal strength compared to noise. |
| SQUID | Superconducting Quantum Interference Device: A highly sensitive tool for measuring magnetic fields. |
| SSA | Singular Spectrum Analysis: A method for breaking down time series data into simpler parts. |
| SSS | Signal Space Separation: A method for separating signal from noise in magnetoencephalography and magnetocardiography. |
| SWT | Stationary Wavelet Transform: A method for analyzing signals without losing time information. |
| VMD | Variational Mode Decomposition: A method for separating signals into different modes for analysis. |
References
- Cardiovascular Diseases (CVDs). Available online: https://www.who.int/health-topics/cardiovascular-diseases/#tab=tab_1 (accessed on 20 May 2024).
- Cardiovascular Diseases (CVDs). Available online: https://www.who.int/news-room/fact-sheets/detail/cardiovascular-diseases-(cvds) (accessed on 20 May 2024).
- Li, P.; Wang, Y.; He, J.; Wang, L.; Tian, Y.; Zhou, T.S.; Li, T.; Li, J.S. High-performance personalized heartbeat classification model for long-term ECG signal. IEEE Trans. Biomed. Eng. 2016, 64, 78–86. [Google Scholar] [CrossRef] [PubMed]
- Tripathi, P.M.; Kumar, A.; Komaragiri, R.; Kumar, M. A review on computational methods for denoising and detecting ECG signals to detect cardiovascular diseases. Arch. Comput. Methods Eng. 2022, 29, 1875–1914. [Google Scholar] [CrossRef]
- Alberdi, A.; Aztiria, A.; Basarab, A. Towards an automatic early stress recognition system for office environments based on multimodal measurements: A review. J. Biomed. Inform. 2016, 59, 49–75. [Google Scholar] [CrossRef]
- Kumar, A.; Tomar, H.; Mehla, V.K.; Komaragiri, R.; Kumar, M. Stationary wavelet transform based ECG signal denoising method. ISA Trans. 2021, 114, 251–262. [Google Scholar] [CrossRef]
- Einthoven, W.; Jaffe, A.; Venge, P.; Lindahl, B. Galvanometrische registratie van het menschelijk Electrocardiography. In Herinneringsbundel Professor SS Rosenstein; Eduard Ijdo: Leiden, The Netherlands, 1902; pp. 101–107. [Google Scholar]
- Kligfield, P. The centennial of the Einthoven Electrocardiography. J. Electrocardiol. 2002, 35, 123. [Google Scholar] [CrossRef]
- Kligfield, P.; Gettes, L.S.; Bailey, J.J.; Childers, R.; Deal, B.J.; Hancock, E.W.; Van Herpen, G.; Kors, J.A.; Macfarlane, P.; Mirvis, D.M.; et al. Recommendations for the standardization and interpretation of the Electrocardiography: Part I: The Electrocardiography and its technology: A scientific statement from the American Heart Association Electrocardiography and Arrhythmias Committee, Council on Clinical Cardiology; the American College of Cardiology Foundation; and the Heart Rhythm Society endorsed by the International Society for Computerized Electrocardiology. Circulation 2007, 115, 1306–1324. [Google Scholar] [PubMed]
- Sanchis, J.; Bodí, V.; Núñez, J.; Bosch, X.; Loma-Osorio, P.; Mainar, L.; Santas, E.; Miñana, G.; Robles, R.; Llàcer, À. Limitations of clinical history for evaluation of patients with acute chest pain, non-diagnostic Electrocardiography, and normal troponin. Am. J. Cardiol. 2008, 101, 613–617. [Google Scholar] [CrossRef]
- Kwong, J.S.; Leithäuser, B.; Park, J.W.; Yu, C.M. Diagnostic value of magnetocardiography in coronary artery disease and cardiac arrhythmias: A review of clinical data. Int. J. Cardiol. 2013, 167, 1835–1842. [Google Scholar] [CrossRef]
- Shin, E.S.; Park, S.G.; Saleh, A.; Lam, Y.Y.; Bhak, J.; Jung, F.; Morita, S.; Brachmann, J. Magnetocardiography scoring system to predict the presence of obstructive coronary artery disease. Clin. Hemorheol. Microcirc. 2018, 70, 365–373. [Google Scholar] [CrossRef]
- Mäntynen, V.; Konttila, T.; Stenroos, M. Investigations of sensitivity and resolution of ECG and MCG in a realistically shaped thorax model. Phys. Med. Biol. 2014, 59, 7141. [Google Scholar] [CrossRef]
- Nenonen, J.; Hämäläinen, M.; Iimoniemi, R. Minimum-norm estimation in a boundary-element torso model. Med. Biol. Eng. Comput. 1994, 32, 43–48. [Google Scholar] [CrossRef] [PubMed]
- Lant, J.; Stroink, G.; ten Voorde, B.; Horacek, B.M.; Montague, T.J. Complementary nature of electrocardiographic and magnetocardiographic data in patients with ischemic heart disease. J. Electrocardiol. 1990, 23, 315–322. [Google Scholar] [CrossRef] [PubMed]
- Brockmeier, K.; Schmitz, L.; Chavez, J.D.J.B.; Burghoff, M.; Koch, H.; Zimmermann, R.; Trahms, L. Magnetocardiography and 32-lead potential mapping: Repolarization in normal subjects during pharmacologically induced stress. J. Cardiovasc. Electrophysiol. 1997, 8, 615–626. [Google Scholar] [CrossRef] [PubMed]
- Tenner, U.; Haueisen, J.; Nowak, H.; Leder, U.; Brauer, H. Source localization in an inhomogeneous physical thorax phantom. Phys. Med. Biol. 1999, 44, 1969. [Google Scholar] [CrossRef]
- Hänninen, H.; Takala, P.; Mäkijärvi, M.; Montonen, J.; Korhonen, P.; Oikarinen, L.; Simelius, K.; Nenonen, J.; Katila, T.; Toivonen, L. Recording locations in multichannel magnetocardiography and body surface potential mapping sensitive for regional exercise-induced myocardial ischemia. Basic Res. Cardiol. 2001, 96, 405–414. [Google Scholar] [CrossRef]
- Oostendorp, T.; Pesola, K. Non-invasive determination of the activation sequence of the heart based on combined ECG and MCG measurements. In Proceedings of the 12th International Conference on Biomagnetism, Espoo, Finland, 13–17 August 2001; pp. 813–820. [Google Scholar]
- Koch, H. Recent advances in magnetocardiography. J. Electrocardiol. 2004, 37, 117–122. [Google Scholar] [CrossRef] [PubMed]
- McKenna, S.; McCord, N.; Diven, J.; Fitzpatrick, M.; Easlea, H.; Gibbs, A.; Mitchell, A. Evaluating the impacts of digital ECG denoising on the interpretive capabilities of healthcare professionals. Eur. Heart J.-Digit. Health 2024, 5, 601–610. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.K.; Krishnan, S. A singular spectrum analysis-based model-free Electrocardiography denoising technique. Comput. Methods Programs Biomed. 2020, 188, 105304. [Google Scholar] [CrossRef]
- Berkaya, S.K.; Uysal, A.K.; Gunal, E.S.; Ergin, S.; Gunal, S.; Gulmezoglu, M.B. A survey on ECG analysis. Biomed. Signal Process. Control 2018, 43, 216–235. [Google Scholar] [CrossRef]
- Chatterjee, S.; Thakur, R.S.; Yadav, R.N.; Gupta, L.; Raghuvanshi, D.K. Review of noise removal techniques in ECG signals. IET Signal Process. 2020, 14, 569–590. [Google Scholar] [CrossRef]
- Sengottuvel, S.; Devi, S.S.; Sasikala, M.; Satheesh, S.; Selvaraj, R.J. An epoch based methodology to denoise Magnetocardiography (MCG) signals and its application to measurements on subjects with implanted devices. Biomed. Phys. Eng. Express 2021, 7, 035006. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Xu, M.; Liang, A.; Yin, Y.; Ma, X.; Gao, Y.; Ning, X. A new wearable multichannel Magnetocardiography system with a SERF atomic magnetometer array. Sci. Rep. 2021, 11, 5564. [Google Scholar] [CrossRef]
- Mariyappa, N.; Sengottuvel, S.; Parasakthi, C.; Gireesan, K.; Janawadkar, M.; Radhakrishnan, T.; Sundar, C. Baseline drift removal and denoising of MCG data using EEMD: Role of noise amplitude and the thresholding effect. Med. Eng. Phys. 2014, 36, 1266–1276. [Google Scholar] [CrossRef]
- Kamada, K.; Ito, Y.; Kobayashi, T. Human MCG measurements with a high-sensitivity potassium atomic magnetometer. Physiol. Meas. 2012, 33, 1063. [Google Scholar] [CrossRef]
- Morales, S.; Corsi, M.; Fourcault, W.; Bertrand, F.; Cauffet, G.; Gobbo, C.; Alcouffe, F.; Lenouvel, F.; Le Prado, M.; Berger, F.; et al. Magnetocardiography measurements with 4He vector optically pumped magnetometers at room temperature. Phys. Med. Biol. 2017, 62, 7267. [Google Scholar] [CrossRef] [PubMed]
- Wikswo, J.P., Jr.; Barach, J.P. Possible sources of new information in the Magnetocardiography. J. Theor. Biol. 1982, 95, 721–729. [Google Scholar] [CrossRef] [PubMed]
- Koch, H.; Haberkorn, W. Magnetic field mapping of cardiac electrophysiological function. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2001, 359, 1287–1298. [Google Scholar] [CrossRef]
- Kandori, A.; Shimizu, W.; Yokokawa, M.; Noda, T.; Kamakura, S.; Miyatake, K.; Murakami, M.; Miyashita, T.; Ogata, K.; Tsukada, K. Identifying patterns of spatial current dispersion that characterise and separate the Brugada syndrome and complete right-bundle branch block. Med. Biol. Eng. Comput. 2004, 42, 236. [Google Scholar] [CrossRef]
- Fenici, R.; Brisinda, D.; Venuti, A.; Sorbo, A.R. Thirty years of clinical magnetocardiography at the Catholic University of Rome: Diagnostic value and new perspectives for the treatment of cardiac arrhythmias. Int. J. Cardiol. 2013, 168, 5113–5115. [Google Scholar] [CrossRef]
- Nenonen, J.T. Solving the inverse problem in magnetocardiography. IEEE Eng. Med. Biol. Mag. 1994, 13, 487–496. [Google Scholar] [CrossRef]
- MacLeod, R.S.; Brooks, D.H. Recent progress in inverse problems in electrocardiology. IEEE Eng. Med. Biol. Mag. 1998, 17, 73–83. [Google Scholar] [CrossRef] [PubMed]
- Takala, P.; Hänninen, H.; Montonen, J.; Mäkijärvi, M.; Nenonen, J.; Oikarinen, L.; Simelius, K.; Toivonen, L.; Katila, T. Magnetocardiographic and electrocardiographic exercise mapping in healthy subjects. Ann. Biomed. Eng. 2001, 29, 501–509. [Google Scholar] [CrossRef] [PubMed]
- Liehr, M.; Haueisen, J.; Goernig, M.; Seidel, P.; Nenonen, J.; Katila, T. Vortex shaped current sources in a physical torso phantom. Ann. Biomed. Eng. 2005, 33, 240–247. [Google Scholar] [CrossRef]
- Upadhyay, P.; Upadhyay, S.; Shukla, K. Schrödinger Equation Based ECG Signal Denoising. Chin. J. Phys. 2022, 77, 2238–2257. [Google Scholar] [CrossRef]
- Malghan, P.G.; Hota, M.K. Grasshopper optimization algorithm based improved variational mode decomposition technique for muscle artifact removal in ECG using dynamic time warping. Biomed. Signal Process. Control 2022, 73, 103437. [Google Scholar] [CrossRef]
- Singhal, A.; Singh, P.; Fatimah, B.; Pachori, R.B. An efficient removal of power-line interference and baseline wander from ECG signals by employing Fourier decomposition technique. Biomed. Signal Process. Control 2020, 57, 101741. [Google Scholar] [CrossRef]
- Members, W.C.; Antman, E.M.; Anbe, D.T.; Armstrong, P.W.; Bates, E.R.; Green, L.A.; Hand, M.; Hochman, J.S.; Krumholz, H.M.; Kushner, F.G.; et al. ACC/AHA guidelines for the management of patients with ST-elevation myocardial infarction-executive summary: A report of the American College of Cardiology/American Heart Association Task Force on Practice Guidelines (Writing Committee to Revise the 1999 Guidelines for the Management of Patients With Acute Myocardial Infarction). Circulation 2004, 110, 588–636. [Google Scholar]
- Sahambi, J.; Tandon, S.; Bhatt, R. Quantitative analysis of errors due to power-line interference and base-line drift in detection of onsets and offsets in ECG using wavelets. Med. Biol. Eng. Comput. 1997, 35, 747–751. [Google Scholar] [CrossRef]
- Velayudhan, A.; Peter, S. Noise analysis and different denoising techniques of ECG signal-a survey. IOSR J. Electron. Commun. Eng. 2016, 1, 40–44. [Google Scholar]
- Khaing, A.S.; Naing, Z.M. Quantitative investigation of digital filters in Electrocardiography with simulated noises. Int. J. Inf. Electron. Eng. 2011, 1, 210–216. [Google Scholar]
- Samann, F.; Schanze, T. Multiple ECG segments denoising autoencoder model. Biomed. Eng. Tech. 2023, 68, 275–284. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, S.; Gupta, A. Fractal and EMD based removal of baseline wander and powerline interference from ECG signals. Comput. Biol. Med. 2013, 43, 1889–1899. [Google Scholar] [CrossRef] [PubMed]
- Van Alste, J.A.; Schilder, T. Removal of base-line wander and power-line interference from the ECG by an efficient FIR filter with a reduced number of taps. IEEE Trans. Biomed. Eng. 1985, BME-32, 1052–1060. [Google Scholar] [CrossRef]
- Chavan, M.S.; Agarwala, R.; Uplane, M. Suppression of baseline wander and power line interference in ECG using digital IIR filter. Int. J. Circuits Syst. Signal Process. 2008, 2, 356–365. [Google Scholar]
- Cuomo, S.; De Pietro, G.; Farina, R.; Galletti, A.; Sannino, G. A novel O (n) numerical scheme for ECG signal denoising. Procedia Comput. Sci. 2015, 51, 775–784. [Google Scholar] [CrossRef]
- Wang, J.; Ye, Y.; Pan, X.; Gao, X.; Zhuang, C. Fractional zero-phase filtering based on the Riemann–Liouville integral. Signal Process. 2014, 98, 150–157. [Google Scholar] [CrossRef]
- Shi, H.; Liu, R.; Chen, C.; Shu, M.; Wang, Y. ECG baseline estimation and denoising with group sparse regularization. IEEE Access 2021, 9, 23595–23607. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, Y.; Shu, M.; Wang, Y.; Dong, A. ECG baseline wander correction and denoising based on sparsity. IEEE Access 2019, 7, 31573–31585. [Google Scholar] [CrossRef]
- Meyer, C.; Keiser, H. Electrocardiography baseline noise estimation and removal using cubic splines and state-space computation techniques. Comput. Biomed. Res. 1977, 10, 459–470. [Google Scholar] [CrossRef]
- Hargittai, S. Efficient and fast ECG baseline wander reduction without distortion of important clinical information. In Proceedings of the 2008 Computers in Cardiology, Bologna, Italy, 14–17 September 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 841–844. [Google Scholar]
- Patil, P.B.; Chavan, M.S. A wavelet based method for denoising of biomedical signal. In Proceedings of the International Conference on Pattern Recognition, Informatics and Medical Engineering (PRIME-2012), Salem, India, 21–23 March 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 278–283. [Google Scholar]
- Ara, I.; Hossain, M.N.; Mahbub, S.Y. Baseline drift removal and de-noising of the ECG signal using wavelet transform. Int. J. Comput. Appl. 2014, 95, 15–17. [Google Scholar] [CrossRef]
- Zhang, D. Wavelet approach for ECG baseline wander correction and noise reduction. In Proceedings of the 2005 IEEE Engineering in Medicine and Biology 27th Annual Conference, Shanghai, China, 17–18 January 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 1212–1215. [Google Scholar]
- Yu, K.; Feng, L.; Chen, Y.; Wu, M.; Zhang, Y.; Zhu, P.; Chen, W.; Wu, Q.; Hao, J. Accurate wavelet thresholding method for ECG signals. Comput. Biol. Med. 2024, 169, 107835. [Google Scholar] [CrossRef] [PubMed]
- Hossain, M.B.; Bashar, S.K.; Lazaro, J.; Reljin, N.; Noh, Y.; Chon, K.H. A robust ECG denoising technique using variable frequency complex demodulation. Comput. Methods Programs Biomed. 2021, 200, 105856. [Google Scholar] [CrossRef]
- Han, G.; Lin, B.; Xu, Z. Electrocardiography signal denoising based on empirical mode decomposition technique: An overview. J. Instrum. 2017, 12, P03010. [Google Scholar] [CrossRef]
- Weng, B.; Blanco-Velasco, M.; Barner, K.E. Baseline wander correction in ECG by the empirical mode decomposition. In Proceedings of the IEEE 32nd Annual Northeast Bioengineering Conference, Easton, PA, USA, 1–2 April 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 135–136. [Google Scholar]
- Xin, Y.; Chen, Y.; Hao, W.T. ECG baseline wander correction based on mean-median filter and empirical mode decomposition. Bio-Med. Mater. Eng. 2014, 24, 365–371. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Ullah, S.W.; Li, B.; Lin, J.; Wang, H. Baseline wander removal for ECG signals based on improved EMD. In Proceedings of the 2020 15th IEEE International Conference on Signal Processing (ICSP), Beijing, China, 6–9 December 2020; IEEE: Piscataway, NJ, USA, 2020; Volume 1, pp. 484–487. [Google Scholar]
- Ding, R.; Li, G.; Wang, Q. The method research on removing baseline wander of ECG. J. Yunnan Univ. Nat. Sci. Ed. 2014, 36, 655–660. [Google Scholar]
- Ur Rehman, N.; Mandic, D.P. Filter bank property of multivariate empirical mode decomposition. IEEE Trans. Signal Process. 2011, 59, 2421–2426. [Google Scholar] [CrossRef]
- Xu, Y.; Luo, M.; Li, T.; Song, G. ECG signal de-noising and baseline wander correction based on CEEMDAN and wavelet threshold. Sensors 2017, 17, 2754. [Google Scholar] [CrossRef]
- Zhao, Z.; Liu, J. Baseline wander removal of ECG signals using empirical mode decomposition and adaptive filter. In Proceedings of the 2010 4th International Conference on Bioinformatics and Biomedical Engineering, Chengdu, China, 18–20 June 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 1–3. [Google Scholar]
- Thakor, N.V.; Zhu, Y.S. Applications of adaptive filtering to ECG analysis: Noise cancellation and arrhythmia detection. IEEE Trans. Biomed. Eng. 1991, 38, 785–794. [Google Scholar] [CrossRef]
- Dai, M.; Lian, S.L. Removal of baseline wander from dynamic Electrocardiography signals. In Proceedings of the 2009 2nd International Congress on Image and Signal Processing, Tianjin, China, 17–19 October 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1–4. [Google Scholar]
- Xiong, P.; Wang, H.; Liu, M.; Zhou, S.; Hou, Z.; Liu, X. ECG signal enhancement based on improved denoising auto-encoder. Eng. Appl. Artif. Intell. 2016, 52, 194–202. [Google Scholar] [CrossRef]
- El B’charri, O.; Latif, R.; Elmansouri, K.; Abenaou, A.; Jenkal, W. ECG signal performance de-noising assessment based on threshold tuning of dual-tree wavelet transform. Biomed. Eng. Online 2017, 16, 26. [Google Scholar] [CrossRef]
- Kumar, A.; Komaragiri, R.; Kumar, M. Heart rate monitoring and therapeutic devices: A wavelet transform based approach for the modeling and classification of congestive heart failure. ISA Trans. 2018, 79, 239–250. [Google Scholar] [CrossRef] [PubMed]
- Hu, L.; Cai, W.; Chen, Z.; Wang, M. A lightweight U-Net model for denoising and noise localization of ECG signals. Biomed. Signal Process. Control 2024, 88, 105504. [Google Scholar] [CrossRef]
- Dias, M.; Probst, P.; Silva, L.; Gamboa, H. Cleaning ECG with Deep Learning: A Denoiser Tested in Industrial Settings. SN Comput. Sci. 2024, 5, 699. [Google Scholar] [CrossRef]
- Cuomo, S.; De Pietro, G.; Farina, R.; Galletti, A.; Sannino, G. A revised scheme for real time ecg signal denoising based on recursive filtering. Biomed. Signal Process. Control 2016, 27, 134–144. [Google Scholar] [CrossRef]
- Jain, S.; Bajaj, V.; Kumar, A. Riemann Liouvelle fractional integral based empirical mode decomposition for ECG denoising. IEEE J. Biomed. Health Inform. 2017, 22, 1133–1139. [Google Scholar] [CrossRef]
- Sharma, R.R.; Pachori, R.B. Baseline wander and power line interference removal from ECG signals using eigenvalue decomposition. Biomed. Signal Process. Control 2018, 45, 33–49. [Google Scholar] [CrossRef]
- Samann, F.; Schanze, T. RunDAE model: Running denoising autoencoder models for denoising ECG signals. Comput. Biol. Med. 2023, 166, 107553. [Google Scholar] [CrossRef]
- Bajaj, A.; Kumar, S. A robust approach to denoise ECG signals based on fractional Stockwell transform. Biomed. Signal Process. Control 2020, 62, 102090. [Google Scholar] [CrossRef]
- Wang, G.; Yang, L.; Liu, M.; Yuan, X.; Xiong, P.; Lin, F.; Liu, X. ECG signal denoising based on deep factor analysis. Biomed. Signal Process. Control 2020, 57, 101824. [Google Scholar] [CrossRef]
- Jin, Y.; Qin, C.; Liu, J.; Liu, Y.; Li, Z.; Liu, C. A novel deep wavelet convolutional neural network for actual ecg signal denoising. Biomed. Signal Process. Control 2024, 87, 105480. [Google Scholar] [CrossRef]
- Peng, H.; Chang, X.; Yao, Z.; Shi, D.; Chen, Y. A deep learning framework for ECG denoising and classification. Biomed. Signal Process. Control 2024, 94, 106441. [Google Scholar] [CrossRef]
- Hung, K.H.; Wang, K.C.; Liu, K.C.; Chen, W.L.; Lu, X.; Tsao, Y.; Lin, C.W. MECG-E: Mamba-based ECG Enhancer for Baseline Wander Removal. arXiv 2024, arXiv:2409.18828. [Google Scholar]
- Kher, R.; Vala, D.; Pawar, T.; Thakar, V. RPCA-based detection and quantification of motion artifacts in ECG signals. J. Med. Eng. Technol. 2013, 37, 56–60. [Google Scholar] [CrossRef] [PubMed]
- Su, L.; Zhao, G. De-noising of ECG signal using translation-invariant wavelet de-noising method with improved thresholding. In Proceedings of the 2005 IEEE Engineering in Medicine and Biology 27th Annual Conference, Shanghai, China, 17–18 January 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 5946–5949. [Google Scholar]
- Singh, B.N.; Tiwari, A.K. Optimal selection of wavelet basis function applied to ECG signal denoising. Digit. Signal Process. 2006, 16, 275–287. [Google Scholar] [CrossRef]
- Ercelebi, E. Electrocardiography signals de-noising using lifting-based discrete wavelet transform. Comput. Biol. Med. 2004, 34, 479–493. [Google Scholar] [CrossRef]
- Poornachandra, S. Wavelet-based denoising using subband dependent threshold for ECG signals. Digit. Signal Process. 2008, 18, 49–55. [Google Scholar] [CrossRef]
- Xiong, F.; Chen, D.; Chen, Z.; Dai, S. Cancellation of motion artifacts in ambulatory ECG signals using TD-LMS adaptive filtering techniques. J. Vis. Commun. Image Represent. 2019, 58, 606–618. [Google Scholar] [CrossRef]
- Lin, H.Y.; Liang, S.Y.; Ho, Y.L.; Lin, Y.H.; Ma, H.P. Discrete-wavelet-transform-based noise removal and feature extraction for ECG signals. IRBM 2014, 35, 351–361. [Google Scholar] [CrossRef]
- Tracey, B.H.; Miller, E.L. Nonlocal means denoising of ECG signals. IEEE Trans. Biomed. Eng. 2012, 59, 2383–2386. [Google Scholar] [CrossRef]
- Lee, Y.; Hwang, D. Periodicity-based nonlocal-means denoising method for electrocardiography in low SNR non-white noisy conditions. Biomed. Signal Process. Control 2018, 39, 284–293. [Google Scholar] [CrossRef]
- Hesar, H.D.; Mohebbi, M. ECG denoising using marginalized particle extended kalman filter with an automatic particle weighting strategy. IEEE J. Biomed. Health Inform. 2017, 21, 635–644. [Google Scholar] [CrossRef]
- Hesar, H.D.; Mohebbi, M. An adaptive particle weighting strategy for ECG denoising using marginalized particle extended Kalman filter: An evaluation in arrhythmia contexts. IEEE J. Biomed. Health Inform. 2017, 21, 1581–1592. [Google Scholar] [CrossRef] [PubMed]
- Hesar, H.D.; Mohebbi, M. An adaptive Kalman filter bank for ECG denoising. IEEE J. Biomed. Health Inform. 2020, 25, 13–21. [Google Scholar] [CrossRef] [PubMed]
- Akhbari, M.; Shamsollahi, M.B.; Jutten, C.; Armoundas, A.A.; Sayadi, O. ECG denoising and fiducial point extraction using an extended Kalman filtering framework with linear and nonlinear phase observations. Physiol. Meas. 2016, 37, 203. [Google Scholar] [CrossRef]
- Mourad, N. ECG denoising based on successive local filtering. Biomed. Signal Process. Control 2022, 73, 103431. [Google Scholar] [CrossRef]
- Rakshit, M.; Das, S. An efficient ECG denoising methodology using empirical mode decomposition and adaptive switching mean filter. Biomed. Signal Process. Control 2018, 40, 140–148. [Google Scholar] [CrossRef]
- Milanesi, M.; Martini, N.; Vanello, N.; Positano, V.; Santarelli, M.F.; Paradiso, R.; De Rossi, D.; Landini, L. Multichannel techniques for motion artifacts removal from electrocardiographic signals. In Proceedings of the 2006 International Conference of the IEEE Engineering in Medicine and Biology Society, New York, NY, USA, 30 August–3 September 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 3391–3394. [Google Scholar]
- Kim, H.; Kim, S.; Van Helleputte, N.; Artes, A.; Konijnenburg, M.; Huisken, J.; Van Hoof, C.; Yazicioglu, R.F. A configurable and low-power mixed signal SoC for portable ECG monitoring applications. IEEE Trans. Biomed. Circuits Syst. 2013, 8, 257–267. [Google Scholar] [CrossRef]
- Beni, N.H.; Jiang, N. Heartbeat detection from single-lead ECG contaminated with simulated EMG at different intensity levels: A comparative study. Biomed. Signal Process. Control 2023, 83, 104612. [Google Scholar] [CrossRef]
- Madan, P.; Singh, V.; Singh, D.P.; Diwakar, M.; Kishor, A. Denoising of ECG signals using weighted stationary wavelet total variation. Biomed. Signal Process. Control 2022, 73, 103478. [Google Scholar] [CrossRef]
- Wang, J.; Ye, Y.; Pan, X.; Gao, X. Parallel-type fractional zero-phase filtering for ECG signal denoising. Biomed. Signal Process. Control 2015, 18, 36–41. [Google Scholar] [CrossRef]
- Jenkal, W.; Latif, R.; Toumanari, A.; Dliou, A.; El B’charri, O.; Maoulainine, F.M. An efficient algorithm of ECG signal denoising using the adaptive dual threshold filter and the discrete wavelet transform. Biocybern. Biomed. Eng. 2016, 36, 499–508. [Google Scholar] [CrossRef]
- Ramos, R.; Mànuel-Làzaro, A.; Del Río, J.; Olivar, G. FPGA-based implementation of an adaptive canceller for 50/60-Hz interference in electrocardiography. IEEE Trans. Instrum. Meas. 2007, 56, 2633–2640. [Google Scholar] [CrossRef]
- Piskorowski, J. Digital Q-varying notch IIR filter with transient suppression. IEEE Trans. Instrum. Meas. 2009, 59, 866–872. [Google Scholar] [CrossRef]
- Wesson, K.D.; Ochshorn, R.M.; Land, B.R. Low-cost, high-fidelity, adaptive cancellation of periodic 60 Hz noise. J. Neurosci. Methods 2009, 185, 50–55. [Google Scholar] [CrossRef]
- Rehman, I.u.; Raza, H.; Razzaq, N.; Frnda, J.; Zaidi, T.; Abbasi, W.; Anwar, M.S. A Computationally Efficient Distributed Framework for a State Space Adaptive Filter for the Removal of PLI from Cardiac Signals. Mathematics 2023, 11, 350. [Google Scholar] [CrossRef]
- Kumar, A.; Ranganatham, R.; Komaragiri, R.; Kumar, M. Efficient QRS complex detection algorithm based on Fast Fourier Transform. Biomed. Eng. Lett. 2019, 9, 145–151. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Li, Y.; Cao, X.; Sun, W.; He, W. Removal of power line interference from ECG signals using adaptive notch filters of sharp resolution. IEEE Access 2019, 7, 150667–150676. [Google Scholar] [CrossRef]
- Singh, P.; Srivastava, I.; Singhal, A.; Gupta, A. Baseline wander and power-line interference removal from ECG signals using Fourier decomposition method. In Machine Intelligence and Signal Analysis; Springer: Singapore, 2019; pp. 25–36. [Google Scholar]
- Shirbani, F.; Setarehdan, S.K. ECG power line interference removal using combination of FFT and adaptive non-linear noise estimator. In Proceedings of the 2013 21st Iranian Conference on Electrical Engineering (ICEE), Mashhad, Iran, 14–16 May 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1–5. [Google Scholar]
- Singh, P.; Joshi, S.D.; Patney, R.K.; Saha, K. The Fourier decomposition method for nonlinear and non-stationary time series analysis. Proc. R. Soc. A Math. Phys. Eng. Sci. 2017, 473, 20160871. [Google Scholar] [CrossRef] [PubMed]
- Suchetha, M.; Kumaravel, N.; Jagannath, M.; Jaganathan, S.K. A comparative analysis of EMD based filtering methods for 50 Hz noise cancellation in ECG signal. Inform. Med. Unlocked 2017, 8, 54–59. [Google Scholar] [CrossRef]
- Suchetha, M.; Kumaravel, N. Empirical mode decomposition based filtering techniques for power line interference reduction in Electrocardiography using various adaptive structures and subtraction methods. Biomed. Signal Process. Control 2013, 8, 575–585. [Google Scholar] [CrossRef]
- Malik, S.A.; Parah, S.A.; Aljuaid, H.; Malik, B.A. An Iterative Filtering Based ECG Denoising Using Lifting Wavelet Transform Technique. Electronics 2023, 12, 387. [Google Scholar] [CrossRef]
- Azzouz, A.; Bengherbia, B.; Wira, P.; Alaoui, N.; Souahlia, A.; Maazouz, M.; Hentabeli, H. An efficient ECG signals denoising technique based on the combination of particle swarm optimisation and wavelet transform. Heliyon 2024, 10, e26171. [Google Scholar] [CrossRef]
- Glover, J. Adaptive noise canceling applied to sinusoidal interferences. IEEE Trans. Acoust. Speech Signal Process. 1977, 25, 484–491. [Google Scholar] [CrossRef]
- Wang, K.; Tu, C.; Qian, C.M.; Lin, R.; Doyle, D.; Fujiwara, Y.; Wang, J. Noise removal in single-lead capacitive ECG with adaptive filtering and singular value decomposition. IEEE Access 2024. [Google Scholar] [CrossRef]
- Chandrakar, C.; Kowar, M. Denoising ECG signals using adaptive filter algorithm. Int. J. Soft Comput. Eng. (IJSCE) 2012, 2, 120–123. [Google Scholar]
- Maniruzzaman, M.; Billah, K.M.S.; Biswas, U.; Gain, B. Least-Mean-Square algorithm based adaptive filters for removing power line interference from ECG signal. In Proceedings of the 2012 International Conference on Informatics, Electronics & Vision (ICIEV), Dhaka, Bangladesh, 18–19 May 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 737–740. [Google Scholar]
- Martens, S.M.; Mischi, M.; Oei, S.G.; Bergmans, J.W. An improved adaptive power line interference canceller for electrocardiography. IEEE Trans. Biomed. Eng. 2006, 53, 2220–2231. [Google Scholar] [CrossRef]
- Bazhyna, A.; Christov, I.; Gotchev, A.; Daskalov, I.; Egiazarian, K. Powerline interference suppression in high-resolution ECG. In Proceedings of the Computers in Cardiology, Thessaloniki, Greece, 21–24 September 2003; IEEE: Piscataway, NJ, USA, 2003; pp. 561–564. [Google Scholar]
- Razzaq, N.; Sheikh, S.A.A.; Salman, M.; Zaidi, T. An intelligent adaptive filter for elimination of power line interference from high resolution Electrocardiography. IEEE Access 2016, 4, 1676–1688. [Google Scholar] [CrossRef]
- Tahir, S.; Raja, M.M.; Razzaq, N.; Mirza, A.; Khan, W.Z.; Kim, S.W.; Zikria, Y.B. Extended Kalman Filter-Based power line interference canceller for Electrocardiography signal. Big Data 2022, 10, 34–53. [Google Scholar] [CrossRef]
- Inam-ur-Rehman; Razzaq, N.; Ullah, E.; Salman, M.; Zaidi, T. State space least mean square adaptive filter for power line interference removal from cardiac signals. In Proceedings of the 2019 IEEE 7th Conference on Systems, Process and Control (ICSPC), Melaka, Malaysia, 13–14 December 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 216–221. [Google Scholar]
- Mian Qaisar, S. Baseline wander and power-line interference elimination of ECG signals using efficient signal-piloted filtering. Healthc. Technol. Lett. 2020, 7, 114–118. [Google Scholar] [CrossRef]
- Chen, Y.S.; Lin, P.Y.; Lin, Y.D. A novel PLI suppression method in ECG by notch filtering with a modulation-based detection and frequency estimation scheme. Biomed. Signal Process. Control 2020, 62, 102150. [Google Scholar] [CrossRef]
- Mir, H.Y.; Singh, O. Powerline interference reduction in ECG signals using variable notch filter designed via variational mode decomposition. Analog Integr. Circuits Signal Process. 2024, 118, 317–328. [Google Scholar] [CrossRef]
- Malghan, P.G.; Hota, M.K. An Improved VME technique via Heap based Optimization Algorithm and AWIT method for PLI and MA noise elimination in ECG. IEEE Access 2023, 11, 54070–54079. [Google Scholar] [CrossRef]
- Jain, P.; Pachori, R.B. An iterative approach for decomposition of multi-component non-stationary signals based on eigenvalue decomposition of the Hankel matrix. J. Frankl. Inst. 2015, 352, 4017–4044. [Google Scholar] [CrossRef]
- Boda, S.; Mahadevappa, M.; Dutta, P.K. A hybrid method for removal of power line interference and baseline wander in ECG signals using EMD and EWT. Biomed. Signal Process. Control 2021, 67, 102466. [Google Scholar] [CrossRef]
- Badreldin, I.S.; El-Kholy, D.S.; Elwakil, A.A. Harmonic adaptive noise canceler for electrocardiography with no power-line reference. In Proceedings of the 2012 16th IEEE Mediterranean Electrotechnical Conference, Yasmine Hammamet, Tunisia, 25–28 March 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1017–1020. [Google Scholar]
- Yang, B.; Dong, Y.; Yu, C.; Hou, Z. Singular spectrum analysis window length selection in processing capacitive captured biopotential signals. IEEE Sens. J. 2016, 16, 7183–7193. [Google Scholar] [CrossRef]
- Singh, P.; Shahnawazuddin, S.; Pradhan, G. An efficient ECG denoising technique based on non-local means estimation and modified empirical mode decomposition. Circuits Syst. Signal Process. 2018, 37, 4527–4547. [Google Scholar] [CrossRef]
- Selesnick, I. Sparsity-assisted signal smoothing (revisited). In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 4546–4550. [Google Scholar]
- Qian, C.; Su, H.; Yu, H. Local means denoising of ECG signal. Biomed. Signal Process. Control 2019, 53, 101571. [Google Scholar] [CrossRef]
- Liu, B.; Li, Y. ECG signal denoising based on similar segments cooperative filtering. Biomed. Signal Process. Control 2021, 68, 102751. [Google Scholar] [CrossRef]
- Kumar, A.; Komaragiri, R.; Kumar, M. Design of wavelet transform based Electrocardiography monitoring system. ISA Trans. 2018, 80, 381–398. [Google Scholar] [CrossRef]
- Alla, M.R.; Nayak, C. A robust ECG signal enhancement technique through optimally designed adaptive filters. Biomed. Signal Process. Control 2024, 95, 106434. [Google Scholar] [CrossRef]
- Prashar, N.; Sood, M.; Jain, S. Design and implementation of a robust noise removal system in ECG signals using dual-tree complex wavelet transform. Biomed. Signal Process. Control 2021, 63, 102212. [Google Scholar] [CrossRef]
- Yadav, S.K.; Sinha, R.; Bora, P.K. Electrocardiography signal denoising using non-local wavelet transform domain filtering. IET Signal Process. 2015, 9, 88–96. [Google Scholar] [CrossRef]
- Singh, P.; Pradhan, G.; Shahnawazuddin, S. Denoising of ECG signal by non-local estimation of approximation coefficients in DWT. Biocybern. Biomed. Eng. 2017, 37, 599–610. [Google Scholar] [CrossRef]
- Revach, G.; Locher, T.; Shlezinger, N.; van Sloun, R.J.; Vullings, R. HKF: Hierarchical Kalman Filtering with Online Learned Evolution Priors for Adaptive ECG Denoising. IEEE Trans. Signal Process. 2024, 72, 3990–4006. [Google Scholar] [CrossRef]
- de Vries, I.R.; de Jong, A.M.; van der Hout-van der Jagt, M.B.; van Laar, J.O.E.H.; Vullings, R. Deep Learing for Sparse Domain Kalman Filtering with Applications on ECG Denoising and Motility Estimation. IEEE Trans. Biomed. Eng. 2024, 71, 2321–2329. [Google Scholar] [CrossRef]
- Hesar, H.D.; Hesar, A.D. Adaptive augmented cubature Kalman filter/smoother for ECG denoising. Biomed. Eng. Lett. 2024, 14, 689–705. [Google Scholar] [CrossRef]
- Hesar, H.D.; Hesar, A.D. Adaptive dual augmented extended Kalman filtering of ECG signals. Measurement 2025, 239, 115457. [Google Scholar] [CrossRef]
- Nguyen, P.; Kim, J.M. Adaptive ECG denoising using genetic algorithm-based thresholding and ensemble empirical mode decomposition. Inf. Sci. 2016, 373, 499–511. [Google Scholar] [CrossRef]
- Kumar, S.; Panigrahy, D.; Sahu, P. Denoising of Electrocardiography (ECG) signal by using empirical mode decomposition (EMD) with non-local mean (NLM) technique. Biocybern. Biomed. Eng. 2018, 38, 297–312. [Google Scholar] [CrossRef]
- Wang, M.; Zhou, Z.; Li, Z.; Zeng, Y. An adaptive denoising algorithm for chaotic signals based on improved empirical mode decomposition. Circuits, Syst. Signal Process. 2019, 38, 2471–2488. [Google Scholar] [CrossRef]
- Tan, C.; Zhang, L.; Wu, H.t. A novel Blaschke unwinding adaptive-Fourier-decomposition-based signal compression algorithm with application on ECG signals. IEEE J. Biomed. Health Inform. 2018, 23, 672–682. [Google Scholar] [CrossRef] [PubMed]
- Selesnick, I. Sparse regularization via convex analysis. IEEE Trans. Signal Process. 2017, 65, 4481–4494. [Google Scholar] [CrossRef]
- Cuomo, S.; Farina, R.; Piccialli, F. An inverse Bayesian scheme for the denoising of ECG signals. J. Netw. Comput. Appl. 2018, 115, 48–58. [Google Scholar] [CrossRef]
- Mourad, N. ECG denoising algorithm based on group sparsity and singular spectrum analysis. Biomed. Signal Process. Control 2019, 50, 62–71. [Google Scholar] [CrossRef]
- Tripathi, P.M.; Kumar, A.; Komaragiri, R.; Kumar, M. A novel approach for real-time ECG signal denoising using Fourier decomposition method. Res. Biomed. Eng. 2022, 38, 1037–1049. [Google Scholar] [CrossRef]
- Ghafari, A.; Pourjafari, N.; Ghaffari, A. Vector Based Post-Processing Method for Improving ECG Denoising Techniques by Re-establishing lead Relationships. IEEE Trans. Instrum. Meas. 2023, 73, 4000809. [Google Scholar] [CrossRef]
- Wang, X.; Chen, B.; Zeng, M.; Wang, Y.; Liu, H.; Liu, R.; Tian, L.; Lu, X. An ECG signal denoising method using conditional generative adversarial net. IEEE J. Biomed. Health Inform. 2022, 26, 2929–2940. [Google Scholar] [CrossRef]
- Chiang, H.T.; Hsieh, Y.Y.; Fu, S.W.; Hung, K.H.; Tsao, Y.; Chien, S.Y. Noise reduction in ECG signals using fully convolutional denoising autoencoders. IEEE Access 2019, 7, 60806–60813. [Google Scholar] [CrossRef]
- Zhang, J.; Bao, R.; Wang, L.; Xu, J.; Chen, Y.; Chen, X. Denoising method of ECG signal based on Channel Attention Mechanism. In Proceedings of the 2022 IEEE International Conference on Trust, Security and Privacy in Computing and Communications (TrustCom), Wuhan, China, 9–11 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1273–1277. [Google Scholar]
- Wang, J.; Pei, S.; Yang, Y.; Wang, H. Convolutional transformer-driven robust Electrocardiography signal denoising framework with adaptive parametric ReLU. Math. Biosci. Eng. 2024, 21, 4286–4308. [Google Scholar] [CrossRef]
- Hou, Y.; Liu, R.; Shu, M.; Xie, X.; Chen, C. Deep neural network denoising model based on sparse representation algorithm for ECG signal. IEEE Trans. Instrum. Meas. 2023, 72, 2507711. [Google Scholar] [CrossRef]
- Kærgaard, K.; Jensen, S.H.; Puthusserypady, S. A comprehensive performance analysis of EEMD-BLMS and DWT-NN hybrid algorithms for ECG denoising. Biomed. Signal Process. Control 2016, 25, 178–187. [Google Scholar] [CrossRef]
- Chen, M.; Li, Y.; Zhang, L.; Liu, L.; Han, B.; Shi, W.; Wei, S. Elimination of Random Mixed Noise in ECG using Convolutional Denoising Autoencoder with Transformer Encoder. IEEE J. Biomed. Health Inform. 2024, 28, 1993–2004. [Google Scholar] [CrossRef]
- Chen, M.; Li, Y.; Zhang, L.; Zhang, X.; Gao, J.; Sun, Y.; Shi, W.; Wei, S. Multitask Learning-Based Quality Assessment and Denoising of Electrocardiography Signals. IEEE Trans. Instrum. Meas. 2024, 73, 2510513. [Google Scholar] [CrossRef]
- Mondal, A.; Manikandan, M.S.; Pachori, R.B. ECG Quality Detection and Noise Classification for Wearable Cardiac Health Monitoring Devices. In Proceedings of the 2024 16th International Conference on Electronics, Computers and Artificial Intelligence (ECAI), Iasi, Romania, 27–28 June 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1–6. [Google Scholar]
- Knappe, S.; Sander, T.H.; Kosch, O.; Wiekhorst, F.; Kitching, J.; Trahms, L. Cross-validation of microfabricated atomic magnetometers with superconducting quantum interference devices for biomagnetic applications. Appl. Phys. Lett. 2010, 97, 133703. [Google Scholar] [CrossRef]
- Bison, G.; Wynands, R.; Weis, A. A laser-pumped magnetometer for the mapping of human cardiomagnetic fields. Appl. Phys. B 2003, 76, 325–328. [Google Scholar] [CrossRef]
- Pei, H.; Pang, H.; Quan, W.; Fan, W.; Yuan, L.; Zhang, K.; Fang, C. Pulsed optical pumping in electron spin vapor. Measurement 2024, 231, 114619. [Google Scholar] [CrossRef]
- Pei, H.; Duan, L.; Ma, L.; Fan, S.; Cai, Z.; Wu, Z.; Fan, W.; Quan, W. Real-time quantum control of spin-coupling damping and application in atomic spin gyroscopes. Cell Rep. Phys. Sci. 2024, 5, 101832. [Google Scholar] [CrossRef]
- Cohen, D.; Edelsack, E.A.; Zimmerman, J.E. Magnetocardiographys taken inside a shielded room with a superconducting point-contact magnetometer. Appl. Phys. Lett. 1970, 16, 278–280. [Google Scholar] [CrossRef]
- Lin, S.; Yuan, Z.; Tang, J.; Lu, J.; Cao, Q.; Zhai, Y. Interaxial time-domain interference in single-beam SERF magnetometer. Measurement 2023, 215, 112890. [Google Scholar] [CrossRef]
- Yang, K.; Wu, D.; Gao, W.; Ni, T.; Zhang, Q.; Zhang, H.; Huang, D. Calibration of SQUID magnetometers in multichannel MCG system based on bi-planar coil. IEEE Trans. Instrum. Meas. 2022, 71, 1002209. [Google Scholar] [CrossRef]
- Fujiwara, K.; Oogane, M.; Kanno, A.; Imada, M.; Jono, J.; Terauchi, T.; Okuno, T.; Aritomi, Y.; Morikawa, M.; Tsuchida, M.; et al. Magnetocardiography and magnetoencephalography measurements at room temperature using tunnel magneto-resistance sensors. Appl. Phys. Express 2018, 11, 023001. [Google Scholar] [CrossRef]
- Jaklevic, R.; Lambe, J.; Silver, A.; Mercereau, J. Quantum interference effects in Josephson tunneling. Phys. Rev. Lett. 1964, 12, 159. [Google Scholar] [CrossRef]
- Ma, Y.; Chen, Y.; Zhao, L.; Luo, G.; Yu, M.; Wang, Y.; Guo, J.; Yang, P.; Lin, Q.; Jiang, Z. The micro-fabrication and performance analysis of non-magnetic heating chip for miniaturized SERF atomic magnetometer. J. Magn. Magn. Mater. 2022, 557, 169495. [Google Scholar] [CrossRef]
- Wang, M.; Wang, Y.; Peng, L.; Ye, C. Measurement of triaxial magnetocardiography using high sensitivity tunnel magnetoresistance sensor. IEEE Sens. J. 2019, 19, 9610–9615. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, K.; Zhang, J.; Wang, Z.; Shang, J. Magnetocardiography measurements by microfabricated atomic magnetometer with a 3-D spherical alkali vapor cell. IEEE Trans. Instrum. Meas. 2021, 70, 4007907. [Google Scholar] [CrossRef]
- Chen, M.; Cheng, Q.; Feng, X.; Zhao, K.; Zhou, Y.; Xing, B.; Tang, S.; Wang, R.; Duan, J.; Wang, J.; et al. Optimized variational mode decomposition algorithm based on adaptive thresholding method and improved whale optimization algorithm for denoising magnetocardiography signal. Biomed. Signal Process. Control 2024, 88, 105681. [Google Scholar] [CrossRef]
- Kurashima, K.; Kataoka, M.; Nakano, T.; Fujiwara, K.; Kato, S.; Nakamura, T.; Yuzawa, M.; Masuda, M.; Ichimura, K.; Okatake, S.; et al. Development of magnetocardiograph without magnetically shielded room using high-detectivity TMR sensors. Sensors 2023, 23, 646. [Google Scholar] [CrossRef]
- Bing, L.; Si, W.; Tan, R.; Han, X.; Liu, F.; Yu, J. Hybrid Fourier-Wavelet Heart Magnetic Field Signal Denoising Based on Sparse Representation. In Proceedings of the 2019 3rd International Conference on Data Science and Business Analytics (ICDSBA), Istanbul, Turkey, 11–12 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 266–268. [Google Scholar]
- Sakib, S.; Fouda, M.M.; Al-Mahdawi, M.; Mohsen, A.; Oogane, M.; Ando, Y.; Fadlullah, Z.M. Deep learning models for magnetic cardiography edge sensors implementing noise processing and diagnostics. IEEE Access 2021, 10, 2656–2668. [Google Scholar] [CrossRef]
- Xie, X.; Zhou, X.; Zhao, F.; Wang, W.; Sun, J. Design of Biplanar Nested Square Uniform Coil in Lightweight Magnetically Shielded Room for Magnetocardiography System. IEEE Trans. Instrum. Meas. 2023, 72, 6011209. [Google Scholar] [CrossRef]
- Dong, Y.; Han, X.; Yin, X.; Li, R.; Xu, Y.; Fan, J.; Xie, F.; Xu, F.; Xiang, M.; Yu, D.; et al. Applying Magnetocardiography to Identify Asymptomatic Ischemic Heart Failure at an Early Stage. Circulation 2023, 148, A15129. [Google Scholar] [CrossRef]
- Haberkorn, W.; Steinhoff, U.; Burghoff, M.; Kosch, O.; Morguet, A.; Koch, H. Pseudo current density maps of electrophysiological heart, nerve or brain function and their physical basis. BioMagn. Res. Technol. 2006, 4, 5. [Google Scholar] [CrossRef]
- Cohen, D.; Hosaka, H. Part II magnetic field produced by a current dipole. J. Electrocardiol. 1976, 9, 409–417. [Google Scholar] [CrossRef] [PubMed]
- Yang, K.; Chen, H.; Lu, L.; Kong, X.; Yang, R.; Wang, J. SQUID array with optimal compensating configuration for magnetocardiography measurement in different environments. IEEE Trans. Appl. Supercond. 2019, 29, 1600707. [Google Scholar] [CrossRef]
- Lu, L.; Yang, K.; Kong, X.; Yang, R.; Wang, Y. A real-time, automatic MCG signal quality evaluation method using the magnetocardiography and electrocardiography. IEEE Trans. Appl. Supercond. 2018, 28, 1602106. [Google Scholar] [CrossRef]
- Dang-Ting, L.; Ye, T.; Yu-Feng, R.; Hong-Wei, Y.; Li-Hua, Z.; Qian-Sheng, Y.; Geng-Hua, C. A novel filter scheme of data processing for SQUID-based Magnetocardiography. Chin. Phys. Lett. 2008, 25, 2714. [Google Scholar] [CrossRef]
- Adachi, Y.; Kawabata, S.; Sasano, T.; Oyama, Y.H.D.; Uehara, G.; Sekihara, K. Biomagnetic measurement system for supine subjects with expanded sensor array and real-time noise reduction. In Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 7071–7074. [Google Scholar]
- Lu, Z.; Ji, S.; Yang, J. Measurement of T wave in magnetocardiography using tunnel magnetoresistance sensor. Chin. Phys. B 2023, 32, 020703. [Google Scholar] [CrossRef]
- Mariyappa, N.; Sengottuvel, S.; Patel, R.; Parasakthi, C.; Gireesan, K.; Janawadkar, M.; Radhakrishnan, T.; Sundar, C. Denoising of multichannel MCG data by the combination of EEMD and ICA and its effect on the pseudo current density maps. Biomed. Signal Process. Control 2015, 18, 204–213. [Google Scholar] [CrossRef]
- Khan, P.F.; Patel, R.; Sengottuvel, S.; Saipriya, S.; Swain, P.P.; Gireesan, K. Application of adaptive filters in denoising Magnetocardiography signals. AIP Conf. Proc. 2017, 1832, 060026. [Google Scholar]
- Patel, R.; Gireesan, K.; Sengottuvel, S.; Janawadkar, M.; Radhakrishnan, T. Suppression of baseline wander artifact in Magnetocardiography using breathing sensor. J. Med. Biol. Eng. 2017, 37, 554–560. [Google Scholar] [CrossRef]
- Mohsen, A.; Al-Mahdawi, M.; Fouda, M.M.; Oogane, M.; Ando, Y.; Fadlullah, Z.M. AI aided noise processing of spintronic based IoT sensor for magnetocardiography application. In Proceedings of the ICC 2020-2020 IEEE International Conference on Communications (ICC), Dublin, Ireland, 7–11 June 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar]
- Sakib, S.; Fouda, M.M.; Al-Mahdawi, M.; Mohsen, A.; Oogane, M.; Ando, Y.; Fadlullah, Z.M. Noise-removal from spectrally-similar signals using reservoir computing for MCG monitoring. In Proceedings of the ICC 2021-IEEE International Conference on Communications, Montreal, QC, Canada, 14–23 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Awal, M.A.; Mostafa, S.S.; Ahmad, M.; Rashid, M.A. An adaptive level dependent wavelet thresholding for ECG denoising. Biocybern. Biomed. Eng. 2014, 34, 238–249. [Google Scholar] [CrossRef]
- Welch, P. The use of fast Fourier transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms. IEEE Trans. Audio Electroacoust. 1967, 15, 70–73. [Google Scholar] [CrossRef]











| Methods | Database | Record | Evaluation Parameters |
|---|---|---|---|
| Variable-frequency complex demodulation (VFCDM) algorithm [59] | MIT-BIH and wearable armband ECG data and NSTDB | 100, 101, 103, 105, 106, 115, 215, 230 | = 4.17 dB, PRD = 5.79%, WEDD = 4.82% (for 20 dB I/P SNR) |
| Singular spectrum analysis and digital filtering [22] | MIT-BIH | 115 | = 29.19 dB, MSE = 0.000307 |
| Fourier decomposition method (FDM) [40] | MIT-BIH | 100, 101, 103, 105, 109, 111, 112, 113, 115, 116, 117, 118, 122, 123, 210, 212 | = 23.0 dB, PRD > 5% (for 5 dB I/P SNR and record 100) |
| Denoising autoencoder (DAE) [45] | 1st China Physiological Signal Challenge 2018 (CPSC) | - | = 13.50 dB (for ) = 20.54 dB (for ) = 23.78 dB (for ) = 25.92 dB (for ) |
| Linear time-invariant filtering and sparse optimization [51] | MIT-BIH | 103, 105, 213 | = 17.87 dB, MSE = 0.003 (for 5 dB I/P SNR and record 103) |
| Recursive filtering [75] | Long-term ST | s20011, s20021, s20031, s20041, s20051, s20061, s20071, s20081, s20091 and s20101 | SNR = 19.12 dB (s20011) |
| Dual-tree wavelet transform [71] | Simulated ECG data | - | = 15.24564 dB, MSE = 0.00044 (for 5 dB I/P SNR) |
| Biorthogonal wavelet transform and Adaptive slope prediction-based threshold [72] | MIT-BIH, BIDMC, PTB, ST | 16 records 15 records 80 + 365 records 17 records | SNR = 28.3821 dB, MSE = 0.0029 |
| Real-time accurate thresholding method and discrete wavelet transform [58] | MIT-BIH | 233 | = 3.03255 dB, RMSE = 0.24123 |
| Recursive filtering [49] | Long-term ST | s20011, s20051, s20061, s20071, s20081 and s20102 | SNR = 14.39 dB (s20012) |
| Riemann–Liouville fractional integral filtering and Savitzky–Golay (SG) filtering and EMD [76] | MIT-BIH | 115 | SNR = 7.6487 dB, MSE = 0.0026 |
| Eigenvalue decomposition of the Hankel matrix [77] | MIT-BIH | 100, 101, 103, 105, 108, 109,111, 112, 113, 115, 116, 117, 118, 121, 122, 123, 210, 211, 212 | = 8.39 dB, PRD ≈ 30% (for 5 dB I/P SNR and record 100) |
| Running denoising autoencoder [78] | Simulated ECG signals | - | ≈ 20 dB, MSE < 0.000005 (for 5 dB I/P SNR) |
| DNN based on the improved DAE and wavelet transform (WT) [70] | MIT-BIH | 103, 105, 111, 116, 122, 205, 213, 219, 223 and 230 | SNR = 23.89 dB, RMSE = 0.025 (for 5 dB I/P SNR and record 103) |
| Fractional Stockwell transform (FrST) [79] | MIT-BIT | 100 and 222 | = 25.0793 dB, RMSE = 0.0397 (for record 100) |
| Methods | Database | Record | Evaluation Parameters |
|---|---|---|---|
| Deep neural network [80] | MIT-BIT | 103, 105, 111, 116, 122, 205, 213, 219, 223 and 230 | SNR = 20.636 dB, RMSE = 0.0446 (for 1.25 dB I/P SNR and avg.) |
| CNN and discrete wavelet transform [81] | MIT-BIH | 103, 105, 111, 116, 122, 205, 213, 219, 223, 230 | SNR = 7.713 dB, RMSE = 0.294 (for 0 dB I/P SNR and avg.) |
| CNN and stationary wavelet transform and transformer encoder [82] | MIT-BIH | 103, 105, 111, 116, 122, 205, 213, 219, 223, 230 | SNR = 29.07 dB, RMSE = 0.017 (for 0 dB I/P SNR) |
| U-Net [73] | PTB-XL, CPSC2018 | Manually label | SNR = 19.51 dB, RMSE = 0.0132 (for 0 dB I/P SNR) |
| Mamba [83] | QT database | - | MSE = 0.3445, PRD = 36.861% |
| Bidirectional gated recurrent units [74] | Experimental data collected using wearable sensors | - | = 20.6 dB, RMSE = 0.024, PRD = 5.5% |
| Methods | Database | Record | Evaluation Parameters |
|---|---|---|---|
| Successive local filtering algorithm [97] | MIT-BIH | 101, 103, 113, 115, 203, 207, 208, 213 | > 8 dB |
| Variable-frequency complex demodulation algorithm [59] | MIT-BIH and NSTDB | 100, 101, 103, 105, 106, 115, 215, 230, Self-acquired data | = 4.17 dB, PRD = 5.79% |
| Stationary wavelet total variation algorithm [102] | MIT-BIH | 100, 103, 105, 113, 115, 117, 119, 122, 200, 215, 213, 230, 231, 234 | SNR = 25.44 dB, RMSE = 0.3940, PRD = 40% |
| Periodic non-local means filter [92] | MIT-BIH | 100, 103, 104, 105, 106, 115, 215 | = 5.804 dB, MSE = 0.0020, PRD > 15% (for 10 dB I/P SNR) |
| Fractional filtering and zero-phase filtering and parallel-type filter [103] | MIT-BIH | 115 | SNR = 13.6817 dB, MSE = 0.0146 |
| Adaptive dual-threshold filter and discrete wavelet transform [104] | MIT-BIH | 115 | MSE = 0.0069 |
| Discrete wavelet transform and electrophysiological morphology [90] | MIT-BIH | All 48 records | = 7.55 dB (for 10 dB I/P SNR) |
| Riemann–Liouville fractional integral filtering and Savitzky–Golay filtering and EMD [76] | MIT-BIH | 115 | SNR = 10.6116 dB, MSE = 0.0013 |
| EMD and adaptive switching mean filter empirical [98] | MIT-BIH | 100, 101, 103, 105, 115, 200, 215, 230 | = 8.7879 dB, MSE = 0.00232, PRD = 11.5257% (for 10 dB I/P SNR) |
| Real-time accurate thresholding method and discrete wavelet transform [58] | MIT-BIH | 233 | = 1.16789 dB, RMSE = 0.12233 |
| CNN and discrete wavelet transform [81] | MIT-BIH | 103, 105, 111, 116, 122, 205, 213, 219, 223, 230 | SNR = 7.738 dB, RMSE = 0.292 (for 0 dB I/P SNR and avg.) |
| CNN and stationary wavelet transform and transformer encoder [82] | MIT-BIH | 103, 105, 111, 116, 122, 205, 213, 219, 223, 230 | SNR = 28.11 dB, RMSE = 0.021 (for 0 dB I/P SNR) |
| U-Net [73] | PTB-XL, CPSC2018 | Manually label | SNR = 16.76 dB, RMSE = 0.0182 (for 0 dB I/P SNR) |
| Bidirectional gated recurrent units [74] | Experimental data collected using wearable sensors | - | = 19.2 dB, RMSE = 0.029, PRD = 6.4% |
| Methods | Database | Record | Evaluation Parameters |
|---|---|---|---|
| Variable-frequency complex demodulation (VFCDM) algorithm [59] | MIT-BIH and wearable armband ECG data and NSTDB | 100, 101, 103, 105, 106, 115, 215, 230 | = 4.17 dB, PRD = 5.79%, WEDD = 4.82% (for 20 dB I/P SNR) |
| Singular spectrum analysis [134] | Simulated data | - | Eave = 0.004 |
| Singular spectrum analysis and digital filtering [22] | MIT-BIH | 115 | Eave = 31.9, MSE = 0.000007 |
| Stationary wavelet transform (SWT) [6] | MIT-BIH | 100, 101, 102, 103, 104, 105, 109, 112, 117, 118, 123, 200, 205, 213, 221, 231, and 234 | = 49.35 dB, RMSE = 0.0006, PRD = 0.254 (for record 100 at 14.32 dB I/P SNR) |
| Fourier decomposition method (FDM) [40] | MIT-BIH | 100, 101, 103, 105, 109, 111, 112, 113, 115, 116, 117, 118, 122, 123, 210, and 212 | = 28.1 dB, PRD > 0% (for 5 dB I/P SNR and record 100) |
| Fractional filtering and zero-phase filtering and parallel-type filter [103] | MIT-BIH | 115 | SNR = 14.2565 dB, MSE = 0.0128 |
| Adaptive dual-threshold filter and discrete wavelet transform [104] | MIT-BIH | 115 | MSE = 0.0015 |
| Biorthogonal wavelet transform and adaptive slope prediction-based threshold [72] | BMDMC | 16 records | SNR = 30.0051 dB, MSE = 0.0008 |
| Riemann–Liouville fractional integral filtering and Savitzky–Golay (SG) filtering and EMD [76] | PTB | 80 + 365 records | SNR = 12.0526 dB, MSE = 0.0096 |
| EMD and adaptive switching mean filter (ASMF) [98] | MIT-BIH | 100, 101, 103, 105, 115, 200, 215, and 230 | > 10 dB, MSE ≈ 0.002, PRD < 10% (for 10 dB I/P SNR) |
| Eigenvalue decomposition of the Hankel matrix [77] | MIT-BIH | 100, 101, 102, 103, 104, 105, 109, 112, 117, 118, 123, 200, 205, 213, 221, 231, and 234 | SNR = 49.35 dB, RMSE = 0.0006, PRD = 0.254 (for record 100 at 14.32 dB I/P SNR) |
| Particle swarm optimization and wavelet transform [117] | MIT-BIH | 100, 102, 103, 105, 109 | SNR = 19.74 dB, MSE = 0.0014, RMSE = 0.0373, PRD = 10.33% (for record 100 at 5 dB I/P SNR) |
| Variational mode decomposition and notch filter [129] | MIT-BIH | 100, 101, 103, 105, 108, 109, 111, 112, 113, 115, 116, 117, 118, 121, 122, 123, 210, and 212 | = 21.09 dB, CC = 0.9898 (for 5 dB I/P SNR and record 100) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, Y.; Pei, H.; Liang, J.; Zhou, Y.; Yang, Y.; Cui, Y.; Xiang, M. Preprocessing and Denoising Techniques for Electrocardiography and Magnetocardiography: A Review. Bioengineering 2024, 11, 1109. https://doi.org/10.3390/bioengineering11111109
Jia Y, Pei H, Liang J, Zhou Y, Yang Y, Cui Y, Xiang M. Preprocessing and Denoising Techniques for Electrocardiography and Magnetocardiography: A Review. Bioengineering. 2024; 11(11):1109. https://doi.org/10.3390/bioengineering11111109
Chicago/Turabian StyleJia, Yifan, Hongyu Pei, Jiaqi Liang, Yuheng Zhou, Yanfei Yang, Yangyang Cui, and Min Xiang. 2024. "Preprocessing and Denoising Techniques for Electrocardiography and Magnetocardiography: A Review" Bioengineering 11, no. 11: 1109. https://doi.org/10.3390/bioengineering11111109
APA StyleJia, Y., Pei, H., Liang, J., Zhou, Y., Yang, Y., Cui, Y., & Xiang, M. (2024). Preprocessing and Denoising Techniques for Electrocardiography and Magnetocardiography: A Review. Bioengineering, 11(11), 1109. https://doi.org/10.3390/bioengineering11111109






