2D/3D Non-Rigid Image Registration via Two Orthogonal X-ray Projection Images for Lung Tumor Tracking
Abstract
1. Introduction
2. Methods
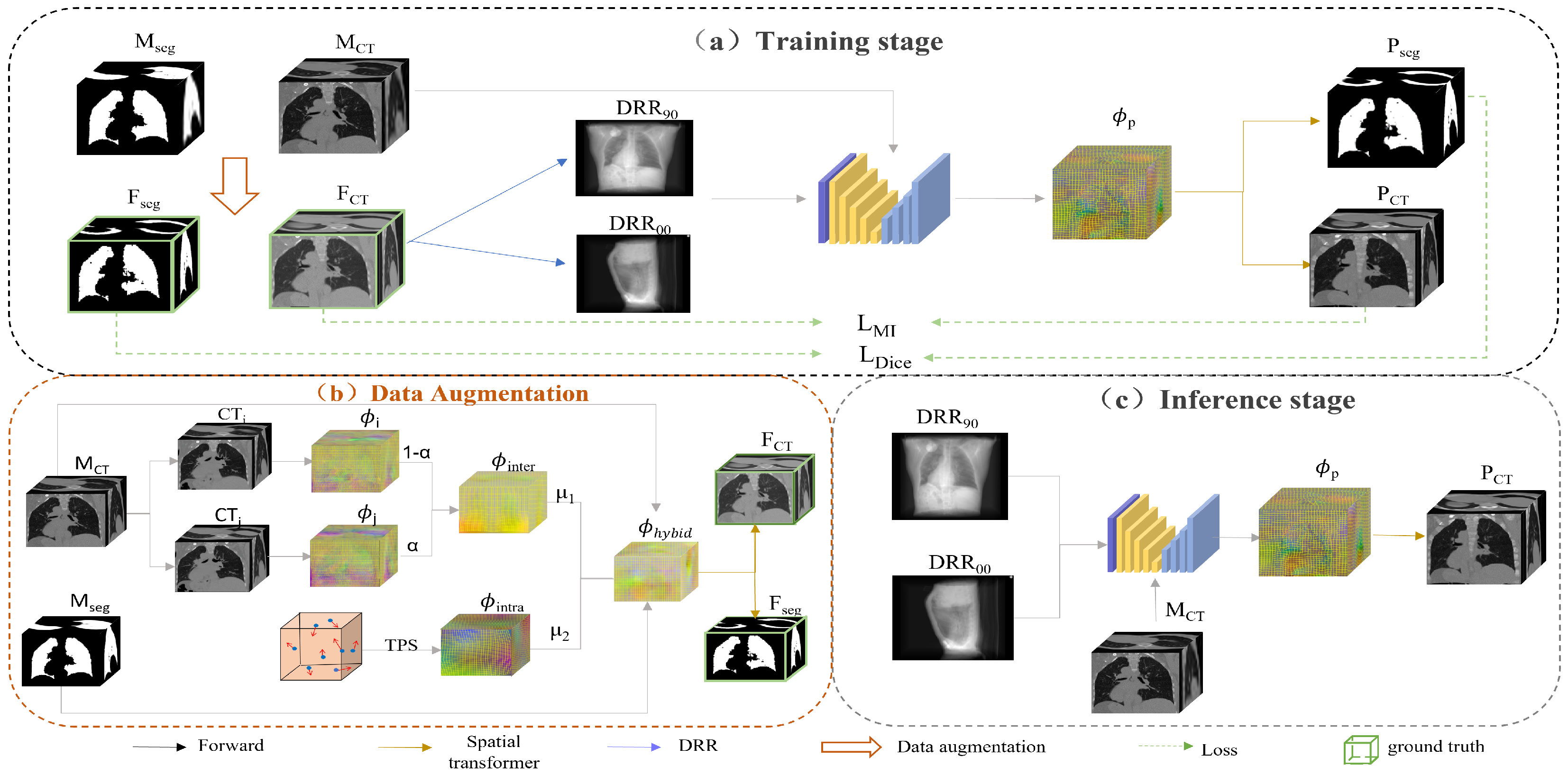
2.1. Overview of the Proposed Method
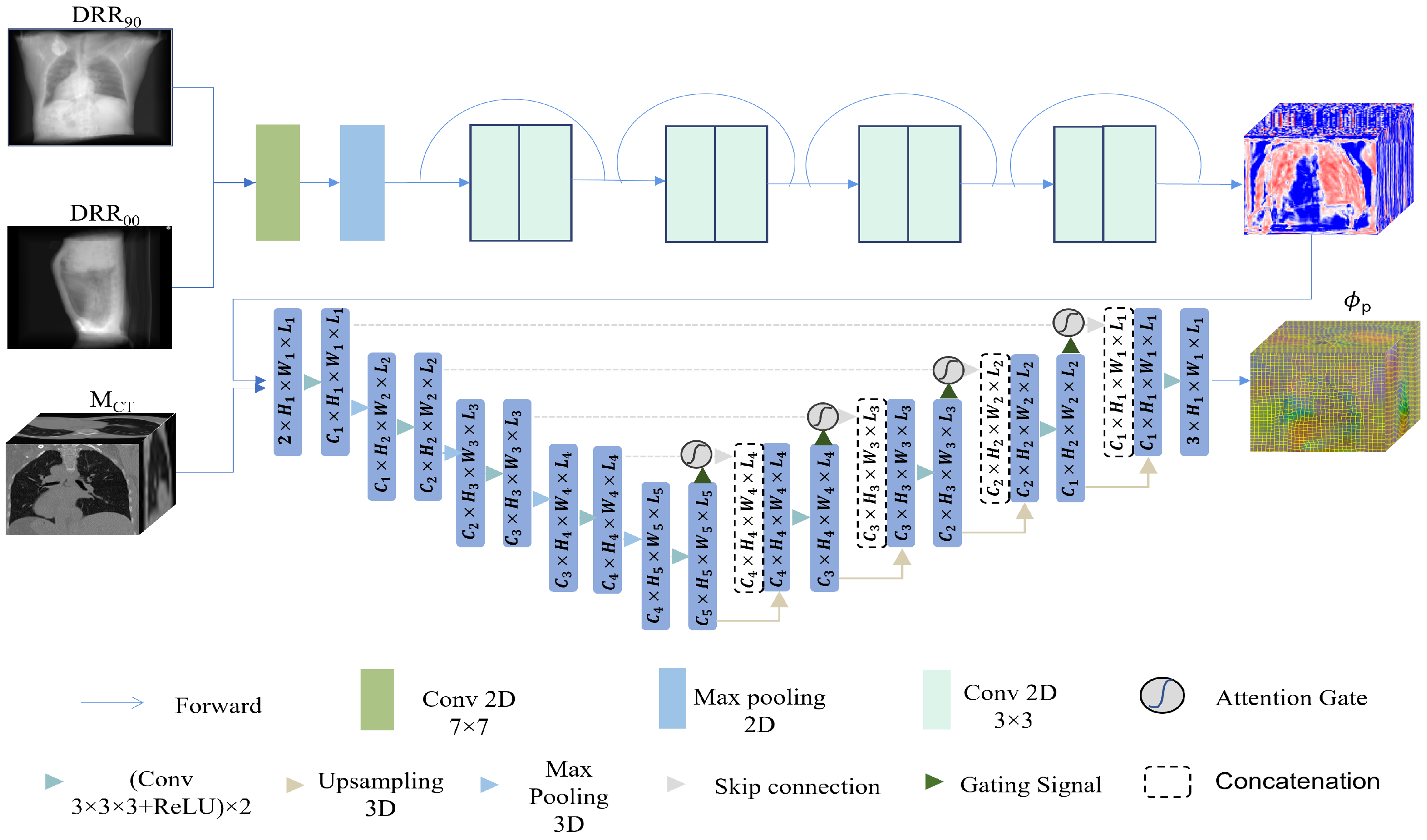
2.2. 2D/3D Registration Network
2.3. Loss Function
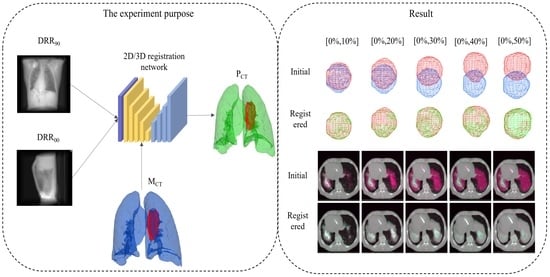
3. Experiment Setups
3.1. Data and Augmentation
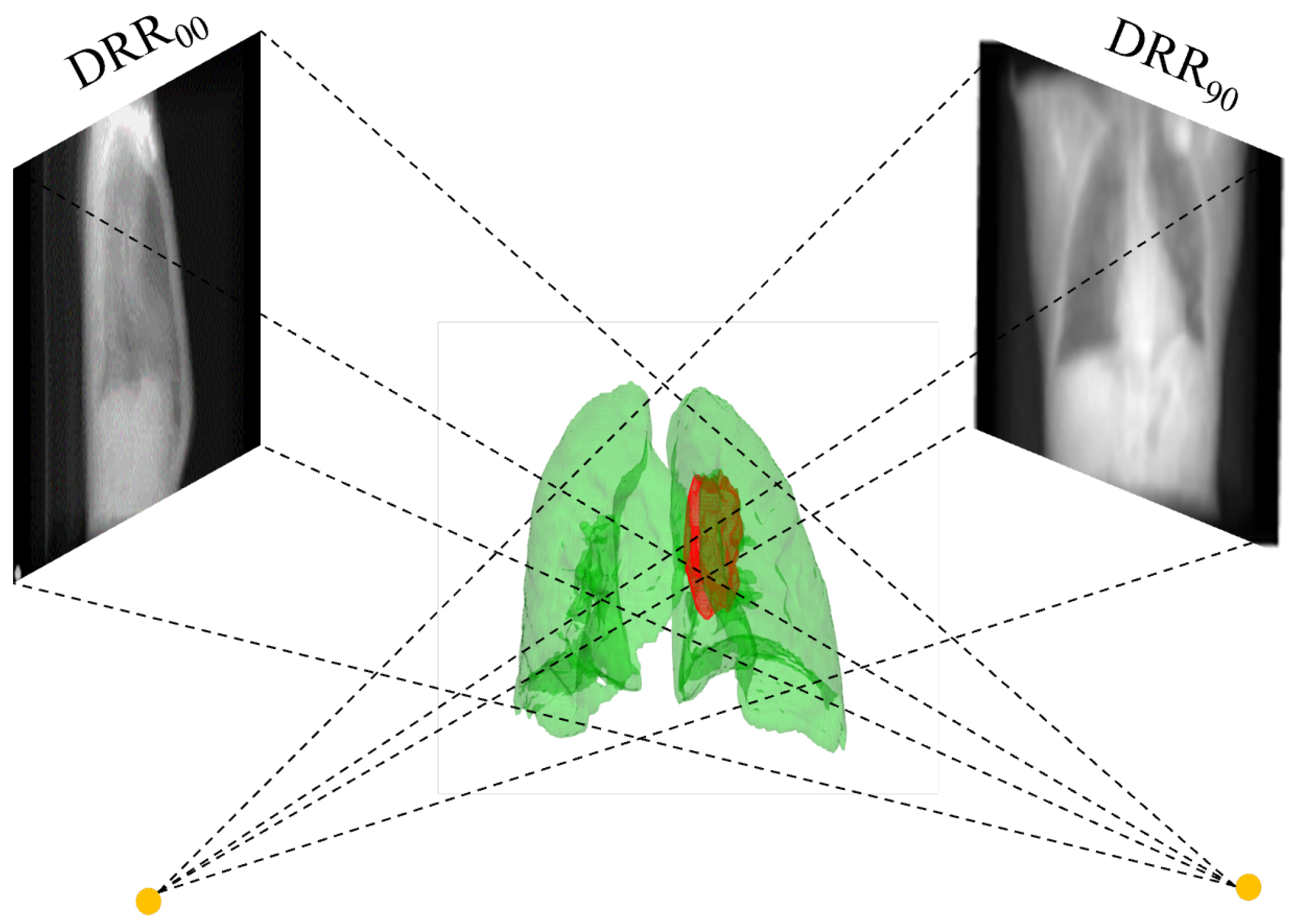
3.2. DRR Image Generation
3.3. Experiment Detail
3.4. Experiment Evaluation
4. Result
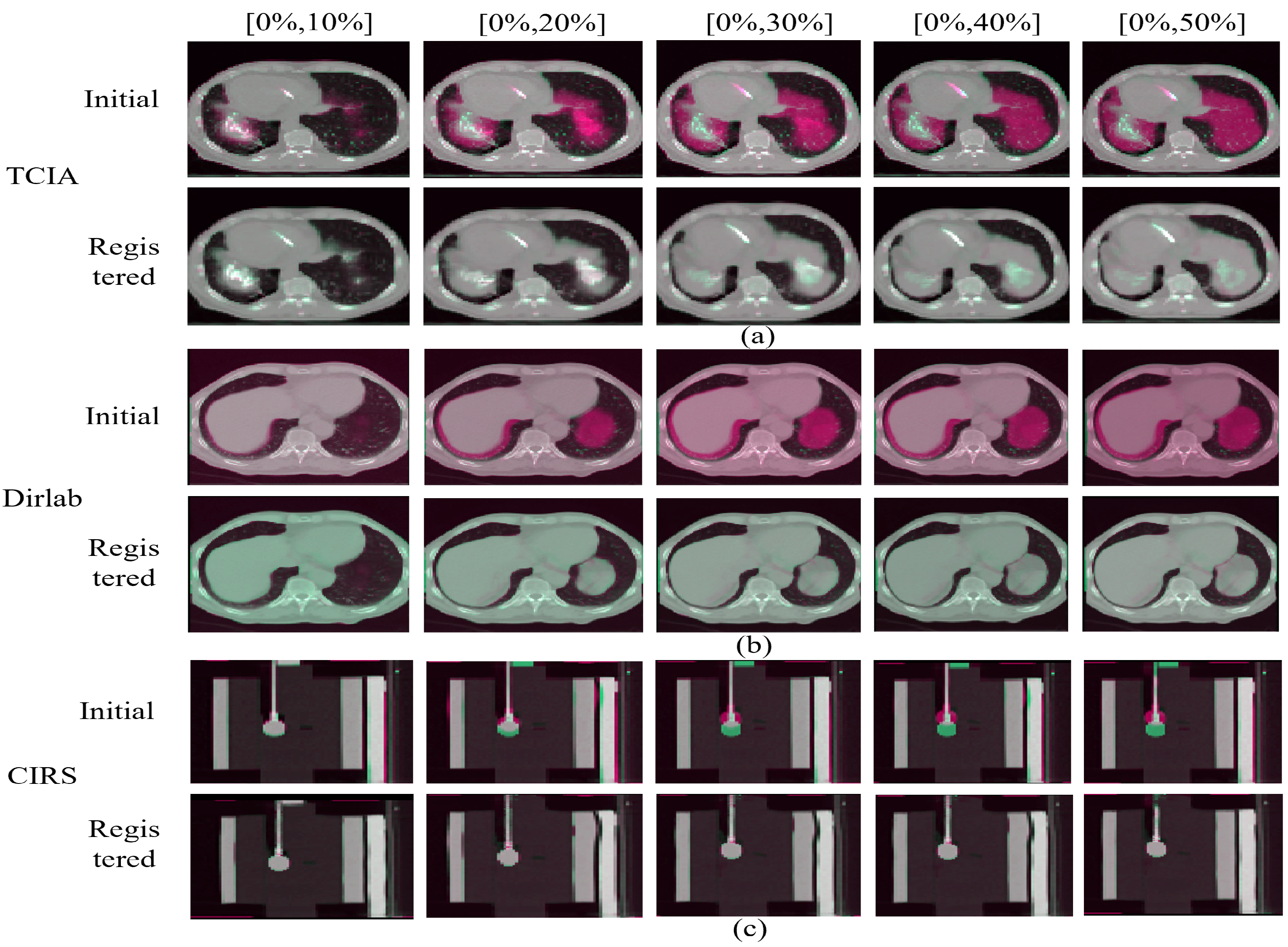
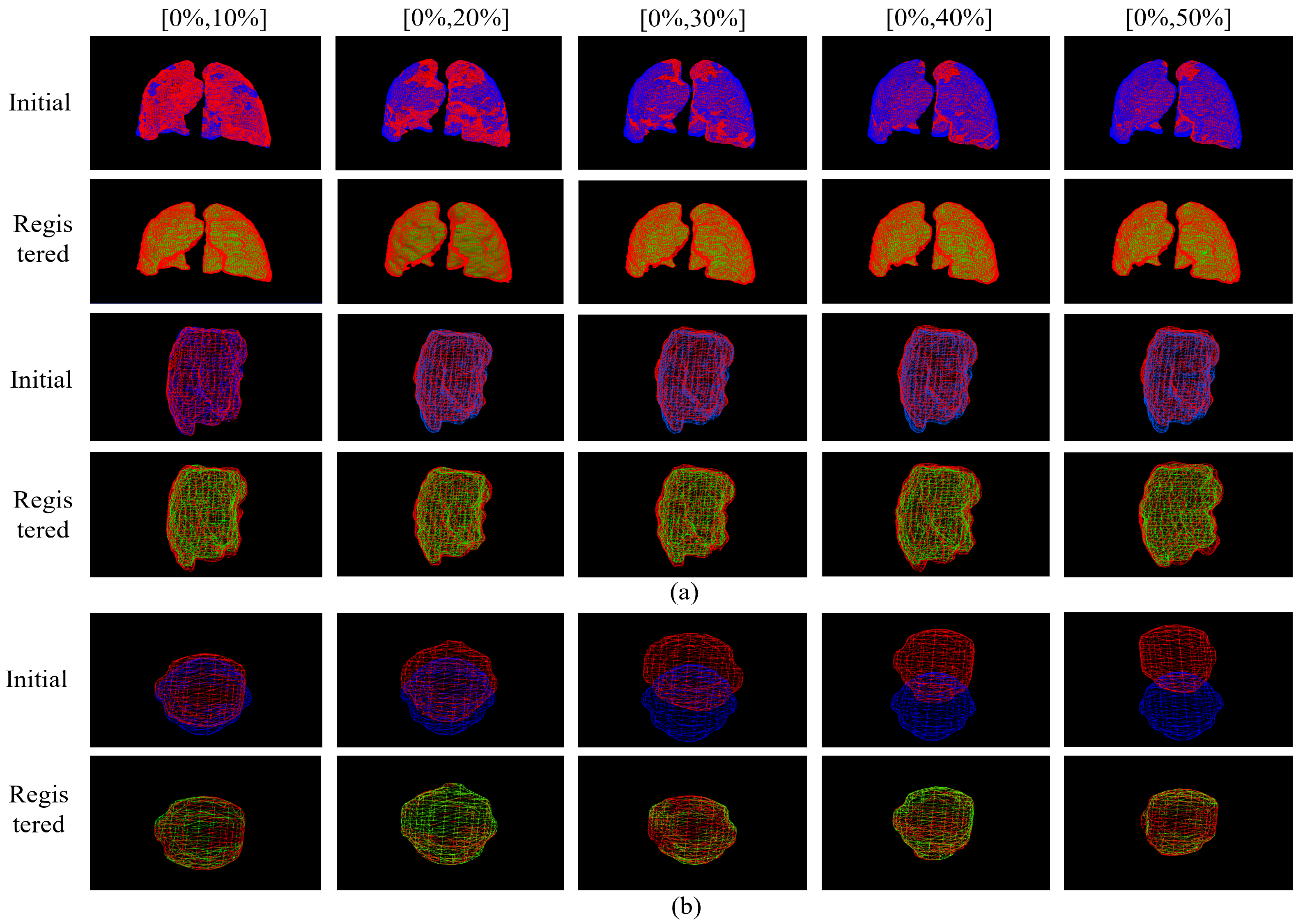
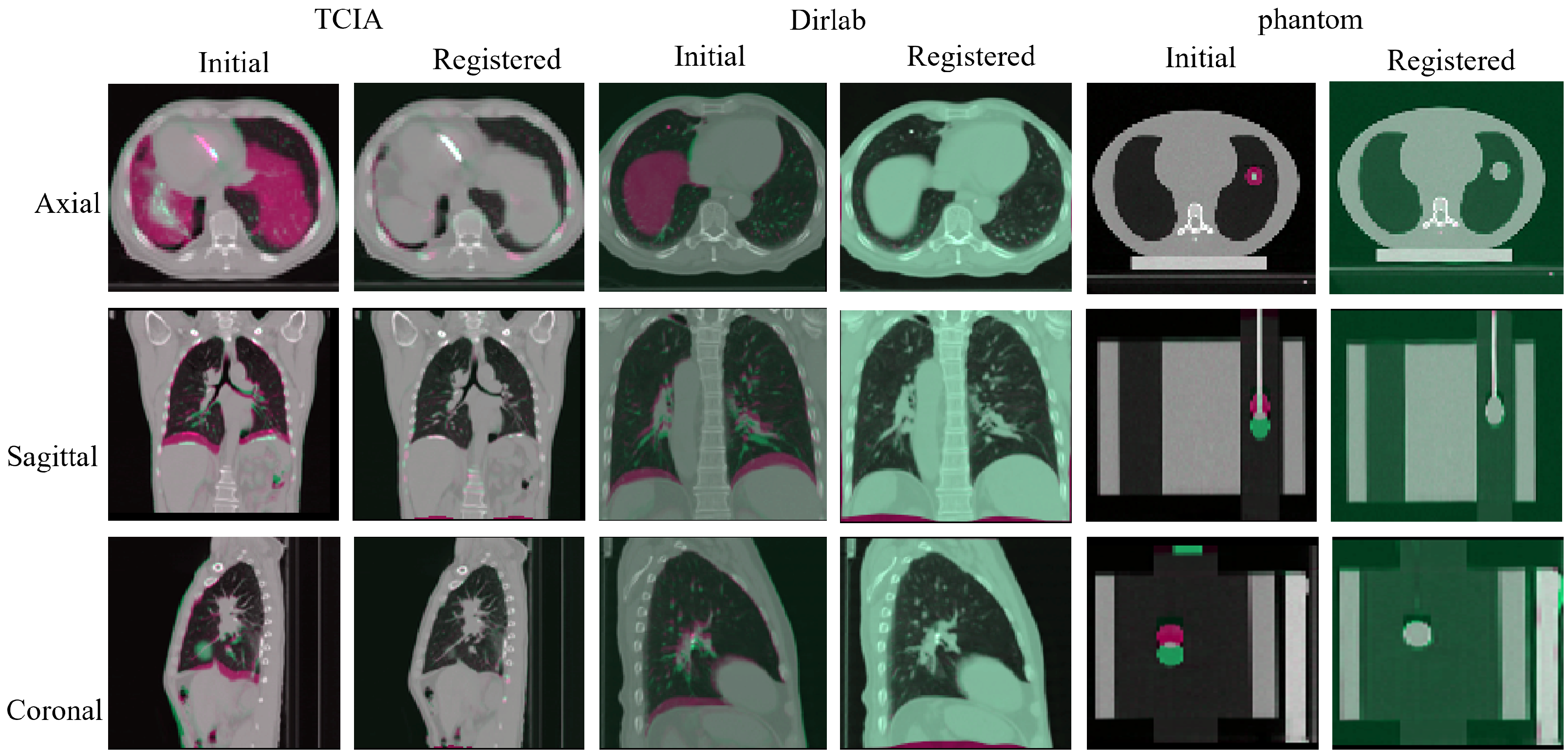
4.1. Registration from the Expiratory End to Each Phase
4.2. Tumor Location
5. Discussion
5.1. Traditional Registration in Data Augmentation
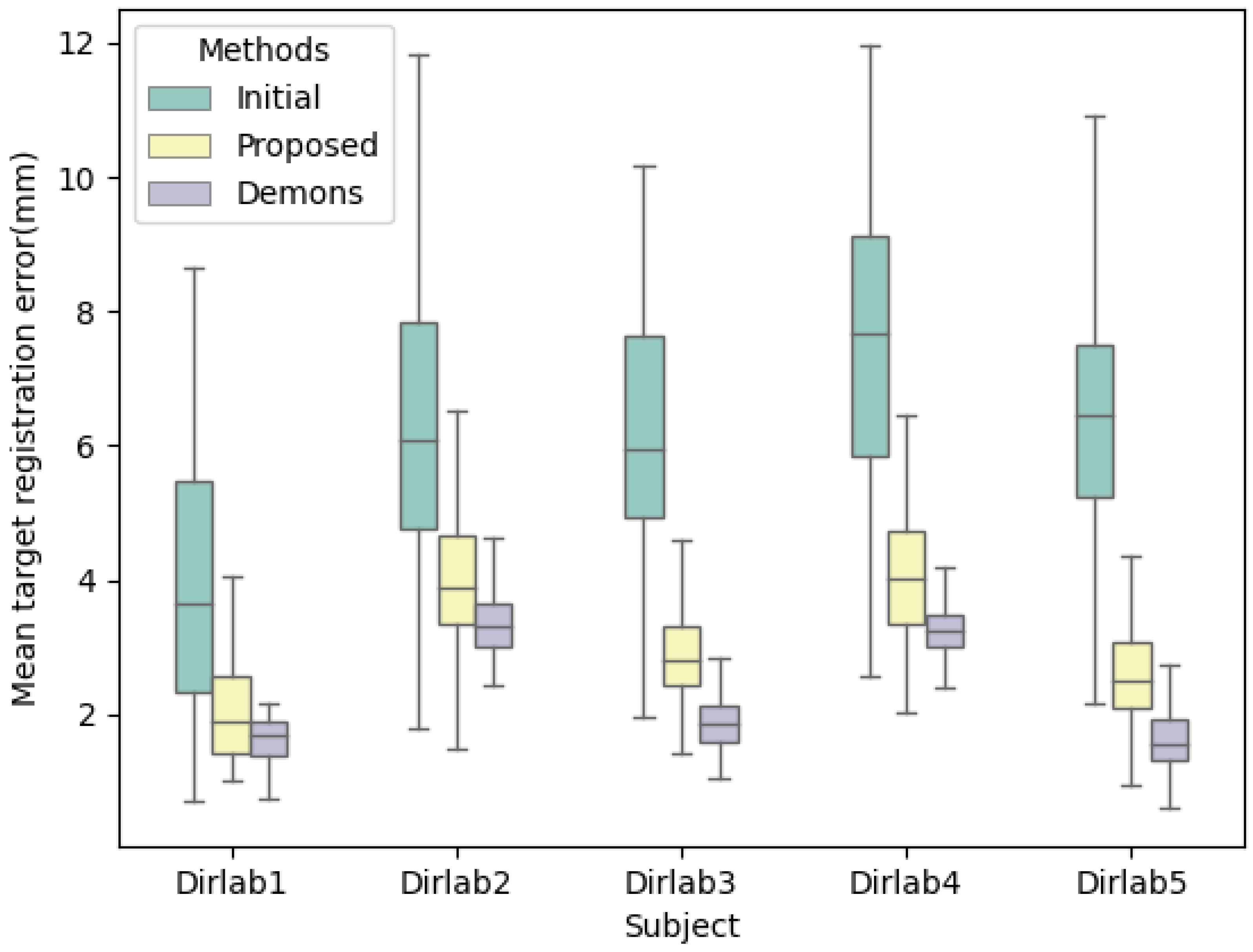
5.2. Landmark Error
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 2D | Two-dimensional |
| 3D | Three-dimensional |
| DSA | Digital Subtraction Angiography |
| CT | Computed Tomography |
| MRI | Magnetic Resonance Imaging |
| DRR | Digitally Reconstructed Radiographs |
| NCC | Normalized cross-correlation |
| PCA | Principal Component Analysis |
| CNN | Convolutional Neural Network |
| GPU | Graphic Processing Unit(GPU) |
| 3D Attu | 3D Attention-U-net |
| MI | Mutual Information |
| TPS | Thin plate spline |
| mTRE | Mean Target Registration Error |
References
- Foote, M.D.; Zimmerman, B.E.; Sawant, A.; Joshi, S.C. Real-time 2D-3D deformable registration with deep learning and application to lung radiotherapy targeting. In Proceedings of the International Conference on Information Processing in Medical Imaging, Hong Kong, 2–7 June 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 265–276. [Google Scholar]
- Frysch, R.; Pfeiffer, T.; Rose, G. A novel approach to 2D/3D registration of X-ray images using Grangeat’s relation. Med. Image Anal. 2021, 67, 101815. [Google Scholar] [CrossRef]
- Van Houtte, J.; Audenaert, E.; Zheng, G.; Sijbers, J. Deep learning-based 2D/3D registration of an atlas to biplanar X-ray images. Int. J. Comput. Assist. Radiol. Surg. 2022, 17, 1333–1342. [Google Scholar] [CrossRef]
- Li, P.; Pei, Y.; Guo, Y.; Ma, G.; Xu, T.; Zha, H. Non-rigid 2D-3D registration using convolutional autoencoders. In Proceedings of the 2020 IEEE 17th International Symposium on Biomedical Imaging (ISBI), Iowa City, IA, USA, 3–7 April 2020; IEEE: New York, NY, USA, 2020; pp. 700–704. [Google Scholar]
- Wang, C.; Xie, S.; Li, K.; Wang, C.; Liu, X.; Zhao, L.; Tsai, T.Y. Multi-View Point-Based Registration for Native Knee Kinematics Measurement with Feature Transfer Learning. Engineering 2021, 7, 881–888. [Google Scholar] [CrossRef]
- Guan, S.; Wang, T.; Sun, K.; Meng, C. Transfer learning for nonrigid 2d/3d cardiovascular images registration. IEEE J. Biomed. Health Inform. 2020, 25, 3300–3309. [Google Scholar] [CrossRef]
- Miao, S.; Wang, Z.J.; Liao, R. A CNN regression approach for real-time 2D/3D registration. IEEE Trans. Med. Imaging 2016, 35, 1352–1363. [Google Scholar] [CrossRef]
- Markova, V.; Ronchetti, M.; Wein, W.; Zettinig, O.; Prevost, R. Global Multi-modal 2D/3D Registration via Local Descriptors Learning. arXiv 2022, arXiv:2205.03439. [Google Scholar]
- Zheng, G. Effective incorporating spatial information in a mutual information based 3D–2D registration of a CT volume to X-ray images. Comput. Med. Imaging Graph. 2010, 34, 553–562. [Google Scholar] [CrossRef]
- Zollei, L.; Grimson, E.; Norbash, A.; Wells, W. 2D-3D rigid registration of X-ray fluoroscopy and CT images using mutual information and sparsely sampled histogram estimators. In Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, CVPR 2001, Kauai, HI, USA, 8–14 December 2021; IEEE: New York, NY, USA, 2001; Volume 2, p. II. [Google Scholar]
- Gendrin, C.; Furtado, H.; Weber, C.; Bloch, C.; Figl, M.; Pawiro, S.A.; Bergmann, H.; Stock, M.; Fichtinger, G.; Georg, D.; et al. Monitoring tumor motion by real time 2D/3D registration during radiotherapy. Radiother. Oncol. 2012, 102, 274–280. [Google Scholar] [CrossRef]
- Gao, C.; Grupp, R.B.; Unberath, M.; Taylor, R.H.; Armand, M. Fiducial-free 2D/3D registration of the proximal femur for robot-assisted femoroplasty. IEEE Trans. Med. Robot. Bionics 2020, 11315, 350–355. [Google Scholar]
- Munbodh, R.; Knisely, J.P.; Jaffray, D.A.; Moseley, D.J. 2D–3D registration for cranial radiation therapy using a 3D kV CBCT and a single limited field-of-view 2D kV radiograph. Med. Phys. 2018, 45, 1794–1810. [Google Scholar] [CrossRef]
- De Silva, T.; Uneri, A.; Ketcha, M.; Reaungamornrat, S.; Kleinszig, G.; Vogt, S.; Aygun, N.; Lo, S.; Wolinsky, J.; Siewerdsen, J. 3D–2D image registration for target localization in spine surgery: Investigation of similarity metrics providing robustness to content mismatch. Phys. Med. Biol. 2016, 61, 3009. [Google Scholar] [CrossRef]
- Yu, W.; Tannast, M.; Zheng, G. Non-rigid free-form 2D–3D registration using a B-spline-based statistical deformation model. Pattern Recognit. 2017, 63, 689–699. [Google Scholar] [CrossRef]
- Li, R.; Jia, X.; Lewis, J.H.; Gu, X.; Folkerts, M.; Men, C.; Jiang, S.B. Real-time volumetric image reconstruction and 3D tumor localization based on a single x-ray projection image for lung cancer radiotherapy. Med. Phys. 2010, 37, 2822–2826. [Google Scholar] [CrossRef]
- Li, R.; Lewis, J.H.; Jia, X.; Gu, X.; Folkerts, M.; Men, C.; Song, W.Y.; Jiang, S.B. 3D tumor localization through real-time volumetric x-ray imaging for lung cancer radiotherapy. Med. Phys. 2011, 38, 2783–2794. [Google Scholar] [CrossRef]
- Zhang, Y.; Tehrani, J.N.; Wang, J. A biomechanical modeling guided CBCT estimation technique. IEEE Trans. Med. Imaging 2016, 36, 641–652. [Google Scholar] [CrossRef]
- Zhang, Y.; Folkert, M.R.; Li, B.; Huang, X.; Meyer, J.J.; Chiu, T.; Lee, P.; Tehrani, J.N.; Cai, J.; Parsons, D. 4D liver tumor localization using cone-beam projections and a biomechanical model. Radiother. Oncol. 2019, 133, 183–192. [Google Scholar] [CrossRef]
- Zhang, Y. An unsupervised 2D–3D deformable registration network (2D3D-RegNet) for cone-beam CT estimation. Phys. Med. Biol. 2021, 66, 074001. [Google Scholar] [CrossRef]
- Ketcha, M.; De Silva, T.; Uneri, A.; Jacobson, M.; Goerres, J.; Kleinszig, G.; Vogt, S.; Wolinsky, J.; Siewerdsen, J. Multi-stage 3D–2D registration for correction of anatomical deformation in image-guided spine surgery. Phys. Med. Biol. 2017, 62, 4604. [Google Scholar] [CrossRef]
- Zhang, Y.; Qin, H.; Li, P.; Pei, Y.; Guo, Y.; Xu, T.; Zha, H. Deformable registration of lateral cephalogram and cone-beam computed tomography image. Med. Phys. 2021, 48, 6901–6915. [Google Scholar] [CrossRef]
- Gao, C.; Liu, X.; Gu, W.; Killeen, B.; Armand, M.; Taylor, R.; Unberath, M. Generalizing spatial transformers to projective geometry with applications to 2D/3D registration. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Lima, Peru, 4–8 October 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 329–339. [Google Scholar]
- Wei, R.; Liu, B.; Zhou, F.; Bai, X.; Fu, D.; Liang, B.; Wu, Q. A patient-independent CT intensity matching method using conditional generative adversarial networks (cGAN) for single x-ray projection-based tumor localization. Phys. Med. Biol. 2020, 65, 145009. [Google Scholar] [CrossRef]
- Wei, R.; Zhou, F.; Liu, B.; Bai, X.; Fu, D.; Liang, B.; Wu, Q. Real-time tumor localization with single X-ray projection at arbitrary gantry angles using a convolutional neural network (CNN). Phys. Med. Biol. 2020, 65, 065012. [Google Scholar] [CrossRef]
- Van Houtte, J.; Gao, X.; Sijbers, J.; Zheng, G. 2D/3D registration with a statistical deformation model prior using deep learning. In Proceedings of the 2021 IEEE EMBS international conference on biomedical and health informatics (BHI), Athens, Greece, NY, USA, 2021, 27–30 July 2021; IEEE: New York; pp. 1–4. [Google Scholar]
- Pei, Y.; Zhang, Y.; Qin, H.; Ma, G.; Guo, Y.; Xu, T.; Zha, H. Non-rigid craniofacial 2D-3D registration using CNN-based regression. In Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support; Springer: Berlin/Heidelberg, Germany, 2017; pp. 117–125. [Google Scholar]
- Tian, L.; Lee, Y.Z.; San José Estépar, R.; Niethammer, M. LiftReg: Limited Angle 2D/3D Deformable Registration. In Proceedings of the Medical Image Computing and Computer Assisted Intervention—MICCAI 2022, Singapore, 18–22 September 2022; Wang, L., Dou, Q., Fletcher, P.T., Speidel, S., Li, S., Eds.; Springer Nature: Cham, Switzerland, 2022; pp. 207–216. [Google Scholar]
- Liao, H.; Lin, W.A.; Zhang, J.; Zhang, J.; Luo, J.; Zhou, S.K. Multiview 2D/3D rigid registration via a point-of-interest network for tracking and triangulation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 12638–12647. [Google Scholar]
- Markova, V.; Ronchetti, M.; Wein, W.; Zettinig, O.; Prevost, R. Global Multi-modal 2D/3D Registration via Local Descriptors Learning. In Proceedings of the Medical Image Computing and Computer Assisted Intervention—MICCAI 2022, Singapore, 18–22 September 2022; Wang, L., Dou, Q., Fletcher, P.T., Speidel, S., Li, S., Eds.; Springer Nature: Cham, Switzerland, 2022; pp. 269–279. [Google Scholar]
- Schaffert, R.; Wang, J.; Fischer, P.; Borsdorf, A.; Maier, A. Learning an attention model for robust 2-D/3-D registration using point-to-plane correspondences. IEEE Trans. Med. Imaging 2020, 39, 3159–3174. [Google Scholar] [CrossRef]
- Schaffert, R.; Wang, J.; Fischer, P.; Borsdorf, A.; Maier, A. Metric-driven learning of correspondence weighting for 2-D/3-D image registration. In Proceedings of the German Conference on Pattern Recognition, Stuttgart, Germany, Germany, 2019, 9–12 October 2019; Springer: Berlin/Heidelberg; pp. 140–152. [Google Scholar]
- Schaffert, R.; Wang, J.; Fischer, P.; Maier, A.; Borsdorf, A. Robust multi-view 2-d/3-d registration using point-to-plane correspondence model. IEEE Trans. Med. Imaging 2019, 39, 161–174. [Google Scholar] [CrossRef]
- Nakao, M.; Nakamura, M.; Matsuda, T. Image-to-Graph Convolutional Network for 2D/3D Deformable Model Registration of Low-Contrast Organs. IEEE Trans. Med. Imaging 2022, 41, 3747–3761. [Google Scholar] [CrossRef]
- Shao, H.C.; Wang, J.; Bai, T.; Chun, J.; Park, J.C.; Jiang, S.; Zhang, Y. Real-time liver tumor localization via a single x-ray projection using deep graph neural network-assisted biomechanical modeling. Phys. Med. Biol. 2022, 67, 115009. [Google Scholar] [CrossRef]
- Liang, X.; Zhao, W.; Hristov, D.H.; Buyyounouski, M.K.; Hancock, S.L.; Bagshaw, H.; Zhang, Q.; Xie, Y.; Xing, L. A deep learning framework for prostate localization in cone beam CT-guided radiotherapy. Med. Phys. 2020, 47, 4233–4240. [Google Scholar] [CrossRef]
- Liang, X.; Li, N.; Zhang, Z.; Xiong, J.; Zhou, S.; Xie, Y. Incorporating the hybrid deformable model for improving the performance of abdominal CT segmentation via multi-scale feature fusion network. Med. Image Anal. 2021, 73, 102156. [Google Scholar] [CrossRef]
- Jaderberg, M.; Simonyan, K.; Zisserman, A.; Kavukcouglu, K. Spatial transformer networks. Adv. Neural Inf. Process. Syst. 2015, 28, 2017–2025. [Google Scholar]
- Schlemper, J.; Oktay, O.; Schaap, M.; Heinrich, M.; Kainz, B.; Glocker, B.; Rueckert, D. Attention gated networks: Learning to leverage salient regions in medical images. Med. Image Anal. 2019, 53, 197–207. [Google Scholar] [CrossRef]
- Hugo, G.D.; Weiss, E.; Sleeman, W.C.; Balik, S.; Keall, P.J.; Lu, J.; Williamson, J.F. Data from 4d lung imaging of nsclc patients. Med. Phys. 2017, 44, 762–771. [Google Scholar] [CrossRef]
- Balik, S.; Weiss, E.; Jan, N.; Roman, N.; Sleeman, W.C.; Fatyga, M.; Christensen, G.E.; Zhang, C.; Murphy, M.J.; Lu, J.; et al. Evaluation of 4-dimensional computed tomography to 4-dimensional cone-beam computed tomography deformable image registration for lung cancer adaptive radiation therapy. Int. J. Radiat. Oncol. Biol. Phys. 2013, 86, 372–379. [Google Scholar] [CrossRef] [PubMed]
- Clark, K.; Vendt, B.; Smith, K.; Freymann, J.; Kirby, J.; Koppel, P.; Moore, S.; Phillips, S.; Maffitt, D.; Pringle, M.; et al. The Cancer Imaging Archive (TCIA): Maintaining and operating a public information repository. J. Digit. Imaging 2013, 26, 1045–1057. [Google Scholar] [CrossRef]
- Roman, N.O.; Shepherd, W.; Mukhopadhyay, N.; Hugo, G.D.; Weiss, E. Interfractional positional variability of fiducial markers and primary tumors in locally advanced non-small-cell lung cancer during audiovisual biofeedback radiotherapy. Int. J. Radiat. Oncol. Biol. Phys. 2012, 83, 1566–1572. [Google Scholar] [CrossRef]
- Castillo, R.; Castillo, E.; Guerra, R.; Johnson, V.E.; McPhail, T.; Garg, A.K.; Guerrero, T. A framework for evaluation of deformable image registration spatial accuracy using large landmark point sets. Phys. Med. Biol. 2009, 54, 1849. [Google Scholar] [CrossRef] [PubMed]
- Vercauteren, T.; Pennec, X.; Perchant, A.; Ayache, N. Diffeomorphic demons: Efficient non-parametric image registration. NeuroImage 2009, 45, S61–S72. [Google Scholar] [CrossRef]
| Dice | Hauf (95%) | NCC | MI | ||
|---|---|---|---|---|---|
| TCIA | [0%,10%] | 0.9814 | 1.1210 | 0.9846 | 0.9796 |
| [0%,20%] | 0.9791 | 1.3811 | 0.9846 | 0.9760 | |
| [0%,30%] | 0.9795 | 1.3811 | 0.9847 | 0.9540 | |
| [0%,40%] | 0.9785 | 1.3811 | 0.9846 | 0.9578 | |
| [0%,50%] | 0.9806 | 1.4196 | 0.9848 | 0.9650 | |
| Dirlab | [0%,10%] | 0.9857 | 1.8839 | 0.9762 | 0.9590 |
| [0%,20%] | 0.9857 | 1.8620 | 0.9723 | 0.9535 | |
| [0%,30%] | 0.9853 | 1.8280 | 0.9691 | 0.9511 | |
| [0%,40%] | 0.9853 | 1.8290 | 0.9680 | 0.9424 | |
| [0%,50%] | 0.9854 | 1.8290 | 0.9753 | 0.9608 | |
| CIRS | [0%,10%] | 0.9862 | 0.9043 | 0.9338 | 0.9135 |
| [0%,20%] | 0.9907 | 1.6713 | 0.9291 | 0.9023 | |
| [0%,30%] | 0.9888 | 2.0000 | 0.9360 | 0.9064 | |
| [0%,40%] | 0.9885 | 1.9087 | 0.9348 | 0.9065 | |
| [0%,50%] | 0.9894 | 1.9087 | 0.9349 | 0.9178 |
| Center Mass (mm) | Dice | |||||
|---|---|---|---|---|---|---|
| X(LR) | Y(AP) | Z(LR) | Center | Tomor | ||
| TCIA | [0%,10%] | 0.0003 | 0.0473 | 0.0844 | 0.0968 | 0.9440 |
| [0%,20%] | 0.0117 | 0.0133 | 0.0260 | 0.0315 | 0.9434 | |
| [0%,30%] | 0.0031 | 0.0023 | 0.0473 | 0.0022 | 0.9023 | |
| [0%,40%] | 0.0032 | 0.0078 | 0.0339 | 0.0350 | 0.9080 | |
| [0%,50%] | 0.0227 | 0.0510 | 0.1251 | 0.1370 | 0.8984 | |
| CIRS | [0%,10%] | 0.0224 | 0.0011 | 0.0270 | 0.0351 | 0.9717 |
| [0%,20%] | 0.0061 | 0.0025 | 0.0081 | 0.0104 | 0.9764 | |
| [0%,30%] | 0.0086 | 0.0018 | 0.0158 | 0.0181 | 0.9609 | |
| [0%,40%] | 0.0174 | 0.0177 | 0.0084 | 0.0262 | 0.9702 | |
| [0%,50%] | 0.0022 | 0.0043 | 0.0477 | 0.0479 | 0.8826 | |
| (mm) | Initial | Proposed (2D/3D) | Demons (3D/3D) |
|---|---|---|---|
| Dirlab1 | 3.9776 (1.8616) | 2.0065 (0.6748) | 1.6297 (0.3196) |
| Dirlab2 | 6.3989 (2.1719) | 4.0079 (1.0077) | 3.3807 (0.5089) |
| Dirlab3 | 6.2138 (1.7843) | 2.9219 (0.7237) | 2.1556 (0.2991) |
| Dirlab4 | 7.6437 (2.3978) | 4.0682 (0.9898) | 3.2525 (0.3918) |
| Dirlab5 | 6.6075 (2.1448) | 2.6253 (0.7719) | 1.6408 (0.4824) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, G.; Dai, J.; Li, N.; Zhang, C.; He, W.; Liu, L.; Chan, Y.; Li, Y.; Xie, Y.; Liang, X. 2D/3D Non-Rigid Image Registration via Two Orthogonal X-ray Projection Images for Lung Tumor Tracking. Bioengineering 2023, 10, 144. https://doi.org/10.3390/bioengineering10020144
Dong G, Dai J, Li N, Zhang C, He W, Liu L, Chan Y, Li Y, Xie Y, Liang X. 2D/3D Non-Rigid Image Registration via Two Orthogonal X-ray Projection Images for Lung Tumor Tracking. Bioengineering. 2023; 10(2):144. https://doi.org/10.3390/bioengineering10020144
Chicago/Turabian StyleDong, Guoya, Jingjing Dai, Na Li, Chulong Zhang, Wenfeng He, Lin Liu, Yinping Chan, Yunhui Li, Yaoqin Xie, and Xiaokun Liang. 2023. "2D/3D Non-Rigid Image Registration via Two Orthogonal X-ray Projection Images for Lung Tumor Tracking" Bioengineering 10, no. 2: 144. https://doi.org/10.3390/bioengineering10020144
APA StyleDong, G., Dai, J., Li, N., Zhang, C., He, W., Liu, L., Chan, Y., Li, Y., Xie, Y., & Liang, X. (2023). 2D/3D Non-Rigid Image Registration via Two Orthogonal X-ray Projection Images for Lung Tumor Tracking. Bioengineering, 10(2), 144. https://doi.org/10.3390/bioengineering10020144