Tactical Helicopter Transportation Planning for Offshore Personnel on the Norwegian Continental Shelf

Abstract

Background: In offshore energy logistics, contracted helicopters frequently transport personnel to and from offshore installations. Regular and efficient transportation is vital to maintain planned activities at the installations. We focus on tactical helicopter planning from a single heliport for a period of stable weekly transport demands in a heliport operating area on the Norwegian Continental Shelf (NCS). This results in the construction of a repetitive weekly flight program, integrating the selection of helicopter resources optimally matching demand with the generation of a weekly timetable of flights assigning them to start times. The purpose of our research is to develop optimisation-based weekly flight program planning algorithms for energy companies operating on the NCS. Methods: We present a developed two-step solution method sequentially generating possible flights and solving a flight-based integer programming model, and an iterative algorithm based on the decomposition of the flight-based model for the construction of cost-optimal weekly flight programs. Results: The developed algorithms were validated on the real instances from Equinor, the largest NCS energy operator. The decomposition-based algorithm was able to solve to optimality all tested instances, with up to 20 installations served from the heliport within less than 9 min. Conclusions: Equinor logistics planners have tested and verified that the developed flight-based model satisfies the goals and planning policies imposed on the NCS for integrated tactical helicopter planning. Considering the advantages of the decomposition-based algorithm performance in solution quality and speed, energy companies on the NCS find it well-suited as a solution engine in the highly demanded automated decision support tools for tactical helicopter transportation planning.

1. Introduction

Offshore-produced oil and gas are important contributors to the world energy mix. There are over 50 countries with offshore oil and gas production [1], with some of the largest producers being Saudi Arabia, Qatar, Iran, Norway, Brazil, the United States, and Mexico. For Norway, the offshore energy industry is of great importance. The country has benefitted from increased welfare due to jobs and technology development since the start of oil and gas exploration in the 1960s. In 2023, Norway was the eighth largest natural gas producer and the 12th largest oil producer in the world [2] with total offshore production at 235 million standard cubic meters of oil equivalents and an export value of around NOK 1200 billion, amounting to 62% of total exports from Norway [3]. The export of natural gas is also vital to the energy supply in Europe, with Norway being the European Union’s largest supplier of natural gas in a gaseous state as of Q3 2024 [4].

This section presents offshore oil and gas operation areas on the Norwegian Continental Shelf (NCS) and the existing upstream logistics infrastructure, with a focus on offshore personnel transportation operations. It is followed by the suggested general definitions of logistics planning levels and the review of research results on transportation of offshore personnel with helicopters. The Section concludes with the goals and objectives of the research presented here, scientific contributions, the practical applicability and adaptivity of research results, and the structure of the paper.

1.1. Offshore Upstream Logistics Infrastructure on the NCS

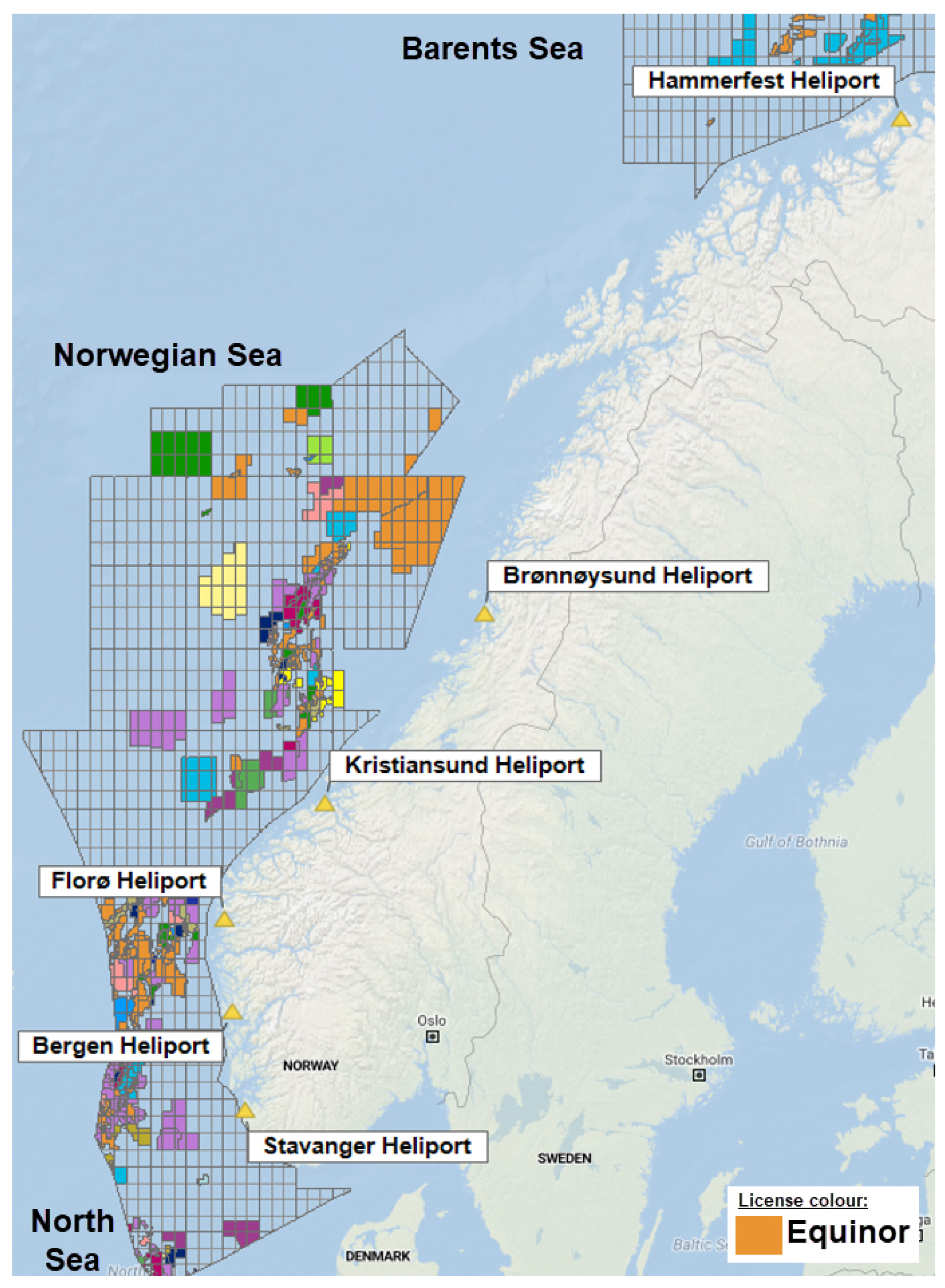
In Norway, oil and gas exploration and production areas are located in the North Sea, the Norwegian Sea, and the Barents Sea on the NCS, divided in blocks as shown in Figure 1. Companies must obtain licenses granted by the Ministry of Energy to explore and produce oil and gas. The colour of the block represents which company is the responsible operator of the licence. Currently, there are 56 fixed offshore installations and at any time approximately 20–30 mobile rigs and vessels operating on the NCS. Among the 17 operator companies with currently active licenses on the NCS [5], the largest is the Norwegian company Equinor, responsible for about 70% of the total NCS oil and gas production [6]. Discoveries may be developed into large offshore fields with a high concentration of installations, like the Sleipner, Oseberg, Troll, Gullfaks, Statfjord, and Snorre fields, all operated by Equinor.

Technological developments have enabled the operators on the NCS to explore and produce further away from shore, in deeper waters and in harsh weather environments, which is challenging not only from an exploration and production perspective but also with regards to logistics. The term upstream offshore logistics is used for activities related to the supply of oil and gas installations with cargo and personnel. This requires frequent planned departures of specialised offshore supply vessels and helicopters from supply bases and airport bases, called heliports, to offshore installations. It is important for the operating companies to guarantee the regular on time transport of cargo and personnel to keep stable production and avoid delays in the planned activities. The existing upstream logistics infrastructure on the NCS shown in Figure 1 includes the heliports in Stavanger, Bergen, Florø, Kristiansund, Brønnøysund, and Hammerfest, with the nearby located onshore supply bases.

This paper is devoted to the tactical helicopter transportation planning for offshore personnel on the NCS. Personnel transportation operations on the NCS are extensive and complex. In 2023, approximately 260,000 passengers were transported to the offshore installations requiring crew change [7], including 165,000 for Equinor. The number of personnel on board (POB) on the NCS ranges from small installations with around 20 POB, to the large, interconnected installations with 400 POB. The number of offshore installations to be served from one heliport just for Equinor can be up to twenty. The information and real industry data on helicopter personnel transportation planning on the NCS as in the other offshore oil and gas operations areas are not publicly available and are mainly presented through research projects conducted in cooperation with industry. The following subsection presents our description of the offshore helicopter transportation planning process, embracing the three planning levels, aiming to make it general for all offshore areas. The suggested definitions of planning inputs and outputs at all levels are based on the analysis of the reviewed references and current research.

1.2. Offshore Helicopter Transportation: Planning Levels and Research Review

Offshore helicopter transportation planning is usually carried out for a specific region or area of operations by the operating company’s own logistics experts, based on planned activities and helicopter services rented in the regional helicopter markets from so-called helicopter operators. The planning process is divided into strategic, tactical, and operational levels, as shown in

Table 1. Planning levels.

Planning Level	Strategic	Tactical	Operational
Planning unit	Yearly	Weekly	Daily
Inputs	Demand forecast for future areas	Planned weekly demand	Daily flight timetable
	Potential heliport locations	Contracts with options	Actual demand
	Helicopter market		Uncertainty factors
Outputs	Logistics network design	Helicopter resources	Flights replanning
	Helicopter sourcing strategy	Weekly flight timetable	Flight rerouting

. The suggested definitions for inputs and outputs are quite general and can have specific content depending on operating company’s polices, region of operations, and country-specific rules and regulations.

Strategic planning addresses decisions regarding logistics network design and helicopter sourcing strategy many years in advance. Network design refers to the selection of possible heliport locations to use for future areas of operations. A helicopter sourcing strategy refers how to purchase the helicopter services in the market. It specifies the timing for tenders, contract lengths, required helicopters, and what type of contract flexibility to request.

Tactical planning is performed when the installations’ locations and their transport demands are stable for a period of several weeks or months. The focus is on determining helicopter resources (fleet composition, helicopters’ allocation, operating times) required for the stable demand period and constructing a repetitive weekly flight timetable for each heliport, satisfying installations’ weekly transport demand. Helicopter sourcing strategy defines the contract types and available options that they provide. For example, a helicopter fleet may be contracted for the whole region, with options for allocation between heliports when demand changes. Or available options in contracts may enable the change of helicopter operating times. A weekly flight timetable specifies flight assignment to helicopters, installations, and start times for each day. Tactical planning for multiple heliports includes, as a preliminary step, the allocation of flights, helicopters, and installations to heliports.

Operational helicopter planning focuses on the replanning of the daily flight timetable due to the revealed actual demand and uncertainty factors causing delays and cancellations. Actual demand includes regular flights, flights postponed from previous days, and ad hoc flights that may occur on the day of departure. Results of operational replanning include flight start time update, flight rerouting, merging flights, additional flights or cancellations.

The majority of research on helicopter offshore personnel transportation planning is related to operational helicopter transportation planning problems encountered in different offshore regions such as the Brazilian basins [8,9,10,11,12,13,14], the NCS [15,16,17,18,19], the Gulf of Mexico [20,21], and the Persian Gulf [22]. These works present optimisation models and solution algorithms for the optimal routing of flights, the assignment of passengers to planned flights, and daily flights replanning.

To our knowledge, the only paper on strategic helicopter offshore personnel transportation planning by Hermeto et al. [23] is dedicated to long-term logistics network planning and fleet analysis in the Brazilian Santos basin. The study presents an optimisation model for heliports location distributing yearly passenger demands between heliports and pre-sizing fleets for hiring for a 20-years’ time horizon.

As far as we know, our paper [24] presenting the first results of the industrial PhD project with Equinor is the first study related to tactical helicopter offshore personnel transportation planning on the NCS. Brazilian studies of Pereira et al. [25] and Mendes et al. [26] on the optimal weekly helicopter allocation refer to Petrobras operations in the Santos and Campos basins. These papers present optimisation models aiming to allocate the contracted helicopter resources between several heliports and to determine how many flights the helicopters have to perform per week [25] or per day [26] within available flight hours to meet the weekly passenger demands from installations. Neither paper provides models for daily flight assignment to start times, and both publications assume fixed helicopter daily operating times.

1.3. Goals, Objectives, and Contributions

The research presented in this paper was initiated and supported by Equinor, the largest Norwegian offshore operator, with the aim of developing optimisation-based decision support tools to be applied for tactical helicopter transportation planning for the heliports on the NCS. Decision support tools developed in this project are designed to address specific key challenges of offshore helicopter planning on the NCS identified in collaboration with Equinor helicopter planners. The project goals include creating problem formulation and optimisation-based solution tools that directly address the most pressing needs in tactical helicopter planning in Equinor, ensuring their relevance and applicability.

Currently, tactical planning at Equinor is performed by estimating required helicopter resources from installation activity plans and then manually constructing a weekly flight timetable for a pre-defined time period using spreadsheets by moving boxes representing flights. This paper builds on the authors’ preliminary research results [24] and presents the first decision support tools for the tactical planning of helicopter resources integrated with weekly flight timetable construction for the real applied planning problem encountered by Equinor. The simultaneous selection of cost-efficient helicopter resources matching weekly flight demand and the assignment of flights to installations to the specific days and start times, while optimally utilising the fleet capacity, is a challenging optimisation problem. The computational complexity of the optimisation model for problem solution, due to its combinatorial nature, joint minimisation of fixed and variable costs, and the large size due to time discretisation, may in some practical cases limit its applicability. This issue is solved through the development of a model-based solution algorithm utilising the decomposition of the original problem formulation by iteratively selecting helicopter resources and allocating flights to days in the first stage and constructing a weekly timetable of flights in the second stage.

This paper presents the results of three research objectives. The first is to present helicopter planning on the NCS at the tactical level with its specific features, and the current manual planning procedure at Equinor. Secondly, to formulate the tactical helicopter planning problem on the NCS as an optimisation problem integrating helicopter resource selection and construction of a weekly flight timetable. Thirdly, to develop an exact algorithm able to solve to optimality all real-size problem instances for the Equinor operations on the NCS. The related objectives are a validation of the developed optimisation tools by the company logistics planners with the verification of solutions for the real problem instances and a discussion of applicability and adaptability of the developed decision support tools in practice.

The contributions of the paper are both scientific and practical. The novelty of research is in the generalised definition of helicopter transportation planning levels for all offshore areas, and the fact that this is the first in the literature of a description of tactical helicopter planning on the NCS with its specific features. The major scientific contributions are the novel formulation of the studied problem as the flight-based optimisation model with pre-generated flights, and the two-stage iterative algorithm based on the decomposition of the flight-based model able to yield optimal solutions to the real problem instances of all sizes. Among the contributions to the industry practices are the validation of the developed flight-based model formulation and the decomposition-based algorithm by the industry planners, verification of the results achieved with optimisation tools for the real Equinor problem instances, and analysis of the optimisation model and algorithm performance by the quality of the results and computational times. An important managerial contribution of this research for companies operating on the NCS is the applicability of the developed optimisation tools for analysis and decision support in helicopter transportation planning, and their flexibility to adapt to various practical challenges and planning policies.

The paper is organised as follows. After the Introduction, Section 2 describes the specific features of tactical helicopter planning on the NCS, and the current manual planning procedure with its output illustrated as an example. In Section 3, tactical helicopter planning on the NCS is formulated as an optimisation problem integrating helicopter resource selection and weekly flight timetable planning. A developed two-step solution method consisting of the flight generation procedure followed by the solution of the flight-based integer programming model is introduced in Section 4. Section 5 presents the iterative solution algorithm developed based on the decomposition of the flight-based model. Section 6 describes the validation of the developed flight-based model and decomposition algorithm and the verification of the solutions generated with the optimisation tools on real Equinor problem instances. It also illustrates the impact of planning policies on results and computational time analysis. Section 7 provides practical contributions of research results to the industry, such as the applicability of the developed planning tools in practice and their adaptivity to the industry needs, outlining possible problem extensions and modifications of the developed tools. Section 8 contains concluding remarks and potential directions of further research.

2. Current Tactical Helicopter Planning on the NCS

This Section provides the prerequisites and the process of tactical helicopter planning on the NCS. First, the outputs from the strategic level planning on the NCS are presented, defining the inputs for tactical planning. Then, the current tactical planning process is described, followed by the illustrative example of the planning output.

2.1. Outputs from Strategic Helicopter Planning on the NCS

Decisions made at the strategic planning level yield important framework conditions for tactical planning. The most important outputs from strategic planning are the decisions related to logistics network design and helicopter sourcing strategy. These two determine service areas for heliports and helicopter availability from options provided by contracts to be used further at the tactical planning level.

2.1.1. Logistics Network Design on the NCS

The helicopter logistics network design defines the heliports to be used for the offshore fields they will cover. The choice of heliport(s) location on strategic level is mainly based on minimising the flight distance to the fields but also other factors like connectivity with commercial fixed-wing flights and existing helicopter capacity available on the heliport. Other socioeconomic considerations may also influence the choice of heliport(s) location. On the NCS, each installation is assigned to a single heliport for the entire duration of its operations. For fixed installations, the heliport is approved in the plan to develop and operate the field and cannot easily be changed without approval. For mobile installations, the heliport is assigned per drilling location. Since installations are assigned for a long period to one heliport per location and there are few changes, the tactical planning on the NCS is performed independently for each heliport for the set of installations assigned to it a priori. This is different from how it is carried out in other regions where at the strategic level several heliports can be assigned to the same offshore area [23], and the assignment of installations to heliports is decided further at the tactical level using optimisation models and algorithms [21,25,26].

2.1.2. Helicopter Sourcing Strategy on the NCS

The sourcing decision made at the strategic level establishes a framework for procuring helicopter services on the helicopter market, guiding the tender process, and ensuring that contracts of preferred length are secured with some flexibility options to be used at the tactical planning level. The sourcing strategies will define the contract lengths or commitments depending on demand and market conditions. Long-term contracts are normal on the NCS, usually for a fixed period of up to five years with options to extend.

Contracts for helicopter services for energy companies operating on the NCS are mainly tendered individually for each heliport, with a scope of work that specifies the number and types of helicopters, and for each helicopter its weekly and daily availability (further called helicopter operating window). The contracts on the NCS may have options to add additional helicopters within an agreed notice period, and options to change the operating window per helicopter, allowing energy operators to match helicopter availability with demand. The helicopter services are compensated through a fixed daily rate for each helicopter, correlated with the selected operating window, while variable costs are based on the actual flight hours utilised. This payment structure places most of the financial risk on energy operators, who must accurately forecast the necessary helicopter resources to meet their demand, as they are responsible for the fixed operational costs, regardless of the helicopters’ actual utilisation rate. These two contract options on the NCS to change the number of helicopters and to change their operating windows give the energy operators the opportunity at the tactical planning level to adjust capacity and thus also fixed costs, enabling them to optimise resources in response to fluctuating flight demand. This is different from helicopter sourcing strategies in the other offshore areas like in Brazil, where the helicopter services are tendered for several heliports [23] and the helicopter fleet [26] and helicopter operating windows [25] are pre-defined at the strategic level and cannot be adjusted during tactical planning to match optimally with the varying flight demand.

An essential component of the sourcing strategy is the selection of approved helicopter types to be included in the tenders. The type of helicopter not only determines the passenger capacity but also defines the operational range for which installations it may reach, both important for tactical planning. The helicopter type currently used on the NCS for offshore personnel transport is the Sikorsky S-92, which has 19 seats [27]. There are currently no alternatives to the heavy-size helicopter type on the NCS, and energy operators have accepted this risk, relying on the strong operational record of the S-92. However, some energy operators plan to introduce super-medium-size helicopters with a passenger capacity of 16 seats to diversify the fleet. Despite these plans, the S-92 remains the primary workhorse, being used for almost all flights on the NCS, and fleet planning is based on a homogenous fleet of helicopters. In Brazil, there is a heterogeneous fleet of helicopters with different sizes and models [25,26]; one of the reasons for the mixed fleet in Brazil is that not all helidecks allow heavy-sized helicopters, while on the NCS all current helidecks can receive the S-92.

2.2. Objectives and Inputs for Tactical Helicopter Planning on the NCS

As follows from the previous subsection, the tactical helicopter planning on the NCS is performed for each heliport separately, using one helicopter type and contract options to change fleet size and operating windows, enabling the optimisation of resources in response to demand. In this subsection, the objectives for tactical helicopter planning for a single heliport on the NCS together with the definitions of the final outputs are provided, and the input characteristics and requirements for planning are described in detail.

2.2.1. Objectives

Tactical helicopter planning for a single heliport is performed for a time period when the locations of installations to serve are fixed and weekly demands are stable, further referred to as a period of stable demand. This period can last from one week to several months. The main objective of tactical planning is to construct a table of flights to installations to be performed from the heliport during each day of week, called the weekly flight timetable. It is assumed that the weekly flight timetable is repeated each week within the period of stable demand to guarantee predictability for the installations and helicopter operators. In the weekly flight timetable, each flight is associated with the installation(s) to visit, a helicopter, and when it is performed (day and start time). In some offshore areas like Brazil where tactical planning is carried out for several heliports simultaneously, the helicopter fleet is cost-optimally allocated between heliports [25], and all flights to an installation are assigned to a single heliport [26]. In this work, we present a new objective identified for tactical helicopter planning for a single heliport, specifically for the NCS, such as a cost-optimal selection of helicopter resources exactly covering the total weekly demand. In what follows, helicopter resources will be defined as a set of helicopters with an assigned operating window for each helicopter, specifying the days and the number of hours per day the helicopter can perform flights. Within the assigned operating window, flights are guaranteed to be delivered. The final output of tactical helicopter planning on the NCS is a weekly flight program defined by cost-efficient helicopter resources and a corresponding weekly flight timetable effectively utilising these resources.

When a period of stable demand is identified, the inputs for tactical planning on the NCS must be provided before the flight planning and estimation of the required helicopter resources. These include weekly demand planning based on future passenger demand and the checking of available helicopter resources, which are explained further in more detail.

2.2.2. Weekly Demand Planning

The demand for passenger transportation of offshore personnel to and from heliports is usually measured in the number of people to transport offshore. Personnel working offshore generally follows regular shift rotations, which involve alternating offshore working periods with rest periods on land. The 2–4 rotation, where employees spend two weeks offshore followed by four weeks onshore, is frequently used on the NCS, although various other rotation patterns are used depending on the nature of the work. Personnel who travel offshore for short-term tasks represent a smaller demand compared to regular shift demand, and such travel requests are typically managed operationally.

To estimate the number of future passengers for a given offshore area, the installations activity master plans containing the number of Personnel on Board (POB) required for all planned activities, together with assumptions of each activity’s rotation scheme, is used. At Equinor, the activity master plan considers the five upcoming years but it is most detailed and precise for the nearest six months. In tactical planning, it is assumed that each person transported to the installation will replace another one who is transported back to shore. This simplification, even ignoring the fact that the number of personnel to be delivered and picked up may be different, is sufficiently accurate for tactical planning.

In the case of one helicopter type, as is the current situation on the NCS, the weekly transportation demand from offshore installation is defined as weekly flight demand. The lower bound for weekly flight demand may be found as a ratio of the number of passengers to be transported per week by the seat capacity of a helicopter rounded up to the nearest integer. For the heterogeneous helicopter fleet, the number of flights to each installation for each helicopter type can be found by using an assignment model as in Pereira et al. [25] under the assumption that all flights are direct (i.e., visit only one offshore installation) and fully-loaded. In practice, the installations themselves provide helicopter planners with their own data on the required number of flights per week, considering capacity buffer to mitigate possible demand fluctuations and weather uncertainty.

On the NCS, because of the single helicopter type with large capacity, it is common to present the installation flight demand as the number of fully loaded direct flights (to an installation and back to the heliport) or the number of fully loaded flights plus one half-loaded flight. For illustration, if the resulting ratio is 6.8, then weekly flight demand will be seven full-loaded direct flights, but for the ratio 7.2, flight demand will be defined as 7.5 with seven full-loaded direct flights and one half-loaded flight. In what follows, the weekly installation flight demand will be measured in the number of half-loaded flights.

2.2.3. Helicopter Resources Planning

To estimate the minimum required helicopter resources for a week, the weekly flight demands from all installations in the heliport service area are aggregated to a heliport level. To find the minimal required total weekly flight hours, the total number of flights can be multiplied by the average return flight duration from the heliport to installations in the service area. In some offshore areas like in Brazil, with the heterogeneous helicopter fleet, all flights are assumed to be direct and fully loaded. This is different on the NCS; even the helicopter fleet is homogeneous. For the offshore installations on the NCS requiring an integer and half number of flights per week, a half-loaded flight can be an underutilised direct flight, as at maximum, only half the helicopter seat capacity is used. In some offshore areas on the NCS, it is cost-efficient for two half-loaded flights to two installations located nearby to use a shared split flight with two landings. This approach makes sense particularly on the NCS, where a large helicopter can accommodate split flights to installations located close to each other. Most energy operators on the NCS limit offshore flights to two landings per flight. According to the Helicopter Safety Study 4 [27], the landing and takeoff phases accounted for 46% of S-92 helicopter accidents from 2010 to 2019 in the NCS and UK sectors, making them the most frequent cause of incidents. Additionally, research by Qian et al. [16] indicates that direct flights are optimal for minimising passenger risks during takeoff and landing. Consequently, logistics planners of energy operators on the NCS prioritise routing as many direct flights as possible while considering split flights with two landings at nearby installations when necessary.

The mixture of direct and split flights makes it difficult for helicopter planners on the NCS to calculate the total weekly flight hours to determine the minimal required helicopter resources to cover the total weekly flight demand. It becomes even more challenging to select the cost-optimal helicopter resources when the contract with helicopter operator offers several options for helicopter operating windows with different fixed costs. The typical operating windows for a helicopter on the NCS may range from 10 to 16 flight hours from Monday to Friday for regular flights. The weekly flight program planning on the NCS is particularly complicated as the helicopter resource planning is integrated with the weekly flight timetable planning, allocating start times for flights. This is why in the weekly flight program on the NCS, each flight is assigned to the installation(s) visited, to a helicopter performing the flight, and to a helicopter operating window option assigned to this helicopter, in addition to flight allocation to a weekday and a start time. This is different from tactical helicopter planning in Brazil, where the set of helicopters and their types are previously known because the decision is taken at the strategic level, and available daily helicopter operating windows are input parameters defined per helicopter type in the charter contracts [13,25] or considered as a single parameter [26]. Tactical planning in Brazil includes decisions on the number of flights performed weekly [25] or on each weekday [26] to each installation by which helicopter and model and from which heliport, while minimising the total cost of flights. Compared to Brazil, on the NCS, the primary objective of tactical planning is to decide the optimal helicopter resources, minimising the total fixed costs of selected operating windows and integrating this with the secondary objective of optimally allocating flight starts, additionally minimising the total cost of flights. This makes the current tactical planning on the NCS quite unique and different from other offshore areas. The weekly flight program planning on the NCS is subject to certain requirements from offshore installations, restrictions related to helicopters and flight time scheduling, and planning policies, as presented in Section 2.2.4.

2.2.4. Flight Program Planning Requirements and Policies

Flight program planning must satisfy several mandatory requirements. The flight demand for all installations must be covered, and only one flight can land at each installation at the same time. Each helicopter may only have one operating window assigned, and all daily flights must be planned within the helicopter’s operating window. The start of the next flight of a helicopter can be planned only after the previous flight has been completed. There is a mandatory one-hour turnaround time between the consecutive flights of the same helicopter, which is required for pilots to plan the next flight, necessary helicopter maintenance, and for the fuelling and check in/boarding of passengers. The flights may only be planned within the installations opening hours. Most fixed installations on the NCS have a helideck crew to receive flights which is only available between 07:00 and 19:00. Mobile rigs may often receive flights during evening and night, but for the passengers, it is not sensible to have offshore landings later than 23:00. Installations on the NCS primarily request planned flights on weekdays only. The constraints on installation flight demand and flight assignment within daily operating windows are also mentioned in Mendes et al. [26] for decisions on the amount of flights per day for an application in Brazil.

Besides the above mandatory requirements, there are some planning policies that do not have an impact on the selection of helicopter resources and costs but improve the quality of the flight timetable. The first is to evenly distribute the flights to an installation over the weekdays. This is conducted to ensure that installations can plan to have some seats available for ad hoc demands throughout the week. This policy also implies that the number of flights performed by a helicopter each day is levelled over the week, providing a stable helicopter workload. Mendes et al. [26] use a different policy for flights distribution over the weekdays, restricting flights to each installation to certain days. The second policy is to shift all daily flights to the beginning of the helicopter operating windows. This means that daily flights are planned without idle time between flights, except for the mandatory turnaround time between two consecutive flights. This ensures that all idle time is accumulated towards the end of the operating window and can be used to catch up from unpredicted delays.

Besides the mandatory constraints on installation transportation demands, flights within the operating window, and flight distribution over the weekdays, the remaining weekly flight program planning constraints are related to the allocation of flight start times, which are so far not presented in known studies. Nevertheless, Mendes et al. [26] suggest as a future research direction to consider, in tactical planning, the complete flight scheduling, assigning the takeoff times of each flight. As the flight demand allocation to helicopters and days in Mendes et al. [26] guarantees the lowest total flights cost, the allocation of flights at start times throughout the day does not change the cost and can be performed separately using the daily allocation of flights as input. It is also mentioned that the objective of daily flights allocation on minimising total operating time will be essential to ensure that flights are performed at the beginning of the daily operating window, like the daily flights shift policy on the NCS. However, on the NCS, it is suboptimal to separate helicopter resource selection and weekly flights assignment to start times because the mandatory requirements and policies for allocation of flights start times influence the selection of helicopter resources with minimal total fixed costs.

2.3. Current Weekly Flight Program Planning Procedure on the NCS

This section first describes the current tactical planning procedure, followed by an illustrative example of the weekly flight program as a planning output.

2.3.1. Current Planning Procedure

The current planning on the NCS is performed sequentially by trial and error. The procedure starts when the period of stable demand is identified, and the installations’ weekly flight demands are known with certainty. The total flight demand for the heliport and available helicopters and operating windows options are used to estimate the initial minimal required helicopter resources. The necessary number of flights selected from all possible generated direct and split flights are allocated to start times within the operating windows of the selected helicopter resources. If the helicopter resources meet the mandatory requirements of the planning policies, and the solution is approved for cost efficiency, the planning is completed. If the helicopter resources do not meet these mandatory requirements or if it is possible to select more cost-efficient resources, a new selection is made within the available helicopter and operating windows options. Within the newly selected helicopter resources, the procedure is repeated until the helicopter resources are sufficient and approved for cost efficiency. The manual iterative procedure commonly applied on the NCS illustrated in Figure 2 may require several iterations, and the result may not be optimal.

2.3.2. Example of Weekly Flight Program

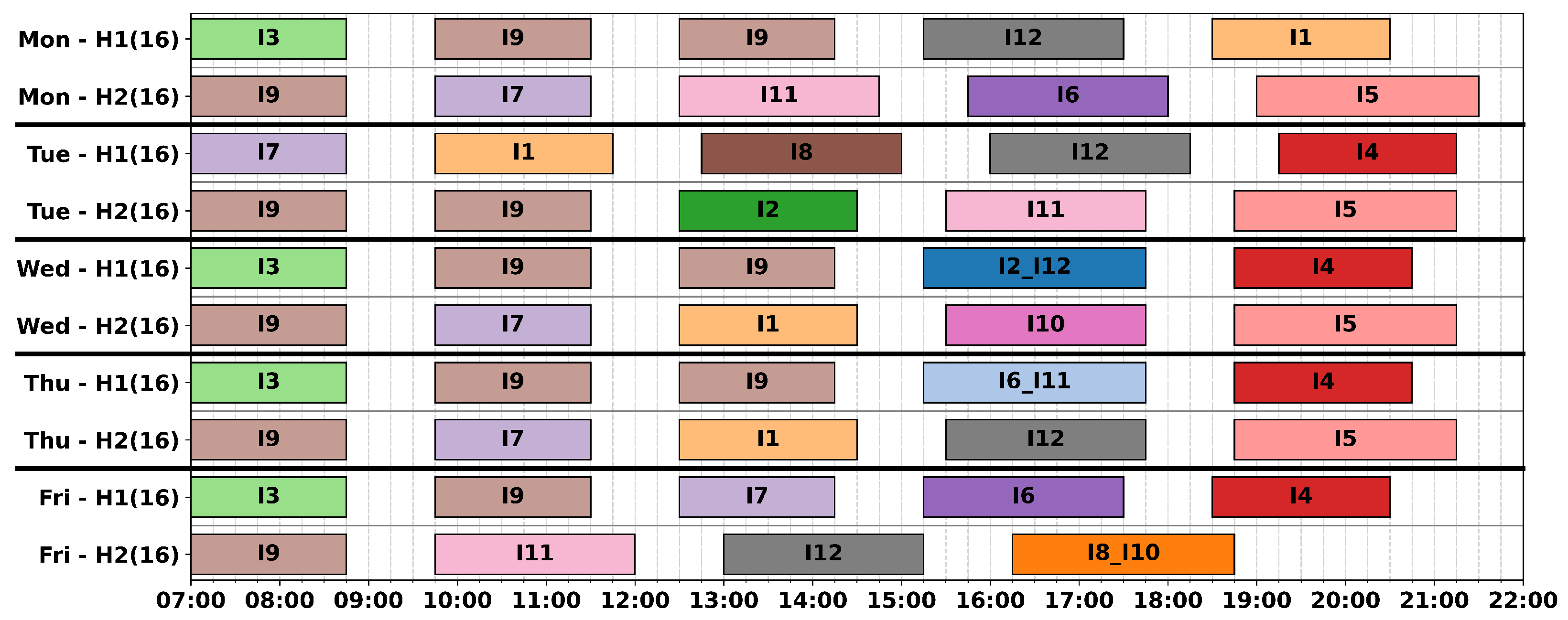
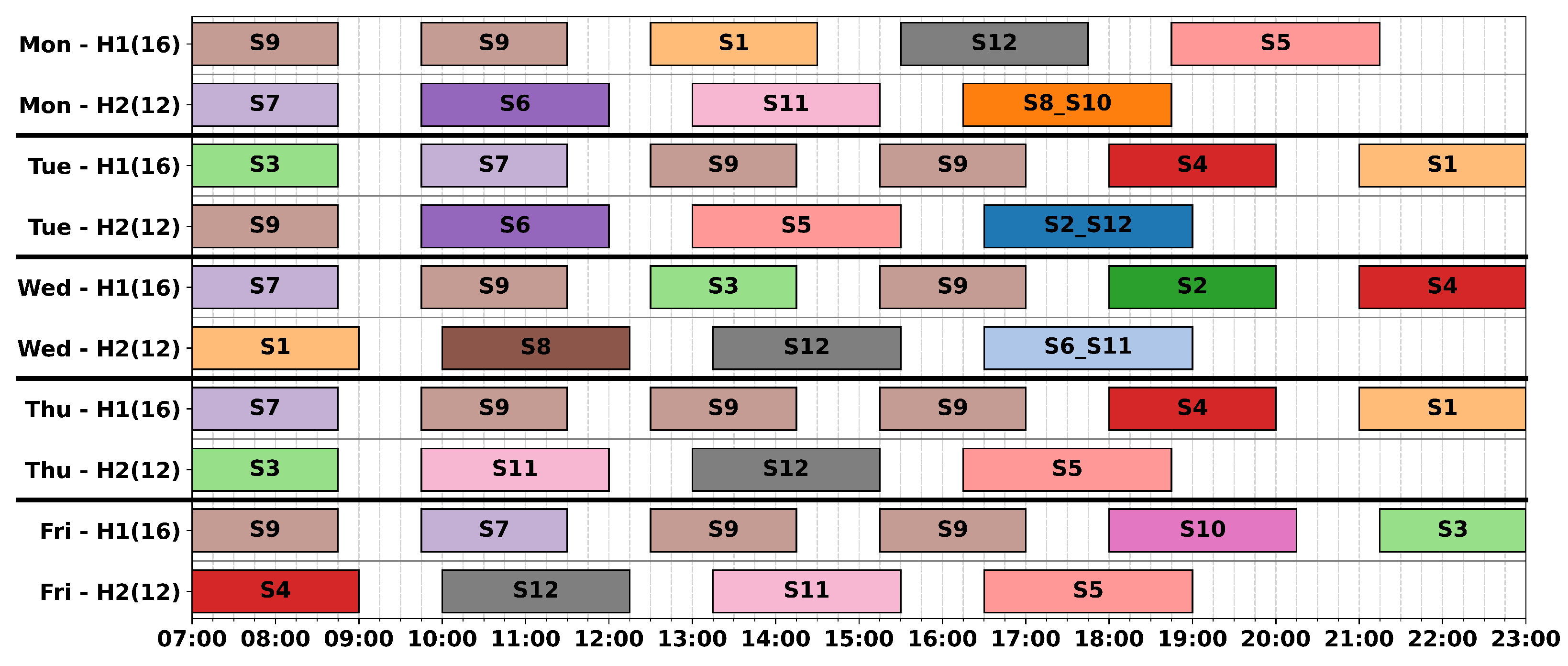
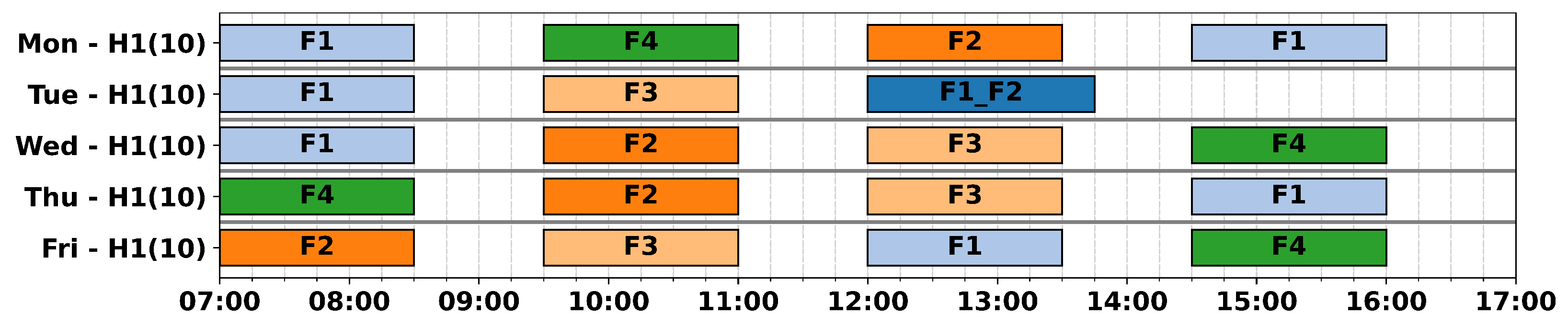
An illustration of a weekly flight program for a heliport on the NCS serving 12 installations (called I1, I2, …, I12) is shown in Figure 3 in the form of a Gannt chart, similar to how it is carried out in practice by tactical helicopter planners. The horizontal axis comprises the time of the day divided into 15 min time slots (which is a reasonable time discretisation for tactical planning) and in the vertical axis are the days from Monday to Friday and the available helicopters and the corresponding operating window. In this example, the helicopter resources selected are two helicopters (H1 and H2) both with 16/5 operating windows, meaning that the helicopter is available 16 h each weekday, from 07:00 to 23:00. The coloured boxes show flights to be performed to installations, specifying for each flight the installation(s) to visit, a weekday, a start time at a specific time slot during the day, and a flight duration rounded to the integer number of time slots. For illustration, we describe the flight timetable for installations I1 and I2. Installation I1 has a demand for four flights per week, and have opening hours from 07:00 to 22:00. The four flights have been planned on Monday 18:30, Tuesday 10:00, and Wednesday and Thursday at 12:30. Installation I2 has a weekly demand for 1.5 flights and opening hours from 07:00 to 18:00. One flight is planned Tuesday 12:30 and another one as a split-flight between I2 and I12 on Wednesday 15:15.

The example shows that all mandatory requirements are fulfilled with flights being planned (their start and duration) only within helicopters’ operating windows, that daily flights of a helicopter do not overlap, that only one helicopter lands at installation at a time, flights land within the installation’s opening hours, and there is a mandatory turnaround time of 1 h. The planning policies are also respected, with flights to each installation spread throughout the week, the number of flights planned for each helicopter are also levelled between the weekdays, and all flights are shifted to the beginning of the helicopter operating windows.

3. Weekly Flight Program Planning Problem Formulation

This section defines the tactical helicopter transportation planning on the NCS as a weekly flight program planning problem and provides problem assumptions specific for the NCS. This planning problem is further formulated as an optimisation problem, with given inputs, solution structure, constraints, objective, and parameters.

The tactical helicopter transportation planning for offshore personnel on the NCS represents a problem of generating a weekly flight program, further referred to as the Weekly Flight Program Planning Problem (WFPPP). The WFPPP is defined for a single heliport, with an assigned set of offshore installations in the heliport operating area on the NCS and for a stable demand period when installations are fixed at their locations and have deterministic and constant weekly demand for personnel transportation. The WFPPP integrates helicopter resource and flight timetable planning for a planning horizon of one week consisting of five workdays from Monday to Friday. The objective of the WFPPP is to select the required helicopter resources defined by a set of helicopters with the assigned operating windows simultaneously with the assignment of each flight to a helicopter, an operating window, a day, and a daily start time, satisfying a set of mandatory requirements and planning policies. The resulting weekly flight program is assumed to be repeated each week during the stable demand period.

The WFPPP is formulated under three basic assumptions with related problem characteristics specific for the tactical helicopter planning on the NCS, described in detail in Section 2. First, a homogeneous fleet of helicopters is considered available at the heliport. It implies that the installations’ weekly demands can be given in the number of flights and not seats as in Brazil [23,26] and in the Gulf of Mexico [21]. Second, it is assumed that helicopter flights can be either direct fully loaded or half-loaded flights, or split flights with landings at two nearby located installations with equally shared helicopter capacity. This is different from the routing options studied in majority of the papers on the operational offshore helicopter routing. The direct full and half-full options imply that the weekly flight demand can be given in integer or integer and a half number of flights, while the split flight option allows to use half-flights as a universal unit of measure for the weekly flight demand. Finally, it is assumed that during the stable demand period, a certain number of helicopters are available at the heliport, and available helicopter operating window options are provided from helicopter contract, defining the number of workdays and the duration of the helicopter’s daily operating window.

The WFPPP can be formulated as an optimisation problem. The problem inputs are weekly flight demands from installations, available helicopters, and available operating windows options agreed upon in the contract with the helicopter operator. The solution to the problem is a weekly flight program, defined by a set of helicopters with the assigned daily operating windows and the weekly timetable assigning flights to helicopters, operating windows, days and start times, satisfying mandatory requirements and planning policies. The objective for the WFPPP on the NCS is to minimise the total cost of the weekly flight program, including both the fixed costs of the helicopter resources and variable costs of the selected flights. The WFPPP solution is challenging as it includes decisions on fleet size, fleet characteristics (helicopter operating windows), the assignment of helicopter resources to flights, and flights’ assignment to days and to start times throughout the week.

The WFPPP installation-related parameters include location data, weekly number of flights, and daily opening hours. Helicopter-related parameters are available fleet size and characteristics of available operating windows options like start time for helicopter operations, duration in hours, and weekly fixed cost. Flight-related parameters include flight hour cost, helicopter speed, deck time at installation, turnaround time between flights, and a threshold value for split flights.

For timetable planning on the NCS time discretisation dividing each day in the numbered time slots of equal duration is commonly used. The durations of operating windows, flights, and turnaround time are counted in the number of time slots. Start times for flights and start times for operating windows are defined by the time slots. An installation’s daily opening hours are defined by the start and end time slots for allowed flight departures from the heliport. The start of opening hours for installations on the NCS is usually the same as start times of available helicopter operating windows.

4. Two-Step Solution Method

This section presents the developed two-step method for the solution of the WFPPP based on the WFPPP formulation starting with the concept and assumptions. It is followed by the description of the flight generation procedure used in the first step, the flight-based model formulation to be solved in the second step, and the details on how the solution method was implemented in practice with the analysis of its computational complexity and scalability.

4.1. Two-Step Solution Method Concept

The presented two-step exact method for the solution of the WFPPP in the first step generates possible flights to the installations served from a given heliport, and in the second step uses the set of possible flights as an input to solve a flight-based integer programming model. The model selects a set of helicopters from the available fleet and assigns to them operating windows from the available options and simultaneously selects flights from the set of possible flights and assigns them to the helicopters, to the weekdays, and to the start times within the operating windows.

The flight generation procedure assumes, as formulated in Section 3, that the helicopter flights on the NCS can be direct flights from the heliport to installation and back to the heliport and split flights, including two stops at installations relatively close to each other.

The assumptions for the flight-based model include a homogeneous helicopter fleet with available operating windows options agreed upon in the contract, and installations’ weekly flight demands being constant for the whole planning period given in the integer or the integer-and-a half number of flights. The last assumption implies that flight demands are measured in half-flights.

For the flights’ assignment into a weekly timetable, it is assumed that helicopter operating windows for each day are discretised into time slots of equal duration (measured in number of minutes) as commonly used in tactical helicopter planning on the NCS. The start time for the flight as well as the start time for the helicopter operating window is defined by a time slot and assumed to be at the beginning of the time slot. For example, a flight starting in time slot 07:00–07:15 is assumed to start at 07:00. This implies that flights start times are multiple of the time slot duration, which is acceptable for tactical planning. Helicopter operating window durations, flight durations, and helicopter turnaround time at the heliport are measured in number of time slots. The daily opening hours for installations on the NCS given by the start time and the end time are defined using a binary two-dimensional parameter indicating time slots for allowed flight departures from the heliport. The start times for daily opening hours for installations are assumed the same as the start times of the available helicopter operating windows.

4.2. Step 1: Flight Generation Procedure

The procedure for flight generation starts with collecting the geographical coordinates of the heliport and installations. Distances between the heliport and each installation are calculated using the Haversine formula, and flight times are derived based on the average helicopter speed. The set of direct flights includes all flights from the heliport to each installation and back to the heliport. Flight duration for these flights is calculated as the sum of twice the flying time from heliport to installation plus the deck stop time. To accommodate for the required helicopter maintenance turnaround time between two consecutive flights, it is included in the flight duration. Next, all pairs of installations are generated to create the set of split flights. Flight duration for split flights is calculated similarly to direct flights, except that the flying time includes the time from the heliport to the first installation, the time between installations, and the time from the second installation back to the heliport. The set of split flights is filtered so that it includes only flights whose time between two installations does not exceed a certain threshold. Calculated flight durations in minutes are converted into the number of time slots by dividing flight duration by the duration of the time slot and rounding up to the nearest integer. Flight cost is defined by an hourly cost and flight duration. The output from the flight generation procedure is a set of all flights, a subset of direct flights, and a subset of split flights, along with the flights’ attributes (costs, durations in the number of time slots), and a binary two-dimensional indicator parameter linking flights to the installations they serve on route.

4.3. Step 2: Flight-Based Model

The flight-based model is solved for five weekdays, where each day is represented by the same number of time slots of equal duration defined by the largest available operating window option. There are two types of decision variables in the model: binary variables for selecting helicopters from the available fleet and assigning to each of them a corresponding operating window and binary variables assigning flights to helicopters, operating windows, weekdays, and daily start time slots. All constraints are divided into four groups. Installation-related constraints include demand constraints, installations’ opening hours, and single flight assignment constraints. Helicopter-related constraints specify a helicopter’s availability inside its operating window and guarantee a single operating window for a helicopter. Flight-related constraints include flights not being able to overlap, flight assignment inside a helicopter operating window, and single flight assignment to a starting time slot. The planning policies constraints represent flights spread and flight shift constraints. The following subsections present model notations, the objective function, and groups of constraints, concluding with the variables’ domains.

4.3.1. Notations

Sets
I	Set of offshore installations;
H	Set of available helicopters;
W	Set of available operating windows;
F	Set of all flights;
$F_1$	Set of direct flights;
$F_2$	Set of split flights;
D	Set of days;
T	Set of daily time slots, where first slot starts from 0.

Parameters
$b_i$	Flight demand for installation i measured in half flights;
$k_w$	Weekly fixed cost for operating window w;
$c_f$	Cost of flight f;
$n_f$	Number of slots including turnaround time occupied by flight f;
l	Number of slots in turnaround time;
$a_{if}$	Equals 1 if installation i is visited on flight f, 0 otherwise;
$p_{it}$	Equals 1 if flight departure to installation i is allowed in slot t, 0 otherwise;
$e_w$	Start slot for operating window w;
$q_{wt}$	Equals 1 if slot t is inside operating window w, 0 otherwise.

Variables
$x_{hwfdt}$	Binary flight assignment variable, 1 if flight f is assigned to helicopter h operating window w on day d in start slot t;
$y_{hw}$	Binary helicopter resource selection variable, 1 if helicopter h is selected and assigned to operating window $w.$

4.3.2. Objective Function

The objective function (1) expresses the sum of the fixed costs of the helicopter resources and the variable costs of flights in the weekly flight program. The fixed costs depend on the durations of operating windows. The model determines the optimal combination of operating windows for helicopters and thus the number of helicopters to form the optimal helicopter resources. The total variable cost depends on the flight time of all planned flights performed during the week, and is based on the distances between the heliport and the installations and the number of landings during flights.

$$minimize\sum _{\mathit{h}\in H}\sum _{\mathit{w}\in W}{k}_{\mathit{w}}{y}_{\mathit{h}\mathit{w}}+\sum _{\mathit{h}\in H}\sum _{\mathit{w}\in W}\sum _{\mathit{f}\in F}\sum _{\mathit{d}\in D}\sum _{\mathit{t}\in T}{c}_{\mathit{f}}{x}_{hwfdt}.$$

(1)

4.3.3. Installation-Related Constraints

Installation flight demand constraints (2) ensure that the demand requirements on the number of flights from installations are met. As the demand is measured in half-flights, it is logical to consider that a direct flight to installation i covers the demand of two half-flights, and for a split flight only one half-flight. The first term in the left-hand side refers to the fact that each direct flight performed to installation i is attributed to covering two half-loaded flights of its flight demand. On the other hand, in a split flight where installation i is visited first or second on the route, one half of the helicopter capacity is allocated to the demand of installation i, and the other half of capacity is allocated to another installation. This contributes to satisfying a half-flight demand that installation i requires.

Installation opening hours constraints (3) ensure that all flights to installation are allowed to depart from the heliport within the installation’s opening hours. It means that flight f performed in a helicopter’s h operating window w on day d starting in time slot t will serve installation i only if installation i is visited on flight f and its departure time slot is within installation’s i opening hours.

Installation single flight assignment constraints (4) guarantee that there is only one flight f planned to installation i on day d starting in time slot t.

$$2\sum _{\mathit{h}\in H}\sum _{\mathit{w}\in W}\sum _{\mathit{f}\in F_1}\sum _{\mathit{d}\in D}\sum _{\mathit{t}\in T}{a}_{\mathit{i}\mathit{f}}{x}_{hwfdt}+\sum _{\mathit{h}\in H}\sum _{\mathit{w}\in W}\sum _{g\in F_2}\sum _{\mathit{d}\in D}\sum _{\mathit{t}\in T}{a}_{\mathit{i}\mathit{f}}{x}_{\mathit{h}\mathit{w}g\mathit{dt}}\ge b_i,\forall \mathit{i}\in I$$

(2)

$$a_{if}{x}_{hwfdt}\le p_{it},\forall i\in I,\forall h\in H,w\in W,f\in F,d\in D,t\in T$$

(3)

$$\sum _{\mathit{h}\in H}\sum _{\mathit{w}\in W}\sum _{\mathit{f}\in F}{a}_{if}{x}_{hwfdt}\le 1,\forall \mathit{i}\in I,\mathit{d}\in D,\mathit{t}\in T.$$

(4)

4.3.4. Helicopter-Related Constraints

The helicopter operating window constraints (5) restrict the availability of helicopter h with respect to helicopter operating window w. Flight f can be performed in the helicopter h operating window w on day d starting in time slot t only if it is specified by the operating window that the helicopter is available on day d in time slot t.

Helicopter single operating window constraints (6) guarantee that there is only one operating window w assigned to helicopter h. There may be, however, more than one helicopter assigned to the same operating window in a weekly flight program.

$$x_{hwfdt}\le q_{\mathit{w}\mathit{t}}{y}_{\mathit{h}\mathit{w}},\forall \mathit{h}\in H,\mathit{w}\in W,\mathit{f}\in F,\mathit{d}\in D,\mathit{t}\in T$$

(5)

$$\sum _{\mathit{w}\in W}{y}_{\mathit{h}\mathit{w}}\le 1,\forall \mathit{h}\in H.$$

(6)

4.3.5. Flight-Related Constraints

The flights non-overlap constraints (7) ensure that the flights performed by the same helicopter do not overlap. If flight f performed in helicopter h operating window w on day d starts in time slot t, then no other flight g is allowed to start in helicopter h operating window w on day d within the duration of flight f where turnaround time is included.

Flight inside helicopter operating window constraints (8) guarantee the availability of helicopter during its operating window while the flight is performed. If flight f is performed in helicopter h operating window w on day d starting in time slot t, then the number of available time slots in helicopter h operating window w on day d should be at least equal to the number of time slots occupied by the flight without its turnaround time.

Flight single assignment constraints (9) ensure that in helicopter h operating window w on day d no more than one flight can start in time slot t.

$$\sum _{g\in F}\sum _{s\in [\mathit{t}+1,min\{\mathit{t}+n_f-1,\left|T\right|\left\}\right]}{x}_{\mathit{h}\mathit{w}g\mathit{d}s}\le (1-x_{hwfdt})\left|T\right|,\forall \mathit{h}\in H,\mathit{w}\in W,\mathit{f}\in F,\mathit{d}\in D,\mathit{t}\in T$$

(7)

$$(n_f-l)x_{hwfdt}\le \sum _{s\in [\mathit{t},min\{\mathit{t}+n_f-l,\left|T\right|-1\left\}\right]}{q}_{\mathit{w}s},\forall \mathit{h}\in H,\mathit{w}\in W,\mathit{f}\in F,\mathit{d}\in D,\mathit{t}\in T$$

(8)

$$\sum _{f\in F}{x}_{hwfdt}\le 1,\forall \mathit{h}\in H,\mathit{w}\in W,\mathit{d}\in D,\mathit{t}\in T.$$

(9)

4.3.6. Planning Policies Constraints

The installation flights spread constraints (10) determine the difference in number of flights between days for each installation. This means that the number of the flights performed to installation i on day d and the number of the flights performed to the same installation on day l are the same or differ in one flight. It allows for spreading the flights to each installation evenly throughout the week, without flights stacking up on one day.

Flight shift to operating window start constraints (11) determine the stacking of the flights on each day to the start time of the operating windows without any time-gaps between flights, allowing for the effective helicopter time to be accumulated at the end of the day. Each flight f of the helicopter h operating window w on day d starting in time slot t should end no later than the sum of number of slots occupied by all flights planned for the helicopter operating window on this day with respect to the operating window start slot.

$$\sum _{\mathit{h}\in H}\sum _{\mathit{w}\in W}\sum _{\mathit{f}\in F}\sum _{\mathit{t}\in T}{a}_{\mathit{i}\mathit{f}}{x}_{hwfdt}-\sum _{\mathit{h}\in H}\sum _{\mathit{w}\in W}\sum _{\mathit{f}\in F}\sum _{\mathit{t}\in T}{a}_{\mathit{i}\mathit{f}}{x}_{\mathit{h}\mathit{wf}\mathit{lt}}\le 1,\forall \mathit{i}\in I;\mathit{d},\mathit{l}\in D$$

(10)

$$(\mathit{t}+n_f)x_{hwfdt}\le \sum _{g\in F}\sum _{s\in T}{n}_g{x}_{\mathit{h}\mathit{w}g\mathit{d}s}+e_w,\forall \mathit{h}\in H,\mathit{w}\in W,\mathit{f}\in F,\mathit{d}\in D,\mathit{t}\in T.$$

(11)

4.3.7. Variables Domain

Constraints (12) impose binary properties upon the respective decision variables.

$$x_{hwfdt}\in \{0,1\},\forall \mathit{h}\in H,\mathit{w}\in W,\mathit{f}\in F,\mathit{d}\in D,\mathit{t}\in T;y_{\mathit{hw}}\in \{0,1\},\forall \mathit{h}\in H,\mathit{w}\in W.$$

(12)

4.4. Two-Step Method Implementation Details and Computational Scalability

The flight generation procedure along with the resulting weekly flight program interface were implemented in Python programming language. The flight-based model was coded using AMPL modelling programming language and solved using Gurobi 12.0.1 solver on a remote computer equipped with an Intel(R) Xeon(R) Gold 6330 CPU @ 2.00 GHz, with six physical cores, 12 logical processors, and 32 GB of RAM, provided by Molde University College.

The computational complexity of the flight-based model is defined by the number of installations to serve from a heliport, the number of generated direct and split flights, the number of available helicopters at the heliport, the number of available helicopter operating windows options in the contract, the number of days helicopters are available, and the number of daily time slots. The daily time discretisation in 64 fifteen-minute time slots used in tactical helicopter planning on the NCS influences the computational scalability of the flight-based model due to the large number of possible combinations of flights assignment to starting time slots. Dimensions of other model inputs such as the number of installations, the number of available helicopters, and operating windows options for the real problem instances on the NCS are not large. Thus, the flight-based model for most of these instances can be solved with a commercial solver in reasonable short times, and is substantially faster than when planning manually by trial and error. To reduce the computational time, the cardinality of the set of available helicopters is defined as a minimum between the number of helicopters available and the upper bound on the fleet size required, calculated from the total weekly demand covered by direct flights within the minimal operating window option.

The results of extensive experiments conducted on real Equinor instances for heliports on the NCS presented in [24] showed that the flight-based model can solve problem instances with up to seven offshore installations and fifteen minutes daily time discretisation to optimality. The experiments with adding and removing constraints in the flight-based model showed that most of the computational efforts and time are used for flights’ assignment to start times, and in particular finding feasible solutions satisfying the flight shift constraints. This finding was a driver for the development of several versions of an iterative solution algorithm utilising various ideas for flight-based model decomposition, in which a flight’s shift to an operating window start is implemented after the helicopter resources are defined in the first stage. The decomposition-based algorithm with the best performance able to solve the largest problem instances on the NCS in a short computational time to optimality, as presented in the next section.

5. Decomposition-Based Algorithm

This section starts with the concept of the developed decomposition-based algorithm and the underlying assumptions. It is followed by the presentation of the Stage 1 and Stage 2 models solved consecutively in each iteration. The last subsection includes the pseudocode with the details of the algorithm implementation, and an analysis of its computational scalability.

5.1. Decomposition-Based Algorithm Concept

The algorithm presented in this section is an iterative procedure, with two stages at each iteration. In the first stage, helicopter resources are selected while minimising total cost, and selected flights are distributed between the weekdays. The assignment of flights to start times in each day is performed in the second stage, aiming to shift flight start times towards the beginning of the corresponding operating windows while utilising the helicopter resources selected in the first stage.

The underlying assumptions for the developed algorithm are the same as for the WFPPP formulation in Section 3 and the flight-based model in Section 4. The algorithm is based on the decomposition of the flight-based model, thus ensuring that the solution satisfies the flight-based model objectives and constraints. The selection of helicopter resources with flights distribution and the assignment of flights in the timetable are made at each iteration of the algorithms consecutively in Stage 1 and Stage 2, solving the corresponding integer programming models. In Stage 1, the cost-efficient set of helicopters with their operating windows and the distribution of selected flights between days is determined by solving the Stage 1 model, without using time slots. In Stage 2, the assignment of flights to start times within the pre-defined operating windows is decided by solving the Stage 2 model for each day separately, satisfying the time slot-related constraints while minimising the sum of start times of the selected flights. The Stage 1 model outputs provide the inputs to the Stage 2 model.

If the Stage 2 model cannot find a feasible flight assignment to start times for at least one day, the algorithm checks if for at least one helicopter in the existing fleet exist operating window option(s) with marginal increase in size. In this case the algorithm selects the operating window option yielding lease-cost increase, this operating window is assigned to the corresponding helicopter, and the algorithm iterates to Stage 1 where the Stage 1 model is solved with the revised helicopter resources. Otherwise, one more helicopter is added to the existing fleet, and each helicopter is assigned the minimal available operating window. The process is repeated until the solutions of the Stage 2 model are found for all days, and an optimal weekly flight program is generated. The optimality of the solution is ensured by the marginal gradual least-cost increase in the helicopter resources in each iteration.

5.2. Models

The following subsections provide description and mathematical formulations of the Stage 1 and Stage 2 models.

5.2.1. Stage 1 Model

The Stage 1 model decision variables include binary helicopter resource selection variables $y_{hw}$ and integer flight distribution variables $x_{hwfd}$, defining for each flight how many times it is performed on each day by the selected helicopters within their operating windows. The objective function (13) minimises fixed and variable costs, and the constraints (14), (15), (16), (17) act as substitutes for constraints (2), (5), (6), and (10). To ensure that the total number of time slots occupied by all flights performed by helicopter h within operating window w on day d (not including turnaround time for the last flight) does not exceed the duration of the helicopter operating window, constraints (18) are added, where parameter $s_w$ is the number of time slots in operating window w. Constraints (19) are only used when iterating from an infeasible solution in Stage 2, ensuring that the helicopter resources are set to be the same as the output values from Stage 2 of the algorithm.

  Model formulation:

Input sets
I	Set of offshore installations;
H	Set of available helicopters;
W	Set of available operating windows;
F	Set of all flights;
$F_1$	Set of direct flights;
$F_2$	Set of split flights;
D	Set of days.

Input parameters
$b_i$	Flight demand for installation i measured in half flights;
$s_w$	Number of slots in operating window w;
$k_w$	Weekly fixed cost for operating window w;
$c_f$	Cost of flight f;
$n_f$	Number of slots including turnaround time occupied by flight f;
l	Number of slots in turnaround time;
$a_{if}$	Equals 1 if installation i is visited on flight f, 0 otherwise;
$m_{hw}^2$	Equals 1 if helicopter h is assigned operating window w in Stage 2, 0 otherwise.

Variables
$x_{hwfd}$	Integer flight distribution variable, number of times flight f is performed by helicopter h within operating window w on day d;
$y_{hw}$	Binary helicopter resource selection variable, 1 if helicopter h is selected and assigned to operating window w.

$$minimize\sum _{\mathit{h}\in H}\sum _{\mathit{w}\in W}{k}_{\mathit{w}}{y}_{\mathit{h}\mathit{w}}+\sum _{\mathit{h}\in H}\sum _{\mathit{w}\in W}\sum _{\mathit{f}\in F}\sum _{\mathit{d}\in D}{c}_{\mathit{f}}{x}_{hwfd}$$

(13)

$$2\sum _{\mathit{h}\in H}\sum _{\mathit{w}\in W}\sum _{\mathit{f}\in F_1}\sum _{\mathit{d}\in D}{a}_{\mathit{i}\mathit{f}}{x}_{hwfd}+\sum _{\mathit{h}\in H}\sum _{\mathit{w}\in W}\sum _{g\in F_2}\sum _{\mathit{d}\in D}{a}_{\mathit{i}\mathit{f}}{x}_{\mathit{h}\mathit{w}g\mathit{d}}\ge b_i,\forall \mathit{i}\in I$$

(14)

$$x_{hwfd}\le s_w{y}_{\mathit{h}\mathit{w}},\forall \mathit{h}\in H,\mathit{w}\in W,\mathit{f}\in F,\mathit{d}\in D$$

(15)

$$\sum _{\mathit{w}\in W}{y}_{\mathit{h}\mathit{w}}\le 1,\forall \mathit{h}\in H$$

(16)

$$\sum _{\mathit{h}\in H}\sum _{\mathit{w}\in W}\sum _{\mathit{f}\in F}{a}_{\mathit{i}\mathit{f}}{x}_{hwfd}-\sum _{\mathit{h}\in H}\sum _{\mathit{w}\in W}\sum _{\mathit{f}\in F}{a}_{\mathit{i}\mathit{f}}{x}_{\mathit{h}\mathit{wf}\mathit{l}}\le 1,\forall \mathit{i}\in I;\mathit{d},\mathit{l}\in D$$

(17)

$$\sum _{\mathit{f}\in F}{n}_f{x}_{hwfd}\le s_w+l,\forall \mathit{h}\in H,\mathit{w}\in W,\mathit{d}\in D$$

(18)

$$y_{hw}\ge m_{hw}^2,\forall \mathit{h}\in H,\mathit{w}\in W.$$

(19)

The outputs of the Stage 1 model, namely optimal helicopter resources and the assignment of flights to days, are used as inputs to the Stage 2 model solved separately for each day. The outputs include set $I^1$ and set $F^1$, defining the installations to serve and the flights to perform on the day. Sets $H^1$ and $W^1$ define helicopters and operating windows common for all days, given by the optimal values of decision variables $y_{hw}$. The integer parameter $g_f^1$ defines the number of flights f for the day. The helicopter resources in the Stage 2 model are defined by the binary parameter $m_{hw}^1$ equal to one if the operating window w is assigned to helicopter h as in the Stage 1 model solution.

5.2.2. Stage 2 Model

The Stage 2 model is solved consecutively for each day, assigning the daily flights to helicopters, operating windows, and time slots using binary variables $x_{hwft}$. The objective function (20) aims to shift all daily flights towards the beginning of the operating windows defined in Stage 1 and ensures that there is no idle time between flights, thus substituting flight shift constraints (11) from the flight-based model. Constraints (21) and (22) set the number of flights and helicopter resources for the day to those found in Stage 1. The remaining constraints are installation opening hours and flight-related constraints (23), (24), (25), (26), and (27) which correspond to constraints (3), (4), (7), (8), and (9) from the flight-based model.

  Model formulation:

Input sets
$I^1$	Set of offshore installations to service in that day found in Stage 1;
$H^1$	Set of helicopters selected in Stage 1;
$W^1$	Set of operating windows selected in Stage 1;
$F^1$	Set of flights to be assigned for that day found in Stage 1;
T	Set of daily time slots, where first slot starts from 0.

Parameters
$m_{hw}^1$	Equals 1 if helicopter h is assigned operating window w in Stage 1, 0 otherwise;
$g_f^1$	Number of flights f to be performed per day found in Stage 1;
$n_f$	Number of slots including turnaround time occupied by flight f;
l	Number of slots in turnaround time;
$a_{if}$	Equals 1 if installation i is visited on flight f, 0 otherwise;
$p_{it}$	Equals 1 if flight departure to installation i is allowed in slot t, 0 otherwise;
$q_{wt}$	Equals 1 if slot t is inside operating window w, 0 otherwise.

Variables
$x_{hwft}$	Binary flight assignment variable, 1 if flight f is assigned to
	helicopter h operating window w on day d with start slot t.

$$minimize\sum _{\mathit{h}\in H^1}\sum _{\mathit{w}\in W^1}\sum _{\mathit{f}\in F^1}\sum _{\mathit{t}\in T}t{x}_{hwft}$$

(20)

$$\sum _{h\in H^1}\sum _{w\in W^1}\sum _{t\in T}{x}_{hwft}\ge g_f,\forall \mathit{f}\in F^1$$

(21)

$$x_{hwft}\le m_{hw},\forall \mathit{h}\in H^1,\mathit{w}\in W^1,\mathit{f}\in F^1,\mathit{t}\in T$$

(22)

$$a_{if}{x}_{hwft}\le p_{it},\forall h\in H^1,w\in W^1,f\in F^1,t\in T$$

(23)

$$\sum _{\mathit{h}\in H}\sum _{\mathit{w}\in W}\sum _{\mathit{f}\in F}{a}_{if}{x}_{hwft}\le 1,\forall \mathit{i}\in I^1,\mathit{t}\in T$$

(24)

$$\sum _{g\in F^1}\sum _{s\in [\mathit{t}+1,min\{\mathit{t}+n_{f-1},\left|T\right|\left\}\right]}{x}_{\mathit{h}\mathit{w}gs}\le (1-x_{hwft})\left|T\right|,\forall \mathit{h}\in H^1,\mathit{w}\in W^1,\mathit{f}\in F^1,t\in T$$

(25)

$$(n_f-l)x_{hwft}\le \sum _{s\in [\mathit{t},min\{\mathit{t}+n_f-l,\left|T\right|-1\left\}\right]}{q}_{\mathit{w}s},\forall \mathit{h}\in H^1,\mathit{w}\in W^1,\mathit{f}\in F^1,\mathit{t}\in T$$

(26)

$$\sum _{f\in F^1}{x}_{hwft}\le 1,\forall \mathit{h}\in H^1,\mathit{w}\in W^1,\mathit{t}\in T.$$

(27)

If the Stage 2 model generates optimal solutions for each day, the resulting weekly flight program is merged from the solutions found for all days. If it is not possible to solve the Stage 2 model for at least one day, the helicopter resources are revised according to the logic described in Section 5.1.

5.3. Decomposition-Based Algorithm Implementation Details and Computational Scalability

The pseudocode of the decomposition-based algorithm is shown in Algorithm 1. The Stage 1 and Stage 2 models of the algorithm are coded using AMPL and solved with Gurobi 12.0.1 solver on the same computer as described in Section 4.4.

The computational scalability of the algorithm is high, mainly due to the separation of decisions on helicopter resources from decisions on flights’ assignments to start times, performed sequentially in two stages and iteratively improving the solution. In this algorithm, in contrast to the manual planning procedure applied on the NCS, helicopter resource selection in the first stage is performed simultaneously with the selection of flights and their distribution between days by solving the Stage 1 model.

The computational complexity of the Stage 1 model is not as high compared to the flight-based model due to the substantial reduction of the flight-related variables and constraints. The computational time to find an initial solution of the Stage 1 model can be reduced by limiting the size of fleet available to the instance-dependent upper bound on the number of helicopters required. Computational time for solving the Stage 1 model in the other iterations (if any) is insignificant as the values of helicopter resource selection variables are fixed.

Algorithm 1: Decomposition-based algorithm for the WFPPP

The computational complexity of Stage 2 of the algorithm is not high because the flights assignment to start times is implemented not for all days simultaneously as in the flight-based model but separately for each day using the Stage 2 model. Computational time for the Stage 2 model is not substantial due to less variables and constraints compared to the flight-based model and the pre-defined daily flights found in Stage 1. In addition, after solution infeasibility for one day is detected, the solution of the Stage 2 model for the consecutive days is not required.

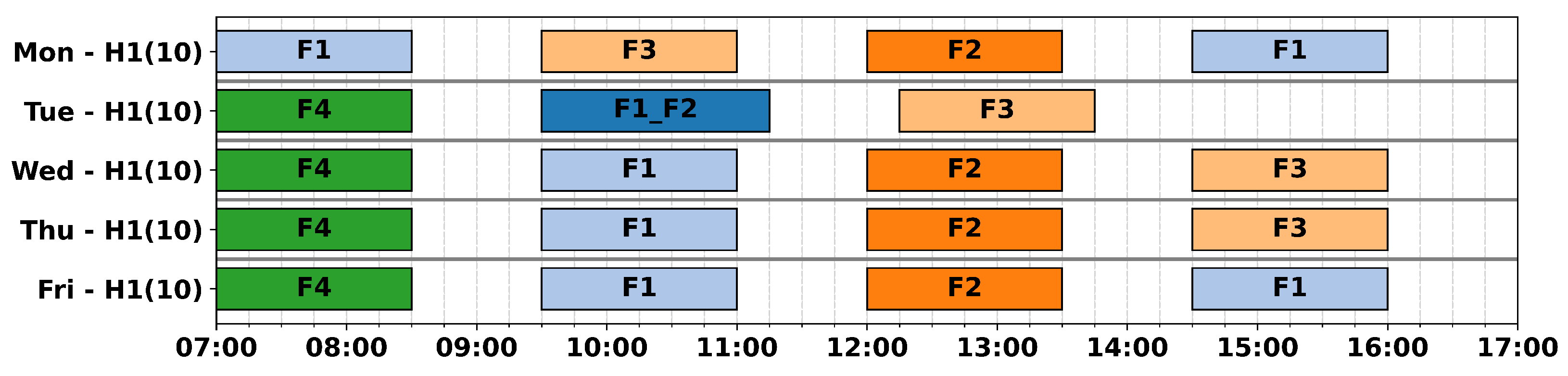
Moreover, the algorithm may terminate fast, after just a few iterations, as it exploits the restrictive enumeration of the limited number of operating window options. The experiments showed that the decomposition-based algorithm can solve the largest instances known on the NCS to optimality in a few iterations in just a few minutes.

6. Validation and Verification

The weekly flight program planning tools developed and presented in this paper were specifically created to address the most pressing needs expressed by Equinor helicopter planners for optimisation-based software to assist the tactical helicopter planning process and to improve manual planning results. The objective of this project was to formulate the WFPPP as an integer programming model that responds directly to the objectives and planning requirements of tactical helicopter planning on the NCS, in close cooperation between industry and academia, ensuring the practical relevance of the formulation. The main goal was to design an algorithm able to solve real problem instances of all sizes in short time, based on model decomposition, and generating optimal solutions using integer programming solver. The flight-based model formulation and the developed decomposition-based algorithm presented in two previous sections were validated and tested on the real Equinor problem instances of different sizes, jointly by the authors and the logistics planners from Equinor, to verify solutions’ quality by comparing them with the actual flight programs. One of the authors is an acting helicopter planner at Equinor, bringing years of first-hand experience to the project. His background has contributed significantly to the development, implementation, and validation of the optimisation-based tools, ensuring that they are grounded in the realities of tactical helicopter planning on the NCS.

The first subsection outlines how the flight-based model formulation and the decomposition-based algorithm for the solution of the WFPPP were validated by Equinor logistics planners, and how their feedback was integrated throughout the development process. The second subsection presents the real Equinor problem instances of small, medium, and large sizes, the generated optimal solutions, and the comparative analysis of the results with the actual flight programs. The third subsection illustrates in one of the real instances the importance of including planning policy constraints in the model formulation and their impact on the quality of the solutions. The last subsection presents the results of the computational time analysis for the tested instances, focusing on the number of iterations and solution speed.

6.1. Validation

The development of the optimisation tools was carried out through a comprehensive five-year collaboration with Equinor’s logistics planners, involving continuous validation of the optimisation tools and extensive experiments for the verification of the solutions generated for real instances. The development process began with an in-depth study of offshore helicopter transportation planning practices, including engagement with energy companies operating on the NCS and other offshore regions to identify similarities and differences in planning approaches. Additionally, the existing logistics system for offshore helicopter operations on the NCS was analysed alongside with studying offshore helicopter markets with a particular focus on sourcing strategies specific for the NCS. Safety studies and regulatory requirements were also reviewed to assess their impact on helicopter planning. These efforts enabled the identification of key input characteristics and assumptions, planning requirements, and a user-friendly interface for the visualisation of results in practice while also highlighting the limitations of the existing manual planning procedure.

Building on these insights, the flight-based optimisation model was first formulated to address the weekly flight program planning by defining decision variables and the objective function while incorporating the mandatory requirements and the planning policies as constraints. Continuous validation with Equinor planners ensured that the flight-based problem formulation was tested, refined, and aligned with the real-world requirements, confirming its practical applicability. In what follows, some important modelling steps are described based on the feedback from helicopter planners.

Model development was initially focused on defining a measure for personnel transport demand specifically for the NCS. In the beginning, the number of passengers to be transported per week was used in the same way as that in the literature regarding offshore helicopter transportation. Then, a novel definition of transport demand measured in number of flights (rounded up to full or half flight) was suggested based on how installations report demand to helicopter planners in practice. After examining the regulations and the planning practices for offshore helicopter transportation on the NCS, the problem formulation was extended to include split flights with up to two landings and measure transport demand in the number of half-full flights. This approach complies with the NCS safety policy on the maximum number of offshore landings and enables the maximisation of helicopter seat capacity utilisation. Planners also gave feedback that this approach captures installation’s transport demand at a correct level of detail for tactical planning.

Early testing of the flight-based model revealed that the level of time discretisation (time slot duration) significantly impacts both the output details and the computational performance. After the feedback from planners, a fifteen-minute time slot used in manual spreadsheets was adopted successfully, improving model accuracy for planning purposes while maintaining the acceptable computational efficiency of the developed solution methods.

The planning policies selected to be included in the model formulation expressed the actual needs for weekly flights to be spread for installations and for helicopters, and the existing practice of daily flight assignment. The spread of flights between weekdays is necessary to maintain planned activities at installations. The suggested formulation of the flights spread constraint was approved by planners because it also ensures equity between installations. Based on the input from planners, a planning policy constraint, levelling for each helicopter the number of flights between days, was formulated with the aim to balance helicopter utilisation throughout the week. This constraint was later removed after testing as the flight spread constraint effectively levelled helicopter utilisation. Flight shift was included as a necessary planning policy constraint after feedback from planners, following their practice to schedule flights as tightly as possible from the start of operations, aiming to accumulate all the helicopter idle time at the end of the operating windows for operational purposes.

Flight-based model testing by planners revealed an unusually large amount of slack at the end of some helicopter operating windows and lower than expected resource utilisation. This was due to the flight generation procedure adding a turnaround time to each flight and the model not accounting for the fact that the turnaround time for the last flight of the day does not need to fit within the helicopter operating window. Adjusting the model to reflect this improved the results.

The solution algorithm based on the decomposition of the flight-based model was approved by the planners as its concept aligns with the iterative planning procedure currently applied on the NCS described in Section 2.3.1. The planners supported the idea that least-cost helicopter resource selection in the first stage should be made simultaneously with the distribution of flights between days defined by the flight spread planning policy. The suggestion to find the flights’ assignments to start times, solving the second-stage model with the objective function to minimise the sum of flights’ start times, was also well met, as it complies with the flight shift planning policy. During the validation of several versions of the algorithm’s implementation, the approach where the Stage 2 model assigns flight start times to each day separately was approved as the most effective and efficient for planning.

Additionally, helicopter planners expressed their wish for a user-friendly solution output to visualise and more easily interpret the results provided by the optimisation tools. This led to the development of a Python script that automatically visualises the results as Gantt charts, which is very close to the visualisations the planners use in their planning spreadsheets. The interface developed also includes options to provide statistics on helicopter utilisation for cost analysis, flights distribution analysis, idle time analysis, and other relevant statistics and performance measures.

6.2. Test Instances, Results and Verification

The following subsections present the real tested Equinor problem instances and how the solutions generated by the developed optimisation tools were verified by comparing results to the actual flight programs at the time.

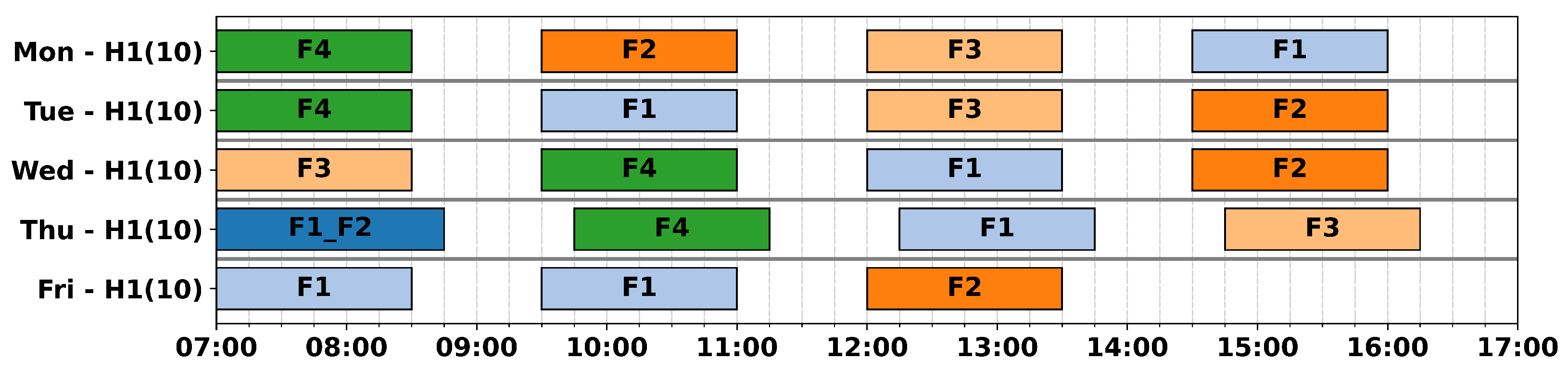
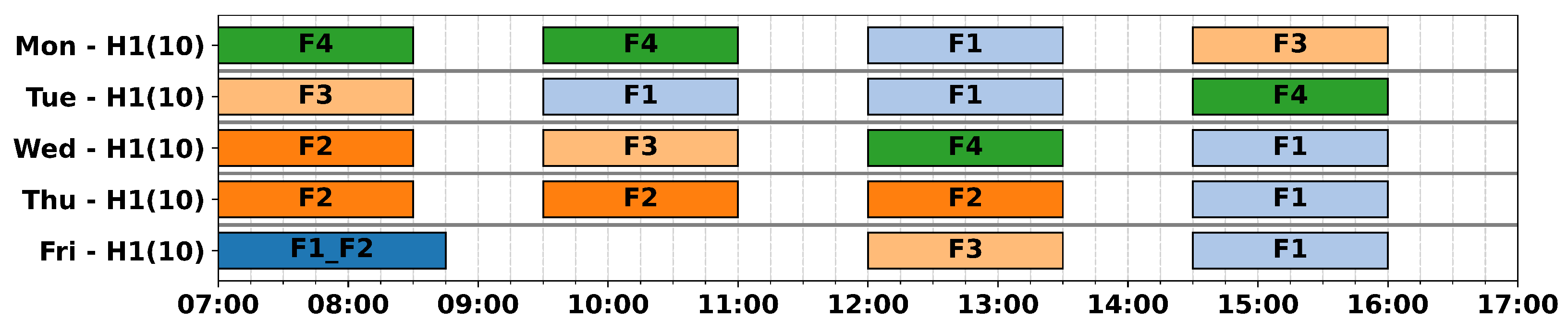
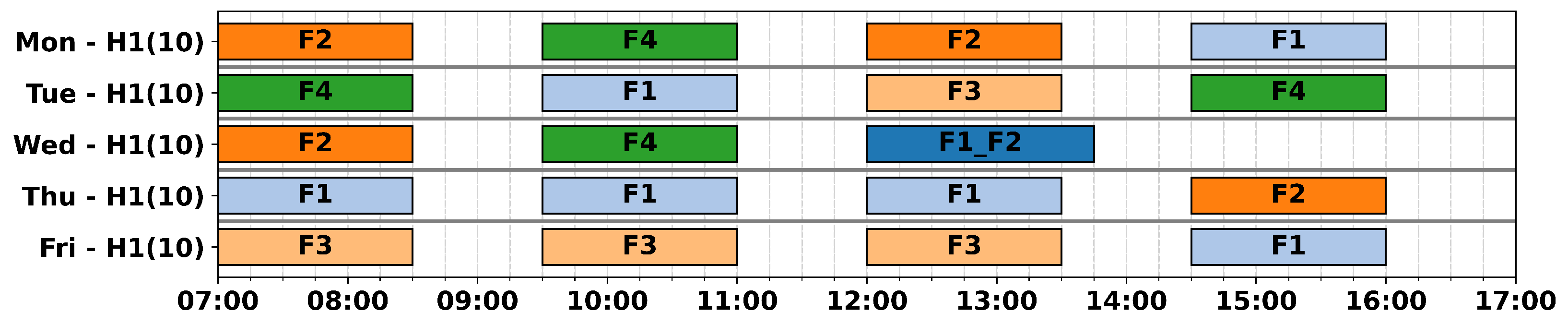
6.2.1. Test Instances

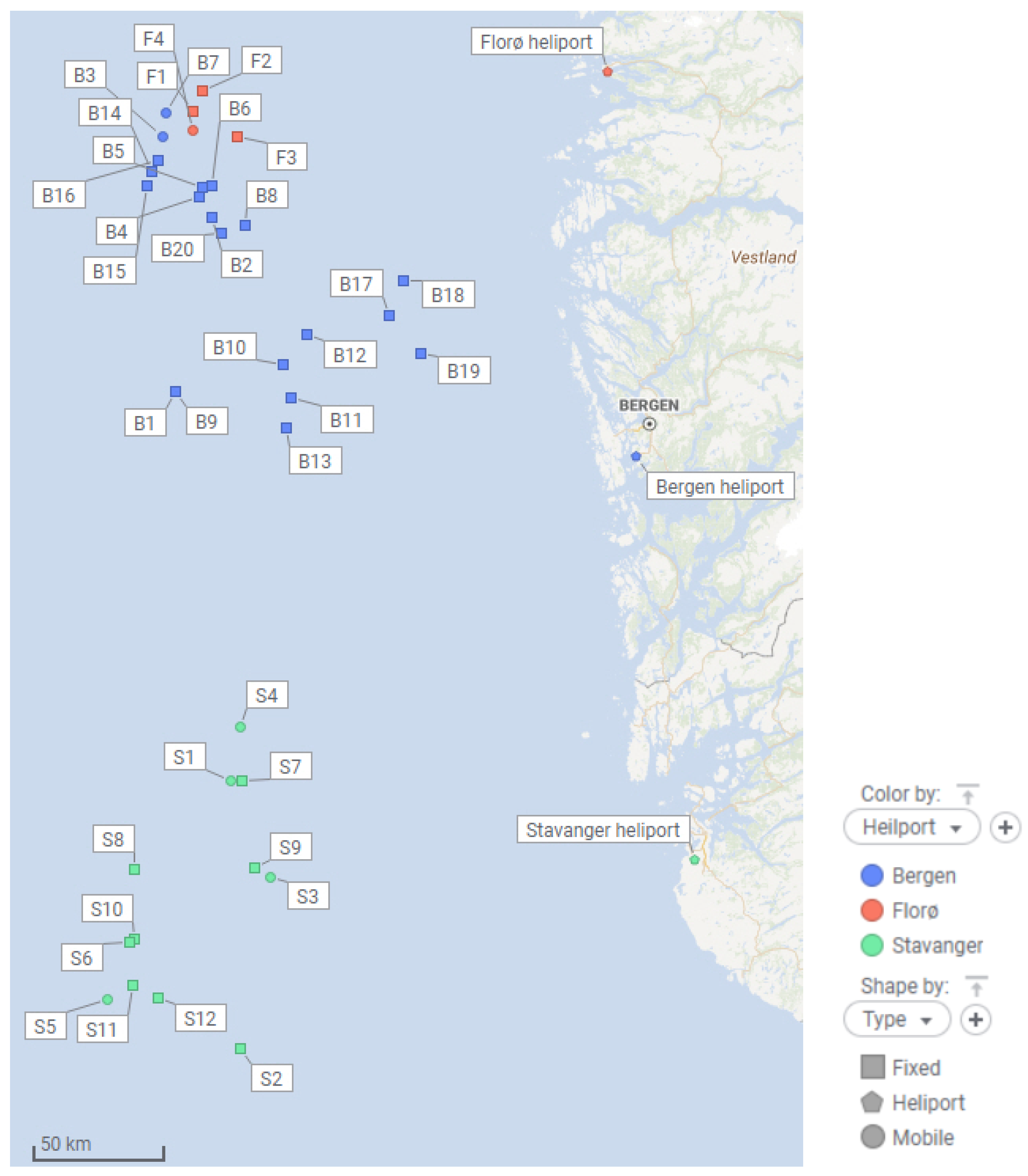
The developed optimisation model and algorithm were tested on three real problem instances representing the Florø, Stavanger, and Bergen heliports, with Equinor weekly flight demands from a period of stable demand in 2024. These heliports were selected because they represent examples of small-, medium-, and large-size instances of the WFPPP on the NCS where a single heliport can serve at a minimum two and at a maximum twenty installations with a total flight demand between approximately 10 and 100 flights per week. The served installations in the instances have varying geographical locations between ca 50 and 120 nautical miles from the heliports, as shown in Figure 4. The installations are named using the first letter of the heliport they are assigned to (F for Florø, S for Stavanger, and B for Bergen). The flight duration for direct flights to the installations varies approximately from one hour to two and a half hours, with the Sikorsky S-92 helicopter average speed of 125 knots, including about ten minutes for the installation deck stop. In addition, one hour of helicopter turnaround time is added to each flight. Split flights are filtered with the threshold of fifteen minutes flight time between any two installations. The duration of a time slot is set to fifteen minutes, and the flight hour cost is 140 in masked units.

The Florø instance represents the small-size instance with four installations, three of them fixed with opening hours that allow flight departure from the heliport from 07:00 to 18:00, one mobile with opening hours from 07:00 to 22:00, and a total weekly demand of 19 flights. The representative medium-size instance is Stavanger, with twelve installations, eight of them fixed with opening hours from 07:00 to 18:00 while four installations are mobile with opening hours from 07:00 to 22:00, and the total demand is 46.5 flights per week. The largest instance is Bergen, with 20 installations, with 18 of them fixed with opening hours from 07:00 to 18:00 while 2 are mobile installations with opening hours from 07:00 to 22:00, and in total 93 flights are demanded per week. The demand and opening hours of each installation are shown in the corresponding tables for each problem instance in Appendix A. The contracts for each heliport define available operating window options that can be selected. For the Florø instances, options of 10-, 12- and 16-h duration are available five days a week, all starting at 07:00. For the Stavanger and Bergen instances, there is an option of 14 h duration in addition to the aforementioned options. For an overview, a summary of the number of installations, the total weekly flight demand, the number of helicopters available, and the available operating window options is shown in

Table 2. Instances data summary.

Instance	Installations	Flight Demand	Helicopters	Operating Windows
Florø	4	19	1	10, 12, 16
Stavanger	12	46.5	3	10, 12, 14, 16
Bergen	20	93	5	10, 12, 14, 16

for each instance.

To ensure solution feasibility and reduce computational time, an upper bound on the number of helicopters that will be required per instance is estimated, as described in Section 4.4. For example, for the Stavanger instance, under the assumption that the total flight demand is covered with direct flights, a total of 626 timeslots per week would be required. This number is divided by 220 which is the total number of timeslots in the minimal helicopter operating window option. The resulting number 2.85 is rounded to three helicopters that at maximum are required to cover the transport demand.

Table 3. Operating windows and their fixed cost.

Operating Window	Fixed Cost
10	5968
12	6625
14	6813
16	7000

shows the fixed costs for the available operating windows in units that mask real cost values, with realistic ratios.

6.2.2. Florø Instance Results and Verification

Figure 5 presents a flight program generated by the flight-based model. The optimal solution has a total cost of 9980, utilising a single helicopter operating within a 10-h window per day. The decomposition-based algorithm finds the optimal solution with the same helicopter resources. The flights are, however, assigned to different days and time slots. There are several valid optimal solutions for flights assignment; however, the solver was configured to output only one.

The actual helicopter resources used at the time were two helicopters, one with 10 h of availability and the other with 16 h. This is one additional 16-h helicopter compared to the optimal solution. The two helicopters were underutilised, and planners considered reducing fleet to one helicopter. However, partly due to an industry-wide shortage of spare parts for the S-92 helicopter model, the decision was made at the time to keep both helicopters. In addition, one of the helicopters was shared with another energy operator, slightly improving total utilisation. The solution clearly demonstrates that based solely on Equinor’s flight demand at the time and the defined planning policies, there was a potential to reduce the fleet by one helicopter. The optimisation tools effectively highlight this opportunity which can be used as a structured input to managerial decisions.

6.2.3. Stavanger Instance Results and Verification

The flight program generated by the decomposition-based algorithm is shown in Figure 6 and has an optimal solution with a cost of 26,642, using two helicopters with operating windows of 12 and 16 h.

The actual helicopter resources used at the time were three helicopters with availabilities of 24, 14 and 12 h. This allocation differs from the optimal solution which required one less helicopter. Several factors explain this discrepancy. The helicopter with the 24-h availability is available for critical demands during the night and is in practice only available for 16 h of regular planned flights, which is the maximum daily planning time horizon. One of the helicopters was shared with another energy operator, improving the utilisation of the third helicopter. There is a clear potential for the reduction of one helicopter based solely on Equinor flight demand in this period.

6.2.4. Bergen Instance Results and Verification

The decomposition-based algorithm required two iterations to find an optimal solution. In the first iteration, the solution of the Stage 1 model assigns four helicopters to operating windows (H1 = 16, H2 = 12, H3 = 10, and H4 = 10) and has a total cost of 47,394. In the following run of the Stage 2 model, it is not possible to find feasible solutions for Monday and Friday. According to the decomposition-based algorithm, the operating window of helicopter H2 is increased from 12 to 14 h, which is the option that provides the least-cost increase. In the second iteration, the Stage 1 model is run again with the increased fixed helicopter resources found by the algorithm. In the following run of the Stage 2 model, an optimal solution for all days is found. The final solution uses four helicopters with operating windows of 16, 14, 10, and 10 h, and has a total cost of 47,582. Figure 7 shows the optimal flight program for the Bergen instance.

The actual helicopter resources used comprised five helicopters, one with 24 h availability, two with 14 h availability, and two with 12 h availability. This is one more helicopter than the optimal solution found, and two helicopters with 12 h availability compared to 10 h in the optimal solution. Similarly to the Stavanger instance, one of the helicopters with 24 h availability is primarily reserved for critical demands outside its availability during daytime. Also, in the Bergen heliport, there is a collaboration with another energy operator with one of the helicopters, increasing the utilisation of the last helicopter. The optimisation tool shows that, considering only Equinor’s demand in this period, it was theoretically possible to reduce the fleet with one helicopter.

Table 4. Characteristics of the optimal flight programs, with the improvements compared to actual solutions.

Heliport	Helicopters	Operating Windows	Total Cost	Total Utilisation
Florø	1 (−1)	10 (−16)	9980 (−41%)	86.82% (+53%)
Stavanger	2 (−1)	16, 12 (−14)	26,642 (−20%)	86.82% (+33%)
Bergen	4 (−1)	16, 14, 10, 10 (−14)	47,582 (−15%)	95.93% (+25%)

presents characteristics of the optimal flight programs for all instances, including optimal helicopter resources (number of helicopters and their operating windows), total cost, and total utilisation of the resources as percentage of time flown within the available operating windows. The improvement compared to the actual resources used at the time is shown in the brackets in each column. For the 24 h available helicopters in the Bergen and Stavanger heliports, it is assumed that these are only available for 16 h regular flights.

It should be mentioned that there could be certain challenges with the implementation of cost-optimal flight programs in practice. Substantial changes in helicopter resources such as fleet reduction and following significant adjustments in weekly flight timetables require thorough alignment with installations and sufficient time for the managerial implementation of such changes.

6.3. Impact of Planning Policy Constraints

During the development of the flight-based model formulation and its validation by Equinor planners, two planning policy requirements were suggested in addition to the mandatory installation-related, helicopter-related, and flight-related constraints. In what follows, it is shown with the Florø instance example why industry planners find the flight shift and the flights spread constraints necessary for weekly flight timetable planning and the impact of these constraints on the quality of the resulting weekly programs.

6.3.1. Impact of Flight Shift Constraints

The Florø problem instance was first solved to optimality with the flight-based model without planning policies using only the mandatory constraints (2), (4), (5), (6), (7), (8), and (9). Figure 8 shows that the optimal selection of helicopter resources is one helicopter with an operating window of 10 h, with 3–4 flights assigned per day. On Friday, there is a longer than one-hour idle time between the first and the second flights. This is inefficient as operational delays for later flights may press the flights outside the opening hours of the installations or the helicopter operating window. This is why a timetable with early flight starts and tightly packed flights is preferred, since it accumulates the idle times towards the end of each day as a natural slack.

Figure 9 shows the solution with the added flight shift constraints (11). The weekly flight program uses the same helicopter resources and flights and thus has the same cost. However, the modified timetable ensures no idle times between flights and all the free capacity is now accumulated at the end of the helicopter operating window on Wednesday. It improves the quality of the flight program as the available helicopter capacity at the end of the operating window may be used as a buffer for natural delays or extra flights operationally scheduled. This exactly mimics the planning policy of helicopter planners in Equinor.

6.3.2. Impact of Flights Spread Constraints

The flight timetable in Figure 9 shows an uneven distribution of flight for installations. Installation F1 has three flights on Thursday while only one flight on all other days. Installation F2 has two flights on Monday and Wednesday and no flights on Friday. Installation F3 has three flights on Friday and one or none all other days. In Figure 10, the installation flight spread constraints (10) are added, ensuring that the difference in the number of flights per installation between any two days is at maximum one. This evens the distribution of flights, giving the flexibility for installations to spread bookings of personnel throughout the week. The constraints also ensure a form of fairness in the daily distribution of flights between the installations. This complies with the company’s helicopter planning policy.

6.4. Computational Time Analysis

As expected, only the small Florø instance was possible to solve to optimality with the flight-based model, in 159 s. For the larger Stavanger and Bergen instances, the model solution process was terminated due to insufficient memory, according to the solver output.

Table 5. Number of iterations and computational time in seconds.

Instance	Iterations	Total Time	Stage 1	Stage 2
Florø	1	4.39	1.97	2.42
Stavanger	1	27.26	16.52	10.74
Bergen	2	492.27	387.41 + 1.33	16.14 + 87.39

shows the number of iterations of the decomposition-based algorithm, the total computational time in seconds, and the computational time used to solve Stage 1 and Stage 2 models for all instances. Solution times for each model at each iteration are shown in the summations. In the column “Stage 1”, these numbers provide time to solve Stage 1 model, while in the column “Stage 2”, they present the total time of running the Stage 2 model until infeasibility was discovered for one of the days, or optimal solutions for all days have been generated. The flight generation procedure and identification of a marginal least-cost increase in helicopter resources took just a few seconds and thus are not reported.

The decomposition-based algorithm found an optimal solution for the Florø instance in one iteration in less than 5 s. The solution for the medium-size Stavanger instance was also found in one iteration, in 27.26 s, with less than 17 s in Stage 1 and less than 11 s in Stage 2. For the largest Bergen instance, the optimal solution was found in two iterations, with an increase in helicopter resources in the second iteration. The total solution time was 492.27 s, with 389 s for both iterations in Stage 1, and 104 s in Stage 2. The solution time for Stage 1 model in the first iteration is substantially larger than in the second iteration where the helicopter resources are already known from the first iteration. In contrast, the time for model solving in Stage 2 is smaller in the first iteration where the Stage 2 model has an infeasible solution already for the first day, while in the second iteration the model generated optimal solutions for all days.

The difference in the computational time for the solution of small and medium instances is approximately 6 times compared to approximately 18 times longer solution time between the medium and the large instance. The three times larger increase in the computational time from the medium to the large instance can be explained by the fact that with eight more installations and two additional helicopters available, the number of possible assignments of operating windows and flights substantially increases. The same explanation is valid for the longer computational time for model solving in Stage 1 than in Stage 2 for all instances.

The computational time analysis shows that the decomposition-based algorithm can generate solutions for small instances of up to four installations within a few seconds, for medium instances for up to twelve installations within half a minute, and for large instances with around twenty installations within nine minutes. The solution time of around 8 min for the largest Equinor instance on the NCS is very fast compared to the manual planning procedure taking days of work. These results show that the developed decomposition-based algorithm will be highly relevant and demanded for all other offshore energy operators on the NCS that have smaller instances compared to Equinor.

7. Applicability and Adaptivity

The flight-based optimisation model for the WFPPP and the iterative decomposition-based algorithm for the construction of cost-optimal weekly flight programs developed in this project are planned to be used as the solution engine of the automated decision support tool for tactical helicopter planning at Equinor. In the first subsection, we describe and illustrate with examples how the developed solution methods for the WFPPP can be used in practice for decision analysis and support at Equinor and by other offshore operators on the NCS. The next subsection presents how the flight-based model formulation and the decomposition algorithm can be adapted to practical industry needs outlining possible problem extensions and the modifications of the developed tools. We also discuss whether the studied problem formulation and the proposed flight-based model and the decomposition-based algorithm could be generalised to be adapted to other offshore regions.

7.1. Applicability

The managerial advantages of the developed optimisation-based tools for decision support in tactical helicopter transportation planning for Equinor and other operating companies on the NCS are substantial. They are suitable for being applied for various practical purposes as further presented and illustrated by examples.

The significant advantage of the developed decomposition-based algorithm is that it enables rapid planning with cost-optimal solutions in accordance with the defined planning policies. It allows planners to thoroughly assess the optimal resource selection and flight assignment each time demand changes. This level of analysis would not typically be performed manually as small changes might only prompt minor adjustments without a comprehensive full evaluation of the solutions.

The practical application of the decomposition-based algorithm makes it possible to use an optimal solution generated as a benchmark for solutions manually created by planners. Planning performed manually may result in subjective outcomes, lead to higher solution cost, and may be prone to errors or solution inefficiency due to the complexity of the task. Benchmarking the solutions will highlight the potential for improved resource selection, cost savings, and flight timetable quality. The application of the developed optimisation-based solution tools will make it possible to objectively evaluate whether helicopter resources selected manually by planners are sufficient and cost-efficient. Comparing tool-generated solutions with actual flights programs will allow the examination of differences and the analysis of why the managerial decisions regarding resource selection and flight timetable planning deviate from the general planning policies modelled in the tools. This enables modelling and testing alternative planning policies.

The other important advantage of the developed model-based solution tools comes from the configuration option of modelling the Gurobi solver to output alternative optimal solutions. This option allows planners and installations to choose between different weekly timetables with the same helicopter resources and total cost.

The tools developed can also be used to generate solutions with changes in installations-related planning policies enabling managers to objectively evaluate the impact on flight program (timetable) quality; for example, evaluating the impact of replacing the even spread of flights to each installation with the installations-defined distribution of flights between days, and evaluating the trade-offs for including preferences for flight assignment from installations.

The application of the flight-based model without and with the flight shift constraints can provide planners with solutions where idle times are either spread between helicopters’ daily flights or accumulated at the end of their operating windows. This information on natural timetable slacks enables planners to measure and evaluate the weekly flight program’s reliability.

The developed tools can be applied to analyse the effects of changes in the number and the combination of operating windows options, installations’ opening hours, the set of installations to serve from the heliport (adding and removing mobile installations), the set of planned days for helicopter operations (adding weekend), and the allowed flight types (flights with more landings).

The following example shows how the number and combination of the available operating window options effect the solution results illustrated using the Stavanger instance. The instance was solved for the following scenarios of available operating window options: one operating window available (10, 12, 16 scenarios), two operating windows available (10 + 12, 10 + 16, 12 + 16 scenarios), and three operating windows available (10 + 12 + 16 scenario).

Table 6. Effects of available operating window options on solution results.

Scenarios of Available Operating Window Options	Helicopter Resources	Total Resource Utilisation	Total Cost
10	10, 10, 10	89.54%	30,921
12	12, 12, 12	75.76%	32,892
16	16, 16	86.91%	27,017
10 + 12	10, 10, 10	89.54%	30,921
10 + 16	16, 16	86.91%	27,017
12 + 16	12, 16	98.50%	26,642
10 + 12 + 16	12, 16	98.50%	26,642

illustrates the solution results for each scenario, showing cost-optimal helicopter resources, total resource utilisation, and total cost. The optimal least-cost solution is as expected for the last scenario where all operating window options are available, with two helicopters of 12 h and 16 h operating window options, the highest utilisation of 98.50%, and the lowest total cost of 26,642. When only two options for operating windows are available, results vary depending on the combination of available options. For example, with the 12 + 16 scenario, the same optimal solution is achieved. With the 10 + 16 scenario, the least-cost solution requires both helicopters operating for 16 h, leading to lower utilisation and higher total cost. However, for the 10 + 12 scenario, three helicopters each operating for 10 h are required, resulting in the highest cost, even with better utilisation. When only one operating window is available, results vary. With the 16 scenario, the result is second best after the optimal solution. For the 10 scenario, the result is as for the 10 + 12 scenario. The worst solution is for the 12 scenario, both in the number of helicopters and the total cost and utilisation. In this example, the best number and combination of available operating window options is scenario 12 + 16. However, the 16 scenario has the best trade-off between cost and free capacity, with only a slightly higher cost and more free capacity. It highlights the importance of testing all scenarios to decide which combination of operating window options to agree on with the helicopter operator for future periods of stable demand.

In the following example, the effect of changes in installations opening hours on resource selection, flight assignment, total cost, and resource utilisation is illustrated on the Florø instance. Figure 11 shows the optimal solution when installation F4 opening hours are reduced to the time interval between 07:00 and 09:00. Here, all flights to F4 starts at 07:00, in contrast to the solution illustrated in Figure 10, where most of the flights to F4 have later start times. This change has no effect on helicopter resources, total cost, and resource utilisation. However, when installation F3 has the same reduction of opening hours, one more helicopter with a 10-h operating window is required, doubling the fixed costs of the solution and reducing resource utilisation from 86.85% to 47.75%.

The developed optimisation tools can also be applied to evaluate the effect of changes in the installations’ numbers and their locations, flight demands, operating windows’ costs, and hourly cost on solution results such as optimal helicopter resources, total resource utilisation, and total cost, and can also be applied for the sensitivity analysis of solutions on the accuracy of parameters’ values. This is especially important for defining new stable demand periods and for informing helicopter operators about the required changes in helicopter resources.

The following example shows how helicopter resources and costs change between future demand periods when additional mobile installations are moving to the operations area illustrated on the Stavanger instance. The following future demand periods were considered: the first period when only one mobile installation is served (S1), the second period when one more installation moves to the area of operations (S1 + S3), the third period when installation S4 arrives (S1 + S3 + S4), and the last period when installation S5 is also planned to move to the area (S1 + S3 + S4 + S5). These installations have different distances from the heliport and to other installations, as shown in Figure 4. The demand for each installation is four flights per week.

Table 7. Changes in solution results when additional installations are moving to the area of operations.

Mobile Installations	Helicopter Resources	Total Resource Utilisation	Fixed Cost	Total Cost
S1	10, 12	92.29%	12,593	22,426
S1 + S3	10, 16	86.96%	12,968	23,717
S1 + S3 + S4	10, 16	95.53%	12,968	24,717
S1 + S3 + S4 + S5	12, 16	98.50%	13,625	26,642

shows changes in optimal helicopter resources, total resource utilisation, and fixed and total cost for each following period after additional installations move to the area of operations. The table analysis shows that helicopter resources change from the first to the second period and then from the third to the fourth period. Adding installation S3 in the second period will require an increase in the operating window for the second helicopter from 12 to 16 h because in the previous period operating windows for both helicopters were 92.29% utilised. However, for the third period when installation S4 is also served in the area, the helicopter resources that are available are enough to cover the increased demand. In the last period, when all four mobile installations are in the area, the operating window for the first helicopter increases from 10 to 12 h, since all available resources in the previous period are 96% utilised. Following the increase in transport demand and thus in the required helicopter resources, the total cost gradually increases, with an increase only in variable cost from the second to the third period. This example illustrates how the optimisation-based solution tools can be used to identify how and why helicopter resources change after new installations move to the area of operations.

The advantages of the developed optimisation-based tools to quickly generate proven optimal solutions for large problem instances make them superior for evaluating the potential benefits of horizontal cooperation between energy operators. By pooling demands and sharing helicopter resources between energy operators, helicopter planners can identify opportunities to optimise helicopter utilisation and lower total costs. Characteristics of the joint flight programs generated for problem instances with installations operated by several energy companies can be used for the analysis of resource allocation and cost sharing between potential collaborating offshore operators. This analysis is required when evaluating whether cooperation between operators could result in significant cost savings through resource sharing.

The tender process for helicopter contracts must objectively evaluate and compare bids from helicopter operators, ensuring transparency and fairness. The developed optimisation tools can generate for every bid a series of flight programs for the whole contract period with the number of helicopters offered, their available operating windows, and variable and fixed costs as inputs. The detailed and accurate comparison of the summarised costs for the series of flight programs for the bids can support the tender process, allowing decision-makers to select the best bidder.

7.2. Adaptivity

The flight-based model and the algorithm based on its decomposition developed for the solution of the formulated basic version of the WFPPP are also suitable to be adapted to practical industry needs. The presented flight-based model formulation can be modified to address various problem extensions by including additional requirements and planning policies. Examples of some relevant problem extensions are presented below, pointing to how the basic model formulation can be modified. At the end, we discuss the challenges related to the generalisation and adaptation of the solution tools developed especially for the NCS to other offshore areas.

7.2.1. Installations Visit Windows

Offshore installations may in some cases require designated visit windows within their opening hours, specifying the days and time slots that are allocated to receive helicopter flights. For example, there is an ongoing practice to try to avoid helicopter landings during planned supply vessel operations at installations. Adding visit windows requirements to the basic model formulation is challenging for the cases when visit windows start later than the helicopter operating windows or when there are several visit windows per day, due to the flight shift planning policy constraints that are imposed. However, this can be implemented in the second stage of the decomposition-based algorithm by replacing the opening hours’ constraints with the new constraints, ensuring that flights occur only within the defined visit windows. Sensitivity analysis can be performed to study the effects of adding different visit windows on the optimal helicopter resources and costs.

7.2.2. Preferences from Installations

In reality, it may happen sometimes that installations express certain individual preferences for flights on specific days and time slots, and on the number of flights per day due to their operational requirements. For example, even though it is physically possible to use the late evening flights for mobile installations, it may not always be the preferred solution for installations’ operations. This can also be the case for other time slots and days that are assigned to flights. To address this, the decomposition-based algorithm can be adapted to include installations’ preferences by introducing indicator parameters specifying which days and time slots the installation prefers. Solutions generated with the objectives to maximise total preference satisfaction and minimising total cost can be used to evaluate the total added cost and level of service for each installation.

7.2.3. Equity in Preferences

For each installation, some time slots for flights may be more preferable and some less preferable. The challenge for planners would be to find solutions with a trade-off between the objectives of maximising individual preferences, the sum of preferences across all installations, the ability to ensure some form of equity between the installations, and to minimise total cost. To address this problem extension, new utility decision variables can be introduced for installations, measuring their satisfaction of the preferences. Different measures of equity can be incorporated into the model formulation, with the goal of finding solutions that balance the total utility, the equity in preferences’ satisfaction, and the total cost.

7.2.4. Reliability

The developed optimisation tools generate weekly timetables with natural time slacks which can be used as a buffer against minor operational changes that may occur. The flight program constructed for a stable demand period guarantees that each week the declared flight demands from installations are covered. The principal assumption in tactical helicopter planning is that the installations’ weekly flight demands do not dynamically vary from week to week during this period. However, during a day or a week within the fixed helicopter operating windows, there may be flight cancellations, postponed flights, ad hoc flights, flights merged, and delays in flight duration and start time because of installations’ operational needs and weather conditions. To adapt for possible disruptions in the flight timetable and ensure that the declared weekly demand will be satisfied, the tactical helicopter planners construct reliable weekly flight programs, adding time slacks to flight durations, in-between flights, and at the end of the helicopter operating windows. Planners may use different policies in order to incorporate the time slacks in the weekly timetable; see, for example, [25,26]. For the construction of cost-efficient and reliable flight programs with the help of the optimisation tools developed in this work, it is possible to incorporate flight slack during flight generation and to include daily time slacks in the flight-based model formulation as the requirements for additional or dummy flights assignment within the designated visit windows. The amount and the distribution of the required slack time in practice is decided by experts while optimisation tools make it possible to analyse how much slack can be added into a timetable without an increase in helicopter resources and cost.

7.2.5. Continuity

In practice, a new period of stable demand is identified when the total weekly flight demand and/or location of installations change substantially to require changes in helicopter resources and the construction of a new flight timetable. Nevertheless, installations usually express their needs for as few changes as possible in flights assignment to days and timeslots so they can continue crew changes in the same days and times. Requesting continuity in flight assignment in the new timetable may lead to a substantial cost increase; thus, planners are interested in solutions with the minimal possible deviations in flights assignment and the least added cost. The developed optimisation tools can be adapted to generate a weekly flight program for a new period of stable demand with continuity in flight assignment by minimising total deviation between current and new timetables. This can be performed by introducing a parameter that specifies which flights should be assigned to the same days and timeslots as in the previous timetable, and variables quantifying deviations in flight assignment. The flight-based model formulation can be modified to minimise the total deviation while imposing constraints on the allowable cost increase, ensuring a trade-off between continuity in flight assignment and cost.

7.2.6. Mixed Fleet

One of the possible directions for further research in tactical helicopter planning on the NCS is an extension of the basic WFPPP formulation from the currently used homogeneous fleet of large helicopters to a mixed fleet, also considering super-medium helicopters in addition to the currently used large helicopters, which will require modifications in the flight-based model and the decomposition algorithm. The preliminary discussions with installations and helicopter planners show that the assumption on measuring transport demand in the number of flights will still hold and split flights will still be relevant now for both helicopter models. The adaptation for super-medium helicopters in the current WFPPP model formulation will require additional sets, parameters, and modifications of installations’ flight demands and other relevant constraints.

7.2.7. Challenges with Generalisation and Adaptation to Other Areas

This paper is focused on tactical helicopter planning, especially for the NCS, based on the knowledge of the largest offshore operating company planning practices specific for this region. This study did not aim to develop a problem formulation general for other offshore areas mainly because of the lack of knowledge and access to other offshore operating companies’ information and data. The currently used prerequisites and assumptions for tactical helicopter planning on the NCS such as the country-regulated assignment of installations to heliports, current homogeneous fleet market, contract options for selection of helicopter operating windows, etc., may not be relevant for other areas, operating companies’ strategies, and planning practices. Based on the available literature from Brazilian authors and direct contacts with helicopter planners in Petrobras energy company operating in Brazilian basins, we were able to be acquainted with their management rules and tactical helicopter planning principles to study similarities and differences. As far as we are aware of, the WFPPP formulation for a single heliport on the NCS with simultaneous selection of helicopter resources and weekly flight timetable planning cannot be applied to the Brazilian cases where mixed fleet pre-sizing and allocation between heliports is performed ahead of the construction of the weekly flight timetables. The first-stage model of our decomposition algorithm has some similar constraints with the intermediate strategic–tactical weekly planning model for flight allocation to the helicopter-model-heliport-installation-day of Mendes et al. [26] but is different in assumptions, decision variables, and objectives. However, the second-stage model of our algorithm assigning pre-defined flights to start times while shifting them to the start of helicopter operating windows has potential to be extended and adapted to the construction of weekly flight timetables in Brazil and probably other offshore areas.

8. Conclusions and Further Research

Tactical helicopter planning for offshore personnel transportation on the Norwegian Continental Shelf (NCS) for a stable demand period focuses on the selection of helicopter resources and the construction of a repetitive weekly timetable of flights to ensure coverage of installations’ weekly transport demands from the heliport while minimising fixed and variable costs. This paper is the first study that formalises the tactical helicopter offshore personnel transportation planning problem for heliports on the NCS. The description of the assumptions, objectives, inputs and outputs for tactical helicopter planning specific for the NCS such as the known assignment of installations to a heliport, period of stable demand, homogeneous fleet, direct and split flights, helicopter resources, operating windows, weekly flight demands, weekly flight program, mandatory requirements, and planning policies are provided, followed by the presentation of the current planning procedure and an illustration of its output. It is the first paper on helicopter weekly flight program planning where helicopter resource selection is integrated with weekly timetable planning assigning start times to flights.

The weekly flight program planning on the NCS is formulated as an optimisation problem and solved in two steps. The pre-generated flights are input to the flight-based integer programming model, selecting the cost-optimal number of helicopters and their operating windows matching the total weekly flight demand. The benefit of the formulation is that it integrates decisions on helicopter resource planning with decisions on the assignment of flights to helicopters, operating windows, and days and start times in a weekly timetable, ensuring sets of installation-, helicopter-, and flight-related mandatory requirements and planning policies that aim to spread flights to each installation between days and to eliminate gaps between flights.

To solve problem instances of all sizes existing on the NCS, an iterative two-stage solution algorithm is developed based on the decomposition of the flight-based model. The least-cost helicopter resources required to cover weekly flight demand are selected by distributing flights between weekdays using the first-stage model. The selected resources are input to the second-stage model, separately for each day, assigning selected flights to start times while shifting them towards the start of operating windows. If solution infeasibility is detected, helicopter resources are revised, exploiting the marginal least-cost increase, and the algorithm iterates to the first-stage model until a feasible least-cost solution is found.

The weekly flight programs generated for Equinor actual instances showed the advantages of the decomposition-based algorithm, enabling ability to solve to optimality problems of large sizes quickly. The results presented in this paper have been validated and verified by Equinor’s helicopter planners. They have confirmed that the developed optimisation algorithm is capable of generating cost-optimal weekly flight programs for real industry problems in a short time and can be used as a solution engine for the automated decision support tool for tactical helicopter planning, providing input for the evaluation of the helicopter contract portfolios. They are suitable for being applied by Equinor and other companies operating on the NCS for improved decision-making, testing expert-generated solutions, evaluating the effects of changes in problem characteristics and parameters, gathering statistics, and assessing new planning policies and contract options. For all offshore energy operators on the NCS, the developed optimisation tools for tactical helicopter transportation planning are currently highly relevant and widely demanded as they can be easily adapted to address industry-required problem extensions and planning requirements.

The most important directions for further research in tactical helicopter planning required by the industry on the NCS include the development of solution methodologies for such problem extensions as the requirement of fairness between installations in preferred flight assignment, a mixed helicopter fleet, and horizontal collaboration with resource sharing and cost allocation between operators.