Using Entropy Metrics to Analyze Information Processing Within Production Systems: The Role of Organizational Constraints
Abstract
1. Introduction
2. Coordination and Network Entropy
3. Graph Theory to Describe Network and Situation Entropy
3.1. Shannon Entropy
3.2. The Complexity of Coordination
3.2.1. Design Complexity
- Extra coordination is needed when Takttime cannot be met at a specific moment or location in the production system.
- Both additional capacity and coordination are required when Takttime is exceeded.
3.2.2. Coordination Complexity
3.2.3. Node Complexity
3.3. Network Simulation
4. Two Examples of Coordination Systems
4.1. Toyota Production System
4.1.1. Slack and Constraints by Design to Deal with Variations
- pi: Processing time for the product with standard features at the department.
- pf,i: Extra processing time due to specific product feature requirements at the department.
- pq,i: Extra processing time of the product due to quality problems at the department.
4.1.2. A Closed-Loop Control System
4.1.3. Complexity in a Coordination Network: At System and at Node Level
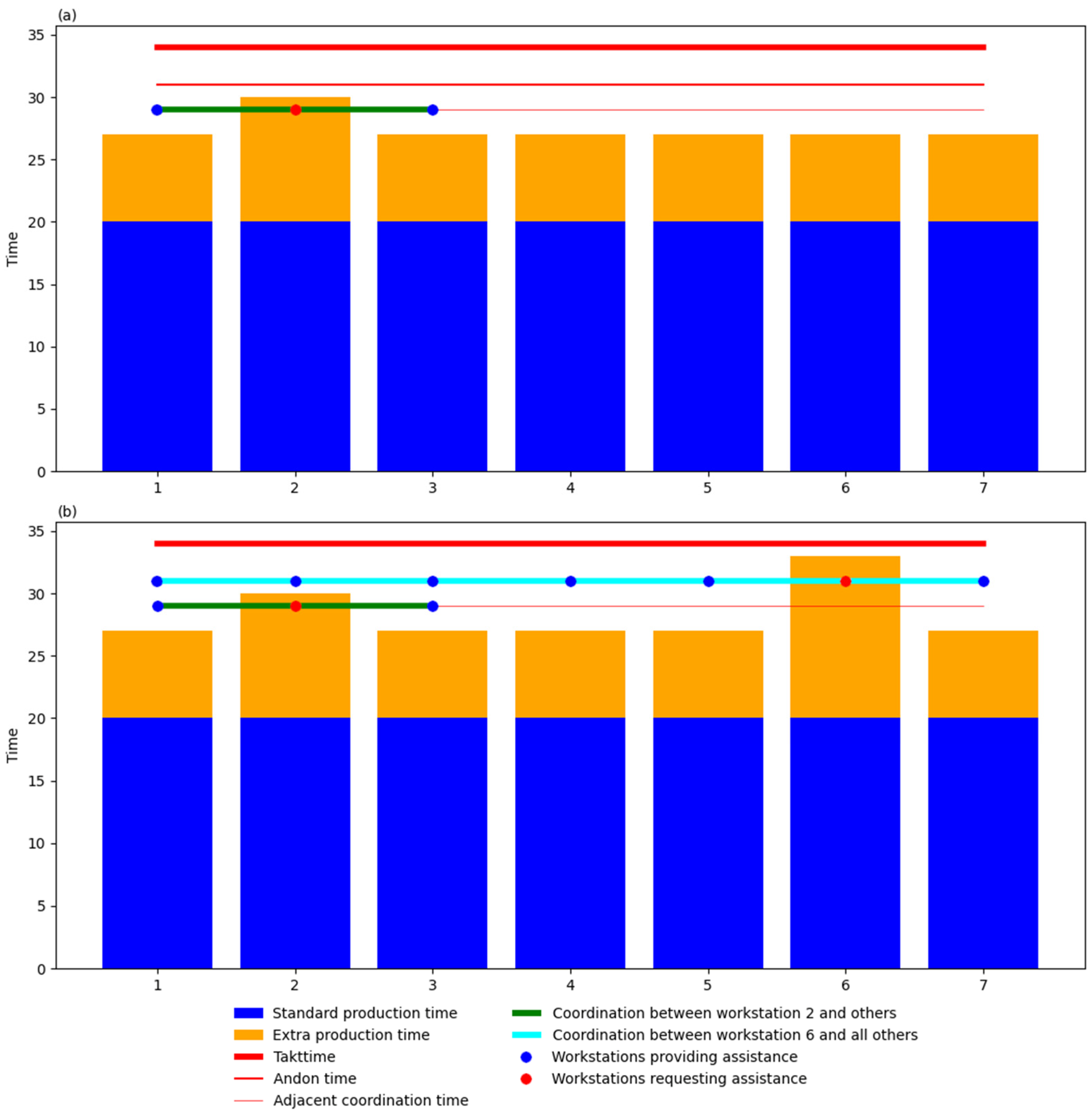
4.1.4. Takttime, Adjacent, and Andon Coordination
- Help time: time when adjacent workstations are asked (and expected) to provide assistance.
- Andon time: time when all workstations are asked (and expected) to provide assistance.
- Below 29 min: no coordination between workstations is needed.
- Between 29 and 31 min: coordination occurs between adjacent workstations.
- Above 31 min: coordination is required from all workstations.
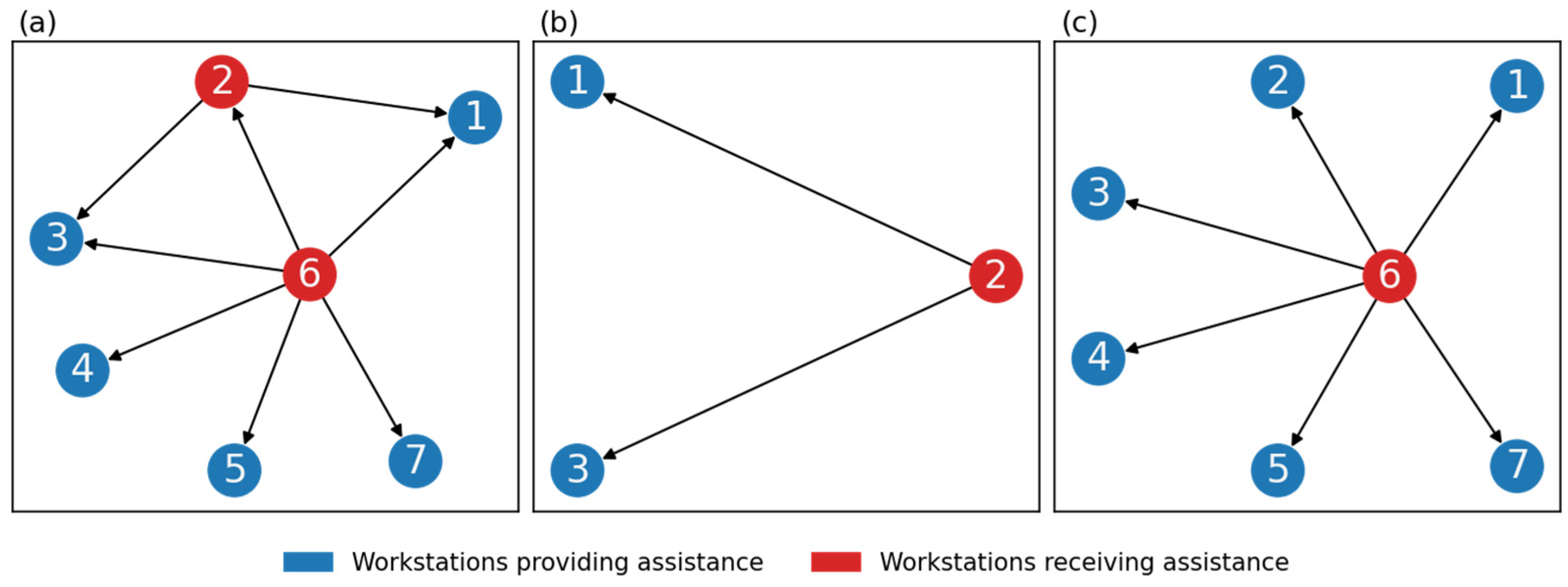
- For workstation 1, workstation 2 becomes involved.
- For workstation 3, both workstations 1 and 2 become involved.
- Situation networks: formed in response to routine coordination demands based on help time.
- Andon networks: formed when andon time is reached, requiring broader coordination.
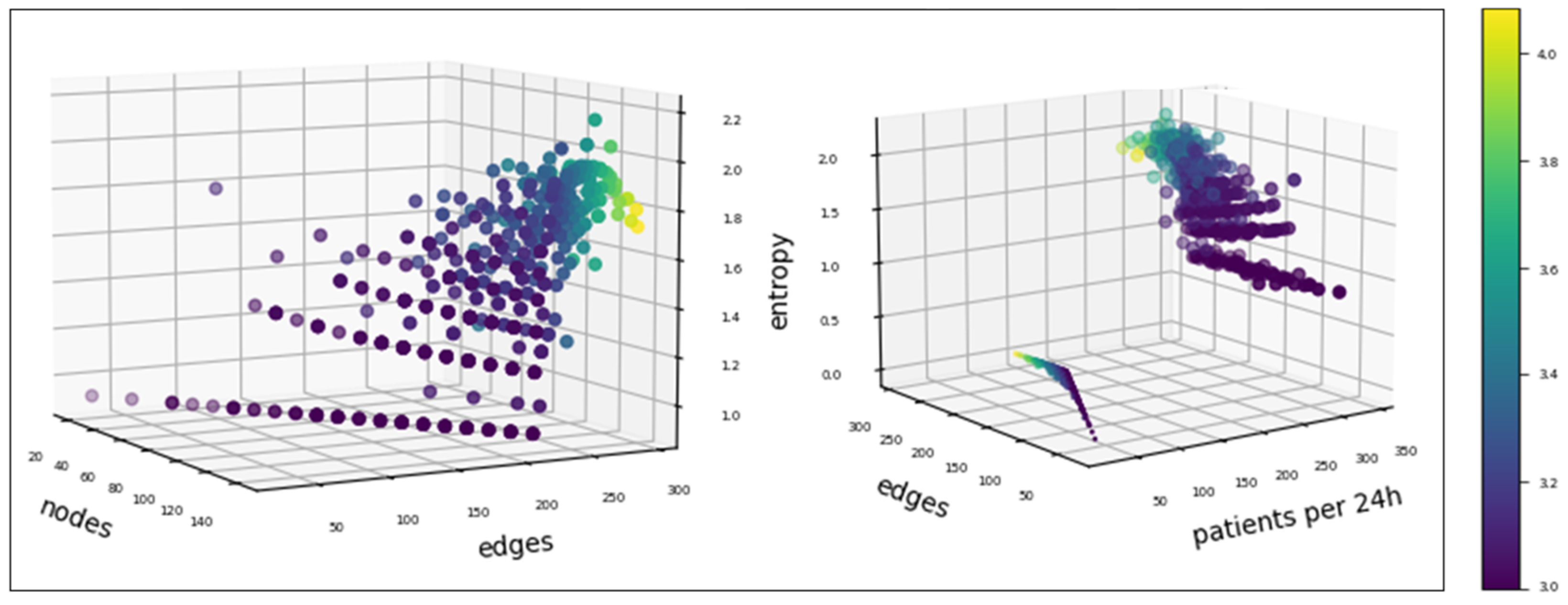
4.1.5. TPS Case Study
Scenario Generator
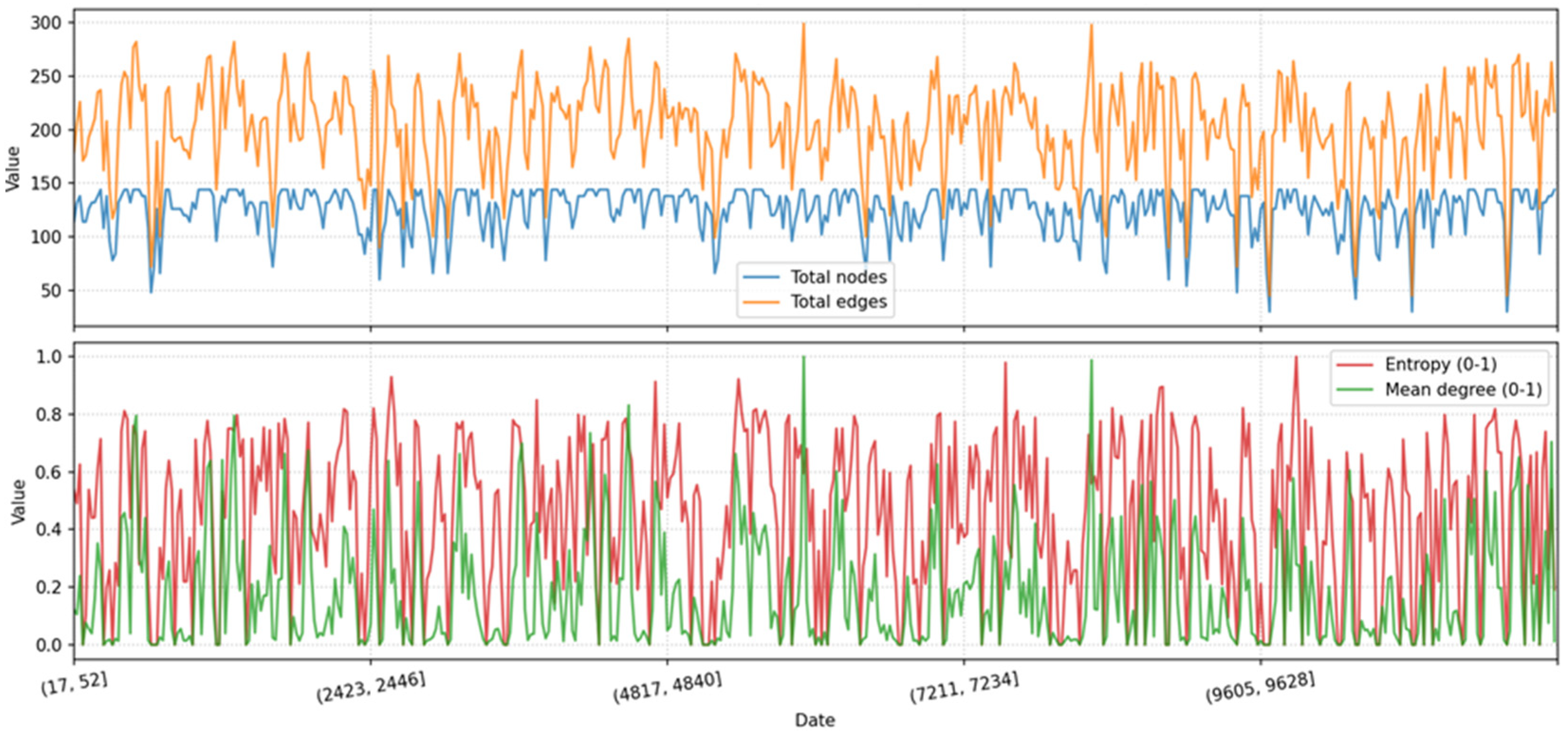
Simulation Results
- No situation or andon entropy (entropy is 0 for both). Occurs when help time, andon time, and maximum duration are identical. Assumes 100% standard process times with no disturbances; in practice, any disturbance would immediately cause the system to fall out of control, as no buffer for coordination exists. This is a highly unrealistic scenario, unless there are no variations in process or task times.
- Situation entropy exists and there is no chance that andon entropy exists. This is only the case when the andon time is set at the maximum duration time. All process time variations are managed locally through help time coordination. Coordination efforts likely result in situation entropy and an increase in local edges. This set up may be deliberate, such as when an organization prioritizes local coordination or lacks sufficient multiskilled workers for broader (andon) coordination. Without multiskill training, andon coordination is infeasible, and local solutions become the default. Alternatively, this way of coordination may also be a matter of choice, such as in organizations where local over andon coordination may be preferred.
- Situation entropy exists and there is a chance that andon entropy develops. It is characterized by the maximum process time exceeding andon time. When the maximum possible process time is above andon time, there is always a chance that andon coordination is activated. The likelihood of andon coordination and its entropy therefore increases with longer andon time zones and decrease with longer help time zones—the latter of which reduces the frequency and impact of andon coordination. The interplay between help time and andon time zones determines the balance between localized (situation) and global (andon) coordination efforts.
4.1.6. Phase Transitions and Complexity
- From “Need Help” to “Andon”. Triggered by breaching help time threshold, prompting localized coordination. Node complexity increases and entropy rises as local coordination networks emerge, particularly for nodes requiring assistance and their adjacent nodes.
- From “Andon” to “Out of Control”. Andon time threshold is surpassed, leading to system-wide coordination or failure. Node complexity becomes concentrated, as certain nodes bear disproportionately high coordination loads. Fluctuation of entropy levels is initially high during widespread coordination, then stabilizes at medium levels if resolved efficiently. Otherwise, it peaks at very high levels if the system is overwhelmed (out of control).
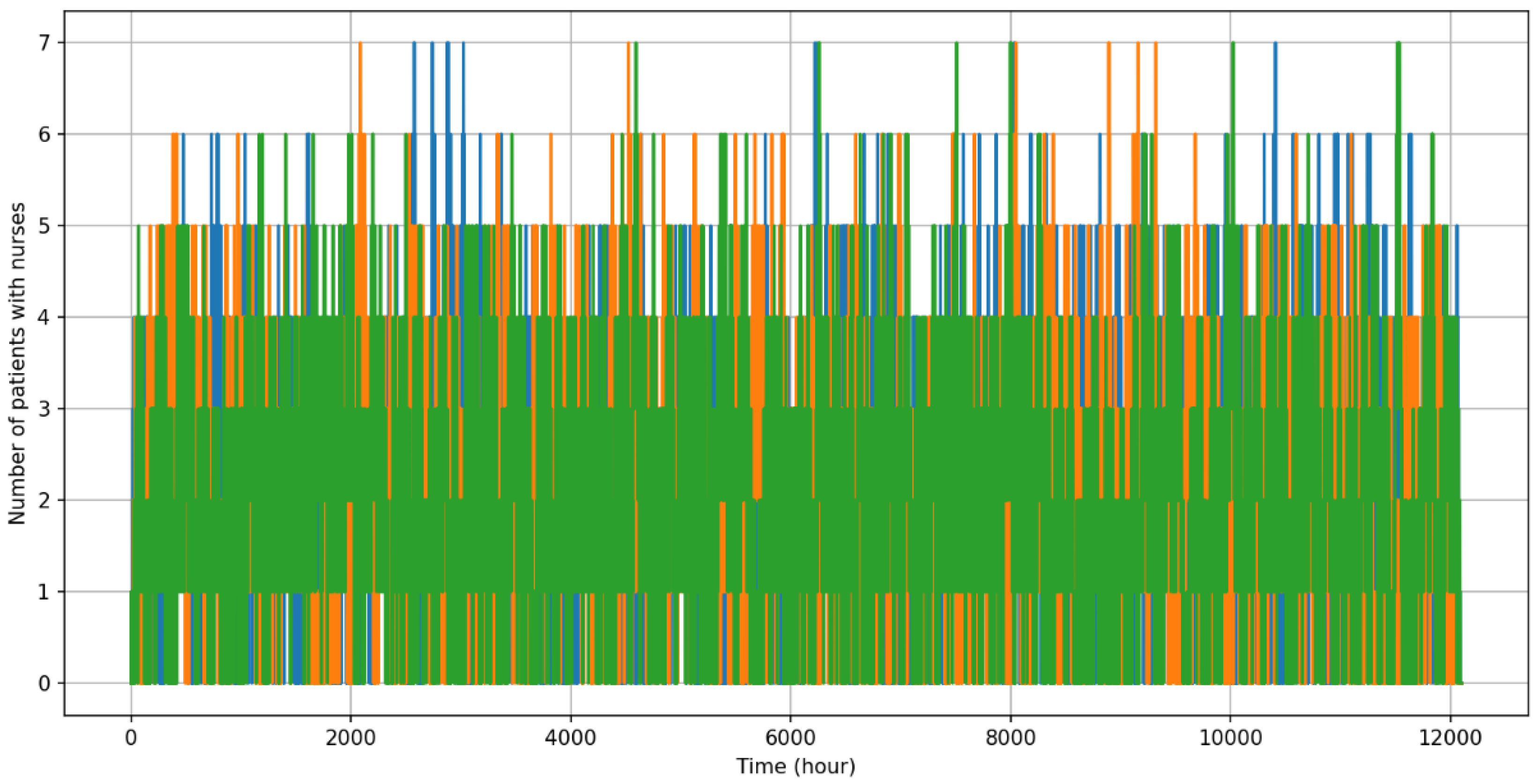
4.2. Obstetrics Case Study
4.2.1. Scenario Generation: Coordination in Different Levels of Occupancy
4.2.2. Model Description
4.2.3. Simulation Results
5. Discussion
5.1. Differences in Entropy and Network Metrics Among TPS and the Obstetrics Clinic
5.2. Design Complexity: Open Versus Closed Loop Systems
5.3. Crises and Shocks
5.4. Entropy Methods
5.5. Limitations and Future Research
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Physical and Information Flows | Type of Coordination Network |
 | (a) No feedback loops. Products and materials flow from upstream stations to downstream stations once ready, independent of the status of the downstream stations. No information is sent upstream, and no coordination occurs. |
 | (b) Local feedback loops. Downstream stations communicate their status to the next upstream workstations, enabling adjustments to their operations. Coordination occurs via local feedback loops, and if feedback times are short, this coordination can operate nearly in real-time at the system level. |
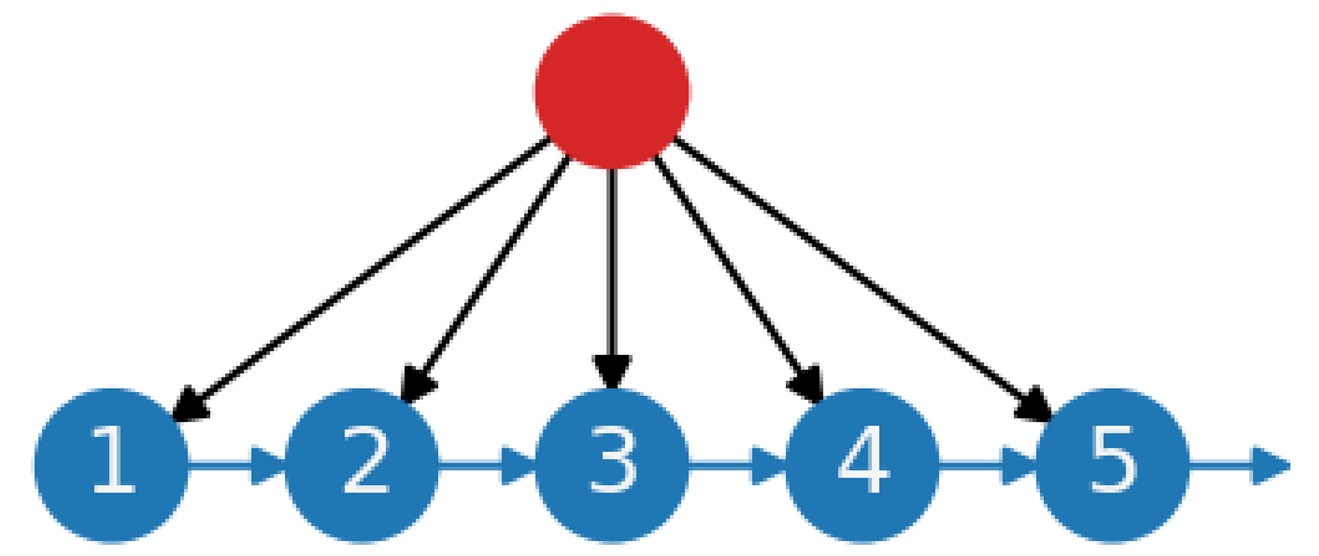 | (c) Central planning without feedback loops. Similar to (a), but with an added central planning function. The planning function has two roles: (1) production leveling: determining the volume, mix, and order of products to meet demand and smooth the workload; and (2) capacity assignment: allocating capacity to workstations. Communication between upstream and downstream stations is absent, and coordination is achieved centrally. This system works best when operations are deterministic. If operations are not fully deterministic, slack capacity must be available at each workstation, and waiting times between workstations should be allowed. Slack capacity and waiting times serve as buffers, but their extent is difficult to predict. |
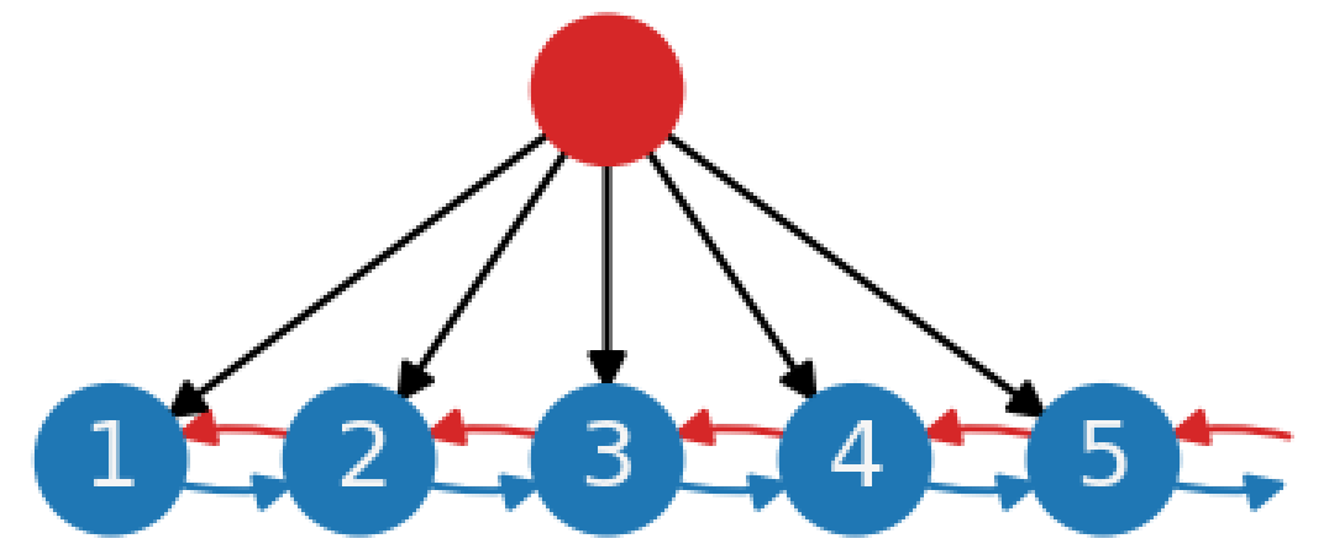 | (d) Central planning with local feedback loops. Combination of (b) and (c). The planning function is the same as in (c), but operational coordination is achieved entirely through local feedback loops. This system is especially useful for production systems with many product variants. Unlike (c), slack capacity and waiting times between workstations are controlled locally. |
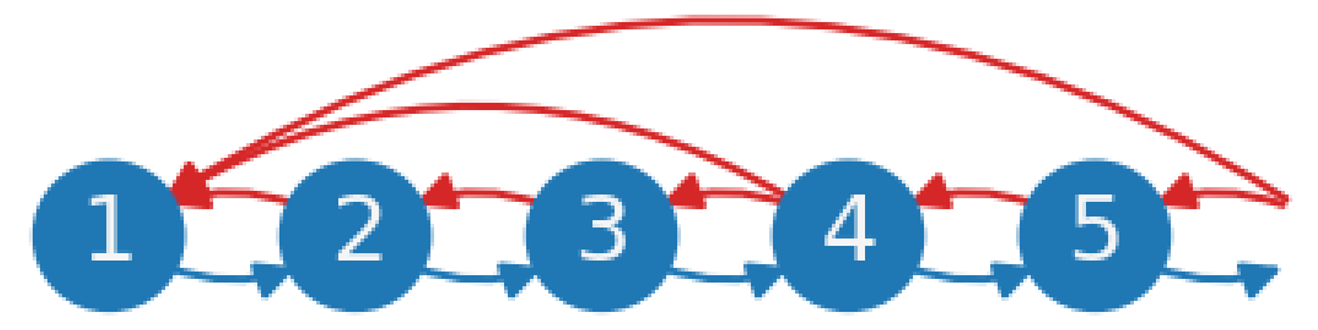 | (e) Local and global feedback loops. This system builds on (b) by incorporating work-in-progress coordination. Order release is influenced by the total amount of work in progress from the last station to the first (upper red line). It is also possible to measure and communicate the workload between the first workstation and an intermediate station to the beginning of the chain (middle red line). This addition of global control to the local feedback loops, contrasting with (b), allows upstream stations to adjust their workload based on downstream constraints, implying the need for assistance from workers from adjacent stations. The extent to which this is possible depends on whether the standard workload plus a surplus factor (including slack) is below a predefined threshold. If this threshold is exceeded, the release of orders stops. |
 | (f) Central planning with local and global feedback loops. Combination of (c) and (e), used for work-in-progress coordination. As in (d), the rationale for the planning loop (in black) is to be found in occasions when many different product variants are to be produced, allowing for the central relocation of workers. |
 | (g) Local and global feedback loops with synchronization. Similar to (e), but applied to multiple production lines. Work in progress is measured from workstations 1 to 4, from workstations ’a’ to 4, from the first to the defined ‘end station’, and from ‘a’ to the ‘end station’. In total, four work-in-progress measurements are used to control the production system. With multiple production lines, synchronization between these lines is necessary. This means that the release of orders across different production lines must be coordinated (e.g., at workstations 1 and ’a’). This system also allows workers from adjacent workstations on different production lines to assist each other. |
References
- Zhu, X.; Hu, S.J.; Koren, Y.; Marin, S.P. Modeling of Manufacturing Complexity in Mixed-Model Assembly Lines. J. Manuf. Sci. Eng. 2008, 130, 051013. [Google Scholar] [CrossRef]
- Hu, S.J.; Zhu, X.; Wang, H.; Koren, Y. Product variety and manufacturing complexity in assembly systems and supply chains. CIRP Ann. —Manuf. Technol. 2008, 57, 45–48. [Google Scholar] [CrossRef]
- Chryssolouris, G.; Efthymiou, K.; Papakostas, N.; Mourtzis, D.; Pagoropoulos, A. Flexibility and complexity: Is it a trade-off? Int. J. Prod. Res. 2013, 51, 6788–6802. [Google Scholar] [CrossRef]
- Ivanov, D. Two views of supply chain resilience. Int. J. Prod. Res. 2024, 62, 4031–4045. [Google Scholar] [CrossRef]
- Aldrighetti, R.; Calzavara, M.; Martignago, M.; Zennaro, I.; Battini, D.; Ivanov, D.A. methodological framework for the design of efficient resilience in supply networks. Int. J. Prod. Res. 2024, 62, 271–290. [Google Scholar] [CrossRef]
- Aldrighetti, R.; Battini, D.; Ivanov, D. Efficient resilience portfolio design in the supply chain with consideration of preparedness and recovery investments. Omega 2023, 117, 102841. [Google Scholar] [CrossRef]
- Riccardo, A.; Daria, B.; Dmitry, I. Increasing supply chain resilience through efficient redundancy allocation: A risk-averse mathematical model. IFAC-Pap. 2021, 54, 1011–1016. [Google Scholar] [CrossRef]
- Aldrighetti, R.; Battini, D.; Ivanov, D.; Zennaro, I. Costs of resilience and disruptions in supply chain network design models: A review and future research directions. Int. J. Prod. Econ. 2021, 235, 108103. [Google Scholar] [CrossRef]
- Bonchev, D.; Rouvray, D. Shannon’s information and complexity. Complex. Chem. Introd. Fundam. 2003, 7, 157–187. [Google Scholar]
- Dehmer, M.; Mowshowitz, A. A history of graph entropy measures. Inf. Sci. 2011, 181, 57–78. [Google Scholar] [CrossRef]
- Benjamin, A.; Chartrand, G.; Zhang, P. The Fascinating World of Graph Theory; University Press: Princeton, NJ, USA, 2015. [Google Scholar]
- Kumar, V. Entropic measures of manufacturing flexibility. Int. J. Prod. Res. 1987, 25, 957–966. [Google Scholar] [CrossRef]
- Battini, D.; Persona, A.; Allesina, S. Towards a use of network analysis: Quantifying the complexity of Supply Chain Networks. Int. J. Electron. Cust. Relatsh. Manag. 2007, 1, 75–90. [Google Scholar] [CrossRef]
- Wang, J.; Wilson, R.C.; Hancock, E.R. Network edge entropy decomposition with spin statistics. Pattern Recognit. 2021, 118, 108040. [Google Scholar] [CrossRef]
- Cheng, C.-Y.; Chen, T.-L.; Chen, Y.-Y. An analysis of the structural complexity of supply chain networks. Appl. Math. Model. 2014, 38, 2328–2344. [Google Scholar] [CrossRef]
- Morzy, M.; Kajdanowicz, T.; Kazienko, P. On measuring the complexity of networks: Kolmogorov complexity versus entropy. Complexity 2017, 2017, 3250301. [Google Scholar] [CrossRef]
- Chaitin, G.J. Algorithmic Information Theory. IBM J. Res. Dev. 1977, 21, 350–359. [Google Scholar] [CrossRef]
- Gell-Mann, M. The Quark and the Jaguar: Adventures in the Simple and the Complex; St. Martin’s Press: New York, NY, USA, 1995. [Google Scholar]
- Gell-Mann, M.; Lloyd, S. Information measures, effective complexity, and total information. Complexity 1996, 2, 44–52. [Google Scholar] [CrossRef]
- Zenil, H.; Kiani, N.A.; Tegnér, J. A Review of Graph and Network Complexity from an Algorithmic Information Perspective. Entropy 2018, 20, 551. [Google Scholar] [CrossRef]
- Martignago, M.; Calzavara, M.; Katiraee, N.; Battini, D. Entropic measurement in supply chain network: Past applications, current trends, and future research. In Proceedings of the Summer School Francesco Turco, Genova, Italy, 6–8 September 2023; Volume 1, pp. 1–7. [Google Scholar]
- Carcassi, G.; Aidala, C.A.; Barbour, J. Variability as a better characterization of Shannon entropy. Eur. J. Phys. 2021, 42, 045102. [Google Scholar] [CrossRef]
- Lin, Y.H.; Wang, Y.; Lee, L.H.; Chew, E.P. Consistency matters: Revisiting the structural complexity for supply chain networks. Phys. A Stat. Mech. Its Appl. 2021, 572, 125862. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Monostori, J. Robustness- and Complexity-oriented Characterization of Supply Networks’ Structures. Procedia CIRP 2016, 57, 67–72. [Google Scholar] [CrossRef]
- Womack, J.P.; Jones, D.T. Lean Thinking—Banish Waste and Create Wealth in Your Corporation; Revised and Updated; Free Press: New York, NY, USA, 2003. [Google Scholar]
- Nye, D.E. America’s Assembly Line; The MIT Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Katiraee, N.; Calzavara, M.; Finco, S.; Battaïa, O.; Battini, D. Assembly line balancing and worker assignment considering workers’ expertise and perceived physical effort. Int. J. Prod. Res. 2023, 61, 6939–6959. [Google Scholar] [CrossRef]
- Liu, C.; González, V.A.; Pavez, I.; Tortorella, G.L.; Abdelmegid, M. Exploring the socio-technical interactions associated with lean implementation: A systematic literature review. Prod. Plan. Control. 2025, 1–33. [Google Scholar] [CrossRef]
- Khakifirooz, M.; Fathi, M.; Dolgui, A.; Pardalos, P.M. Assessing resiliency in scale-free supply chain networks: A stress testing approach based on entropy measurements and value-at-risk analysis. Int. J. Prod. Res. 2024, 1–34. [Google Scholar] [CrossRef]
- Sharma, S.K.; Srivastava, P.R.; Kumar, A.; Jindal, A.; Gupta, S. Supply chain vulnerability assessment for manufacturing industry. Ann. Oper. Res. 2023, 326, 653–683. [Google Scholar] [CrossRef]
- Van Rossum, G.; Drake, F.L., Jr. The Python Language Reference; Python Software Foundation: Wilmington, DE, USA, 2014. [Google Scholar]
- The Pandas Development Team. pandas-dev/pandas: Pandas 2.2.3; Zenodo: Genève, Switzerland, 2021. [Google Scholar]
- McKinney, W. Data Structures for Statistical Computing in Python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010; Walt, S.É.V.D., Millma, J., Eds.; scipy.org: Austin, TX, USA, 2010; pp. 56–61. [Google Scholar]
- Caswell, T.A.; Droettboom, M.; Lee, A.; Sales De Andrade, E.; Hoffmann, T.; Hunter, J.; Klymak, J.; Firing, E.; Stansby, D.; Varoquaux, N.; et al. matplotlib/matplotlib: REL, v3.5.2; Zenodo: Genève, Switzerland, 2022. [Google Scholar]
- Hunter, J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Plotly_Technologies. Plotly Open Source Graphing Library for Python. 2023. Available online: https://plotly.com/python/?_ga=2.202387800.891488512.1698351200-1657284833.1677516886 (accessed on 27 October 2023).
- Sievert, C. Interactive Web-Based Data Visualization with R, Plotly, and Shiny; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Harris, C.R.; Millman, K.J.; Van Der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- Hagberg, A.; Schult, D.; Swart, P. Networkx, Version 2.8; NetworkX Developers: Los Alamos, NM, USA, 2022.
- Hagberg, A.; Swart, P.; Chult, D.S. Exploring Network Structure, Dynamics, and Function Using NetworkX; Los Alamos National Lab. (LANL): Los Alamos, NM, USA, 2008. [Google Scholar]
- Passos, N.A.R.A.; Carlini, E.; Trani, S. NetworkX-Temporal: Building, Manipulating, and Analyzing Dynamic Graph Structures; Zenodo: Genève, Switzerland, 2024. [Google Scholar]
- Liker, J.K.; Meier, D. The Toyota Way Field Book; Tata McGraw-Hill Publishing Company: New Delhi, India, 2006; p. 475. [Google Scholar]
- Black, J.T. Design rules for implementing the Toyota Production System. Int. J. Prod. Res. 2007, 45, 3639–3664. [Google Scholar] [CrossRef]
- Mönch, T.; Huchzermeier, A.; Bebersdorf, P. Variable takt times in mixed-model assembly line balancing with random customisation. Int. J. Prod. Res. 2021, 59, 4670–4689. [Google Scholar] [CrossRef]
- Mönch, T.; Huchzermeier, A.; Bebersdorf, P. Variable takt time groups and workload equilibrium. Int. J. Prod. Res. 2020, 60, 1535–1552. [Google Scholar] [CrossRef]
- Munavalli, J.R.; Vasudevarao, S.; Srinivasan, A.; Manjunath, U.; van Merode, G.G. A Robust Predictive Resource Planning under Demand Uncertainty to Improve Waiting Times in Outpatient Clinics. J. Health Manag. 2017, 19, 563–583. [Google Scholar] [CrossRef] [PubMed]
- Munavalli, J.R.; Rao, S.V.; Srinivasan, A.; van Merode, G.G. intelligent real-time scheduler for out-patient clinics: A multi-agent system model. Health Inform. J. 2020, 26, 2383–2406. [Google Scholar] [CrossRef] [PubMed]
- Munavalli, J.R.; Boersma, H.J.; Rao, S.V.; van Merode, G.G. Real-Time Capacity Management and Patient Flow Optimization in Hospitals Using AI Methods. In Artificial Intelligence and Data Mining in Healthcare; Masmoudi, M., Jarboui, B., Siarry, P., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 55–69. [Google Scholar]
- Masuda, N.; Holme, P. Detecting sequences of system states in temporal networks. Sci. Rep. 2019, 9, 795. [Google Scholar] [CrossRef] [PubMed]
- Moctar, A.O.M.; Sarr, I.; Tanzouak, J.V. Snapshot Setting for Temporal Networks Analysis. In e-Infrastructure and e-Services for Developing Countries; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar]
- Bushuyev, S.D.; Sochnev, S.V. Entropy measurement as a project control tool. Int. J. Proj. Manag. 1999, 17, 343–350. [Google Scholar] [CrossRef]
- Hopp, W.J.; Spearman, M.L. Factory Physics: Foundations of Manufacturing Management, 2nd ed.; Irwin/McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Meng, K.; Ba, Z.; Liu, L. A Network Portrait Divergence Approach to Measure Science-Technology Linkages; Springer Nature: Cham, Switzerland, 2024. [Google Scholar]
- Bagrow, J.P.; Bollt, E.M. An information-theoretic, all-scales approach to comparing networks. Appl. Netw. Sci. 2019, 4, 45. [Google Scholar] [CrossRef]
- Bagrow, J.P.; Bollt, E.M.; Skufca, J.D.; ben-Avraham, D. Portraits of complex networks. Europhys. Lett. 2008, 81, 68004. [Google Scholar] [CrossRef]
- Van Merode, F.; Groot, W.; Somers, M. Slack Is Needed to Solve the Shortage of Nurses. Healthcare 2024, 12, 220. [Google Scholar] [CrossRef]
| Section | Topics Addressed |
|---|---|
| 2. Coordination and network entropy | How can coordination be modeled as networks? To what extent can entropy of these networks measure the coordination complexity? |
| 3. Graph theory to describe network and situation entropy | What types of coordination complexity do occur? Where do these occur in coordination networks? How can coordination networks be simulated? What are the metrics used to evaluate the characteristics of coordination networks? |
| 4. Two examples of coordination systems | Introduction of concepts of Takttime, adjacent and andon coordination and temporal coordination networks Comparison of coordination of Toyota Production System (TPS) with University Obstetric Clinic Simulation of scenarios for both examples |
| 5. Discussion | What are the differences between the coordination networks of TPS and the University Obstetric Clinic? What do these differences mean? What is the design complexity of the TPS and the University Obstetric Clinic? Limitation of this study |
| 6. Conclusions | What is the insight into the complexity of coordination in both examples? |
| Variable | Meaning |
|---|---|
| Number of nodes | The number of agents (such as workers, machines, or entities) involved in coordination within the system. |
| Number of edges | The total number of coordination links (connections) between the nodes in the network. |
| Node degree | The sum of incoming and outgoing edges associated with a node. It signals the relative involvement of a node in the coordination network. |
| Average node degree | The mean degree of all nodes in the network, i.e., the total number of edges divided by the total number of nodes in the graph. |
| Maximum node degree | The highest degree among all the nodes in the network, indicating the most involved agent in coordination. The difference between the average and maximum degree of nodes is used to measure the centralization of coordination within the network. |
| Entropy | In this context, entropy refers to graph entropy as a measure of the structural complexity of the coordination network. |
| Parameter Description | Parameter Value | |
|---|---|---|
| c1 | Time without features (standard time) | 60 |
| c2 | Mean extra time (due to product features or quality issues, based on uniform distribution) | range (5, 25, 5) |
| c3 | Help time (trigger time for coordination from adjacent workstations, added to c2) | range (5, 15, 5) |
| c4 | Andon time (trigger time for coordination from all workstations, added to c2) | range (10, 25, 5) |
| c5 | Takttime (maximum time per cycle) | 100 |
| Situation Networks (Local Coordination) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Max Degree | Average Degree | Entropy | |||||||||
| 0.00 | 0.86 | 0.99 | 1.15 | 1.38 | 1.45 | 1.56 | 1.66 | 1.84 | 1.95 | ||
| 2 | 1.71 | 0.00% | 2.43% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% |
| 2.00 | 38.49% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | |
| 3 | 2.00 | 0.00% | 0.00% | 0.00% | 7.09% | 0.00% | 0.00% | 4.64% | 0.00% | 0.00% | 0.00% |
| 2.29 | 0.00% | 7.15% | 0.00% | 0.00% | 0.28% | 7.41% | 0.00% | 0.00% | 0.00% | 0.00% | |
| 2.57 | 0.00% | 0.00% | 1.88% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | |
| 4 | 2.00 | 0.00% | 0.00% | 0.00% | 0.00% | 5.69% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% |
| 2.29 | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 3.34% | 9.31% | 0.00% | 3.04% | |
| 2.57 | 0.00% | 0.00% | 0.00% | 0.00% | 3.96% | 0.00% | 0.36% | 0.00% | 4.60% | 0.00% | |
| 2.86 | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.35% | 0.00% | 0.00% | 0.00% | |
| Andon Networks (Global Coordination) | |||||
|---|---|---|---|---|---|
| Maximum Degree | Average Degree | Andon Entropy | |||
| 0.00 | 0.59 | 0.86 | 0.99 | ||
| 2 | 2.00 | 76.62% | 0.00% | 0.00% | 0.00% |
| 8 | 3.71 | 0.00% | 5.12% | 0.00% | 0.00% |
| 5.14 | 0.00% | 0.00% | 6.38% | 0.00% | |
| 6.29 | 0.00% | 0.00% | 0.00% | 5.96% | |
| 7.14 | 0.00% | 0.00% | 0.00% | 3.68% | |
| 7.71 | 0.00% | 0.00% | 1.71% | 0.00% | |
| 8.00 | 0.55% | 0.00% | 0.00% | 0.00% | |
| Average Degree | Entropy (Normalized Between 0 and 1) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.0–0.1 | 0.1–0.2 | 0.2–0.3] | 0.3–0.4 | 0.4–0.5 | 0.5–0.6 | 0.6–0.7 | 0.7–0.8 | 0.8–0.9 | 0.9–1.0 | |
| 0.0–0.1 | 11.80% | 1.80% | 12.00% | 9.40% | 8.20% | 3.20% | 1.40% | 0.00% | 0.00% | 0.00% |
| 0.1–0.2 | 0.00% | 0.60% | 0.00% | 1.40% | 3.20% | 3.20% | 3.20% | 1.80% | 0.20% | 0.00% |
| 0.2–0.3 | 0.00% | 0.00% | 0.00% | 0.80% | 0.60% | 1.60% | 3.60% | 4.00% | 0.20% | 0.00% |
| 0.3–0.4 | 0.00% | 0.00% | 0.00% | 0.00% | 0.40% | 0.80% | 1.40% | 3.20% | 0.80% | 0.40% |
| 0.4–0.5 | 0.00% | 0.00% | 0.00% | 0.00% | 0.20% | 0.20% | 2.00% | 2.80% | 2.60% | 0.40% |
| 0.5–0.6 | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.20% | 3.40% | 1.40% | 0.20% |
| 0.6–0.7 | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.60% | 1.80% | 0.40% | 0.00% |
| 0.7–0.8 | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.20% | 0.60% | 2.00% | 0.20% | 0.00% |
| 0.8–0.9 | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.20% | 0.60% | 0.00% | 0.00% |
| 0.9–1.0 | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.20% | 0.60% | 0.00% | 0.00% | 0.00% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
van Merode, F.; Boersma, H.; Tournois, F.; Winasti, W.; Reis de Almeida Passos, N.A.; Ham, A.v.d. Using Entropy Metrics to Analyze Information Processing Within Production Systems: The Role of Organizational Constraints. Logistics 2025, 9, 46. https://doi.org/10.3390/logistics9020046
van Merode F, Boersma H, Tournois F, Winasti W, Reis de Almeida Passos NA, Ham Avd. Using Entropy Metrics to Analyze Information Processing Within Production Systems: The Role of Organizational Constraints. Logistics. 2025; 9(2):46. https://doi.org/10.3390/logistics9020046
Chicago/Turabian Stylevan Merode, Frits, Henri Boersma, Fleur Tournois, Windi Winasti, Nelson Aloysio Reis de Almeida Passos, and Annelies van der Ham. 2025. "Using Entropy Metrics to Analyze Information Processing Within Production Systems: The Role of Organizational Constraints" Logistics 9, no. 2: 46. https://doi.org/10.3390/logistics9020046
APA Stylevan Merode, F., Boersma, H., Tournois, F., Winasti, W., Reis de Almeida Passos, N. A., & Ham, A. v. d. (2025). Using Entropy Metrics to Analyze Information Processing Within Production Systems: The Role of Organizational Constraints. Logistics, 9(2), 46. https://doi.org/10.3390/logistics9020046






