Abstract
Background: Nowadays, variable domination structure is instrumental in studying multiobjective decision making problems. We investigate multiobjective location problems with respect to variable domination structure and its applications in supply chain management. Methods: We formulate practical problems in supply chain management as an optimization problem with a variable domination structure. Moreover, we present the mathematical methods to solve such problems. We investigate two kinds of solutions derived from the concept of minimal and nondominated solutions from vector optimization problems with respect to variable domination structure. Furthermore, we explore how these solution concepts are characterized in practical problems. Results: We ex- pose how those solutions are beneficial in practical problems. However, these results hold true for multiobjective decision making problems with a continuous feasible set; we present a practical problem in the case of a finite set of feasible locations. Conclusions: In many multiobjective location problems, each location’s characterizations, preferences, and restrictions are involved in the decision making process. This study investigates the decision making problems, where different preferences of objective functions at each location are assumed. Moreover, we present a numerical experiment for selecting a new hub airport.
1. Introduction
Multicriteria decision-making (MCDM) problems deal with solving problems to determine the feasible solution/solutions according to the considered criteria. In many classifications, MCDM problems are divided into two sections: multiobjective decision-making (MODM) problems and multiattribute decision-making (MADM) problems [1].
Facility location decisions play an important role in logistics planning, business management, strategic management, industrial engineering, etc. The facility location problem asks for a new facility location such that one or more objective functions are to be optimized. In the formulation of the objective function of many location problems, distances between existing facilities and a new facility are involved, see [1,2]. In real-world applications, other objectives may affect the decision, including cost (e.g., land cost, labor cost, production cost, material cost, logistics cost, and the like), time, financial risks, laws and regulations, quality, economic factors, etc.
Melo et al. [3] reviewed the literature on facility location problems in supply chain management.
The multiobjective facility location problem plays a critical role in the strategic design of supply chain management, especially the logistics part of supply chain management. Some objectives in supply chain management are optimizing quality, minimizing logistics costs (transportation costs, administration costs, and inventory carrying costs), optimizing customer satisfaction, optimizing inventory, optimizing delivery speed, minimizing the ordering time, etc.
Thus far, multiobjective location problems assume a fixed ordering cone and find the optimal solution/solutions considering this fixed ordering cone.
Recently, vector optimization problems with respect to (w.r.t.) variable domination structure has been significant for studying MODM problems. The variable domination structure was first introduced by Yu [4], and he used variable cones in preference modeling [4,5]. To find Pareto optimal solutions in MODM problems, one uses an ordering cone C in the image space. Yu introduced an optimal element of a vector optimization problem w.r.t. a variable domination structure called the non-dominated element, which is not dominated by another element of objective space w.r.t. the associated set to this other point. Chen, Huang and Yang [6] defined minimal elements of the vector optimization problem w.r.t. variable domination structure which is not dominated by another element of objective space, w.r.t. the associated set to this candidate point [7]. Many researchers have subsequently investigated different solution concepts and applications of variable domination structures. Bao, Mordukhovich, and Soubeyran developed mathematical models of variable domination structure in behavioral sciences [8,9]. Eichfelder [10,11,12] discussed variable ordering structures and demonstrated an application of variable ordering structures in medical engineering. Soleimani et al. [7,13] introduced concepts for approximate minimal, approximate non-dominated, and an approximate minimizer for vector optimization problems w.r.t. variable ordering structure. Tammer et al. proposed decision support for location problems in town planning and multicriteria location routing problems for travel management in tourism [14,15].
Table 1 presents some studies on multiobjective location problems.

Table 1.
Literature review [16,17,18,19,20].
In [21], we studied multiobjective location problems w.r.t. variable domination structure; we introduced an inverse variational inequality to investigate the solutions of such problems. Since each location has its characterization, preferences, and restrictions in many multiobjective location problems, these characterization, preferences, and restrictions affect the value of optimizing each objective function. For instance, in one feasible location, minimizing the time is more preferred to minimizing the cost, while, in the other feasible location, it could be vice-versa. Variable domination structure represents these variable preferences of objective functions in multiobjective location problems.
Therefore, the locations are compared in terms of their preferences and restrictions. The aim of this study is to show that certain problems arising in Logistics lead to optimization problems w.r.t. variable domination structure. Furthermore, we developed the mathematical methods for solving such problems, see [21]. Multiobjective location problems w.r.t. variable domination structure is proposed where different preferences of objective functions are assumed at each location.
Xiong and Yu [22] studied selecting a hub airport based on a Steiner tree model. Paul [23] investigated assessment of constraints for market power on the transfer market and in the local catchment for European Hub Airports. This paper is organized as follows: Section 2 discusses the fundamental concepts of vector optimization problems w.r.t. variable domination structures. Section 3 presents a mathematical method to solve MCDM problems with variable criteria weights based on alternative preferences. We use the result of Proposition 1 to present two types of solutions in MODM problems w.r.t. variable domination structure. The advantage of this model is that alternatives are compared with the corresponding preferences. Section 4 investigates a numerical experiment for selecting a new hub airport. We discuss the importance of the two types of solutions in more detail.
2. Preliminaries
To present solution concepts for MCDM problems with a variable domination structure, we present some basic concepts of a Pareto efficient solution. Afterward, minimal and non-dominated elements in vector optimization problems w.r.t. variable domination structure are presented.
Let be a set of alternatives or locations (in the location problems). X is called feasible set, and . Let objective function be defined as
where , , for . The spaces and are called decision space and objective space, respectively.
The concept of Pareto efficiency assumes a fixed ordering cone (in this case, we assume ) The vector optimization problem w.r.t. fixed ordering cone is given by
and a point is called Pareto efficient solution for if
Consider the objective function defined in (1); let be a set-valued mapping, known as a variable domination map. The vector optimization problem corresponding to this variable domination structure is expressed as
In the sequel of this study, minimal and non-dominated solutions for the problem are used under Definition 1 (compare to [24]).
Definition 1.
Let . For problem , we say that:
- (i)
- is a minimal solution of if is a minimal element of w.r.t. the domination map , i.e,The set of all minimal elements of w.r.t is denoted by
- (ii)
- is a non-dominated solution of if is a non-dominated element of w.r.t. the domination map , i.e,The set of all non-dominated elements of w.r.t is denoted by
- (iii)
- is a weakly non-dominated solution of if is a weakly non-dominated element of w.r.t. the domination map , i.e,In this case, it is assumed that , for all . The set of all weakly non-dominated elements of w.r.t. is denoted by
Remark 1.
Properties and relationships in these solutions have been investigated in several studies, including [10,13].
In [21], the authors derive a new method for solving multiobjective location problems using definitions of minimal and weakly non-dominated solutions. In the next section, we also use these concepts.
3. Minimal and Weakly Non-Dominated Solutions of Vector Optimization Problems and Inverse Variational Inequality
The following assumption is used through this study; it describes a formula for a special domination map.
Assumption A1.
Let be a vector function, , , and where for , and whenever . Assume that for , is a convex domination map defined as
We recall the following proposition, which discusses a result concerning the sufficient conditions of the minimal and weakly non-dominated solutions of problem [16,21].
Proposition 1.
[21]. Let Assumption 1 be fulfilled. Consider , , , for and .
- If the following inequality holds for all ,Then, is a weakly non-dominated element of w.r.t. .
- Furthermore, for , , if the following assertion holds true for all ,is a minimal element of w.r.t. .
4. MCDM Problems w.r.t. Variable Domination Structures
This section demonstrates relationships between vector optimization problems, w.r.t. variable domination structures and MCDM problems. In this section, we consider a finite set of alternatives/locations and criteria/objective functions. We show that it is possible to obtain more appropriate solutions for MCDM problems by considering vector optimization w.r.t. appropriate domination structures, where different preferences of objective functions related to each alternative/location are at hand. We begin with the formulation of MCDM problems.
4.1. MCDM Problems
MCDM problems deals with finding the best alternative or ranking of them in terms of considered objective functions or criteria [25]. In multiobjective location problems, a decision maker must select the best location among a set of candidate locations, w.r.t. a set of objective functions. This section recalls basic concepts of MCDM problems, solutions for these problems, and methods for addressing them. A decision-making process contains the following steps:
- Determining the goal of the decision-making process;
- Selecting the set of criteria or objective functions;
- Collecting the alternatives or locations in location problems (feasible set);
- Considering a cone in order to compare the objective function values;
- Choosing a weighting method to represent the relative importance of criteria (if needed);
- Choosing a method to solve the MCDM problem.
Further details can be found in [25,26,27].
Here, we consider a special case of problem , where is a finite feasible set of alternatives, locations, or possible actions. A function represents the value of each alternative on p different criteria, where is the objective space [4,27]. We consider the following MCDM problem:
where the solution concepts of are introduced in Definition 1.
Remark 2.
For all The concept of Pareto-optimal solutions is an important special case of non-dominated solutions, see [4].
After obtaining the set of all images of alternatives , we obtain a family of points in the space . There are several methods for finding solutions to MCDM problems. For instance, the simple additive weighting (SAW) method was first introduced to address a portfolio selection problem. In this method, a weight vector is assigned, and solutions are determined based on computations of all utilities of alternatives , i.e., , where (see [25], Section 4.1 for more detail on this method). In addition, in fuzzy multi-attribute decision-making (FMADM) problems, if we assume that there is a mutually independent relationship among the criteria, the fuzzy simple additive weighting (FSAW) method is used. For other methods, we refer to [25,28,29] for more detail.
Section 4.3 presents the solution concepts of MCDM problems w.r.t. variable domination structure.
4.2. Decision Matrix and Weight Matrix
This section presents some notions to solve MCDM problems, using a decision matrix and a weight matrix. A decision matrix helps to prioritize which decisions meet our goals. Table 2 collects alternatives and objective functions, for which columns and rows are created to derive a decision matrix, representing the alternatives and objective function values, respectively, where and represent the alternatives and objective functions, respectively.

Table 2.
Decision table.
Here, , represents the performance of the jth alternative to the ith criterion. A corresponding decision matrix to solve the problem is given using Table 1 as follows:
In MCDM problems, it is helpful to normalize the decision matrix to allow aggregation of criteria with numerical and comparable data. Normalization is a conversion process to create numerical and comparable data using a common scale. After collecting data in the decision matrix, pre-processing is necessary for helpful decision modeling. Jahan et al. [30] evaluated and compared different normalization techniques. We present the vector normalization and linear normalization techniques in Table 3, see [31].

Table 3.
Normalization techniques.
Where for .
Based on the decision matrix (), we introduce the normalized decision matrix
where represents the element of a normalized matrix to the ith criteria and the jth alternative.
After deriving the normalized decision matrix, we define a weight matrix which represents the relative importance of each criterion. In many MCDM problems, the weights are different for different alternatives. Therefore, we assume that the weights are not the same for different alternatives (locations). This is different from approaches in the literature that consider the fixed domination structure for all locations or alternatives [26,32,33]. The current study assigns different weights to the criteria. According to the characterization of each location. For instance, a selected strategy can affect the relative importance of the criteria. An appropriate weight vector is considered for each location, and all weight vectors are collected in a weight matrix . We denote the rows of the weight matrix (weight vectors) by , . To compute the weight matrix, we suppose that is the weight of the ith criteria w.r.t. the jth alternative. The formulation of the weight matrix is given as
There are several methods for obtaining weight vectors (criteria weights), such as Entropy, Linmap, and Eigenvector [32,34]. The authors in [35] show how to determine weights by considering objective and subjective weights. The aforementioned methods have several advantages and have been studied from mathematical and practical perspectives [26,36]. In other techniques, a decision maker uses a pairwise comparison matrix to assign the weight vector.
A pairwise comparison method of weighting compares criteria weights in pairs to judge which criterion is preferred. In the MCDM process, a pairwise comparison matrix determines the criteria weights [37]. A pairwise comparison matrix is constructed with the criteria in rows and columns. A numeric value from 1–9 is assigned (9 if the criterion is strongly preferred, one if the compared criteria are equally important). The criteria weights are calculated by normalizing a comparison matrix, and each value in the matrix is divided by the sum of the values in its column. If the pairwise comparison matrix is a consistent matrix (see the condition of consistency [37]), a decision maker can use a normalization technique to determine the weight vector [37,38]. In this study, we assume the pairwise comparison matrix has a condition of consistency, and we use linear normalization to obtain the weight vectors [31]. In the next section, we use the weight matrix and the decision matrix to generate solutions for MCDM problems.
4.3. Solution Concepts for MCDM Problems w.r.t. Variable Domination Structure
In this section, we consider problem . In the literature, one takes a fixed weight vector w.r.t. each criterion and obtains a solution by minimizing Considering the formulation of the general weight matrix given in (7).
However, in many practical problems, it is necessary to consider different weights corresponding to different alternatives. For instance, if the goal is to select the proper location among candidate locations, it is more beneficial to consider a please replace by: various criteria weights according to each location. These criteria could be quality, cost, stakeholder satisfaction, time, proximity to market, proximity to a supplier, and other objectives. Minimizing proximity to the market is preferred at some locations, and minimizing proximity to the supplier is preferred at other locations. In the problem , we assume that the set of alternatives can be separated into different groups of candidates with . Here, contains ‘similar’ candidates in that the candidates have similar preferences. In this study, we assume that each location has different preferences. In this section, .
We suppose that problem is equipped with domination map given by (2), where , are given. The role of this domination structure is to compare different candidate alternatives. To define solutions for problem , we use the decision matrix and the weight matrix introduced in the previous section. Let , where denotes the transpose matrix to :
where, represents the performance of alternative corresponding to the weight vector , i.e., .
We recall two types of solutions for problem [16].
Definition 2.
Consider , .
- is a solution of Type I of if the performance of this alternative (corresponding to its weight vector ) does not exceed the performances of other alternatives corresponding to the weight vector . This is equivalent tofor all .
- is a solution of Type II of if the performance of this alternative (corresponding to an arbitrary weight vector ) does not exceed the performances of alternative corresponding to its weight vector , for all . This is equivalent tofor all .
5. Selection of a New Hub Airport Using the MCDM Problem w.r.t. Variable Domination Structure
Investigating the selection of a new hub facility is related to the development and operation of a hub transport network. It has many applications in operations research, economics, strategic management, logistics, etc. Several operational research methods involve determining the route structure and the location of one or a few hubs by minimizing the total cost of the transport operator.
The goal is to select a new hub airport, i.e., a hypothetical European Union hub (EU hub), to be a hub transport within the EU market. Janic and Reggiani have investigated a similar problem with a fixed domination structure [39]. However, the results given in Proposition 1 hold true for a continues feasible set; here, we assume a finite set of feasible locations. The candidate airports create the set of alternatives; the criteria are defined to identify and compare the given alternatives.
The European air transport system contains airlines, airports, and air traffic controls. The service and the condition of airports are investigated for both passengers and freight. Figure 1 depicts the busiest European airports with passenger traffic of over one million in 2019 [40].
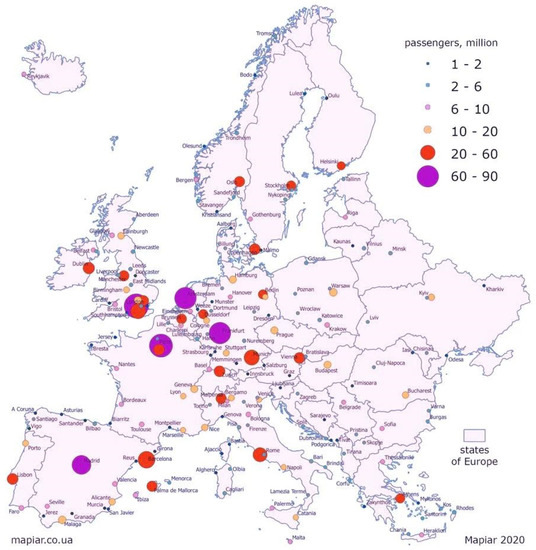
Figure 1.
The busiest airports in Europe in 2019 [40].
Figure 2 depicts the European freighter hubs in 2020, as reported by Air Cargo News. Note that these statistical data vary from time to time. Therefore, the purpose behind presenting these problems is just to show the application of the multicriteria location problem with respect to the variable domination structure.
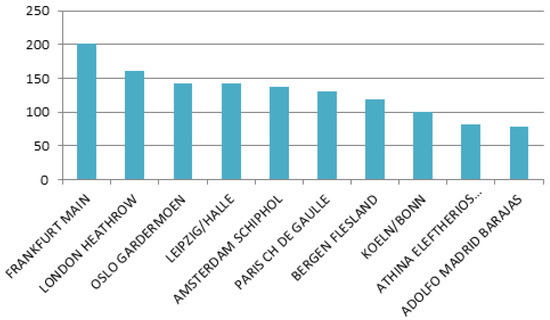
Figure 2.
Average daily movement for the busiest European freighter hubs.
Some EU airlines desire to establish a new hub airport abroad as an appropriate option to build up their market position within the EU and reduce the risk of failure. Therefore, establishing a hub airport is considered by both national and international EU airlines. For instance, Finnair, which operates hub in the Vantaa Airport in Helsinki, has proposed the Arlanda Airport in Stockholm as a potential new hub. Iberia, whose hub is in the Barajas Airport in Madrid, has considered the Schiphol Airport in Amsterdam or Frankfurt-Main Airport as its second hub.
However, the actual data of the problem may be different in recent years, and these numerical data are considered in this section just to show how a most preferred solution can be selected for a new hub airport w.r.t. the variable domination structure. Let us consider a set of alternatives and attributes as presented in [39]. Suppose that an EU airline already utilizes a network with a hub located at Rome’s Leonardo da Vinci Airport. The airline is going to consider a new hub.
The following criteria can be considered as relevant for selecting a new hub [39]:
- Climatological characteristics of the airport;
- Geographical location and proximity to most in-demand destinations;
- Airport size (millions of passengers per year);
- The market size of the airport;
- Airport capacity;
- Number of destinations served;
- Number of gates at the airport;
- Per capita income;
- Generalized access cost;
- Total airline cost of operating this hub;
- Market share at the given airport;
- The efficiency of airport capacity throughout the peaks.
In the case of the fixed domination structure, the corresponding MCDM problem can be solved by taking a vector of the criteria’s weight and using the proper MCDM solution method [38].
Since the mentioned attributes’ preferences are different for each alternative (i.e., airport), applying the variable domination structure is proposed to solve such problem. For instance, the climatic characteristics constitute a more critical criterion up to the geographical location of the airport. In contrast, in the other airport, up to the condition of the airport, the efficiency of the airport capacity during peaks is preferred to the other criteria.
In addition, politics, social and governmental regulations, and environmental and financial risks can be different at the given candidate airports. All these aspects impact the preferences of the alternatives, and they are considered by variable domination structures.
Consider X is a set of feasible airports where .
The decision maker is looking for a facility x for a new hub airport considering seven objective functions. The laws and regulations of each country, even each state, affect the value of optimizing each objective function. A variable domination structure represents these variable preferences of optimizing each objective function. The decision maker considers MODM problem with
- Feasible set:
- The decision maker collects a set of candidate airports for a new hub. represents a feasible airport, , . For a numerical experiment, the decision maker considers seven feasible airports as : Amsterdam-Schiphol, : Brussels, : Düsseldorf, : Frankfurt-Main, : London-Heathrow, : Milan-Malpensa, and : Paris-Charles de Gaulle CDG. Moreover, we propose
- Objective functions:
- The decision maker proposes the following seven objective functions:
- : Airport size (millions of passengers per year);
- : Airport capacity (aircraft/hour);
- : Population of the airport (million);
- : Per capita income (ECU/inhabitant);
- : Total airline cost of operating two hubs (million euros);
- : Generalized access cost (euros/passenger); and
- : the average airport cost per service (euros/WLU).
Let be the objective function, defined bywhere , for . - Preference relation:
- The social, political, and governmental regulations and financial risks are different in each country/state. For instance, optimizing generalized access cost has different preferences at each airport than optimizing the other objective functions; the decision maker assigns an appropriate parameter for each objective function at each feasible location by a pairwise comparison matrix.
The preferences of the decision maker are described by a variable domination structure given by
where and represents the preference of the decision maker. The corresponding multi-objective decision-making problem w.r.t. variable domination structure defined in (10) is given by
To present the practical application, we consider the MCDM problem investigated by Janic and Reggiani [39] in terms of the variable domination structure.
Note that we present this application to show how we formulate the multiobjective location problem based on the variable domination structure and finding the solution for such problems. For more details on the given criteria and how they could be obtained, we can refer to [39].
Criteria , , , and will be maximized, while criteria , , and should be minimized. The decision maker assigns the domination map, defined in (10), to each criterion and up to each location (i.e., airport).
In the following, we find the solution/solutions of problem (11) to select the most preferred location for a new airport hub.
Suppose that an EU airline already utilizes a network with a hub located at Leonardo da Vinci Airport in Rome and decided to consider a new hub in one of the given airports.
The decision matrix represents the relevant value of each objective function for each alternative airport. The normalized decision matrix is given in Table 4. In this case, we consider the normalized decision matrix presented by Janic and Reggiani in [39].

Table 4.
Normalized decision matrix for the given example.
Consider each row of Table 5 as a vector of and denote the ith component of the jth row by , for and . Compare to the definitions of the domination map and in (2).

Table 5.
The relative weights of objective functions corresponding to the given alternatives.
We are looking to find a Type I solution and a Type II solution. The Type I solution expresses that the most preferred location is a selected hub airport regarding the airports’ current characterization and conditions. On the other hand, the Type II solution selects an appropriate hub airport based on the preferences of other candidate airports.
The matrix is calculated using (8) as
The decision maker chooses the most preferred solution for the corresponding problems. When one needs to find a solution that is an efficient solution considering the other candidate’s preferences and conditions, we propose a non-dominated solution. A minimal solution is proposed on the condition that the decision maker seeks the solution using the corresponding domination structure for the alternatives.
Considering Definition 2, we obtain that solution Type I is the Brussels airport, and the Milan-Malpensa airport is a solution Type II. It refers that the Brussels airport is appropriate to select as a hub location considering the corresponding preferences and conditions of the airports. If the Brussels airport is also solution Type II; it means that it is also an appropriate hub location even by considering the other candidate airports’ preferences.
Up to the condition of the problem, the decision maker selects which type of solution is appropriate for the problem.
6. Conclusions
In many real-world MODM problems, there are variable preferences of objective functions for different alternatives or locations (in location problems). Consideration of these preferences by variable domination structure helps improve the decision-making process. The current study considered MODM problems w.r.t. variable ordering structure, and an application of this new method is presented to select a new hub airport. This study formulated the practical problem in logistics as an multiobjective location problem w.r.t variable domination structure. To solve such a problem, the mathematical results are applied; afterward, we expose these solutions in a numerical experiment. The application of MODM problems w.r.t.variable domination structure in strategic management is a subject of future research.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
I wish to express my special thanks to Christiane Tammer for her valuable comments on this study. I am also grateful to Rosalind Elster for her constructive advice.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zanjirani Farahani, R.; Steadie Seifi, M.; Asgari, N. Multiple criteria facility location problems: A survey. Appl. Math. Model. 2010, 34, 1689–1709. [Google Scholar] [CrossRef]
- Zargini, B. Solution concepts in multiobjective location problems with variable domination structure. Eur. J. Appl. Sci. 2021, 9, 175–188. [Google Scholar]
- Melo, T.; Nickel, S.; Saldanha da Gama, F. Facility Location and Supply Chain Management—A Review. Eur. J. Oper. Res. 2009, 196, 401–412. [Google Scholar] [CrossRef]
- Yu, P.L. Cone convexity, cone extreme points, and non-dominated solution in decision problems with multi-objectives. J. Optim. Theory Appl. 1974, 14, 319–337. [Google Scholar] [CrossRef]
- Yu, P.L. A class of solution for group decision problems. Manag. Sci. 1973, 19, 936–946. [Google Scholar] [CrossRef]
- Chen, G.Y.; Huang, X.; Yang, X. Vector Optimization: Set-Valued and Variational Analysis; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Soleimani, B. Characterization of Approximate Solutions of Vector Optimization Problems with a Variable Order Structure. J. Optim. Theory Appl. 2014, 162, 605–632. [Google Scholar] [CrossRef]
- Bao, T.Q.; Mordukhovich, B.S.; Soubeyran, A. Variational Analysis in Psychological Modeling. J. Optim. Theory Appl. 2014, 164, 290–315. [Google Scholar] [CrossRef]
- Bao, T.Q.; Mordukhovich, B.S.; Soubeyran, A. Variational principles in models of behavioral sciences. arXiv 2013, arXiv:1311.6017. [Google Scholar]
- Eichfelder, G. Variable Ordering Structures in Vector Optimization; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Eichfelder, G. Optimal elements in vector optimization with a variable ordering structure. J. Optim. Theory Appl. 2011, 151, 217–240. [Google Scholar] [CrossRef]
- Eichfelder, G. Vector Optimization in Medical Engineering. In Mathematics Without Boundaries; Pardalos, P., Rassias, T., Eds.; Springer: New York, NY, USA, 2014; pp. 181–215. [Google Scholar]
- Soleimani, B.; Tammer, C. Concepts for Approximate Solutions of Vector Optimization Problems with Variable Order Structure. Vietnam. J. Math. 2014, 42, 543–566. [Google Scholar] [CrossRef]
- Neumann, G.; Tammer, C.; Weinkauf, R. Multi-criteria Location-Routing Problems for Traveling Management in Tourism. In Methods of Multicriteria Decision Theory and Applications; Shaker-Verlag: Aachen, Germany, 2009; pp. 115–136. [Google Scholar]
- Tammer, C.; Patz, R.; Spitzner, J. Decision support for location problems in town planning. Int. Trans. Oper. Res. 2002, 9, 261–278. [Google Scholar]
- Zargini, B. Multiobjective decision making problems with respect to variable domination structures. J. Oper. Res. Soc. Jpn. 2022, in press. [Google Scholar]
- Alzorba, S.; Günther, C.; Popovici, N.; Tammer, C. A new algorithm for solving planar multiobjective location problems involving the Manhattan norm. Eur. J. Oper. Res. 2017, 258, 35–46. [Google Scholar] [CrossRef]
- Eiselt, H.A.; Marianov, V. Foundations of Location Problems; Springer: New York, NY, USA, 2011. [Google Scholar]
- Bierwirth, C.; Kirschstein, T.; Sackmann, D. Preface: Logistics Management; Springer: New York, NY, USA, 2019. [Google Scholar]
- Behnke, M.; Kirschstein, T.; Bierwirth, C. A column generation approach for an emission-oriented vehicle routing problem on a multigraph. Eur. J. Oper. Res. 2020, 288, 794–809. [Google Scholar] [CrossRef]
- Zargini, B.; Doagooei, A.R. Multi-objective location problems with variable domination structure. Rev. Investig. Oper. 2018, 39, 449–462. [Google Scholar]
- Xiong, J.; Yu, G. Research on hub airport selection based on steiner tree model. In Proceedings of the 3rd International Conference on Information Management (ICIM), Chengdu, China, 21–23 April 2017; pp. 457–460. [Google Scholar] [CrossRef]
- Paul, A. European Hub Airports—Assessment of Constraints for Market Power in the Local Catchment and on the Transfer Market. Ph.D. Thesis, Technische Universität Dresden Fakultät Verkehrswissenschaften “Friedrich List” Institut für Wirtschaft und Verkehr, Dresden, Germany, 2018. [Google Scholar]
- Durea, M.; Strugariu, R.; Tammer, C. On set-valued optimization problems with variable ordering structure. J. Glob. Optim. 2015, 61, 745–767. [Google Scholar] [CrossRef]
- Tzeng, G.H.; Huang, J.H. Multiple Attribute Decision Making Methods and Applications; CRC Press Taylor and Francis Group: Boca Raton, FL, USA, 2011; pp. 57–105. [Google Scholar]
- Agarwal, P.; Sahai, M.; Mishra, V.; Bag, M.; Singh, V. A review of multi-criteria decision making techniques for supplier evaluation and selection. Int. J. Ind. Eng. Comput. 2011, 2, 801–810. [Google Scholar] [CrossRef]
- Bergstresser, K.; Charnes, A.; Yu, P.L. Generalization of Domination Structures and Non-dominated Solutions in Multi-criteria Decision Making. J. Optim. Theory Appl. 1976, 18, 3–13. [Google Scholar] [CrossRef]
- Brans, J.P.; Vincke, P. A Preference Ranking Organisation Method: The PROMETHEE Method for Multiple Criteria Decision-Making. Manag. Sci. 1985, 31, 647–656. [Google Scholar] [CrossRef]
- Khadam, I.; Kaluarachchi, J. Multi-criteria decision analysis with probabilistic risk assessment for the management of contaminated ground water. Environ. Impact Assess. Rev. 2003, 23, 683–721. [Google Scholar] [CrossRef]
- Jahan, A.; Edwards, K.L. A state-of-the-art survey on the influence of normalization techniques in ranking: Improving the materials selection process in engineering design. Mater. Des. 2015, 65, 335–342. [Google Scholar] [CrossRef]
- Vafaei, N.; Ribeiro, R.A.; Camarinha-Matos, L.M. Normalization Techniques for Multi-Criteria Decision Making: Analytical Hierarchy Process Case Study. Technol. Innov. Cyber-Phys. Syst. 2016, 470, 261–269. [Google Scholar]
- Choo, E.U.; Schoner, B.; Wedley, W. Interpretation of criteria weights in multi-criteria decision-making. Comput. Ind. Eng. 1999, 37, 527–541. [Google Scholar] [CrossRef]
- Tzeng, G.-H.; Chen, T.-Y.; Wang, J.C. A weight-assessing method with habitual domains. Eur. J. Oper. Res. 1998, 110, 342–367. [Google Scholar] [CrossRef]
- Borcherding, K.; Eppel, T.; Von Winterfeldt, D. Comparison of weighting judgments in multiattribute utility measurement. Manag. Sci. 1991, 37, 1603–1619. [Google Scholar] [CrossRef]
- Zoraghi, N.; Amiri, M.; Talebi, G.; Zowghi, M. A fuzzy MCDM model with objective and subjective weights for evaluating service quality in hotel industries. J. Ind. Eng. Int. 2013, 9, 1–13. [Google Scholar] [CrossRef]
- Gao, S.; Zhang, Z. Calculating Weights Methods in Complete Matrices and Incomplete Matrices. J. Softw. 2010, 5, 304–311. [Google Scholar] [CrossRef][Green Version]
- Saaty, T.L. The Analytic Hierarchy Process; McGraw-Hill: New York, NY, USA, 1980; Section 2; pp. 22–23. [Google Scholar]
- Asgharpour, M.J. Multiple Criteria Decision Making; Tehran University Publication: Tehran, Iran, 1998; pp. 201–203. [Google Scholar]
- Janic, M.; Reggiani, M. An Application of the Multiple Criteria Decision Making (MCDM) Analysis to the Selection of a New Hub Airport. Eur. J. Transp. Infrastruct. Res. 2002, 2, 113–141. [Google Scholar]
- The Busiest Airport in European Countries. Mapiar. 2020. Available online: https://mapiar.co.ua/en/2020/02/28/largest-airports-in-europe/ (accessed on 3 December 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).