1. Introduction
Chaos theory describes complex dynamical systems that are highly sensitive to initial conditions, leading to unpredictable and irregular behavior over time. The stabilization of such systems, a process known as chaos control, is achieved by applying small, carefully timed perturbations that guide the system toward a desired state or trajectory. Over the past decades, numerous strategies have been developed to suppress chaotic dynamics in various physical, biological, and engineering contexts. Methodological advancements range from general frameworks like model-free deep reinforcement learning [
1] or the partial control method for maintaining trajectories within safe bounds [
2] to highly specialized applications.
In engineering and physics, for instance, recent studies have applied these techniques to solve challenges in robotics, such as the control of under-actuated robot manipulators [
3], and to stabilize high-dimensional mechanical systems like double rotor models [
4]. Applications extend to aerospace for the control of chaotic satellite systems [
5] and to materials science for optimizing crystal growth processes [
6]. Further applications include manipulating chaos in cavity optomechanical systems for secure communications [
7,
8] and securing digital media with chaotic watermarking [
9]. The principles of chaos control are equally impactful in stabilizing population dynamics in ecological models, such as those for host–parasitoid or prey–predator interactions [
10,
11,
12]. In medicine, recent applications of chaos control range from suppressing spiral-wave chaos in cardiac arrhythmias using low-energy electrical pulses [
13,
14] to analyzing epidemiological models for diseases like syphilis to better understand stabilization [
15]. In economics, chaos control can be used to investigate and manage the stability of econometric systems, providing insights into economic cycles [
16].
The principles of chaos control are particularly relevant to oncology. While the term chaos is often used colloquially in oncology to describe the seemingly disordered and complex nature of tumor progression [
17], it is crucial to distinguish this from its rigorous mathematical definition. Specifically, the rapid or unbounded growth of cancer cells, a hallmark of the disease, is not a form of deterministic chaos. Mathematically, chaotic dynamics are intrinsically bounded—the system’s evolution is confined to a finite region in phase space known as a strange attractor [
18]. Unbounded growth, in contrast, represents a trajectory that diverges to infinity and is typically an artifact of models that do not incorporate realistic biological constraints, such as nutrient and space limitations [
19]. In the context of cancer-immune models, true chaos signifies a more complex phenomenon: a sustained, irregular, and unpredictable interaction between the tumor and the host immune system. This mathematically defined chaotic behavior corresponds to the irregular tumor growth patterns and unpredictable responses to therapies that can lead to treatment resistance and disease progression [
20]. Recent studies emphasize the significant role that deterministic chaos can play in cancer progression, particularly in cellular networks, gene expression patterns, and tumor-immune system interactions [
21,
22,
23]. Other mathematical frameworks, such as integro-differential systems based on the kinetic theory of active particles, have also been developed to analyze the complex interactions and blow-up phenomena of cancer cells under immune response [
24]. This highlights the critical need for mathematical modeling to understand and ultimately control the chaotic behaviors inherent to cancer systems [
25].
In response to this challenge, various chaos control strategies have been adapted for cancer models. These approaches aim to stabilize unpredictable tumor dynamics, guiding the system toward a steady or periodic state. Methods range from continuous feedback control, with which interventions like chemotherapy are modeled as persistent inputs [
26], to adaptive control, which adjusts inputs in response to system errors, as demonstrated by the controller in [
27] that effectively stabilizes tumor and immune cell counts. Another prominent strategy is optimal control, which seeks to identify the most effective intervention based on a predefined set of objectives. This approach has been used to derive necessary controller inputs for achieving asymptotic stability, even in systems with unknown parameters [
28], and to manage complex dynamics like cancer self-remission [
29]. Optimal control is also applied for designing clinically relevant strategies like combinatorial therapies that maximize immune response while minimizing tumor size and drug toxicity [
30]. To solve these complex optimization problems, especially in non-linear fractional-order systems, some studies employ computational methods like particle swarm optimization and genetic algorithms to find the ideal drug dosing [
31]. Another analytical approach involves state-space exact linearization, which employs nonlinear feedback based on Lie algebra to transform the original chaotic system into a linear, controllable one [
32]. Beyond these, other techniques such as state feedback and hybrid control have been applied to mitigate chaotic behavior, particularly in discretized fractional-order models that describe the tumor-immune interaction in both benign and malignant cases [
33].
This study investigates the chaotic dynamics of the three-dimensional cancer model presented in [
34], which describes the complex interactions between tumor cells, healthy tissue, and the activated immune system. While the original work rigorously established the existence of chaos in this system, the primary aim of this paper is to compare the efficacy of several distinct strategies for controlling these chaotic dynamics. All strategies investigated in this paper share a common theoretical framework: that of exogenous intervention, where an external corrective force is applied to a system that is already in a chaotic state. The objective is the complete suppression of the chaotic dynamics and the stabilization of the involved populations onto a specific, regular, unstable periodic orbit. This approach differs fundamentally from studies that use bifurcation analysis to understand how chaos can be managed or delayed by tuning the system’s endogenous parameters. For instance, a recent study on a prey–predator model demonstrated that predator-induced fear can act as an intrinsic parameter that effectively delays the onset of chaos and stabilizes population dynamics under certain conditions [
35]. In contrast, our work addresses the challenge of imposing stability when the system’s biological parameters are already fixed within a chaotic regime, a scenario that is highly relevant to clinical applications where a patient’s underlying system parameters cannot be easily altered. With this framework in mind, the investigation in this study begins with continuous control to establish a baseline for stabilization. Subsequently, intermittent control is explored as a strategy to reduce the therapeutic burden by activating interventions only when the system deviates from a target trajectory. This approach is then refined into an improved intermittent strategy that incorporates a minimum activation duration to suppress undesirable high-frequency switching. Finally, an adaptive intermittent control strategy is introduced, designed to account for inherent uncertainties by allowing control parameters to adjust automatically. A central goal of this paper is to provide a comparative analysis of these methods, evaluating their efficiency, responsiveness, and biological relevance for stabilizing this well-established cancer model. A key motivation for exploring intermittent strategies is the recognition that continuous interventions, while effective in mathematical models, often translate poorly to clinical settings due to issues like drug toxicity, patient burden, and the development of resistance. Therefore, this study places particular emphasis on control methods that reduce the overall therapeutic intervention.
The remainder of this paper is structured as follows.
Section 2 addresses the materials and methods:
Section 2.1 describes the analyzed mathematical model and its chaotic dynamics,
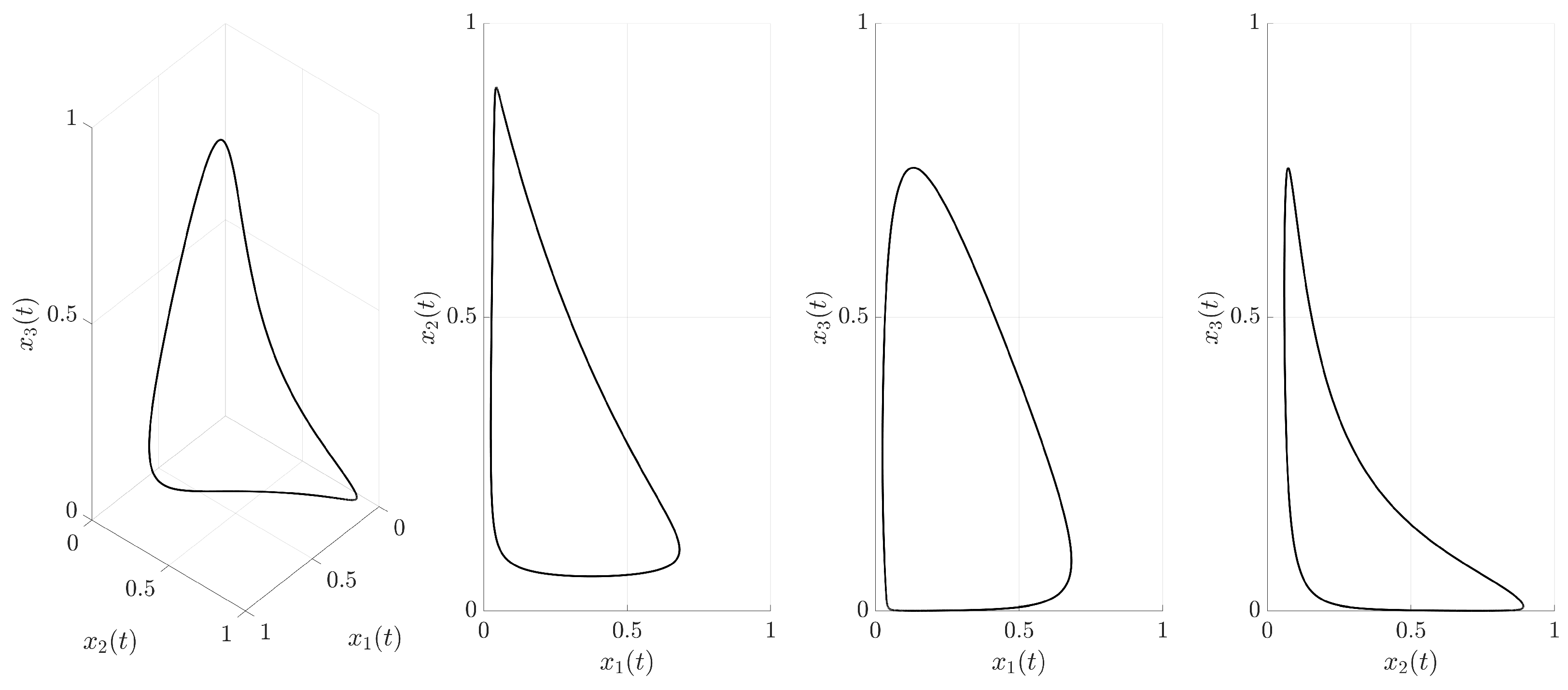
Section 2.2 details the identification of the target unstable periodic orbit, and
Section 2.3 establishes the general framework for the applied techniques.
Section 3 contains the main results, presenting several chaos suppression strategies. These include continuous external force control (
Section 3.1), intermittent control (
Section 3.2), an improved intermittent strategy with a minimum activation duration (
Section 3.3), and adaptive intermittent control (
Section 3.4). A comparative evaluation of these methods is provided in
Section 3.5. Concluding remarks are given in the final
Section 4.
3. Results
3.1. Continuous External Force Control
The first strategy investigated is continuous external force control. This method applies a corrective force that is always active (for
) and is proportional to the error between the current system state,
, and the corresponding state of the target UPO,
. This control force is defined as follows:
where
is an adjustable control parameter determining the strength of the corrective action. Incorporating this control force into the system dynamics (
1) yields the following set of controlled equations:
This control is applied continuously for
. The effectiveness of this continuous control strategy, using
, is visualized in
Figure 3,
Figure 4 and
Figure 5. Note that the value of
K was selected based on preliminary numerical simulations as a value sufficient to achieve robust stabilization, thereby providing a consistent parameter to fairly compare the performances of the different control strategies.
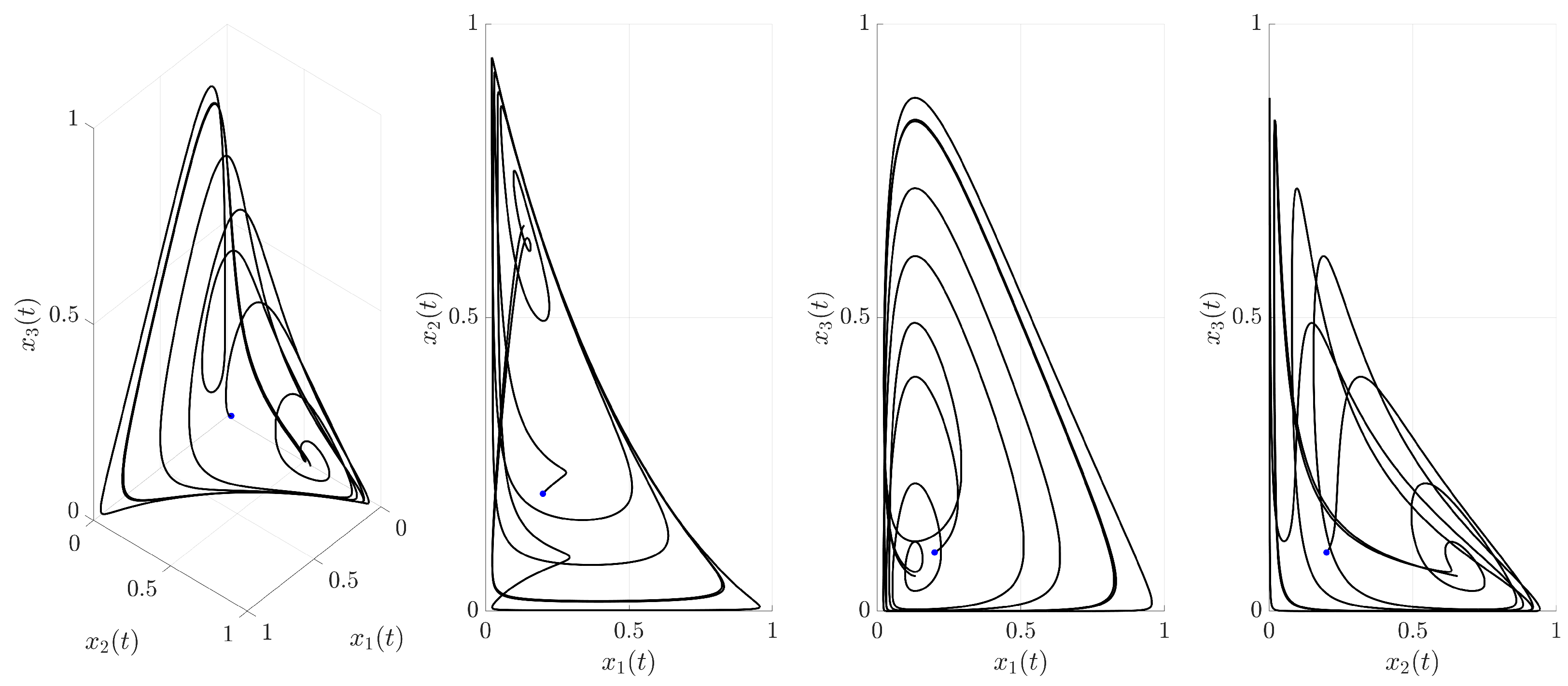
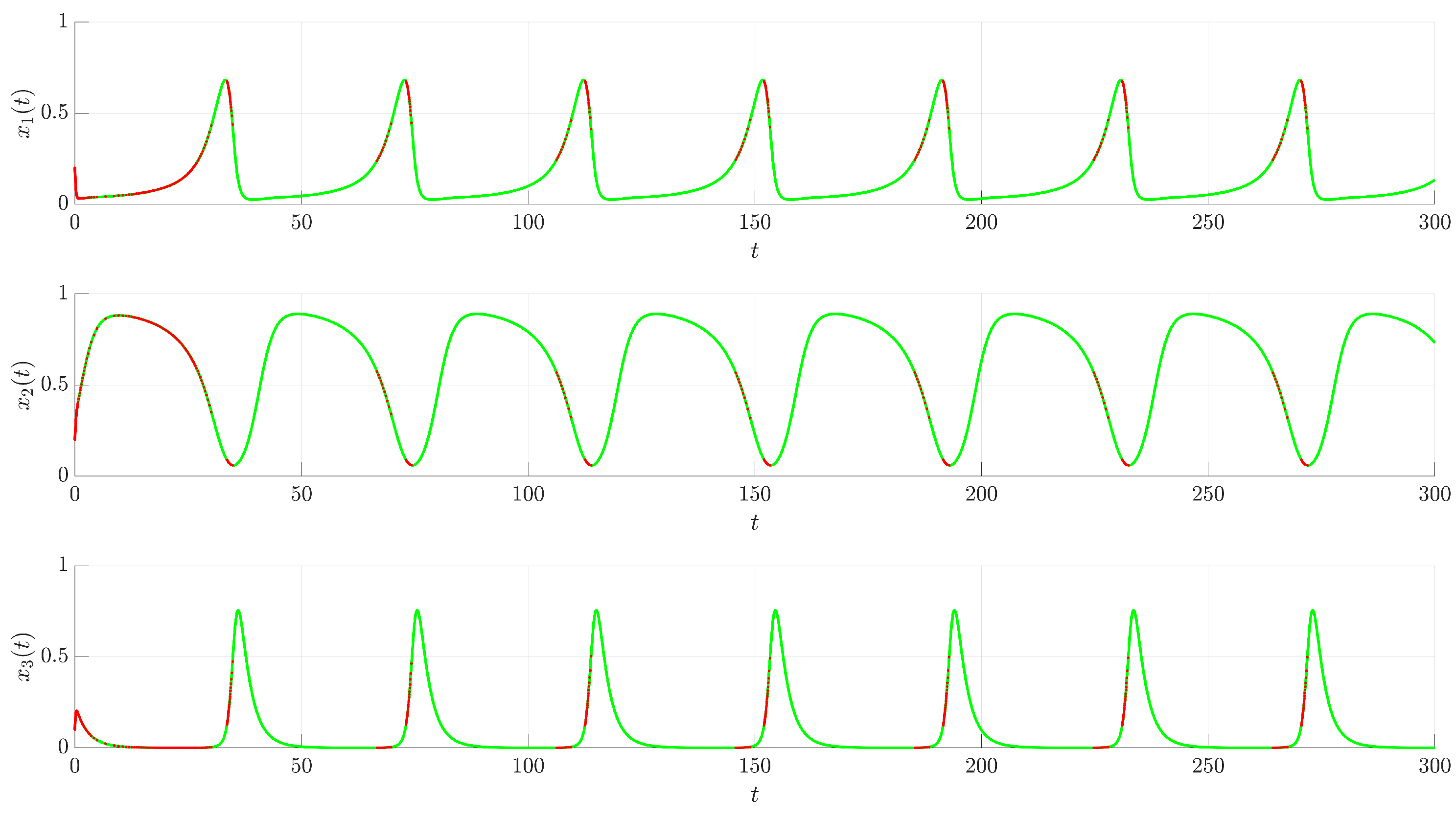
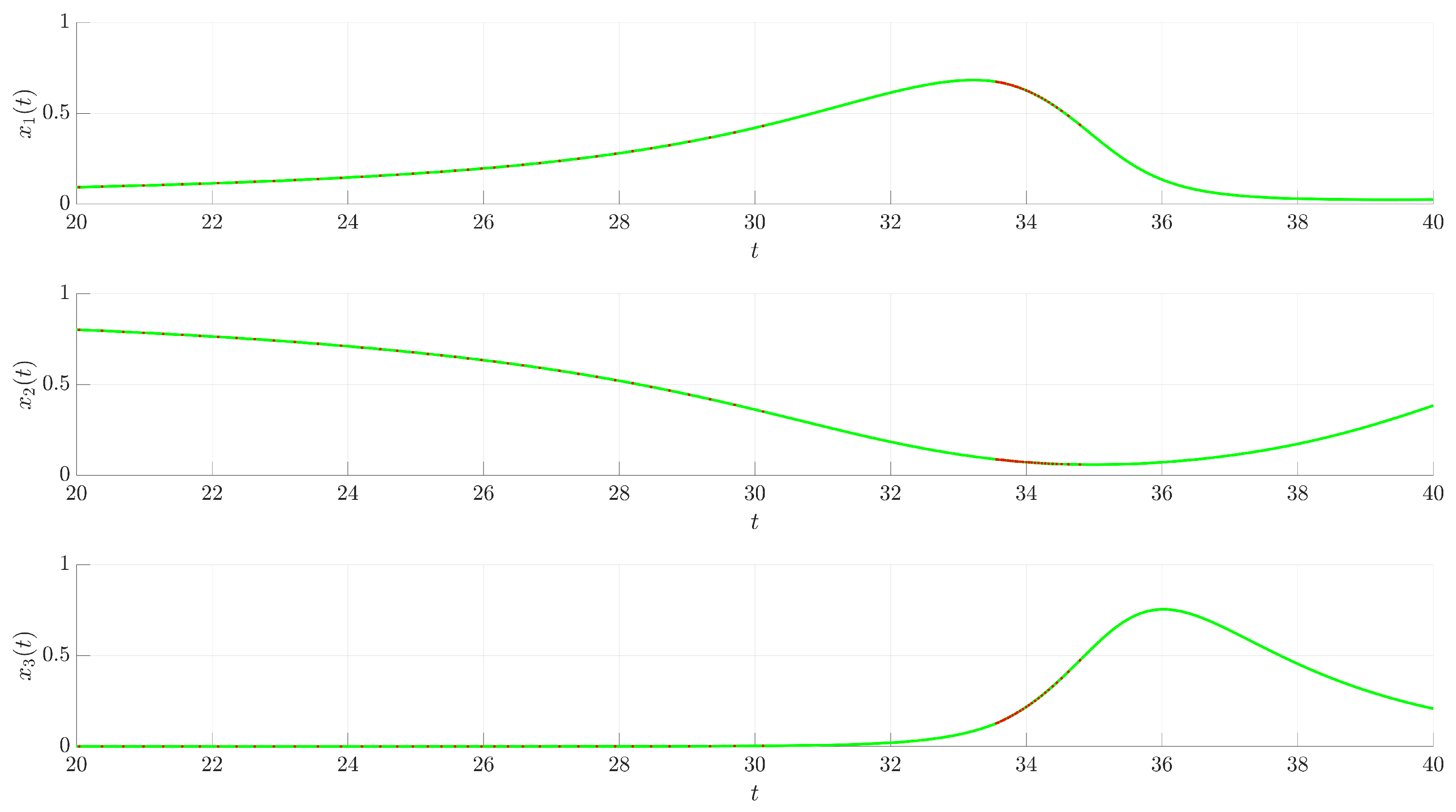
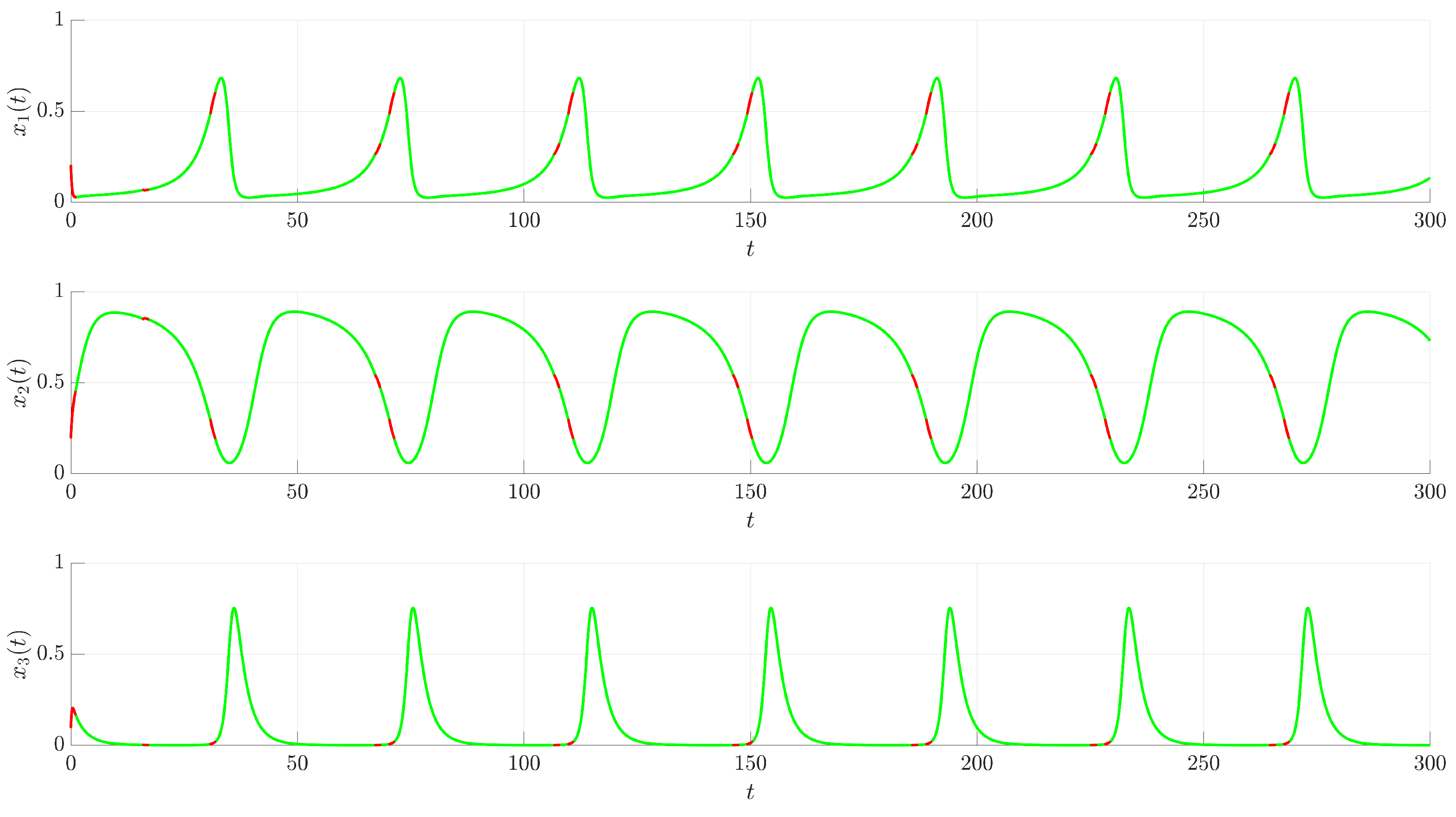
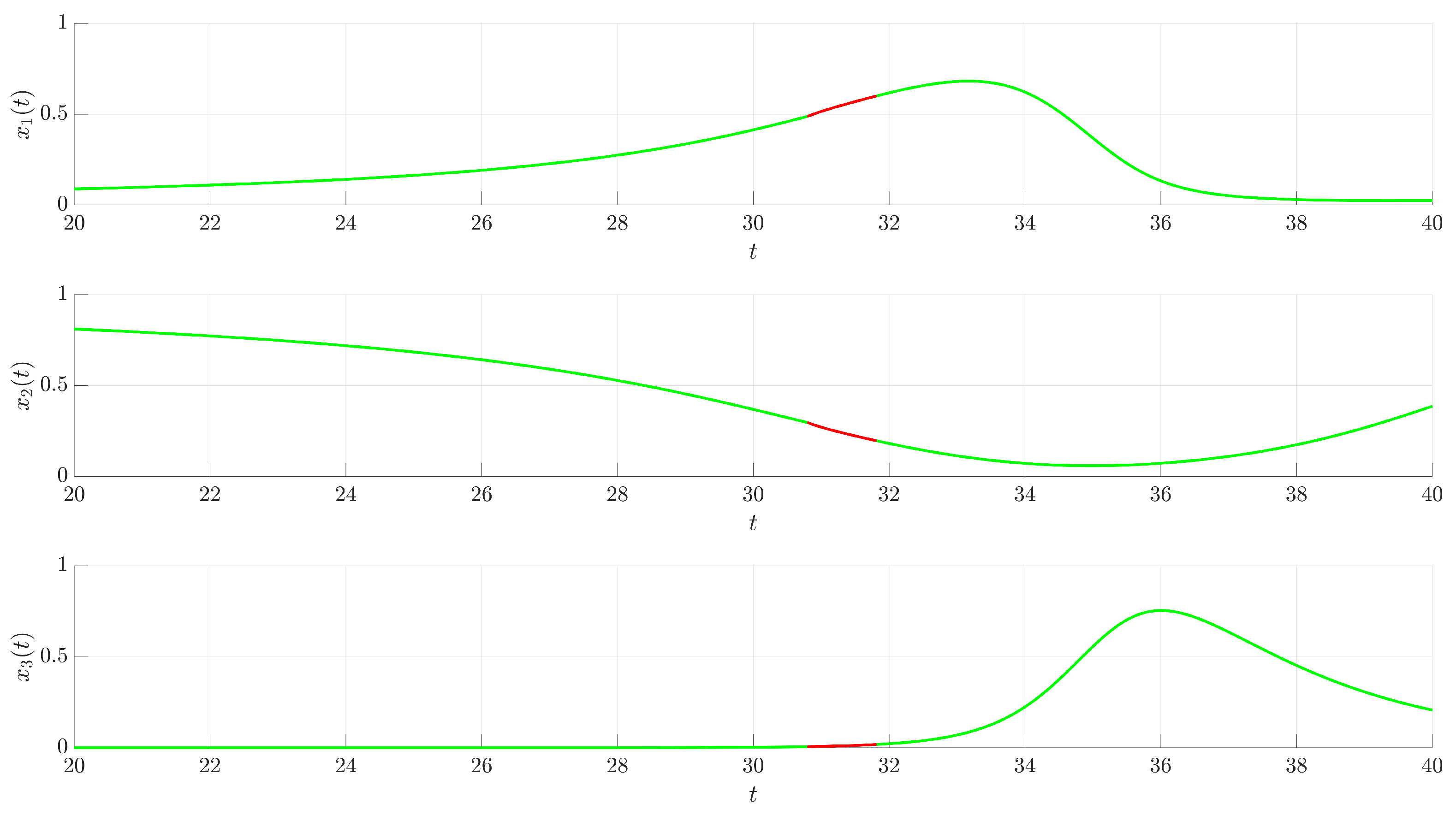
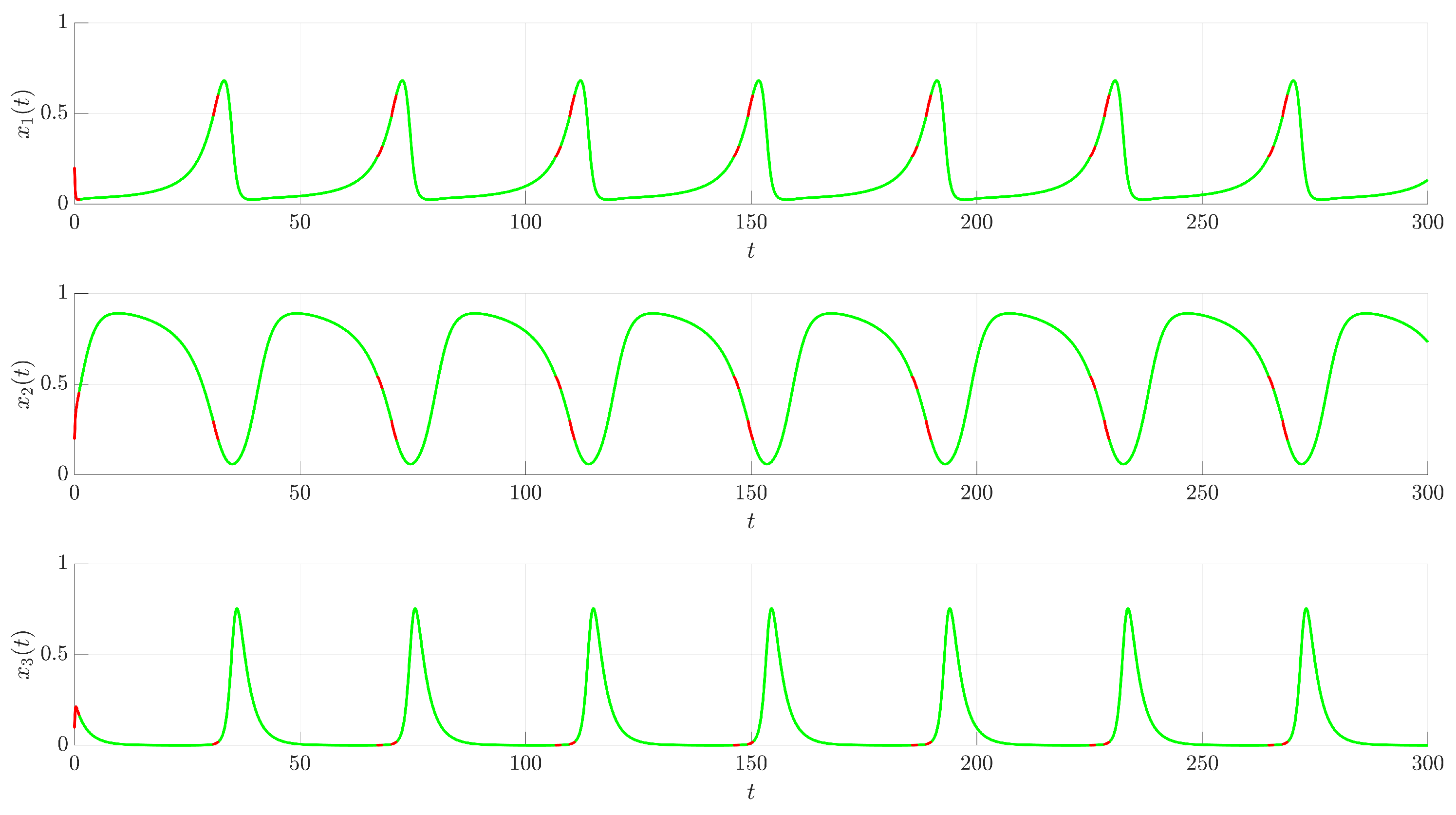
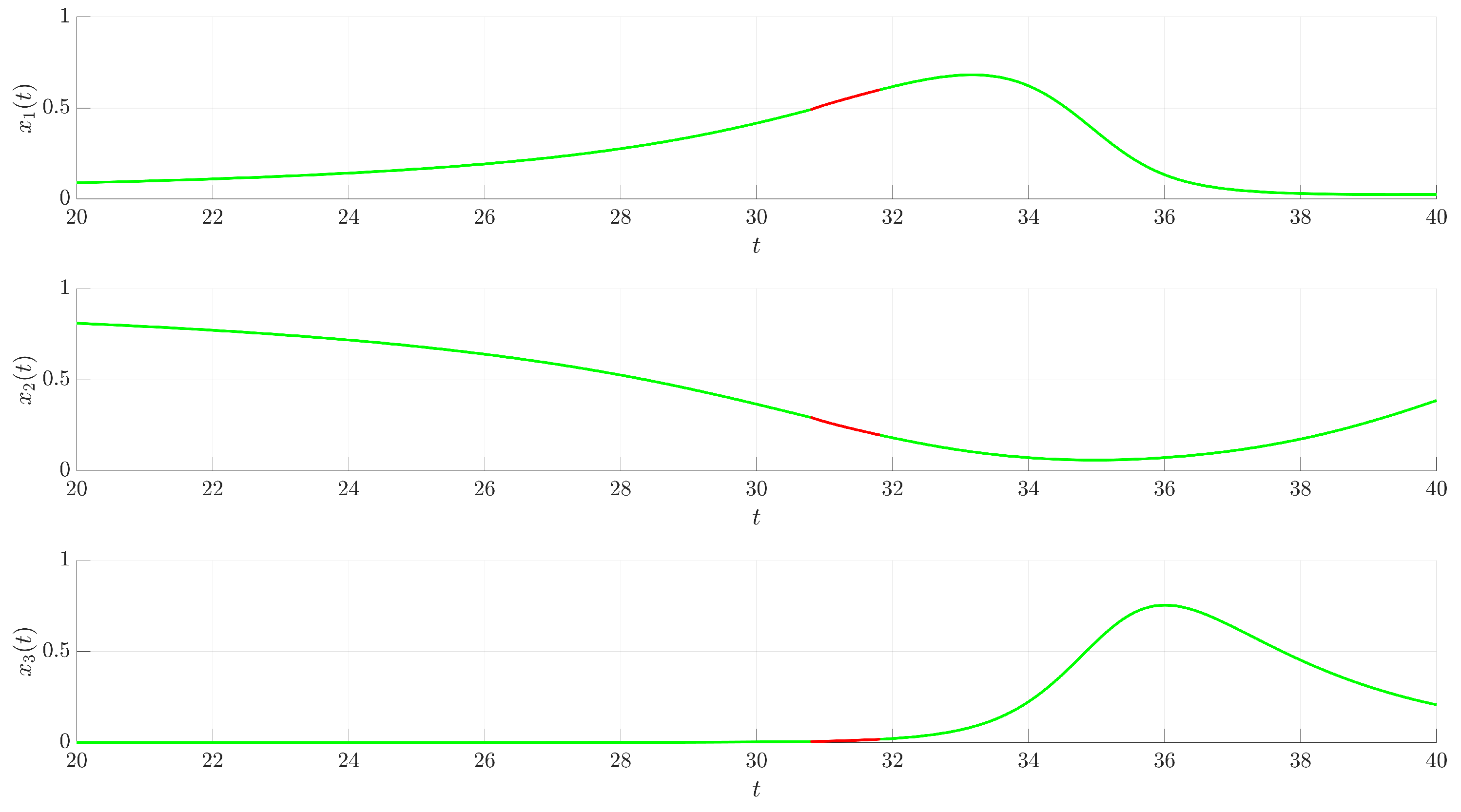
Figure 3 illustrates the time evolution of the state variables
,
, and
. For comparison, the uncontrolled chaotic trajectory originating from the same initial condition is shown in green. When the continuous control is activated at
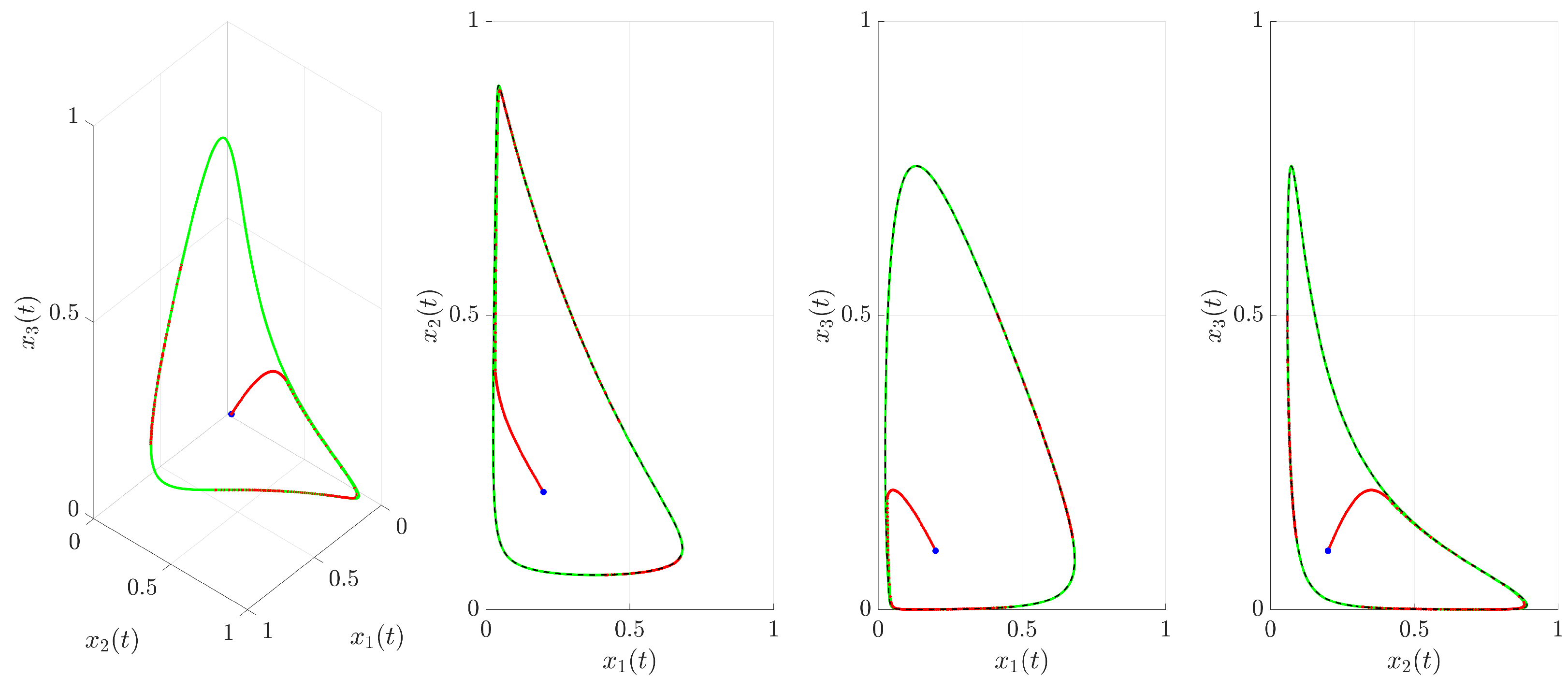
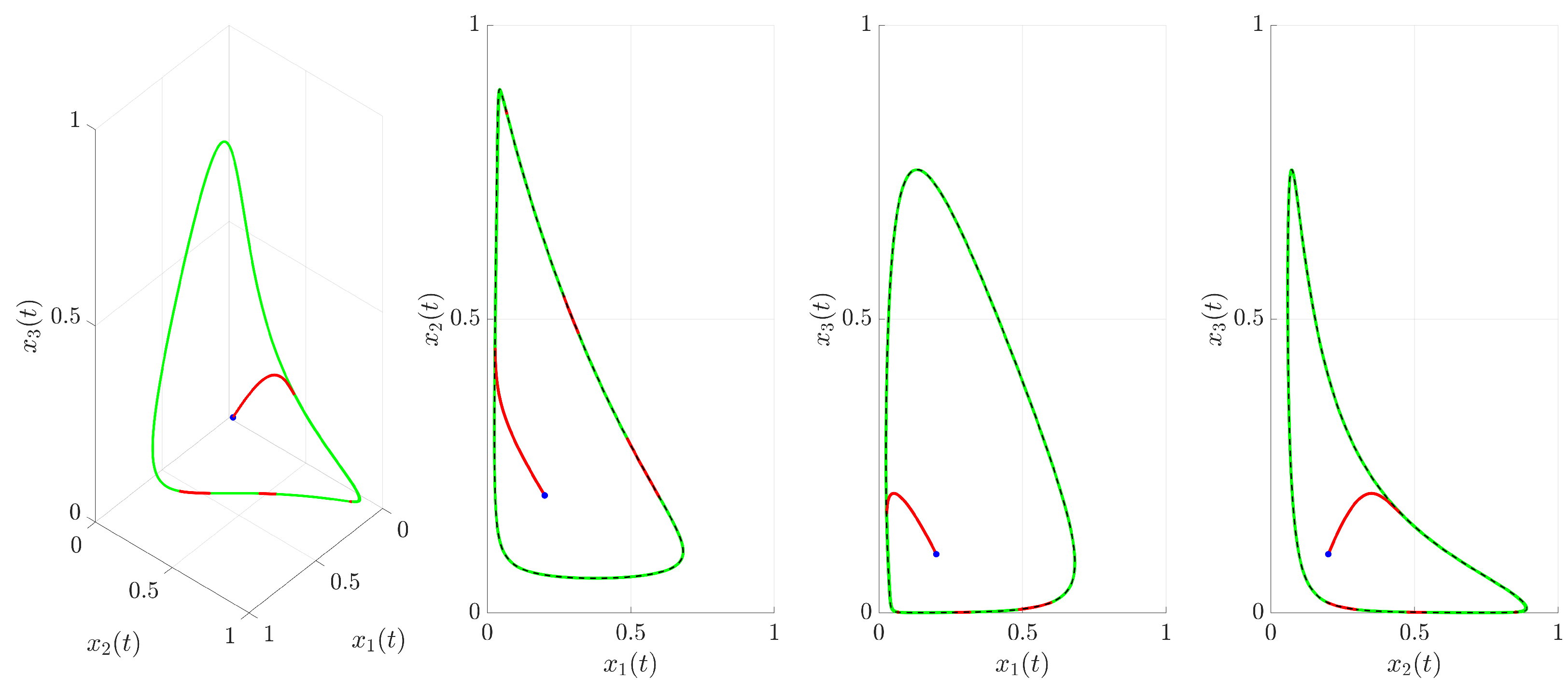
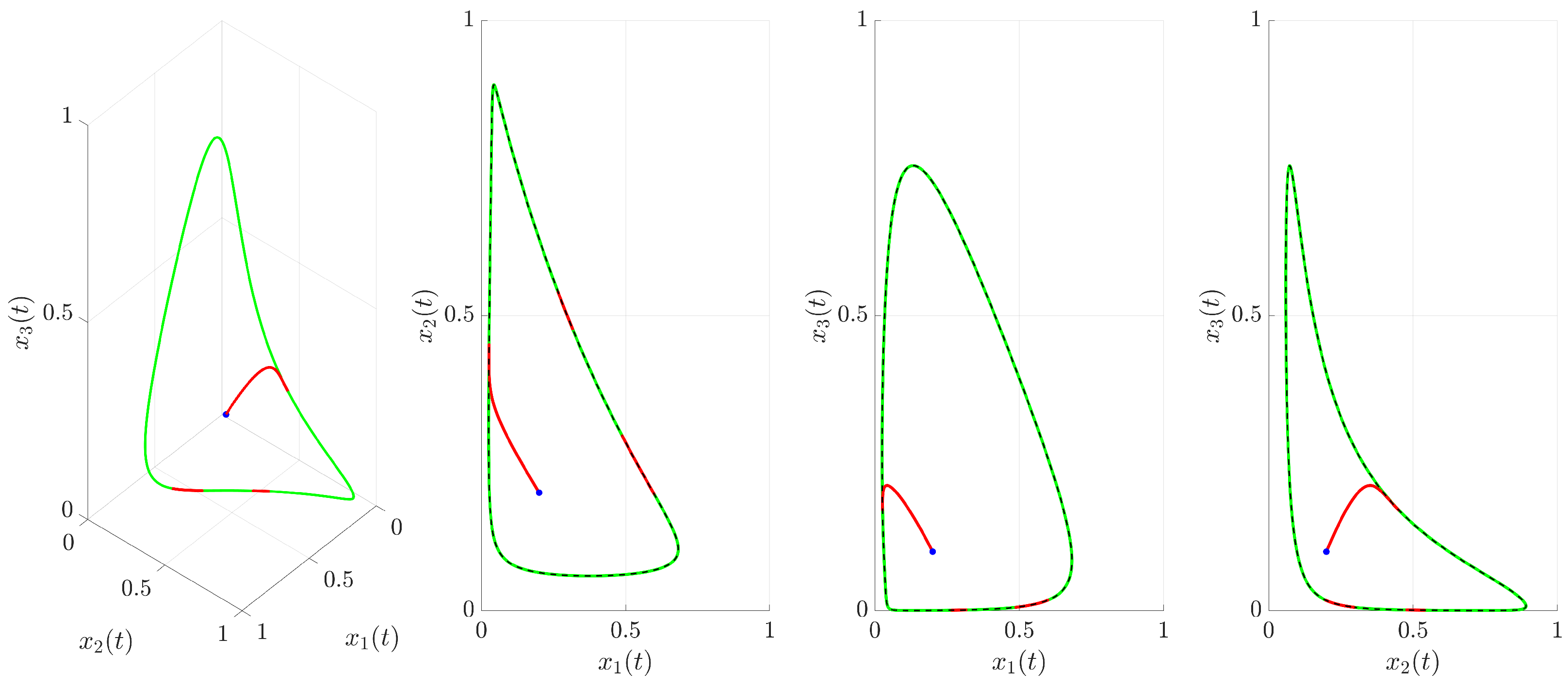
(red trajectory), the state variables rapidly converge to a regular, periodic pattern corresponding to the target UPO. This demonstrates the control’s ability to suppress the inherent chaotic dynamics and enforce the desired periodic behavior. The stabilization is also evident in the phase portrait and its projections shown in
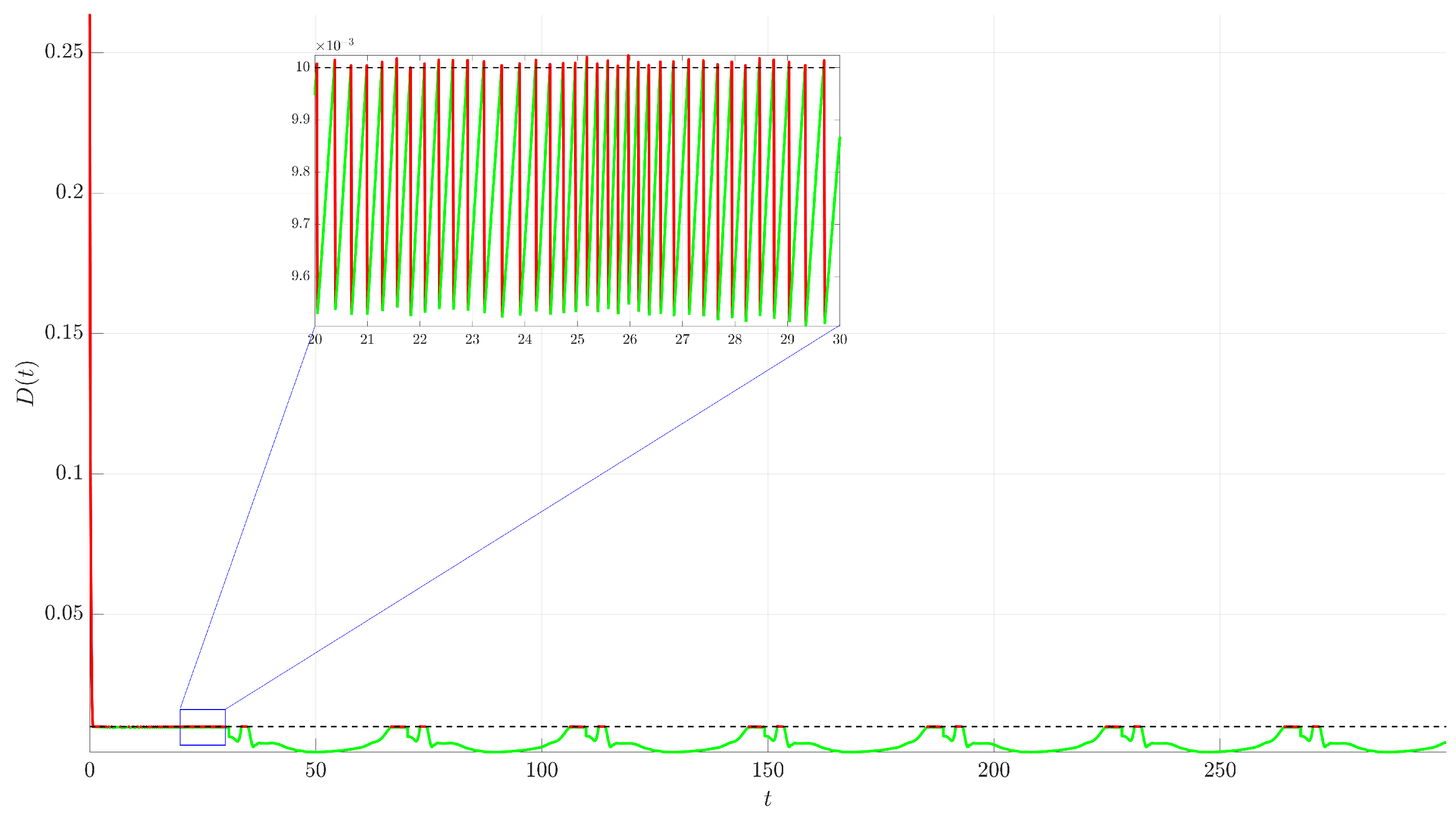
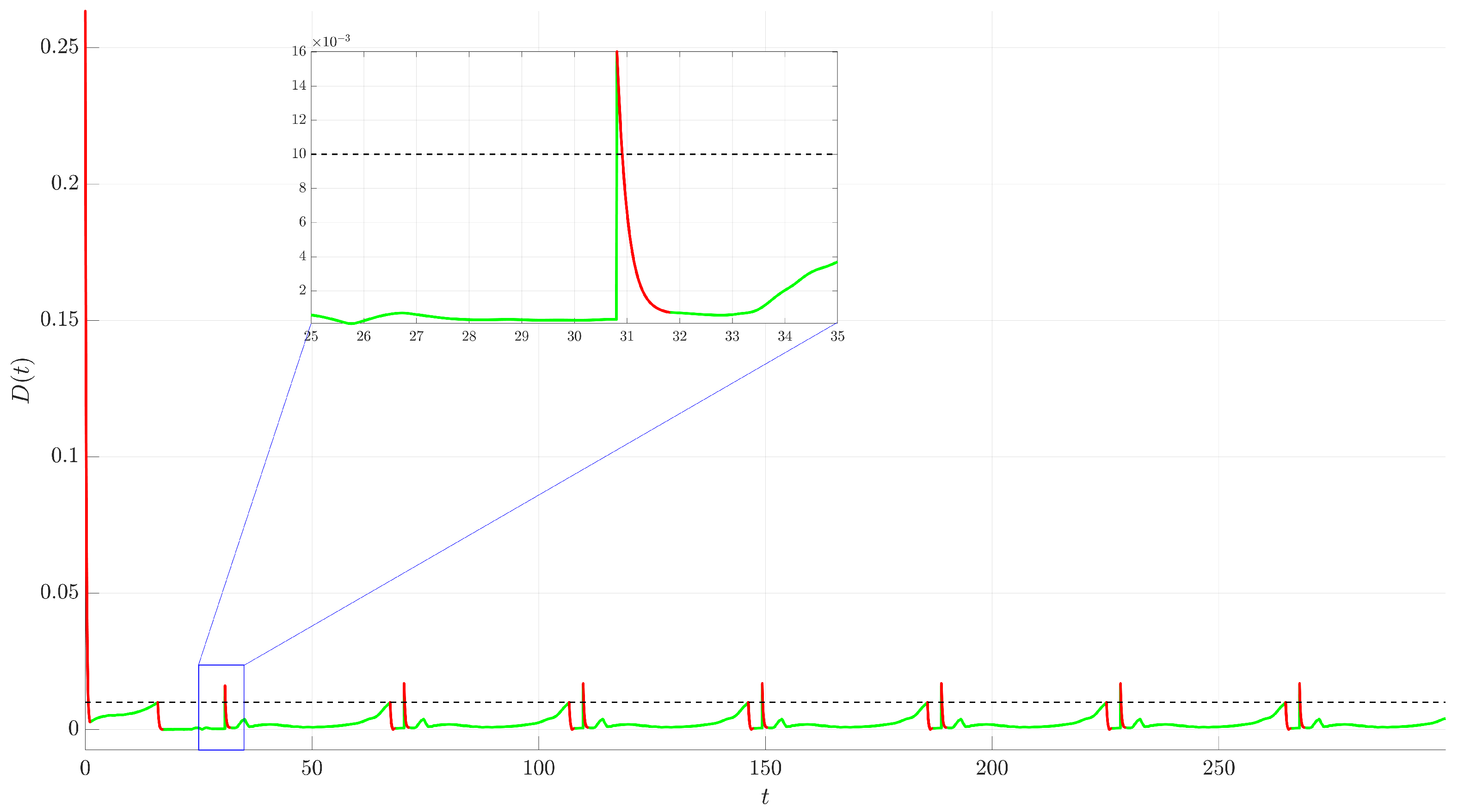
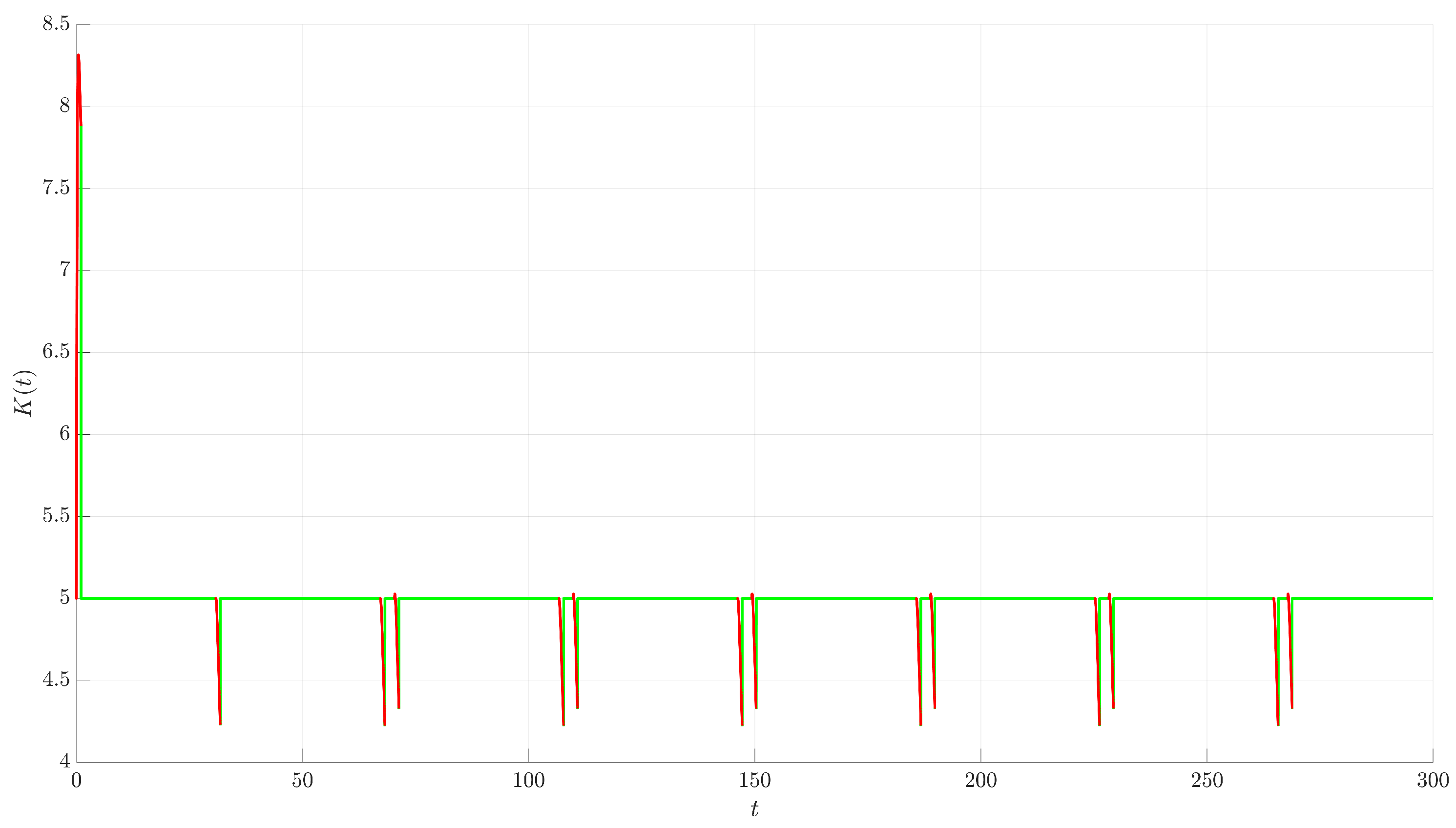
Figure 4. The controlled trajectory (red) rapidly converges towards the target UPO (dashed black line). The convergence is quantified by the Euclidean distance
between the controlled state and the UPO, depicted in
Figure 5. The distance sharply decreases after control activation at
and remains close to zero thereafter.
From a clinical perspective, this continuous control method represents an idealized therapeutic regimen, analogous to a continuous infusion of a therapeutic agent. While this strategy provides a valuable theoretical benchmark for stabilization, its inherent requirement for persistent intervention poses significant practical limitations. Continuous application can be undesirable or infeasible due to cumulative toxicity, patient discomfort, economic burden, and the high selective pressure it places on cancer cells, which can accelerate the development of drug resistance.
These considerations motivate the investigation of intermittent control strategies wherein the control mechanism is applied discontinuously and activated or deactivated based on the system’s stabilization status. The following subsections, therefore, explore intermittent control strategies designed to maintain stability while significantly reducing the total control effort.
3.2. Intermittent External Force Control
The intermittent approach applies the same control force as in (
3) but switches it on or off based on the system’s proximity to the target UPO. The control activation is determined by the distance
:
where
is the activation threshold. The control activates only when the system’s trajectory is beyond the
-neighborhood of the UPO. The goal is to maintain the trajectory near the UPO using minimal control action. The simulations shown use
and
. The behavior under this strategy is illustrated in
Figure 6,
Figure 7,
Figure 8 and
Figure 9.
Figure 6 shows the time evolution of the state variables. Unlike the continuous case, the trajectory now alternates between controlled segments (red, when
) and uncontrolled segments (green, when
). The system is corrected when it strays too far from the UPO and is allowed to evolve according to its natural dynamics once it is within the prescribed tolerance. This demonstrates the on–off nature of the control.
Figure 7 provides a zoomed-in view of the time series from
Figure 6. This magnification reveals a potential issue with this simple switching logic: chattering. As the trajectory oscillates around the boundary
, the control rapidly switches on and off. This high-frequency switching might be undesirable or damaging in practical implementations.
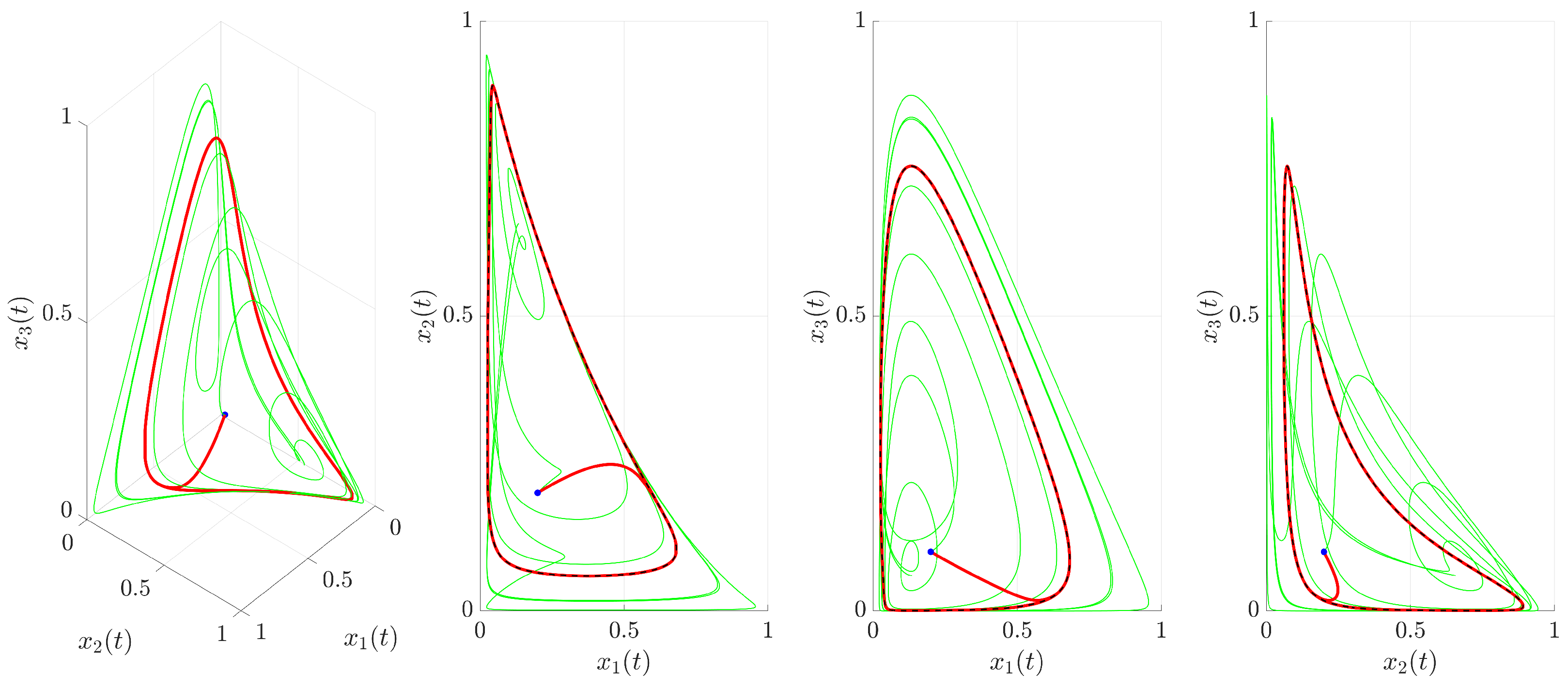
The phase portrait and its projections are shown in
Figure 8. The trajectory remains confined near the target UPO (dashed black line), indicating successful stabilization. The alternating red and green segments highlight the periods of active control and free evolution, respectively.
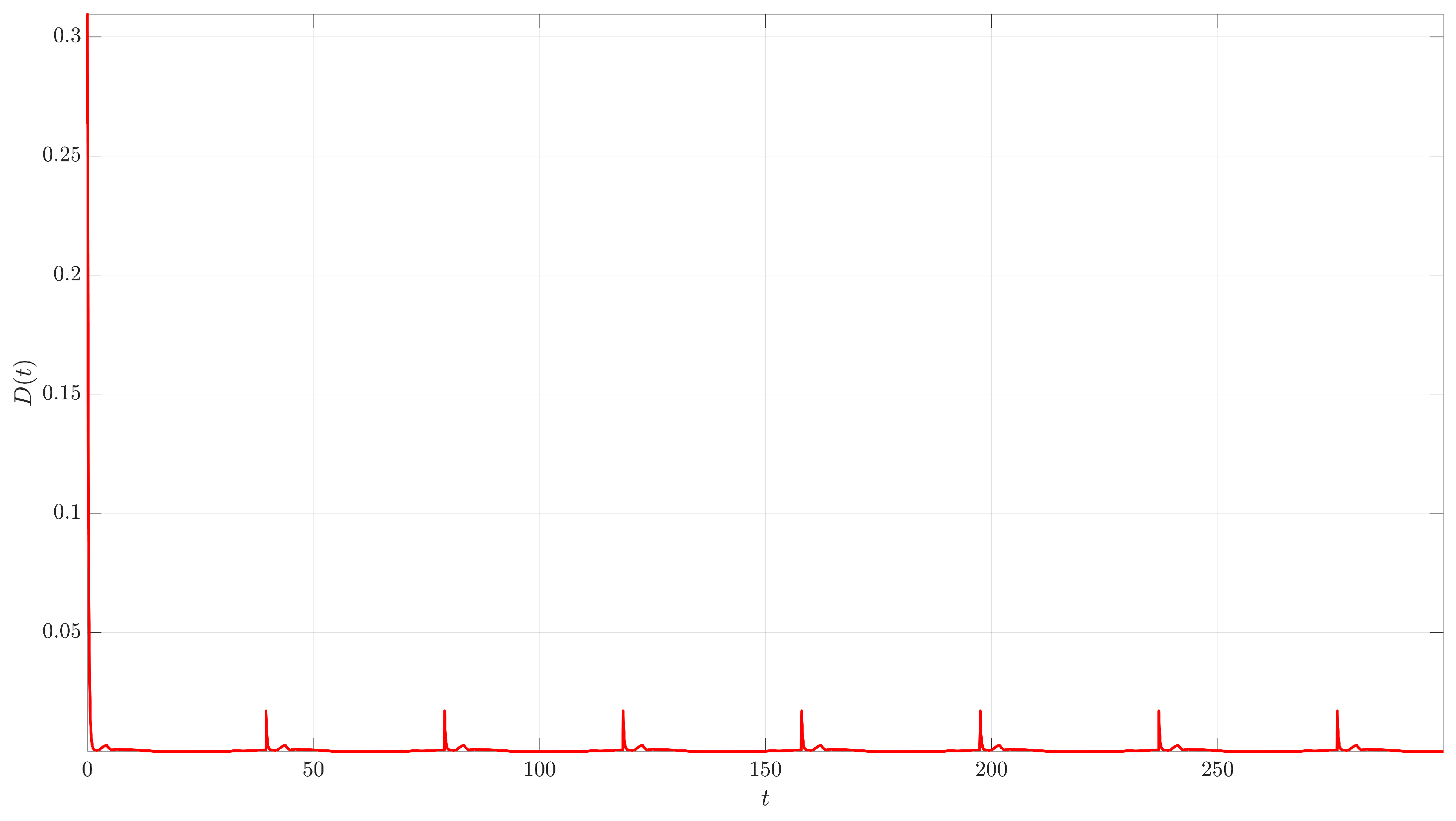
Figure 9 plots the distance
and clearly shows the switching dynamics. The control activates (red segments) when
exceeds
(dashed black line) and deactivates (green segments) when
drops below
. The inset highlights the chattering phenomenon through which the distance frequently crosses the threshold, leading to rapid control switching.
The therapeutic interpretation of this strategy is that of a reactive or on-demand therapy, where treatment is initiated only when the tumor burden crosses a specific threshold. However, the chattering phenomenon revealed in the analysis (
Figure 9) corresponds to a clinically unfeasible scenario. It would imply starting and stopping a therapeutic intervention at an extremely high frequency, which is not only impractical to administer but could also lead to unpredictable drug concentrations in the patient, potentially fostering the evolution of resistant cancer cell populations. This highlights the need for a control logic that prevents such rapid switching.
3.3. Intermittent Control with Minimum Activation Duration
To address the chattering issue observed in the simple state-dependent intermittent strategy, a modification is introduced that enforces a minimum duration for which the control must remain active once triggered. This strategy aims to prevent rapid switching by ensuring the control acts for a substantial period once turned on, allowing the system state to move well within the
-neighborhood before deactivation is considered. The control force is modulated by a switching signal
, such that the overall control input is as follows:
The switching signal
is governed by a logic designed to prevent rapid toggling. The control activates (
switches from 0 to 1) at time
when the distance,
, first exceeds the threshold
. Once active, the control is guaranteed to remain on for a minimum duration of
. Deactivation (
switching from 1 to 0) is only permitted when two conditions are met simultaneously: the minimum activation time has elapsed (
), and the system’s trajectory has returned to the desired neighborhood (
). If these conditions for deactivation are not met after the minimum time, the control remains on until the trajectory is successfully stabilized within the
-neighborhood. For the simulations, the parameter values
,
, and
were used. The results of this modified strategy are shown in
Figure 10,
Figure 11,
Figure 12 and
Figure 13.
Figure 10 displays the time evolution of the state variables. The trajectory alternates between controlled (red,
) and uncontrolled (green,
) segments. Compared to
Figure 6, the red segments are visibly longer and less frequent.
The zoomed-in view in
Figure 11 shows the effect of the minimum activation duration. Once control activates (start of red segment), it remains on for at least
. Even if
drops below
during this initial period, the control persists. Deactivation (start of green segment) only occurs after
and
. This effectively eliminates the high-frequency chattering seen previously.
The phase portrait and its projections in
Figure 12 show the trajectory successfully stabilized near the target UPO (dashed black line). Again, the switching between controlled (red) and uncontrolled (green) dynamics is less frequent than in
Figure 8.
Figure 13 plots the distance
. When
exceeds
(dashed black line), control activates (red segment begins) and stays active for at least
. If
is still above
when
, the control remains on until
eventually drops below or equals
. The inset demonstrates the successful suppression of chattering; the distance remains below
for significant periods before control is potentially reactivated.
This modified strategy has a much more direct and realistic clinical analogue. The introduction of the minimum activation time directly corresponds to the administration of a standard treatment cycle. In clinical practice, therapies are prescribed over a defined period (e.g., several days or weeks) and are not stopped instantaneously based on an immediate biological response. This control method, therefore, represents a treat-and-wait strategy where a full course of therapy is initiated when the tumor burden grows beyond a set limit. By eliminating chattering, this approach models a far more practical approach to cancer management.
3.4. Adaptive Intermittent Control
Building upon the chatter-suppressed intermittent strategy, this section introduces an adaptive mechanism for the control parameter,
K, allowing the system to automatically adjust the control strength. The control force is given as follows:
where
is the time-varying adaptive control gain, and
is the chatter-suppressing switching signal from
Section 3.3.
The main difference lies in the adaptation law for the gain,
, which consists of two parts: a continuous update rule applied when the control is active, and a discrete reset rule applied at the moment of deactivation. When the control is active (
), the gain,
, evolves according to the differential equation:
This law increases the gain when the trajectory is outside the
-neighborhood and decreases it when the trajectory is inside, dynamically tuning the control strength based on performance. At the instant the control deactivates (i.e., when
switches from 1 to 0), the gain is immediately reset to its initial value
. During the subsequent inactive period (
), the gain remains constant at this reset value until the next activation.
For the simulations, the same switching parameters and were used, alongside an adaptation rate and an initial gain .
The performance of the adaptive strategy is illustrated in
Figure 14,
Figure 15,
Figure 16 and
Figure 17. The time evolution of the state variables (
Figure 14 and
Figure 15), phase portrait and its projections (
Figure 16), and distance from the UPO (
Figure 17) demonstrate that the system is successfully stabilized. The resulting dynamics appear qualitatively similar to the non-adaptive case from
Section 3.3, indicating that stability is robustly maintained even as the control gain varies.
The evolution of
is depicted in
Figure 18. Starting at
, the parameter is adjusted dynamically during the control-on periods (red segments). When control activates because
,
initially increases. If control is effective and
drops below
while
is still 1 (due to
),
decreases. This adaptive strategy successfully stabilizes the system while automatically modulating the control based on performance relative to the threshold
.
This control strategy represents the most sophisticated and clinically forward-thinking technique investigated in this study—adaptive therapy. This approach moves beyond simple on–off switching based on a fixed-dosage plan. By allowing the control gain to vary in response to the system’s error, the strategy models a treatment where the dosage or intensity is actively modulated during the treatment cycle based on the patient’s observed response. For example, a less-than-optimal response could trigger an increase in dosage, while a strong response could allow for a dose reduction to mitigate side effects. This method directly aligns with the goals of personalized medicine, aiming to steer the tumor dynamics using the minimum necessary intervention to manage toxicity and delay the onset of resistance.
3.5. Comparative Analysis of Control Strategies
To provide a comprehensive evaluation, this section compares the performance of the four implemented control strategies. The goal is to quantify the trade-offs between stabilization accuracy and the required control effort, highlighting the distinct advantages and disadvantages of each method.
The comparison is based on a simulation run for each strategy over a total duration of
time units, starting from the same initial condition
. Performance is quantified using three key metrics, summarized in
Table 1. The first, total distance, is the time integral of the Euclidean distance,
, which represents the accumulated tracking error over the entire simulation. The second metric, control-on time, is the percentage of the total simulation time during which the control force was active, quantifying the temporal burden of the control. The third, total control impulse, is the time integral of the magnitude of the control force vector, serving as a measure of the total energy or resources expended by the controller.
An analysis of the results in
Table 1 reveals a clear hierarchy of performance and efficiency. The continuous control acts as a performance benchmark. As expected, it achieves the highest precision with the lowest total distance. However, this comes at the maximum possible cost, with a control-on time of 100% and the highest total control impulse.
Switching to the simple intermittent control strategy results in a dramatic reduction in control effort, as evidenced by its minimal control-on time. This efficiency, however, is gained at the expense of performance, as the total distance increases significantly. This method also suffers from the chattering phenomenon, where the controller rapidly switches on and off near the boundary of the activation threshold.
The intermittent control with minimum activation duration successfully addresses these shortcomings. By eliminating chattering and ensuring that the control acts for a more substantial period once triggered, it cuts the total distance in half compared to the simple intermittent method. This significant improvement in accuracy comes with a slight increase in the control-on time.
Finally, the adaptive intermittent control demonstrates a further refinement. It achieves the best performance among the intermittent strategies, with the lowest total distance and total control impulse in this category. Its primary advantage is its ability to achieve this robust performance without requiring manual tuning of the control gain, K. It automatically adjusts the gain based on system performance, finding an effective balance dynamically.
It is crucial to emphasize that the intermittent and adaptive strategies introduce additional parameters, which act as new degrees of freedom for tuning the controller. The results presented in
Table 1 correspond to the specific parameter values used earlier in this study, namely an activation threshold of
, a minimum activation time of
, an initial gain of
, and an adaptation rate of
. A different choice of these parameters would lead to different quantitative results; for instance, a larger threshold
would further reduce control effort but likely increase the tracking error. The purpose of this study was not to perform an exhaustive parameter optimization but, rather, to introduce and compare the fundamental mechanics and inherent trade-offs of these distinct control frameworks. For any practical application, a careful tuning of these parameters would be a necessary subsequent step.
4. Conclusions
This study implemented and compared four distinct external force control strategies for suppressing the chaotic dynamics of a well-established three-dimensional cancer model [
34]. The objective was to stabilize a target UPO embedded within the system’s strange attractor, thereby transforming the unpredictable, chaotic behavior into a regular, periodic dynamic.
The investigation first established a baseline using continuous control, which, while highly precise in tracking the target UPO, required constant intervention and the largest control effort. In contrast, a simple intermittent control strategy drastically reduced the control effort, but at the cost of significantly lower accuracy and the introduction of high-frequency chattering. To address this, a modified intermittent controller incorporating a minimum activation duration was introduced. This method successfully eliminated chattering and substantially improved tracking performance, demonstrating a favorable balance between control accuracy and efficiency.
The most promising results were obtained with the adaptive intermittent control strategy. This approach not only matched the improved performance of the chatter-free method but also achieved the lowest total control impulse among the intermittent strategies. Its principal advantage lies in its ability to dynamically tune the control gain, showcasing a robust mechanism for self-optimization. The findings underscore that both chatter-suppressed and adaptive intermittent control offer more practical and efficient alternatives to continuous intervention, which is an important consideration for therapeutic applications. By minimizing the duration and intensity of the intervention, these strategies could potentially lead to treatments with fewer side effects, lower economic costs, and a reduced likelihood of developing treatment resistance, making them more practical and sustainable for patient care.
The scope of this work was a comparative analysis of the control frameworks, rather than an exhaustive optimization of their parameters. Future research should focus on a systematic investigation of the parameter space (e.g., , , ) to formally optimize the trade-off between control effort and stabilization accuracy. Further valuable extensions could include applying these adaptive and intermittent strategies to more complex cancer models that incorporate additional biological factors, such as pharmacokinetics or different immune cell populations. Finally, investigating the robustness of these controllers to system noise and parameter uncertainty, which are inherent to all biological systems, would be a critical step toward assessing their potential for real-world application.