A Hybrid Approach for Reachability Analysis of Complex Software Systems Using Fuzzy Adaptive Particle Swarm Optimization Algorithm and Rule Composition
Abstract
1. Introduction
2. Background
2.1. Model Checking
2.2. Graph Transformation System
2.3. Particle Swarm Optimization Algorithm
| Algorithm 1. Pseudo Code for PSO Algorithm |
| 1. Initialization a. Initialize the particle’s position xi(t) for (t = 0, i:1…N) b. Initialize the particle’s best position to its initial position pi(t) = xi(t) for (t = 0, i:1…N) c. Calculate the fitness of each particle f (xi (t)) for (t = 0, i:1…N) d. if f (xi (0)) ≤ f (xj (0)) then Initialize the global best as g-best = xj(t) for each i,j:1…N, i≠j) 2. while a stopping criterion is not met repeat the following steps: Update the velocity vi for each particle: vi(t + 1) = W*vi(t) + C1(p-besti − xi(t)) R1 + C2(g-best − xi(t)) R2 Update the position xi for each particle: xi(t + 1) = xi(t) + vi(t + 1) Evaluate the fitness f(xi(t + 1)) for each particle. if f(xi(t + 1)) ≥ f(p-besti) then Update personal best: p-besti = xi(t + 1) if f(xi(t + 1)) ≥ f(g-best) then Update personal best: g-best = xi(t + 1) At the end of iterative process, the best solution is represented by g-best. |
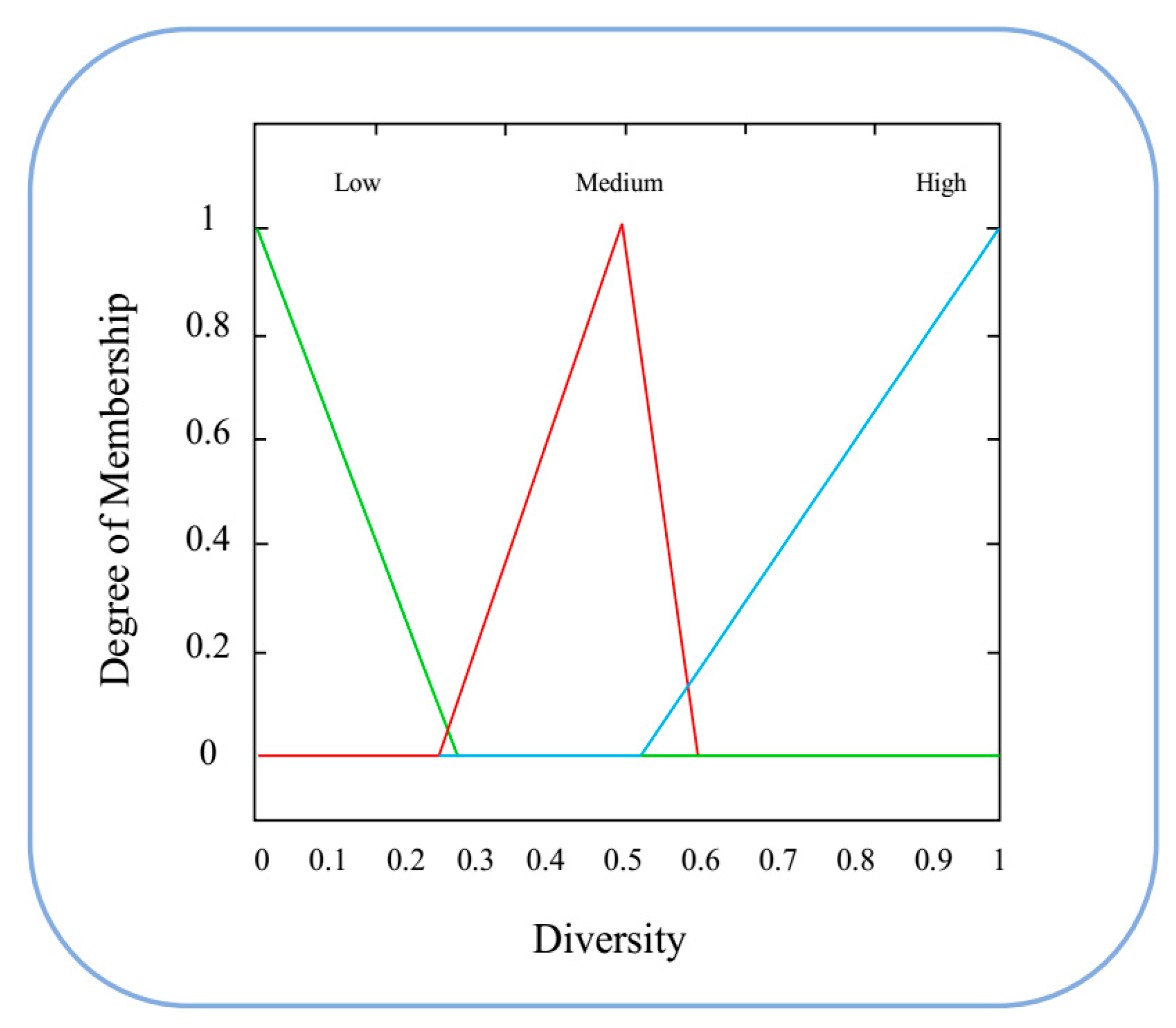
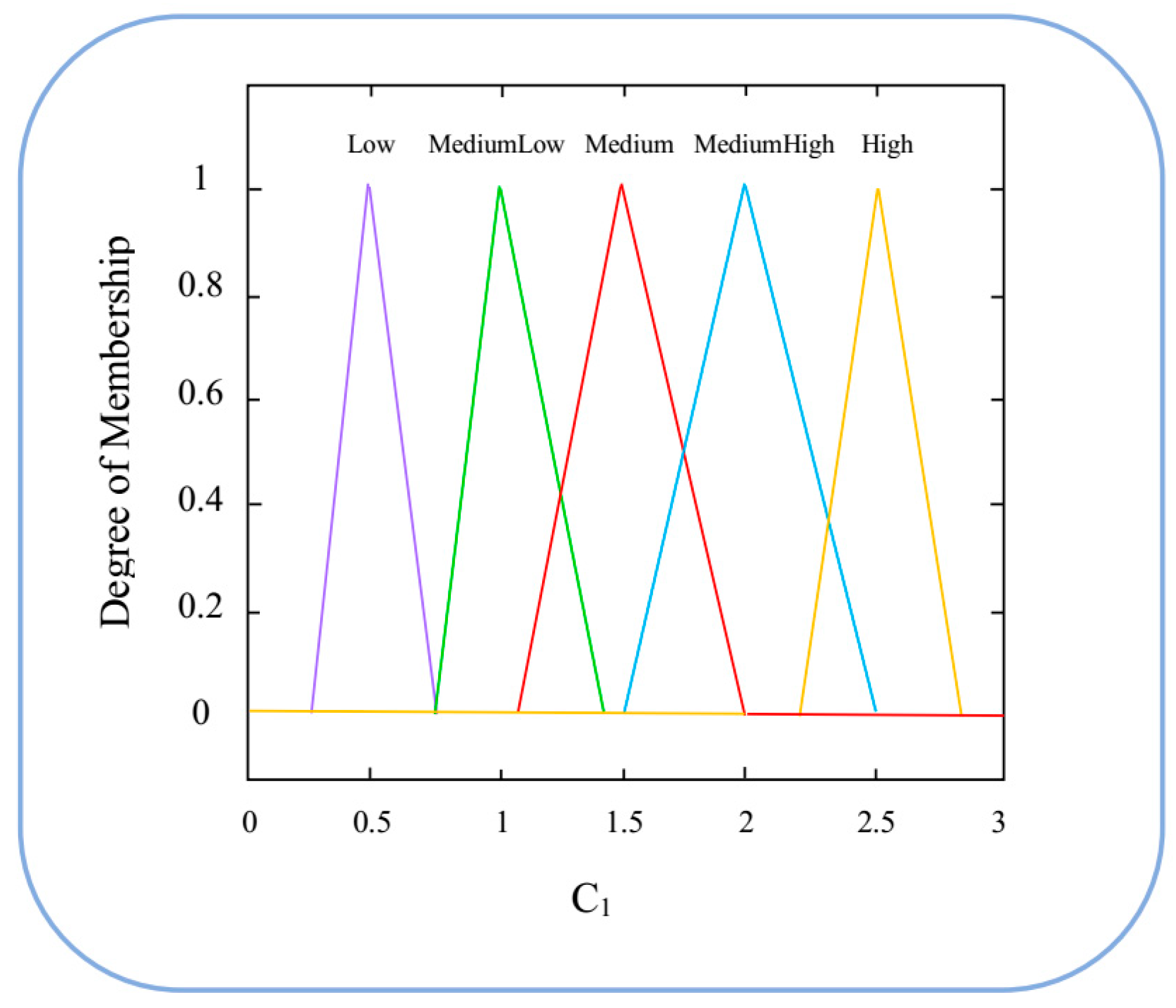
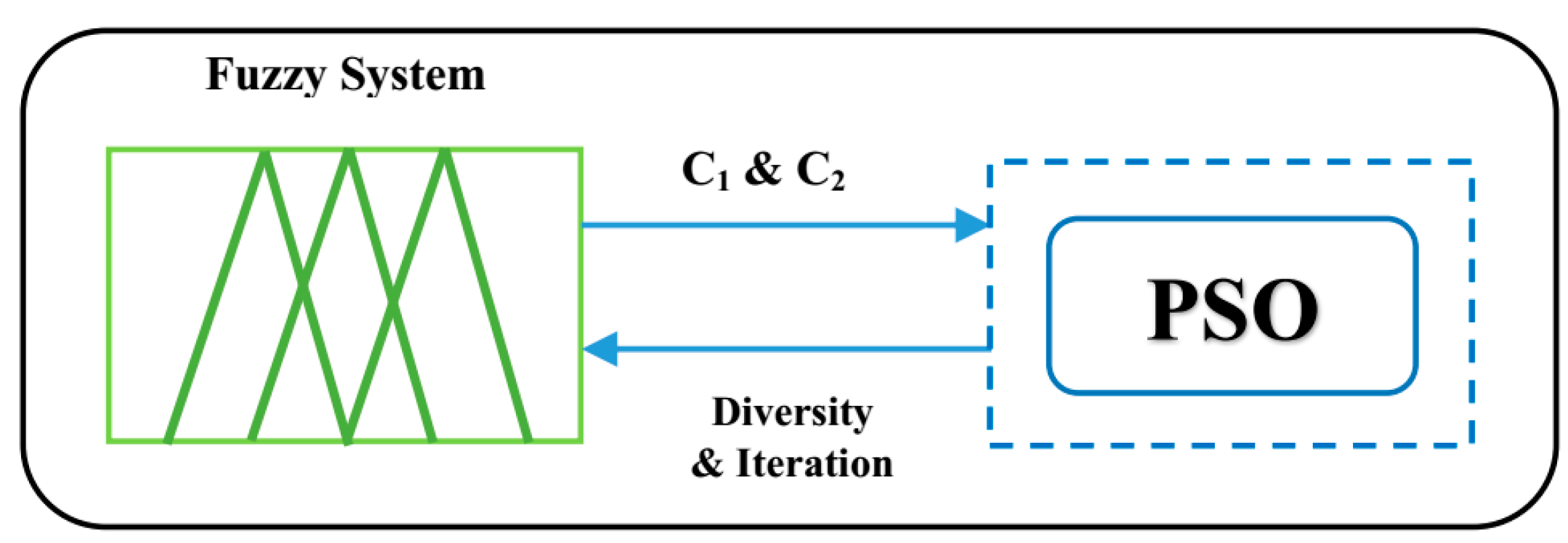
2.4. Fuzzy Inference System
- In the fuzzification process, the linguistic variables (for both inputs and outputs) are defined.
- The FIS defines the rules that describe how the system works and maps inputs to outputs.
- In the defuzzification process, the outputs are calculated.
- The input and output variables.
- The fuzzy membership functions.
- The fuzzy rules.
- The parameters used in defining the membership functions and rules.
3. The Proposed Approaches
3.1. Problem Formulation
- A fuzzy inference system for dynamic adjustment of PSO parameters based on iteration progress and particle diversity, improving exploration and convergence.
- A domain-specific fitness function that evaluates graph similarity and penalizes violations of Negative Application Conditions (NACs), allowing more precise navigation of GTS-based state spaces.
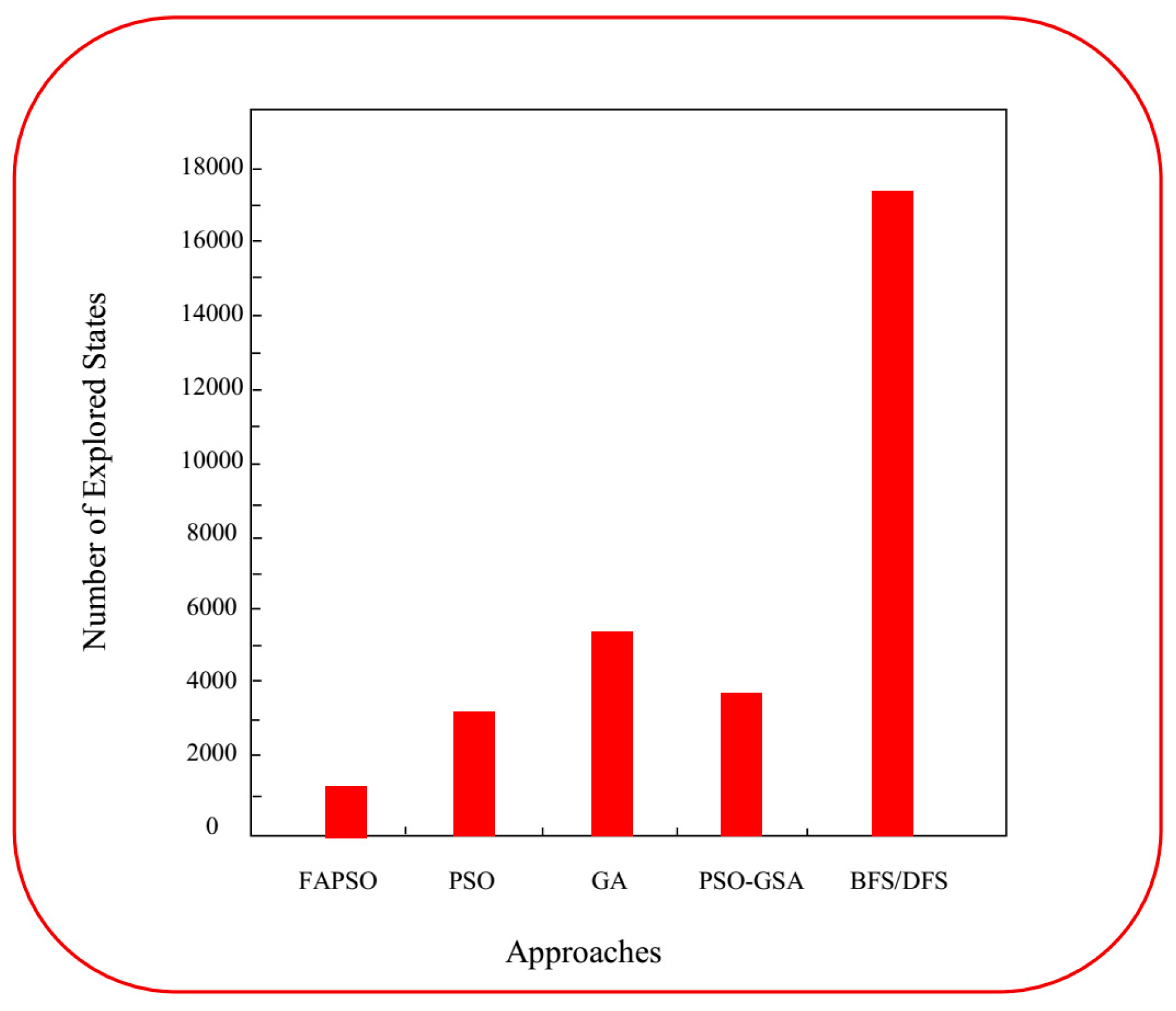
- Integration with rule composition to reduce model complexity and the number of explored states.
- Gh maximally matches the structural and semantic features of Gp;
- No NAC conditions are violated in Gh;
- The number of explored intermediate states and computational time are minimized.
- TG is the Type graph, specifying the meta-model of the system;
- HG is the host graph, representing the initial configuration of the system;
- R = {r1, r2, …, rk} is the rule set, where each rule ri = (LHSi, RHSi, NACi) defines a transformation on graphs.
- Applying π\piπ to HG yields a graph Gh = π(HG);
- Gh maximally matches Gp in structure and labels;
- Gh does not violate any NACs defined for Gp;
- The path length |π| and the number of explored states is minimized.
- Maximize Similarity (Gp, Gh) − PenaltyNAC (Gh, NACp)
- Subject to Gh = π(HG), π∈Rn Gh satisfies all structural constraints of TG
- Similarity (Gp, Gh) is a domain-specific function measuring graph isomorphism or structural resemblance (e.g., node/edge label matches);
- PenaltyNAC penalizes configurations that violate the Negative Application Conditions associated with Gp.
- Thinking, Hungry, HasLeft, Eating, HasRight.
- r1: GoHungry;
- r2: GetLeft;
- r3: GetRight;
- r4: ReleaseLeft;
- r5: ReleaseRight.
- No forks are shared (NAC);
- All graph transformations are valid under the GTS semantics.
- The similarity function Similarity (Gp, Gh) counts matched philosopher states labelled HasLeft and correctly allocated forks.
- The penalty function PenaltyNAC ensures no philosopher has picked both forks, which would violate the deadlock property.
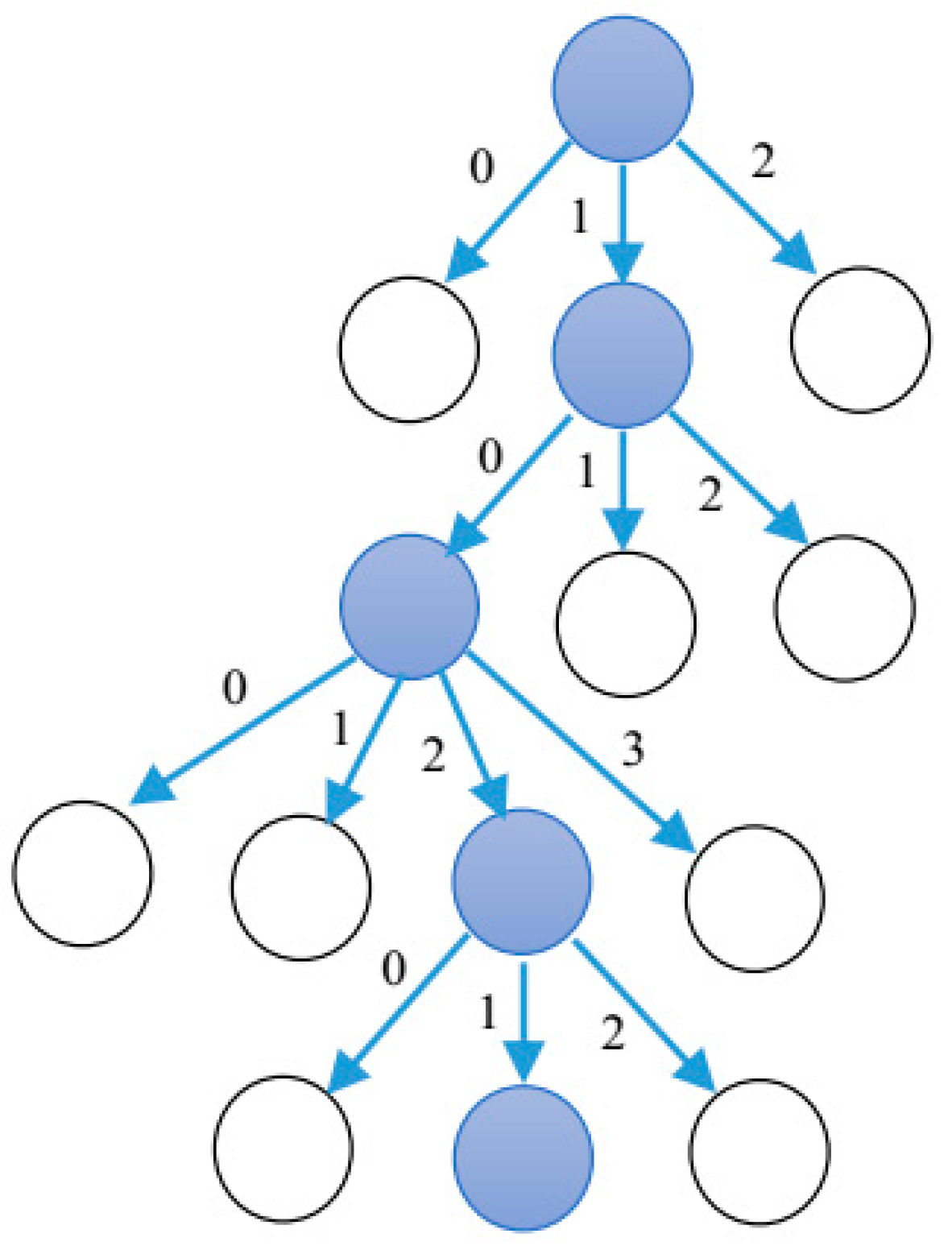
3.2. Particle Encoding
3.3. Fitness Function
- Identify pairs of nodes where the first node belongs to the given property graph (excluding NAC nodes) and the second node belongs to the last state of the path specified by the particle, ensuring that they have the same labels.
- Count the total number of pairs found in the first step.
- Count the total number of each NAC node and edge for the given properties occurring in the graph that represents the path’s last state, encoded by the given particle.
- The fitness value is the difference between the total calculated in step 2 and the total from step 3.
| Algorithm 2. Fitness Function for PSO and FAPSO Approaches |
| 1. Input and Output: a. Input: h: a particle and p: a given reachability property to be checked b. Output: the fitness value of h 2. Initialization: a. Initialize NodeList member Npi with node ith of Gp (i: 0 to Number of nodes Gp) b. Initialize EdgeList member Epi with edge ith of Gp (i: 0 to Number of edge Gp) c. Initialize NodeList member Nhi with node ith of Gh (i: 0 to Number of nodes Gh) d. Initialize EdgeList member Ehi with edge ith of Gh (i: 0 to Number of edge Gh) e. Initialize BooleanList member hVisitedij with false f. Initialize BooleanList member pVisitedij with false g. Initialize BooleanList member Visitedij with false (For part e, f and g: i: 0 to Number of nodes Gh and j: 0 to Number of nodes Gp) 3. For each Nhi for each Npj EdgeList ENP = all edges of Ep whose source node is Npj EdgeList ENH = all edges of Eh whose source node is Nhi E-Countij = The number of pairs (p,h) which (p) is from ENP and (h) is from ENH as p′s label is equal to h’s label; PE-Countij = size of ENP DE-Countij = E-Countij − PE-Countij end for end for 4. EQ-Count = 0 while all Visitedij is not true do Find the smallest DE-Countij that Visitedij = false Visitedij = true if pVisitedij is not true && hVisitedij is not true then EQ-Count += E-Countij; pVisitedij = true hVisitedij = true end if end while 5. Find all NACs of Gp and store in ArrayList of NACs allNAC NEQ-Count = 0 for each NACi in allNAC do NEQ-Count += The number of edges and nodes of NACi occurring in Gh end for return EQ-Count − NEQ-Count |
3.4. PSO-Based Approach
3.5. FAPSO-Based Approach
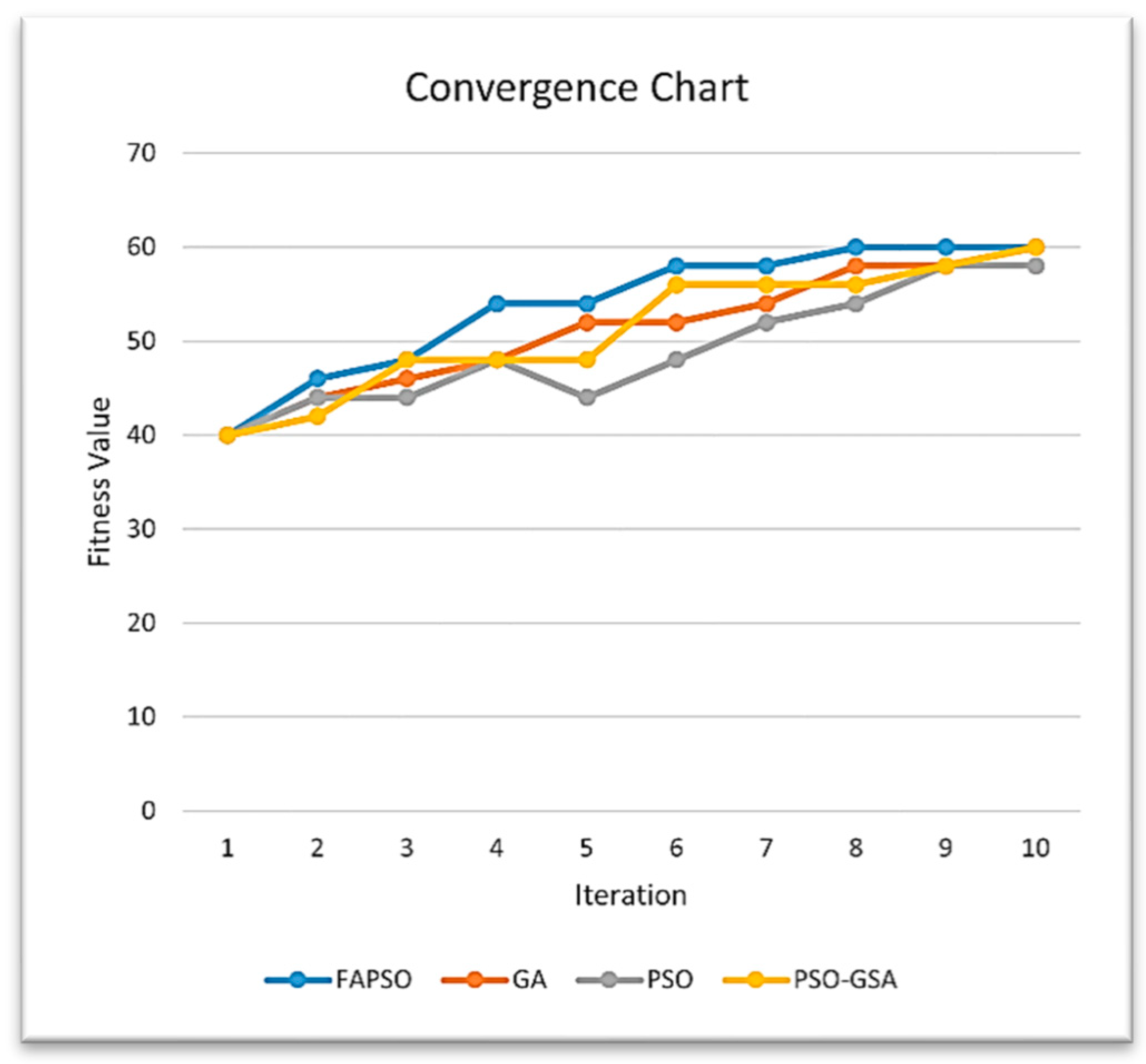
4. Experimental Results
4.1. Basic Models
4.1.1. Dinning Philosopher’s Problem
4.1.2. Pac-Man Game Problem
4.1.3. Process Life Cycle Problem
4.1.4. Shopping Problem
4.1.5. N-Queen Problem
4.1.6. 8-Puzzle Problem
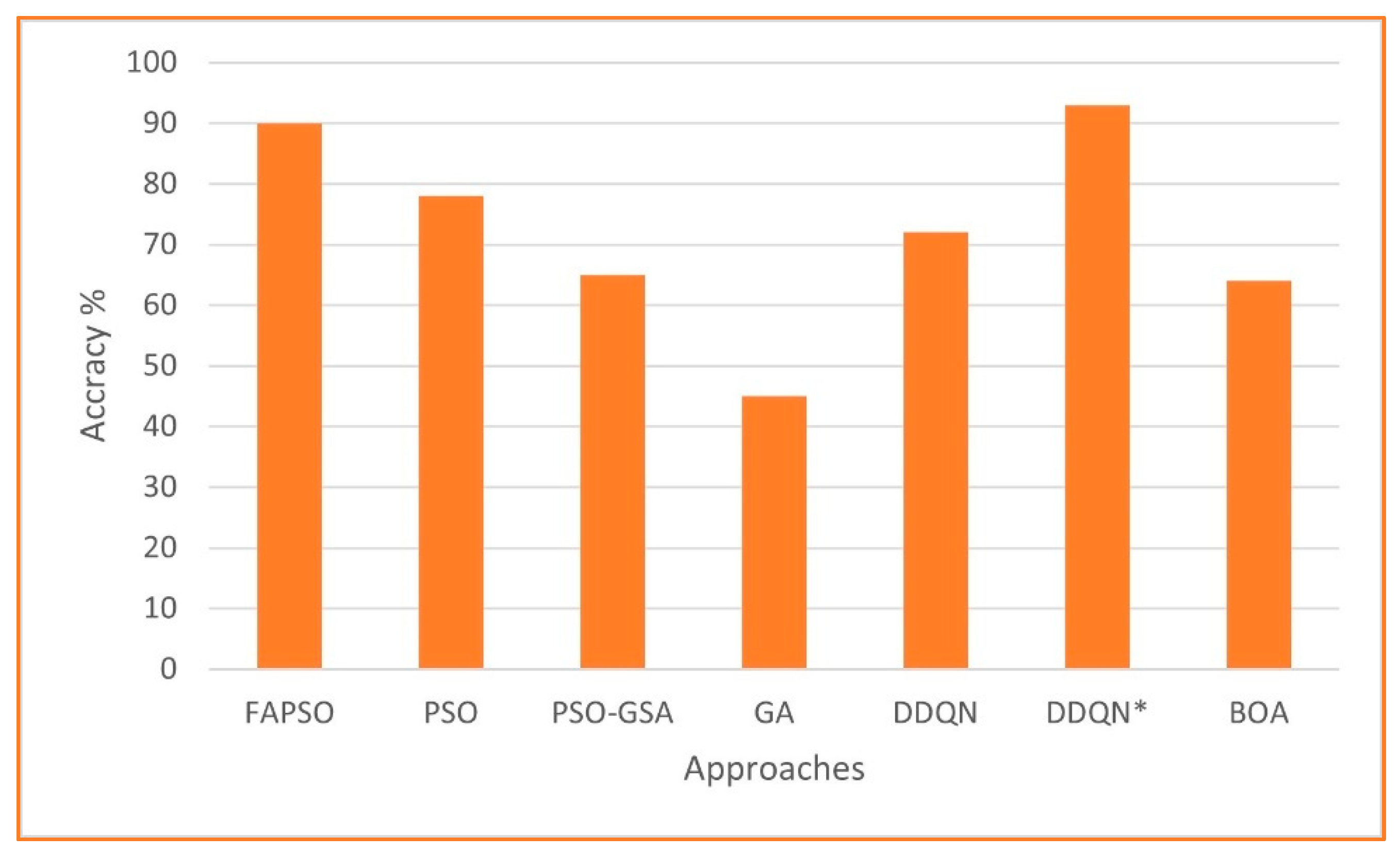
4.1.7. Positioning FAPSO Against Machine Learning-Based Approaches
4.2. Models Applied for Rule Composition
4.2.1. Dinning Philosopher’s Problem
- GoHungry: The philosopher transitions from the “Thinking” state to the “Hungry” state.
- GetLeft: The philosopher picks up the left fork and transitions to the “HasLeft” state.
- GetRight: The philosopher picks up the right fork and transitions to the “Eating” state.
- ReleaseLeft: The philosopher releases the left fork and transitions to the “HasRight” state.
- ReleaseRight: The philosopher releases the right fork and returns to the “Thinking” state.
- GoHungry-GetLeft: The philosopher picks up the left fork and transitions from the “Thinking” state to the “HasLeft” state.
- GetRight: The philosopher picks up the right fork and transitions to the “Eating” state.
- ReleaseLeft: The philosopher releases the left fork.
- ReleaseRight: The philosopher releases the right fork and returns to the “Thinking” state.
4.2.2. Shopping Problem
- TakeCart: The customer initiates the shopping process by picking up a cart.
- CreateBill: An unpaid bill is generated for the customer.
- SelectGood: The customer picks up an item from the rack and places it in their cart.
- DeselectGood: The customer returns an item from the cart to the rack.
- BillGood: The customer′s items in the cart are added to the bill to begin the payment process.
- PayBill: The customer′s bill is paid once all items have been added to the bill.
- SettleBill: The shopping process concludes, and the customer′s shopping flag is deactivated.
- Finish: The customer releases the cart, and their bill is deleted.
- TakeCart-CreateBill: The customer initiates the shopping process by picking up a cart, and an unpaid bill is generated for the customer.
- SelectGood: The customer picks up an item from the rack and places it in their cart.
- DeselectGood: The customer returns an item from the cart to the rack.
- BillGood: To begin the payment process, the customer′s items in the cart are added to their bill.
- PayBill-SettleBill: The customer′s bill is paid once all items have been added, and the shopping process concludes by deactivating the customer′s shopping flag.
- Finish: The customer releases the cart, and their bill is deleted.
- Validation through Formal Methods: The modified rules have been formally verified to ensure that they do not change the expected system behaviour.
- Checking Intermediate States: Rule composition did not remove critical intermediate states that affect the reachability of essential states.
- Structural Consistency: The graph transformation rules maintain structural constraints to ensure the logical flow remains intact.
5. Discussion
6. Conclusions
- Enhancing the fuzzy system through refined membership functions and rules.
- Extending the fitness function to verify other properties such as safety, liveness, and fairness.
- Applying FAPSO to broader optimization benchmarks and real-world case studies.
- Automating rule composition to reduce manual effort and improve scalability.
- Exploring hybrid integrations with machine learning techniques for further performance improvements.
- Finally, while the current work relied on classic benchmark models, an important direction for future research is the integration of real-world GTS datasets. These may include configurations extracted from software repositories, business process models, and cyber-physical system simulations. Such expansions will allow for deeper insight into the algorithm’s adaptability and performance under diverse, large-scale, and non-synthetic conditions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Denil, J.; Jukss, M.; Verbrugge, C.; Vangheluwe, H. Search-Based Model Optimization Using Model Transformations. In System Analysis and Modeling: Models and Reusability; Springer International Publishing: Berlin/Heidelberg, Germany, 2014; pp. 80–95. [Google Scholar]
- Yousefian, R.; Rafe, V.; Rahmani, M. A heuristic solution for model checking graph transformation systems. Appl. Soft Comput. 2014, 24, 169–180. [Google Scholar] [CrossRef]
- Baresi, L.; Heckel, R. Tutorial introduction to graph transformation: A software engineering perspective. In Graph Transformation: First International Conference, ICGT 2002, Barcelona, Spain, 7–12 October 2002; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Lafuente, A.L. Symmetry reduction and heuristic search for error detection in model checking. In Proceedings of the Workshop on Model Checking and Artificial Intelligence, Acapulco, Mexico, 10 August 2003. [Google Scholar]
- Clarke, E.; McMillan, K.L.; Campos, S.V.A.; Hartonas-Garmhausen, V.I. Symbolic Model Checking. Available online: https://www.cs.cmu.edu/~emc/papers/Conference%20Papers/Symbolic%20Model%20Checking.pdf (accessed on 15 April 2025).
- Edelkamp, S.; Leue, S.; Lafuente, A.L. Directed Explicit-state model checking in the validation of communication protocols. Int. J. Softw. Tools Technol. Transf. (STTT) 2004, 5, 247–267. [Google Scholar] [CrossRef]
- Gyuris, V.; Sistla, A.P. On-the-fly model checking under fairness that exploits symmetry. Form. Methods Syst. Des. 1999, 15, 217–238. [Google Scholar] [CrossRef]
- Lin, F.J.; Chu, P.M.; Liu, M.T. Protocol verification using reachability analysis: The state space explosion problem and relief strategies. In Proceedings of the ACM Workshop on Frontiers in Computer Communications Technology, Stowe, VT, USA, 11–13 August 1987; ACM: New York, NY, USA; pp. 126–135. [Google Scholar]
- Yang, C.H.; Dill, D.L. Validation with guided search of the state space. In Proceedings of the DAC’98: Proceedings of the 35th Annual Design Automation Conference, San Francisco, CA, USA, 15–19 June 1998; ACM: New York, NY, USA, 1998; pp. 599–604. [Google Scholar]
- Edelkamp, S.; Reffel, F. OBDDs in Heuristic Search. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1998; pp. 81–92. [Google Scholar]
- Friedman, G.; Hartman, A.; Nagin, K.; Shiran, T. Projected state machine coverage for software testing. In Proceedings of the ACM SIGSOFT International Symposium on Software Testing and Analysis, Rome, Italy, 22–24 July 2002; ACM: New York, NY, USA, 2002; pp. 134–143. [Google Scholar]
- Francesca, G.; Santone, A.; Vaglini, G.; Villani, M.L. Ant Colony Optimization for Deadlock Detection in Concurrent Systems. In Proceedings of the 35th IEEE Annual Computer Software and Applications Conference, Munich, Germany, 18–22 July 2011; pp. 108–117. [Google Scholar]
- Duarte, L.M.; Foss, L.; Wagner, R.; Heimfarth, T. Model Checking the Ant Colony Optimisation. In Distributed, Parallel and Biologically Inspired Systems, IFIP Advances in Information and Communication Technology; Springer: Berlin/Heidelberg, Germany, 2010; pp. 221–232. [Google Scholar]
- Alba, E.; Troya, J.M. Genetic Algorithms for Protocol Validation. In Proceedings of the International Conference on Parallel Problem Solving from Nature (PPSN IV), Berlin, Germany, 22–26 September 1996; Springer: Berlin/Heidelberg, Germany, 1996; pp. 869–879. [Google Scholar]
- Vardhan, A. Learning to Verify Systems. Ph.D. Thesis, University of Illinois at Urbana-Champaign, Champaign, IL, USA, 2006. [Google Scholar]
- Alba, E.; Chicano, F. Finding safety errors with ACO. In Proceedings of the 9th Annual Conference on Genetic and Evolutionary Computation, London, UK, 7–11 July 2007; pp. 1066–1073. [Google Scholar]
- Alba, E.; Chicano, F. Searching for Liveness Property Violations in Concurrent Systems with ACO. In Proceedings of the 10th Annual Conference on Genetic and Evolutionary Computation, Atlanta, GA, USA, 12–16 July 2008; ACM: New York, NY, USA, 2008. [Google Scholar]
- Moradi, M.; Rafe, V.; Yousefian, R.; Nikanjam, A. A Meta-Heuristic Solution for Automated Refutation of Complex Software Systems Specified through Graph Transformations. Appl. Soft Comput. 2015, 33, 136–149. [Google Scholar]
- Pira, E.; Rafe, V.; Nikanjam, A. EMCDM: Efficient Model Checking by Data Mining for Verification of Complex Software Systems Specified through Architectural Styles. Appl. Soft Comput. 2016, 44, 1185–1201. [Google Scholar] [CrossRef]
- Pira, E.; Rafe, V.; Nikanjam, A. Deadlock detection in complex software systems specified through graph transformation using Bayesian optimization algorithm. J. Syst. Softw. 2017, 131, 181–200. [Google Scholar] [CrossRef]
- Partabian, J.; Bagherifard, K.; Rafe, V.; Parvin, H.; Nejatian, S. Checking Reachability Property in Complex Concurrent Software Systems with a Knowledge Discovery Approach. J. Soft Comput. Inf. Technol. 2023, 12, 41–51. [Google Scholar]
- Nejati, F.; Hamid, N.A.W.A.; Koohi, S.Z.; Zadeh, Z.R. An Incremental Optimization Algorithm for Efficient Verification of Graph Transformation Systems. IEEE Access 2023, 11, 75748–75760. [Google Scholar] [CrossRef]
- Pira, E. Using Deep Learning Techniques for Solving AI Planning Problems Specified through Graph Transformations. Soft Comput. 2022, 26, 12217–12234. [Google Scholar] [CrossRef]
- Mehrabi, M.J.; Rafe, V. Using Deep reinforcement learning to search reachability properties in systems specified through graph transformation. Soft Comput. 2022, 26, 9635–9663. [Google Scholar] [CrossRef]
- Lambers, L. Certifying Rule-Based Models Using Graph Transformation. Ph.D. Thesis, Technische Universität Berlin, Berlin, Germany, 2019. ISBN 978-3-8381-1650-1. [Google Scholar]
- Große, M.; Presicce, F.P.; Simeoni, M. Refinements of Graph Transformation Systems via Rule Expressions. In Theory and Application of Graph Transformation: 6th International Workshop, TAGT'98 Paderborn, Germany, 16–20 November 1998; Springer: Berlin/Heidelberg, Germany, 2000; pp. 368–382. [Google Scholar]
- Taentzer, G. Parallel high-level replacement systems. Theor. Comput. Sci. TCS 1997, 186, 43–81. [Google Scholar] [CrossRef]
- Rensink, A.; Schmidt, Á.; Varró, D. Model Checking Graph Transformations: A Comparison of Two Approaches. In International Conference on Graph Transformation; Springer: Berlin/Heidelberg, Germany, 2004; pp. 226–241. [Google Scholar]
- Heckel, R. Graph Transformation in a Nutshell. Electron. Notes Theor. Comput. Sci. (ENTCS) 2006, 148, 187–198. [Google Scholar] [CrossRef]
- Kennedy, J. Particle Swarm Optimization. In Encyclopedia of Machine Learning; Springer: Berlin/Heidelberg, Germany, 2010; pp. 760–766. [Google Scholar]
- Kastenberg, H.; Rensink, A. Model Checking Dynamic States in GROOVE. In Model Checking Software: International SPIN Workshop, Vienna, Austria, 30 March–1 April 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 299–305. [Google Scholar]
- Melin, P.; Olivas, F.; Castillo, O.; Valdez, F.; Soria, J.; Valdez, M. Optimal design of fuzzy classification systems using PSO with dynamic parameter adaptation through fuzzy logic. Expert Syst. Appl. 2013, 40, 3196–3206. [Google Scholar] [CrossRef]
- Olivas, F.; Castillo, O. Particle Swarm Optimization with Dynamic Parameter Adaptation Using Fuzzy Logic for Benchmark Mathematical Functions. In Recent Advances on Hybrid Intelligent Systems; Springer: Berlin/Heidelberg, Germany, 2013; pp. 247–258. [Google Scholar]
- Schmidt, A. Model Checking of Visual Modeling Languages. Master’s Thesis, Budapest University of Technology, Budapest, Hungary, 2004. [Google Scholar]
- Hausmann, J.H. Dynamic Meta Modeling: A Semantics Description, Technique for Visual Modeling Techniques. Ph.D. Thesis, University of Paderborn, Paderborn, Germany, 2005. [Google Scholar]
- Gaschnig, J. Performance Measurement and Analysis of Certain Search Algorithms. Ph.D. Thesis, Carnegie Mellon University, Pittsburgh, PA, USA, 1979. technical report. [Google Scholar]

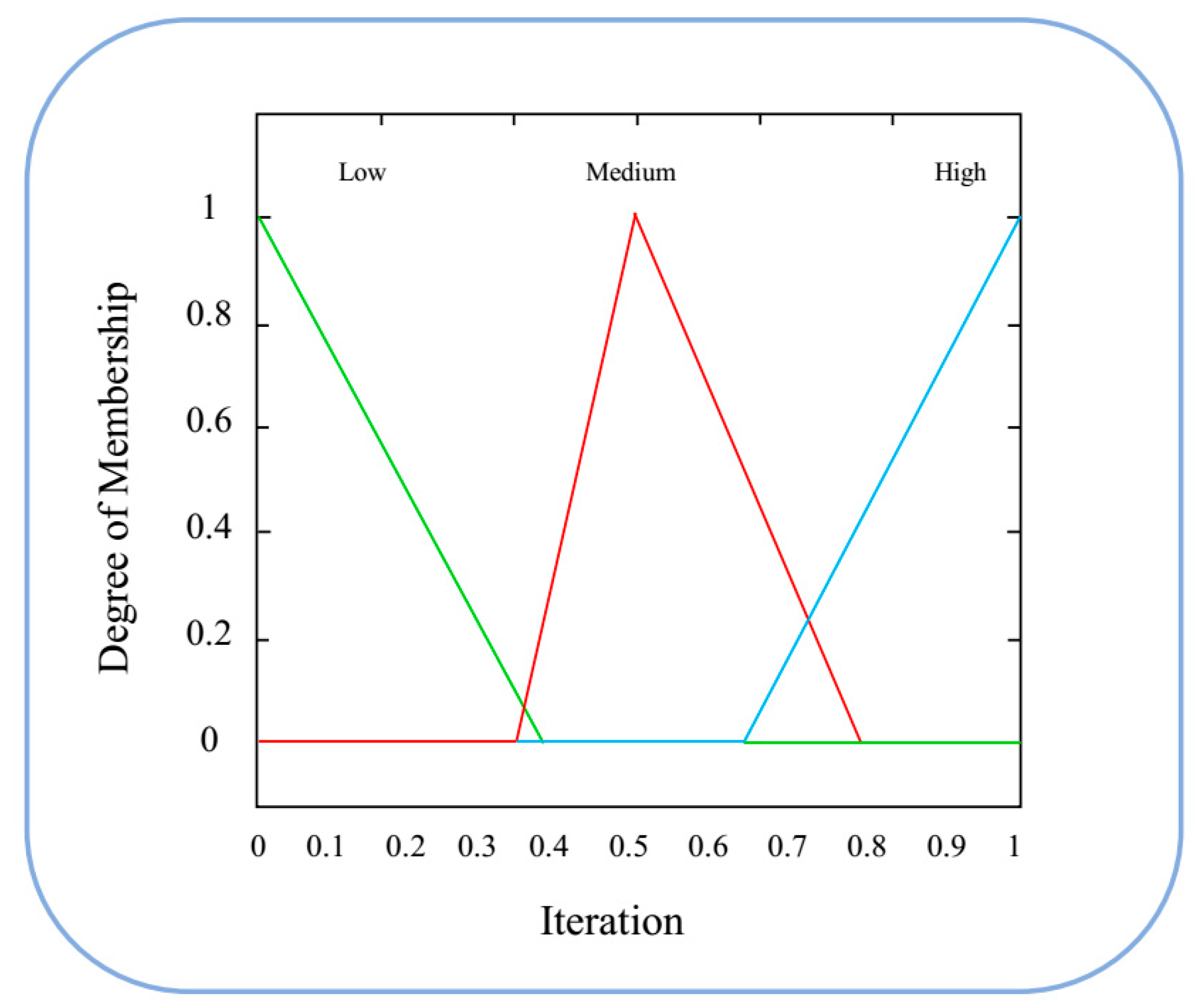


| Iteration | Low | Medium | High | |
|---|---|---|---|---|
| Diversity | ||||
| Low | High | MediumHigh | Medium | |
| Medium | MediumHigh | Medium | MediumLow | |
| High | MediumHigh | MediumLow | Low | |
| Iteration | Low | Medium | High | |
|---|---|---|---|---|
| Diversity | ||||
| Low | Low | MediumLow | High | |
| Medium | Medium | Medium | MediumHigh | |
| High | MediumLow | MediumHigh | High | |
| Iteration | 100 |
|---|---|
| C1 | 2 |
| C2 | 2 |
| W | 0.8 |
| Number of Philosophers | Depth Limit | Population | FAPSO (Second) | GA (Second) | PSO (Second) | PSO-GSA (Second) |
|---|---|---|---|---|---|---|
| 10 | 50 | 15 | 2.81 | 6.27 | 8.12 | 7.06 |
| 20 | 100 | 20 | 29.2 | 22 | 85 | 68 |
| 25 | 150 | 40 | 38.52 | 41 | 112 | 90 |
| 30 | 200 | 60 | 49.86 | 91 | 137 | 109 |
| Dimension of Pac-Man Game | Depth Limit | Population | FAPSO (Second) | GA (Second) | PSO (Second) | PSO-GSA (Second) |
|---|---|---|---|---|---|---|
| 4 × 4 | 100 | 40 | 4.13 | 4.88 | 15.07 | 12.49 |
| 4 × 5 | 100 | 60 | 7.96 | 11.15 | 36.79 | 27.31 |
| 5 × 6 | 100 | 80 | 17.59 | 72.03 | 59.1 | 60.26 |
| Process Life Cycle | Depth Limit | Population | FAPSO (Second) | GA (Second) | PSO (Second) | PSO-GSA (Second) |
|---|---|---|---|---|---|---|
| 20 process 8 memory | 180 | 20 | 7.08 | 6.58 | 37.09 | 17.66 |
| 30 process 8 memory | 280 | 40 | 7.28 | 8.16 | 37.61 | 16.92 |
| 40 process 8 memory | 350 | 60 | 19.52 | 125.4 | 80.28 | 54.13 |
| 50 process 8 memory | 450 | 80 | 40.95 | Out of Memory | ||
| Shopping Dimension | Depth Limit | Population | FAPSO (Second) | GA (Second) | PSO (Second) | PSO-GSA (Second) |
|---|---|---|---|---|---|---|
| 10 customer 30 good | 160 | 20 | 2.45 | 2.01 | 3.89 | 4.14 |
| 15 customer 30 good | 170 | 30 | 10.53 | 32.74 | 34.5 | 27.62 |
| 20 customer 30 good | 180 | 40 | 33.58 | Out of Memory | ||
| N-Queen Dimension | Depth Limit | Population | FAPSO (Second) | GA (Second) | PSO (Second) | PSO-GSA (Second) |
|---|---|---|---|---|---|---|
| 8 × 8 | 100 | 20 | 3.0 7 | 1.45 | 6.83 | 2.17 |
| 16 × 16 | 120 | 30 | 24.17 | Out of Memory | ||
| Initial Arrangement | Depth Limit | Population | FAPSO (Second) | GA (Second) | PSO (Second) | PSO-GSA (Second) |
|---|---|---|---|---|---|---|
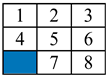 | 100 | 40 | 2.77 | 1.79 | 11.37 | 12.45 |
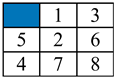 | 100 | 50 | 6.57 | 5.91 | 47.13 | 61.9 |
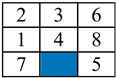 | 100 | 60 | 34.93 | 26.3 | 126.03 | 276.35 |
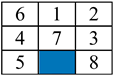 | 100 | 70 | 102.5 | 116.51 | 209.23 | 380.52 |
| Approaches |
8-Puzzle (Second) |
N-Queen (Second) |
Dining Philosophers (Second) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
 |  |  |  | 8 | 12 | 16 | 40 | 70 | 90 | |
| FAPSO | 2.77 | 6.57 | 34.93 | 102.5 | 3.07 | 12.54 | 24.17 | 55.23 | 97.18 | 131.11 |
| DDQN * | 1.98 | 6.04 | 33.9 | 836.45 | 21.54 | 34.33 | 87.85 | 2.09 | 4.07 | 8.27 |
| DDQN | 2.32 | 5.65 | 195.6 | 1759.55 | 40.78 | 242.57 | 522.58 | 12.04 | 75.46 | 265.23 |
| Number of Philosophers | Depth Limit | Population | Basic Model | Modified Model | ||
|---|---|---|---|---|---|---|
| FAPSO (Second) | PSO (Second) | FAPSO (Second) | PSO (Second) | |||
| 10 | 50 | 15 | 2.81 | 8.12 | 1.77 | 7.05 |
| 20 | 100 | 20 | 29.2 | 85 | 11.93 | 18.62 |
| 30 | 200 | 60 | 49.86 | 137 | 15.18 | 37.87 |
| 40 | 200 | 60 | Out of Memory | 66.4 | 304.1 | |
| 60 | 200 | 60 | Out of Memory | 98.6 | 389.6 | |
| Number of Philosophers | Depth Limit | Population | Basic Model | Modified Model | ||
|---|---|---|---|---|---|---|
| FAPSO | PSO | FAPSO | PSO | |||
| 10 | 50 | 15 | 1124 | 3212 | 64 | 95 |
| 20 | 100 | 20 | 5080 | 7730 | 273 | 531 |
| 30 | 200 | 60 | 5766 | 8450 | 465 | 850 |
| 40 | 200 | 60 | Out of Memory | 972 | 2422 | |
| 60 | 220 | 60 | Out of Memory | 6177 | 11,046 | |
| Shopping Dimension | Depth Limit | Population | Basic Model | Modified Model | ||
|---|---|---|---|---|---|---|
| FAPSO (Second) | PSO (Second) | FAPSO (Second) | PSO (Second) | |||
| 10 customer 30 good | 160 | 20 | 2.45 | 3.89 | 0.98 | 2.5 |
| 15 customer 30 good | 170 | 30 | 10.53 | 34.5 | 2.16 | 8.41 |
| 20 customer 30 good | 180 | 40 | 33.58 | Out of Memory | 2.82 | 12.58 |
| 25 customer 30 good | 180 | 50 | Out of Memory | 3.24 | 13.16 | |
| 30 customer 30 good | 180 | 50 | Out of Memory | 5.61 | 14.3 | |
| Shopping Dimension | Depth Limit | Population | Basic Model | Modified Model | ||
|---|---|---|---|---|---|---|
| FAPSO | PSO | FAPSO | PSO | |||
| 10 customer 30 good | 150 | 20 | 243 | 287 | 133 | 142 |
| 15 customer 30 good | 160 | 30 | 482 | 603 | 131 | 151 |
| 20 customer 30 good | 170 | 40 | 765 | Out of Memory | 155 | 161 |
| 25 customer 30 good | 180 | 50 | Out of Memory | 152 | 158 | |
| 30 customer 30 good | 180 | 50 | Out of Memory | 167 | 164 | |
| Approach Problem | Depth Limit | Population | FAPSO (Second) | BOA (Second) | GA (Second) | PSO (Second) | PSO-GSA (Second) | BFA (Second) | BS (Second) |
|---|---|---|---|---|---|---|---|---|---|
| dining philosophers (10 philosophers) | 25 | 15 | 4.41 | 0.71 ± 0.15 | 10.12 | 13.45 | 38.92 | 0.94 | 3.85 |
| dining philosophers (20 philosophers) | 100 | 20 | 29.2 | 1.04 ± 0.15 | 23 | 158 | 170 | 1.9 | 4.12 |
| process life cycle (40-process-8-memory) | 350 | 60 | 19.52 | 1.44 ± 0.8 | Not found | Not found | 939.45 | Not found | Not found |
| process life cycle (50-process-8-memory) | 450 | 80 | 40.95 | 1.81 ± 0.39 | Not found | Not found | Not found | Not found | Not found |
| 8-puzzle (Second argument) | 100 | 50 | 6.57 | 1.15 ± 0.33 | 35.81 | 94.72 | 16.7 | 0.16 | 1.33 |
| 8-puzzle (Third argument) | 100 | 60 | 34.93 | Not found | 165 | 165.51 | 147.7 | 3.5 | 2.33 |
| Approaches | FAPSO-GA | FAPSO-PSO | FAPSO-BFA | FAPSO-BS | FAPSO-A * | FAPSO-DDQN |
| Z Asymp. Sig. (2-tailed) | 0.001 | 0.001 | 0.03 | 0.007 | 0.03 | 0.042 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salimi, N.; Soleimani, S.; Rafe, V.; Khodadad, D. A Hybrid Approach for Reachability Analysis of Complex Software Systems Using Fuzzy Adaptive Particle Swarm Optimization Algorithm and Rule Composition. Math. Comput. Appl. 2025, 30, 65. https://doi.org/10.3390/mca30030065
Salimi N, Soleimani S, Rafe V, Khodadad D. A Hybrid Approach for Reachability Analysis of Complex Software Systems Using Fuzzy Adaptive Particle Swarm Optimization Algorithm and Rule Composition. Mathematical and Computational Applications. 2025; 30(3):65. https://doi.org/10.3390/mca30030065
Chicago/Turabian StyleSalimi, Nahid, Seyfollah Soleimani, Vahid Rafe, and Davood Khodadad. 2025. "A Hybrid Approach for Reachability Analysis of Complex Software Systems Using Fuzzy Adaptive Particle Swarm Optimization Algorithm and Rule Composition" Mathematical and Computational Applications 30, no. 3: 65. https://doi.org/10.3390/mca30030065
APA StyleSalimi, N., Soleimani, S., Rafe, V., & Khodadad, D. (2025). A Hybrid Approach for Reachability Analysis of Complex Software Systems Using Fuzzy Adaptive Particle Swarm Optimization Algorithm and Rule Composition. Mathematical and Computational Applications, 30(3), 65. https://doi.org/10.3390/mca30030065








