Impact Loading on a Patient-Specific Head Model: The Significance of Brain Constitutive Models and Loading Location
Abstract
1. Introduction
2. Materials and Methods
2.1. Head Model Geometry
2.2. Model MPs
2.3. Interface and Boundary Conditions
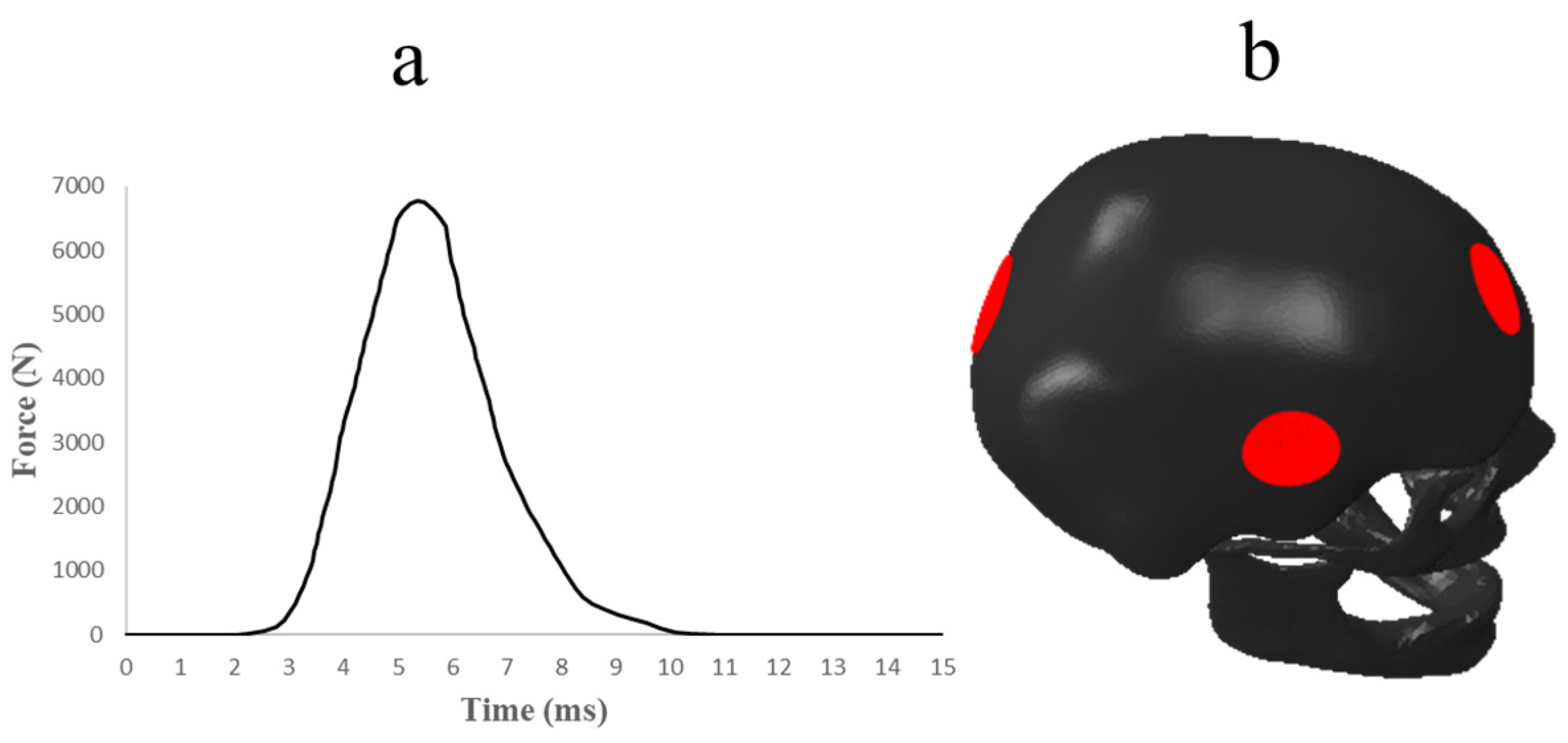
2.4. Loading Conditions
3. Results and Discussion
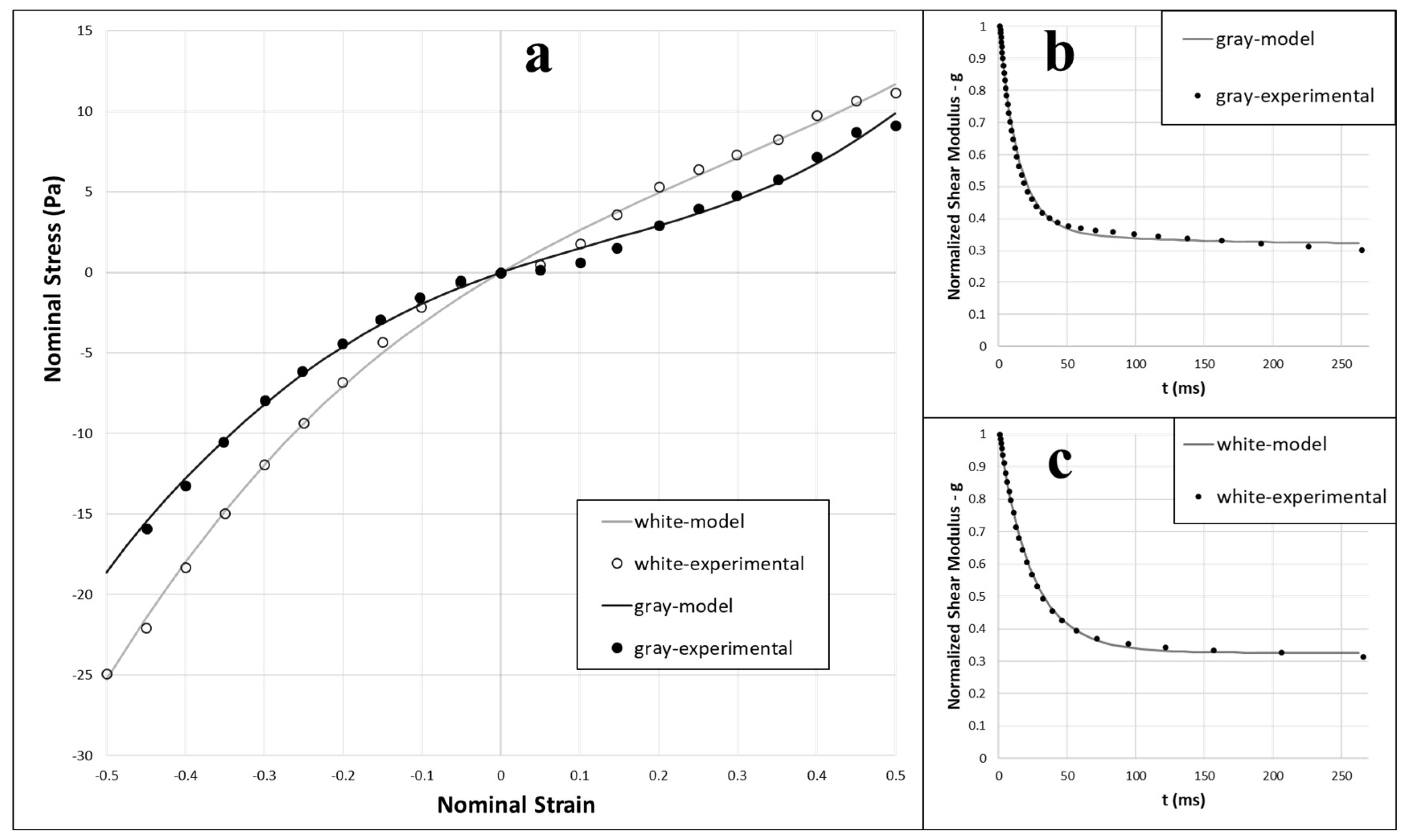
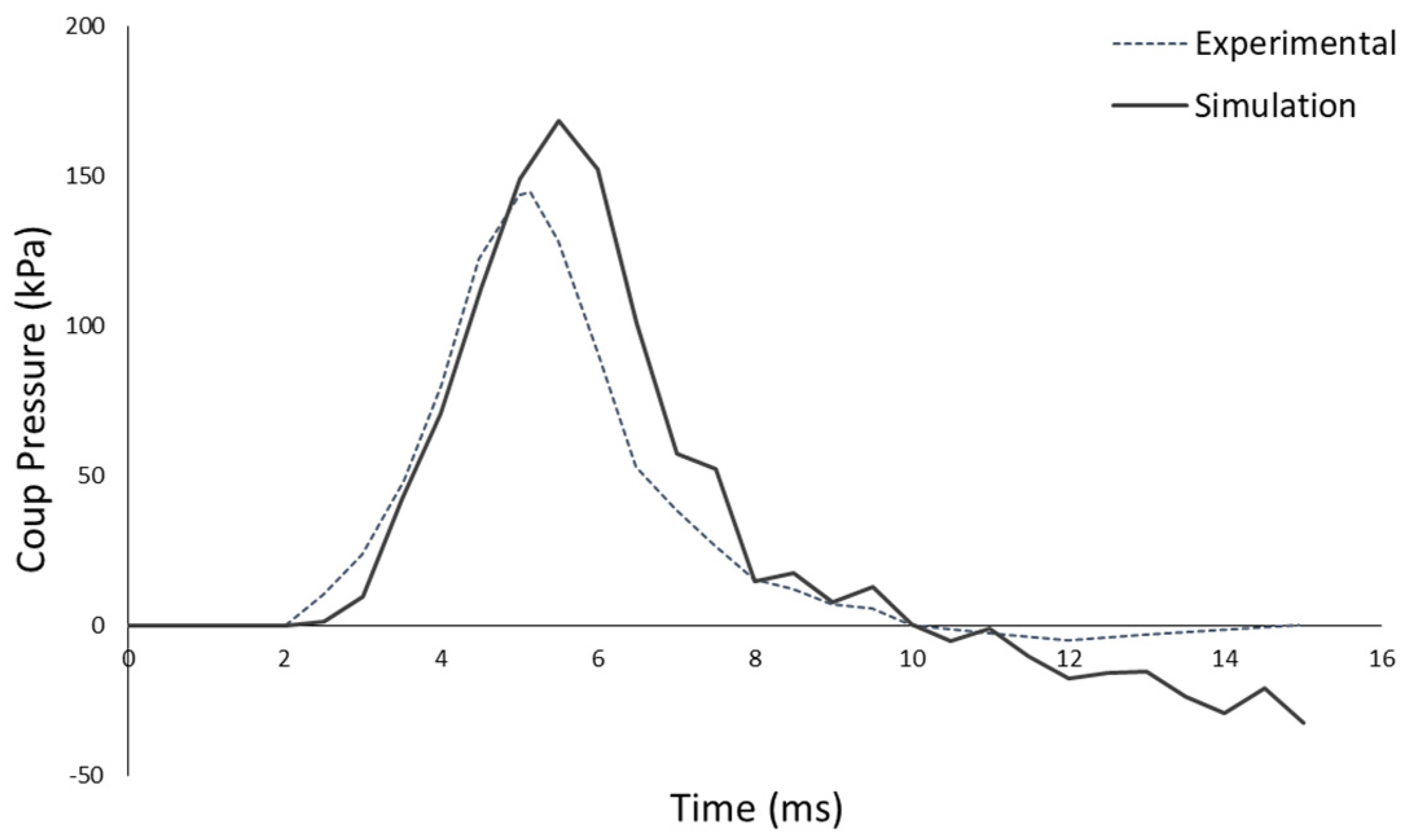
3.1. Model Verification
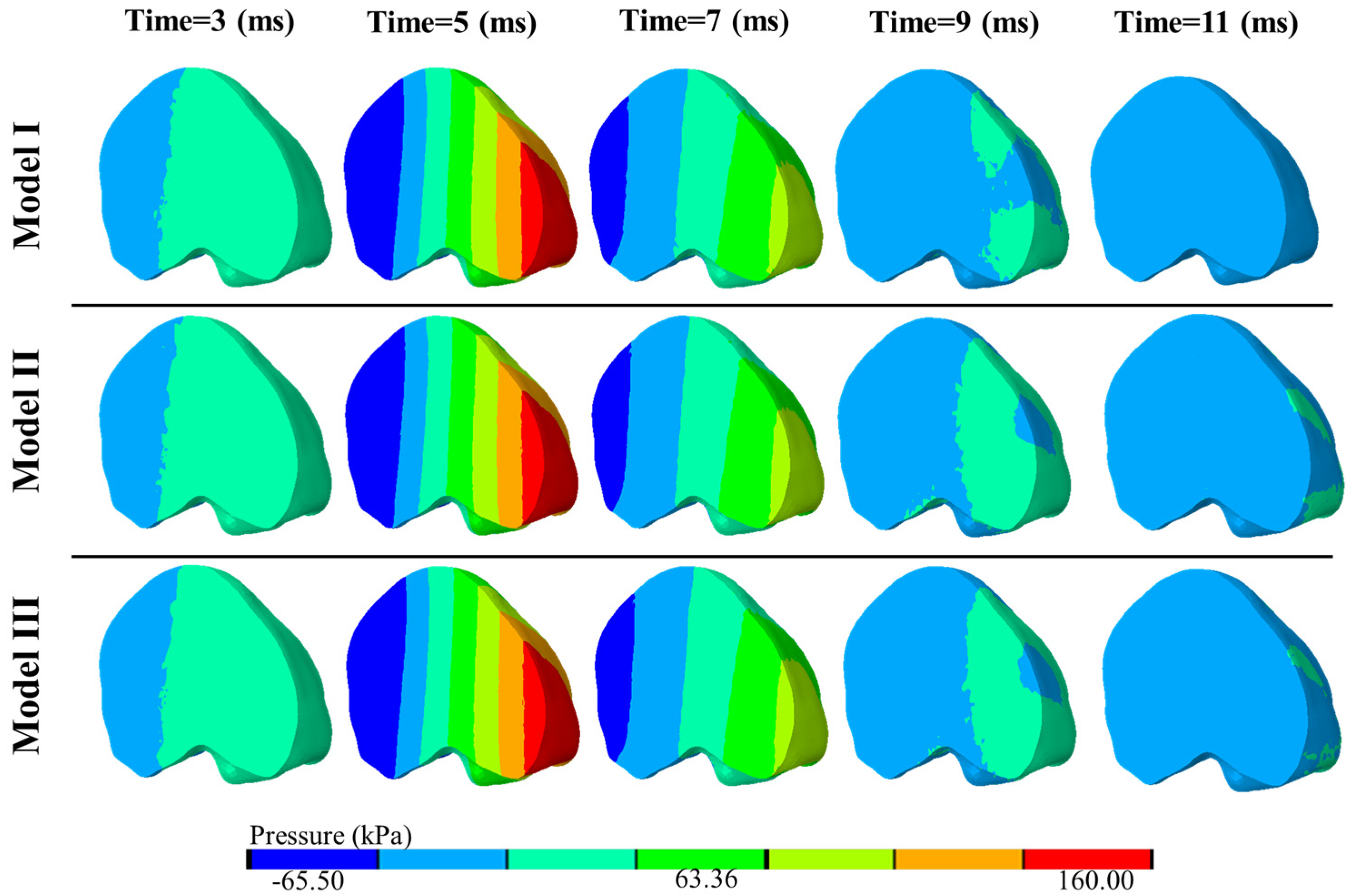
3.2. Significance of Brain MPs
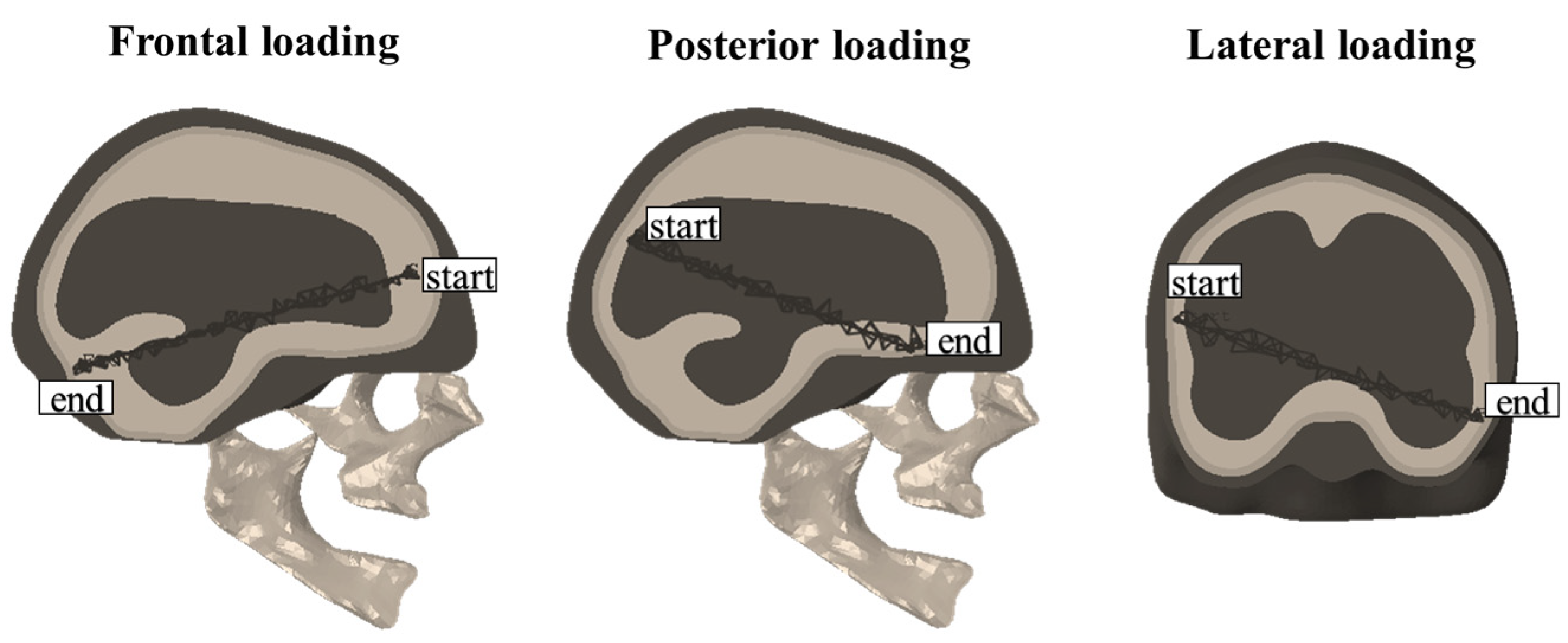
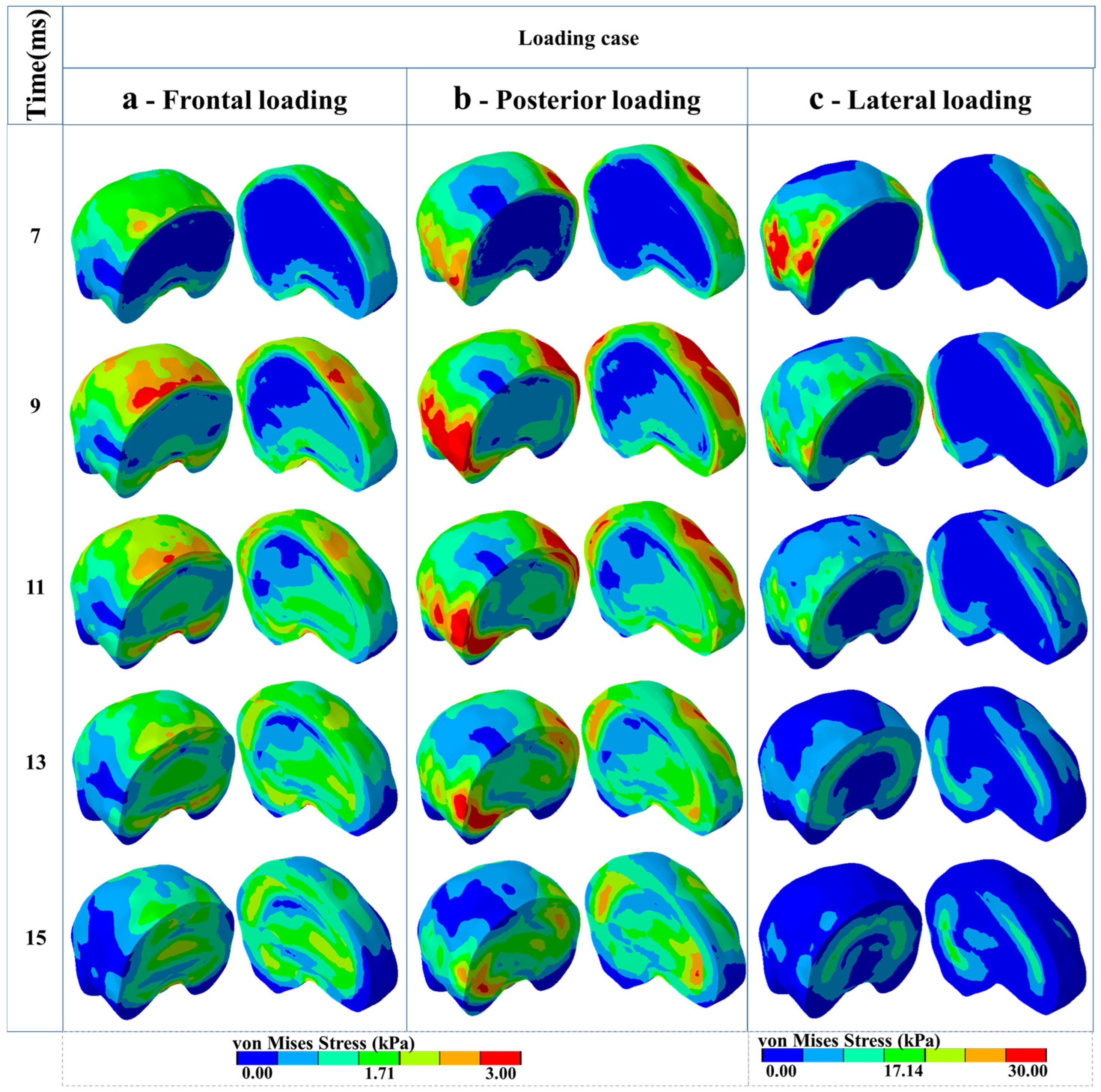
3.3. Effect of Loading Location
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nguyen, R.; Fiest, K.M.; McChesney, J.; Kwon, C.S.; Jette, N.; Frolkis, A.D.; Atta, C.; Mah, S.; Dhaliwal, H.; Reid, A.; et al. The international incidence of traumatic brain injury: A systematic review and meta-analysis. Can. J. Neurol. Sci. 2016, 43, 774–785. [Google Scholar] [CrossRef]
- Taylor, C.A.; Bell, J.M.; Breiding, M.J.; Xu, L. Traumatic brain injury–Related emergency department visits, hospitalizations, and deaths—United States, 2007 and 2013. MMWR Surveill. Summ. 2017, 66, 1–16. [Google Scholar] [CrossRef]
- Tse, K.M.; Lim, S.P.; Tan, V.B.C.; Lee, H.P. A Review of Head Injury and Finite Element Head Models. Am. J. Eng. Technol. Soc. 2015, 1, 28–52. [Google Scholar]
- Fernandes, F.A.O.; Alves de Sousa, R.J.; Ptak, M. Head Injury Simulation in Road Traffic Accidents; Springer International Publishing: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Fernandes, F.A.; Tchepel, D.; de Sousa, R.J.A.; Ptak, M. Development and validation of a new finite element human head model: Yet another head model (YEAHM). Eng. Comput. 2018, 35, 477–496. [Google Scholar] [CrossRef]
- Cinelli, I.; Destrade, M.; McHugh, P.; Trotta, A.; Gilchrist, M.; Duffy, M. Head-to-nerve analysis of electromechanical impairments of diffuse axonal injury. Biomech. Model. Mechanobiol. 2019, 18, 361–374. [Google Scholar] [CrossRef] [PubMed]
- Miller, K.; Chinzei, K. Constitutive modelling of brain tissue: Experiment and theory. J. Biomech. 1997, 30, 1115–1121. [Google Scholar] [CrossRef] [PubMed]
- Miller, K.; Chinzei, K. Mechanical properties of brain tissue in tension. J. Biomech. 2002, 35, 483–490. [Google Scholar] [CrossRef]
- Coats, B.; Margulies, S.S. Material properties of porcine parietal cortex. J. Biomech. 2006, 39, 2521–2525. [Google Scholar] [CrossRef] [PubMed]
- Franceschini, G.; Bigoni, D.; Regitnig, P.; Holzapfel, G. Brain tissue deforms similarly to filled elastomers and follows consolidation theory. J. Mech. Phys. Solids 2006, 54, 2592–2620. [Google Scholar] [CrossRef]
- Jin, X.; Zhu, F.; Mao, H.; Shen, M.; Yang, K.H. A comprehensive experimental study on material properties of human brain tissue. J. Biomech. 2013, 46, 2795–2801. [Google Scholar] [CrossRef]
- Finan, J.D.; Sundaresh, S.N.; Elkin, B.S.; McKhann, G.M.; Morrison, B. Regional mechanical properties of human brain tissue for computational models of traumatic brain injury. Acta Biomater. 2017, 55, 333–339. [Google Scholar] [CrossRef]
- Budday, S.; Sommer, G.; Birkl, C.; Langkammer, C.; Haybaeck, J.; Kohnert, J.; Bauer, M.; Paulsen, F.; Steinmann, P.; Kuhl, E.; et al. Mechanical characterization of human brain tissue. Acta Biomater. 2017, 48, 319–340. [Google Scholar] [CrossRef] [PubMed]
- Budday, S.; Sommer, G.; Haybaeck, J.; Steinmann, P.; Holzapfel, G.; Kuhl, E. Rheological characterization of human brain tissue. Acta Biomater. 2017, 60, 315–329. [Google Scholar] [CrossRef] [PubMed]
- Murphy, M.C.; Huston, J.; Ehman, R.L. MR elastography of the brain and its application in neurological diseases. NeuroImage 2019, 187, 176–183. [Google Scholar] [CrossRef] [PubMed]
- Arani, A.; Manduca, A.; Ehman, R.L.; Huston, J. Harnessing brain waves: A review of brain magnetic resonance elastography for clinicians and scientists entering the field. Br. J. Radiol. 2021, 94, 20200265. [Google Scholar] [CrossRef]
- Ueno, K.; Melvin, J.W.; Li, L.; Lighthall, J.W. Development of Tissue Level Brain Injury Criteria by Finite Element Analysis. J. Neurotrauma 2009, 12, 695–706. [Google Scholar] [CrossRef]
- Miller, K.; Chinzei, K.; Orssengo, G.; Bednarz, P. Mechanical properties of brain tissue in-vivo: Experiment and computer simulation. J. Biomech. 2000, 33, 1369–1376. [Google Scholar] [CrossRef]
- Claessans, M.; Sauren, F.; Wismans, J. Modeling of the human head under impact conditions: A parametric study. In Stapp Car Crash; SAE International: Warrendale, PA, USA, 1997; pp. 315–328. [Google Scholar]
- Tse, K.M.; Bin Tan, L.; Lee, S.J.; Lim, S.P.; Lee, H.P. Development and validation of two subject-specific finite element models of human head against three cadaveric experiments. Int. J. Numer. Methods Biomed. Eng. 2014, 30, 397–415. [Google Scholar] [CrossRef]
- Yang, B.; Tse, K.-M.; Chen, N.; Tan, L.-B.; Zheng, Q.-Q.; Yang, H.-M.; Hu, M.; Pan, G.; Lee, H.-P. Development of a finite element head model for the study of impact head injury. BioMed Res. Int. 2014, 2014, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Gonzalez, D.; Jayamohan, J.; Sotiropoulos, S.; Yoon, S.-H.; Cook, J.; Siviour, C.; Arias, A.; Jérusalem, A. On the mechanical behaviour of PEEK and HA cranial implants under impact loading. J. Mech. Behav. Biomed. Mater. 2017, 69, 342–354. [Google Scholar] [CrossRef]
- Schroder, A.; Lawrence, T.; Voets, N.; Garcia-Gonzalez, D.; Jones, M.; Peña, J.M.; Jerusalem, A. A Machine Learning Enhanced Mechanistic Simulation Framework for Functional Deficit Prediction in TBI. Front. Bioeng. Biotechnol. 2021, 9, 587082. [Google Scholar] [CrossRef]
- Ruan, J.S.; Khalil, T.; King, A.I. Dynamic response of the human head to impact by three-dimensional finite element analysis. J. Biomech. Eng. 1994, 116, 44–50. [Google Scholar] [CrossRef]
- Zhou, C.; Khalil, T.B.; King, A.I. A New Model Comparing Impact Responses of the Homogeneous and Inhomogeneous Human Brain; SAE transactions: Warrendale, PA, USA, 1995; pp. 121–137. [Google Scholar]
- Garcia-Gonzalez, D.; Race, N.S.; Voets, N.L.; Jenkins, D.R.; Sotiropoulos, S.N.; Acosta, G.; Cruz-Haces, M.; Tang, J.; Shi, R.; Jérusalem, A. Cognition based bTBI mechanistic criteria; a tool for preventive and therapeutic innovations. Sci. Rep. 2018, 8, 1–14. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, K.H.; Dwarampudi, R.; Omori, K.; Li, T.; Chang, K.; Hardy, W.N.; Khalil, T.B.; King, A.I. Recent Advances in Brain Injury Research: A New Human Head Model Development and Validation. SAE Tech. Pap. 2001. [Google Scholar] [CrossRef]
- Tzschätzsch, H.; Kreft, B.; Schrank, F.; Bergs, J.; Braun, J.; Sack, I. In vivo time-harmonic ultrasound elastography of the human brain detects acute cerebral stiffness changes induced by intracranial pressure variations. Sci. Rep. 2018, 8, 17888. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Ostoja-Starzewski, M. MRI-based finite element modeling of head trauma: Spherically focusing shear waves. Acta Mech. 2010, 213, 155–167. [Google Scholar] [CrossRef]
- Gomez-Cruz, C.; la Torre, M.F.; Lachowski, D.; Prados-De-Haro, M.; Hernández, A.E.d.R.; Perea, G.; Muñoz-Barrutia, A.; Garcia-Gonzalez, D. Mechanical and Functional Responses in Astrocytes under Alternating Deformation Modes Using Magneto-Active Substrates. Adv. Mater. 2024, 36, 2312497. [Google Scholar] [CrossRef] [PubMed]
- Deng, X.; Du, Z.; Feng, H.; Wang, S.; Luo, H.; Liu, Y. Investigation on the Modeling and Reconstruction of Head Injury Accident Using ABAQUS/Explicit. Bioengineering 2022, 9, 723. [Google Scholar] [CrossRef]
- Abdi, H.; Sánchez-Molina, D.; García-Vilana, S.; Rahimi-Movaghar, V. Revealing the role of material properties in impact-related injuries: Investigating the influence of brain and skull density variations on head injury severity. Heliyon 2024, 10, e29427. [Google Scholar] [CrossRef] [PubMed]
- Kleiven, S. Predictors for traumatic brain injuries evaluated through accident reconstructions. Stapp Car Crash J. 2007, 51, 81–114. [Google Scholar] [CrossRef]
- Subramaniam, D.R.; Unnikrishnan, G.; Sundaramurthy, A.; Rubio, J.E.; Kote, V.B.; Reifman, J. Cerebral Vasculature Influences Blast-Induced Biomechanical Responses of Human Brain Tissue. Front. Bioeng. Biotechnol. 2021, 9, 744808. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Zhou, Z.; Kleiven, S. An anatomically detailed and personalizable head injury model: Significance of brain and white matter tract morphological variability on strain. Biomech. Model. Mechanobiol. 2021, 20, 403–431. [Google Scholar] [CrossRef] [PubMed]
- Franceschini, G. The Mechanics of Human Brain Tissue; The University of Trento: Trento, Italy, 2006. [Google Scholar]
- Li, X.; Sandler, H.; Kleiven, S. The importance of nonlinear tissue modelling in finite element simulations of infant head impacts. Biomech. Model. Mechanobiol. 2017, 16, 823–840. [Google Scholar] [CrossRef] [PubMed]
- Elkin, B.S.; Gabler, L.F.; Panzer, M.B.; Siegmund, G.P. Brain tissue strains vary with head impact location: A possible explanation for increased concussion risk in struck versus striking football players. Clin. Biomech. 2019, 64, 49–57. [Google Scholar] [CrossRef] [PubMed]
- Giudice, J.S.; Park, G.; Kong, K.; Bailey, A.; Kent, R.; Panzer, M.B. Development of Open-Source Dummy and Impactor Models for the Assessment of American Football Helmet Finite Element Models. Ann. Biomed. Eng. 2018, 47, 464–474. [Google Scholar] [CrossRef] [PubMed]
- Takhounts, E.G.; Ridella, S.A.; Hasija, V.; Tannous, R.E.; Campbell, J.Q.; Malone, D.; Danelson, K.; Stitzel, J.; Rowson, S.; Duma, S. Investigation of traumatic brain injuries using the next generation of simulated injury monitor (SIMon) finite element head model. Stapp Car Crash J. 2008, 52, 1–31. [Google Scholar] [CrossRef] [PubMed]
- Takhounts, E.G.; Eppinger, R.H.; Campbell, J.Q.; Tannous, R.E.; Power, E.D.; Shook, L.S. On the Development of the SIMon Finite Element Head Model; SAE Tech Pap 2003-Octob; SAE: Warrendale, PA, USA, 2003. [Google Scholar] [CrossRef]
- Ruan, J.S.; Khalil, T.B.; King, A.I. Finite element modeling of direct head impact. In Proceedings of the Stapp Car Crash Conference, Warrendale, PA, USA, 1 November 1993. [Google Scholar]
- Lüsebrink, F.; Sciarra, A.; Mattern, H.; Yakupov, R.; Speck, O. T1-weighted in vivo human whole brain MRI dataset with an ultrahigh isotropic resolution of 250 μm. Sci. Data 2017, 4, 170062. [Google Scholar] [CrossRef] [PubMed]
- Viano, D.C.; Casson, I.R.; Pellman, E.J.; Zhang, L.; King, A.I.; Yang, K.H. Concussion in professional football: Brain responses by finite element analysis: Part 9. Neurosurgery 2005, 57, 891–916. [Google Scholar] [CrossRef] [PubMed]
- Yoganandan, N.; Pintar, F.A.; Zhang, J.; Baisden, J.L. Physical properties of the human head: Mass, center of gravity and moment of inertia. J. Biomech. 2009, 42, 1177–1192. [Google Scholar] [CrossRef] [PubMed]
- Mao, H.; Gao, H.; Cao, L.; Genthikatti, V.V.; Yang, K.H. Development of high-quality hexahedral human brain meshes using feature-based multi-block approach. Comput. Methods Biomech. Biomed. Eng. 2013, 16, 271–279. [Google Scholar] [CrossRef]
- Belingardi, G.; Chiandussi, G.; Gaviglio, I. Development and validation of a new finite element model of human head. In Proceedings of the 19th International Technical Conference of the Enhanced Safety of Vehicle (ESV), Washington, DC, USA, 6–9 June 2005. [Google Scholar]
- Mihai, L.A.; Chin, L.; Janmey, P.A.; Goriely, A. A comparison of hyperelastic constitutive models applicable to brain and fat tissues. J. R. Soc. Interface 2015, 12, 20150486. [Google Scholar] [CrossRef] [PubMed]
- Taghizadeh, H.; Tafazzoli-Shadpour, M.; Shadmehr, M.B.; Fatouraee, N. Evaluation of biaxial mechanical properties of aortic media based on the lamellar microstructure. Materials 2015, 8, 302–316. [Google Scholar] [CrossRef]
- Nahum, A.M.; Smith, R.; Ward, C.C. Intracranial pressure dynamics during head impact. In Proceedings of the Stapp Car Crash Conference Proceedings, New Orleans, LO, USA, 19–21 October 1977. [Google Scholar]
- Abdi, H.; Sanchez-Molina, D.; Garcia-Vilana, S.; Rahimi-Movaghar, V. Quantifying the effect of cerebral atrophy on head injury risk in elderly individuals: Insights from computational biomechanics and experimental analysis of bridging veins. Injury 2023, 54, 111125. [Google Scholar] [CrossRef] [PubMed]
- Martin, G. Traumatic brain injury: The first 15 milliseconds. Brain Inj. 2016, 30, 1517–1524. [Google Scholar] [CrossRef] [PubMed]



| Mass (kg) | COG Coordinates (cm) | IXX (kg.cm2) | IYY (kg.cm2) | IZZ (kg.cm2) | |||
|---|---|---|---|---|---|---|---|
| X | Y | Z | |||||
| Head Model | 3.92 | 1.4 | −0.2 | 3.4 | 159 | 230 | 129 |
| Experimental Measurement [45] | 3.88 ± 0.47 | 1.3 ± 0.28 | −0.1 ± 0.13 | 2.5 ± 1.08 | 174.9 ± 45.2 | 219.3 ± 50.8 | 159 ± 25.7 |
| Model Components | Elastic Modulus (MPa) | Poisson’s Ratio | Density (kg/m3) | References |
|---|---|---|---|---|
| Skull | 10,000 | 0.21 | 1800 | [46,47] |
| CSF | 1.314 | 0.4999 | 1040 | [20] |
| Model Type | Brain Component | Ogden Material Parameters | Viscoelastic Parameters in Prony Series | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| μ1 (Pa) | α1 (-) | μ2 (Pa) | α2 (-) | μ3 (Pa) | α3 (-) | μ4 (Pa) | α4 (-) | g1 (-) | τ1 (ms) | g2 (-) | τ2 (ms) | g3 (-) | τ3 (ms) | ||
| Model I (hyperelastic) | Gray matter | −5877 | 2 | 5043 | −2 | 2322 | 4 | −1002 | −4 | - | - | - | - | - | - |
| White matter | |||||||||||||||
| Model II (hyperelastic) | Gray matter | 45,670 | 1 | −55,270 | 3 | 22,150 | 5 | −6976 | −2 | - | - | - | - | - | - |
| White matter | 22,860 | 1 | −15,790 | 3 | 7356 | 5 | −4928 | −2 | - | - | - | - | - | - | |
| Model III (hyper-viscoelastic) | Gray matter | 45,670 | 1 | −55,270 | 3 | 22,150 | 5 | −6976 | −2 | 0.1091 | 10 | 0.5237 | 15 | 0.0474 | 100 |
| White matter | 22,860 | 1 | −15,790 | 3 | 7356 | 5 | −4928 | −2 | 0.0578 | 15 | 0.6116 | 25 | 0.0082 | 250 | |
| Load Case | Frontal | Posterior | Lateral |
|---|---|---|---|
| Maximum brain pressure (kPa) | 159.4 | 178.8 | 467.9 |
| Maximum von Mises stress of midbrain (kPa) | 1.9 | 2.2 | 7.7 |
| Maximum nominal strain of midbrain | 0.078 | 0.089 | 0.284 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gandomirouzbahani, A.; Taghizadeh, H.; Oskui, I.Z.; Fernandes, F.A.O. Impact Loading on a Patient-Specific Head Model: The Significance of Brain Constitutive Models and Loading Location. Math. Comput. Appl. 2025, 30, 21. https://doi.org/10.3390/mca30020021
Gandomirouzbahani A, Taghizadeh H, Oskui IZ, Fernandes FAO. Impact Loading on a Patient-Specific Head Model: The Significance of Brain Constitutive Models and Loading Location. Mathematical and Computational Applications. 2025; 30(2):21. https://doi.org/10.3390/mca30020021
Chicago/Turabian StyleGandomirouzbahani, Amirhossein, Hadi Taghizadeh, Iman Z. Oskui, and Fábio A. O. Fernandes. 2025. "Impact Loading on a Patient-Specific Head Model: The Significance of Brain Constitutive Models and Loading Location" Mathematical and Computational Applications 30, no. 2: 21. https://doi.org/10.3390/mca30020021
APA StyleGandomirouzbahani, A., Taghizadeh, H., Oskui, I. Z., & Fernandes, F. A. O. (2025). Impact Loading on a Patient-Specific Head Model: The Significance of Brain Constitutive Models and Loading Location. Mathematical and Computational Applications, 30(2), 21. https://doi.org/10.3390/mca30020021







