Advanced Hybrid Brain Tumor Segmentation in MRI: Elephant Herding Optimization Combined with Entropy-Guided Fuzzy Clustering

Abstract

Accurate and early detection of brain tumors is essential for improving clinical outcomes and guiding effective treatment planning. Traditional segmentation techniques in MRI often struggle with challenges such as noise, intensity variations, and complex tumor morphologies, which can hinder their effectiveness in critical healthcare scenarios. This study proposes an innovative hybrid methodology that integrates advanced metaheuristic optimization and entropy-based fuzzy clustering to enhance segmentation precision in brain tumor detection. This method combines the nature-inspired Elephant Herding Optimization (EHO) algorithm with Entropy-Driven Fuzzy C-Means (EnFCM) clustering, offering significant improvements over conventional methods. EHO is utilized to optimize the clustering process, enhancing the algorithm’s ability to delineate tumor boundaries, while entropy-based fuzzy clustering accounts for intensity inhomogeneity and diverse tumor characteristics, promoting more consistent and reliable segmentation results. This approach was evaluated using the BraTS challenge dataset, a benchmark in the field of brain tumor segmentation. The results demonstrate marked improvements across several performance metrics, including Dice similarity, mean squared error (MSE), peak signal-to-noise ratio (PSNR), and the Tanimoto coefficient (TC), underscoring this method’s robustness and segmentation accuracy. By managing image noise and reducing computational demands, the EHO-EnFCM approach not only captures intricate tumor structures but also facilitates efficient image processing, making it suitable for real-time clinical applications. Overall, the findings reveal the potential of this hybrid approach to advance MRI-based tumor detection, offering a promising tool that enhances both accuracy and computational efficiency for medical imaging and diagnosis.

1. Introduction

Brain tumors, characterized by abnormal cell proliferation that forms masses, pose a significant health challenge. These tumors may be benign, in which case, although non-cancerous, they can still disrupt nearby tissues due to increased pressure, or malignant, being cancerous and capable of invading adjacent structures, with the potential for metastasis [1,2]. The prevalence of brain tumors varies across age groups, with a higher incidence among individuals over 65. For example, in India, approximately 30,000 new brain tumor cases are reported annually, inflicting significant emotional and financial strain on affected families [3]. Although brain tumors constitute a smaller percentage of cancer cases, their impact is profound, necessitating accurate diagnostic tools and effective treatments [4]. Symptoms often include persistent headaches, seizures, and cognitive or sensory impairments, emphasizing the importance of early medical evaluation to ensure accurate diagnosis. The etiology remains unclear, though factors like aging, radiation exposure, immune suppression, environmental influences, and prolonged cell phone use may be contributary [5]. Advanced diagnostic modalities, including CT, MRI, and biopsies, play crucial roles in tumor detection. Notably, MRI stands out as a non-invasive imaging method that leverages magnetic fields and radio waves to produce highly detailed soft-tissue images, making it an indispensable tool for assessing brain tumors [6,7,8,9]. Furthermore, emerging technologies, particularly machine learning and deep learning, show promise in enhancing early detection and improving diagnostic accuracy, highlighting their potential for transformative advancements in patient care.

1.1. Current Research and Challenges

Brain tumor segmentation in medical imaging is an essential step for accurate diagnosis, treatment planning, and follow-up monitoring. The challenge of segmenting brain tumors is exacerbated by several issues, such as noise, intensity inhomogeneity, and tumor heterogeneity. These issues create significant challenges in differentiating tumor regions from healthy tissue in MRI images. In many cases, the tumor boundaries are not clearly visible due to overlapping intensity distributions and the presence of other anatomical structures. Consequently, improving segmentation methods for more accurate tumor delineation has become a key research focus [10]. Fuzzy C-Means (FCM) clustering is a widely used technique for image segmentation, including for brain tumor images. FCM improves upon traditional k-means clustering by allowing overlapping membership between clusters, which is essential in medical images where regions such as tumors and surrounding tissues often overlap. FCM has been widely used in image processing due to its ability to handle uncertainty and overlap between different regions [11]. However, this technique still faces challenges, including the need for a predefined number of clusters, high computational costs, and sensitivity to initialization parameters. This method’s reliance on fixed membership functions can also limit its flexibility when handling complex, noisy datasets [12].

To address these limitations, entropy-based fuzzy clustering (EnFCM) was introduced. EnFCM improves clustering by dynamically determining the most appropriate cluster centers based on entropy measures, thus addressing issues related to noise and overlapping regions. By assigning data points with lower entropy values as cluster centers, EnFCM ensures that the clusters formed are cohesive and less sensitive to outliers. This entropy-based approach has demonstrated superior performance in the presence of noise and partial volume effects, particularly in complex medical images such as MRI scans [13,14]. In the realm of medical image segmentation, optimization algorithms play a vital role in refining the clustering process. Many metaheuristic algorithms, including the Elephant Herding Optimization (EHO) algorithm, have shown promising results in this field. The EHO algorithm, inspired by the social behaviors of elephant herds, effectively explores the solution space by employing clan updating and separation mechanisms. This makes EHO particularly useful for solving complex, nonlinear optimization problems inherent in medical image segmentation, where traditional methods often fail [15].

While there are other metaheuristic algorithms such as Genetic Algorithms, Particle Swarm Optimization, and Differential Evolution, EHO was chosen due to its superior ability to balance exploration and exploitation. It effectively finds optimal solutions in complex and high-dimensional spaces, which are typical in medical image segmentation tasks. Furthermore, EHO’s design minimizes the risk of becoming trapped in local minima, which is a common problem in many optimization techniques [16].

1.2. Proposed Solution

This research presents a hybrid approach that integrates the EnFCM clustering algorithm with the EHO optimization algorithm for enhanced segmentation of brain tumors in MRI scans. The combination of these two algorithms addresses the key challenges in medical image segmentation, including noise reduction, handling intensity inhomogeneity, and dealing with overlapping tumor regions. The EnFCM algorithm’s ability to adapt to the complexities of medical images, coupled with EHO’s ability to optimize cluster centers, makes this hybrid approach more robust and accurate than traditional methods [17,18]. The motivation behind selecting this specific hybrid metaheuristic approach lies in the complementary strengths of EnFCM and EHO. While EnFCM excels in handling uncertainty and overlapping regions in data, EHO effectively refines the cluster centers by optimizing the segmentation process. This synergy allows for a more precise and accurate delineation of tumor and non-tumor regions, thereby improving the overall quality of brain tumor segmentation. Previous studies have demonstrated the effectiveness of hybrid approaches, but our focus is on leveraging the specific advantages of EnFCM and EHO for medical image applications, where the challenges of noise, intensity variation, and heterogeneity are particularly pronounced [19].

Additionally, several other hybrid metaheuristic algorithms have been explored in the literature for solving medical image segmentation problems. For instance, hybrid Genetic Algorithms (GAs) and Particle Swarm Optimization (PSO) have been applied in medical imaging with some success. However, these methods often struggle with local optima and slow convergence, especially in high-dimensional optimization spaces. Differing from these approaches, the EHO-based method is designed to avoid such pitfalls and offers faster convergence and better overall performance, making it more suitable for complex brain tumor segmentation tasks. Our approach was evaluated using the BraTS challenge dataset, which is widely regarded as a benchmark for brain tumor segmentation. In preliminary tests, the proposed hybrid method outperformed several other metaheuristic-based segmentation algorithms in terms of segmentation accuracy and robustness. Specifically, when compared to traditional methods like FCM and other hybrid approaches like GA-PSO, the EnFCM-EHO hybrid demonstrated superior performance in handling the noisy and heterogeneous nature of MRI scans [20].

The key contributions of integrating EHO and Entropy-driven FCM for brain tumor segmentation are listed below.

• Enhanced initialization: EHO solves the prevalent problem of inadequate initialization in traditional FCM algorithms by optimally initializing the cluster centers for the FCM process.
• Improved convergence: speedy and more consistent convergence is guaranteed by the combination method, which cuts down on computing time without sacrificing segmentation accuracy.
• Scalability and robustness: the hybrid approach is appropriate for use in clinical settings since it can manage big, high-dimensional MRI datasets with ease.
• Superior segmentation accuracy: High-quality segmentation results can be achieved by combining the precision of entropy-driven FCM with the optimization of EHO, both of which are essential for accurate tumor analysis and identification.

In conclusion, the hybrid EnFCM-EHO approach addresses the limitations of previous methods by combining the strengths of both clustering and optimization algorithms. The proposed method not only improves segmentation accuracy but also offers a more robust solution that can be applied to a variety of medical imaging problems. Future work will explore the use of other hybrid metaheuristics and evaluate the proposed approach in clinical settings to further assess its practical applicability.

2. Related Works

This Section reviews recent advancements in brain tumor segmentation using clustering and optimization techniques, focusing on their methodologies, results, benefits, and limitations.

In recent years, researchers have investigated numerous clustering and optimization techniques aimed at improving brain tumor segmentation accuracy. For instance, Malathi and Sinthia [21] developed a convolutional neural network (CNN)-based methodology that leverages high-resolution glioma images from the BraTS 2015 dataset for automated tumor segmentation. Their model, implemented with TensorFlow and Anaconda frameworks, brought about notable improvements in tumor identification and classification. Balaha and Hassan [22] proposed a segmentation and classification method employing the Sparrow Search Algorithm (SpaSA) and UNet models, achieving 99.19% accuracy across datasets with varying classes. Their method demonstrated effective discriminative learning and optimization, highlighting its advantages in automatic tumor segmentation. Kurdi et al. [23] addressed edge feature preservation using the Harris Hawks optimized convolutional neural network (HHOCNN), achieving 98% tumor identification accuracy on Kaggle datasets. Their candidate region approach enhanced edge detection robustness, significantly reducing misclassification error rates. Zheng et al. [24] used Zernike moments and support vector machine (SVM)-based classification for brain tumor segmentation, demonstrating high effectiveness on the Figshare dataset. Their approach optimized segmentation accuracy through modified arithmetic operations, showcasing significant improvements compared to traditional methods.

Ren et al. [25] developed a pipeline integrating feature extraction with an artificial neural network (ANN) using the water strider algorithm for MRI-based cancer diagnosis. This metaheuristic approach enhanced feature selection and classification performance, as validated using the Brain-Tumor-Progression dataset. Sajjad et al. [26] employed deep CNNs and data augmentation techniques for brain tumor grading, significantly improving classification accuracy. Their method highlighted the efficacy of deep learning in capturing complex tumor features, demonstrating robust performance in tumor categorization. Habiba et al. [27] used transfer learning with InceptionV3 and DenseNet201 models for brain tumor classification, emphasizing the effectiveness of dense convolutional layers in feature extraction. Their model achieved a classification accuracy of 96.3%, showcasing substantial improvements in classification outcomes. Ranjbarzadeh et al. [28] proposed a cascade CNN approach for brain tumor segmentation, achieving superior Dice scores on the BraTS 2018 dataset. Their method addressed overfitting and computational complexity, demonstrating improved segmentation performance.

Gul et al. [29] reviewed state-of-the-art methods for liver tumor segmentation, comparing traditional research results and dataset information. Their comprehensive review provides insights into performance measures and methodologies, aiding future scholars in understanding traditional approaches. Togacar et al. [30] introduced BrainMRNet, utilizing CNN and hypercolumn algorithms for effective feature extraction in brain tumor segmentation. Their approach outperformed traditional methods, demonstrating superior segmentation accuracy and efficiency. Oreiller et al. [31] employed U-net for the automatic segmentation of neck and head cancers in CT and PET images, achieving a Dice value of 75.91% for tumor volume dissection. Their method highlighted the applicability of U-net for multimodal image segmentation. Zarinbal et al. [32] proposed a fuzzy clustering approach based on relative entropy for noise reduction and precise membership assignment in brain tumor segmentation. Their method optimized cluster distinction and noise recognition across various datasets, demonstrating significant improvements in segmentation accuracy.

Cocosco et al. [33] applied a minimum spanning tree and K-NN classifier for abnormality detection in brain tissues, showcasing improved segmentation accuracy. Their method enhanced tissue probability map refinement and classification, providing a novel approach to brain tumor segmentation. Zhang et al. [34] employed a Hidden Markov Random Field (HMRF) system with Expectation–Maximization for automatic brain MRI segmentation. Despite its computational costs and susceptibility to noise, their method offered insights into enhancing segmentation robustness. Rajinikanth et al. [35] established a technique using meta-heuristic optimization for tumor and edema extraction in brain MRI. Their method, tested on FLAIR, T1-CE, and T2 images, integrated entropy and active-contour-based segmentation, demonstrating improved segmentation accuracy. Firouzian et al. [36] introduced an energy reduction strategy to create a geodesic active region for intracranial aneurysm segmentation in CTA images. Their method, tested on 11 datasets, provided more accurate segmentation outcomes than manual methods.

Chaudhury and Sau [37] proposed an automatic segmentation approach using computational and artificial intelligence for identifying breast cancer in raw medical images. Their method, employing Gated Recurrent Units (GRUs), outperformed traditional recurrent neural networks (RNNs) and was validated on the Wisconsin Diagnostic Breast Cancer (WDBC) dataset. Heidari et al. [38] used deep learning algorithms for lung cancer classification and malignant lung nodule identification in lung CT images. Their model, utilizing Federated Learning (FL) and CapsNets, demonstrated robust performance across multiple datasets, including the CIA dataset, Kaggle Data Science Bowl (KDSB), and LUNA 16.

Although there have been significant advancements in detecting and outlining abnormalities in multimodal images, there is still potential for improving performance metrics. This research introduces a new EHO-EnFCM algorithm designed to boost accuracy and improve the Dice Score while also speeding up computation. This unique combination of methods is novel and has yet to be extensively explored or shared within the scientific community.

3. Materials and Methods

3.1. Dataset Description

This study leverages the Brain Tumor Segmentation (BraTS) dataset, a globally recognized benchmark for brain tumor segmentation research. This dataset includes both real and synthetic multimodal MRI scans, which capture two primary tumor types: high-grade gliomas (HGGs) and low-grade gliomas (LGGs). This dataset is classified into four MRI modalities, each contributing unique diagnostic information:

• T1-weighted MRI, which offers high-resolution anatomical detail for the precise localization of brain structures
• T2-weighted MRI, which highlights regions with elevated water content, often indicative of edema;
• T1-CE (contrast-enhanced) MRI, in which contrast agents are used to enhance tumor visibility, emphasizing active regions;
• FLAIR (fluid-attenuated inversion recovery) MRI, which suppresses cerebrospinal fluid signals to improve the contrast of lesions near fluid-filled regions.

The combination of these imaging modalities facilitates comprehensive analysis of tumor morphology, significantly enhancing segmentation accuracy and reliability [39,40].

3.2. Magnetic Resonance Imaging (MRI)

MRI is a widely used non-invasive imaging technique for generating high-resolution images of the brain. In this technique, strong magnetic fields and radio waves are used to produce detailed tissue contrasts, essential for distinguishing between healthy and pathological regions. Each MRI modality provides unique diagnostic insights: T1-weighted imaging provides high-resolution anatomical detail, suitable for analyzing the normal structure of the brain. T2-weighted imaging highlights differences in water content, making it effective for detecting edema and other fluid-related abnormalities. In T1-CE imaging, contrast agents are employed to enhance the visibility of tumor regions, particularly active areas. FLAIR imaging suppresses cerebrospinal fluid signals, enhancing the contrast of lesions adjacent to fluid-filled spaces. These modalities collectively enable comprehensive tumor evaluation, aiding in the accurate differentiation of tumor boundaries and improving segmentation outcomes [2,41,42].

3.3. Data Collection and Quality

The BraTS dataset was compiled based on information from multiple institutions, representing a wide range of imaging protocols and scanner configurations. This diversity mirrors real-world clinical conditions, where variability in scanner hardware and imaging protocols is common. Despite these variations, this dataset has been carefully compiled to ensure its uniformity and reliability for research purposes.

The preprocessing steps applied to this dataset include skull-stripping, eliminating non-brain tissues from MRI images to focus on brain regions; spatial alignment, registering images to a standardized anatomical template to ensure consistent orientation; and intensity normalization, adjusting intensity values across images to reduce variability and improve algorithm robustness. These preprocessing techniques minimize inconsistencies within the dataset, enabling the proposed EHO-EnFCM segmentation method to achieve optimal performance. By addressing challenges such as scanner variability and intensity heterogeneity, the BraTS dataset supports the development and evaluation of reliable brain tumor segmentation techniques.

3.4. Implementation of Brain Segmentation Methods

In this study, we implemented a novel hybrid approach combining Elephant Herding Optimization (EHO) with Entropy-Driven Fuzzy C-Means (EnFCM) clustering to segment brain tumors from the MRI images in the BraTS dataset. Elephant Herding Optimization (EHO) is an algorithm inspired by the natural herding behavior of elephants. It enhances the clustering process by improving efficiency and precision, leading to more accurate and computationally effective segmentation. Entropy-Driven Fuzzy C-Means (EnFCM) clustering incorporates entropy measures to handle the inherent variability and uncertainty in medical images. This helps in distinguishing between tumor and non-tumor regions more effectively. The integration of EHO with EnFCM is intended to overcome the limitations of traditional segmentation methods, such as sensitivity to noise and intensity inhomogeneity. By leveraging the strengths of both techniques, our approach achieves more robust and precise segmentation of brain tumors.

3.5. EHO—Elephant Herding Optimization

Elephants are sociable animals that reside in families made up of females and their young. The elephant is one of the biggest mammals in Africa and Asia. There are various subspecies of elephants in both Asia and Africa. Elephants use subsonic vibrations that travel faster than sound through the ground and air, enabling interpersonal communication over large distances.Elephant males communicate with their clans by sending low-frequency vibrations. This optimization method has been modelled after the traits of elephants, which include living in clans under the direction of a matriarch and separating male elephants from their clans once they reach puberty. The males typically reside elsewhere, whereas females choose to reside with relatives. Until they entirely separate from their families, they will progressively become detached from them. After researching actual elephant herding behavior, Wu et al. [43] proposed the EHO method with the following presumptions are considered.

• The elephant population is made up of a few clans with predetermined amounts of elephants.
• In every generation, a preassigned number of male elephants will be detached from their clans to reside separately in a remote area far from the chief elephant community.
• The elephants in every clan are led by a matriarch.

3.5.1. Updating Operator

Elephants within a clan, led by a matriarch, live and operate under her guidance, maintaining order and structure. Each clan, represented as Ci, contains a constant number of elephants. The position of each elephant within a clan is determined by the matriarch’s influence, which is modeled in the Elephant Herding Optimization (EHO) algorithm through the “Clan Updating” operator. This operator adjusts the positions of elephants based on the leadership of the matriarch ci. For example, the new position of an individual elephant, like elephant j, is updated based on the matriarch’s control.

• Updating Individual Elephant Positions

Xnew_i,j = Xold_i,j + α ∗ (Xbest_i − Xold_i,j) ∗ r

(1)

• Xnew_i,j denotes the new position of the j-th elephant in the i-th clan.
• Xold_i,j denotes the current position of the j-th elephant in the i-th clan.
• Xbest_i denotes the best position found so far in the i-th clan (matriarch).
• α is a scaling factor that controls the step size of the update. It is a random number between 0 and 1.
• r is a random number between 0 and 1.

This equation updates the position of each elephant so that it moves towards the best position within its clan, with the step size determined by the scaling factor α and a random factor r.

• Updating the Best Elephant

Xnew_i,j = β ∗ Xcenter_i

(2)

• Xnew_i,j denotes the new position of the best elephant in the i-th clan.
• β is a scaling factor between 0 and 1.
• Xcenter_i denotes the center of mass of the i-th clan.

This equation updates the position of the best elephant in the clan such that it moves towards the center of the clan. The scaling factor β controls the extent of this movement.

• Calculating the Center of Mass

Xcenter_i,d = (1/nci) ∗ Σ(Xc_i,j,d) for j = 1 to nci

(3)

The clan center is modified by (3).

• Xcenter_i,d denotes the d-th dimension of the center individual of the i-th clan.
• nci is the number of elephants in the i-th clan.
• Xc_i,j,d denotes the d-th dimension of the j-th elephant in the i-th clan.

The pseudo code for Elephant Herding Optimization is as follows.

# EHO Pseudo Code

# Step 1: Initialization

MaxGen = <maximum generations> # Set maximum generations

P = initialize_population() # Randomly initialize population P

# Step 2: Main Optimization Loop

while not stopping_criterion_met():

# 2.1: Sort Population by Fitness

P = sort_population_by_fitness(P)

# 2.2: Update Positions for Each Clan

for clan in clans:

for elephant in clan:

# Generate a new candidate position based on formula (1)

X_new = generate_new_position(elephant, clan_leader)

# Compare and update elephant’s position if the new one is better

if fitness(X_new) > fitness(elephant):

elephant = update_position(elephant, X_new) # Apply formula (2)

# 2.3: Replace the Worst Elephant in Each Clan

for clan in clans:

worst_elephant = find_worst_elephant(clan)

# Replace the worst elephant with a new position (Formula 4)

new_elephant = generate_new_position_randomly()

replace_elephant(clan, worst_elephant, new_elephant)

# 2.4: Recompute Fitness for All Elephants

P = evaluate_fitness_for_population(P)

# 2.5: Increment Generation Counter

generation += 1

# Step 3: End Loop

3.5.2. Separating Operator

In natural elephant behavior, when male elephants reach adulthood, they leave their family herds to live independently. The Elephant Herding Optimization (EHO) algorithm reflects this behavior through the “Separation Operator”, used during its iterative process. The male elephant with the lowest fitness in each clan is subjected to this separation mechanism and represented as having been removed from the clan, mimicking the real-world behavior of adult male elephants leaving their groups.

$$x_{worst,ci}=x_{min}+\left(x_{max}-x_{min}+1\right)\ast rand$$

(4)

where

• ${\mathit{x}}_{\mathit{w}\mathit{o}\mathit{r}\mathit{s}\mathit{t},\mathit{c}\mathit{i}}$ = the worst individual in clan ci;
• ${\mathit{x}}_{\mathit{m}\mathit{i}\mathit{n}}$ = lower bound;
• ${\mathit{x}}_{\mathit{m}\mathit{a}\mathit{x}}$ = upper bound;
• rand = stochastic distribution [0, 1].

The following Figure 1 and Figure 2, depict the elephant life cycle and how EHO algorithms work, respectively.

3.6. Fuzzy C-Means (FCM) Algorithm

The Fuzzy C-Means (FCM) algorithm, introduced by Dunn and extended by Bezdek, is a clustering approach that assigns a degree of membership to each data point across multiple clusters. This contrasts with hard clustering techniques, which rigidly classify each data point into a single cluster [44]. The FCM algorithm’s flexibility allows for overlapping membership, where the association of data points with clusters is iteratively refined based on the number of clusters predefined by the user. A detailed explanation with sub sections and illustration of the FCM process (Figure A1) are available in the Appendix A.

Consider X = {x_1, x_2, …, x_n} as the finite set of elements and v = {v_1, v_2, …, v_c} as the cluster center. The objective function of FCM is

$$J_{FCM}={{\displaystyle \sum }}_{i=1}^N{{\displaystyle \sum }}_{j=1}^c{u}_{ij}^m\Vert x_i-{v_j\Vert }^2,$$

(5)

where

• N is the number of samples;
• c denotes the number of clusters;
• m denotes the fuzzy exponent (m > 1);
• x_i denotes the grayscale value at i-th pixel (the k-dimensional data measured);
• v_j denotes the cluster center (d-dimensional vector);
• u_ij denotes the membership degree of x_i in the cluster j (0 ≤ u_ij ≤ 1);
• ‖x_i − v_j‖² denotes the Euclidean distance between the i-th pixel and cluster center v_j.

The membership function u_ij is

$$u_{ij}={\displaystyle \frac{1}{{{\displaystyle \sum }}_{k=1}^c{\left(\Vert x_i-{v_j\Vert }^2/\Vert x_i-{v_k\Vert }^2\right)}^{1/\left(m-1\right)}}}$$

(6)

The cluster center v_j is

$$v_j={\displaystyle \frac{{{\displaystyle \sum }}_{i=1}^N{u}_{ij}^m{x}_i}{{{\displaystyle \sum }}_{i=1}^N{u}_{ij}^m}}$$

(7)

The iteration process continues until the termination condition is satisfied.

$$ma{x}_{ij}\left\{\left|u_{ij}^{\left(k+1\right)}-u_{ij}^{\left(k\right)}\right|\right\}<\epsilon$$

where $\epsilon$ is the stopping criterion between 0 and 1, and $k$ is the iteration count.

This approach is affined to a J_FCM local minimum. In the noiseless image, FCM leads to improved accuracy and is especially responsive to noisy images. By including greyscale and local information between pixels in the FCM clustering, effectiveness is increased.

Despite its popularity, FCM has certain limitations:

• Noise sensitivity: This algorithm is prone to misclassification when noise or outliers are present, reducing its segmentation accuracy.
• Dependency on initialization: Performance is highly influenced by the initial placement of cluster centroids, which can lead to suboptimal clustering.
• Static membership values: FCM struggles with dynamic intensity variations in images as the membership values are fixed, which can cause inaccuracies in defining boundaries.

To address these issues, Entropy-based FCM enhances the standard algorithm by incorporating entropy to manage uncertainties. This approach dynamically adjusts membership values based on image characteristics, significantly improving robustness against noise and achieving more-accurate segmentation results.

3.7. Entropy-Based Fuzzy Clustering (EnFCM)

In accordance with the degree of similarity at every point in the data, entropy is determined. The data point at the center of a cluster exhibits a relatively small entropy value, making it more probable that it will be selected as the cluster core. The initial cluster node is proposed to be the data point with the lowest entropy. Data points are removed from the cluster center selection list if they fall below a threshold equivalent to this cluster center in the subsequent rounds. The data points that closely resemble the chosen cluster center should fit there with the greatest likelihood, and it is uncertain whether they belong to any other cluster centers. The iterations will be repeated till there are no more data points [45]. This approach has benefits over more traditional ones in that (i) there are fewer computation challenges because entropy is assessed once and (ii) fewer parameters are required for the calculation. The entropy parameter typically guides the following steps when processing images.

• The entropy values of each pixel are considered.
• A pixel with a low entropy value is picked to represent the center of the cluster and margined over a specific area in the image.
• FCM will then cluster the pixels that are closest to the cluster center or have a high degree of similarity.
• Additional pixels with differences are grouped under other clusters for better organization.
• This operation causes border cohesion/overlap while marginating the pixels, and it also takes longer to build the boundaries.

Consider a set of N data points in M dimensions, where a vector of M values (i.e., x_i1, x_i2, …, x_iM) represents each data point x_i, i = 1, …, N. In the range [0.0, 1.0], the values of each dimension are standardized.

The Euclidean distance between any two data points (e.g., i and j) is assessed as follows:

$$D_{ij}=\sqrt{{{\displaystyle \sum }}_{k=1}^M{\left(X_{ik}-X_{jk}\right)}^2},$$

(8)

where D_ij = the distance between x_i and x_j data points. The similarity between any two points can be determined as follows:

$$S_{ij}=e^{-\alpha D_{ij}}$$

(9)

where S_ij is the similarity between x_i and x_j normalized in the range of [0.0, 1.0].

The entropy for a data point relative to another data point is as follows:

$$E=-S{\log }_{2}S-\left(1-S\right){\log }_2\left(1-S\right),$$

(10)

where S is the similarity measure and E assumes a maximum of 1.0 if S is 0.5 and a minimum of 0.0 if S is 0.0 or 1.0. At data point $x_i$, the average entropy for all other data points is calculated as follows:

$$E_i=-{{\displaystyle \sum }}_{j\in X}^{j\ne i}\left(S_{ij}{log}_2{S}_{ij}+\left(1-S_{ij}\right){log}_2\left(1-S_{ij}\right)\right)$$

(11)

If similarity versus distance is plotted, a larger curvature will be observed for a larger α value. The similarity value is set to 0.5 to automatically calculate α only when the distance between two data points equals the mean distance of all data point pairs, as represented below:

$$\alpha =-ln0.5/\overline{D}$$

where $\overline{D}$ is the mean distance between the data points pairs.

The threshold is between the data points in the same cluster, according to the interpretation of the β parameter, which can be thought of as a resemblance or correlation. The range of β is in between [0.0, 1.0]. The input data with N data points are represented by the threshold value ‘T’ in the algorithm. The Entropy-Based Fuzzy Clustering (EnFCM) algorithm is given below:

• Calculate entropy for every x_i in T for i = 1, …, N.
• Choose $x_{i_{min}}$ with the least entropy.
• Reject $x_{i_{min}}$ and the data points similar to $x_{i_{min}}$ larger than β from T.
• If T is not empty, then go to Step 2.

Define correlated data points

$$x_{i_{corr}}\le \beta \in T$$

(12)

The parameter $x_{i_{corr}}$ represents the correlated data points that fall below the threshold β. These data points are deemed to belong to or comply with the threshold set by T. This parameter introduces a novel approach to clustering by accounting for the objective function in a way that ensures the following:

• Accuracy: Enhances the precision of clustering outcomes by considering well-defined cluster boundaries.
• Boundary Definition: Ensures that the cluster boundaries are neither cohesive, disoriented, nor blurred, thereby maintaining clarity and separability among clusters.

By introducing $x_{i_{corr}}$, this method adds reliability to the clustering process, addressing challenges associated with ambiguous or overlapping cluster regions.

Therefore, the minimum FCM objective function can be modified or reformulated as follows:

$$J\left(U,C\right)={{\displaystyle \sum }}_{i=1}^N{{\displaystyle \sum }}_{j=1}^C{\left(u_{ij}\right)}^m\Vert x_{i_{corr}}-c_j\Vert , 1\le m\le \infty$$

(13)

By integrating the clustering method, the updated position of elephant j in clan c_i can be determined using the following equation:

$$x_{new,ci,j}=x_{ci,j}+\alpha \ast \left(J\left(U,C\right)-x_{ci,j}\right)\ast r$$

(14)

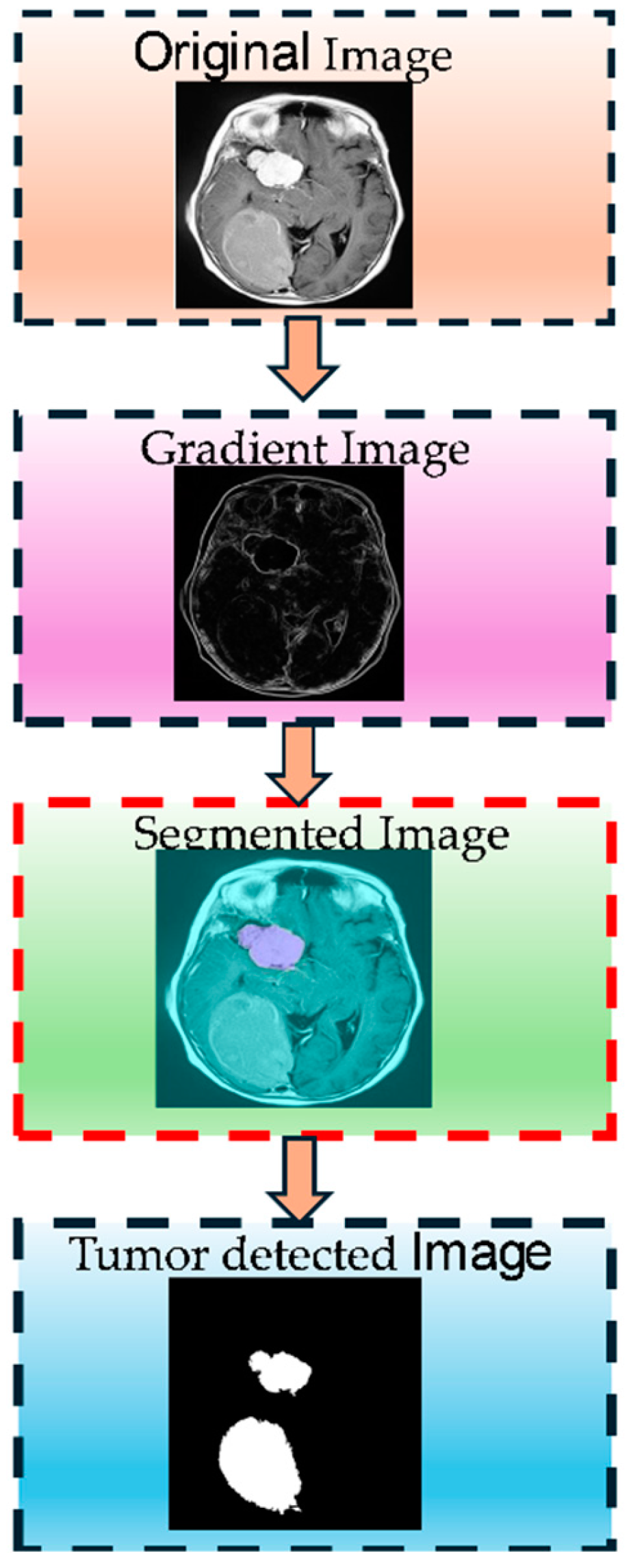
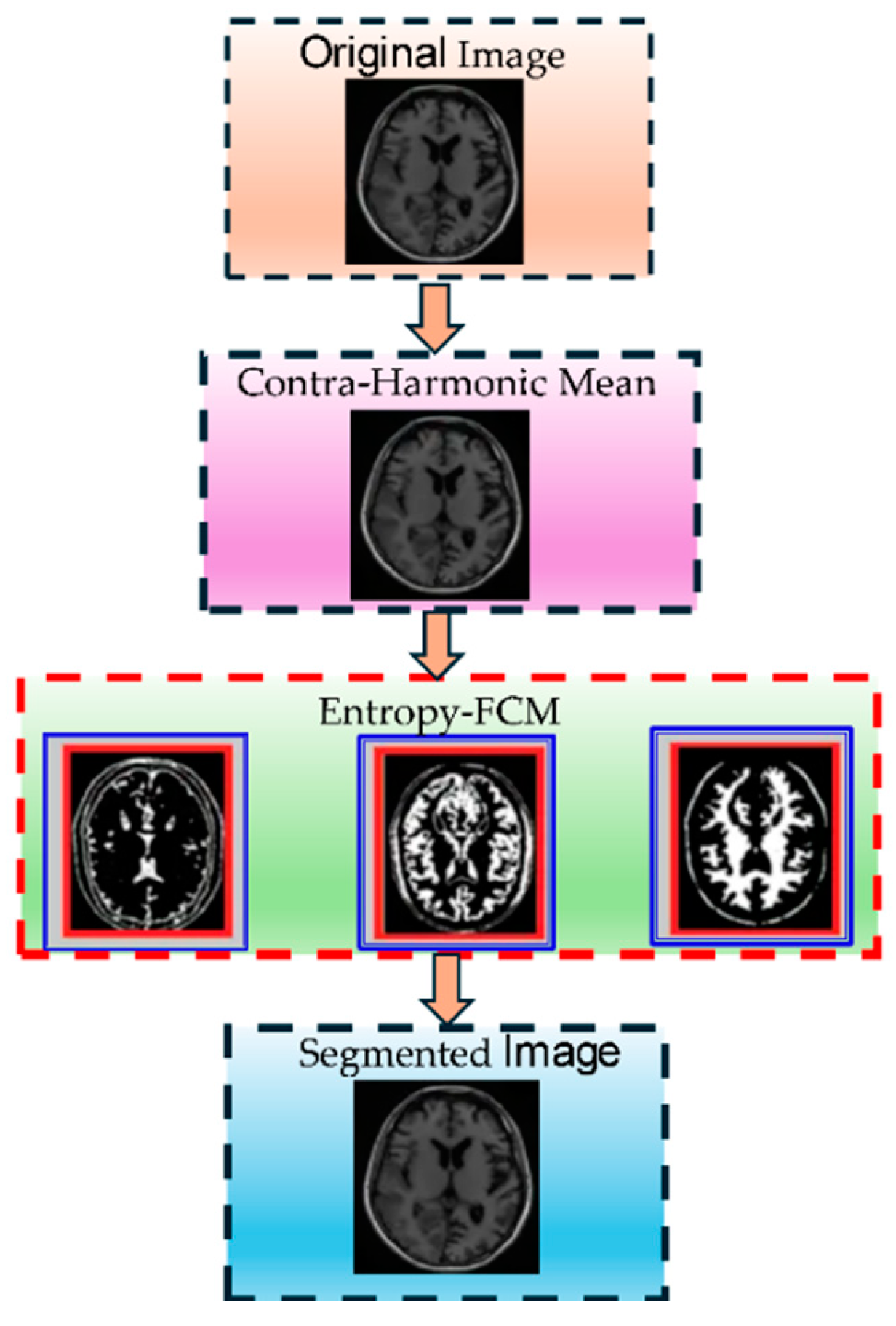
Figure 3 shows the Entropy-Driven Fuzzy C-Means (EnFCM) clustering process step by step. The figure illustrates the stepwise process of MRI brain tumor segmentation implemented in this study. Initially, the input MRI images undergo preprocessing to standardize quality through skull stripping, alignment, and intensity normalization. Next, feature enhancement techniques, such as noise reduction and contrast adjustment, are applied to amplify critical details. Multiple MRI modalities (T1, T2, FLAIR, and T1-CE) are then integrated to utilize their complementary information. The enhanced images are segmented using a hybrid Elephant Herding Optimization (EHO) and Entropy-Driven Fuzzy C-Means (EnFCM) clustering approach, producing the final segmented output, highlighting tumor regions effectively. This comprehensive pipeline addresses challenges like image variability, noise, and intensity inhomogeneity, ensuring accurate tumor identification.

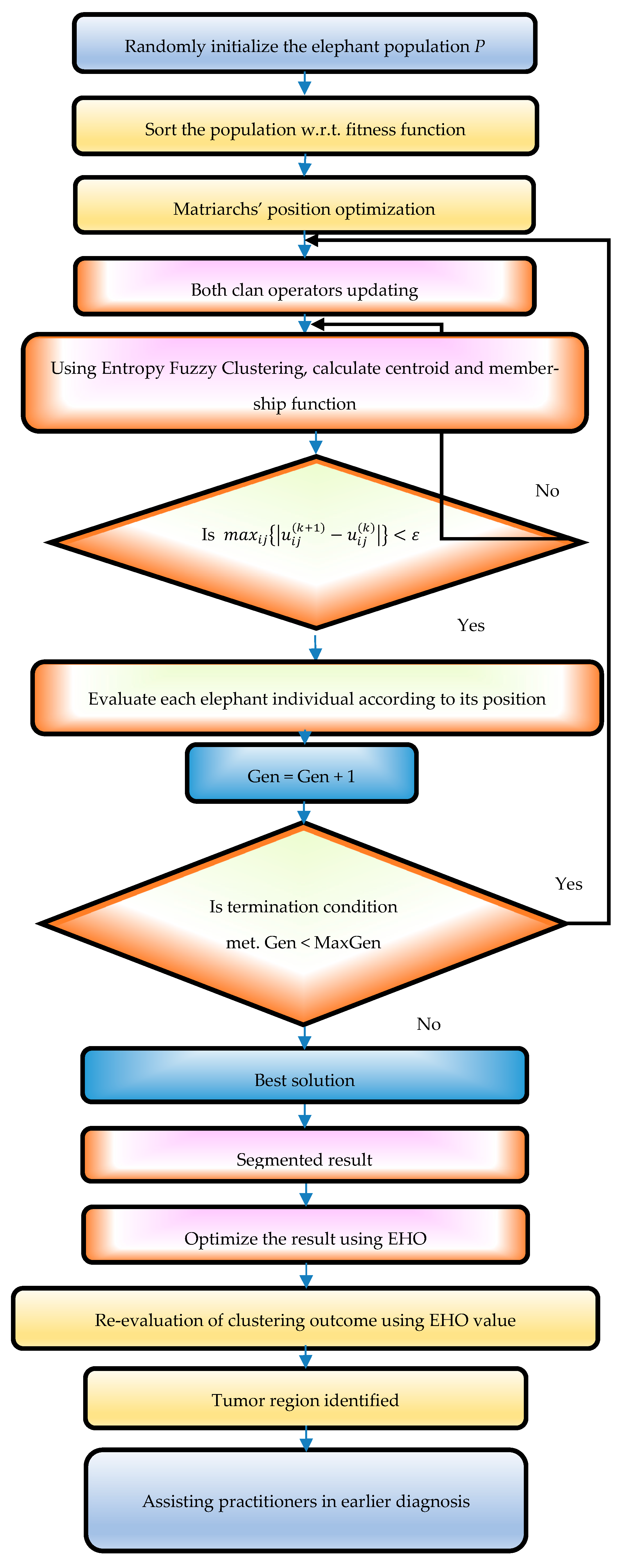
3.8. Proposed EHO-Based EnFCM Clustering Approach

The suggested approach employs Entropy-Based Fuzzy C-Means (EnFCM) clustering enhanced by the Elephant Herding Optimization (EHO) algorithm to accurately identify execution. The key advantages of integrating EHO with EnFCM are as follows.

Enhanced convergence speed: EHO mitigates exhaustive search space limitations, expediting convergence. Optimization efficiency: following clustering, EHO rapidly pinpoints optimal pixel locations, refining the clustering process. Precise localization: this method ensures accurate localization of tumor regions while maintaining clear discrimination of brain tissue in MRI images. Balanced performance: it achieves efficient segmentation outcomes without sacrificing accuracy or speed. A flow chart of the proposed method is shown in Figure 4.

The proposed Elephant Herding Optimization (EHO) combined with Entropy-Driven Fuzzy C-Means (EnFCM) method shows significant advancements in brain tumor segmentation for MRI images. This hybrid approach addresses critical challenges in medical image segmentation, such as noise, intensity inhomogeneity, and tumor heterogeneity, which are common issues in brain tumor detection. Its performance was thoroughly evaluated through various metrics and comparisons to demonstrate its robustness.

4. Results and Discussion

4.1. Segmentation Performance Improvement

This work proposes a novel development in medical picture segmentation via the combination of Elephant Herding Optimization (EHO) with Entropy-Based Fuzzy C-Means (EnFCM), particularly regarding the identification and analysis of intricate tumor formations. EHO, drawing inspiration from the social and evolutionary behaviors of elephant herds, enhances the segmentation process by effectively identifying the most precise cluster topologies. Concurrently, EnFCM improves this methodology by integrating entropy metrics to more effectively address the uncertainties and ambiguities present in medical imaging data.

This hybrid technique exhibits resilience and flexibility by using the BraTS 2013 and BraTS 2015 datasets, known for their significant variability and complex tumor areas. These datasets include a diverse array of tumor kinds, sizes, and complexity, offering a stringent evaluation platform for segmentation algorithms. In contrast to conventional methods, which often produce inconsistent outcomes or fail to adequately delineate complex tumor margins, the EHO-EnFCM framework demonstrates superior accuracy and reliability across various contexts.

This synergy rectifies the deficiencies of traditional segmentation methods while also creating opportunities for precise and quick tumor identification, hence enhancing clinical decision making and treatment planning.

4.2. Performance Metrics Analysis

The metrics used to assess the efficacy of the proposed hybrid technique, as shown in

Table 1. Performance metrics.

Performance Metrics	Formula	Description
Mean Squared Error (MSE)	$MSE={\displaystyle \frac{1}{CD}}{\displaystyle {\displaystyle \sum }_{i=0}^{C-1}}{\displaystyle {\displaystyle \sum }_{j=0}^{D-1}}{[A\left(i,j\right)-B\left(i,j\right)]}^2$ where $C$ denotes rows; $D$ denotes columns; $i$ denotes rows’ incremental operators; $j$ denotes columns’ incremental operators;	Measures the average difference between predicted and actual pixel values. Lower values are better.
Computational Time (T)	NA	Measures the time taken to process an image. Lower values are better.
Dice Score (DS)	$D\left(A,G\right)=2\times {\displaystyle \frac{T\left(A,G\right)}{1+T\left(A,G\right)}}$	Measures the similarity between two sets of pixels. Higher values are better.
Tanimoto Coefficient index (TC)	$T\left(A,G\right)={\displaystyle \frac{\left|A\cap G\right|}{\left|A\cup G\right|}}$	Measures the overlap between two sets of pixels. Higher values are better.
Peak Signal-to-Noise Ratio (PSNR)	$PSNR=10 lo{g}_{10 }\left({\displaystyle \frac{Peak Valu{e}^2}{MSE}}\right)$	Measures the quality of an image compared to a perfect image. Higher values are better.

, include the Mean Squared Error (MSE), Dice Score (DS), Tanimoto Coefficient (TC), Peak Signal-to-Noise Ratio (PSNR), and Computational Time. These measures combined allow a thorough evaluation of segmentation precision, resilience, and efficacy.

Table 2. Performance metric values of proposed EHO-EnFCM algorithm.

Data Resource	Mean Squared Error	Processing Time (s)	Dice Score (%)	Tanimoto Co-Efficient (%)	Peak Signal-to-Noise Ratio (dB)
BraTS Dataset	0.3067	27.34	80.1212	58.0497	53.2981
	0.3193	27.58	79.0521	57.5378	53.1231
	0.2556	26.16	79.2907	59.1461	54.0886
	0.2724	27.14	80.4956	59.6745	53.813
	0.2731	26.7	80.0431	58.1525	53.802
	0.2583	26.66	79.0834	57.5488	54.0441
	0.2944	27.43	80.207	56.0985	53.475
	0.3199	25.86	79.9319	59.9806	53.1145
	0.2832	25.81	80.7672	56.8906	53.644
	0.2517	25.01	79.5889	55.8948	54.1561
	0.2643	27.86	80.9894	56.2128	53.9431
	0.3064	26.53	80.9651	55.385	53.3021
	0.2848	27.1	80.3245	58.7678	53.6199
	0.3165	27.47	80.1553	56.1506	53.1607
	0.2788	25.77	79.3731	59.5731	53.7118
	0.2981	26.05	79.4034	55.7011	53.4208
	0.3137	25.83	80.6473	58.8856	53.2003
	0.3091	25.99	80.6379	59.6507	53.2644
	0.28	25.53	79.9314	57.4057	53.6926
	0.2958	27.5	80.467	58.4739	53.4543
AVG	0.29	26.57	80.07	57.76	53.57

illustrates the average values attained using the EHO-EnFCM technique, underscoring its enhanced efficacy relative to conventional methods.

The hybrid model attained a notably low Mean Squared Error (MSE) of 0.29, indicating little divergence between the segmented areas and the ground truth from the BraTS datasets. This signifies a high degree of accuracy in delineating tumor margins and capturing their complex characteristics. This low MSE guarantees the model’s precision in segmentation while reducing the likelihood of misclassification, which is essential for clinical applications. Precise delineation of tumor locations is critical for informing treatment strategies, including radiation planning, surgical procedures, or tracking disease progression.

The decreased MSE further emphasizes the dependability of the EHO-EnFCM approach in managing intricate medical pictures characterized by significant unpredictability. The hybrid approach improves output reliability by reducing segmentation mistakes, making it a significant asset for healthcare practitioners. This accuracy immediately improves patient outcomes by facilitating more precise diagnosis and customized treatment strategies.

The Dice Score (DS) of 80.07% indicates that the EHO-EnFCM technique has considerable accuracy in tumor area segmentation, achieving substantial overlap with the ground-truth annotations. The DS metric, an essential measure of segmentation precision, underscores the hybrid method’s proficiency in accurately classifying tumor pixels while reducing the incidence of false positives and false negatives. This great accuracy not only demonstrates the efficacy of the EHO-EnFCM technique but is also essential for preserving diagnostic dependability. Precise segmentation directly influences the trust of radiologists and physicians, guaranteeing that a model’s outputs conform to professional expectations and clinical norms. This accuracy facilitates advanced applications, including automated tumor surveillance and therapy response evaluation.

The Tanimoto Coefficient (TC) obtained, averaging 57.76%, indicates the efficacy of the EHO-EnFCM approach in differentiating tumor regions from non-tumor areas. The TC, albeit somewhat more conservative than the DS metric, accurately assesses overlap while considering discrepancies, hence offering superior insights into segmentation quality. This performance is particularly crucial in medical imaging contexts where tumor and non-tumor areas may be detected in close proximity or perhaps partly overlap. The EHO-EnFCM approach provides distinct segmentation outputs that allow precise identification of tumor borders, essential for clarity in medical analysis. This difference is crucial for accurate treatment planning, allowing doctors to successfully target tumor areas while preserving healthy tissues.

The model attained a notable Peak Signal-to-Noise Ratio (PSNR) of 53.57 dB, reflecting markedly decreased noise levels in the segmented pictures. A high PSNR value is an essential metric of picture quality, especially in medical imaging, since it guarantees that the segmented output preserves clarity and detail while reducing distortions or artifacts. Improved picture quality is crucial for precisely viewing tumor structures, allowing doctors to discern even minor borders and abnormalities that may be concealed by noise. The EHO-EnFCM approach maintains the integrity of small details, providing a dependable basis for further diagnostic evaluations, such as tumor grading and treatment planning. The elevated PSNR highlights our method’s resilience in managing the intrinsic unpredictability and complexity of medical pictures from datasets like BraTS.

Although computing time (T) may vary depending on hardware specifications and picture complexity, the EHO-EnFCM approach brought about a significant increase in efficiency relative to traditional segmentation methods. The decrease in processing time is especially crucial in clinical applications, where rapid image processing is vital for facilitating swift and informed decision making. Accelerated processing speeds enable radiologists and oncologists to examine data more swiftly, thereby allowing prompt diagnoses and hastening the commencement of essential therapies such as surgery, chemotherapy, or radiation therapy. Moreover, the enhanced efficiency of the EHO-EnFCM technique guarantees its scalability, rendering it appropriate for incorporation into high-throughput workflows and real-time applications within contemporary healthcare systems. In Table 2, each row represents an individual image’s performance metrics.

4.3. Comparative Analysis

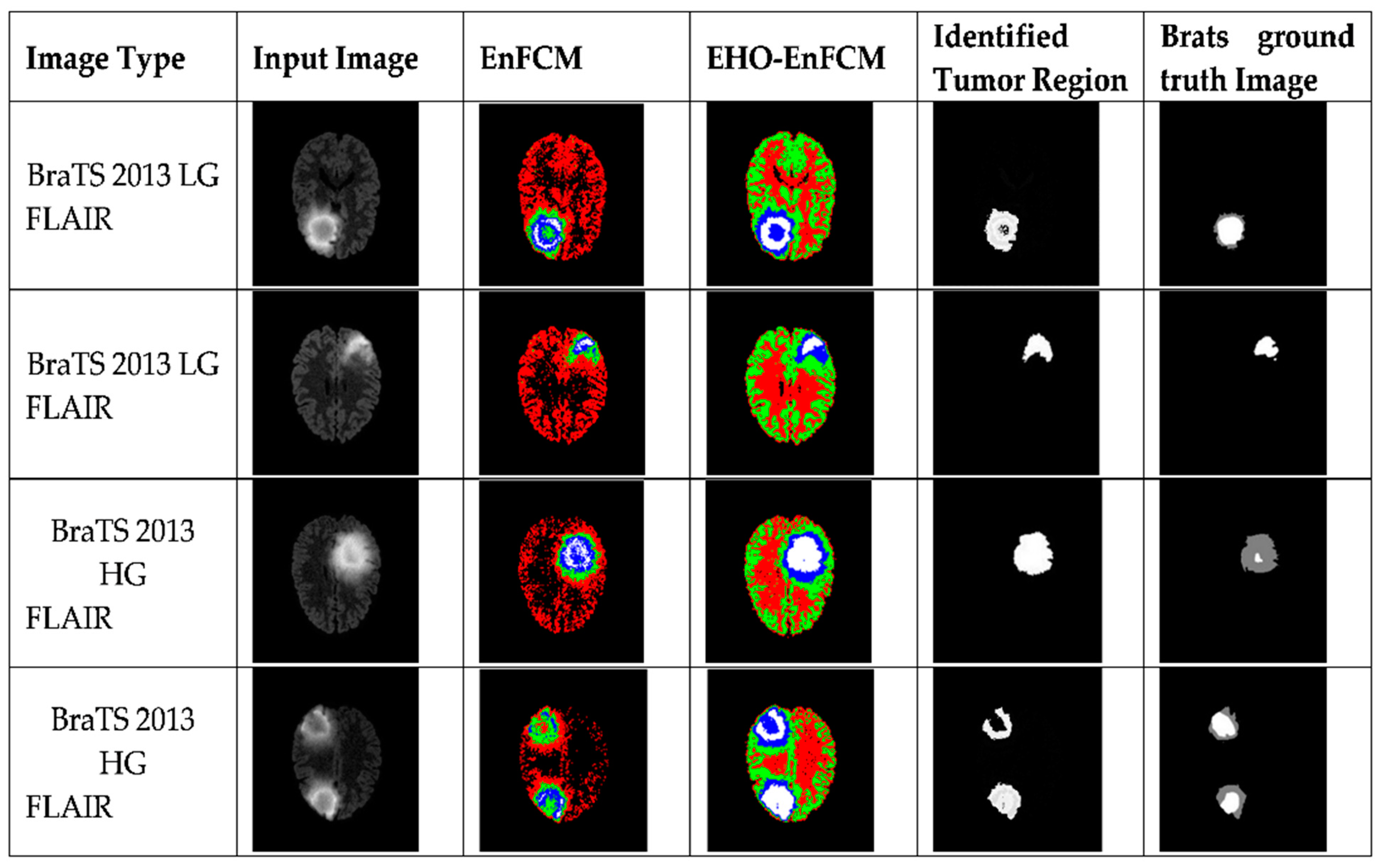
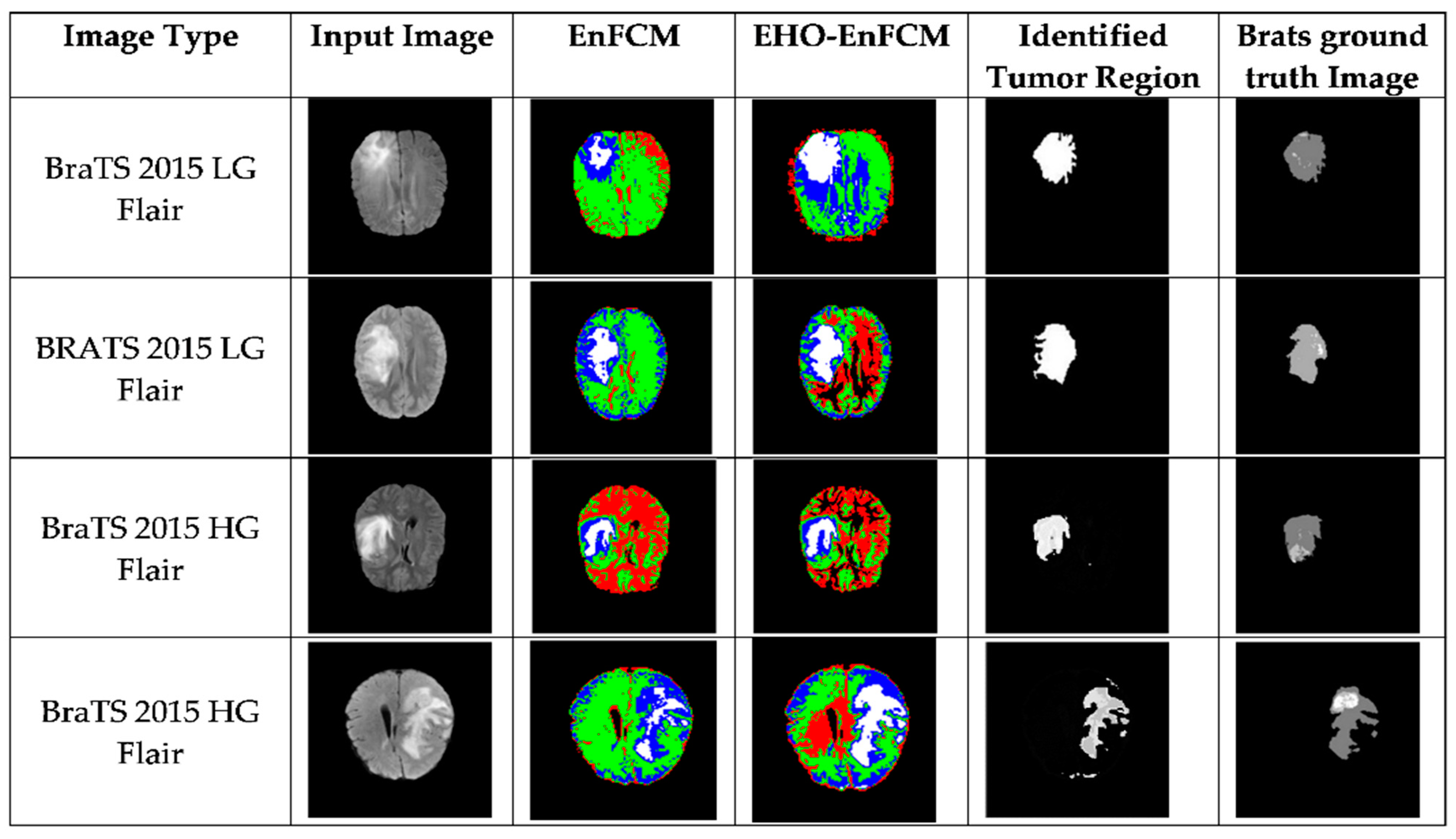
Figure 5 and Figure 6 provide a comprehensive comparison of segmentation outcomes between the standalone Entropy-Based Fuzzy C-Means (EnFCM) technique and the proposed hybrid method, EHO-EnFCM, with respect to the BraTS 2013 and 2015 datasets, respectively. The EHO-EnFCM technique distinctly demonstrated its capacity to overcome the limitations of traditional EnFCM, such as imprecise tumor boundary identification and increased segmentation noise. The hybrid approach significantly enhanced accuracy by integrating the optimization potential of the Elephant Herding Optimization (EHO) algorithm with the entropy-driven clustering strength of EnFCM.

In Figure 5 and Figure 6, the differences in tumor segmentation are visually evident. The tumor regions segmented using EHO-EnFCM align more closely with the ground-truth data than the results obtained using the standalone EnFCM method. This highlights the effectiveness of EHO-EnFCM in addressing the challenges posed by blurred boundaries and noise interference, both of which are commonly encountered in MRI scans. A clear delineation of tumor boundaries and reduced segmentation noise further demonstrate the algorithm’s robustness.

The integration of EHO enhances the clustering process by refining segmentation precision and improving noise resilience. Specifically, the optimization capabilities of EHO allow the hybrid model to effectively manage the complex textures and irregular forms characteristic of tumor regions. This makes it particularly relevant for medical imaging, where accurate identification of tumor margins is critical for diagnosis, treatment planning, and prognosis assessment.

Moreover, the EHO-EnFCM approach demonstrates superior resilience to background noise by effectively distinguishing tumor areas from surrounding tissues, thus improving the signal-to-noise ratio. The improved segmentation clarity and reduced noise ensure more-dependable results are obtained, which are essential for clinical application. The visual contrast highlighted in Figure 5 and Figure 6 underscores the substantial advancements achieved through the hybrid technique, validating its potential as a reliable tool for medical image analysis.

Additionally, a detailed explanation of the color scheme in Figure 5 and Figure 6 has been included. In the segmentation outcomes, color differentiation is used to distinguish tumor regions from non-tumorous areas, enabling a more intuitive understanding of the improvements offered by the proposed approach. These figures, combined with the performance data in the revised Table 3, clearly demonstrate the superiority of the EHO-EnFCM method.

Low-grade and high-grade glioma images from the BraTS 2013 and 2015 datasets were utilized to validate the efficacy of the developed EHO-EnFCM methodology. The identified tumor regions are represented in three distinct colors:

• Gray—non-enhancing tumor;
• White—enhancing tumor;
• Black—edema portion.

This color scheme enables a more detailed understanding of the segmented tumor regions and highlights the enhanced precision offered by EHO-EnFCM.

4.4. Comparison of Performance with That of Existing Methods

Table 3 provides the results of a comprehensive comparative analysis of the performance metrics of the proposed EHO-EnFCM method and various existing tumor segmentation techniques. This revised table consolidates the data to ensure that a more streamlined and direct comparison can be made. The comparison spans several key evaluation criteria: the Mean Squared Error (MSE), Computational Time (CT), Dice Similarity (DS), the Tanimoto Coefficient (TC), and the Peak Signal-to-Noise Ratio (PSNR). This unified presentation simplifies the evaluation of the proposed system against state-of-the-art methods.

A critical observation from Table 3 is the improved Dice Similarity (DS) and Tanimoto Coefficient (TC) values achieved by EHO-EnFCM. These metrics are crucial in evaluating segmentation accuracy, as higher values indicate better overlap between the segmented tumor regions and the ground truth. While EHO-EnFCM has consistently higher values for most metrics, it does not outperform all state-of-the-art algorithms in terms of the DS metric. This observation is discussed in greater depth in Section 5 to provide clarity and context.

Additionally, the PSNR values for EHO-EnFCM show a marked improvement, reflecting superior image quality after segmentation, which is essential for clinical evaluation and further processing. In terms of Mean Squared Error (MSE), EHO-EnFCM maintains a low MSE, indicating minimal discrepancy between the segmented image and the actual ground truth. This is particularly important in medical imaging, where precision is critical for accurate diagnosis and treatment planning.

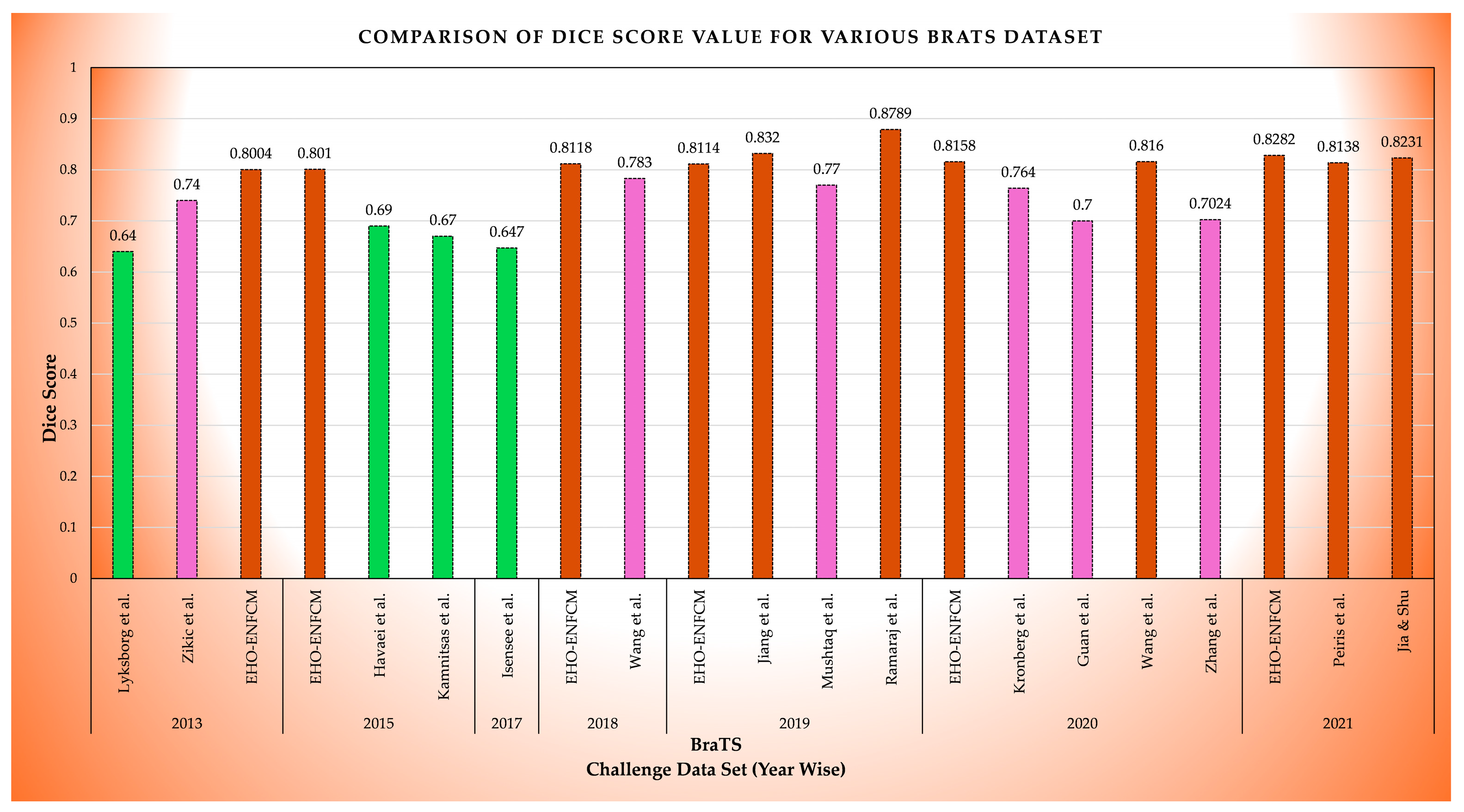
The computational efficiency of EHO-EnFCM, reflected in its relatively lower Computational Time (CT), is another key advantage. Despite achieving higher accuracy metrics, EHO-EnFCM demonstrates faster processing, making it suitable for real-time applications in clinical environments. Figure 7 illustrates the comparative performances of brain tumor segmentation methods using Dice Score values across various studies on the BraTS dataset from 2013 to 2021, emphasizing the consistent performance of the proposed EHO-ENFCM method [3,46,47,48,49,50,51,52,53,54,55,56,57,58,59].

Table 3. Results of the comparison [3,49,50,51,52,53,54,55,57,58,59].

BraTS Challenge Data Set (Year)	Method by	MSE	CT(Sec)	DS (%)	TC (%)	PSNR (dB)
2015	Kamnitsas et al.	0.27	26.5	67	50.45	35.89
2017	Isensee et al.	0.36	27.15	64.7	45.15	25.11
2018	Wang et al.	0.37	27.05	78.3	49.32	29.43
2019	Jiang et al.	0.36	27.18	83.2	55.89	50.22
2019	Mushtaq et al.	0.37	27.1	77	48.45	29.12
2019	Ramaraj et al.	0.30	27.5	87.89	56.34	33.56
2020	Kronberg et al.	0.38	27.3	76.4	48.12	28.9
2020	Guan et al.	0.36	27.25	70	45.45	26.45
2020	Zhang et al.	0.37	27.12	70.24	49.89	27.11
2021	Peiris et al.	0.31	27.12	81.38	48.23	50.14
2021	Jia and Shu	0.37	27.08	82.31	56.34	50.32
2013 & 2015	EHO-EnFCM	0.29	26.57	80.07	57.76	53.57

Table 3. Results of the comparison [3,49,50,51,52,53,54,55,57,58,59].

BraTS Challenge Data Set (Year)	Method by	MSE	CT(Sec)	DS (%)	TC (%)	PSNR (dB)
2015	Kamnitsas et al.	0.27	26.5	67	50.45	35.89
2017	Isensee et al.	0.36	27.15	64.7	45.15	25.11
2018	Wang et al.	0.37	27.05	78.3	49.32	29.43
2019	Jiang et al.	0.36	27.18	83.2	55.89	50.22
2019	Mushtaq et al.	0.37	27.1	77	48.45	29.12
2019	Ramaraj et al.	0.30	27.5	87.89	56.34	33.56
2020	Kronberg et al.	0.38	27.3	76.4	48.12	28.9
2020	Guan et al.	0.36	27.25	70	45.45	26.45
2020	Zhang et al.	0.37	27.12	70.24	49.89	27.11
2021	Peiris et al.	0.31	27.12	81.38	48.23	50.14
2021	Jia and Shu	0.37	27.08	82.31	56.34	50.32
2013 & 2015	EHO-EnFCM	0.29	26.57	80.07	57.76	53.57

4.5. Key Insights of EHO-EnFCM

This Section elaborates on the ability of EHO-EnFCM to effectively address three critical challenges in medical image segmentation: noise reduction, intensity inhomogeneity, and tumor heterogeneity. The metrics in Table 3 provide evidence of the method’s effectiveness in these areas, as supported by quantitative and qualitative analyses.

4.5.1. Noise Reduction

Noise in MRI scans is a common issue that can hinder the accurate segmentation of tumors. EHO-EnFCM enhances the clustering process by minimizing the impact of noise, ensuring that the segmented tumor regions are more accurate and reflective of the actual structure. The PSNR values in Table 3 provide a quantitative measure of the improvement in image quality, where higher PSNR values indicate reduced noise and better signal clarity. This ability to effectively reduce noise makes EHO-EnFCM more robust in real-world applications where MRI scans often suffer from artifacts and interference.

4.5.2. Intensity Inhomogeneity

MRI scans are susceptible to intensity inhomogeneity, where varying intensity levels within the same tumor region can cause segmentation inaccuracies. Traditional methods often struggle to account for these variations, leading to imprecise tumor boundary identification. The hybrid nature of EHO-EnFCM, combining EHO optimization with Entropy-Based Fuzzy C-Means (EnFCM), significantly improves its ability to deal with intensity inhomogeneity. By enhancing the clustering process, EHO-EnFCM can better distinguish between tumor and non-tumor regions, even in areas with varying intensities. This improvement is reflected in the DS and TC values in Table 3, which are significantly higher for EHO-EnFCM than for traditional methods.

4.5.3. Tumor Heterogeneity

Tumors often exhibit heterogeneous characteristics, such as irregular shapes, varying textures, and differing sizes, which pose additional challenges for accurate segmentation. EHO-EnFCM’s ability to adapt to these variations is one of its most significant advantages. By refining the clustering process, the EHO algorithm enhances the method’s ability to segment tumors of varying shapes and textures. This flexibility is critical for segmenting both low-grade and high-grade gliomas, which can display significantly different characteristics. The improved accuracy and robustness in handling tumor heterogeneity are evident in the enhanced performance metrics shown in Table 3.

4.6. Computational Efficiency

High computational efficiency is essential for an algorithm’s practical application in medical imaging, where the rapid processing of large datasets is often required. The proposed EHO-EnFCM method strikes a remarkable balance between segmentation accuracy and computational efficiency. As illustrated in Table 3, EHO-EnFCM achieves competitive performance in terms of segmentation metrics while maintaining relatively low computational time compared to other state-of-the-art methods.

One of the key aspects contributing to the computational efficiency of the EHO-EnFCM algorithm is the use of the Elephant Herding Optimization (EHO) algorithm. EHO is known for its fast convergence and ability to find the global optimum without requiring extensive iterations. By integrating EHO with the Entropy-Based Fuzzy C-Means (EnFCM) algorithm, the hybrid method benefits from both the optimization capabilities of EHO and the clustering strength of EnFCM, resulting in efficient segmentation with high accuracy.

The computational efficiency of the EHO-EnFCM algorithm, coupled with its high accuracy, demonstrates its suitability for real-world medical imaging applications, where both processing time and segmentation accuracy are essential.

4.7. Qualitative and Quantitative Analysis

To further assess the effectiveness of the proposed EHO-EnFCM algorithm, both qualitative and quantitative analyses were performed. The qualitative analysis involved visual inspection of the segmentation results, while the quantitative analysis relied on established performance metrics, such as Dice Similarity (DS), the Tanimoto Coefficient (TC), Mean Squared Error (MSE), and the Peak Signal-to-Noise Ratio (PSNR), which are presented in Table 3.

4.7.1. Qualitative Analysis

The qualitative results presented in Figure 5 and Figure 6 provide a clear visual comparison of the tumor segmentation outcomes obtained by applying the proposed EHO-EnFCM method to the BraTS 2013 and 2015 datasets. The visual contrast between the tumor regions segmented by EHO-EnFCM and the ground truth data highlights the effectiveness of the hybrid approach in accurately identifying tumor boundaries.

4.7.2. Quantitative Analysis

In addition to qualitative assessments, the proposed method was evaluated using a series of quantitative performance metrics, as shown in Table 2 and Table 3. The DS and TC values for EHO-EnFCM are notably higher values, demonstrating the superiority of this algorithm in terms of segmentation accuracy. The MSE and PSNR values further reinforce the reliability and precision of EHO-EnFCM in tumor segmentation.

Together, the qualitative and quantitative results highlight the overall effectiveness of the EHO-EnFCM algorithm in tumor segmentation. The proposed method outperforms other existing approaches across multiple metrics, providing evidence of its potential for use in clinical applications.

4.8. Limitations and Future Scope

The EHO-EnFCM method has demonstrated significant potential in brain tumor segmentation, particularly for gliomas and aneurysms. However, its current applicability is limited to these specific tumor types. To enhance its generalizability and clinical impact, future work should aim to expand this method’s scope to include a wider range of brain lesions, such as metastatic tumors, meningiomas, and other space-occupying lesions. This would not only enhance the versatility of this method but also broaden its utility in neuro-oncology diagnostics, making it applicable to a larger variety of clinical cases.

Additionally, future research should focus on refining MRI parameter utilization and incorporating more-detailed MRI protocols. Although this method has shown promising results for the datasets currently used, integrating comprehensive MRI characteristics into the segmentation process would improve the interpretability, accuracy, and reproducibility of the results across different clinical environments. A deeper understanding of how various MRI parameters, such as intensity inhomogeneity, noise reduction, and tumor heterogeneity, affect segmentation outcomes would further bolster this method’s robustness in diverse clinical scenarios. In terms of performance enhancement, future efforts should prioritize improving standard metrics such as the PSNR, TC, and Dice Score. While these metrics provide valuable insights into segmentation quality, their improvement in parallel with a reduction in computational time is critical. By optimizing computational efficiency, this algorithm can be adapted to handle larger datasets and more complex clinical cases. This optimization will also make this method suitable for real-time clinical applications, where time-sensitive decision making is crucial.

Lastly, a comparative analysis of the algorithm’s performance with respect to other existing methods, including in relation to processing time and segmentation accuracy, would provide concrete evidence of its potential advantages. This would further solidify the algorithm’s position as a viable solution for clinical use. By addressing these limitations and broadening its scope, the EHO-EnFCM method has the potential to evolve into a comprehensive, robust, and adaptable tool for brain tumor segmentation. These advancements will not only improve its clinical applicability but also contribute to the broader field of medical imaging and neuro-oncology research.

5. Conclusions

The proposed EHO-EnFCM algorithm successfully addresses critical challenges in MRI-based brain tumor segmentation, demonstrating superior performance in noise reduction, handling intensity inhomogeneity, and managing tumor heterogeneity. By integrating the optimization capabilities of EHO with the clustering strength of EnFCM, the hybrid approach achieves a balance between segmentation accuracy and computational efficiency, as reflected in the enhanced performance metrics presented in Table 1 and Table 3.

Enhanced segmentation accuracy: The EHO-EnFCM approach significantly improves tumor boundary identification and reduces segmentation noise, making it a reliable tool for clinical applications. This improved precision enables radiologists to make more accurate diagnoses and treatment plans.

Noise reduction capabilities: The hybrid algorithm effectively minimizes the impact of noise in MRI scans, as evidenced by the superior PSNR values. This reduction in noise ensures clearer visualization of tumor regions, which is critical for further medical analysis and decision making.

The ability to handle intensity inhomogeneity: By addressing varying intensity levels within tumor regions, EHO-EnFCM ensures more precise segmentation results can be obtained. This capability is essential for overcoming one of the most persistent challenges in MRI-based segmentation, enabling consistent and reliable tumor delineation.

Robustness to tumor heterogeneity: The proposed method demonstrates adaptability to irregular shapes, textures, and sizes, which are critical features for accurate glioma segmentation. This adaptability ensures that EHO-EnFCM can handle diverse tumor characteristics effectively, improving its utility in various clinical scenarios.

Computational efficiency: Faster processing times coupled with high segmentation accuracy make EHO-EnFCM suitable for real-time clinical environments. This efficiency not only reduces the workload for medical professionals but also facilitates the integration of this algorithm into existing clinical workflows.

Future prospects and broader applicability: While achieving significant advancements, further refinements are necessary to enhance Dice Similarity (DS) scores and address overlapping region accuracy. Additionally, this methodology can potentially be extended to other medical imaging domains, such as cardiac or liver imaging, to validate its generalizability and efficacy. Larger-scale clinical trials should be conducted to test the robustness and adaptability of EHO-EnFCM across diverse patient populations and imaging conditions.

In conclusion, the EHO-EnFCM method offers a comprehensive solution to longstanding challenges in MRI-based brain tumor segmentation. By addressing the limitations of traditional approaches and demonstrating significant improvements in segmentation precision, computational efficiency, and adaptability, it holds great promise for transforming clinical practices. This innovation not only facilitates timely and accurate tumor diagnostics but also contributes to the broader goal of improving patient care and treatment outcomes.