Using Symmetries to Investigate the Complete Integrability, Solitary Wave Solutions and Solitons of the Gardner Equation

Abstract

In this paper, using a scaling symmetry, it is shown how to compute polynomial conservation laws, generalized symmetries, recursion operators, Lax pairs, and bilinear forms of polynomial nonlinear partial differential equations, thereby establishing their complete integrability. The Gardner equation is chosen as the key example, as it comprises both the Korteweg–de Vries and modified Korteweg–de Vries equations. The Gardner and Miura transformations, which connect these equations, are also computed using the concept of scaling homogeneity. Exact solitary wave solutions and solitons of the Gardner equation are derived using Hirota’s method and other direct methods. The nature of these solutions depends on the sign of the cubic term in the Gardner equation and the underlying mKdV equation. It is shown that flat (table-top) waves of large amplitude only occur when the sign of the cubic nonlinearity is negative (defocusing case), whereas the focusing Gardner equation has standard elastically colliding solitons. This paper’s aim is to provide a review of the integrability properties and solutions of the Gardner equation and to illustrate the applicability of the scaling symmetry approach. The methods and algorithms used in this paper have been implemented in Mathematica, but can be adapted for major computer algebra systems.

1. Introduction

Several physically important nonlinear partial differential equations (PDEs) are completely integrable by the inverse scattering transform (IST) method, which can be viewed as the nonlinear analog of the Fourier transform method (see [1,2,3] and references therein). Arguably, the most well-known completely integrable PDEs are the Korteweg–de Vries (KdV), modified KdV (mKdV), nonlinear Schrödinger, and sine-Gordon equations. They model wave phenomena in a wide range of applications in modern theoretical and mathematical physics, including fluid dynamics, nonlinear optics, and plasma physics, to name a few.

“Complete integrability” is an elusive term [4], but completely integrable equations have remarkable properties and a rich mathematical structure. For instance, they possess infinitely many conservation laws and high-order symmetries. They admit a Lax pair where the nonlinear PDE is replaced by a pair of linear equations whose compatibility only holds on solutions of the nonlinear PDE. They can be viewed as infinite dimensional Hamiltonian systems with two or three different Hamiltonians. By applying a change of dependent variable, completely integrable PDEs can be transformed into equations that are homogeneous of degree (second or higher) in that new variable and be recast in bilinear form in terms of Hirota operators [5,6]. Most importantly, completely integrable PDEs have solitary waves solutions that maintain their shape and speed while propagating at a constant velocity, and soliton solutions made up of such solitary waves that collide elastically. Nowadays, the terms solitary wave and soliton are used interchangeably, without reference to the elastic scattering property.

To obtain an initial idea about the possible complete integrability of a PDE, one should check if the equation has the Painlevé property [1,2], meaning that its solutions have no worse singularities than movable poles. To do so, one runs the so-called Painlevé test [7], which is algorithmic and can be performed with our Mathematica code PainleveTest.m [8]. If a PDE passes the Painlevé test, there is no guarantee that it is completely integrable, but it is more likely than not to have special properties, viz., conservation laws, generalized symmetries, and so on.

In this paper we use the concept of scaling homogeneity to symbolically compute conserved densities, fluxes, higher-order symmetries, Lax pairs, bilinear forms, and Miura-type transformations for polynomial systems of PDEs, thereby testing their complete integrability in a variety of ways. To keep the paper accessible to non-experts, we only cover PDEs in $(1+1)$ dimensions, i.e., one space variable $\left(x\right)$ in addition to time $\left(t\right)$. To illustrate the steps of the computations we focus on the Gardner equation, which comprises the KdV and mKdV equations as special cases. Therefore, the results for these two important soliton equations are obtained without extra effort. This paper’s purpose is to provide a review of the integrability properties and solutions of the Gardner equation and illustrate the applicability of the scaling symmetry approach for investigating the complete integrability of polynomial nonlinear PDEs.

Scaling homogeneity is a feature common to many nonlinear PDEs, and it provides an elegant way to find, e.g., densities and higher-order symmetries. Indeed, these scalar quantities can be derived as linear combinations with undetermined (constant) coefficients of scaling homogeneous polynomial terms in the dependent variables and their derivatives. Since the defining equations for these quantities are linear, the method comes down to solving linear systems for the undetermined coefficients.

For conservation laws, the time derivative of a candidate density must be the total derivative of an unknown flux. To test this type of “exactness” we use the Euler operator from the calculus of variations. An automated computation of the corresponding fluxes requires integration by parts on the so-called jet space. In essence, one needs to integrate expressions involving arbitrary functions. Unfortunately, computer algebra systems (CAS) often fail at that task. To circumvent this shortcoming, we use the homotopy operator from differential geometry, which reduces the problem to a one-dimensional integral with respect to an auxiliary parameter.

The existence of a sufficiently large number of non-trivial densities suffices to establish complete integrability of a given PDE. In most cases, the corresponding fluxes are not needed. However, for some equations, e.g., the Kadomtsev–Petviashvili equation [1,2], it is necessary to swap the independent variables to be able to rewrite the PDE as a system of evolution equations. In doing so, the roles of density and flux become interchanged, and that is why we also show the computation of the flux.

The computation of higher-order symmetries is performed with the same methodology without having to rely on the relationship between symmetries and conservation laws, as expressed through Noether’s theorem. The scaling symmetry argument and the method of undetermined coefficients also apply to recursion operators, which connect the generalized symmetries. Of course, the recursion operator is hard to compute because it involves total derivatives and anti-derivatives. Fortunately, the defining equation for the recursion operator is linear, which again reduces the problem to solving a linear system. By applying the recursion operator to a low-order generalized symmetry, one can generate all higher-order symmetries one after another. Thus, the existence of a recursion operator provides proof that a nonlinear PDE is completely integrable. With the recursion operator, one can build a hierarchy of completely integrable equations which have the same properties as the original nonlinear PDE. For example, the well-known Lax equation [5,9], which is of fifth order in x, is the first higher-order generalized symmetry of the KdV equation [10]. When encountering a allegedly “new” nonlinear PDE of high-order in the literature, one should verify that it does not belong to the hierarchy of symmetries of a well-studied PDE of lower order.

The computation of Lax pairs based on scaling homogeneity is more challenging because the defining equation is no longer linear, and thus the method of undetermined coefficients leads to an algebraic system with quadratic terms. It is still quite straightforward to solve; however, if parameters are present, finding the conditions of the parameters for which solutions exist is substantially harder. The knowledge of a Lax pair is essential to apply the IST, which allows one to solve the initial value problem for a nonlinear PDE and, consequently, find solitary wave solutions and solitons. Obtaining a Lax pair is the first step in the application of the IST and Riemann–Hilbert method to find soliton solutions. Using the Lax pair one can also derive conservation laws and many other properties of the nonlinear PDE.

The same thing happens when applying the scaling homogeneity method to compute the Miura and Gardner transformations. Here, one has to solve quadratic systems for the undetermined coefficients. The Miura transformation, which connects the KdV and mKdV equations, had a profound impact on the discovery of conservation laws of both equations and, in general, the early development of the notion of complete integrability of PDEs and soliton theory.

To apply Hirota’s direct method for finding solitary waves and solitons, the given PDE must be cast in bilinear form. Finding that bilinear representation is a non-trivial task which requires some insight, experience, and often ingenuity as explained in [5], our scaling-homogeneity approach is still helpful, but has its limitations— in particular, if finding a bilinear representation requires splitting an expression into two parts in such a way that each part can be written in bilinear form. This is exactly what must be conducted with regard to the mKdV and Gardner equations and, as far as we know, there is no algorithmic way to achieve this. Once the bilinear representation is found, special solutions, including solitary waves and solitons, can be computed algorithmically.

As we will also show in Section 9, the Gardner equation can be transformed into the mKdV equation via a Galilean transformation. Consequently, any time new solutions of the mKdV equation are discovered, one obtains additional solutions to the Gardner equation, and vice versa [11]. The search for new solutions, in particular for the defocusing mKdV equation, is still an active area of research (see, e.g., refs. [12,13,14,15]). Over the last two decades, our research team has designed and implemented fast algorithms [16,17,18] to test the integrability of nonlinear PDEs based on the concept of scaling symmetry [9,10,19,20,21,22,23]. In addition, we have implemented a simplified version of Hirota’s method [5,24] and other direct methods [25,26] to find exact solutions for nonlinear PDEs. As a matter of fact, the computations in this paper have been largely performed with our software packages, which are written in Mathematica syntax, but could be adapted for other computer algebra systems such as Maple and REDUCE.

The paper is organized as follows. In Section 2 we introduce the Gardner equation and mention some of its applications. As shown in Section 3, the Gardner equation passes the Painlevé test, which indicates that the equation likely has many interesting properties. In Section 4, we discuss the scaling symmetry of the Gardner equation, as well as the KdV and mKdV equations. Section 5 is devoted to the computation of conservation laws. Section 6 and Section 7 cover the computation of generalized symmetries and the recursion operator that connects them. In Section 8, we turn our attention to the computation of a Lax pair for the Gardner equation. The derivation of a bilinear representation is covered in Section 9. The computation of the Gardner transformation (connecting solutions of the Gardner equation and KdV equations) is shown in Section 10.

With the important quantities of the Gardner equation being computed, we show in Section 11 and Section 12 how our results translate to the KdV and mKdV equations. Solitary wave solutions and solitons are covered in Section 13 and Section 14, where we show that the nature of the solutions of the Gardner and mKdV equations depends on the sign of the cubic nonlinearity. A brief discussion of our software packages used in this study is given in Section 15. Finally, in Section 16, we draw some conclusions and mention a few topics for future work.

2. The Gardner Equation

The Gardner equation [27] is the nonlinear PDE

$$u_t+\alpha u{u}_x+\beta u^2{u}_x+u_{3x}=0,$$

(1)

where $u(x,t)$ is the dependent variable (or field) which is a function of space variable x and time t. The subscripts denote partial derivatives, i.e., $u_t={\displaystyle \frac{\partial u}{\partial t}},u_x={\displaystyle \frac{\partial u}{\partial x}},$ and $u_{3x}={\displaystyle \frac{{\partial }^{3}u}{\partial x^3}}.$ The parameters $\alpha$ and $\beta$ are real numbers for which the values $\pm 1$ and $\pm 6$ are frequently used in the literature.

The Gardner equation has the KdV and mKdV equations as special cases. Therefore, (1) is sometimes called the combined or mixed KdV-mKdV equation. Indeed, for $\beta =0$, (1) reduces to the ubiquitous Korteweg–de Vries equation [28],

$$u_t+\alpha u{u}_x+u_{3x}=0,$$

(2)

which models, e.g., shallow water waves [29], ion-acoustic waves in plasmas [1,2,30], and many other nonlinear wave phenomena where solitons arise. When $\alpha =0$, (1) becomes the mKdV equation [1,27],

$$u_t+\beta u^2{u}_x+u_{3x}=0,$$

(3)

which models internal ocean waves, electromagnetic surface waves, waves in plasmas, and more [1].

Equation (1) appears for the first time in [31,32] in the context of the Miura transformation (see Section 10), which connects the mKdV and KdV equations. The Gardner equation has a long history [27,33] and many applications [34] in fluid dynamics: in particular, for modeling long internal water waves [35,36], the dynamics of undular bores [37], and waves in multi-species plasma physics [38,39,40,41]. There is a wealth of information available about the Gardner equation. The equation appears in most books about solitons and integrability (see, e.g., ref. [29], which includes a list of soliton books).

Without loss of generality, we take $\alpha \ge 0$ in (1), because if $\alpha <0$, replacing u by $-u$ would make the coefficient of $u{u}_x$ positive again. However, no discrete symmetries of $x,t,$ or u will flip the sign of the coefficient of $u^2{u}_x$, so the cases for positive and negative $\beta$ will have to be treated separately. Exact solutions of (1) with $\beta >0$, called the focusing Gardner equation, are quite different from these of the defocusing case, where $\beta <0$.

We focus on (1) because it is a typical example of a scalar $(1+1)$-dimensional evolution equation,

$$u_t=F(x,t,u,u_x,u_{xx},\cdots ,u_{nx}),$$

(4)

of order n in x and first order in t, with $n=3$ in (1). More importantly, many of the results for (1) lead to the corresponding results for the KdV and mKdV equations by setting $\beta =0$ or $\alpha =0$, respectively. Like the latter two equations, the Gardner equation is known to be completely integrable for both signs of $\beta$, but the solutions are quite different for $\beta >0$ and $\beta <0$. The latter case is the hardest to deal with. The solitary wave solutions and solitons for the focusing Gardner equation follow from those of a focusing mKdV equation to which the Gardner equation can be reduced. The so-called “table-top” or “flat-top” soliton, corresponding to a large amplitude, only exists for the defocusing Gardner equation.

In some applications, the coefficients $\alpha$ and $\beta$ are time dependent [35]. In that case, (1) has only a couple of conservation laws (conservation of mass and wave action flux, see Section 5) and is non-integrable. The treatment of (1) with varying coefficients is outside the scope of this paper.

3. Painlevé Analysis

In this Section we check if (1) has the Painlevé property. Performing the Painlevé test is straightforward but usually involves lengthy computations best performed with a software package such as PainleveTest.m [8]. In essence, one investigates a Laurent series solution for (1),

$$u(x,t)=g{(x,t)}^{\sigma }\sum _{k=0}^{\infty }{u}_k(x,t)g{(x,t)}^k,$$

(5)

in which the coefficients $u_k(x,t)$ are analytic functions in a neighborhood of the singular manifold $g(x,t)$. Furthermore, $g(x,t)=0$ determines the poles and $g(x,t)$ is assumed to be non-characteristic (i.e., $g_x(x,t)\ne 0$). The negative integer $\sigma$ determines the leading order term, $u_0{g}^{\sigma }$, in (5). We summarize the main steps of the Painlevé test below; refer to [7] for details.

• Step 1: Compute the leading order term. To determine $\sigma$ and $u_0$, substitute $u_0{g}^{\sigma }$ into (1). Balance the minimal power terms in g, namely, $g^{3\sigma -1}$ and $g^{\sigma -3}$, to get $\sigma =-1$. Next, require that the leading terms (in $g^{-4})$ vanish, yielding

  $$\begin{array}{ccc}\hfill u_0& =& \pm \sqrt{-\frac{6}{\beta }}{g}_x\mathrm{if}\beta <0,\mathrm{or}\hfill \end{array}$$

  (6)

  $$\begin{array}{ccc}\hfill u_0& =& \pm i\sqrt{\frac{6}{\beta }}{g}_x\mathrm{if}\beta >0.\hfill \end{array}$$

  (7)
• Step 2: Compute the resonances. In this step, one determines which functions $u_k(x,t)$ in (5) will remain arbitrary. That happens at specific values of k, called resonances, denoted by r. To find the resonances, substitute $u_0{g}^{\sigma }+u_r{g}^{\sigma +r}$, with $\sigma =-1$ and $u_0$ given in (6) or (7) into (1), and equate the coefficients of the dominant terms (in $g^{r-4}$) that are linear in $u_r$ to get the characteristic equation

  $$(r-4)(r-3)(r+1)u_r{g}_x^3=0.$$

  (8)

  Since $g_x\ne 0,$ the resonances are $r_1=-1,r_2=3$, and $r_3=4.$ Resonance $r_1=-1$ corresponds to the arbitrariness of g.

• Step 3: Check the compatibility conditions. To do so, substitute

  $$u={\displaystyle \frac{1}{g}}\sum _{k=0}^4{u}_k{g}^k,$$

  (9)

  into (1) and verify that $u_1$ and $u_2$ can be unambiguously determined. Verify also that $u_3$ and $u_4$ are indeed arbitrary functions, meaning that no compatibility conditions arise. For (1), one readily determines the real functions,

  $$\begin{array}{ccc}\hfill u_1& =& -{\displaystyle \frac{\alpha }{2\beta }}\pm \frac{1}{2}\sqrt{-\frac{6}{\beta }}\left({\displaystyle \frac{g_{xx}}{g_x}}\right),\hfill \end{array}$$

  (10)

  $$\begin{array}{ccc}\hfill u_2& =& \pm \left({\displaystyle \frac{4\beta g_x{g}_t-{\alpha }^2{g}_x^2-6\beta g_{xx}^2+4\beta g_x{g}_{3x}}{4\beta \sqrt{-6\beta }{g}_x^3}}\right),\hfill \end{array}$$

  (11)

  when $\beta <0$ (and complex expressions when $\beta >0$). At resonance $r=3$, the compatibility condition (arising as the coefficient of $g^{-3}$),

  $$\left(u_0^2\left(\alpha +2\beta u_1\right)-6\left({\left(u_0\right)}_x{g}_x+u_0{g}_{xx}\right)\right)g_x-\beta u_0^2{\left(u_0\right)}_x=0,$$

  (12)

  is identically satisfied upon substitution of (6) and (10). Likewise, a long but straightforward computation shows that the compatibility condition at $r=4$ (appearing at order $g^{-2}$),

  $$\begin{array}{ccc}& & \left(u_0{u}_1\left(\alpha +\beta u_1\right)+\beta u_0^2{u}_2+3{\left(u_0\right)}_{xx}\right)g_x+u_0{g}_t-u_0{\left(u_0\right)}_x\left(\alpha +2\beta u_1\right)\hfill \\ & & -\beta u_0^2{\left(u_1\right)}_x+3{\left(u_0\right)}_x{g}_{xx}+u_0{g}_{3x}=0,\hfill \end{array}$$

  (13)

  is identically satisfied upon substitution of (6), (10), and (11).

Thus, at least in the neighborhood of $g(x,t)=0$, solution (9) is free of algebraic and logarithmic movable branch points. Apart from possible essential singularities (which the test is unable to detect), the movable singularities of its general solution are poles determined by $g(x,t)=0$. Note that (5) serves as a general solution because, as required by the Cauchy–Kovalevskaya theorem, (1) is of order 3 in x and that number agrees with 3 arbitrary functions $g(x,t)$, $u_3(x,t),$ and $u_4(x,t)$ in (5).

Moreover, notice that truncating the Laurent series at the constant level term yields an auto-Bäcklund transformation,

$$u(x,t)=\pm i\sqrt{\frac{6}{\beta }}\left(\frac{g_x}{g}\right)+u_1(x,t)=\pm i\sqrt{\frac{6}{\beta }}{\left(lng\right)}_x+u_1(x,t),$$

(14)

because for an arbitrary $g(x,t)$, both $u(x,t)$ and $u_1(x,t)$ must then be solutions of (1) with $\beta >0$. Setting $u_1(x,t)=0$ in (14) motivates the Hirota transformation discussed in Section 9, where it is shown that only for $\beta >0$ one can find soliton solutions of (1).

In conclusion, the Gardner equation passes the Painlevé test and, therefore, has the Painlevé property, which is a good predictor that the equation has conservation laws, generalized symmetries, and so on. The investigation and actual computation of these quantities is based on a scaling symmetry of (1), which we will discuss next.

4. Scaling Symmetry

As stated, when $\beta =0$, the Gardner equation reduces to the KdV Equation (2), which is scaling homogeneous under the scaling (dilation) symmetry

$$(x,t,u)\to ({\kappa }^{-1}x,{\kappa }^{-3}t,{\kappa }^{2}u)=(\tilde{x},\tilde{t},\tilde{u}),$$

(15)

where $\kappa \ne 0$ is an arbitrary scaling parameter. Indeed, replacing $(x,t,u)$ in the KdV equation in terms of $(\tilde{x},\tilde{t},\tilde{u})$ yields

$${\kappa }^{-5}({\tilde{u}}_{\tilde{t}}+\alpha \tilde{u}{\tilde{u}}_{\tilde{x}}+{\tilde{u}}_{3\tilde{x}})=0.$$

(16)

A fast way to compute (15) is to introduce the notions of weight, rank, and uniformity of rank. The weight, W, of a variable is the exponent of $\kappa$ that multiplies that variable. Thus, based on (15), $W\left(x\right)=-1,W\left(t\right)=-3$, and $W\left(u\right)=2$. Equivalently, $W\left({\displaystyle \frac{\partial }{\partial x}}\right)=1$ and $W\left({\displaystyle \frac{\partial }{\partial t}}\right)=3.$ The rank of a monomial is defined as the total weight of the monomial. For example, $\alpha u{u}_x$ has rank 5 since the parameter $\alpha$ has no weight. An expression (or equation) is uniform in rank if all its monomial terms have equal rank.

Now, if (15) were not known yet, it could quickly be found by requiring that the KdV equation is uniform in rank, yielding

$$W\left(u\right)+W\left({\displaystyle \frac{\partial }{\partial t}}\right)=2W\left(u\right)+W\left({\displaystyle \frac{\partial }{\partial x}}\right)=W\left(u\right)+3W\left({\displaystyle \frac{\partial }{\partial x}}\right).$$

(17)

Solving (17) gives $W\left({\displaystyle \frac{\partial }{\partial t}}\right)=3W\left({\displaystyle \frac{\partial }{\partial x}}\right)$ and $W\left(u\right)=2W\left({\displaystyle \frac{\partial }{\partial x}}\right).$ Since $\kappa$ is arbitrary, without loss of generality one can set $W\left({\displaystyle \frac{\partial }{\partial x}}\right)=1$, resulting in $W\left({\displaystyle \frac{\partial }{\partial t}}\right)=3$ and $W\left(u\right)=2.$ Thus, requiring uniformity in rank of a PDE allows one to compute the weights of the variables (and, hence, the scaling symmetry) with linear algebra.

Setting $\alpha =0$, the Gardner equation becomes the mKdV equation. Requiring uniformity in rank readily yields $W\left({\displaystyle \frac{\partial }{\partial t}}\right)=3$ and $W\left(u\right)=1.$ Hence, the mKdV equation is scaling homogeneous under the transformation

$$(x,t,u)\to ({\kappa }^{-1}x,{\kappa }^{-3}t,\kappa u).$$

(18)

Because $W\left(u\right)$ is different for the KdV and mKdV equations, the Gardner equation (1) will not be uniform in rank unless we use a trick. We will let the parameter $\alpha$ scale with some power of $\kappa$. Doing so, we must solve

$$W\left(u\right)+W\left({\displaystyle \frac{\partial }{\partial t}}\right)=W\left(\alpha \right)+2W\left(u\right)+W\left({\displaystyle \frac{\partial }{\partial x}}\right)=3W\left(u\right)+W\left({\displaystyle \frac{\partial }{\partial x}}\right)=W\left(u\right)+3W\left({\displaystyle \frac{\partial }{\partial x}}\right),$$

(19)

yielding

$$W\left({\displaystyle \frac{\partial }{\partial x}}\right)=1,W\left({\displaystyle \frac{\partial }{\partial t}}\right)=3,W\left(u\right)=1,W\left(\alpha \right)=1,$$

(20)

which expresses that (1) has the scaling symmetry

$$(x,t,u,\alpha )\to ({\kappa }^{-1}x,{\kappa }^{-3}t,\kappa u,\kappa \alpha ).$$

(21)

Starting with conservation laws, in what follows, we will use scaling symmetry to compute important quantities related to (1), thereby establishing its complete integrability.

5. Conservation Laws

A conservation law of (4) is an equation of the form

$${\mathrm{D}}_t\rho +{\mathrm{D}}_{x}J\dot{=}0,$$

(22)

where the dot means that the equality should only hold on solutions $u(x,t)$ of (4). $\rho$ is called a conserved density (or charge), and J is the corresponding flux (or current).

The scalar functions $\rho$ and J are functions of u and its partial derivatives with respect to x. All subsequent computations are performed on the jet space, which means that u and its partial derivatives with respect to x are treated as independent, alongside all monomials such as $u^3,u_x^2,$ etc. The density and flux could also explicitly depend on x and t, but we will not cover such exceptional cases.

In (22), ${\mathrm{D}}_t$ is the total derivative with respect to $t,$ defined by

$${\mathrm{D}}_t\rho ={\displaystyle \frac{\partial \rho }{\partial t}}+{\rho }^{\prime }\left[u_t\right]={\displaystyle \frac{\partial \rho }{\partial t}}+\sum _{k=0}^M{\displaystyle \frac{\partial \rho }{\partial u_{kx}}}{\mathrm{D}}_x^k{u}_t,$$

(23)

where ${\rho }^{\prime }\left[u_t\right]$ is the Fréchet derivative of $\rho$ in the direction of $u_t$, and M is the highest order of $\rho$ in x. In practice, one simply applies the chain rule for differentiation with respect to t, treating $u,u_x,u_{xx}$, etc., as independent functions.

Likewise, ${\mathrm{D}}_x$ is the total derivative with respect to x,

$${\mathrm{D}}_{x}J={\displaystyle \frac{\partial J}{\partial x}}+\sum _{k=0}^N{\displaystyle \frac{\partial J}{\partial u_{kx}}}{\mathrm{D}}_x\left(u_{kx}\right)={\displaystyle \frac{\partial J}{\partial x}}+\sum _{k=0}^N{\displaystyle \frac{\partial J}{\partial u_{kx}}}{u}_{(k+1)x},$$

(24)

where N is the order of J.

Since (22) is linear in the densities (and fluxes), a linear combination of densities with constant coefficients is still a density. The matching flux would, of course, be a linear combination of the corresponding fluxes with the same constant coefficients.

Returning to (1), one can readily verify that

$$\begin{array}{ccc}& & {\mathrm{D}}_t\left(u\right)+{\mathrm{D}}_x(\frac{1}{2}\alpha u^2+\frac{1}{3}\beta u^3+u_{xx})=0,\hfill \end{array}$$

(25)

$$\begin{array}{ccc}& & {\mathrm{D}}_t\left(u^2\right)+{\mathrm{D}}_x(\frac{2}{3}\alpha u^3+\frac{1}{2}\beta u^4-u_x^2+2u{u}_{xx})=0,\hfill \end{array}$$

(26)

$$\begin{array}{ccc}& & {\mathrm{D}}_t(\alpha u^3+\frac{1}{2}\beta u^4-3u_x^2)+{\mathrm{D}}_x\left(\frac{3}{4}{\alpha }^2{u}^4+\alpha \beta u^5+\frac{1}{3}{\beta }^2{u}^6-6\alpha u{u}_x^2-6\beta u^2{u}_x^2\right.\hfill \\ & & \left.+3\alpha u^2{u}_{xx}+2\beta u^3{u}_{xx}+3u_{xx}^2-6u_x{u}_{3x}\right)=0.\hfill \end{array}$$

(27)

Indeed, (25) is (1) written as a conservation law. Next, (26) straightforwardly follows after multiplication of (1) by $2u$ and a bit of integration by parts. Clearly, (27) is far less obvious and will require a computational strategy [9,23] and the use of codes like InvariantsSymmetries.m [17] or ConservationLawsMD.m [18].

Notice that the above densities are uniform in rank. Indeed, ${\rho }^{\left(1\right)}=u$ has rank 1, ${\rho }^{\left(2\right)}=u^2$ has rank 2, and ${\rho }^{\left(3\right)}$ is of rank 4. The corresponding fluxes are also uniform, with ranks $3,4,$ and $6.$ As a matter of fact, the entire conservation laws themselves are uniform in rank, with ranks $4,5,$ and 7, respectively. This comes as no surprise because the defining Equation (22) is only non-trivial if evaluated on solutions of the PDE, and therefore the densities, fluxes, and conservation laws “inherit” (or adopt) the scaling homogeneity of the given PDE (and all its other continuous and discrete symmetries, for that matter).

It turns out that the list of conservation laws of (1) continues ad infinitum. The Gardner equation has infinitely many conservation laws, which is a clear indication that the PDE is completely integrable.

Using the scaling symmetry (21), we will now show how to compute (27), which is the shortest possible density of rank 4, since it is free of any terms that could be moved into the flux.

• Step 1: Construct a candidate density of rank 4 as follows: Make a list of all monomials in u and $\alpha$ of rank 4 or less, i.e., $\{\{u^4,\alpha u^3,{\alpha }^2{u}^2,{\alpha }^{3}u,{\alpha }^4\}$, $\{u^3,\alpha u^2,{\alpha }^{2}u,{\alpha }^3\}$, $\{u^2,\alpha u,{\alpha }^2\}$, $\{u,\alpha \}$, $\left\{1\right\}\}$. For the construction of candidate densities, the constant terms ${\alpha }^4,{\alpha }^3,\dots ,1$ can be removed. Then, for each monomial in that list, apply the correct number of x-derivatives so that the resulting term has exactly rank 4. The terms in the first sublist need no derivatives. Those in the second sublist need a single derivative. The next set of terms need two derivatives, etc. For example, for the first element in the third sublist, ${\mathrm{D}}_x^2{u}^2=2u_x^2+2u{u}_{xx}.$ Obviously, if we carry out partial integration, the highest derivative term $u{u}_{xx}$ only differs from $u_x^2$ by the x-derivative of $\frac{1}{2}{u}^2$ and therefore can be ignored. Likewise, terms like $u^2{u}_x$, $\alpha u{u}_x$, ${\alpha }^2{u}_x$, $\alpha u_{xx},$ and $u_{3x}$ can be neglected because they are x-derivatives of single-term monomials (${\displaystyle \frac{1}{3}}{u}^3$, $\frac{1}{2}\alpha u^2$, etc.). There is no need to put terms like $u{u}_{xx}$, $u^2{u}_x$ in the density because they can be moved to the flux.

Gather the resulting monomials after stripping off numerical factors and removing scalar multiples of single-term densities of lower rank (with regard to (25) and (26) these are ${\alpha }^{3}u$ and ${\alpha }^2{u}^2$). Finally, linearly combine the remaining terms with constant coefficients, yielding

$$\rho =c_1{u}^4+c_2\alpha u^3+c_3{u}_x^2,$$

(28)

which is of first order in x ($M=1$).

• Step 2: Compute the undetermined coefficients. Using (23), first compute

  $${\mathrm{D}}_t\rho =(4c_1{u}^3\mathrm{I}+3\alpha c_2{u}^2\mathrm{I}+2c_3{u}_x{\mathrm{D}}_x)\left[u_t\right]=(4c_1{u}^3+3\alpha c_2{u}^2)u_t+2c_3{u}_x{u}_{xt},$$

  (29)

  where ${\mathrm{D}}_x^0=\mathrm{I}$ is the identity operator. Replace $u_t$ and $u_{xt}=u_{tx}$ from (1) to get

  $$\begin{array}{ccc}\hfill E& =& -\left((4c_1{u}^3+3\alpha c_2{u}^2)(\alpha u{u}_x+\beta u^2{u}_x+u_{3x})+\left(2c_3{u}_x\right){(\alpha u{u}_x+\beta u^2{u}_x+u_{3x})}_x\right)\hfill \\ & =& -\left(\alpha (4c_1+3\beta c_2)u^4{u}_x+4\beta c_1{u}^5{u}_x+4c_1{u}^3{u}_{3x}+3{\alpha }^2{c}_2{u}^3{u}_x+3\alpha c_2{u}^2{u}_{3x}\right.\hfill \\ & & \left.+2\alpha c_3{u}_x^3+2\alpha c_{3}u{u}_x{u}_{xx}+4\beta c_{3}u{u}_x^3+2\beta c_3{u}^2{u}_x{u}_{xx}+2c_3{u}_x{u}_{4x}\right).\hfill \end{array}$$

  (30)

  Next, find the constants $c_1,c_2,$ and $c_3$ so that $E={\mathrm{D}}_t\rho$ matches $-{\mathrm{D}}_{x}J$ for some flux J (to be computed in Step 3 below). Mathematically, this means that E must be exact. The Euler operator (variational derivative),

  $$\begin{array}{c}\hfill {\mathcal{L}}_{u\left(x\right)}=\sum _{k=0}^K{(-{\mathrm{D}}_x)}^k{\displaystyle \frac{\partial }{\partial u_{kx}}}={\displaystyle \frac{\partial }{\partial u}}-{\mathrm{D}}_x{\displaystyle \frac{\partial }{\partial u_x}}+{\mathrm{D}}_x^2{\displaystyle \frac{\partial }{\partial u_{xx}}}-{\mathrm{D}}_x^3{\displaystyle \frac{\partial }{\partial u_{3x}}}+{\mathrm{D}}_x^4{\displaystyle \frac{\partial }{\partial u_{4x}}}+\dots ,\end{array}$$

  (31)

  allows one to test exactness [21,22,23,42], where K is the order of the expression the Euler operator is applied to. Therefore, $K=4$ for E in (30). Consequently, (31) will terminate after five terms. E will be exact if ${\mathcal{L}}_{u\left(x\right)}E\equiv 0$ on the jet space (treating $u,u_x,u_{xx}$, etc., and also all monomials in such variables as independent). The computation of the terms in (31) involves nothing more than partial differentiations followed by (total) differentiations with respect to x. Of a total of 30 terms (not listed) generated, many terms are canceled, and one is left with

  $${\mathcal{L}}_{u\left(x\right)}E=-4(6c_1+\beta c_3)(u_x^3+3u{u}_x{u}_{xx})-6\alpha (3c_2+c_3)u_x{u}_{xx},$$

  (32)

  which must vanish identically, yielding the linear system $6c_1+\beta c_3=0$ and $3c_2+c_3=0$ with solution $c_1=\frac{1}{2}\beta ,c_2=1,c_3=-3$. Substitute these constants into (28) to obtain

  $${\rho }^{\left(3\right)}=\alpha u^3+\frac{1}{2}\beta u^4-3u_x^2,$$

  (33)

  the same expression as in (27). If one were only interested in the density, the computation would finish here. To continue with the computation of the flux (in the next step), substitute the constants into (30), yielding

  $$\begin{array}{ccc}\hfill E& =& -\left(5\alpha \beta u^4{u}_x+2{\beta }^2{u}^5{u}_x+2\beta u^3{u}_{3x}+3{\alpha }^2{u}^3{u}_x+3\alpha u^2{u}_{3x}\right.\hfill \\ & & \left.-6\alpha u_x^3-12\beta u{u}_x^3-6\alpha u{u}_x{u}_{xx}-6\beta u^2{u}_x{u}_{xx}-6u_x{u}_{4x}\right).\hfill \end{array}$$

  (34)
• Step 3: Compute the flux. Since ${\mathrm{D}}_x{J}^{\left(3\right)}=-{\mathrm{D}}_t{\rho }^{\left(3\right)}=-E$, to get $J^{\left(3\right)}$ one must integrate E with respect to x and reverse the sign. There is a tool from differential geometry, called the homotopy operator [43] p. 372, to carry out integration by parts on the jet space. As will be shown below, application of the homotopy operator reduces the integration on the jet space to a standard one-dimensional integration with respect to an auxiliary variable which will be denoted by $\lambda$.

The homotopy operator for variable $u\left(x\right),$ acting on a exact expression E of order K, is given [21,22,23,42,44] by

$${\mathcal{H}}_{u\left(x\right)}E={\int }_0^1\left(I_{u}E\right)\left[\lambda u\right]{\displaystyle \frac{d\lambda }{\lambda }},$$

(35)

with integrand

$$\begin{array}{ccc}\hfill I_{u}E& =& \sum _{k=1}^K\left(\sum _{i=0}^{k-1}{u}_{ix}{(-{\mathrm{D}}_x)}^{k-(i+1)}\right){\displaystyle \frac{\partial E}{\partial u_{kx}}}\hfill \\ & =& (u\mathrm{I})({\displaystyle \frac{\partial E}{\partial u_x}})+(u_x\mathrm{I}-u{\mathrm{D}}_x)({\displaystyle \frac{\partial E}{\partial u_{xx}}})+(u_{xx}\mathrm{I}-u_x{\mathrm{D}}_x+u{\mathrm{D}}_x^2)({\displaystyle \frac{\partial E}{\partial u_{3x}}})\hfill \\ & & +(u_{3x}\mathrm{I}-u_{xx}{\mathrm{D}}_x+u_x{\mathrm{D}}_x^2-u{\mathrm{D}}_x^3)({\displaystyle \frac{\partial E}{\partial u_{4x}}})+\dots .\hfill \end{array}$$

(36)

In (35), $\left(I_{u}E\right)\left[\lambda u\right]$ means that once $I_{u}E$ is computed one must replace u by $\lambda u$, $u_x$ by $\lambda u_x$, $u_{xx}$ by $\lambda u_{xx}$, etc. Use (34), to get

$$\begin{array}{ccc}\hfill {\mathrm{I}}_{u}E& =& \left(u\mathrm{I}\right)(-5\alpha \beta u^4-2{\beta }^2{u}^5-3{\alpha }^2{u}^3+18\alpha u_x^2+36\beta u{u}_x^2+6\alpha u{u}_{xx}+6\beta u^2{u}_{xx}+6u_{4x})\hfill \\ & & +(u_x\mathrm{I}-u{\mathrm{D}}_x)(6\alpha u{u}_x+6\beta u^2{u}_x)+(u_{xx}\mathrm{I}-u_x{\mathrm{D}}_x+u{\mathrm{D}}_x^2)(-3\alpha u^2-2\beta u^3)\hfill \\ & & +(u_{3x}\mathrm{I}-u_{xx}{\mathrm{D}}_x+u_x{\mathrm{D}}_x^2-u{\mathrm{D}}_x^3)\left(6u_x\right)\hfill \\ & =& -\left(3{\alpha }^2{u}^4+5\alpha \beta u^5+2{\beta }^2{u}^6-18\alpha u{u}_x^2-24\beta u^2{u}_x^2+9\alpha u^2{u}_{xx}+8\beta u^3{u}_{xx}\right.\hfill \\ & & \left.+6u_{xx}^2-12u_x{u}_{3x}\right),\hfill \end{array}$$

(37)

which already has the terms of $J^{\left(3\right)}$, but still with incorrect coefficients (and the opposite sign). Finally, using (35),

$$\begin{array}{ccc}\hfill J^{\left(3\right)}& =& -{\mathcal{H}}_{u\left(x\right)}\left(E\right)=-{\int }_0^1\left(I_u\left(E\right)\right)\left[\lambda u\right]{\displaystyle \frac{d\lambda }{\lambda }}\hfill \\ & =& {\int }_0^1\left(3{\alpha }^2{\lambda }^3{u}^4+5\alpha \beta {\lambda }^4{u}^5+2{\beta }^2{\lambda }^5{u}^6-18\alpha {\lambda }^{2}u{u}_x^2-24\beta {\lambda }^3{u}^2{u}_x^2\right.\hfill \\ & & \left.+9\alpha {\lambda }^2{u}^2{u}_{xx}+8\beta {\lambda }^3{u}^3{u}_{xx}+6\lambda u_{xx}^2-12\lambda u_x{u}_{3x}\right)d\lambda \hfill \\ & =& \frac{3}{4}{\alpha }^2{u}^4+\alpha \beta u^5+\frac{1}{3}{\beta }^2{u}^6-6\alpha u{u}_x^2-6\beta u^2{u}_x^2+3\alpha u^2{u}_{xx}+2\beta u^3{u}_{xx}\hfill \\ & & +3u_{xx}^2-6u_x{u}_{3x},\hfill \end{array}$$

(38)

which is exactly the flux in (27).

We close this section with a remark about the use of conserved densities and constants of motion. If J vanishes at infinity (because u and its x-derivatives decay to zero), then integration of (22) with respect to x yields

$${\displaystyle \frac{d}{dt}}{\int }_{-\infty }^{\infty }\rho dx=0.$$

(39)

Hence,

$$P={\int }_{-\infty }^{\infty }\rho dx$$

(40)

is constant in time and often referred to as a conserved quantity or constant of motion. Depending on the physical setting, the first few constants of motion express conservation of mass, momentum, and energy. Preserving these types of quantities plays an important role in testing the accuracy of numerical integrators. For example, some symmetric time-stepping methods [45] and explicit finite-difference schemes [46,47] preserve two of these three conserved quantities of low degree, while the more general symplectic integrators preserve the Hamiltonian structure [48,49]. The reader is referred to, e.g.,  [50,51,52,53] for an in-depth discussion of this subject.

6. Generalized Symmetries

A second criterion to establish the complete integrability of (1) is to show that the PDE has infinitely many generalized (higher-order) symmetries. As we will see, the computation of a hierarchy of such symmetries [10] is algorithmic and easier than for conservation laws.

A scalar function $G(x,t,u,u_x,u_{xx},\dots ,u_{mx})$ is called a generalized symmetry of (4) if and only if it leaves (4) invariant under the replacement $u\to u+ϵG$ within order $ϵ$, that is,

$${\mathrm{D}}_t(u+ϵG)\dot{=}F(u+ϵG)$$

(41)

must hold up to order $ϵ$ on the solutions of (4). Consequently, G must satisfy the linearized equation

$${\mathrm{D}}_{t}G={\displaystyle \frac{\partial G}{\partial t}}+F^{\prime }\left[G\right],$$

(42)

where $F^{\prime }$ is the Fréchet derivative of F in the direction of G:

$$\begin{array}{ccc}\hfill F^{\prime }\left[G\right]& =& {\displaystyle \frac{\partial }{\partial ϵ}}F{(u+ϵG)}_{|ϵ=0}\hfill \end{array}$$

(43)

$$\begin{array}{ccc}& =& \sum _{k=0}^n{\displaystyle \frac{\partial F}{\partial u_{kx}}}{\mathrm{D}}_x^{k}G={\displaystyle \frac{\partial F}{\partial u}}\mathrm{I}G+{\displaystyle \frac{\partial F}{\partial u_x}}{\mathrm{D}}_{x}G+{\displaystyle \frac{\partial F}{\partial u_{xx}}}{\mathrm{D}}_x^{2}G+{\displaystyle \frac{\partial F}{\partial u_{3x}}}{\mathrm{D}}_x^{3}G+\dots ,\hfill \end{array}$$

(44)

where n is the (highest) order of F. In (41) and (43), one must not only replace u by $u+ϵG,$ but also $u_x$ by $u_x+ϵ{\mathrm{D}}_{x}G$,   $u_{xx}$ by $u_{xx}+ϵ{\mathrm{D}}_x^{2}G$, etc. As before, $\mathrm{I}$ is the identity operator. The total derivative operators, ${\mathrm{D}}_t$ and ${\mathrm{D}}_x$, were defined in (23) and (24), respectively. Since the defining Equation (42) is evaluated on solutions of the PDE, the higher-order symmetries inherit the scaling homogeneity of (4).

As we will show, (1) has infinitely many generalized symmetries, starting with

$$\begin{array}{ccc}\hfill G^{\left(1\right)}& =& u_x,\hfill \end{array}$$

(45)

$$\begin{array}{ccc}\hfill G^{\left(2\right)}& =& \alpha u{u}_x+\beta u^2{u}_x+u_{3x},\hfill \end{array}$$

(46)

$$\begin{array}{ccc}\hfill G^{\left(3\right)}& =& \frac{5}{6}{\alpha }^2{u}^2{u}_x+\frac{5}{3}\alpha \beta u^3{u}_x+\frac{5}{6}{\beta }^2{u}^4{u}_x+\frac{5}{3}\beta u_x^3+\frac{10}{3}\alpha u_x{u}_{xx}+\frac{20}{3}\beta u{u}_x{u}_{xx}\hfill \\ & & +\frac{5}{3}\alpha u{u}_{3x}+\frac{5}{3}\beta u^2{u}_{3x}+u_{5x}.\hfill \end{array}$$

(47)

With regard to the weights in (20), the above symmetries are of ranks $2,4$, and 6, respectively.

Except for $G^{\left(1\right)}$, each of these symmetries leads to a completely integrable nonlinear PDE, $u_t+G^{\left(j\right)}=0,j=2,3,\dots$, where the weight of t increases as j increases. Notice that $u_t+G^{\left(2\right)}=0$ corresponds to (1) itself.

Although the computation of symmetries is algorithmic [10] and technically simpler than for densities, it still requires the computation of a plethora of terms, and is best handled with symbolic software such as InvariantsSymmetries.m [10]. As an example, we show how to compute $G^{\left(3\right)}$ of rank 6.

• Step 1: Construct a candidate symmetry of rank 6 as follows: List all monomials in u and $\alpha$ of rank 6 or less, i.e.,  $\{\{u^6,\alpha u^5,{\alpha }^2{u}^4,{\alpha }^3{u}^3,{\alpha }^4{u}^2,{\alpha }^{5}u\}$, $\{u^5,\dots ,{\alpha }^{4}u\}$, $\{u^4,\dots ,{\alpha }^{3}u\}$, $\{u^3,\alpha u^2,{\alpha }^{2}u\}$, $\{u^2,\alpha u\}$, $\left\{u\right\}\}$, without the constant terms ${\alpha }^6,{\alpha }^5,\dots ,\alpha ,1$.

Then, apply the correct number of x-derivatives to the monomials in each of the six sublists so that the resulting terms have exactly rank 6. The elements in the first sublist need no derivatives. Those in the second sublist need a single derivative, etc. For example, for the first element in the fourth sublist, compute ${\displaystyle \frac{{\partial }^3{u}^3}{\partial x^3}}=6u_x^3+18u{u}_x{u}_{xx}+3u^2{u}_{3x}.$ Do this for each element in all sublists and gather the resulting monomials after stripping off numerical factors. To avoid lower-rank symmetries being recomputed, remove scalar multiples of single-term symmetries of lower rank, as well as scalar multiples of the highest-derivative term in multiple-term symmetries of lower rank. Thus, with regard to (45) and (46), the monomials ${\alpha }^4{u}_x$ and ${\alpha }^2{u}_{3x}$ can be removed. Finally, linearly combine the remaining terms with constant coefficients, yielding

$$\begin{array}{ccc}\hfill G& =& c_1{u}^6+\alpha c_2{u}^5+{\alpha }^2{c}_3{u}^4+{\alpha }^3{c}_4{u}^3+{\alpha }^4{c}_5{u}^2+{\alpha }^5{c}_{6}u+c_7{u}^4{u}_x+\alpha c_8{u}^3{u}_x\hfill \\ & & +{\alpha }^2{c}_9{u}^2{u}_x+{\alpha }^3{c}_{10}u{u}_x+c_{11}{u}^2{u}_x^2+c_{12}{u}^3{u}_{xx}+\alpha c_{13}u{u}_x^2+\alpha c_{14}{u}^2{u}_{xx}+{\alpha }^2{c}_{15}{u}_x^2\hfill \\ & & +{\alpha }^2{c}_{16}u{u}_{xx}+{\alpha }^3{c}_{17}{u}_{xx}+c_{18}{u}_x^3+c_{19}u{u}_x{u}_{xx}+c_{20}{u}^2{u}_{3x}+\alpha c_{21}{u}_x{u}_{xx}\hfill \\ & & +\alpha c_{22}u{u}_{3x}+c_{23}{u}_{xx}^2+c_{24}{u}_x{u}_{3x}+c_{25}u{u}_{4x}+\alpha c_{26}{u}_{4x}+c_{27}{u}_{5x}\hfill \end{array}$$

(48)

which is of fifth order ($m=5$).

• Step 2: Find the undetermined coefficients. Compute ${\mathrm{D}}_{t}G$ and use (4) to remove $u_t,u_{xt}$, etc. This produces an expression with 176 terms (not listed). Next, compute (44) using

  $$F=-(\alpha u{u}_x+\beta u^2{u}_x+u_{3x})$$

  (49)

  and G from (48), yielding 193 terms (not listed). Then, ${\mathrm{D}}_{t}G-F^{\prime }\left[G\right]$, which has 138 terms, must vanish identically on the jet space, yielding a linear system of 20 equations for the nine nonzero coefficients $(c_7,c_8,c_9$, $c_{18}$ through $c_{22}$, and $c_{27})$:

  $$\begin{array}{ccc}& & 2(3c_{20}-5\beta c_{27})=0,\alpha (3c_{22}-5c_{27})=0,\hfill \\ & & \phantom{,,\alpha (3c_{22}-5c_{27})=0,}⋮\phantom{\alpha (3c_{22}-5c_{27})=0}\hfill \\ & & 3\alpha (12c_8-c_{19}-2\beta c_{21}-4\beta c_{22})=0,6(3c_{18}+2c_{19}+c_{20}-20\beta c_{27})=0.\hfill \end{array}$$

  (50)

  For brevity, we have shown only a couple of the shortest equations (coming from $u{u}_x{u}_{5x}$ and $u_x{u}_{5x}$, respectively) and two of the longest equations (coming from $u{u}_x^2{u}_{xx}$ and $u_x{u}_{xx}{u}_{3x}$, respectively). The 18 coefficients $c_1$ through $c_6$, $c_{10}$ through $c_{17}$, and $c_{23}$ through $c_{26}$ are all zero. Solving the system yields

  $$\begin{array}{ccc}& & c_7=\frac{5}{6}{\beta }^2{c}_{27},c_8=\frac{5}{3}\beta c_{27},c_9=\frac{5}{6}{c}_{27},c_{18}=\frac{5}{3}\beta c_{27},c_{19}=\frac{20}{3}\beta c_{27},\hfill \\ & & c_{20}=\frac{5}{3}\beta c_{27},c_{21}=\frac{10}{3}{c}_{27},c_{22}=\frac{5}{3}{c}_{27}.\hfill \end{array}$$

  (51)

  Set $c_{27}=1$ and substitute (51) into (48) to obtain

  $$\begin{array}{ccc}\hfill G& =& \frac{5}{6}{\alpha }^2{u}^2{u}_x+\frac{5}{3}\alpha \beta u^3{u}_x+\frac{5}{6}{\beta }^2{u}^4{u}_x+\frac{5}{3}\beta u_x^3+\frac{10}{3}\alpha u_x{u}_{xx}+\frac{20}{3}\beta u{u}_x{u}_{xx}\hfill \\ & & +\frac{5}{3}\alpha u{u}_{3x}+\frac{5}{3}\beta u^2{u}_{3x}+u_{5x}.\hfill \end{array}$$

  (52)

  which matches $G^{\left(3\right)}$ in (47).

The code InvariantsSymmetries.m can also be used to verify if an evolution equation, e.g., $u_t+G^{\left(3\right)}=0$, with $G^{\left(3\right)}$ of rank 6, belongs to the hierarchy of completely integrable equations of a PDE of lower order. When asked to compute a symmetry of rank 4 for $u_t+G^{\left(3\right)}=0$, the software returns $G^{\left(2\right)}$ in (46), confirming that $u_t+G^{\left(3\right)}=0$ corresponds to a generalized symmetry of $u_t+G^{\left(2\right)}=0$.

7. Recursion Operator

To prove that there are infinitely many higher-order symmetries, we will compute the recursion operator, which generates those symmetries sequentially, starting from the lowest order symmetry $G^{\left(1\right)}$ in (45).

As expected, the recursion operator for the Gardner equation is a combination of the well-known recursion operators for the KdV and mKdV equations (see p. 312 of [43] and [54]):

$$\mathcal{R}={\mathrm{D}}_x^2+\frac{2}{3}\left(\alpha u+\beta u^2\right)\mathrm{I}+\frac{1}{3}\alpha u_x{\mathrm{D}}_x^{-1}+\frac{2}{3}\beta u_x{\mathrm{D}}_x^{-1}\left(u\mathrm{I}\right),$$

(53)

where ${\mathrm{D}}_x^{-1}$ denotes the anti-derivative (or integral) operator. $\mathcal{R}$ connects the symmetries sequentially (without gaps in this case; for examples with gaps, we refer to [55]):

$$G^{(j+1)}=\mathcal{R}{G}^{\left(j\right)},j=1,2,\dots .$$

(54)

For example,

$$\begin{array}{ccc}\hfill \mathcal{R}{u}_x& =& \left({\mathrm{D}}_x^2+\frac{2}{3}\left(\alpha u+\beta u^2\right)\mathrm{I}+\frac{1}{3}\alpha u_x{\mathrm{D}}_x^{-1}+\frac{2}{3}\beta u_x{\mathrm{D}}_x^{-1}\left(u\mathrm{I}\right)\right)u_x\hfill \\ & =& u_{3x}+\frac{2}{3}\left(\alpha u+\beta u^2\right)u_x+\frac{1}{3}\alpha u_x{\mathrm{D}}_x^{-1}\left(u_x\right)+\frac{2}{3}\beta u_x{\mathrm{D}}_x^{-1}{\left(\frac{1}{2}{u}^2\right)}_x\hfill \\ & =& \alpha u{u}_x+\beta u^2{u}_x+u_{3x},\hfill \end{array}$$

(55)

which is $G^{\left(2\right)}$, and

$$\begin{array}{ccc}\hfill \mathcal{R}{G}^{\left(2\right)}& =& \left({\mathrm{D}}_x^2+\frac{2}{3}\left(\alpha u+\beta u^2\right)\mathrm{I}+\frac{1}{3}\alpha u_x{\mathrm{D}}_x^{-1}+\frac{2}{3}\beta u_x{\mathrm{D}}_x^{-1}\left(u\mathrm{I}\right)\right)\left(\alpha u{u}_x+\beta u^2{u}_x+u_{3x}\right)\hfill \\ \hfill & =& u_{5x}+\frac{5}{3}\alpha u{u}_{3x}+\frac{5}{3}\beta u^2{u}_{3x}+\dots +\frac{\alpha }{3}{u}_x{\mathrm{D}}_x^{-1}{\left(\frac{1}{2}\alpha u^2+\frac{1}{3}\beta u^3+u_{xx}\right)}_x\hfill \\ \hfill & & +\frac{2}{3}\beta u_x{\mathrm{D}}_x^{-1}{\left(\frac{1}{3}\alpha u^3+\frac{1}{4}\beta u^4+u{u}_{xx}-\frac{1}{2}{u}_x^2\right)}_x\hfill \\ \hfill & =& \frac{5}{6}{\alpha }^2{u}^2{u}_x+\frac{5}{3}\alpha \beta u^3{u}_x+\frac{5}{6}{\beta }^2{u}^4{u}_x+\frac{5}{3}\beta u_x^3+\frac{10}{3}\alpha u_x{u}_{xx}+\frac{20}{3}\beta u{u}_x{u}_{xx}\hfill \\ \hfill & & +\frac{5}{3}\alpha u{u}_{3x}+\frac{5}{3}\beta u^2{u}_{3x}+u_{5x},\hfill \end{array}$$

(56)

which is $G^{\left(3\right)}$.

Even for scalar equations like (1), the computation of recursion operators [55] is lengthy, but can be performed with specialized software such as PDERecursionOperator.m [16]. One can also use computer algebra to verify that $\mathcal{R}$ is a hereditary operator [56].

If $\mathcal{R}$ is a recursion operator for (4), then the Lie derivative [19,43,57,58] of $\mathcal{R}$ is zero, yielding

$${\mathrm{D}}_t\mathcal{R}+[\mathcal{R},F^{\prime }]={\displaystyle \frac{\partial \mathcal{R}}{\partial t}}+{\mathcal{R}}^{\prime }\left[F\right]+\mathcal{R}\circ F^{\prime }-F^{\prime }\circ \mathcal{R}\dot{=}0,$$

(57)

where $[,]$ and ∘ denote the commutator and composition of operators, respectively. $F^{\prime }$ is the Fréchet derivative operator, defined as

$$F^{\prime }=\sum _{k=0}^n{\displaystyle \frac{\partial F}{\partial u_{kx}}}{\mathrm{D}}_x^k,$$

(58)

where n is the order of F in (4). ${\mathcal{R}}^{\prime }\left[F\right]$ is the Fréchet derivative of $\mathcal{R}$ in the direction of F. For recursion operators of the form

$$\mathcal{R}=\sum _{j=1}^T{U}_j(u,u_x,u_{xx},\dots ,u_{m_{1}x}){\mathcal{S}}_j({\mathrm{D}}_x,{\mathrm{D}}_x^2,\dots ,{\mathrm{D}}_x^{-1})\left(V_j(u,u_x,u_{xx},\dots ,u_{m_{2}x})\mathrm{I}\right),$$

(59)

where T is the total number of terms in $\mathcal{R}$, and  $m_1$ and $m_2$ are the orders of U and V, respectively, one has

$${\mathcal{R}}^{\prime }\left[F\right]=\sum _{j=0}^{m_1}\left({\mathrm{D}}_x^{j}F\right){\displaystyle \frac{\partial U_j}{\partial u_{jx}}}{\mathcal{S}}_j\left(V_j\mathrm{I}\right)+\sum _{j=0}^{m_2}{U}_j{\mathcal{S}}_j\left(\left({\mathrm{D}}_x^{j}F\right){\displaystyle \frac{\partial V_j}{\partial u_{jx}}}\mathrm{I}\right).$$

(60)

With regard to (53), $\mathcal{R}$ is a linear integro-differential operator [59,60] which naturally splits into two pieces [55,58,61],

$$\mathcal{R}={\mathcal{R}}_0+{\mathcal{R}}_1,$$

(61)

where ${\mathcal{R}}_0$ is a local differential operator and ${\mathcal{R}}_1$ is a non-local integral operator. ${\mathcal{R}}_0$ is a linear combination of monomials involving ${\mathrm{D}}_x$, u, and parameters with weight (if applicable) so that each monomial has the correct rank. Note also that ${\mathrm{D}}_x$ will always be “propagated” to the right in ${\mathcal{R}}_0$. For example,

$${\mathrm{D}}_x^2\left(u\mathrm{I}\right)={\mathrm{D}}_x\left(u_x\mathrm{I}+u{\mathrm{D}}_x\right)=u_{xx}\mathrm{I}+2u_x{\mathrm{D}}_x+u{\mathrm{D}}_x^2.$$

(62)

Based on the theory of recursion operators, ${\mathcal{R}}_1$ is a linear combination with constant coefficients of terms of the form

$$G^{\left(i\right)}{\mathrm{D}}_x^{-1}{\mathcal{L}}_u\left({\rho }^{\left(j\right)}\right),$$

(63)

where $G^{\left(i\right)}$ is a symmetry and ${\mathcal{L}}_u\left({\rho }^{\left(j\right)}\right)$ is a cosymmetry (Euler operator applied to a density ${\rho }^{\left(j\right)})$, selected such that ${\mathcal{R}}_1$ has the correct rank [58,62]. To standardize the form of ${\mathcal{R}}_1$, one propagates ${\mathrm{D}}_x$ to the left. For example, ${\mathrm{D}}_x^{-1}{u}_x{\mathrm{D}}_x=u_x\mathrm{I}-{\mathrm{D}}_x^{-1}{u}_{xx}\mathrm{I}$. The local and non-local operators are then added to obtain a candidate recursion operator.

We will now show how (53) is computed. Since the ranks $G^{\left(1\right)}$ and $G^{\left(2\right)}$ (as well as $G^{\left(2\right)}$ and $G^{\left(3\right)}$) differ by 2, $\mathcal{R}$ must have rank 2. Based on (20), $W\left({\mathrm{D}}_x^{-1}\right)=-1$, and one can readily verify that all the terms in (53) have rank 2.

• Step 1: Compute the candidate recursion operator. Using (20), list all monomials in ${\mathrm{D}}_x,u$, and $\alpha$ of rank 2 or less, i.e.,  $\left\{\right\{{\mathrm{D}}_x^2,u{\mathrm{D}}_x,\alpha {\mathrm{D}}_x$, $u^2\mathrm{I},\alpha u\mathrm{I}\}$, $\{{\mathrm{D}}_x,u\mathrm{I}\}\}$, where the trivial terms $\alpha \mathrm{I}$ and ${\alpha }^2\mathrm{I}$ have been removed. Apply the correct number of x-derivatives to the monomials in each of the two sublists to assure that each term has rank 2. No action is needed on the first sublist. The elements in the second sublist need a single derivative, yielding $\{{\mathrm{D}}_x^2,u_x\mathrm{I},u{\mathrm{D}}_x\}$. After stripping off numerical factors and removing duplicates, linearly combine the resulting monomials with constant coefficients to obtain a candidate local operator

  $${\mathcal{R}}_0=c_1{\mathrm{D}}_x^2+c_{2}u{\mathrm{D}}_x+\alpha c_3{\mathrm{D}}_x+c_4{u}^2\mathrm{I}+\alpha c_{5}u\mathrm{I}+c_6{u}_x\mathrm{I}.$$

  (64)

  Using symmetry $G^{\left(1\right)}=u_x$ and densities ${\rho }^{\left(1\right)}=u$ and ${\rho }^{\left(2\right)}=u^2$ (all of low rank), compute ${\mathcal{L}}_u{\rho }^{\left(1\right)}=1$ and ${\mathcal{L}}_u{\rho }^{\left(2\right)}=2u$. Then, with terms of type (63), make the candidate non-local operator

  $${\mathcal{R}}_1=\alpha c_7{u}_x{\mathrm{D}}_x^{-1}+c_8{u}_x{\mathrm{D}}_x^{-1}\left(u\mathrm{I}\right),$$

  (65)

  so that each term has rank 2. Add both pieces to get the candidate recursion operator

  $$\mathcal{R}=c_1{\mathrm{D}}_x^2+(c_{2}u+\alpha c_3){\mathrm{D}}_x+(c_4{u}^2+\alpha c_{5}u+c_6{u}_x)\mathrm{I}+\alpha c_7{u}_x{\mathrm{D}}_x^{-1}+c_8{u}_x{\mathrm{D}}_x^{-1}\left(u\mathrm{I}\right).$$

  (66)
• Step 2: Compute the undetermined coefficients. Separately compute all the pieces in (57), beginning with

  $$\begin{array}{ccc}\hfill {\mathrm{D}}_t\mathcal{R}& =& c_2{u}_t{\mathrm{D}}_x+(2c_{4}u{u}_t+\alpha c_5{u}_t+c_6{u}_{xt})\mathrm{I}+\alpha c_7{u}_{xt}{\mathrm{D}}_x^{-1}\hfill \\ & & +c_8{u}_{xt}{\mathrm{D}}_x^{-1}\left(u\mathrm{I}\right)+c_8{u}_x{\mathrm{D}}_x^{-1}\left(u_t\mathrm{I}\right)\hfill \\ & =& c_{2}F{\mathrm{D}}_x+(2c_{4}uF+\alpha c_{5}F+c_6{\mathrm{D}}_{x}F)\mathrm{I}+\alpha c_7\left({\mathrm{D}}_{x}F\right){\mathrm{D}}_x^{-1}\hfill \\ & & +c_8\left({\mathrm{D}}_{x}F\right){\mathrm{D}}_x^{-1}\left(u\mathrm{I}\right)+c_8{u}_x{\mathrm{D}}_x^{-1}\left(F\mathrm{I}\right),\hfill \end{array}$$

  (67)

  which can also be computed using (60). With F given in (49), insert

  $${\mathrm{D}}_{x}F=F_x=-(\alpha u_x^2+\alpha u{u}_{xx}+2\beta u{u}_x^2+\beta u^2{u}_{xx}+u_{4x})$$

  (68)

  into (67), expand, and simplify. This yields an expression of 27 terms (not listed). Some of the terms have ${\mathrm{D}}_x$ and $\mathrm{I}$; others involve ${\mathrm{D}}_x^{-1}$, ${\mathrm{D}}_x^{-1}\left(u\mathrm{I}\right)$, ${\mathrm{D}}_x^{-1}\left(u{u}_x\mathrm{I}\right)$, ${\mathrm{D}}_x^{-1}\left(u^2{u}_x\mathrm{I}\right)$, and ${\mathrm{D}}_x^{-1}\left(u_{3x}\mathrm{I}\right)$. Next, using (58), compute

  $$F^{\prime }=-\left({\mathrm{D}}_x^3+(\alpha +\beta u)u{\mathrm{D}}_x+(\alpha +2\beta u)u_x\mathrm{I}\right).$$

  (69)

  With (66) and (69), then compute

  $$\begin{array}{ccc}\hfill \mathcal{R}\circ F^{\prime }& =& -\left(\left(c_1{\mathrm{D}}_x^2+(c_{2}u+\alpha c_3){\mathrm{D}}_x+(c_4{u}^2+\alpha c_{5}u+c_6{u}_x)\mathrm{I}+\alpha c_7{u}_x{\mathrm{D}}_x^{-1}\right.\right.\hfill \\ & & \left.\left.+c_8{u}_x{\mathrm{D}}_x^{-1}\left(u\mathrm{I}\right)\right)\circ \left({\mathrm{D}}_x^3+(\alpha +\beta u)u{\mathrm{D}}_x+(\alpha +2\beta u)u_x\mathrm{I}\right)\right),\hfill \end{array}$$

  (70)

  using, for example,

  $$\begin{array}{ccc}\hfill {\mathrm{D}}_x^2\left(u^2{\mathrm{D}}_x\right)& =& {\mathrm{D}}_x(2u{u}_x{\mathrm{D}}_x+u^2{\mathrm{D}}_x^2)\hfill \\ & =& 2u_x^2{\mathrm{D}}_x+2u{u}_{xx}{\mathrm{D}}_x+4u{u}_x{\mathrm{D}}_x^2+u^2{\mathrm{D}}_x^3,\hfill \end{array}$$

  (71)

  to consistently move the operator ${\mathrm{D}}_x$ from the left to the right. To be able to match the integral terms in (67) which are mentioned below (68), repeated integration by parts is needed [55]. For example,

  $$\begin{array}{ccc}\hfill {\mathrm{D}}_x^{-1}\left(u{\mathrm{D}}_x^3\right)& =& u{\mathrm{D}}_x^2-{\mathrm{D}}_x^{-1}\left(u_x{\mathrm{D}}_x^2\right)\hfill \\ & =& u{\mathrm{D}}_x^2-u_x{\mathrm{D}}_x+{\mathrm{D}}_x^{-1}\left(u_{xx}{\mathrm{D}}_x\right)\hfill \\ & =& u{\mathrm{D}}_x^2-u_x{\mathrm{D}}_x+u_{xx}\mathrm{I}-{\mathrm{D}}_x^{-1}\left(u_{3x}\mathrm{I}\right),\hfill \end{array}$$

  (72)

  converts the integral ${\mathrm{D}}_x^{-1}\left(u{\mathrm{D}}_x^3\right)$ into ${\mathrm{D}}_x^{-1}\left(u_{3x}\mathrm{I}\right)$ by moving the ${\mathrm{D}}_x$ operator under the ${\mathrm{D}}_x^{-1}$ operator from the right to the left. After integration by parts, $\mathcal{R}\circ F^{\prime }$ has 58 terms (not listed). Next, compute

  $$\begin{array}{ccc}\hfill F^{\prime }\circ \mathcal{R}& =& -\left(\left({\mathrm{D}}_x^3+(\alpha +\beta u)u{\mathrm{D}}_x+(\alpha +2\beta u)u_x\mathrm{I}\right)\circ \left(c_1{\mathrm{D}}_x^2+(c_{2}u+\alpha c_3){\mathrm{D}}_x\right.\right.\hfill \\ & & \left.\left.+(c_4{u}^2+\alpha c_{5}u+c_6{u}_x)\mathrm{I}+\alpha c_7{u}_x{\mathrm{D}}_x^{-1}+c_8{u}_x{\mathrm{D}}_x^{-1}\left(u\mathrm{I}\right)\right)\right).\hfill \end{array}$$

  (73)
  To move the operator ${\mathrm{D}}_x$ to the right, use, for example,

  $$\begin{array}{ccc}\hfill {\mathrm{D}}_x^3\left(u_x{\mathrm{D}}_x^{-1}\left(u\mathrm{I}\right)\right)& =& {\mathrm{D}}_x^2\left(u_{xx}{\mathrm{D}}_x^{-1}\left(u\mathrm{I}\right)+u{u}_x\mathrm{I}\right)\hfill \\ \hfill & =& {\mathrm{D}}_x\left(u_{3x}{\mathrm{D}}_x^{-1}\left(u\mathrm{I}\right)+2u{u}_{xx}\mathrm{I}+u_x^2\mathrm{I}+u{u}_x{\mathrm{D}}_x\right)\hfill \\ \hfill & =& u_{4x}{\mathrm{D}}_x^{-1}\left(u\mathrm{I}\right)+4u_x{u}_{xx}\mathrm{I}+3u{u}_{3x}\mathrm{I}+3u{u}_{xx}{\mathrm{D}}_x+2u_x^2{\mathrm{D}}_x+u{u}_x{\mathrm{D}}_x^2,\hfill \end{array}$$

  (74)

  and similar formulas (expressed in a more general form in [55]). The expanded expression for $F^{\prime }\circ \mathcal{R}$ has 73 terms. Substitute the simplified expressions for (67), (70), and (73) into (57) and require that the resulting expression (which has 36 terms) vanishes identically, i.e., all monomials in $u,u_x,\dots ,\mathrm{I}$, ${\mathrm{D}}_x,{\mathrm{D}}_x^2$, ⋯, should be treated as independent. This yields $c_2=c_3=c_6=0$ and a linear system,

  $$\begin{array}{ccc}& & 2(3c_4-2\beta c_1)=0,\alpha (3c_5-2c_1)=0,\alpha (3c_7-c_1)=0,3c_8-2\beta c_1=0,\hfill \\ & & 3\alpha (c_7+c_5-c_1)=0,3(c_8+2c_4-2\beta c_1)=0,\hfill \end{array}$$

  (75)

  involving the remaining nonzero constants. Solve the system to get

  $$c_4=\frac{2}{3}\beta c_1,c_5=\frac{2}{3}{c}_1,c_7=\frac{1}{3}{c}_1,c_8=\frac{2}{3}\beta c_1.$$

  (76)
  Finally, set $c_1=1$ and substitute (76) into (66), yielding

  $$\mathcal{R}={\mathrm{D}}_x^2+\frac{2}{3}\left(\alpha u+\beta u^2\right)\mathrm{I}+\frac{1}{3}\alpha u_x{\mathrm{D}}_x^{-1}+\frac{2}{3}\beta u_x{\mathrm{D}}_x^{-1}\left(u\mathrm{I}\right),$$

  (77)

  which matches $\mathcal{R}$ in (53).

8. Lax Pair

Another way to prove the complete integrability of a nonlinear PDE of type (4) is to construct a Lax pair consisting of two linear PDEs in an auxiliary function whose compatibility requires that the original PDE is satisfied.

There are two flavors of Lax pairs. One is an operator formulation where the Lax pair consists of a pair of differential operators which leads to a higher order linear equation involving an auxiliary function. Alternatively, in the matrix formulation, the Lax pair is a set of two matrices satisfying a system of equations of first order in x and t, respectively. Only Lax pairs in operator form will be covered in this section. The reader is referred to the literature [1,2,63] for the matrix formalism (also called the zero curvature representation).

Finding a Lax pair in operator form is a nontrivial task and requires an educated guess about the order of the differential operators. But once the order is selected, one can take advantage of the scaling symmetry of the given PDE to construct a candidate for each operator because they inherit that scaling symmetry. Here again, the defining equation for a Lax pair is evaluated on solutions of the given PDE which supports that claim.

Using the KdV equation as prime example, Lax [64] showed that a completely integrable nonlinear PDE has an associated system of linear PDEs involving a pair of linear differential operators $(\mathcal{L},\mathcal{M})$ and an auxiliary function $\psi (x,t)$,

$$\mathcal{L}\psi =\lambda \psi ,{\psi }_t=\mathcal{M}\psi ,$$

(78)

where $\mathcal{L}$ and $\mathcal{M}$ are expressed in powers of ${\mathrm{D}}_x$ with coefficients depending on $u,u_x$, etc., and  $\psi$ is an eigenfunction of $\mathcal{L}$ corresponding to eigenvalue $\lambda$. To guarantee complete integrability of (4), at least one non-trivial Lax pair $(\mathcal{L},\mathcal{M})$ should exist, and the eigenvalue should not change in time which makes the problem isospectral.

We will show below that a one-parameter family of Lax pairs of (1) is given by

$$\begin{array}{ccc}\hfill \mathcal{L}& =& {\mathrm{D}}_x^2+2ϵu{\mathrm{D}}_x+\frac{1}{6}\left((6{ϵ}^2+\beta )u^2+\alpha u+(6ϵ\pm \sqrt{-6\beta })u_x\right)\mathrm{I},\hfill \end{array}$$

(79)

$$\begin{array}{ccc}\hfill \mathcal{M}& =& -4{\mathrm{D}}_x^3-12ϵu{\mathrm{D}}_x^2-\left((12{ϵ}^2+\beta )u^2+\alpha u+(12ϵ\pm \sqrt{-6\beta })u_x\right){\mathrm{D}}_x\hfill \\ & & -\left(\frac{1}{3}ϵ(12{ϵ}^2+2\beta )u^3+\frac{1}{2}\alpha ϵu^2+(12{ϵ}^2+\beta \pm ϵ\sqrt{-6\beta })u{u}_x\right.\hfill \\ & & \left.+\frac{1}{2}\alpha u_x+\frac{1}{2}(6ϵ\pm \sqrt{-6\beta })u_{xx}\right)\mathrm{I},\hfill \end{array}$$

(80)

where $ϵ$ is any real or complex number (not necessarily small). Substituting $\mathcal{L}$ and $\mathcal{M}$ into (78) yields

$$\begin{array}{ccc}\hfill {\mathrm{D}}_x^2\psi & =& -2ϵu{\mathrm{D}}_x\psi +\left(\lambda -({ϵ}^2+\frac{1}{6}\beta )u^2-\frac{1}{6}\alpha u-(ϵ\pm \frac{1}{6}\sqrt{-6\beta })u_x\right)\psi ,\hfill \end{array}$$

(81)

$$\begin{array}{ccc}\hfill {\mathrm{D}}_t\psi & =& -4{\mathrm{D}}_x^3\psi -12ϵu{\mathrm{D}}_x^2\psi -\left((12{ϵ}^2+\beta )u^2+\alpha u+(12ϵ\pm \sqrt{-6\beta })u_x\right){\mathrm{D}}_x\psi \hfill \\ & & -\left(\frac{1}{3}ϵ(12{ϵ}^2+2\beta )u^3+\frac{1}{2}\alpha ϵu^2+(12{ϵ}^2+\beta \pm ϵ\sqrt{-6\beta })u{u}_x\right.\hfill \\ & & \left.+\frac{1}{2}\alpha u_x+\frac{1}{2}(6ϵ\pm \sqrt{-6\beta })u_{xx}\right)\psi .\hfill \end{array}$$

(82)

The first equation is a Schrödinger-type equation for the arbitrary eigenfunction $\psi$ with eigenvalue $\lambda$ and potential $({ϵ}^2+\frac{1}{6}\beta )u^2$ $+\frac{1}{6}\alpha u$ $+(ϵ\pm \frac{1}{6}\sqrt{-6\beta })u_x$. The second equation describes the time evolution of the eigenfunction.

A lengthy computation shows that the compatibility condition for (81) and (82) can be written as

$$\begin{array}{ccc}& & {\mathrm{D}}_t{\mathrm{D}}_x^2\psi -{\mathrm{D}}_x^2{\mathrm{D}}_t\psi =\frac{1}{6}\left((6ϵ\pm \sqrt{-6\beta }){\mathrm{D}}_x(u_t+\alpha u{u}_x+\beta u^2{u}_x+u_{3x})\right.\hfill \\ & & \left.+(\alpha +2(6{ϵ}^2+\beta )u)(u_t+\alpha u{u}_x+\beta u^2{u}_x+u_{3x})\right)\psi \hfill \\ & & +2ϵ(u_t+\alpha u{u}_x+\beta u^2{u}_x+u_{3x}){\mathrm{D}}_x\psi ,\hfill \end{array}$$

(83)

where (81) and (82) were used repeatedly to eliminate ${\mathrm{D}}_{xt}\psi$, ${\mathrm{D}}_t\psi$, ${\mathrm{D}}_x^5\psi$, ${\mathrm{D}}_x^4\psi$, ${\mathrm{D}}_x^3\psi$, and ${\mathrm{D}}_x^2\psi$, in that order. From (83), it is clear that (81) and (82) will only be compatible on solutions of (1).

The compatibility of the equations in (78) may be expressed directly in terms of the operators $\mathcal{L}$ and $\mathcal{M}$ as follows

$${\mathrm{D}}_t\left(\mathcal{L}\psi \right)={\mathcal{L}}_t\psi +\mathcal{L}\left({\mathrm{D}}_t\psi \right)=\lambda {\mathrm{D}}_t\psi ,$$

(84)

where

$${\mathcal{L}}_t\psi \equiv {\mathrm{D}}_t\left(\mathcal{L}\psi \right)-\mathcal{L}\left({\mathrm{D}}_t\psi \right).$$

(85)

With (78), one has

$${\mathcal{L}}_t\psi +\mathcal{L}\left(\mathcal{M}\psi \right)=\lambda \mathcal{M}\psi =\mathcal{M}\left(\lambda \psi \right)=\mathcal{M}\left(\mathcal{L}\psi \right).$$

(86)

For a non-trivial Lax pair for (4) to exist, (86) should vanish only on solutions of (4). If (88) is satisfied identically, i.e., without evaluation on solutions of the PDE, then the Lax operators $\mathcal{L}$ and $\mathcal{M}$ are considered trivial). Rearranging the terms yields

$$\left({\mathcal{L}}_t+\mathcal{L}\circ \mathcal{M}-\mathcal{M}\circ \mathcal{L}\right)\psi =\left({\mathcal{L}}_t+\left[\mathcal{L},\mathcal{M}\right]\right)\psi \dot{=}0,$$

(87)

or, expressed in operator form by suppressing the $\psi$,

$${\mathcal{L}}_t+\left[\mathcal{L},\mathcal{M}\right]\dot{=}\mathcal{O},$$

(88)

where $\dot{=}$ means that equality holds only on solutions of the original PDE (4). As before, $[,]$ is the commutator of the operators, and $\mathcal{O}$ is the zero operator. Equation (88) is called the Lax equation. We now show how the Lax pair $(\mathcal{L},\mathcal{M})$ can be computed using the method discussed in [65].

• Step 1: Construct a candidate for $\mathcal{L}$ and $\mathcal{M}$. Since the KdV and mKdV equations are special cases of (1), it makes sense to search for $\mathcal{L}$ of rank 2 and $\mathcal{M}$ of rank 3. To construct $\mathcal{L}$, list all monomials in ${\mathrm{D}}_x,u$, and $\alpha$ of rank 2 or less, i.e.,  $\left\{\right\{{\mathrm{D}}_x^2$, $u{\mathrm{D}}_x$, $\alpha {\mathrm{D}}_x$, $u^2\mathrm{I}$, $\alpha u\mathrm{I}\}$, $\{{\mathrm{D}}_x$, $u\mathrm{I}\left\}\right\}$, where the trivial terms $\alpha \mathrm{I}$ and ${\alpha }^2\mathrm{I}$ have been removed. As explained in Section 7, apply ${\mathrm{D}}_x$ to the elements in the second sublist and, as in (62), propagate ${\mathrm{D}}_x$ to the right, yielding $\{{\mathrm{D}}_x^2,u_x\mathrm{I},u{\mathrm{D}}_x\}$. After removing duplicates, linearly combine the monomials from both sublists with constant coefficients to get a candidate for $\mathcal{L}$:

  $$\mathcal{L}={\mathrm{D}}_x^2+(c_{1}u+\alpha c_2){\mathrm{D}}_x+(c_3{u}^2+\alpha c_{4}u+c_5{u}_x)\mathrm{I},$$

  (89)

  where the coefficient of ${\mathrm{D}}_x^2$ has been set to one (for normalization).

To make a candidate for $\mathcal{M}$, list all monomials in ${\mathrm{D}}_x,u$, and $\alpha$ of rank 3 or less, i.e.,  $\left\{\right\{{\mathrm{D}}_x^3$, $u{\mathrm{D}}_x^2$, $\alpha {\mathrm{D}}_x^2$, $u^2{\mathrm{D}}_x$, $\alpha u{\mathrm{D}}_x$, ${\alpha }^2{\mathrm{D}}_x$, $u_x{\mathrm{D}}_x$, $u^3\mathrm{I}$, $\alpha u^2\mathrm{I}$, ${\alpha }^{2}u\mathrm{I}\}$, $\{{\mathrm{D}}_x^2$, $u{\mathrm{D}}_x$, $\alpha {\mathrm{D}}_x$, $u^2\mathrm{I}$, $\alpha u\mathrm{I}\}$, $\{{\mathrm{D}}_x$, $u\mathrm{I}\left\}\right\}$, where the trivial terms $\alpha \mathrm{I}$, ${\alpha }^2\mathrm{I}$, and  ${\alpha }^3\mathrm{I}$ have been removed. Apply ${\mathrm{D}}_x$ to the elements in the second sublist, yielding $\{{\mathrm{D}}_x^3$, $u_x{\mathrm{D}}_x$, $u{\mathrm{D}}_x^2$, $\alpha {\mathrm{D}}_x^2$, $2u{u}_x\mathrm{I}$, $u^2{\mathrm{D}}_x$, $\alpha u_x\mathrm{I}$, $\alpha u{\mathrm{D}}_x\}$. Apply ${\mathrm{D}}_x^2$ to the elements in the third sublist and use (62) to obtain $\{{\mathrm{D}}_x^3$, $u_{xx}\mathrm{I}$, $2u_x{\mathrm{D}}_x$, $u{\mathrm{D}}_x^2\}$. After stripping off numerical factors and removing duplicates, linearly combine the resulting monomials with constant coefficients to obtain a candidate for $\mathcal{M}$:

$$\begin{array}{ccc}\hfill \mathcal{M}& =& c_6{\mathrm{D}}_x^3+(c_{7}u+\alpha c_8){\mathrm{D}}_x^2+(c_9{u}^2+\alpha c_{10}u+{\alpha }^2{c}_{11}+c_{12}{u}_x){\mathrm{D}}_x\hfill \\ & & +(c_{13}{u}^3+\alpha c_{14}{u}^2+{\alpha }^2{c}_{15}u+c_{16}u{u}_x+\alpha c_{17}{u}_x+c_{18}{u}_{xx})\mathrm{I}.\hfill \end{array}$$

(90)

• Step 2: Compute the undetermined coefficients. First, compute

  $$\begin{array}{ccc}\hfill {\mathcal{L}}_t& =& c_1{u}_t{\mathrm{D}}_x+(2c_{3}u{u}_t+\alpha c_4{u}_t+c_5{u}_{xt})\mathrm{I}\hfill \\ & =& c_{1}F{\mathrm{D}}_x+(2c_{3}uF+\alpha c_{4}F+c_5{\mathrm{D}}_{x}F)\mathrm{I},\hfill \end{array}$$

  (91)

  which, after substituting F from (49) to replace $u_t$ and $u_{xt}$, yields 14 terms. Next, compute

  $$\begin{array}{ccc}\hfill \mathcal{L}\circ \mathcal{M}& =& \left({\mathrm{D}}_x^2+(c_{1}u+\alpha c_2){\mathrm{D}}_x+(c_3{u}^2+\alpha c_{4}u+c_5{u}_x)\mathrm{I}\right)\circ \hfill \\ & & \left(c_6{\mathrm{D}}_x^3+(c_{7}u+\alpha c_8){\mathrm{D}}_x^2+(c_9{u}^2+\alpha c_{10}u+{\alpha }^2{c}_{11}+c_{12}{u}_x){\mathrm{D}}_x\right.\hfill \\ & & \left.+(c_{13}{u}^3+\alpha c_{14}{u}^2+{\alpha }^2{c}_{15}u+c_{16}u{u}_x+\alpha c_{17}{u}_x+c_{18}{u}_{xx})\mathrm{I}\right),\hfill \end{array}$$

  (92)

  which upon expansion has 125 terms, and

  $$\begin{array}{ccc}\hfill \mathcal{M}\circ \mathcal{L}& =& \left(c_6{\mathrm{D}}_x^3+(c_{7}u+\alpha c_8){\mathrm{D}}_x^2+(c_9{u}^2+\alpha c_{10}u+{\alpha }^2{c}_{11}+c_{12}{u}_x){\mathrm{D}}_x\right.\hfill \\ & & \left.+(c_{13}{u}^3+\alpha c_{14}{u}^2+{\alpha }^2{c}_{15}u+c_{16}u{u}_x+\alpha c_{17}{u}_x+c_{18}{u}_{xx})\mathrm{I}\right)\circ \hfill \\ & & \left({\mathrm{D}}_x^2+(c_{1}u+\alpha c_2){\mathrm{D}}_x+(c_3{u}^2+\alpha c_{4}u+c_5{u}_x)\mathrm{I}\right),\hfill \end{array}$$

  (93)

  which after expansion has 126 terms.

Substitute (91)–(93) into (88). The resulting expression (with 105 terms) should be identically equal to zero for any function $\psi (x,t)$. Set the coefficients of $\psi ,{\psi }_x$, and ${\psi }_{xx}$ equal to zero, and then set the coefficients of all monomials in u and its x-derivatives separately equal to zero. This yields a nonlinear system of 24 equations for the undetermined coefficients:

$$\begin{array}{ccc}& & 2c_7-3c_1{c}_6=0,4c_9-6c_3{c}_6-c_1{c}_7=0,\hfill \\ & & \phantom{c_7-3c_1{c}_6=0,}⋮\phantom{4c_9-6c_3{c}_6-c_1{c}_7=0,}\hfill \\ & & c_{12}+2c_{18}-c_1-c_1{c}_6-3c_5{c}_6=0,\alpha (c_{17}-c_4+c_2{c}_{18}-c_4{c}_6-c_5{c}_8)=0.\hfill \end{array}$$

(94)

For brevity, we have shown only a couple of the shortest equations (coming from $u_x{\mathrm{D}}_x^3$ and $u{u}_x{\mathrm{D}}_x^2,$ respectively), and two of the longest equations (coming from $u_{3x}{\mathrm{D}}_x$ and $u_{3x}\mathrm{I}$, respectively). Since each equation has a mixture of linear and and nonlinear terms, several solution branches occur. Mathematica’s Solve function returns five non-trivial solutions. Three of these solutions lead to Lax pairs of lower order or degenerate Lax pairs which will not be discussed. Instead, we focus on the two solutions that lead to Lax pairs that are useful in, e.g., the application of the inverse scattering transform (IST) and the Riemann–Hilbert methods to solve the Gardner equation. They have coefficients

$$\begin{array}{ccc}& & c_2={\displaystyle \frac{6c_4-1}{3c_1}},c_3=\frac{1}{12}(3c_1^2+2\beta ),c_5=\frac{1}{6}(3c_1\pm \sqrt{-6\beta }),c_6=-4,c_7=-6c_1,\hfill \\ & & c_9=-(3c_1^2+\beta ),c_{10}=c_1{c}_8-1,c_{11}={\displaystyle \frac{(1-6c_4)(1-6c_4-c_1{c}_8)}{3c_1^2}},\hfill \\ & & c_{12}=-(6c_1\pm \sqrt{-6\beta }),c_{13}=-\frac{1}{6}{c}_1(3c_1^2+2\beta ),\hfill \\ & & c_{14}=-{\displaystyle \frac{3c_1^2+2\beta (1-6c_4)-c_1{c}_8(3c_1^2+2\beta )}{12c_1}},\hfill \\ & & c_{15}={\displaystyle \frac{c_4(c_1{c}_8+6c_4-1)}{c_1}},c_{16}=-\frac{1}{2}(6c_1^2+2\beta \pm c_1\sqrt{-6\beta }),\hfill \\ & & c_{17}={\displaystyle \frac{3c_1(c_1{c}_8-1)\pm (c_1{c}_8+6c_4-1)\sqrt{-6\beta }}{6c_1}},c_{18}=-\frac{1}{2}(3c_1\pm \sqrt{-6\beta }),\hfill \end{array}$$

(95)

where $c_1,c_4,$ and $c_8$ are arbitrary constants. To be able to obtain the Lax pair for the KdV equation where $c_1=0$, one should require that $c_4=\frac{1}{6}$ and $c_8=0$, otherwise $c_2$, $c_{11}$, $c_{14}$, and $c_{17}$ would become infinite. Notice that both requirements allow one to clear $c_1$ from all denominators. Furthermore, the coefficients then simplify into

$$\begin{array}{ccc}& & c_2=0,c_3=\frac{1}{12}(3c_1^2+2\beta ),c_4=\frac{1}{6},c_5=\frac{1}{6}(3c_1\pm \sqrt{-6\beta }),c_6=-4,c_7=-6c_1,\hfill \\ & & c_8=0,c_9=-(3c_1^2+\beta ),c_{10}=-1,c_{11}=0,c_{12}=-(6c_1\pm \sqrt{-6\beta }),\hfill \\ & & c_{13}=-\frac{1}{6}{c}_1(3c_1^2+2\beta ),c_{14}=-\frac{1}{4}{c}_1,c_{15}=0,c_{16}=-\frac{1}{2}(6c_1^2+2\beta \pm c_1\sqrt{-6\beta }),\hfill \\ & & c_{17}=-\frac{1}{2},c_{18}=-\frac{1}{2}(3c_1\pm \sqrt{-6\beta }).\hfill \end{array}$$

(96)

Finally, substitute the coefficients into (89) and (90) to get

$$\begin{array}{ccc}\hfill \mathcal{L}& =& {\mathrm{D}}_x^2+c_{1}u{\mathrm{D}}_x+\frac{1}{6}\left(\frac{1}{2}(3c_1^2+2\beta )u^2+\alpha u+(3c_1\pm \sqrt{-6\beta })u_x\right)\mathrm{I},\hfill \end{array}$$

(97)

$$\begin{array}{ccc}\hfill \mathcal{M}& =& -4{\mathrm{D}}_x^3-6c_{1}u{\mathrm{D}}_x^2-\left((3c_1^2+\beta )u^2+\alpha u+(6c_1\pm \sqrt{-6\beta })u_x\right){\mathrm{D}}_x\hfill \\ & & -\left(\frac{1}{6}{c}_1(3c_1^2+2\beta )u^3+\frac{1}{4}\alpha c_1{u}^2+\frac{1}{2}(6c_1^2+2\beta \pm c_1\sqrt{-6\beta })u{u}_x\right.\hfill \\ & & \left.+\frac{1}{2}\alpha u_x+\frac{1}{2}(3c_1\pm \sqrt{-6\beta })u_{xx}\right)\mathrm{I},\hfill \end{array}$$

(98)

where the constant $c_1$ is arbitrary. Hence, this is a one-parameter family of Lax pairs. Set $c_1=2ϵ$ to get (79) and (80). With (97) and (98)

$$\begin{array}{ccc}& & {\mathcal{L}}_t+[\mathcal{L},\mathcal{M}]=\frac{1}{6}\left((3c_1\pm \sqrt{-6\beta }){\mathrm{D}}_x(u_t+\alpha u{u}_x+\beta u^2{u}_x+u_{3x})\right.\hfill \\ & & \left.+(\alpha +(3c_1^2+2\beta )u)(u_t+\alpha u{u}_x+\beta u^2{u}_x+u_{3x})\right)\mathrm{I}\hfill \\ & & +c_1(u_t+\alpha u{u}_x+\beta u^2{u}_x+u_{3x}){\mathrm{D}}_x,\hfill \end{array}$$

(99)

which, after setting $c_1=2ϵ$, is equivalent to (83).

9. Bilinear Form

In this section we show how the Gardner equation (1) can be transformed into the mKdV Equation (3) and how that helps with deriving Hirota’s bilinear representation [6] and, eventually, solitary wave and soliton solutions of (1). The existence of multi-soliton solutions (i.e., soliton solutions of any order) is yet another proof that the Gardner equation is completely integrable.

A simple shift of u allows one to remove the quadratic term $\alpha u{u}_x$. Indeed, set $u=\tilde{u}-{\displaystyle \frac{\alpha }{2\beta }}$ to replace (1) by

$${\tilde{u}}_t-{\displaystyle \frac{{\alpha }^2}{4\beta }}{\tilde{u}}_x+\beta {\tilde{u}}^2{\tilde{u}}_x+{\tilde{u}}_{3x}=0,$$

(100)

which is still in the original independent variables x and t. As will be shown below, the linear term in ${\tilde{u}}_x$ can also be removed by a change of independent variables.

• Step 1: Construct a bilinear form as follows: first, integrate (100) with respect to x,

  $${\partial }_t\left({\int }^x\tilde{u}dx\right)-{\displaystyle \frac{{\alpha }^2}{4\beta }}\tilde{u}+\frac{1}{3}\beta {\tilde{u}}^3+{\tilde{u}}_{xx}=0,$$

  (101)

  setting the integration “constant” $c\left(t\right)$ equal to zero. As with the mKdV equation [5], substitute the Hirota transformation

  $$\tilde{u}=i\sqrt{{\displaystyle \frac{6}{\beta }}}{\left(ln\left({\displaystyle \frac{f+ig}{f-ig}}\right)\right)}_x=2\sqrt{{\displaystyle \frac{6}{\beta }}}{\left(\mathrm{Arctan}\left(\frac{f}{g}\right)\right)}_x=2\sqrt{{\displaystyle \frac{6}{\beta }}}\left({\displaystyle \frac{f_{x}g-f{g}_x}{f^2+g^2}}\right)$$

  (102)

  into (101). Then, divide by $-2\sqrt{\frac{6}{\beta }}$ and regroup the terms, yielding

  $$\begin{array}{ccc}& & \left(f^2+g^2\right)\left(g{f}_t-f{g}_t+3f_x{g}_{xx}-3g_x{f}_{xx}-f{g}_{3x}+g{f}_{3x}-{\displaystyle \frac{{\alpha }^2}{4\beta }}\left(f{g}_x-g{f}_x\right)\right)\hfill \\ & & -6\left(g{f}_x-f{g}_x\left)\right(f{f}_{xx}+g{g}_{xx}-f_x^2-g_x^2\right)=0.\hfill \end{array}$$

  (103)

  Next, set the factors multiplying $f^2+g^2$ and $g{f}_x-f{g}_x$ separately equal to zero, to obtain

  $$\begin{array}{ccc}& & g{f}_t-f{g}_t+3f_x{g}_{xx}-3g_x{f}_{xx}-f{g}_{3x}+g{f}_{3x}-{\displaystyle \frac{{\alpha }^2}{4\beta }}\left(f{g}_x-g{f}_x\right)=0,\hfill \end{array}$$

  (104)

  $$\begin{array}{ccc}& & f{f}_{xx}+g{g}_{xx}-f_x^2-g_x^2=0.\hfill \end{array}$$

  (105)
  Based on the scaling symmetry of (1) with weights (20) and the structure of the bilinear form of the mKdV equation [5], recast the above equations in bilinear form,

  $$\begin{array}{ccc}& & (c_1{D}_t+c_2{D}_x^3+{\alpha }^2{c}_3{D}_x)(f·g)=0,\hfill \end{array}$$

  (106)

  $$\begin{array}{ccc}& & c_4{D}_x^2(f·f+g·g)=0,\hfill \end{array}$$

  (107)

  with undetermined coefficients $c_1,c_2,c_3$, and $c_4$. Notice that with $W\left(f\right)=W\left(g\right)=0$, all terms in (104) and (106) have weights of three, whereas the terms in (105) and (107) have weights of two.

The bilinear operators $D_x$ and $D_t$ (not to be confused with total derivatives used in earlier sections) are defined as

$$\begin{array}{ccc}\hfill D_x^m(f·g)& =& {({\partial }_x-{\partial }_{x^{\prime }})}^{m}f(x,t)g(x^{\prime },t){|}_{x^{\prime }=x}=\sum _{j=0}^m{\displaystyle \frac{{(-1)}^{m-j}m!}{j!(m-j)!}}\left({\displaystyle \frac{{\partial }^{j}f}{\partial x^j}}\right)\left({\displaystyle \frac{{\partial }^{m-j}g}{\partial x^{m-j}}}\right),\hfill \end{array}$$

(108)

$$\begin{array}{ccc}\hfill D_t^n(f·g)& =& {({\partial }_t-{\partial }_{t^{\prime }})}^{n}f(x,t)g(x,t^{\prime }){|}_{t^{\prime }=t}=\sum _{j=0}^n{\displaystyle \frac{{(-1)}^{n-j}n!}{j!(n-j)!}}\left({\displaystyle \frac{{\partial }^{j}f}{\partial t^j}}\right)\left({\displaystyle \frac{{\partial }^{n-j}g}{\partial t^{n-j}}}\right),\hfill \end{array}$$

(109)

which represent the Leibniz rule for x-derivatives (and t-derivatives, respectively) of products of functions with every other sign flipped. Explicitly,

$$\begin{array}{ccc}\hfill (c_1{D}_t+c_2{D}_x^3+{\alpha }^2{c}_3{D}_x)(f·g)& =& c_1(g{f}_t-f{g}_t)+c_2(3f_x{g}_{xx}-3g_x{f}_{xx}+g{f}_{3x}-f{g}_{3x})\hfill \\ \hfill & & +{\alpha }^2{c}_3(g{f}_x-f{g}_x),\hfill \end{array}$$

(110)

$$\begin{array}{ccc}\hfill c_4{D}_x^2(f·f+g·g)& =& 2c_4(f{f}_{xx}+g{g}_{xx}-f_x^2-g_x^2).\hfill \end{array}$$

(111)

• Step 2: Compute the undetermined coefficients. Equate (106) and (110) and treat all monomials in f and g and their derivatives as independent to get $c_1=c_2=1,$ and $c_3={\displaystyle \frac{1}{4\beta }}.$ Perform the same with (107) and (111) to get $c_4={\displaystyle \frac{1}{2}}$. Finally, substitute the constants into (106) and (107) and clear common factors to get a bilinear representation of (100):

  $$(D_t+D_x^3+{\displaystyle \frac{{\alpha }^2}{4\beta }}{D}_x)(f·g)=0,D_x^2(f·f+g·g)=0,$$

  (112)

  which, in light of (102), will only lead to real solutions for the focusing Gardner equation $(\beta >0)$.

The above bilinear formulation is expressed in the original variables x and t. Of course, the term ${\displaystyle \frac{{\alpha }^2}{4\beta }}{D}_x$ in (112) can be removed at the cost of introducing a new variable X. Indeed, using the chain rule for differentiation, one can readily verify that the Galilean transformation $(x,t,u(x,t\left)\right)⟶(X,T,U(X,T\left)\right)$ where

$$X=x+{\displaystyle \frac{{\alpha }^2}{4\beta }}t,T=t,u(x,t)=U(X,T)-{\displaystyle \frac{\alpha }{2\beta }},$$

(113)

takes (1) into

$$U_T+\beta U^2{U}_X+U_{3X}=0,$$

(114)

with bilinear representation [5]

$$(D_T+D_X^3)(F·G)=0,D_X^2(F·F+G·G)=0.$$

(115)

Once particular solutions $F(X,T)$ and $G(X,T)$ of

$$\begin{array}{ccc}& & G{F}_t-F{G}_t+3F_x{G}_{xx}-3G_x{F}_{xx}-F{G}_{3x}+G{F}_{3x}=0,\hfill \end{array}$$

(116)

$$\begin{array}{ccc}& & F{F}_{xx}+G{G}_{xx}-F_x^2-G_x^2=0,\hfill \end{array}$$

(117)

are computed,

$$U(X,T)=2\sqrt{{\displaystyle \frac{6}{\beta }}}\left({\displaystyle \frac{F_{X}G-F{G}_X}{F^2+G^2}}\right)$$

(118)

will solve (114). Solutions $u(x,t)$ of (1) then follow from

$$u(x,t)=2\sqrt{{\displaystyle \frac{6}{\beta }}}\left({\displaystyle \frac{F_{X}G-F{G}_X}{F^2+G^2}}\right)-{\displaystyle \frac{\alpha }{2\beta }},$$

(119)

after using (113) to return to the original variables u, x, and t.

10. Gardner Transformation

In this section we discuss a slight generalization of the Miura transformation [31], sometimes called the Gardner transformation or Gardner transform [32,66,67,68],

$$u={\displaystyle \frac{\beta }{\gamma }}\left(v^2\pm \sqrt{-\frac{6}{\beta }}{v}_x+{\displaystyle \frac{\alpha }{\beta }}v\right),$$

(120)

which connects solutions $v(x,t)$ of the Gardner equation,

$$v_t+\alpha v{v}_x+\beta v^2{v}_x+v_{3x}=0,$$

(121)

with $\beta \ne 0$, to solutions $u(x,t)$ of the KdV equation,

$$u_t+\gamma u{u}_x+u_{3x}=0,$$

(122)

with arbitrary coefficient $\gamma \ne 0$. The use of $\gamma$ will avoid confusion with $\alpha$ in (121) and, more importantly, allow us to set $\alpha =0$ to get the standard Miura transformation (see Section 12).

Substituting (120) into (122), it is straightforward to verify that

$$u_t+\gamma u{u}_x+u_{3x}\dot{=}\frac{\beta }{\gamma }\left((2v+\frac{\alpha }{\beta })\mathrm{I}\pm \sqrt{-\frac{6}{\beta }}{\mathrm{D}}_x\right)\left(v_t+\alpha v{v}_x+\beta v^2{v}_x+v_{3x}\right),$$

(123)

where $\dot{=}$ means that the left hand side is evaluated on solutions of (121). As before, $\mathrm{I}$ is the identity operator and ${\mathrm{D}}_x$ is the total derivative operator defined in (24). Clearly, the Gardner transformation will only be real for the defocusing Gardner equation.

We will show how (120) can be computed using the scaling symmetries of the KdV and Gardner equations discussed in Section 4. Recall that $W\left(u\right)=2$, $W\left(v\right)=W\left(\alpha \right)=1$, and $W\left(\gamma \right)=W\left(\beta \right)=0$. Therefore, (120) is uniform in rank of rank two.

• Step 1: Construct a candidate for the Gardner transformation. Make the list $\{\{v^2,\alpha v,{\alpha }^2\}$, $\{v,\alpha \}\}$ of monomials in v and $\alpha$ of rank 2 or less. By differentiating its elements, replace the second sublist by $\left\{v_x\right\}$. Linearly combine the resulting elements with undetermined coefficients,

  $$u=c_1{v}^2+\alpha c_{2}v+{\alpha }^2{c}_3+c_4{v}_x,$$

  (124)

  to generate a candidate for the Gardner transformation.
• Step 2: Compute the undetermined coefficients. Substitute (124) into (122) and, using (121), replace $v_t$ and $v_{tx}$. The resulting expression must vanish on the jet space, leading to $c_2{c}_3=c_3{c}_4=0$ and half a dozen more complicated equations. For $c_4=0$, (124) would become an algebraic transformation. Hence, $c_3=0$ and, after simplification of the more complicated equations, one is left with the following nonlinear system

  $$\begin{array}{c}\hfill \gamma c_1-\beta =0,\gamma c_2-1=0,6c_1+\gamma c_4^2=0,3\gamma c_1{c}_2-\beta c_2-2c_1=0.\end{array}$$

  (125)

  Substitute the solution, $c_1=\frac{\beta }{\gamma }$, $c_2=\frac{1}{\gamma }$, $c_4=\pm {\displaystyle \frac{1}{\gamma }}\sqrt{-6\beta }$, and $c_3=0$, into (124) to get (120).

Of course, the  “uniformity-in-rank” argument also applies to (123), and therefore can be used to derive that equation. Observe that the ranks of the left and right hand sides of (123) match. Since the terms of the KdV equation (left) and Gardner equation (right) have ranks five and four, respectively, the operator that connects them must have rank one. Thus, only $v\mathrm{I}$, $\alpha \mathrm{I}$, and ${\mathrm{D}}_x$ can occur in that operator. Apply the candidate for the operator,

$$(C_{1}v+\alpha C_2)\mathrm{I}+C_3{\mathrm{D}}_x,$$

(126)

to (121), and equate the resulting expression to (122) after substitution of (120) but without evaluation on solutions of (121). After simplification, this yields the linear system

$$\begin{array}{c}\hfill \gamma C_1-2\beta =0,\gamma C_2-1=0,\gamma C_3\pm \sqrt{-6\beta }=0,\gamma C_1+\beta \gamma C_2-3\beta =0.\end{array}$$

(127)

Solve the system to obtain $C_1=\frac{2\beta }{\gamma }$, $C_2=\frac{1}{\gamma }$, and $C_3=\pm \frac{1}{\gamma }\sqrt{-6\beta }$. Substitute the solution into (126) to get (123).

Using (120), some solutions for the KdV equation could be obtained from those of the Gardner equation (see, e.g., [11]). For $\alpha =0$, (120) reduces to the Miura transformation, allowing one to generate solutions of the KdV equation from those of the mKdV equation. Although this is worthy of investigation, it is beyond the scope of this article. For an in-depth discussion of connections between the KdV, mKdV, and Gardner equations and additional applications of the Gardner and Miura transformations, we refer to [11,66,68].

11. The Korteweg–de Vries Equation

Since the KdV equation is a special case of the Gardner equation, its conservation laws, higher-order symmetries, and recursion operator immediately follow from those of (1) by setting $\beta =0$ in (25)–(47), (45)–(47), and (53), respectively. The conservation laws for the KdV equation have been known since the 1970s [32,69] and have played an important role in the development of the concept of complete integrability. Its symmetries and recursion operator have been studied in, e.g.,  [54].

The well-known Lax pair [64] for the KdV equation,

$$\mathcal{L}={\mathrm{D}}_x^2+\frac{1}{6}\alpha u\mathrm{I},\mathcal{M}=-4{\mathrm{D}}_x^3-\alpha u{\mathrm{D}}_x-\frac{1}{2}\alpha u_x\mathrm{I},$$

(128)

follows from (79) and (80) by setting $\beta =ϵ=0$.

The bilinear form for the KdV equation is much simpler than the one for the mKdV equation, and so are its soliton solutions. The interested reader is referred to [1,5,6,30] for the bilinear formulation and explicit formulas for the two-, three-, and  N-soliton solutions.

For completeness, we only include the solitary wave and cnoidal wave solutions, which were first derived in [28],

$$\begin{array}{ccc}\hfill u(x,t)& =& {\displaystyle \frac{12k^2}{\alpha }}{\mathrm{sech}}^2(kx-4k^{3}t+\delta )={\displaystyle \frac{12k^2}{\alpha }}\left(1-{tanh}^2(kx-4k^{3}t+\delta )\right),\hfill \end{array}$$

(129)

$$\begin{array}{ccc}\hfill u(x,t)& =& {\displaystyle \frac{8k^2}{\alpha }}(1-m)+{\displaystyle \frac{12k^2}{\alpha }}m{\mathrm{cn}}^2(kx-4k^{3}t+\delta ;m),\hfill \end{array}$$

(130)

where $m\in (0,1)$ is the modulus of the Jacobi elliptic cosine ($\mathrm{cn}$) function. Both solutions are depicted in Figure 1. When m approaches 1, the peaks of the $\mathrm{cn}$-squared solution become a bit taller, and the valleys become lower and flatter before they spread out horizontally to become the $\mathrm{sech}$-squared solution. Both solutions (129) and (130) satisfy ${lim}_{\left|x\right|\to \infty }u(x,t)=0$ for all t. The more general expressions corresponding to a nonzero boundary condition can be found in, e.g., refs. [1,2,29].

The soliton solutions of (2) can be computed with our code PDESolitonSolutions.m [24]. A discussion of their properties is outside the scope of this paper. Instead, we refer to [1,2,5,30] and the references given in [29].

12. The Modified Korteweg–de Vries Equation

Without extra work, we have the first three conservation laws [32] and higher-order symmetries [54] for the mKdV equation by setting $\alpha =0$ in (25)–(27) and (45)–(47), respectively. The recursion operator [54] connecting those symmetries follows from (53) with $\alpha =0$.

Likewise, a one parameter Lax pair for the mKdV equation follows from (79) and (80) by setting $\alpha =0$:

$$\begin{array}{ccc}\hfill \mathcal{L}& =& {\mathrm{D}}_x^2+2ϵu{\mathrm{D}}_x+\frac{1}{6}\left((6{ϵ}^2+\beta )u^2+(6ϵ\pm \sqrt{-6\beta })u_x\right)\mathrm{I},\hfill \end{array}$$

(131)

$$\begin{array}{ccc}\hfill \mathcal{M}& =& -4{\mathrm{D}}_x^3-12ϵu{\mathrm{D}}_x^2-\left((12{ϵ}^2+\beta )u^2+(12ϵ\pm \sqrt{-6\beta })u_x\right){\mathrm{D}}_x\hfill \\ \hfill & & -\left(\frac{1}{3}ϵ(12{ϵ}^2+2\beta )u^3+(12{ϵ}^2+\beta \pm ϵ\sqrt{-6\beta })u{u}_x+\frac{1}{2}(6ϵ\pm \sqrt{-6\beta })u_{xx}\right)\mathrm{I},\hfill \end{array}$$

(132)

which for $ϵ=0$ simplify into

$$\begin{array}{ccc}\hfill \mathcal{L}& =& {\mathrm{D}}_x^2+\frac{1}{6}\left(\beta u^2\pm \sqrt{-6\beta }{u}_x\right)\mathrm{I},\hfill \end{array}$$

(133)

$$\begin{array}{ccc}\hfill \mathcal{M}& =& -4{\mathrm{D}}_x^3-(\beta u^2\pm \sqrt{-6\beta }{u}_x){\mathrm{D}}_x-(\beta u{u}_x\pm \frac{1}{2}\sqrt{-6\beta }{u}_{xx})\mathrm{I}.\hfill \end{array}$$

(134)

To our knowledge, this Lax pair first appeared in [70,71]. A further discussion of other Lax pairs for the mKdV equation can be found in [63,72]. In the latter paper, a more comprehensive algorithm to compute Lax pairs in operator form is presented, with the mKdV equation among its examples.

The Miura transformation [31,32,67],

$$u={\displaystyle \frac{\beta }{\gamma }}\left(v^2\pm \sqrt{-\frac{6}{\beta }}{v}_x\right),$$

(135)

which connects solutions of the mKdV Equation (3) (with dependent variable $v(x,t)$) to solutions $u(x,t)$ of the KdV Equation (122) readily follows from (120) by setting $\alpha =0$. Likewise, (123) reduces to

$$u_t+\gamma u{u}_x+u_{3x}\dot{=}\frac{\beta }{\gamma }\left(2v\mathrm{I}\pm \sqrt{-\frac{6}{\beta }}{\mathrm{D}}_x\right)\left(v_t+\beta v^2{v}_x+v_{3x}\right).$$

(136)

Various types of solutions for both the focusing and defocusing mKdV equations have been reported in the literature [14,15,34], including bright and dark solitons, breathers, rational solutions, kinks, etc. In this paper we mainly focus on solitary wave and soliton solutions of the mKdV equation. The nature of the solutions of (114) depends on the sign of $\beta$. Two cases have to be considered.

• Case I: The focusing mKdV equation ($\beta >0$).
  The mKdV Equation (114) has solutions involving a cosh-function,

  $$U(X,T)=U_0+{\displaystyle \frac{3k^2}{\beta \left(U_0\pm \sqrt{U_0^2+\frac{3k^2}{2\beta }}cosh\Theta \right)}},$$

  (137)

  with $\Theta =kX-(\beta U_0^2+k^2)kT+\delta$, where the boundary value $U_0$, wave number k, and phase $\delta$ are arbitrary constants. To prevent blow-up in finite time we will only consider the plus sign in (137). The solution satisfying ${lim}_{\left|X\right|\to \infty }U(X,T)=U_0$ has been computed with Hirota’s method in [73], where only the case $\beta >0$ was considered. Solution (137) is also valid for $\beta <0$ with a caveat (see below). For $U_0=0$ the solution reduces to the well-known $\mathrm{sech}$-solution,

  $$U(X,T)=\pm \sqrt{\frac{6}{\beta }}k\mathrm{sech}\left(kX-k^{3}T+\delta \right),$$

  (138)

  where the ± sign is due to the invariance of (114) under the discrete symmetry $U\to -U$.

The soliton solutions of the focusing mKdV equation have been known for a long time and can be computed with a variety of methods. Adhering to Hirota’s method [5,6], the one-soliton solution readily follows from substitution of

$$F={\mathrm{e}}^{\Theta }={\mathrm{e}}^{kX-\omega T+\delta }\mathrm{and}G=1$$

(139)

into (116), yielding $\omega =k^3$ and (117), which is identically satisfied. From (118), one then obtains

$$\begin{array}{ccc}\hfill U(X,T)& =& 2\sqrt{{\displaystyle \frac{6}{\beta }}}\left({\displaystyle \frac{F_x}{1+F^2}}\right)=2\sqrt{{\displaystyle \frac{6}{\beta }}}k\left({\displaystyle \frac{{\mathrm{e}}^{\Theta }}{1+{\mathrm{e}}^{2\Theta }}}\right)=\sqrt{\frac{6}{\beta }}k\mathrm{sech}\Theta \hfill \\ & =& \sqrt{\frac{6}{\beta }}k\mathrm{sech}(kX-k^{3}T+\delta )=2\sqrt{\frac{6}{\beta }}K\mathrm{sech}\left(2KX-8K^{3}T+\delta \right),\hfill \end{array}$$

(140)

where $K={\displaystyle \frac{k}{2}}$, which matches (138). The two-soliton solution [5] follows from

$$F={\mathrm{e}}^{{\Theta }_1}+{\mathrm{e}}^{{\Theta }_2}\mathrm{and}G=1-a_{12}{\mathrm{e}}^{{\Theta }_1+{\Theta }_2},$$

(141)

with ${\Theta }_i=k_{i}X-k_i^{3}T+{\delta }_i$ and $a_{12}={\left({\displaystyle \frac{k_1-k_2}{k_1+k_2}}\right)}^2$. Then, from (118)

$$U(X,T)=2\sqrt{{\displaystyle \frac{6}{\beta }}}\left({\displaystyle \frac{k_1{\mathrm{e}}^{{\Theta }_1}+k_2{\mathrm{e}}^{{\Theta }_2}+a_{12}(k_1{\mathrm{e}}^{{\Theta }_2}+k_2{\mathrm{e}}^{{\Theta }_1}){\mathrm{e}}^{{\Theta }_1+{\Theta }_2}}{{\displaystyle 1+{\mathrm{e}}^{2{\Theta }_1}+{\mathrm{e}}^{2{\Theta }_2}+\frac{8k_1{k}_2}{{(k_1+k_2)}^2}{\mathrm{e}}^{{\Theta }_1+{\Theta }_2}+a_{12}^2{\mathrm{e}}^{2{\Theta }_1+2{\Theta }_2}}}}\right).$$

(142)

Details of the derivation are given in [5] and [6], where formulas for the three- and N-soliton solutions can also be found.

• Case II: The defocusing mKdV equation ($\beta <0$).
  Using the Zakharov–Shabat method, the defocusing mKdV equation was solved in [74]. Solution (137) with X replaced by $-X$ corresponds to the case $N=1$ in [74]. Notice that when $\beta <0$, solution (137) will only exist if $k^2<\frac{2\left|\beta \right|}{3}{U}_0^2.$ This will be discussed in greater detail in the next section.

A new exact two-soliton solution of (114) with $\beta <0$ is presented in [12]:

$$u(X,T)=\sqrt{-{\displaystyle \frac{6}{\beta }}}\left({\displaystyle \frac{sinh(\Phi +2\delta ){\mathrm{e}}^{-2\Psi }+sinh(\Phi -2\delta ){\mathrm{e}}^{2\Psi }+2sinh(\Phi )(1-{sinh}^2\left(2\delta \right))\mathrm{sech}\left(2\delta \right)}{cosh(\Phi +2\delta ){\mathrm{e}}^{-2\Psi }+cosh(\Phi -2\delta ){\mathrm{e}}^{2\Psi }+2cosh(\Phi )cosh\left(2\delta \right)}}\right)$$

(143)

with $\Phi =X+2T,$ and $\Psi =\left(X+2(1+2{\mathrm{sech}}^2\left(2\delta \right))T+X_0\right)tanh\left(2\delta \right),$ with $\delta >0$ and $X_0$ arbitrary real parameters. This solution is obtained as the limit for the modulus going to one of a dark breather solution (involving Jacobi elliptic functions and elliptic integrals) of the defocusing mKdV equation.

Solutions (137) and (138) will be used in the next section to find table-top and hump-shaped solutions of (1). In turn, solution (143) will lead to a two-soliton solution of the defocusing Gardner equation.

13. Solitary Wave and Periodic Solutions

As pointed out in [37], the fact that (1) is invariant under the transformation

$$u\to -\left(u+\frac{\alpha }{\beta }\right)$$

(144)

makes it possible to have solutions of different polarity for that equation, most notably, “bright” as well as “dark” solitons, depending on the initial conditions. However, a solution that vanishes at $x=\pm \infty$ will be transformed by (144) into one that goes to $-\frac{\alpha }{\beta }$ as $x\to \pm \infty$. In this section we only cover a subset of the many types of solutions that (1) admits [75].

Depending on the sign of $\beta$ in (1), it is straightforward [76] to find kink- and hump-type solitary waves solutions as well as periodic solutions in terms of the Jacobi elliptic sine and cosine functions. Indeed, using our symbolic code PDESpecialSolutions.m [26] for the tanh, $\mathrm{sech}$, and Jacobi elliptic function methods, at a click of a button, one obtains simple exact solutions, which we cover first.

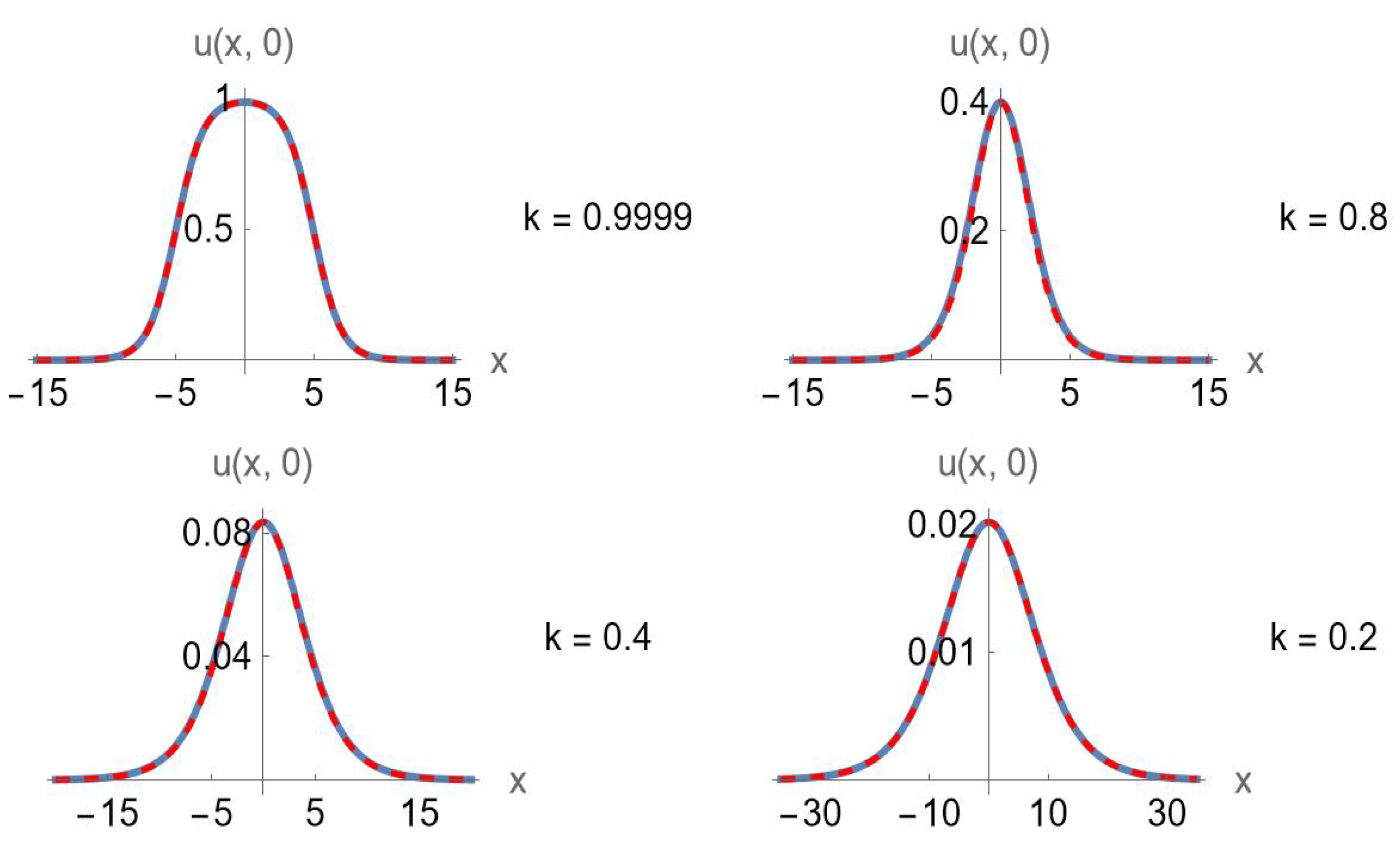
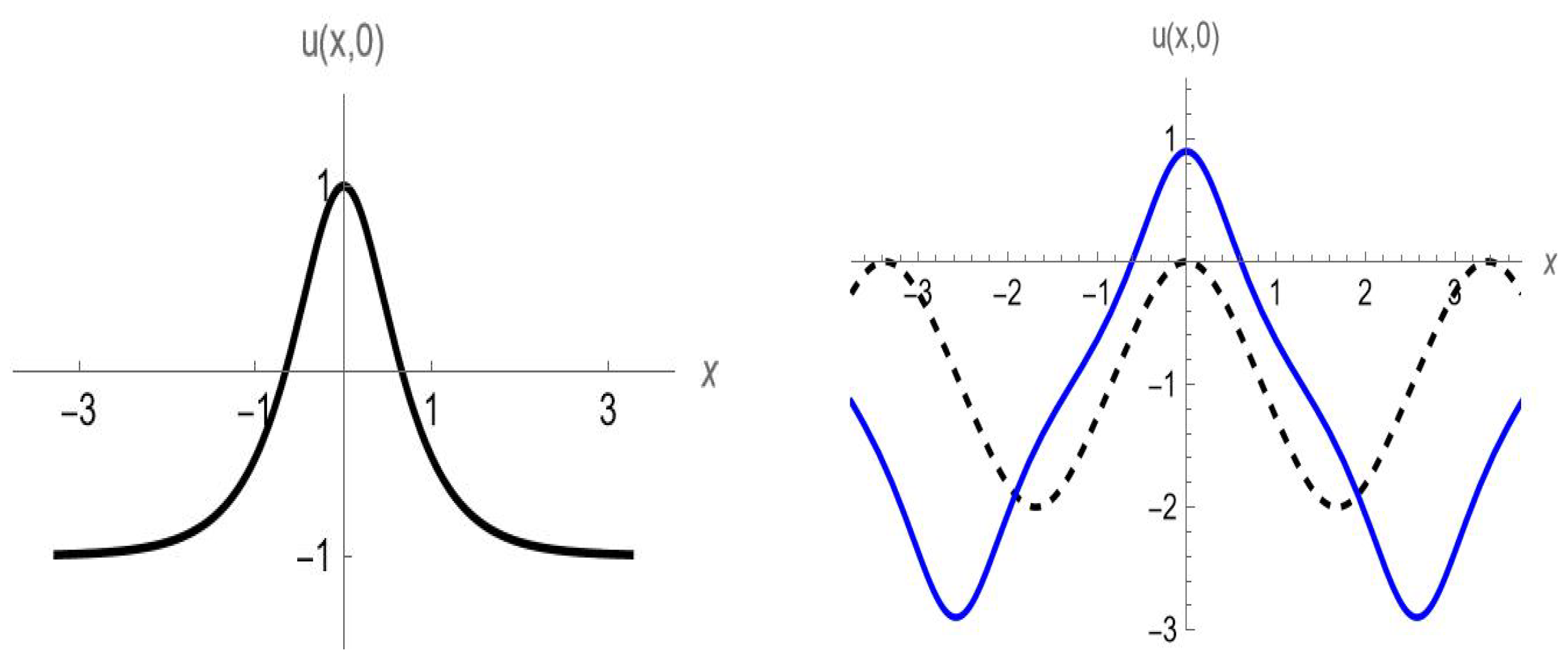
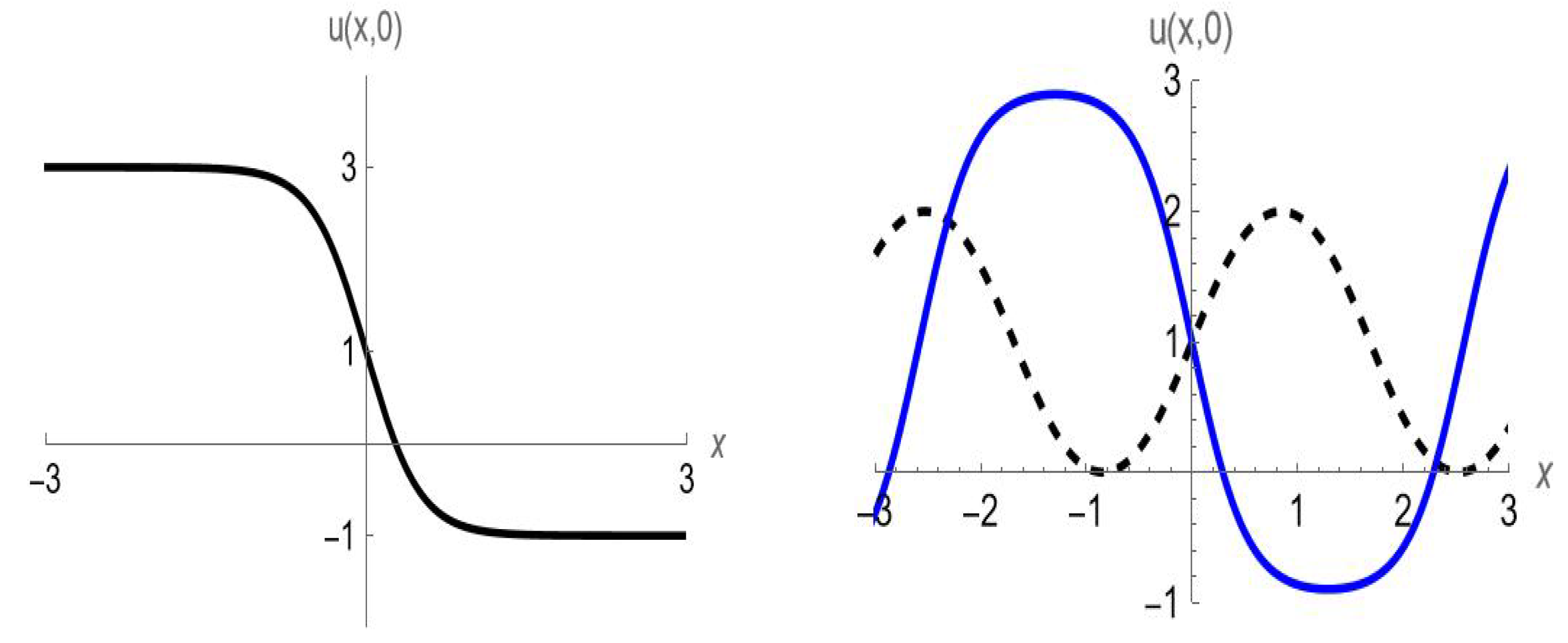
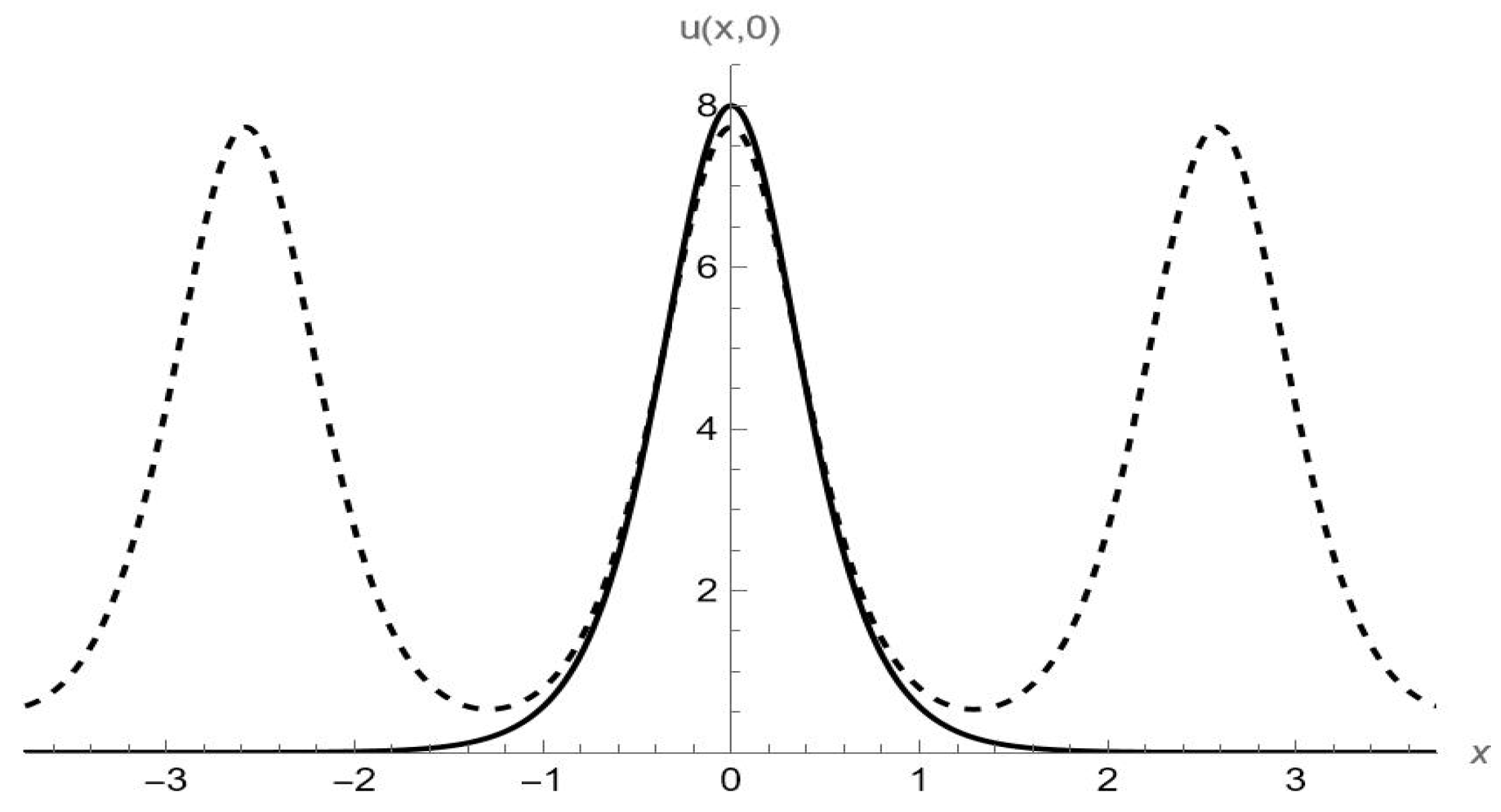
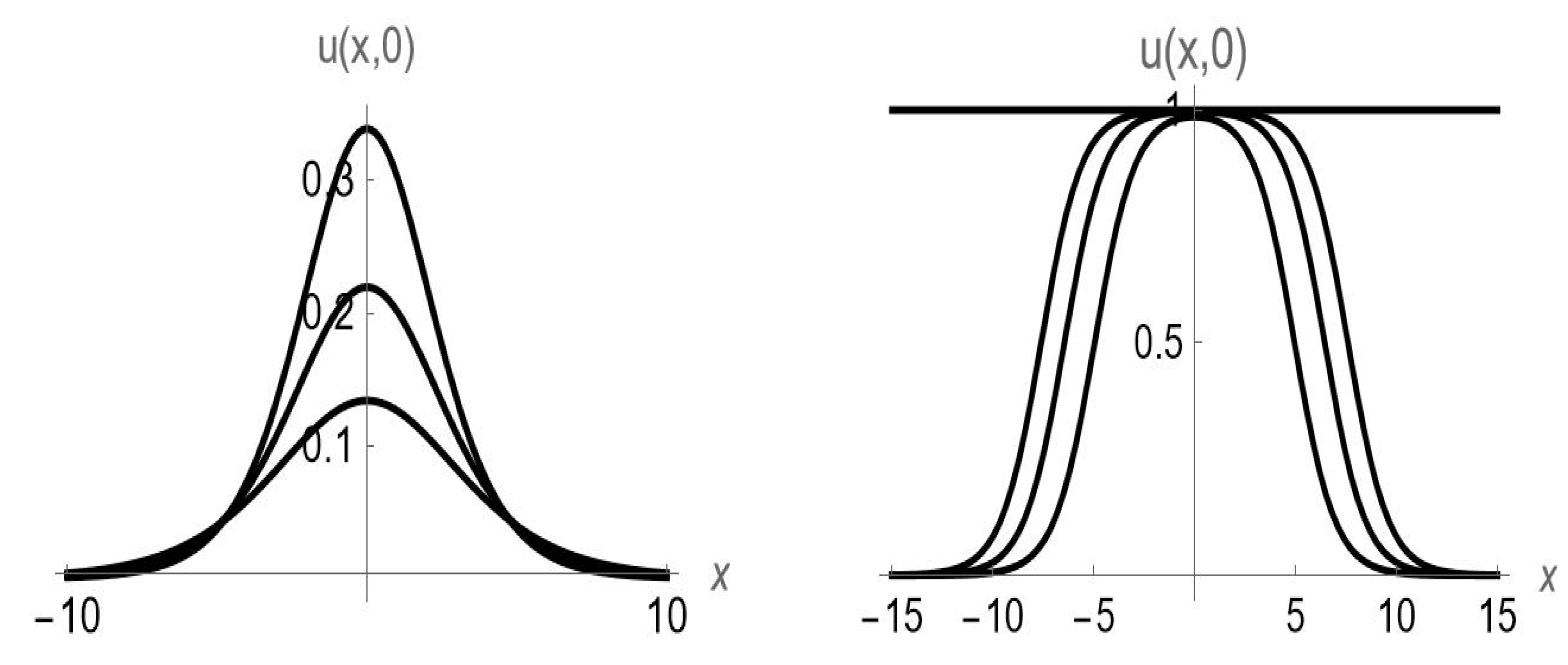
• Case I: The focusing Gardner equation $(\beta >0)$.
  The most well-known solutions are

  $$u(x,t)=-\left(\frac{\alpha }{2\beta }\pm \sqrt{\frac{6}{\beta }}k\mathrm{sech}\theta \right),$$

  (145)

  with $\theta =kx-(k^2-\frac{{\alpha }^2}{4\beta })kt+\delta$, and

  $$u(x,t)=-\left(\frac{\alpha }{2\beta }\pm \sqrt{\frac{6}{\beta }}k\sqrt{m}\mathrm{cn}(\theta ;m)\right),$$

  (146)

  with $\theta =kx+\left((1-2m)k^2+\frac{{\alpha }^2}{4\beta }\right)kt+\delta$. Both solutions for the minus sign (in front of the square root) are shown in Figure 2. Observe that as the value of m gets closer to 1, the $\mathrm{cn}$-function starts taking the shape of a $\mathrm{sech}$-profile.
  Of course, (145) also follows directly from (138) upon application of the transformation (113). Using (137) in the same way yields

  $$u(x,t)=U_0-{\displaystyle \frac{\alpha }{2\beta }}+{\displaystyle \frac{3k^2}{\beta \left(U_0+\sqrt{U_0^2+\frac{3k^2}{2\beta }}cosh\theta \right)}},$$

  (147)

  with $\theta =kx-(k^2+\beta U_0^2-\frac{{\alpha }^2}{4\beta })kt+\delta$ and where $U_0$ is arbitrary. Setting $U_0=\frac{\alpha }{2\beta }$ yields

  $$u(x,t)={\displaystyle \frac{6k^2}{\alpha (1+\sqrt{1+\frac{6\beta }{{\alpha }^2}{k}^2}cosh\theta )}},$$

  (148)

  with $\theta =kx-k^{3}t+\delta =k(x-Vt)+\delta$, where $V=k^2$ denotes the speed of the wave and $k^{-1}$ is the effective width of the solitary wave. This special solution is frequently used in the literature [35,66,76,77,78,79] and could also be computed via a Darboux transformation (see, e.g., [78]). For $\beta >0$, (148) is valid for all values of V, and since $V>0$ the wave is travelling to the right.
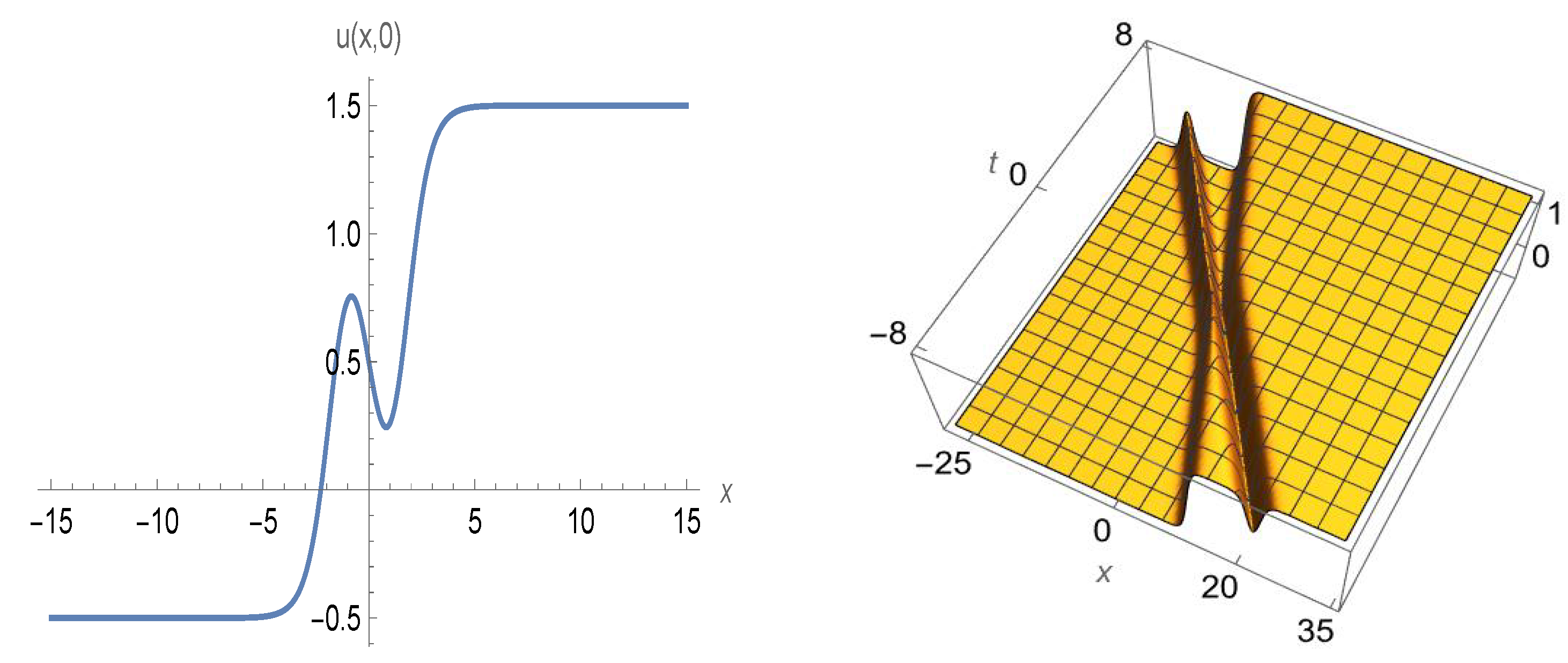
• Case II: The defocusing Gardner equation ($\beta <0$).
  The simplest exact solutions are

  $$u(x,t)=-\left(\frac{\alpha }{2\beta }\pm \sqrt{-\frac{6}{\beta }}ktanh\theta \right),$$

  (149)

  with $\theta =kx+(2k^2+\frac{{\alpha }^2}{4\beta })kt+\delta$, and

  $$u(x,t)=-\left(\frac{\alpha }{2\beta }\pm \sqrt{-\frac{6}{\beta }}k\sqrt{m}\mathrm{sn}(\theta ;m)\right),$$

  (150)

  with $\theta =kx+\left((1+m)k^2+\frac{{\alpha }^2}{4\beta }\right)kt+\delta$. In each of these solutions, $\delta$ is an arbitrary constant phase. The shock wave solution (149) and periodic solution (150) can be found in, e.g., ref. [74]. Both solutions for the minus sign (in front of the square root) are shown in Figure 3. As the value of m draws closer to 1, the $\mathrm{sn}$-function starts taking the shape of a $\tanh$-profile.
  With respect to (148) where $V=k^2$, note that when $\beta <0$, the argument of the square root, $1+\frac{6\beta }{{\alpha }^2}{k}^2$, will be zero when $V=V_{\mathrm{crit}}=\frac{{\alpha }^2}{6\left|\beta \right|}$. Thus, (148) is only valid when the speed is below that critical value ($V<V_{\mathrm{crit}}$). Thus, when dealing with the defocusing Gardner equation, if  $V\ge V_{\mathrm{crit}}$, there is no solution of type (148). Turning the argument around, solutions for (148) of large amplitude (which is proportional to $\frac{k^2}{\alpha }$) or fast traveling waves (since $V=k^2$) can only occur if $\left|\beta \right|$ is relatively small in comparison with $\alpha$. For example, for $k=2$, one must require that $\left|\beta \right|<\frac{{\alpha }^2}{24}$.

Figure 2. Graphs of (145) (left) and (146) (right) both with the minus signs in front of the square roots, and both for $\alpha =12$, $\beta =6$, $\delta =0$, and $k=2$. The curves on the right correspond to $m=0.25$ (dashed line) and $m=0.9$ (solid line).

Figure 2. Graphs of (145) (left) and (146) (right) both with the minus signs in front of the square roots, and both for $\alpha =12$, $\beta =6$, $\delta =0$, and $k=2$. The curves on the right correspond to $m=0.25$ (dashed line) and $m=0.9$ (solid line).

Figure 3. Graphs of (149) (left) and (150) (right), both for $\alpha =12$, $\beta =-6$, $\delta =0$, and $k=2$. The curves on the right correspond to $m=0.25$ (dashed line) and $m=0.9$ (solid line).

Figure 3. Graphs of (149) (left) and (150) (right), both for $\alpha =12$, $\beta =-6$, $\delta =0$, and $k=2$. The curves on the right correspond to $m=0.25$ (dashed line) and $m=0.9$ (solid line).

The graphs in Figure 4 are for $\alpha =6$, $\beta =-6$, and $\delta =0$ (i.e., $V<V_{\mathrm{crit}}$ is equivalent to $k^2<1$), for which (148) simplifies into

$$u(x,t)={\displaystyle \frac{k^2}{1+\sqrt{1-k^2}cosh(kx-k^{3}t)}}.$$

(151)

As the value of k increases, the solitary wave get taller and narrower. At $t=0$ and values of k very close to 1, the waves become flat at the top, hence the name table-top (or flat-top) waves. For the critical value $k=1$, the wave degenerates into a horizontal line corresponding to

$$\underset{k\to 1}{lim}\left({\displaystyle \frac{k^2}{1+\sqrt{1-k^2}cosh\left(kx\right)}}\right)=1.$$

(152)

For values of k near 1, solution (151) can be very well approximated by a kink–antikink pair [79],

$$u(x,t)=\frac{1}{2}\left(tanh\left(\frac{k}{2}(x-k^{2}t+\Delta )\right)-tanh\left(\frac{k}{2}(x-k^{2}t-\Delta )\right)\right),$$

(153)

where $\Delta =2k^{-1}\mathrm{Arctanh}(1-\sqrt{1-k^2})$ serves as a measure for the width of the table-top wave. These kink and anti-kink solutions, which correspond to the left and right flanks of the table-top solutions, are clearly visible in Figure 4 where k approaches 1. Although the expressions do not match analytically, Figure 5 shows that the graphs of (151) and (153) for $t=0$ nearly overlap even when k is not close to 1.

Parenthetically, Grosse [80] (Equation (24)) computed a two-soliton solution of the defocusing mKdV equation. His analytic solution supposedly describes the interaction of two kink-solutions. It does not satisfy the equation exactly, but appears to be an excellent approximation to a solution, and therefore warrants further investigation.

Notice that all the above solutions follow the scaling homogeneity (21). Functions like $\cosh$, tanh, $\mathrm{cn}$, etc., have no weights. With regard to the weights (20), $W\left(\frac{\alpha }{2\beta }\right)=1$, as it should, because $W\left(u\right)=1.$ Furthermore, $W\left(k\right)=1$ because $W\left(x\right)=-1$ and $W\left(kx\right)=0$. All terms in any $\theta$ must have weight zero, in particular, $W\left(\delta \right)=0$, and $W\left(m\right)=0$, where m is the modulus of any of the Jacobi elliptic functions. From $W\left(t\right)=-3$, it follows that $W\left(V\right)=2$ and $W\left(\omega \right)=3$, where $\omega$ is the angular frequency in $\theta =kx-\omega t+\delta =k(x-Vt)+\delta$. Hence, if $\omega$ and V are polynomials in k, then $\omega$ can only have terms proportional to $k^3,\alpha k^2,$ and ${\alpha }^{2}k$, and V can only have terms in $k^2,\alpha k$, and ${\alpha }^2$. The proportionality factors could have any powers of $\beta$ since $W\left(\beta \right)=0$.

14. Soliton Solutions

When considering solitons we again must make the distinction between the focusing and defocusing Gardner equations.

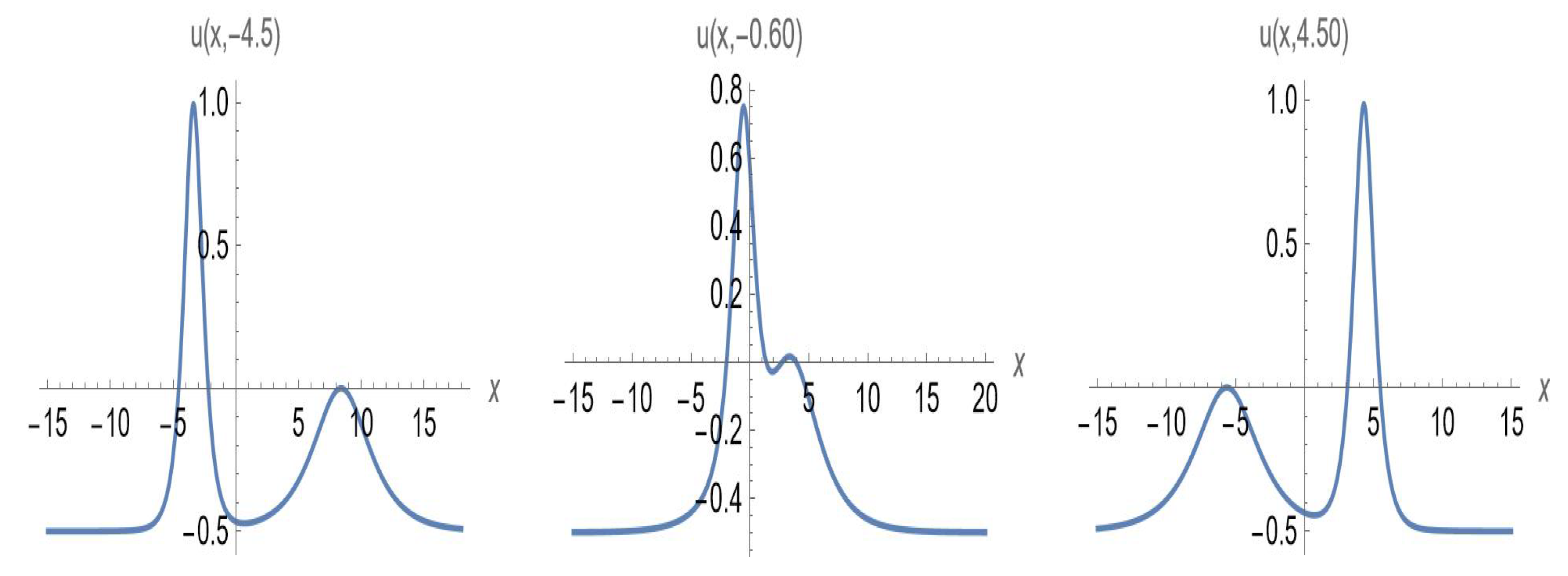
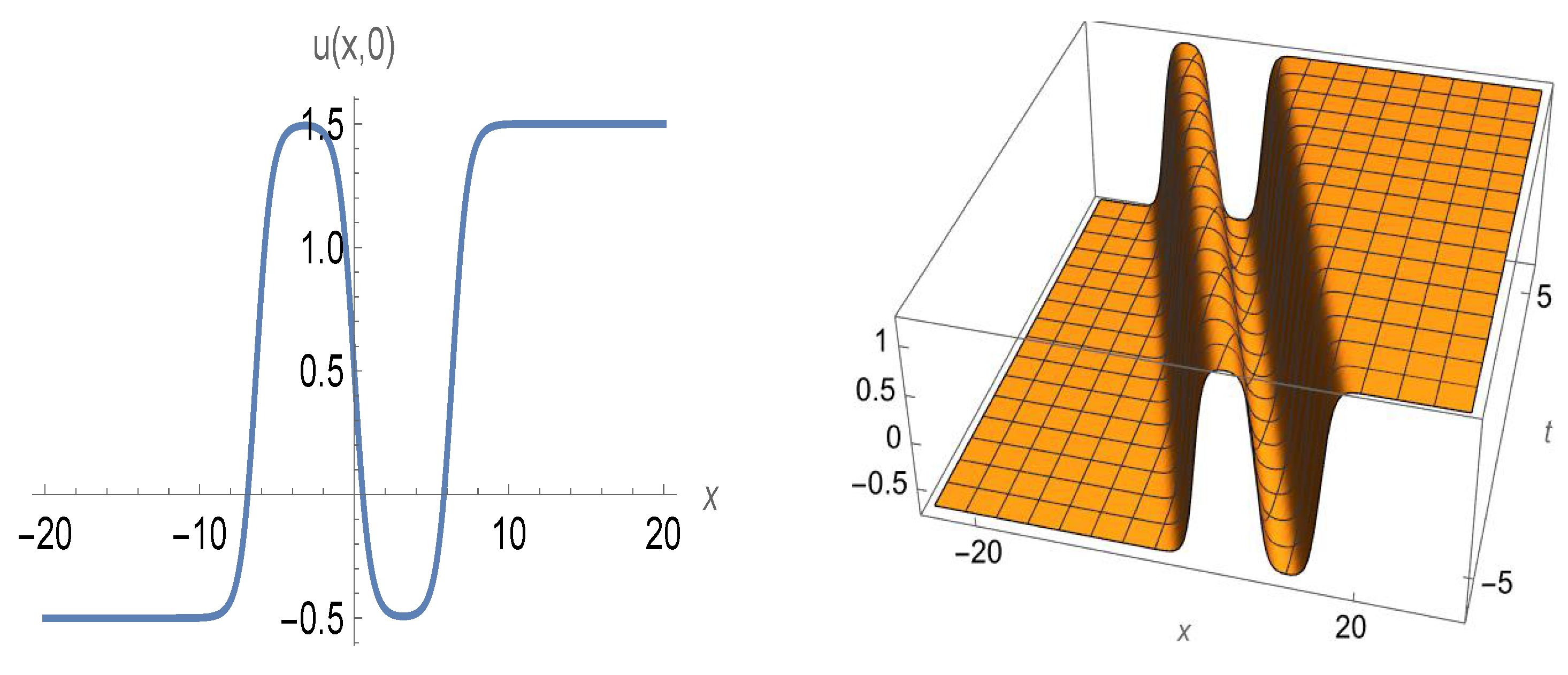
• Case I: The focusing Gardner equation ($\beta >0$).
  Using (113), solutions $u(x,t)$ of the focusing version of (1) are given by

  $$u(x,t)=U(X(x,t),T\left(t\right))-\frac{\alpha }{2\beta },$$

  (154)

  where $U(X,T)$ is any soliton solution of the focusing mKdV equation and $X(x,t)=x+\frac{{\alpha }^2}{4\beta }t$ and $T=t$. For example, the two-soliton solution of (1) reads

  $$u(x,t)=-{\displaystyle \frac{\alpha }{2\beta }}+2\sqrt{{\displaystyle \frac{6}{\beta }}}\left({\displaystyle \frac{k_1{\mathrm{e}}^{{\theta }_1}+k_2{\mathrm{e}}^{{\theta }_2}+a_{12}(k_1{\mathrm{e}}^{{\theta }_2}+k_2{\mathrm{e}}^{{\theta }_1}){\mathrm{e}}^{{\theta }_1+{\theta }_2}}{{\displaystyle 1+{\mathrm{e}}^{2{\theta }_1}+{\mathrm{e}}^{2{\theta }_2}+\frac{8k_1{k}_2}{{(k_1+k_2)}^2}{\mathrm{e}}^{{\theta }_1+{\theta }_2}+a_{12}^2{\mathrm{e}}^{2{\theta }_1+2{\theta }_2}}}}\right),$$

  (155)

  where ${\theta }_i=k_{i}x-(k_i^2-\frac{{\alpha }^2}{4\beta })k_{i}t+{\delta }_i$ and $a_{12}={\left({\displaystyle \frac{k_1-k_2}{k_1+k_2}}\right)}^2$. The elastic scattering of two solitons for the focusing Gardner equation is shown in Figure 6 and Figure 7, which have 2D and 3D graphs of (155) for $\alpha =\beta =6$ with $k_1=\frac{3}{2}$, $k_2=\frac{1}{2}$, and ${\delta }_1={\delta }_2=0$.

Figure 6. Graph of the two-soliton solution (155) of the focusing Gardner equation at three different moments in time.

Figure 6. Graph of the two-soliton solution (155) of the focusing Gardner equation at three different moments in time.

Figure 7. Bird’s eye view of a two-soliton collision for the focusing Gardner equation. Notice the phase shift after collision: the taller (faster) soliton is shifted forward and the shorter (slower) soliton backward relative to where they would have been if they had not collided.

Figure 7. Bird’s eye view of a two-soliton collision for the focusing Gardner equation. Notice the phase shift after collision: the taller (faster) soliton is shifted forward and the shorter (slower) soliton backward relative to where they would have been if they had not collided.

The Gardner equation has solitons of all orders N, which confirms once more that it is a completely integrable PDE.

In general, the existence of a two-soliton solution is no guarantee that the given PDE is completely integrable, but the existence of three-soliton solutions is a good indicator that the PDE is completely integrable. Indeed, as shown in [5], there are PDEs that have at most two-soliton solutions but no three-soliton solutions.

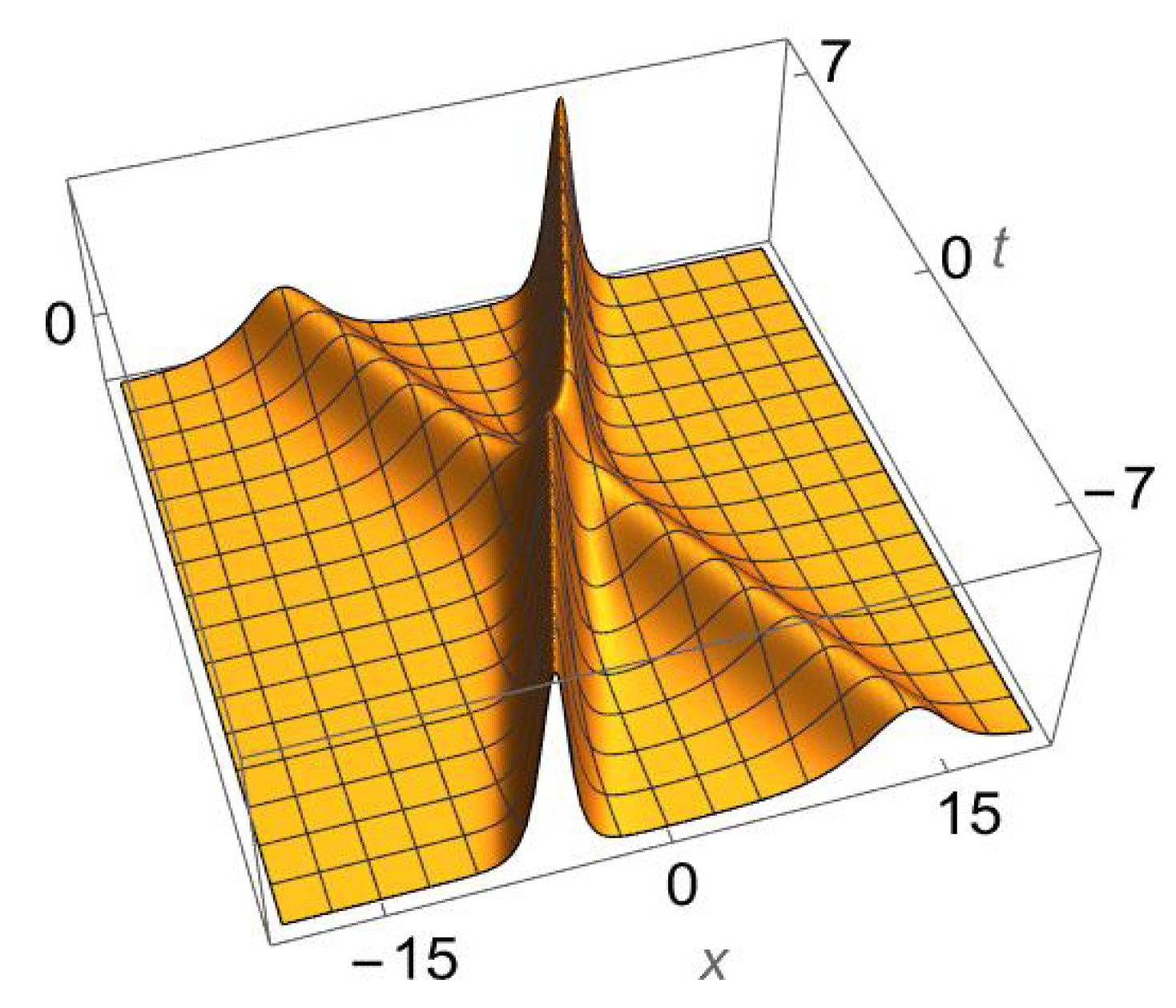
• Case II: The defocusing Gardner equation ($\beta <0$).
  Based on (143), one obtains a two-soliton solution

  $$\begin{array}{ccc}\hfill \phantom{.}& & u(x,t)=-{\displaystyle \frac{\alpha }{2\beta }}\hfill \\ \hfill & & +\sqrt{-{\displaystyle \frac{6}{\beta }}}\left({\displaystyle \frac{sinh(\theta +2\delta ){\mathrm{e}}^{-2\eta }+sinh(\theta -2\delta ){\mathrm{e}}^{2\eta }+2sinh\left(\theta \right)(1-{sinh}^2\left(2\delta \right))\mathrm{sech}\left(2\delta \right)}{cosh(\theta +2\delta ){\mathrm{e}}^{-2\eta }+cosh(\theta -2\delta ){\mathrm{e}}^{2\eta }+2cosh\left(\theta \right)cosh\left(2\delta \right)}}\right),\hfill \end{array}$$

  (156)

  with $\theta =x+\left(2+{\displaystyle \frac{{\alpha }^2}{4\beta }}\right)t,$ and $\eta =\left(x+\left(2+{\displaystyle \frac{{\alpha }^2}{4\beta }}+4{\mathrm{sech}}^2\left(2\delta \right)\right)t+x_0\right)tanh\left(2\delta \right),$ with $\delta >0$ and $x_0$ arbitrary real parameters. Solution (156), which describes the coalescence of two wave fronts, is pictured in 2D and 3D in Figure 8 and Figure 9 for two different values of $\delta$.

15. Symbolic Software

Using the concept of scaling homogeneity, we have been able to create powerful algorithms to investigate the complete integrability of systems of polynomial nonlinear PDEs. In this section, we give a brief summary of the available codes.

Our Mathematica code PainleveTest.m [8] automates the Painlevé test, which allows one to verify if a nonlinear PDE has the Painlevé property [7] as discussed in Section 3.

The Mathematica code InvariantsSymmetries.m [17] computes polynomial conserved densities and higher-order symmetries of nonlinear $(1+1)$-dimensional PDEs that can be written as a polynomial system of evolution equations. If a PDE has arbitrary parameters, the code allows one to derive conditions on these parameters so that the PDE admits conserved quantities or generalized symmetries. An example of such a “classification” problem is given in [9]. A discussion of the scope and limitations of the code can be found in [9,10].

To cover conservation laws of nonlinear PDEs in more than one space variable [23,44,81], we developed ConservationLawsMD.m [18], a Mathematica package to compute polynomial conservation laws of polynomial systems of nonlinear PDEs in space variables $(x,y,z)$ and time t.

In [55], the authors show details of the algorithm to compute recursion operators for systems of nonlinear PDEs of type (4), including formulas for handling integro-differential operators used in Section 7. The Mathematica package PDERecursionOperator.m [16] performs the symbolic computation of recursion operators of systems of polynomial nonlinear evolution equations.

In Appendix B of [65], Larue presents LaxpairTester.m, a Mathematica code to verify Lax pairs in operator and matrix form. In [63], an algorithm is presented to compute Lax pairs in operator form, but that algorithm has not been implemented yet.

In addition, we developed the Mathematica package PDESpecialSolutions.m [25] to compute solitary wave solutions based on the tanh-method and generalizations for the $\mathrm{sech}$, $\mathrm{sn}$, and $\mathrm{cn}$ functions [26].

Recently, we added the Mathematica code PDESolitonSolutions.m [24] to compute soliton solutions of polynomial PDEs based on a simplified version of Hirota’s method described in [5].

Since our codes only use tools from calculus, linear algebra, the calculus of variations, and differential geometry, these algorithms are fairly straightforward to implement in the syntax of computer algebra systems such as Mathematica, Maple, and REDUCE. Our software is open source and available in the public domain. All our Mathematica packages and notebooks are available on the Internet at https://people.mines.edu/whereman/ (accessed on 1 October 2024). A summary of the codes used in this paper can also be found at https://community.wolfram.com/groups/-/m/t/3275116 (accessed on 23 September 2024).

16. Conclusions and Future Work

The approach described in this paper and related software is applicable to large classes of nonlinear PDEs, which can be expressed as polynomial systems of evolution equations. As a prototypical example, we gave a detailed integrability analysis of the Gardner equation by computing its densities (and fluxes), higher-order symmetries, recursion operator, Lax pair, Hirota’s bilinear representation, and soliton solutions. The corresponding results for the KdV and mKdV equations were obtained by setting the coefficient of the cubic and quadratic term equal to zero, respectively.

We also showed how to compute the Gardner (Miura, resp.) transformation, which connects solutions of the Gardner (mKdV, resp.) equation to those of the KdV equation. With the Gardner transformation, some solutions of the KdV equation could be obtained from those of the Gardner equation shown in this paper. Likewise, applying the Miura transformation to solutions of the mKdV equation will lead to solutions of the KdV equation. When new solutions of the Gardner and mKdV equations are discovered, it would be worthwhile to investigate which solutions of the KdV equation they correspond to and, more importantly, if new solutions of the KdV equation could be computed that way (see, e.g., ref. [11]).

The crux of our computational strategy is a skillful use of the scaling symmetry of the PDE and relies on the observation that the defining equations for conservation laws, generalized symmetries, recursion operator, Lax pair, bilinear representation, and Gardner transformation should only hold on solutions of the given PDE. Consequently, the quantities (or operators) one computes inherit the scaling symmetry of the given PDE.

Since their defining equations are similar, it would also be possible to use this approach to compute symplectic and Hamiltonian (co-symplectic) operators of PDEs. In doing so, it would be possible to verify whether or not a PDE has a bi-Hamiltonian (or tri-Hamiltonian) structure, which is yet another criterion for its complete integrability. Further exploration of this idea, as well as the design of algorithms and codes for the computation of symplectic and Hamiltonian operators, is left for future work.

The methodology discussed in this paper might also apply to the Gardner equation in $(2+1)$ dimensions [82,83], which is a combination of the Kadomtsev–Petviashvili (KP) and the modified KP equations.

The algorithms used in this paper are coded in Mathematica syntax, but can be adapted for major computer algebra systems such as Maple and REDUCE.