Innovative Solutions to the Fractional Diffusion Equation Using the Elzaki Transform
Abstract
1. Introduction
2. Basic Definitions
Transformation of Fractional Derivatives via the Elzaki Transform
3. Variational Iteration Transform Method (VITM)
4. Application
4.1. Example-(I)
4.2. Example-(II)
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Du, M.; Wang, Z.; Hu, H. Measuring memory with the order of fractional derivative. Sci. Rep. 2013, 3, 3431. [Google Scholar] [CrossRef] [PubMed]
- Caputo, M. Elasticita Dissipazione (Elasticity and Anelastic Dissipation); Zanichelli: Bologna, Italy, 1969; Volume 4, p. 98. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; John Wiley & Sons: New York, NY, USA, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Scalas, E.; Gorenflo, R.; Mainardi, F. Fractional calculus and continuous-time finance. Phys. A Stat. Mech. Its Appl. 2000, 284, 376–384. [Google Scholar] [CrossRef]
- West, B.J.; Turalska, M.; Grigolini, P. Fractional calculus ties the microscopic and macroscopic scales of complex network dynamics. New J. Phys. 2015, 17, 045009. [Google Scholar] [CrossRef]
- Tarasov, V.E. Fractional vector calculus and fractional Maxwell’s equations. Ann. Phys. 2008, 323, 2756–2778. [Google Scholar] [CrossRef]
- Tao, H.; Anjum, N.; Yang, Y.J. The Aboodh transformation-based homotopy perturbation method: New hope for fractional calculus. Front. Phys. 2023, 11, 1168795. [Google Scholar] [CrossRef]
- Ain, Q.T.; Anjum, N.; Din, A.; Zeb, A.; Djilali, S.; Khan, Z.A. On the analysis of Caputo fractional order dynamics of Middle East Lungs Coronavirus (MERS-CoV) model. Alex. Eng. J. 2022, 61, 5123–5131. [Google Scholar] [CrossRef]
- Zhang, Y.; Anjum, N.; Tian, D.; Alsolami, A.A. Fast And Accurate Population Forecasting with Two-Scale Fractal Population Dynamics and Its Application to Population Economics. Fractals 2024, 32, 2450082. [Google Scholar] [CrossRef]
- Anjum, N.; Ain, Q.T.; Li, X.X. Two-scale mathematical model for tsunami wave. GEM-Int. J. Geomath. 2021, 12, 10. [Google Scholar] [CrossRef]
- Alhejaili, W.; Az-Zo’bi, E.; Shah, R.; El-Tantawy, S.A. On the analytical soliton approximations to fractional forced Korteweg-de Vries equation arising in fluids and Plasmas using two novel techniques. Commun. Theor. Phys. 2024, 76, 085001. [Google Scholar] [CrossRef]
- Noor, S.; Albalawi, W.; Shah, R.; Al-Sawalha, M.M.; Sherif, M.E.; Ismaeel, S.M.E.; El-Tantawy, S.A. On the approximations to fractional nonlinear damped Burger’s-type equations that arise in fluids and plasmas using Aboodh residual power series and Aboodh transform iteration methods. Front. Phys. 2024, 12, 1374481. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Noor, S.; Albalawi, W.; Shah, R.; Shafee, A.; Sherif, M.E.; Ismaeel, S.M.E.; El-Tantawy, S.A. A comparative analytical investigation for some linear and nonlinear time-fractional partial differential equations in the framework of the Aboodh transformation. Front. Phys. 2024, 12, 1374049. [Google Scholar] [CrossRef]
- Bekir, A.; Aksoy, E.; Cevikel, A.C. Exact solutions of nonlinear time fractional partial differential equations by sub-equation method. Math. Methods Appl. Sci. 2015, 38, 2779–2784. [Google Scholar] [CrossRef]
- Khuri, S.A.; Sayfy, A. A Laplace variational iteration strategy for the solution of differential equations. Appl. Math. Lett. 2012, 25, 2298–2305. [Google Scholar] [CrossRef]
- Nadeem, M.; Li, F.; Ahmad, H. Modified Laplace variational iteration method for solving fourth-order parabolic partial differential equation with variable coefficients. Comput. Math. Appl. 2019, 78, 2052–2062. [Google Scholar] [CrossRef]
- Nadeem, M.; He, J.H.; Sedighi, H.M. Numerical analysis of multi-dimensional time-fractional diffusion problems under the Atangana-Baleanu Caputo derivative. Math. Biosci. Eng. 2023, 20, 8190–8207. [Google Scholar] [CrossRef]
- Anjum, N.; He, J.H. Laplace transform: Making the variational iteration method easier. Appl. Math. Lett. 2019, 92, 134–138. [Google Scholar] [CrossRef]
- Ul Rahman, J.; Lu, D.; Suleman, M.; He, J.H.; Ramzan, M. He-Elzaki method for spatial diffusion of biological population. Fractals 2019, 27, 1950069. [Google Scholar] [CrossRef]
- Ji-Huan, H.E.; Anjum, N.; Chun-Hui, H.E.; Alsolami, A.A. Beyond Laplace and Fourier transforms Challenges and Future Prospects. Therm. Sci. 2023, 27, 5075–5089. [Google Scholar]
- El-Tantawy, S.A.; Matoog, R.T.; Shah, R.; Alrowaily, A.W.; Ismaeel, S.M.E. On the shock wave approximation to fractional generalized Burger–Fisher equations using the residual power series transform method. Phys. Fluids 2024, 36, 023105. [Google Scholar] [CrossRef]
- Gorenflo, R.; Mainardi, F. Some recent advances in theory and simulation of fractional diffusion processes. J. Comput. Appl. Math. 2009, 229, 400–415. [Google Scholar] [CrossRef]
- Jiang, X.; Xu, M.; Qi, H. The fractional diffusion model with an absorption term and modified Fick’s law for non-local transport processes. Nonlinear Anal. Real World Appl. 2010, 11, 262–269. [Google Scholar] [CrossRef]
- Sokolov, I.M.; Chechkin, A.V.; Klafter, J. Fractional diffusion equation for a power-law-truncated Levy process. Phys. A Stat. Mech. Its Appl. 2004, 336, 245–251. [Google Scholar] [CrossRef]
- Meerschaert, M.M.; Zhang, Y.; Baeumer, B. Particle tracking for fractional diffusion with two time scales. Comput. Math. Appl. 2010, 59, 1078–1086. [Google Scholar] [CrossRef]
- Goychuk, I.; Hanggi, P. Fractional diffusion modeling of ion channel gating. Phys. Rev. E 2004, 70, 051915. [Google Scholar] [CrossRef] [PubMed]
- Berestycki, H.; Roquejoffre, J.M.; Rossi, L. The periodic patch model for population dynamics with fractional diffusion. Discret. Contin. Dyn. Syst. Ser. S 2011, 4, 1–13. [Google Scholar] [CrossRef]
- Cartea, A.; del-Castillo-Negrete, D. Fractional diffusion models of option prices in markets with jumps. Phys. A Stat. Mech. Its Appl. 2007, 374, 749–763. [Google Scholar] [CrossRef]
- Marom, O.; Momoniat, E. A comparison of numerical solutions of fractional diffusion models in finance. Nonlinear Anal. Real World Appl. 2009, 10, 3435–3442. [Google Scholar] [CrossRef]
- Elzaki, T.M. The new integral transform Elzaki transform. Glob. J. Pure Appl. Math. 2011, 7, 57–64. [Google Scholar]
- Elzaki, T.M. Application of new transform “Elzaki transform” to partial differential equations. Glob. J. Pure Appl. Math. 2011, 7, 65–70. [Google Scholar]
- Elzaki, T.M.; Ezaki, S.M. On the Elzaki transform and ordinary differential equation with variable coefficients. Adv. Theor. Appl. Math. 2011, 6, 41–46. [Google Scholar]
- Elzaki, T.M. Applications of New Transform “Elzaki Transform” to Mechanics, Electrical Circuits and Beams Problems; Research India Publications: Delhi, India, 2012; Volume 4. [Google Scholar]
- El-Tantawy, S.A.; Wazwaz, A.-M. Anatomy of modified Korteweg–de Vries equation for studying the modulated envelope structures in non-Maxwellian dusty plasmas: Freak waves and dark soliton collisions. Phys. Plasmas 2018, 25, 092105. [Google Scholar] [CrossRef]
- El-Tantawy, S.A.; Shan, S.A.; Mustafa, N.; Alshehri, M.H.; Duraihem, F.Z.; Bin Turki, N. Homotopy perturbation and Adomian decomposition methods for modeling the nonplanar structures in a bi-ion ionospheric superthermal plasma. Eur. Phys. J. Plus 2021, 136, 561. [Google Scholar] [CrossRef]
- Aljahdaly, N.; El-Tantawy, S.A.; Ashi, H.; Wazwaz, A.-M. Exponential time differencing scheme for Modeling the dissipative Kawahara solitons in a two-electrons collisional plasma. Rom. Rep. Phys. 2022, 74, 109. [Google Scholar]
- El-Tantawy, S.A.; Wazwaz, A.-M.; Ali Shan, S. On the nonlinear dynamics of breathers waves in electronegative plasmas with Maxwellian negative ions. Phys. Plasmas 2017, 24, 022105. [Google Scholar] [CrossRef]
- El-Tantawy, S.A.; Alharbey, R.A.; Salas, A.H. Novel approximate analytical and numerical cylindrical rogue wave and breathers solutions: An application to electronegative plasma. Chaos Solitons Fractals 2022, 155, 111776. [Google Scholar] [CrossRef]
- El-Tantawy, S.A.; Salas, A.H.; Alyousef, H.A.; Alharthi, M.R. Novel approximations to a nonplanar nonlinear Schrödinger equation and modeling nonplanar rogue waves/breathers in a complex plasma. Chaos Solitons Fractals 2022, 1635, 112612. [Google Scholar] [CrossRef]
- Elzaki, T.M.; Elzaki, S.M.; Elnour, E.A. On the New Integral Transform “ELzaki Transform” Fundamental Properties Investigations and Applications. Glob. J. Math. Sci. 2012, 4, 1–13. [Google Scholar]
- Elzaki, T.M.; Elzaki, S.M. On the Connections between Laplace and ELzaki Transforms. Adv. Theor. Appl. Math. 2014, 6, 1–10. [Google Scholar]
- Neamaty, A.; Agheli, B.; Darzi, R. New Integral Transform for Solving Nonlinear Partial Di erential Equations of fractional order. Theory Approx. Appl. 2016, 10, 69–86. [Google Scholar]
- Elzaki, T.M.; Kim, H. The solution of radial diffusivity and shock wave equations by Elzaki variational iteration method. Int. J. Math. Anal. 2015, 9, 1065–1071. [Google Scholar] [CrossRef]
- He, J.H. A variational iteration approach to nonlinear problems and its applications. Mech. Appl. 1998, 20, 30–31. [Google Scholar]
- Noor, S.; Albalawi, W.; Shah, R.; Al-Sawalha, M.M.; Ismaeel, S.M.E. Mathematical frameworks for investigating fractional nonlinear coupled Korteweg-de Vries and Burger’s equations. Front. Phys. 2024, 12, 1374452. [Google Scholar] [CrossRef]
- Wang, K.L.; He, C.H. A remark on Wang’s fractal variational principle. Fractals 2019, 27, 1950134. [Google Scholar] [CrossRef]

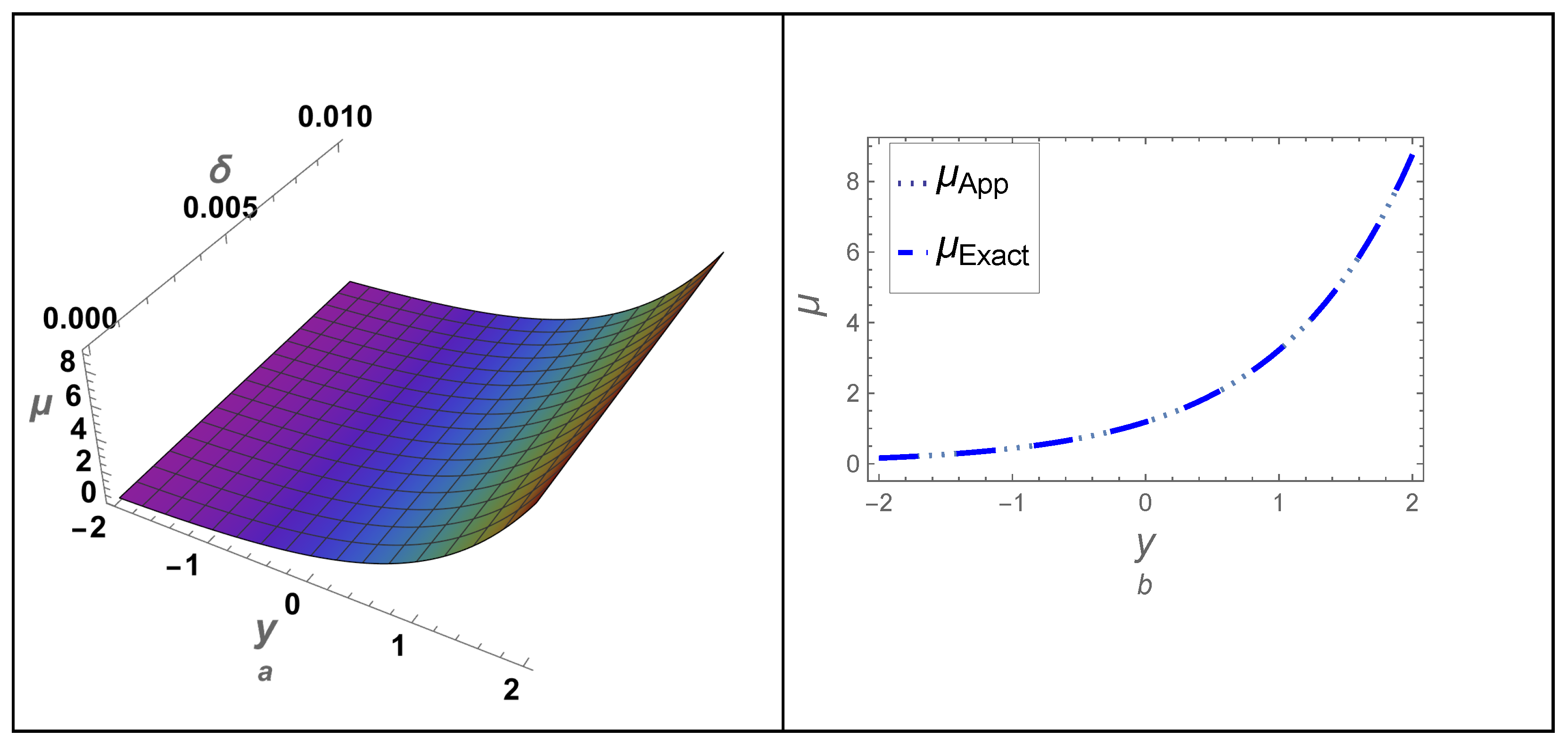
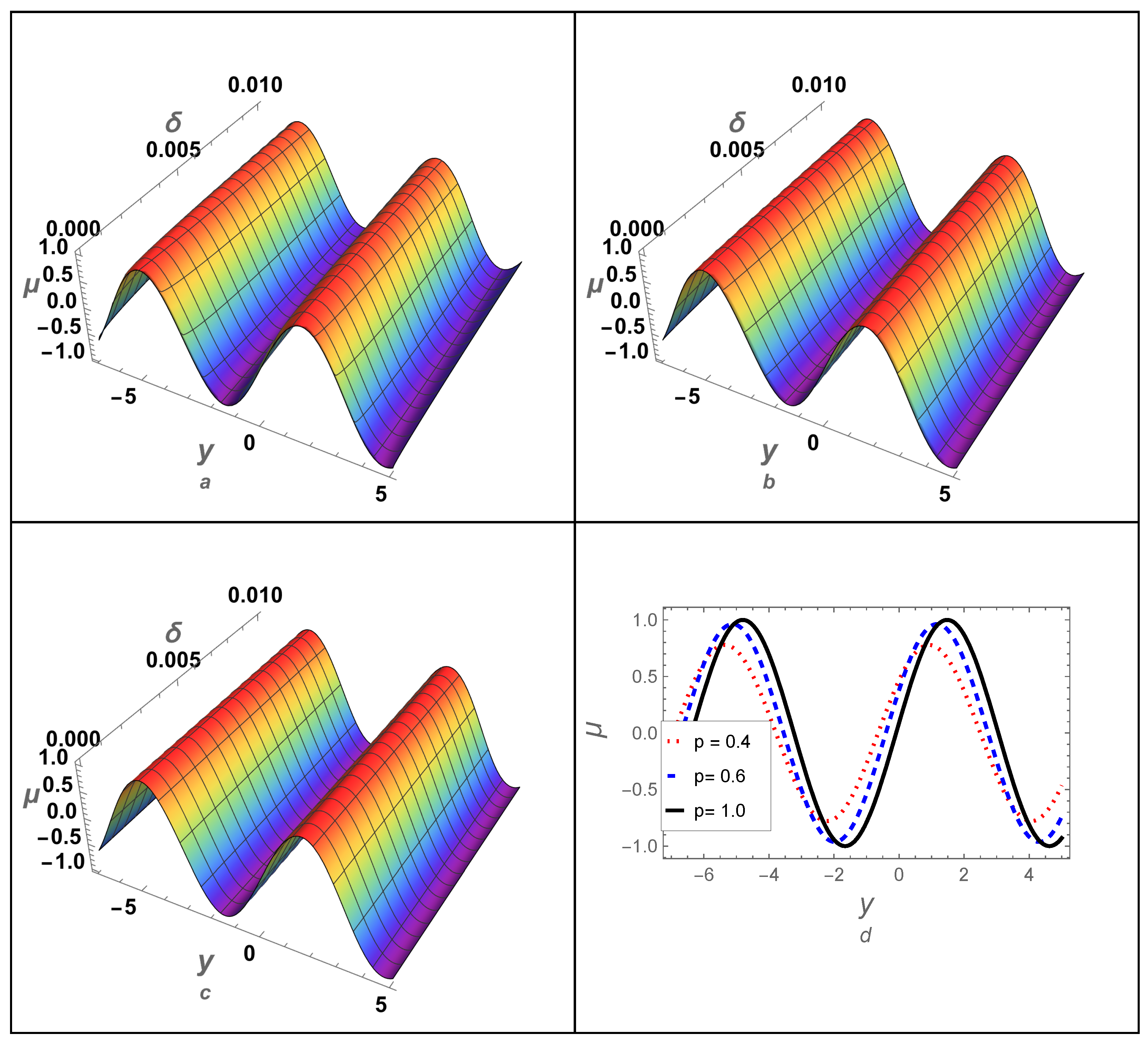

| y | |||
|---|---|---|---|
| −0.5 | 0.738599 | 0.738599 | 1.4432899320127035 |
| −0.4 | 0.816278 | 0.816278 | 1.6653345369377348 |
| −0.3 | 0.902127 | 0.902127 | 1.887379141862766 |
| −0.2 | 0.997004 | 0.997004 | 1.9984014443252818 |
| −0.1 | 1.10186 | 1.10186 | 2.220446049250313 |
| 0. | 1.21774 | 1.21774 | 2.4424906541753444 |
| 0.1 | 1.34582 | 1.34582 | 2.6645352591003757 |
| 0.2 | 1.48736 | 1.48736 | 2.886579864025407 |
| 0.3 | 1.64378 | 1.64378 | 3.3306690738754696 |
| 0.4 | 1.81666 | 1.81666 | 3.774758283725532 |
| 0.5 | 2.00772 | 2.00772 | 3.9968028886505635 |
| y | |||||
|---|---|---|---|---|---|
| −0.5 | 0.738599 | 0.738602 | 0.738599 | 1.44329 | 3.31707 |
| −0.4 | 0.816278 | 0.816282 | 0.816278 | 1.66533 | 3.66593 |
| −0.3 | 0.902127 | 0.902131 | 0.902127 | 1.88738 | 4.05148 |
| −0.2 | 0.997004 | 0.997009 | 0.997004 | 1.9984 | 4.47758 |
| −0.1 | 1.10186 | 1.10187 | 1.10186 | 2.22045 | 4.94849 |
| 0. | 1.21774 | 1.21775 | 1.21774 | 2.44249 | 5.46893 |
| 0.1 | 1.34582 | 1.34582 | 1.34582 | 2.66454 | 6.0441 |
| 0.2 | 1.48736 | 1.48736 | 1.48736 | 2.88658 | 6.67976 |
| 0.3 | 1.64378 | 1.64379 | 1.64378 | 3.33067 | 7.38228 |
| 0.4 | 1.81666 | 1.81667 | 1.81666 | 3.77476 | 8.15868 |
| 0.5 | 2.00772 | 2.00773 | 2.00772 | 3.9968 | 9.01673 |
| y | |||
|---|---|---|---|
| −0.5 | −0.476791 | −0.476791 | 1.7763568394002505 |
| −0.4 | −0.386653 | −0.386653 | 1.8318679906315083 |
| −0.3 | −0.292653 | −0.292653 | 1.887379141862766 |
| −0.2 | −0.195728 | −0.195728 | 1.9984014443252818 |
| −0.1 | −0.096848 | −0.096848 | 2.0122792321330962 |
| 0. | 0.003 | 0.003 | 2.024855977333928 |
| 0.1 | 0.102818 | 0.102818 | 2.0261570199409107 |
| 0.2 | 0.201609 | 0.201609 | 1.9984014443252818 |
| 0.3 | 0.298385 | 0.298385 | 1.9984014443252818 |
| 0.4 | 0.39218 | 0.39218 | 1.887379141862766 |
| 0.5 | 0.482056 | 0.482056 | 1.7763568394002505 |
| y | |||||
|---|---|---|---|---|---|
| −0.5 | −0.476791 | −0.476788 | −0.476791 | 1.77636 | 2.13763 |
| −0.4 | −0.386653 | −0.386652 | −0.386653 | 1.83187 | 1.73163 |
| −0.3 | −0.292653 | −0.292652 | −0.292653 | 1.88738 | 1.30832 |
| −0.2 | −0.195728 | −0.195727 | −0.195728 | 1.9984 | 0.871945 |
| −0.1 | −0.096848 | −0.0968475 | −0.096848 | 2.01228 | 0.426855 |
| 0. | 0.003 | 0.00299997 | 0.003 | 2.02486 | 0.0225 |
| 0.1 | 0.102818 | 0.102818 | 0.102818 | 2.02616 | 0.47163 |
| 0.2 | 0.201609 | 0.201608 | 0.201609 | 1.9984 | 0.916048 |
| 0.3 | 0.298385 | 0.298384 | 0.298385 | 1.9984 | 1.35131 |
| 0.4 | 0.39218 | 0.392178 | 0.39218 | 1.88738 | 1.77308 |
| 0.5 | 0.482056 | 0.482054 | 0.482056 | 1.77636 | 2.17712 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noor, S.; Alrowaily, A.W.; Alqudah, M.; Shah, R.; El-Tantawy, S.A. Innovative Solutions to the Fractional Diffusion Equation Using the Elzaki Transform. Math. Comput. Appl. 2024, 29, 75. https://doi.org/10.3390/mca29050075
Noor S, Alrowaily AW, Alqudah M, Shah R, El-Tantawy SA. Innovative Solutions to the Fractional Diffusion Equation Using the Elzaki Transform. Mathematical and Computational Applications. 2024; 29(5):75. https://doi.org/10.3390/mca29050075
Chicago/Turabian StyleNoor, Saima, Albandari W. Alrowaily, Mohammad Alqudah, Rasool Shah, and Samir A. El-Tantawy. 2024. "Innovative Solutions to the Fractional Diffusion Equation Using the Elzaki Transform" Mathematical and Computational Applications 29, no. 5: 75. https://doi.org/10.3390/mca29050075
APA StyleNoor, S., Alrowaily, A. W., Alqudah, M., Shah, R., & El-Tantawy, S. A. (2024). Innovative Solutions to the Fractional Diffusion Equation Using the Elzaki Transform. Mathematical and Computational Applications, 29(5), 75. https://doi.org/10.3390/mca29050075








