Predictive Modeling and Control Strategies for the Transmission of Middle East Respiratory Syndrome Coronavirus
Abstract
:1. Introduction
2. Model Formulation
3. Basic Reproduction Number
Analysis of Sensitivity
4. Equilibria Points
4.1. Local Stability
4.2. Analysis of Global Stability
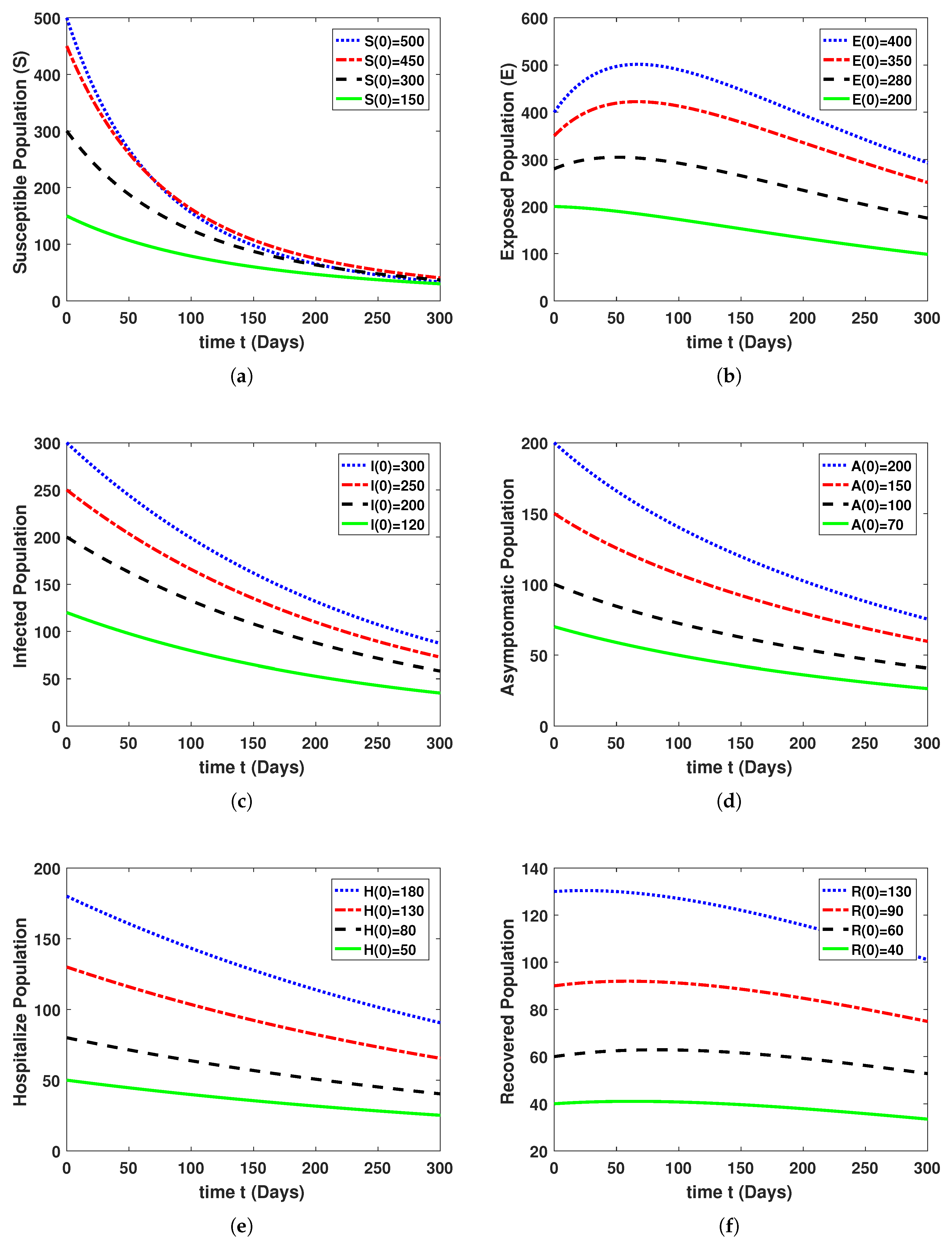
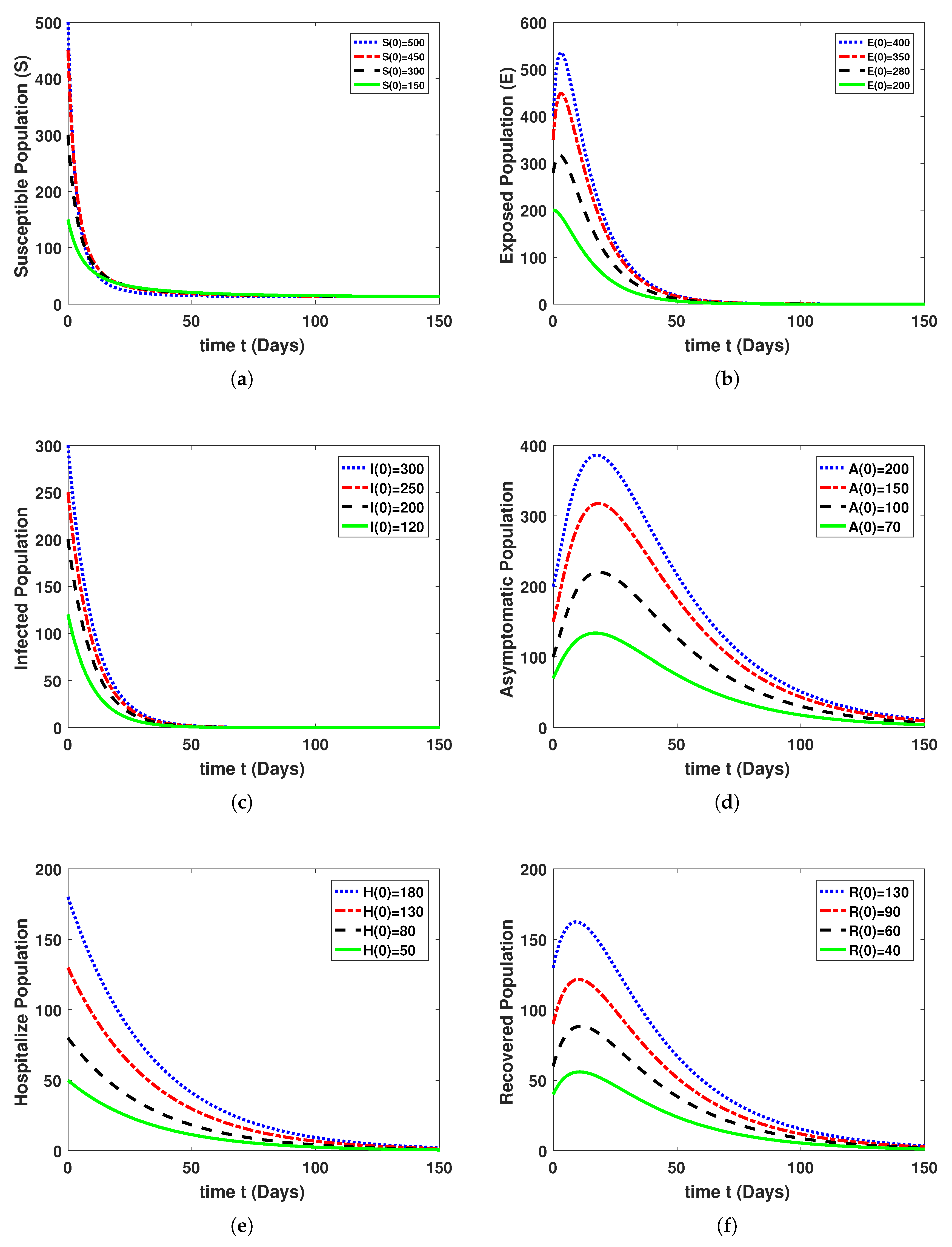
5. Results and Discussion
Used Algorithm
6. Analysis of Optimal Control
6.1. Methods
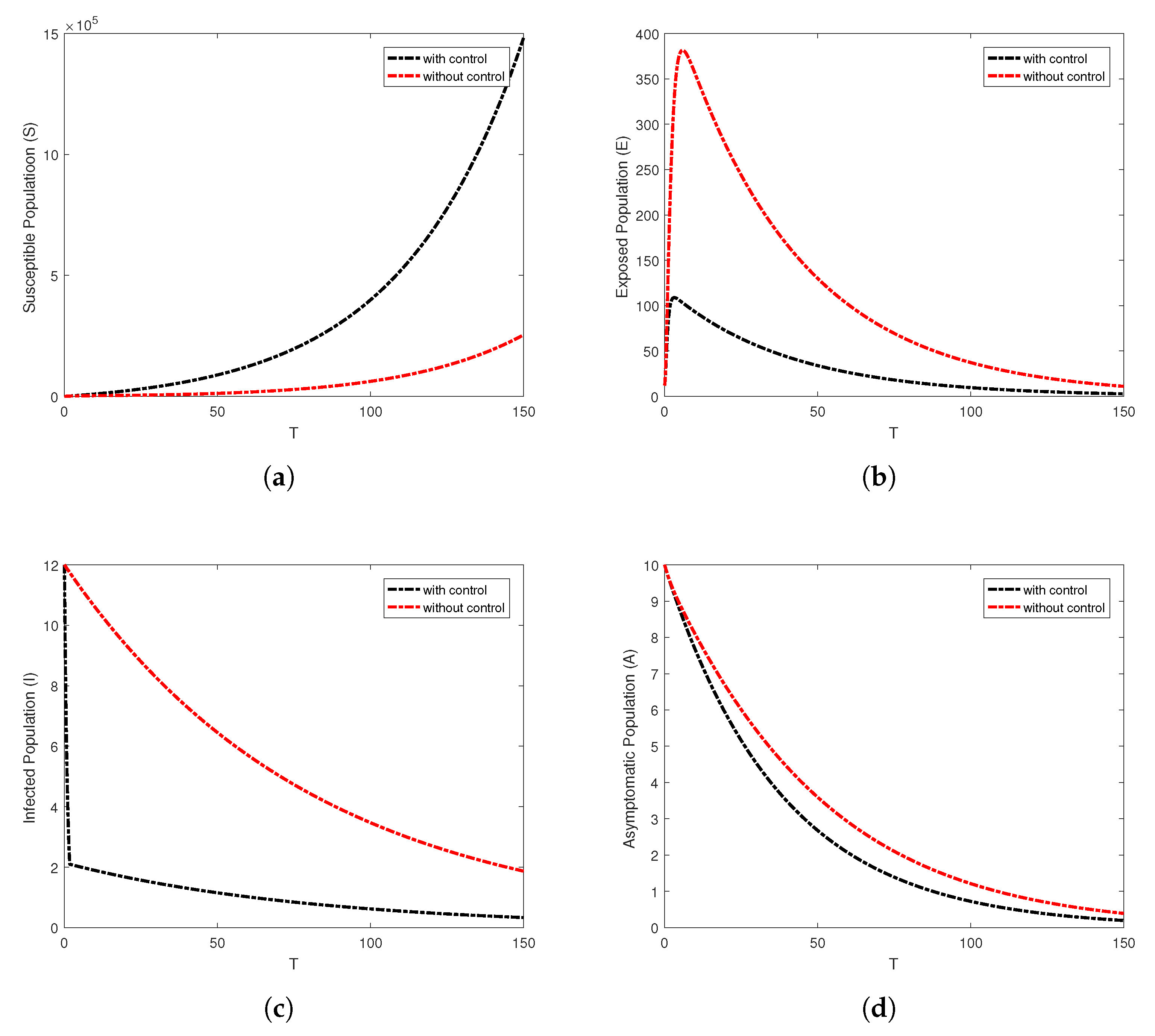
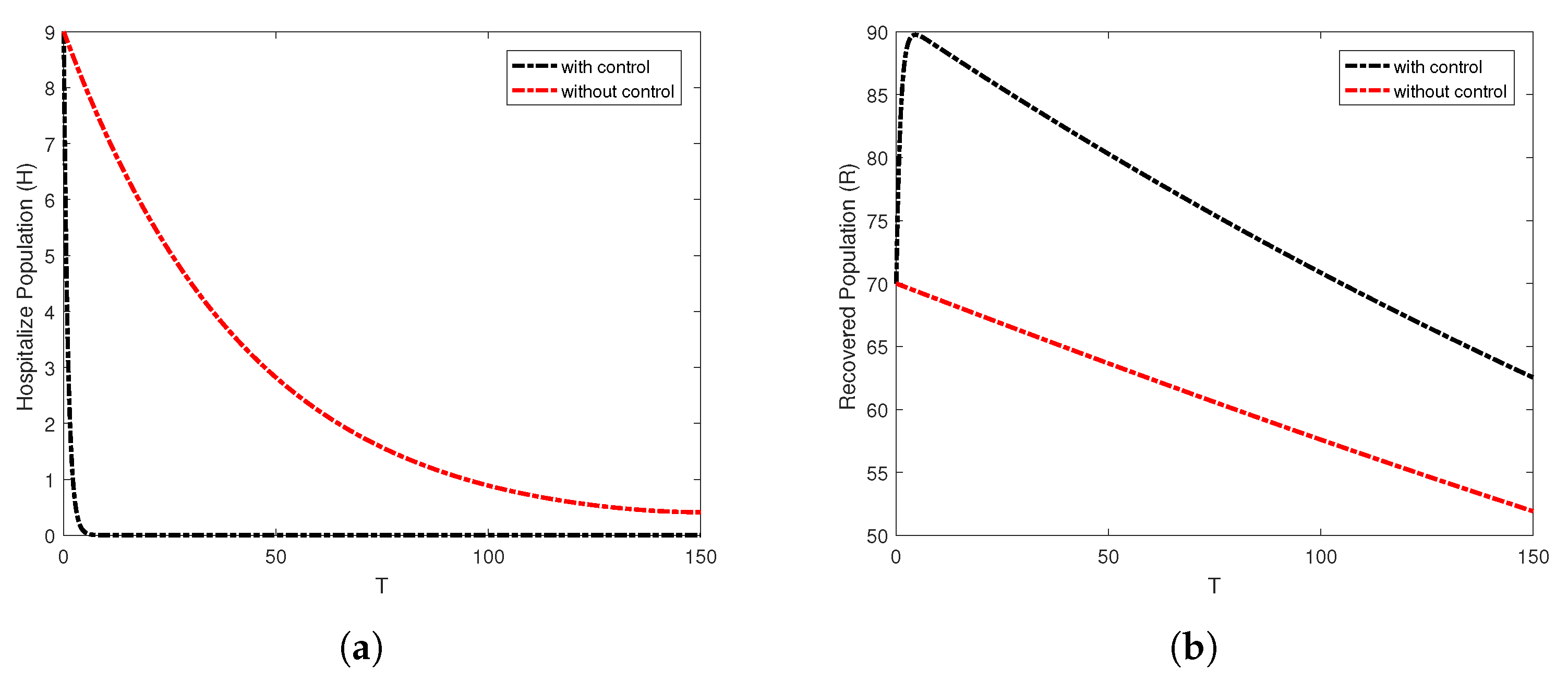
6.2. Results and Discussion for Optimal Control
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- AlTawfiq, J.A.; Hinedi, K.; Ghandour, J. Middle East respiratory syndrome coronavirus: A case-control study of hospitalized patients. Clin. Infect. Dis. 2014, 59, 160–165. [Google Scholar] [CrossRef] [PubMed]
- Azhar, E.I.; Kafrawy, E.I.; Hassan, S.A.; Al-Saeed, A.M.; Hashem, M.S.; Madani, A.M. Evidence for camel to human transmission of MERS coronavirus. N. Engl. J. Med. 2014, 370, 2499–2505. [Google Scholar] [CrossRef] [PubMed]
- Arabi, Y.M.; Arifi, A.A.; Balkhy, H.H. Clinical course and outcomes of critically ill patients with Middle East respiratory syndrome coronavirus infection. Ann. Intern. Med. 2014, 160, 389–397. [Google Scholar] [CrossRef] [PubMed]
- Madani, T.A.; Azhar, E.I.; Hashem, A.M. Evidence for camel-to-human transmission of MERS coronavirus. N. Engl. J. Med. 2014, 371, 1360. [Google Scholar] [PubMed]
- Breban, R.; Riou, J.; Fontanent, A. Interhuman transmissibility of Middle East respiratory coronavirus: Estimation of pandemic risk. Lancet 2013, 382, 694–699. [Google Scholar] [CrossRef]
- Fisman, D.N.; Ashleigh, R.T. The epidemiology of MERS-CoV. Lancet Infect. Dis. 2014, 14, 6–7. [Google Scholar] [CrossRef]
- Zhong, N.S.; Zheng, B.J.; Li, Y.M.; Poon, L.L.M.; Xie, Z.H.; Chan, K.H.; Li, P.H.; Tan, S.Y.; Chang, Q.; Xie, J.P.; et al. Epidemiology and cause of severe acute respiratory syndrome (SARS) in Guangdong, People’s Republic of China, in February, 2003. Lancet 2003, 362, 1353–1358. [Google Scholar] [CrossRef]
- Ksiazek, T.G.; Erdman, D.; Goldsmith, C.S.; Zaki, S.R.; Peret, T.; Emery, S.; Tong, S.; Urbani, C.; Comer, J.A.; Lim, W.; et al. A novel coronavirus associated with severe acute respiratory syndrome. N. Engl. J. Med. 2003, 348, 1953–1966. [Google Scholar] [CrossRef]
- Zaki, A.M.; Van Boheemen, S.; Bestebroer, T.M.; Osterhaus, A.D.; Fouchier, R.A. Isolation of a novel coronavirus from a man with pneumonia in Saudi Arabia. N. Engl. J. Med. 2012, 367, 1814–1820. [Google Scholar] [CrossRef]
- Ciotti, M.; Ciccozzi, M.; Terrinoni, A.; Jiang, W.C.; Wang, C.B.; Bernardini, S. The COVID-19 pandemic. Crit. Rev. Clin. Lab. Sci. 2020, 57, 365–388. [Google Scholar] [CrossRef]
- Mandal, M.; Jana, S.; Nandi, S.K.; Khatua, A.; Adak, S.; Kar, T.K. A model based study on the dynamics of COVID-19: Prediction and control. Chaos Solitons Fractals 2020, 136, 109889. [Google Scholar] [CrossRef] [PubMed]
- Atede, A.O.; Omame, A.; Inyama, S.C. A fractional order vaccination model for COVID-19 incorporating environmental transmission: A case study using Nigerian data. Bull. Biomath. 2023, 1, 78–110. [Google Scholar] [CrossRef]
- Shen, Z.H.; Chu, Y.M.; Khan, M.A.; Muhammad, S.; Al-Hartomy, O.A.; Higazy, M. Mathematical modeling and optimal control of the COVID-19 dynamics. Results Phys. 2021, 31, 105028. [Google Scholar] [CrossRef] [PubMed]
- Alqarni, M.S.; Alghamdi, M.; Muhammad, T.; Alshomrani, A.S.; Khan, M.A. Mathematical modeling for novel coronavirus (COVID-19) and control. Numer. Methods Partial. Differ. Equ. 2022, 38, 760–776. [Google Scholar] [CrossRef]
- Tsay, C.; Lejarza, F.; Stadtherr, M.A.; Baldea, M. Modeling, state estimation, and optimal control for the US COVID-19 outbreak. Sci. Rep. 2020, 10, 10711. [Google Scholar] [CrossRef]
- Libotte, G.B.; Lobato, F.S.; Platt, G.M.; Neto, A.J.S. Determination of an optimal control strategy for vaccine administration in COVID-19 pandemic treatment. Comput. Methods Programs Biomed. 2020, 196, 105664. [Google Scholar] [CrossRef]
- Ullah, I.; Ahmad, S.; Al-Mdallal, Q.; Khan, Z.A.; Khan, H.; Khan, A. Stability analysis of a dynamical model of tuberculosis with incomplete treatment. Adv. Differ. Equ. 2020, 2020, 499. [Google Scholar] [CrossRef]
- Hajji Mohamed, A.; Al-Mdallal, Q. Numerical simulations of a delay model for immune system-tumor interaction. Sultan Qaboos Univ. J. Sci. (SQUJS) 2018, 23, 19–31. [Google Scholar]
- Asif, M.; Haider, N.; Al-Mdallal, Q.; Khan, I. A Haar wavelet collocation approach for solving one and two-dimensional second-order linear and nonlinear hyperbolic telegraph equations. Numer. Methods Partial. Differ. Equ. 2020, 36, 1962–1981. [Google Scholar] [CrossRef]
- Kermack, W.O.; McKendrick, A.G. Contributions to the mathematical theory of epidemics, part 1. Proc. R. Soc. Edinburgh. Sect. A Math. 1927, 115, 700–721. [Google Scholar]
- Cauchemez, S.; Fraser, C.; Van Kerkhove, M.D.; Donnelly, C.A.; Riley, S.; Rambaut, A.; Enouf, V.; van der Werf, S.; Ferguson, N.M. Middle East respiratory syndrome coronavirus: Quantification of the extent of the epidemic, surveillance biases, and transmissibility. Lancet Infect. Dis. 2013, 14, 50–56. [Google Scholar] [CrossRef]
- Chowell, G.; Blumberg, S.; Simonsen, L.; Miller, M.A.; Viboud, C. Synthesizing data and models for the spread of MERS-CoV, 2013: Key role of index cases and hospital transmission. Epidemics 2014, 9, 40–51. [Google Scholar] [CrossRef] [PubMed]
- Assiri, A.; Al-Tawfiq, J.A.; Al-Rabeeah, A.A.; Al-Rabiah, F.A.; Al-Hajjar, S.; Al-Barrak, A. Epidemiological, demographic, and clinical characteristics of 47 cases of Middle East respiratory syndrome coronavirus disease from Saudi Arabia: A descriptive study. Lancet Infect. Dis. 2013, 13, 752–761. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Eskandari, Z.; Avazzadeh, Z. Dynamical behaviors of an SIR epidemic model with discrete time. Fractal Fract. 2022, 6, 659. [Google Scholar] [CrossRef]
- Li, B.; Eskandari, Z. Dynamical analysis of a discrete-time SIR epidemic model. J. Frankl. Inst. 2023, 360, 7989–8007. [Google Scholar] [CrossRef]
- Li, B.; Eskandari, Z.; Avazzadeh, Z. Strong resonance bifurcations for a discrete-time prey–predator model. J. Appl. Math. Comput. 2023, 69, 2421–2438. [Google Scholar] [CrossRef]
- Jiang, X.; Li, J.; Li, B.; Yin, W.; Sun, L.; Chen, X. Bifurcation, chaos, and circuit realisation of a new four-dimensional memristor system. Int. J. Nonlinear Sci. Numer. Simul. 2022. [Google Scholar] [CrossRef]
- Sabbar, Y. Asymptotic extinction and persistence of a perturbed epidemic model with different intervention measures and standard lévy jumps. Bull. Biomath. 2023, 1, 58–77. [Google Scholar] [CrossRef]
- Adoum, A.H.; Haggar, M.S.D.; Ntaganda, J.M. Mathematical modelling of a glucose-insulin system for type 2 diabetic patients in Chad. Math. Model. Numer. Simul. Appl. 2022, 2, 244–251. [Google Scholar] [CrossRef]
- Ahmed, I.; Akgül, A.; Jarad, F.; Kumam, P.; Nonlaopon, K. A Caputo-Fabrizio fractional-order cholera model and its sensitivity analysis. Math. Model. Numer. Simul. Appl. 2023, 3, 170–187. [Google Scholar] [CrossRef]
- Singh, T.; Vaishali; Adlakha, N. Numerical investigations and simulation of calcium distribution in the alpha-cell. Bull. Biomath. 2023, 1, 40–57. [Google Scholar] [CrossRef]
- Odionyenma, U.B.; Ikenna, N.; Bolaji, B. Analysis of a model to control the co-dynamics of Chlamydia and Gonorrhea using Caputo fractional derivative. Math. Model. Numer. Simul. Appl. 2023, 3, 111–140. [Google Scholar] [CrossRef]
- Yao, T.-T.; Qian, J.-D.; Zhu, W.-Y.; Wang, Y.; Wang, G.-Q. A systematic review of lopinavir therapy for SARS coronavirus and MERS coronavirus—A possible reference for coronavirus disease-19 treatment option. J. Med. Virol. 2020, 92, 556–563. [Google Scholar] [CrossRef] [PubMed]
- Fatima, B.; Yavuz, M.; Rahman, M.u.; Al-Duais, F.S. Modeling the epidemic trend of middle eastern respiratory syndrome coronavirus with optimal control. Math. Biosci. Eng. 2023, 20, 11847–11874. [Google Scholar] [CrossRef]
- Afshar, Z.M.; Ebrahimpour, S.; Javanian, M.; Koppolu, V.; Vasigala, V.K.R.; Hasanpour, A.H.; Babazadeh, A. Coronavirus disease 2019 (COVID-19), MERS and SARS: Similarity and difference. J. Acute Dis. 2020, 9, 194–199. [Google Scholar]
- Ahmad, S.; Dong, Q.; Rahman, M.u. Dynamics of a fractional-order COVID-19 model under the nonsingular kernel of Caputo-Fabrizio operator. Math. Model. Numer. Simul. Appl. 2022, 2, 228–243. [Google Scholar] [CrossRef]
- ur Rahman, M.; Arfan, M.; Baleanu, D. Piecewise fractional analysis of the migration effect in plant-pathogen-herbivore interactions. Bull. Biomath. 2023, 1, 1–23. [Google Scholar] [CrossRef]
- Yunhwan, K.; Sunmi, L.; Chaeshin, C.; Seoyun, C.; Saeme, H.; Youngseo, S. The Characteristics of Middle Eastern Respiratory Syndrome Coronavirus Transmission Dynamics in South Korea. Osong Public Health Res. Perspect. 2016, 7, 49–55. [Google Scholar]
- Driessch, V.; Watmough, J. Reproduction numbers and sub threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Van Den Driessche, P.; Watmough, J. Mathematical Epidemiology; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Chitnis, N.; Cushing, J.M.; Hyman, J.M. Bifurcation analysis of a mathematical model for malaria transmission. SIAM J. Appl. Math. 2006, 67, 24–45. [Google Scholar] [CrossRef]
- Khan, T.; Zaman, G.; Chohan, M.I. The transmission dynamic and optimal control of acute and chronic hepatitis B. J. Biol. Dyn. 2017, 11, 172–189. [Google Scholar] [CrossRef]
- Zaman, G.; Han Kang, Y.; Jung, I.H. Stability analysis and optimal vaccination of an SIR epidemic model. Biosystems 2008, 93, 240–249. [Google Scholar] [CrossRef] [PubMed]
- LaSalle, J.P. The Stability of Dynamical System; SIAM: Philadelphia, PA, USA, 1976. [Google Scholar]
- LaSalle, J.P. Stability of nonautonomous system. Nonlinear Anal. 1976, 1, 83–90. [Google Scholar] [CrossRef]
- Khan, T.; Ullah, Z.; Ali, N.; Zaman, G. Modeling and control of the hepatitis b virus spreading using an epidemic model. Chaos Solitons Fractals 2019, 124, 1–9. [Google Scholar] [CrossRef]
- Kamien, M.; Schwartz, N. Dynamic Optimization, 2nd ed.; North-Holland: Amsterdam, The Netherlands, 1991. [Google Scholar]
- Hattaf, K.; Yousfi, N. Optimal control of a delayed HIV infection model with immune response using an efficient numerical method. Int. Sch. Res. Not. 2012, 2012, 215124. [Google Scholar] [CrossRef]
- Evirgen, F.; Ozköse, F.; Yavuz, M.; Ozdemir, N. Real data-based optimal control strategies for assessing the impact of the Omicron variant on heart attacks. AIMS Bioeng. 2023, 10, 218–239. [Google Scholar] [CrossRef]
- Lashari, A.A.; Zaman, G. Global dynamics of vector-borne diseases with horizontal transmission in host population. Comput. Math. Appl. 2001, 61, 745–754. [Google Scholar] [CrossRef]
- Aseev, S.M.; Kryazhimskii, A.V. The Pontryagin maximum principle and optimal economic growth problems. Proc. Steklov Inst. Math. 2007, 257, 1–255. [Google Scholar] [CrossRef]


| Notation | Sensitivity Values | Notation | Sensitivity Values |
|---|---|---|---|
| 0.0384651 | −0.058565 | ||
| −0.00000453 | −0.93704 | ||
| −0.001464128 | −0.041392 | ||
| 0.99999 | q | 0.0000476 | |
| 0.99999 | 0.000432 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fatima, B.; Yavuz, M.; ur Rahman, M.; Althobaiti, A.; Althobaiti, S. Predictive Modeling and Control Strategies for the Transmission of Middle East Respiratory Syndrome Coronavirus. Math. Comput. Appl. 2023, 28, 98. https://doi.org/10.3390/mca28050098
Fatima B, Yavuz M, ur Rahman M, Althobaiti A, Althobaiti S. Predictive Modeling and Control Strategies for the Transmission of Middle East Respiratory Syndrome Coronavirus. Mathematical and Computational Applications. 2023; 28(5):98. https://doi.org/10.3390/mca28050098
Chicago/Turabian StyleFatima, Bibi, Mehmet Yavuz, Mati ur Rahman, Ali Althobaiti, and Saad Althobaiti. 2023. "Predictive Modeling and Control Strategies for the Transmission of Middle East Respiratory Syndrome Coronavirus" Mathematical and Computational Applications 28, no. 5: 98. https://doi.org/10.3390/mca28050098
APA StyleFatima, B., Yavuz, M., ur Rahman, M., Althobaiti, A., & Althobaiti, S. (2023). Predictive Modeling and Control Strategies for the Transmission of Middle East Respiratory Syndrome Coronavirus. Mathematical and Computational Applications, 28(5), 98. https://doi.org/10.3390/mca28050098







