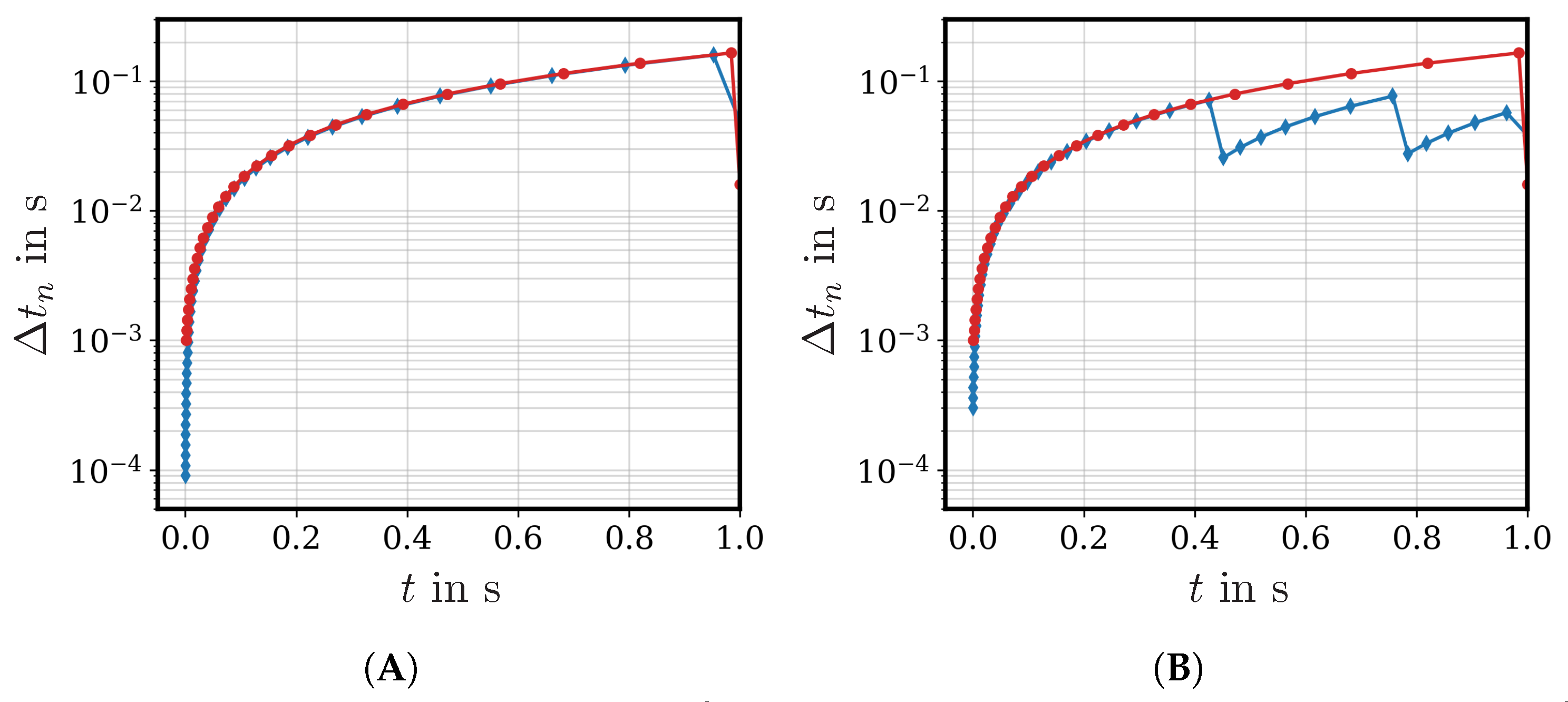
1. Introduction
Nearly all commonly applied engineering materials possess, depending on the detail of investigation, some heterogeneous microstructure, e.g., fiber-reinforced polymers or rolled steel alloys, where the grains can have preferential directions because of the manufacturing process. Since this heterogeneous microstructure can significantly influence the response of these materials to mechanical loading, it is of particular interest to consider the microstructure already in numerical simulations. The development of constitutive models for materials with heterogeneous microstructures is challenging in both aspects, phenomenological constitutive modeling and subsequent experimental calibration. Thus, the so-called FE
method has been developed by [
1,
2,
3,
4,
5,
6]—to mention only a few—for coupled numerical simulation of structures at macro- and microscale with finite elements. There, in contrast to common finite element computations, a constitutive model is not assigned to an integration point at macroscale. Instead, the stress and consistent tangent quantities are obtained by solving an initial boundary value problem with finite elements on a particular microstructure followed by a numerical homogenization technique. In this context, the microstructure is usually denoted as a representative volume element (RVE). In addition to the aforementioned works, in [
7], a comprehensive description of the FE
-method for the numerical solution of these coupled boundary value problems on different scales is provided. In general, there exist further methods to obtain the response of heterogeneous microstructures, such as Discrete Fourier Transforms or Fast Fourier Transforms; see, for example, [
8]. Even the finite cell method is applicable for the homogenization of heterogeneous microstructures; see, for example, [
9]. However, in this work, deep neural networks are applied to replace the computationally costly solution of initial boundary value problems at microscale.
Currently, various applications of methods of artificial intelligence exist in the field of solid mechanics. A comprehensive overview of applications in continuum material mechanics is given in [
10]. Further reviews are provided in [
11,
12] for applications in experimental solid mechanics and [
13] for material development in additive manufacturing employing machine learning methods. Ref. [
14] provides a general introduction to the application of machine learning techniques in material modeling and design of materials. Additionally, in [
15], a review and investigation of the ability to apply machine learning in constitutive modeling is provided; however, it is in the context of soils. Most applications of machine learning methods aim to obtain feasible information from huge amounts of data or to increase the speed of particular computations. The source of the data could either be simulations, as in the present work, or directly experimental data, as in the
data-driven mechanics approach, which was introduced by the aithors of [
16], where it is not required to learn the response of constitutive models from simulations.
The application of artificial neural networks for data-based constitutive modeling was originally introduced in [
17] and is frequently used in representing the material behavior for finite element simulations since then; see, for example, [
18,
19]. Recently, different approaches have been published to advance numerical simulations with machine learning methods. An investigation into deep learning surrogate models for accelerating numerical simulations is presented in [
20]. Ref. [
21] contains a proposal of a combination of physics-based finite element analysis and convolutional neural networks for predicting the mechanical response of materials. In contrast, ref. [
22] contains an application of deep learning techniques for extracting rules that are inherent in computational mechanics to propose a new numerical quadrature rule that shows results superior to the well-known Gauss–Legendre quadrature.
Learning material behavior from simulations is generally covered with versatile approaches. In this context, the authors of [
23] describe a material modeling framework for hyperelasticity and plasticity, where different architectures of neural networks are employed. Model-free procedures that fit into the data-driven mechanics approach for representing material behavior are described in [
24,
25,
26,
27], among others. Model-free approaches are suitable, especially for the consideration of elastoplastic material behavior; see [
28,
29] as well. Artificial neural networks could also be applied for calibrating known constitutive models from experimental data (parameter identification). First attempts are presented in [
30,
31], whereas in [
32], modern deep reinforcement learning techniques are applied for the calibration of history-dependent models. Since the measurement techniques to obtain experimental data have evolved in recent years, modern calibration techniques can consider full-field data, e.g., from digital image correlation; see [
33]. Instead of calibrating constitutive models from experimental data with neural networks, where an error is introduced from choosing the constitutive model, the experimental data can be directly employed for discovering the material models from data. This approach is introduced in [
34] for hyperelasticity and later on extended to cover elastoplasticity [
35] and generalized materials [
36]. Similar work with automated discovery of suitable hyperelastic materials is provided in [
37], where
constitutive artificial neural networks are applied, introduced in [
38].
Many different machine learning methods are successfully used for multiscale applications in solid mechanics. There, the main objective is to obtain the homogenized response from heterogeneous microstructures. One of the first works in this context is provided in [
39], wherein the authors applied neural networks for the homogenization of non-linear elastic materials. Ref. [
40] contains a proposal of a data-driven two-scale approach to predict homogenized quantities even for inelastic deformations by drawing on clustering techniques. The ability to replace microscale evaluations with artificial neural networks requires a suitable accuracy of the network after the training process. Regarding this issue, the authors of ref. [
41] make use of artificial neural networks as constitutive relation surrogates for nonlinear material behavior. However, based on the evaluation of quality indicators, a reduced-order model can be employed instead of the neural network within an adaptive switching method. The authors of ref. [
42] describe the so-called
Structural-Genome-Driven approach for FE
computations of composite structures, wherein even model reduction techniques are applied.
Advanced neural network architectures such as convolutional or recurrent neural networks are regularly applied to predict the homogenized response of microstructures. Here, atomistic data can also be used showing significant acceleration compared to molecular statics [
43]. Elastic material behavior is investigated in [
44,
45,
46,
47]. In ref. [
48], significant speed up in homogenization is reached when applying three-dimensional convolutional neural networks in broad ranges of different microstructures, phase fractions, and material parameters. The authors of ref. [
49] provide the generalization of data to obtain three-dimensional nonlinear elastic material laws under arbitrary loading conditions. Considering anisotropy, teh authors of ref. [
50] predict effective material properties of RVEs with randomly placed and shaped inclusions. The suitability of different machine learning methods for homogenizing polycrystalline materials is studied in [
51]. Besides the purely mechanical homogenization approaches, the authors of ref. [
52] show that neural networks can be even applied to computational homogenization of electrostatic problems. Moreover, researchers in ref. [
53] employ
CT data within a data-driven multiscale framework to study open-cell foam structures.
According to [
54], replacing microscale computations in the FE
method by surrogate models can be denoted as a
data-driven multiscale finite element method. The authors of ref. [
55] perform multiscale computations with feedforward neural networks and recurrent neural networks for RVEs with inelastic material behavior and further investigate the ability to generalize for unknown loading paths. Researchers in ref. [
56] present a hybrid methodology denoted as a model-data-driven one. Therein, the authors apply a combination of conventional constitutive models and a data-driven correction component as a multiscale methodology. Moreover, it is beneficial to incorporate physical knowledge into the development of neural network surrogates. This is achieved, for example, in [
57]. The authors propose
thermodynamics-based artificial neural networks (TANNs) and apply them for multiscale simulations of inelastic lattice structures, while later extending the framework to evolution TANNs [
58]. The application of particular physical constraints by using problem-specific invariants as input quantities and the Helmholtz free energy density as output is provided in [
59]. The authors provide FE
as a data-driven multiscale framework and minimize the number of microscale simulations, which serve as training data, by following an autonomous data mining approach.
Further, probabilistic approaches can be employed while developing the surrogate models; in [
60], more accurate results are achieved with Sobolev training [
61] compared to regular training for hyperelasticity. In this context, for an extension to multiscale plasticity with geometric machine learning methods, we refer to [
62,
63]. Elastoplastic solid materials are investigated in [
64] using recurrent neural networks and in [
65] where the authors employ two separated neural networks for the homogenized stress and tangent information. The authord of ref. [
66] apply DeepONet as a surrogate model for the microscale level with two-dimensional elastoplasticity and hyperelasticity. Currently, the authors of ref. [
67] demonstrate the applicability of the encoder/decoder approach for multiscale computations with path-dependent material behavior on the microscale.
Another research track are the so-called
deep material networks (DMNs), which provide an efficient data-driven multiscale framework to reproduce the homogenized response of RVEs. The introduction of DMNs for two-phase heterogeneous materials is provided in [
68] together with an extension to three-dimensional microstructures [
69]. The authors of ref. [
70] further extend the technique to take into account diverse fiber orientations, applying DMNs for multiscale analysis of composites with full thermo-mechanical coupling [
71]. Researchers in ref. [
72] employ DMNs with the computation of the tangent operator in a closed form as an output of the network.
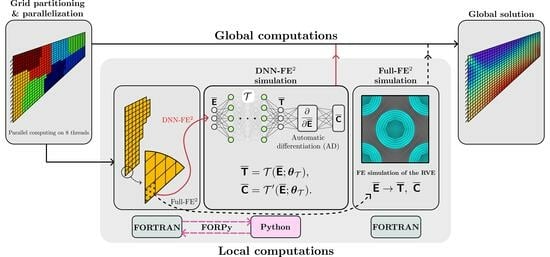
The main objective of the present work is to provide a consistent approach for employing deep neural networks (DNN) as surrogate models in step-size controlled multiscale FE
computations. As mentioned afore, various publications already deal with embedding artificial neural networks into numerical simulations especially for accelerating computational costly multiscale simulations. A novelty of the present work is that we provide a clear description of the algorithmic structure, which is in general a Multilevel–Newton algorithm (MLNA) that simplifies to a Newton–Raphson algorithm when employing DNN surrogate models. Further, current publications leave out required information; for example, the ways in which the consistent tangent at macroscale integration points is obtained from the microscale information, meaning whether the computations are performed by automatic differentiation, neural network models, or by numerical differentiation. Concerning this objective, we start in
Section 2 with an explanation of the underlying equations and the algorithmic structure in FE
computations, where we restrict ourselves to small strains and quasi-static problems. Afterwards, two different architectures of neural networks and specific considerations of physical knowledge during the training process are described. Since the amount of training data required to obtain sufficient accuracies in the neural network outputs is of particular interest, this is investigated as well while using regular training and Sobolev training. As another novel contribution, we develop a method for efficiently coupling the different programming codes of the trained neural network and the multiscale finite element code. There, the application of high-performance computing libraries and just-in-time compilation yields significantly higher speed up of the DNN-FE
approach in load-step size controlled computations compared to the results presented in the current literature. Furthermore, the DNN surrogate is even able to overcome load-step size limitations that are apparent in FE
computations.
The notation in use is defined in the following manner: geometrical vectors are symbolized by and second-order tensors by bold-faced Roman letters. In addition, we introduce column vectors and matrices at the global finite element level symbolized by bold-type italic letters and column vectors and matrices on the local (element) level using bold-type Roman letters . Further, to distinguish quantities on macroscale and microscale levels, we indicate microscale quantities by . Calligraphic letters denote deep neural network surrogate models.
3. Deep Neural Networks
In this section, a brief introduction is provided to deep neural networks and state-of-the-art frameworks for the implementation of these learning methodologies. First, a fully connected deep neural network—also known as a multilayer perceptron (MLP)—is considered. An MLP consists of a consecutive repetition of so-called layers. Each layer contains a set of nodes, so-called neurons, which are densely connected to the nodes of the preceding and succeeding layers. A deep neural network (DNN) is a neural network with multiple layers between the input and output layers which are the so-called hidden layers. Data sample
in space
and the corresponding target output
in space
are considered. Then, the objective of a deep neural network is to learn the mapping,
, from the data by minimizing a scalar-valued loss function
for all the samples in the training data set, where
represents the trainable parameters of the network. To this end, the data are processed through each layer
i as
where
and
are the input and output of the
ith layer with the number of neurons
in the previous layer and
neurons in the current layer. Further,
holds.
represents a weighting matrix and
is the bias vector.
symbolizes the element-wise applied activation function in layer
i. Parameters
of the network are determined by applying a gradient-descent optimization technique for minimizing the loss function on the training data set. The updates of the parameters are obtained as
where
denotes the learning rate. The gradient of the loss function with respect to the trainable parameters can be obtained using automatic differentiation (AD) [
80]. All the neural networks discussed in this study were developed applying machine learning software frameworks developed by Google Research called TensorFlow [
81] and JAX [
82].
Automatic differentiation (AD), also known as
algorithmic differentiation or “auto-diff” (automatic differentiation), is a family of methods for evaluating the derivatives of numeric functions expressed as computer programs efficiently and accurately through the accumulation of values during code execution. AD has an extensive application in machine learning and also well-established use cases in computational fluid dynamics [
83], atmospheric sciences [
84], and engineering design optimization [
85]. In the field of computational solid mechanics, see [
86] and the literature cited therein. The idea behind AD is to break down the function into its elementary operations and compute the derivative of each operation using symbolic rules of differentiation. This means that instead of relying on numerical approximations or finite differences to compute the derivative, AD can provide exact derivatives with machine precision. To do this, AD keeps track of the derivative values at each stage of the computation applying a technique called forward or reverse mode differentiation. This allows AD computing the derivative of the overall composition of the function by combining the derivatives of the constituent operations through the chain rule. The benefit of AD is that it can be applied to a wide range of computer programs, allowing for the efficient and accurate computation of derivatives. This makes it a powerful tool for scientific computing, optimization, and machine learning, where derivatives are needed for tasks such as gradient descent, optimization, and training of neural networks. AD techniques include forward and reverse accumulation modes. Forward-mode AD is efficient for functions
, while for cases
where
, AD in its reverse accumulation mode is preferred [
80]. For state-of-the-art deep learning models,
n can be as large as millions or billions. In this research work, we utilized reverse-mode AD for the training of the neural networks and also for obtaining the Jacobian of the outputs with respect to the inputs. This should be demonstrated for both applied frameworks, TensorFlow and JAX. If one considers a batch of input vectors
and the corresponding outputs
, then the Jacobian matrix
can be easily computed in batch mode using AD via TensorFlow and JAX according to Algorithm 3.
| Algorithm 3: Computing the Jacobian matrix of function f via reverse mode AD in TensorFlow and JAX frameworks for a batch of samples . |
| TensorFlow: | JAX: |
| def Jacobian(f, ): | Jacobian = jax.vmap(jax.jacrev(f)) |
| with tf.GradientTape() as tape: | = Jacobian() |
| tape.watch() | |
| = f() | |
| return tape.batch_jacobian(, ) | |
| = Jacobian(f, ) | |
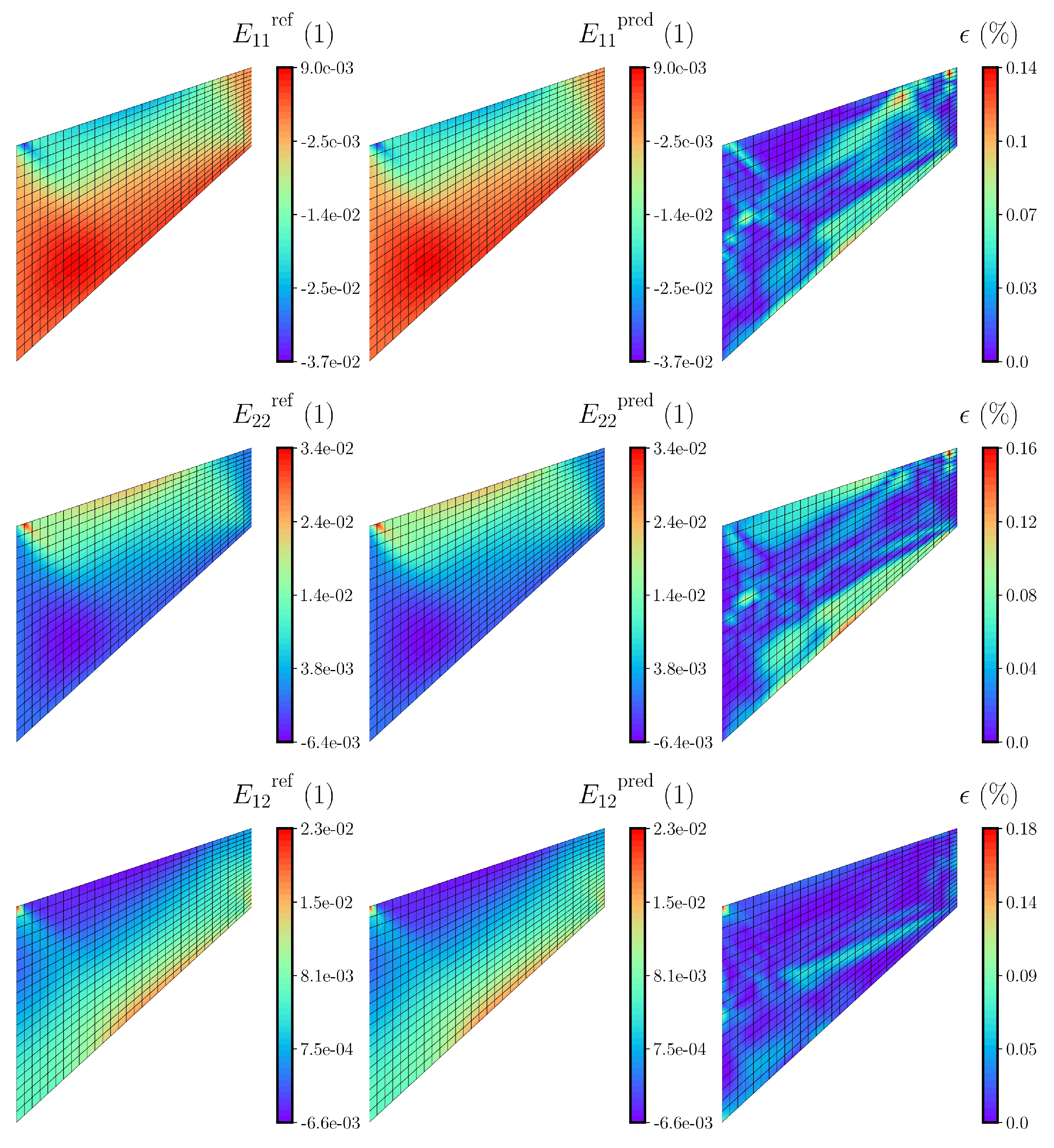
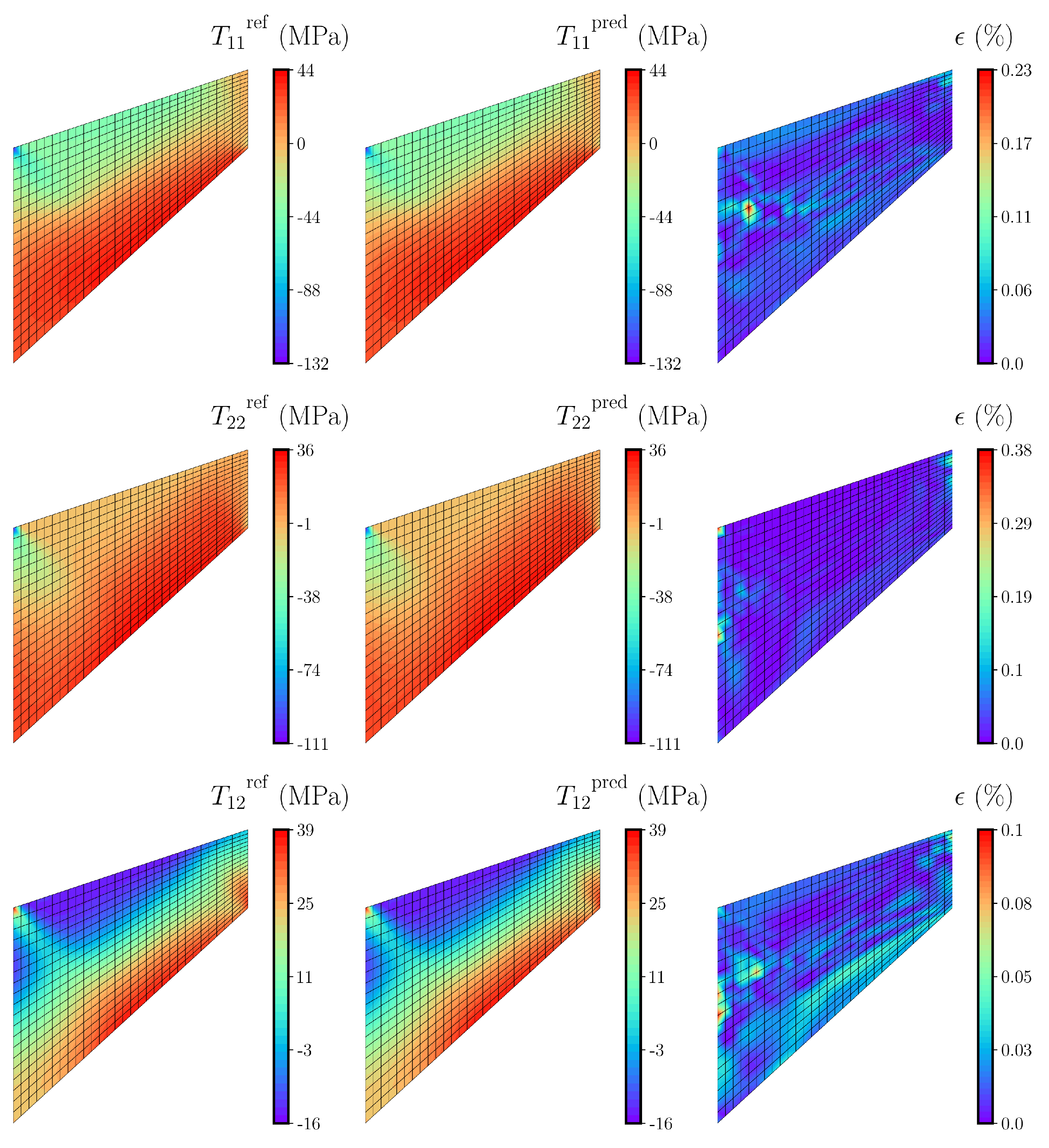
3.1. Deep Neural Networks as Surrogate Models for Local RVE Computations
In the MLNA described in
Section 2.2.1, the computations on local macroscale level are very expensive to perform. Thus, the objective is to develop a data-driven surrogate model for substituting the local macroscale computations with deep neural networks. To this end, the macroscale strains
at each integration point
and time (load-step)
are taken as the input and macroscale stresses
and the consistent tangent matrix
are provided as the output of the surrogate model. In the following, the FE
analysis is performed in a quasi-static setting with the restriction to small strains. For the sake of simplicity of the notation and for a two-dimensional set-up, we refer to the input of the surrogate model as
,
, and to the outputs as
,
, and
,
. Here, it should be mentioned that we do not employ the symmetry of the consistent tangent matrix due to the application of AD, where we compute the Jacobian matrix of the neural network containing the partial derivatives of each element of
with respect to each element of the input
. Thus, we apply a soft symmetry constraint to the Jacobian matrix of the neural network by the data.
The inputs of the surrogate model are computed using an MPI (message passing interface) parallelized FORTRAN code. We employ FORPy [
87], a library for FORTRAN-Python interoperability, to perform the data communications between FORTRAN and Python codes in an efficient and parallel manner. In particular, we load the required Python libraries and the DNN models only once and conduct the RVE computations in parallel, which leads to a considerable speed-up. The obtained outputs from the RVE surrogate model are passed to the FORTRAN code for further computations.
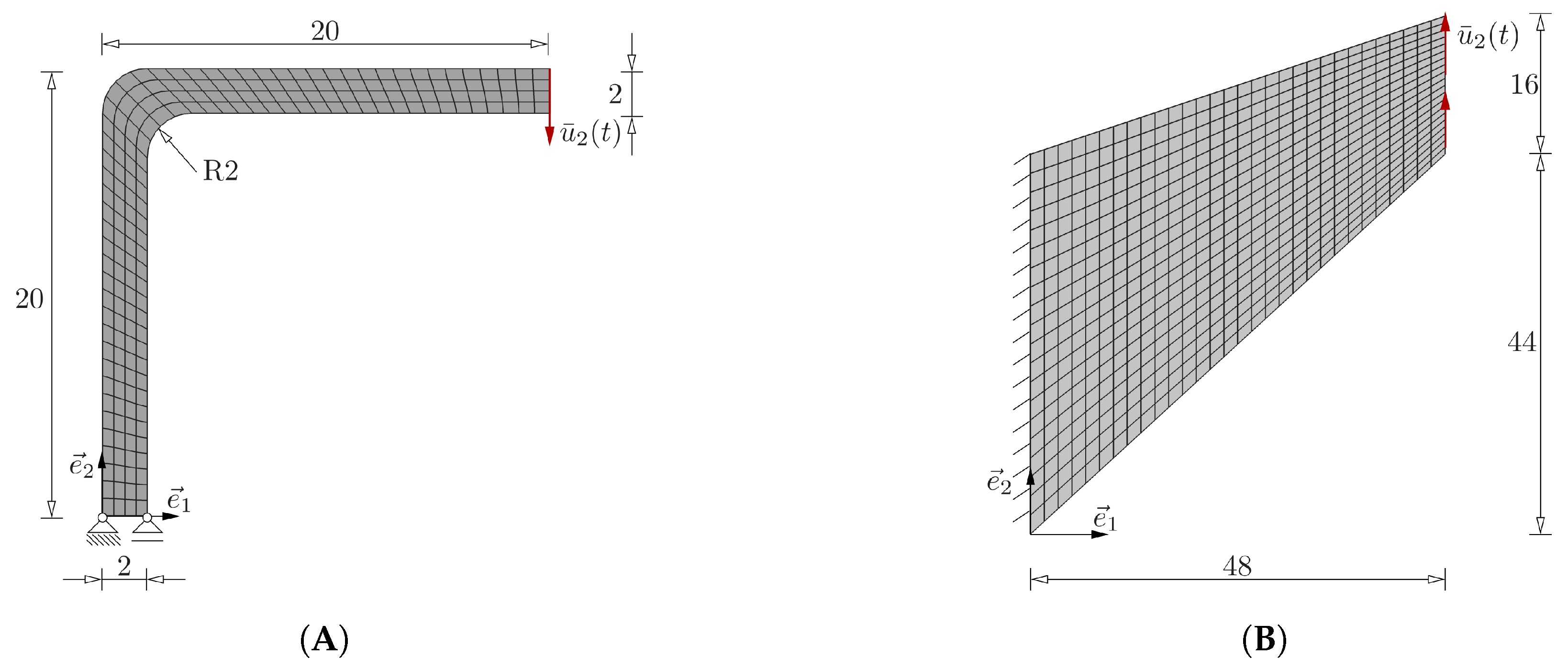
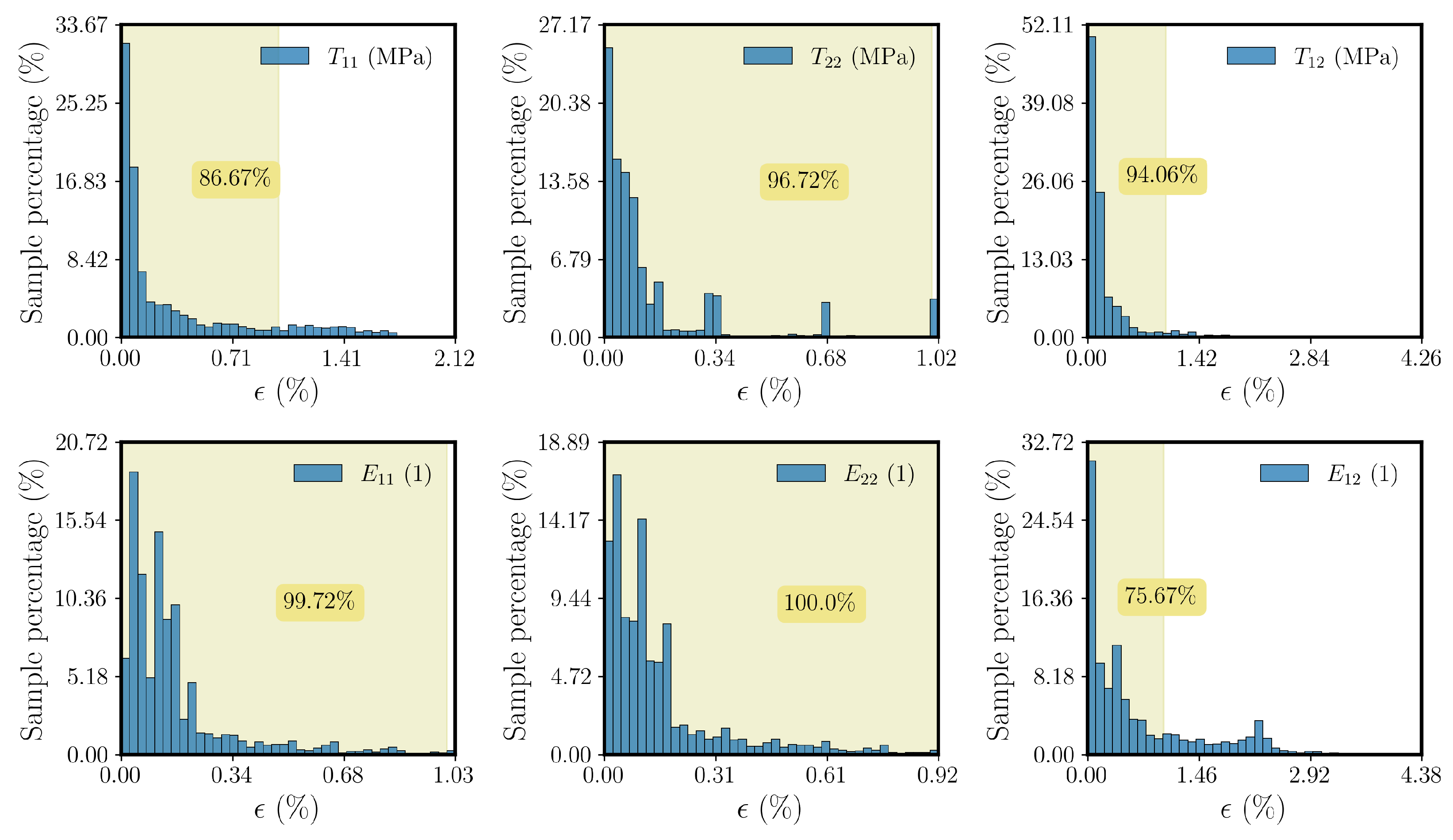
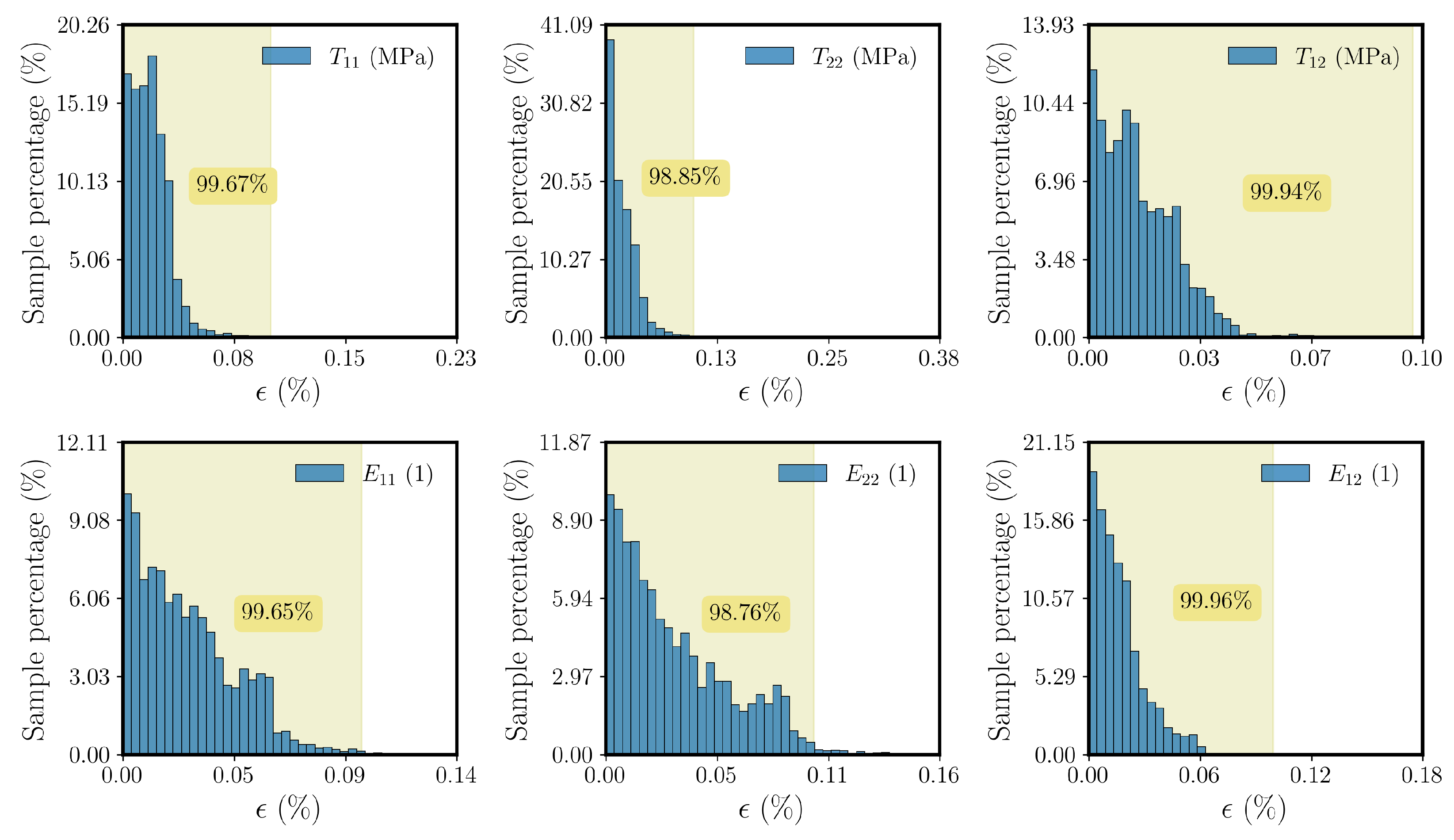
3.2. Training and Validation Datasets
Since the FE
framework in
Section 2 is derived for the case of small strains, we consider a domain of application for our surrogate model with the upper and lower bounds of
and
, respectively, where
represents the
ith component of the strain input
. A dataset is generated by imposing different strain inputs to an RVE and computing the corresponding stress components and consistent tangent matrices. We utilized Latin hypercube sampling (LHS) [
88] to efficiently sample from the input space. To generate the data, we consider two global symmetries in the input space:
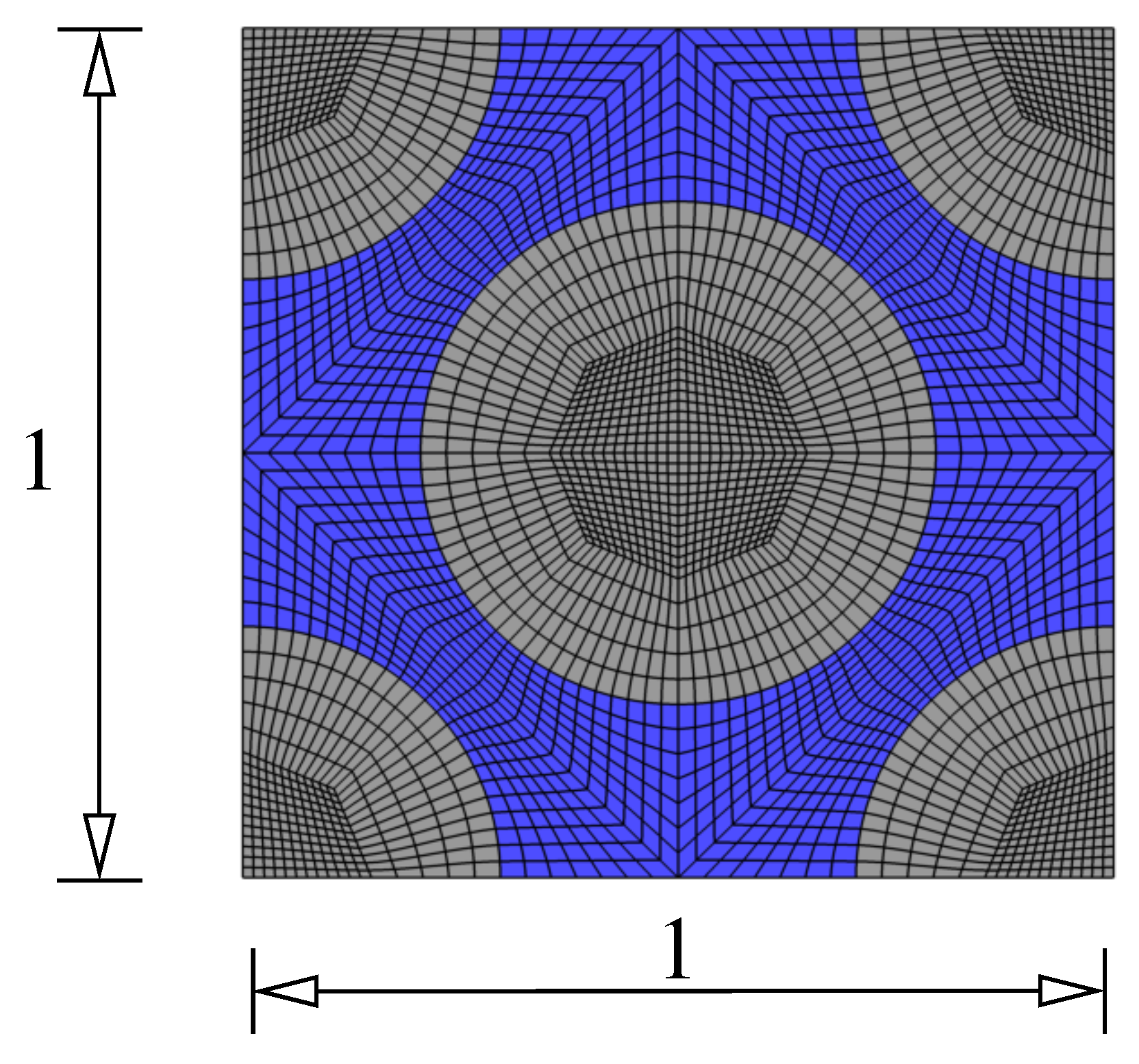
It is important to mention that the assumed symmetries can be employed as long as the materials in the RVE show no tension–compression asymmetry, anisotropy, or rate- or path-dependent behavior, i.e., the reduction in the input space is not applicable for more complex behavior such as plasticity or anisotropic behavior. Thus, the data are generated using the numerical solver for one quarter of the input space according to the region marked by blue in
Figure 1.
The dataset is augmented by transforming the generated data through the aforementioned global symmetries (
62) and (
63). This leads to a reduction in the computation time required for the preparation of the training data. After generating the dataset, it is decomposed into 80% for training and 20% for validation. Later on, in
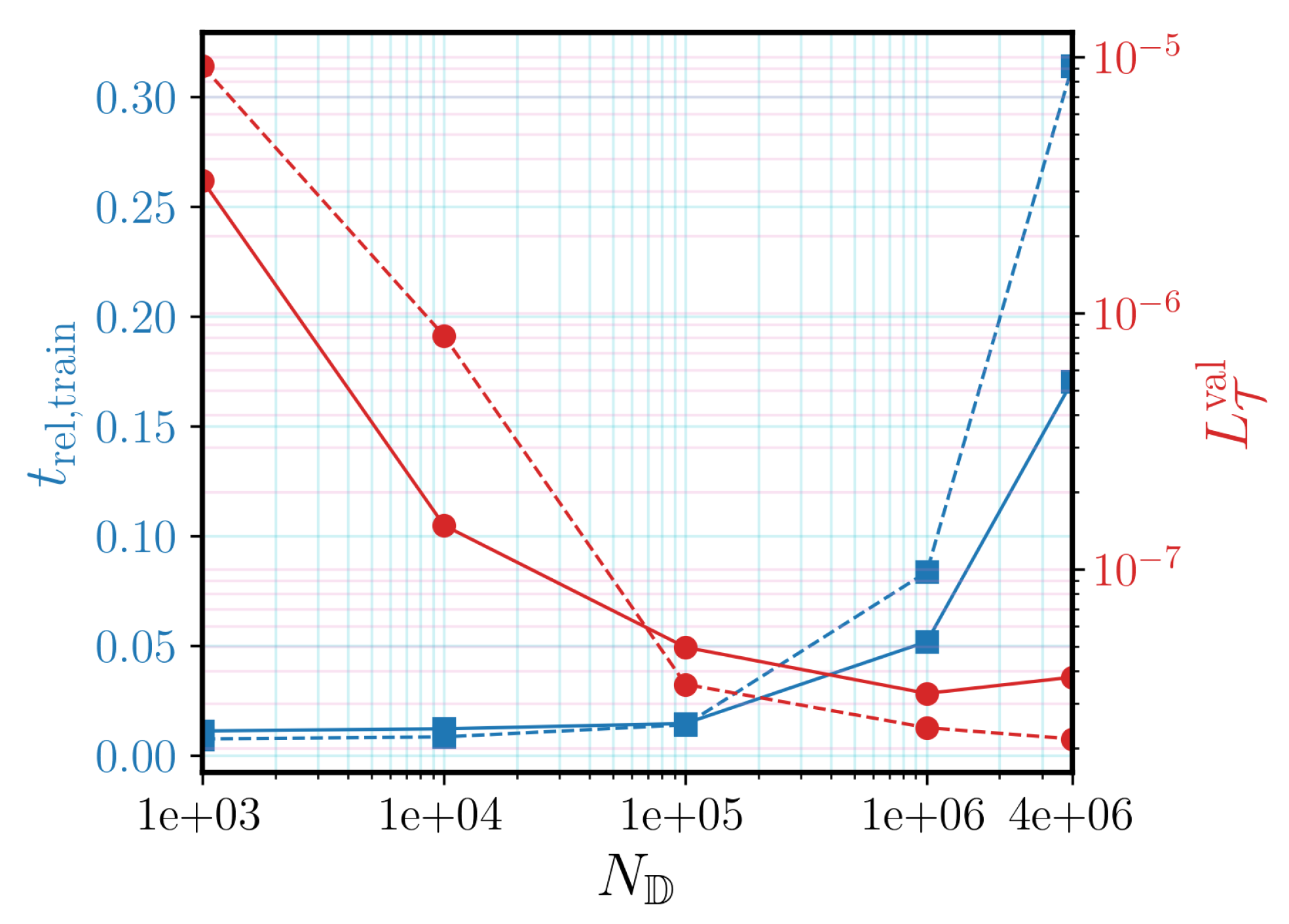
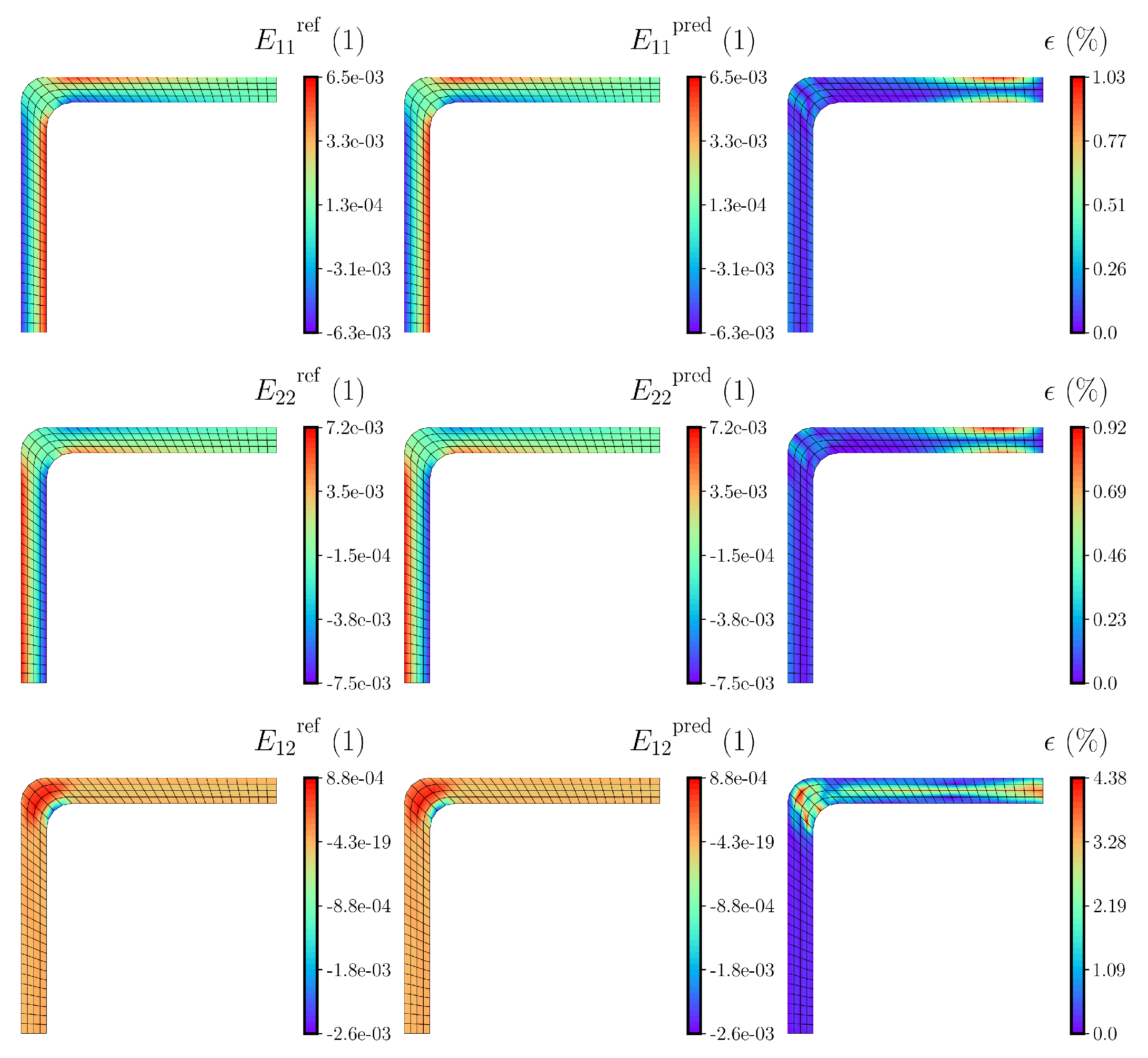
Section 4.2, the effect of the size of the training dataset on the accuracy of the final solution obtained from the DNN-based FE
simulation is investigated. It should be noted that the DNN models are tested by conducting DNN-FE
simulations and comparing the obtained solutions with those of the reference FE
simulations.
3.3. Architecture and Training Process
As it was mentioned in
Section 2.2 and
Section 3.1, the surrogate model for the local RVE takes
as the input and predicts
and
as the outputs. The obtained stress components and the consistent tangent matrix are assembled at the global finite element level for computation of the next global iteration in the Newton–Raphson method. In this work, two model architectures for our DNN-based surrogate models are considered, both are developed based on MLPs. In the first architecture, two separate neural networks
and
are implemented that map
to
and
,
where
and
represent the trainable parameters of deep neural network,
and
, respectively. The notation in use indicates that the deep neural networks are evaluated for strain inputs
with the given parameters after training the neural network. Throughout the article, this architecture is denoted as NN–2. However, this architecture does not consider that the consistent tangent matrix is the functional matrix of the stress components with respect to the strains,
where
and
are the corresponding entries in
and
, respectively. Thus, this is taken into account in the second architecture by computing
as the output of the Jacobian function
as
where
is obtained by applying reverse mode AD on the deep neural network surrogate
, which is parameterized with trainable parameters
. This architecture is denoted as NN–AD. Moreover, this approach is known as the so-called Sobolev training [
61] in which both the target and its derivative with respect to the input are considered for supervised learning. Particular explanations regarding the application of Sobolev training in multiscale simulations are provided in [
63], while the method is also employed in [
60]. By optimizing the parameters of neural networks to approximate not only the function’s outputs but also the function’s derivatives, the model can encode additional information about the target function within its parameters. Therefore, the quality of the predictions, the data efficiency, and generalization capabilities of the learned neural network can be improved.
In the following, we provide a detailed discussion on the data pre-processing, model training, model selection, and hyperparameter tuning.
3.3.1. Data Pre-Processing
We perform a standardization step on both input and outputs of the model to obtain efficient training of the networks using the statistics of the training dataset. A training dataset
is considered with its mean and standard deviation over the samples as vectors
and
, respectively. For training of the NN–2 model, the input and the outputs are standardized independently with their means and standard deviations,
where
represents the
ith component of
or
with the mean and standard deviation
and
, respectively. In contrast, for the NN–AD model, the consistent tangent matrix
should be scaled consistently with the scaling of
and
so that their relationship is preserved. Therefore, scaling (
67) is performed for the NN–AD model for the strains and stresses, while the components of
are scaled as
3.3.2. Training
In the following, a detailed discussion of the training process of all DNNs implemented in this research work is provided. We utilize an extended version of the stochastic gradient descent algorithm, known as
Adam [
89], for optimizing the parameters of the network during the training process. The weights and biases of the DNN are initialized using the Glorot uniform algorithm [
90] and zero initialization, respectively. All the neural networks are trained for 4000 epochs with an exponential decay of learning rate of
where
represents the learning rate.
is the initial learning rate and
is the decay rate. Here, a decay step of 1000 is employed. The decay of the learning rate is applied according to Equation (
69) every 1000 epochs to obtain a staircase behavior. For different sizes of the training dataset, the batch size is set such that 100 batches are obtained in order to have the same number of training updates for different sizes of the training dataset. The mean squared error (MSE) is utilized as the loss function. For the NN–2 model, the loss for a sample can be obtained as
where
and
indicate the loss for the mapping
and
, respectively. Here,
denotes the reference stress value and
is the prediction of the neural network. Accordingly,
is the reference value in the consistent tangent and
is the corresponding prediction.
The loss for a data sample for the NN–AD architecture is computed as
where
and
are the weighting coefficients for the two components of the loss. In all the cases, the loss for a batch of data is calculated by taking the average of the per-sample losses in the batch.
3.3.3. Model Selection
During the training process of each model, we track the validation loss and save the parameters of the model which lead to the lowest validation loss as the best model parameters. This helps to avoid overfitting of our deep neural networks. As mentioned earlier, the data are decomposed randomly into 80% for training and 20% for validation.
3.3.4. Hyperparameter Tuning
Hyperparameters in machine learning are the parameters that are defined by the user. Their values are set before starting the learning process of the model, such as number of neurons and hidden layers. The values of the hyperparameters remain unchanged during the training process and the following prediction. In machine learning applications, it is important to set the hyperparameters of a model such that the best performance is obtained regarding both prediction and generalization. Here, we perform hyperparameter tuning using a simple grid search algorithm to optimize the model performance on the validation dataset. For this experiment, a dataset with the size of is selected. We investigate three hyperparameters, i.e., the number of hidden layers , the number of neurons per each hidden layer , and the activation function , and carry out the hyperparameter tuning for the NN–2 architecture. Further, the same hyperparameters are employed for the NN–AD architecture for the sake of comparability. Moreover, for the NN–AD model, the weighting coefficients of the two components of the loss, and , are studied as well.
Results of the hyperparameter tuning for the number of hidden layers
, the number of neurons per each hidden layer
, and the activation function
are reported in
Appendix A. We observe that a model with eight hidden layers, 128 neurons per each hidden layer, and a
swish activation function leads to
and
. Moreover, our results show that increasing the model complexity to more than the aforementioned values would not lead to a significant gain in the model accuracy. Thus, we select these model hyperparameters for further analysis.
Other hyperparameters for the NN–AD model are the weighting coefficients
and
of the components of the loss, i.e.,
and
. Here, the effect of the weighting on the obtained validation losses is investigated. The results are reported in
Table 1.
We choose for all the cases and change from to 100. It can be observed that having a small may lead to an imbalanced training where a difference of almost two orders of magnitude between validation losses and exists. However, a of one or larger results in a more balanced training leading to validation losses with nearly the same scale. According to the results of this study, we select a model with and for further analysis.