Routing, Modulation Level, and Spectrum Assignment in Elastic Optical Networks—A Serial Stage Approach with Multiple Sub-Sets of Requests Based on Integer Linear Programming
Abstract
1. Introduction
- i
- Proposal of five new ILP alternatives based on RML+SA strategy, as follows:
- Link-oriented routing, with split traffic flow, and one set of requests.
- Link-oriented routing, with split traffic flow, and multiple sub-sets of requests.
- Link-oriented routing, with unsplit traffic flow, and multiple sub-sets of requests.
- Path-oriented routing, with split traffic flow, and multiple sub-sets of requests.
- Path-oriented routing, with unsplit traffic flow, and multiple sub-sets of requests.
- ii
- Performance of simulations to study the advantages and limitations of the proposed RML+SA approaches.
2. Related Works
- Optimization approaches:
- Two-stage serial optimization: In this approach, algorithms obtain the solution in two stages; the RML problem is solved first, and then the SA problem is approached as a coloring problem. This approach has been called RML+SA, where the RML phase calculates an ideal cost for the RMLSA problem [6]. On the other hand, it is also possible to calculate the solution in an SA+RML approach [30,31]; however, this approach is outside the scope of this study.
- Request management:
- Multiple sub-sets of requests: The set of requests is divided into several smaller sub-sets, and then the light-paths are calculated and installed consecutively for each sub-set [28].
- Routing strategies:
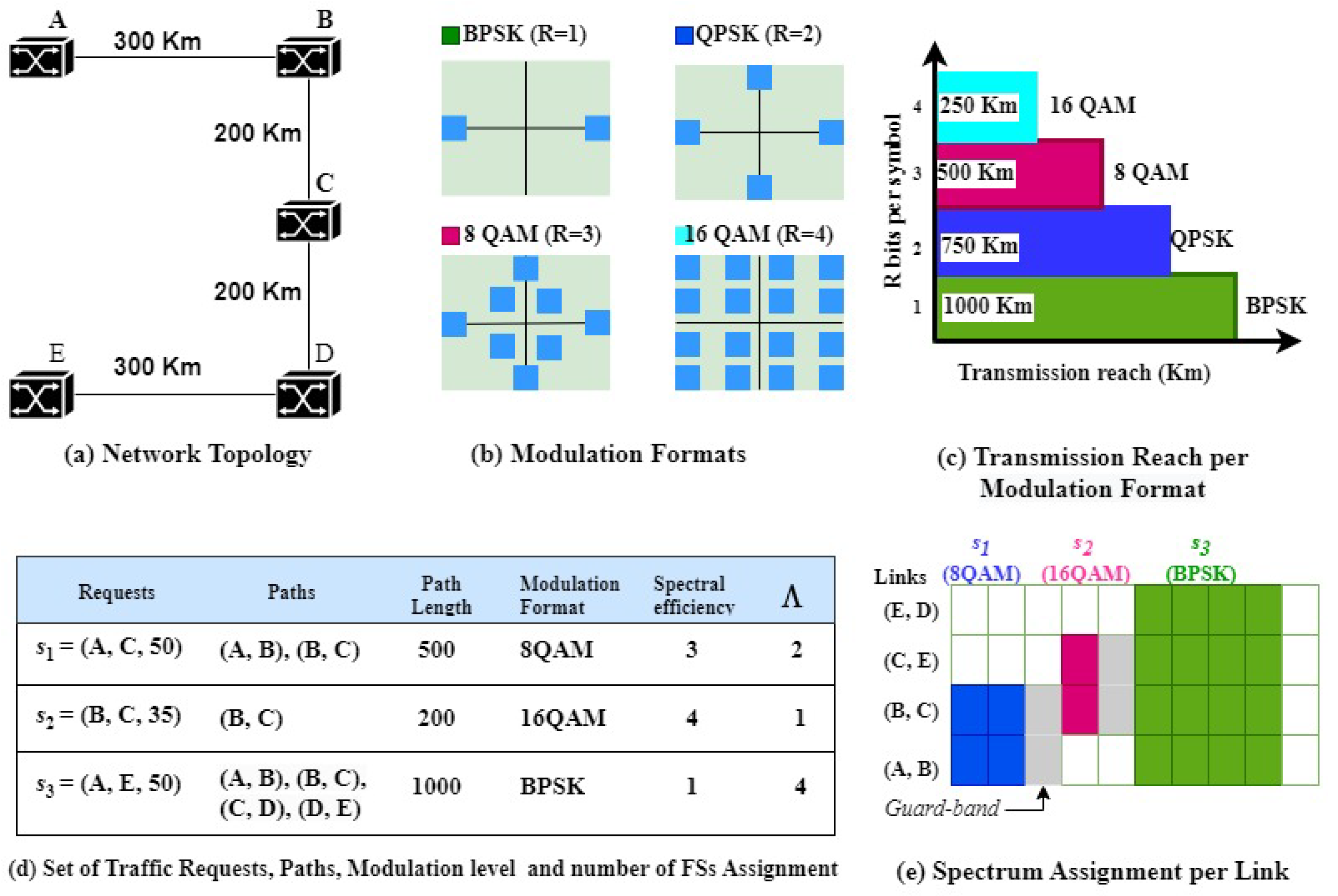
- Path-oriented routing: Routing algorithms select a path for a request from pre-computed paths [6], typically the k shortest paths.
- Link-oriented routing: Routing algorithms have all possible routes available [14]; all network links are candidates to be part of a route. No pre-calculated path is necessary.
- Traffic flow division:
3. Mathematical Programming Models
- 1LM = One set of requests, link-oriented routing, and multiple traffic sub-flows.
- MLM = Multiple sub-sets of requests, link-oriented routing, and multiple traffic sub-flows.
- ML1 = Multiple sub-sets of requests, link-oriented routing, and one traffic flow.
- MPM = Multiple sub-sets of requests, path-oriented routing, and multiple traffic sub-flows.
- MP1 = Multiple sub-sets of requests, path-oriented routing, and one traffic flow.
3.1. Problem Statement
- Satisfy all the source—destination connection demands, determining the route, the modulation format, and the spectrum assignment for each traffic request;
- Optimize spectrum usage minimizing the maximum index of slot used on all optical fibers in the network.
- The spectral bandwidth of each optical fiber is divided into slots.
- The fiber optic capacity in slots terms is equally limited in all links.
- Connection demands are bidirectional, and RMLSA algorithms calculate a light-path for each request.
- Between two light-paths using the same link, there is at least one slot as a guard-band.
- A request is represented by a 3-tuple: s = (, , ), indicating the source node, the destination node and the requested bandwidth (data rate).
- Multiple sub-sets imply a scheme to approach the problem studied in this work, which does not imply management requirements in the upper layers of the network.
- For the division of traffic flows we consider sliceable bandwidth-variable transponders (SBVTs) mentioned in [13].
3.2. Calculation Process for the Multiple Sub-Sets of Requests Approaches
| Algorithm 1: for Multiple Sub-sets of Requests Process |
|
3.3. RML Phase Formulation for MPM
3.4. RML Phase Formulation for MLM
3.5. SA Phase Formulation
3.6. ILP Models Summary
- RML phase: the following particular cases should be taken into account
- One set of requests: in Equations (4) and (11), we have that = 0 when the value of = ∅, since there was no previous request; and therefore it represents only the maximum slot used by incoming requests.
- Multiple traffic sub-flows: inequality (12) limits to one the number of paths to be used per request considering . This affects Equation (23), causing it to assign all the required slots to a single path for each request.
- SA phase:
4. Simulation Test
- To determine the benefits of dividing the requests into sub-sets and the advantages in term of computational time of path-based routing over link-based routing.
- To study the performance of the proposed models (MLM, MPM, ML1, MP1, and 1LM) compared to the state-of-the-art models (1L1, 1PM, and 1P1).
4.1. Computational Environment
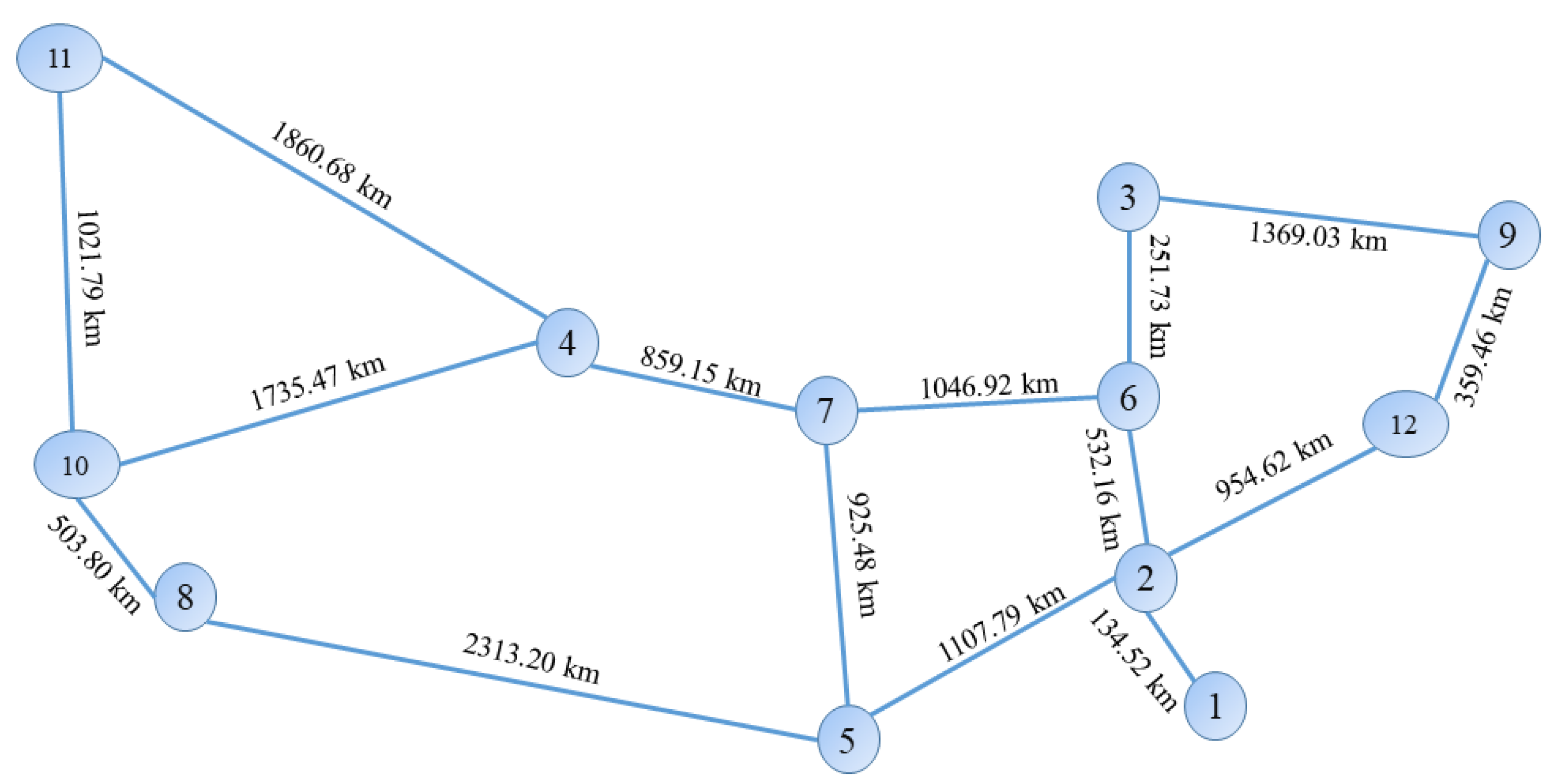
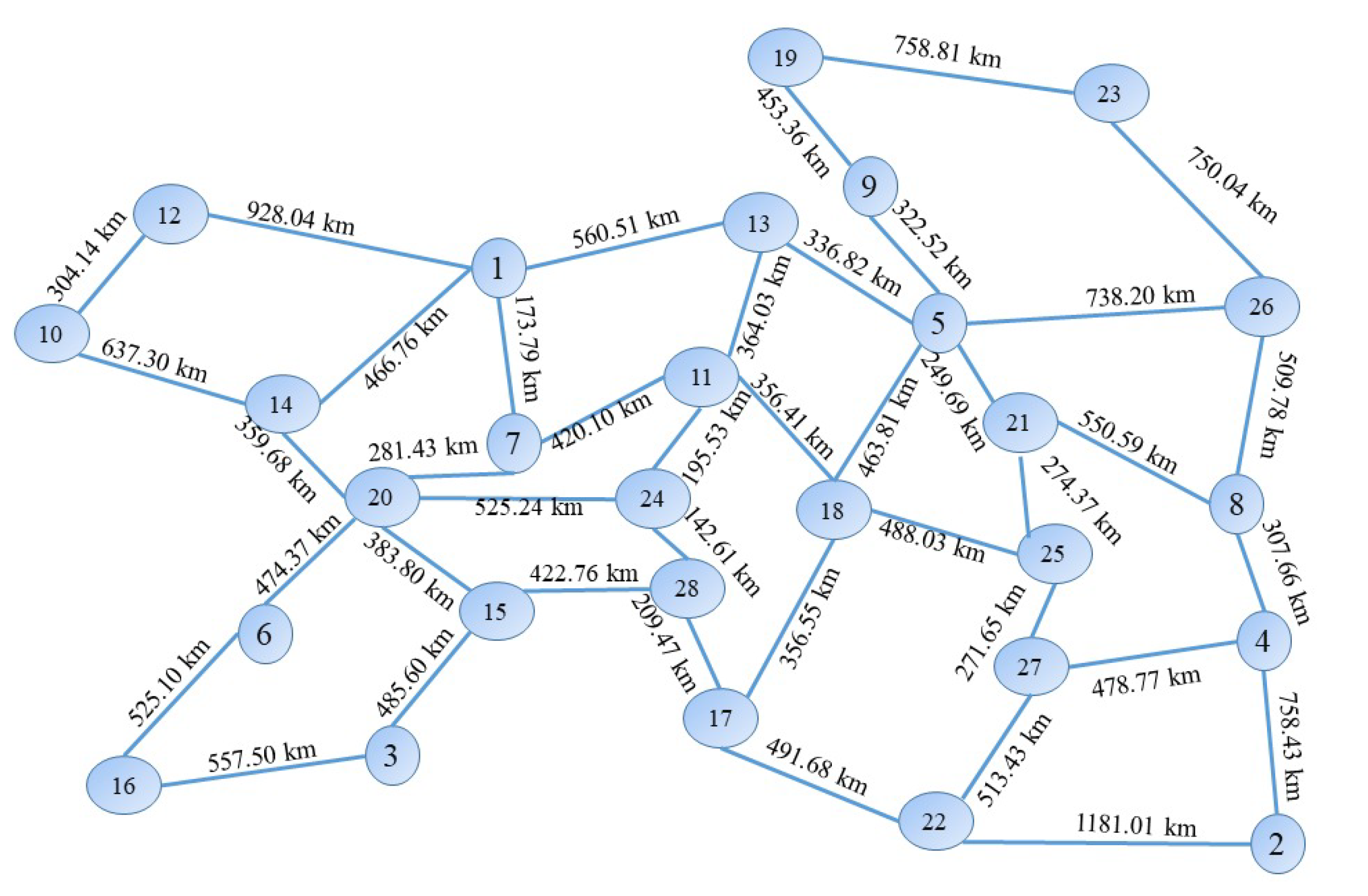
4.2. Network Topologies
4.3. Simulation Scheme
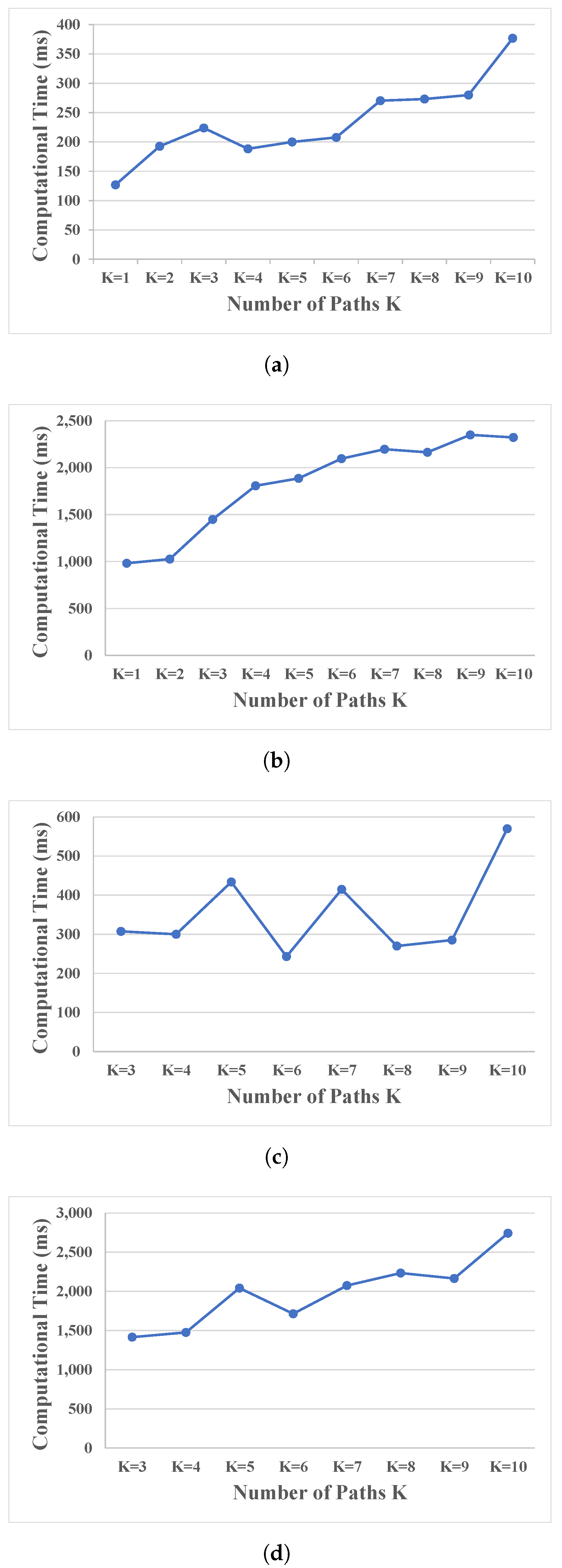
- Research Question 1: What would happen as the number of sub-sets of the requests increases as they are divided into smaller sub-sets?
- Research Question 2: Are unsplit traffic flow models worse concerning spectrum efficiency and computational time than split traffic flow models? Up to how many sub-demands is convenient to split each request?
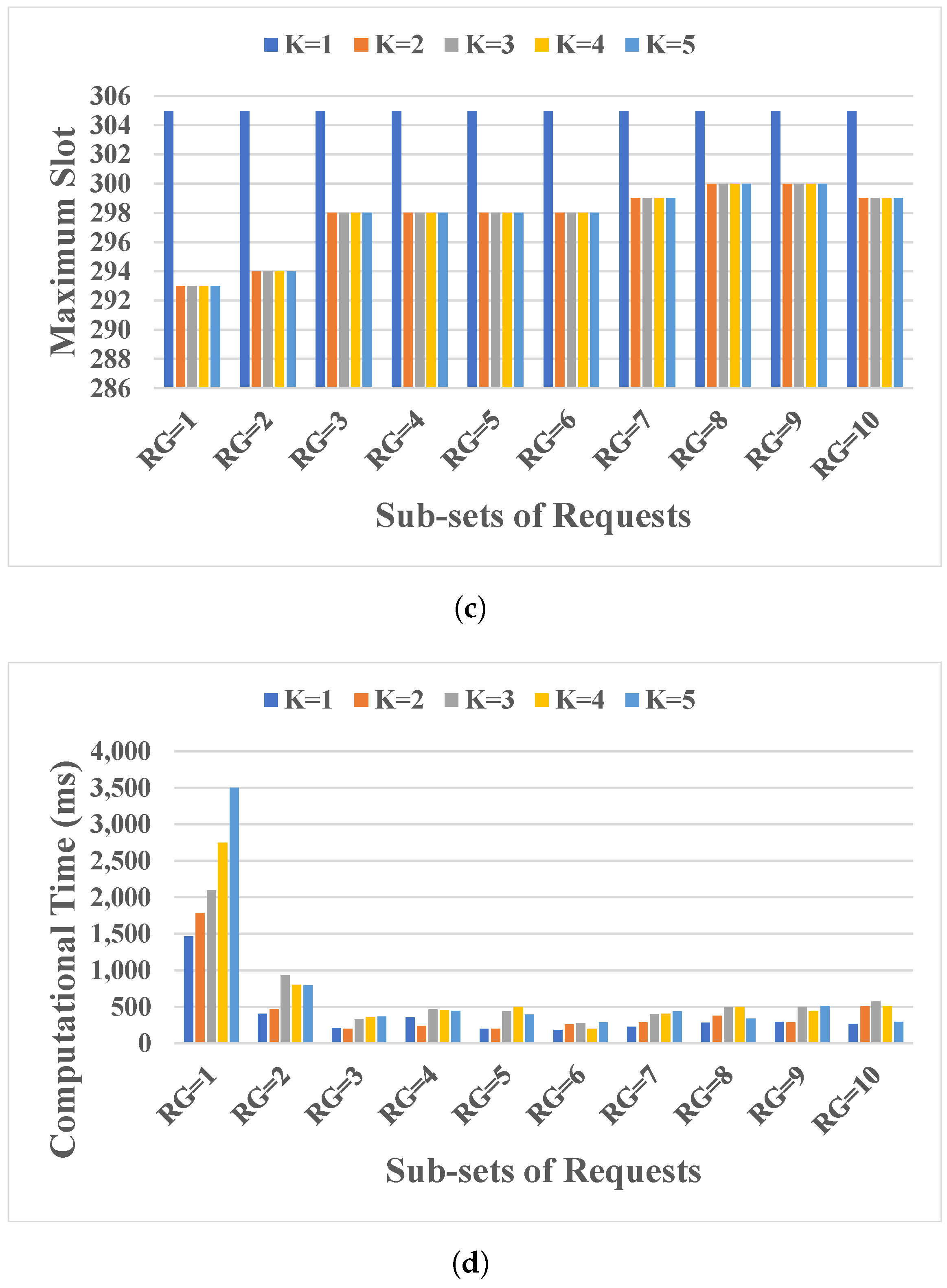
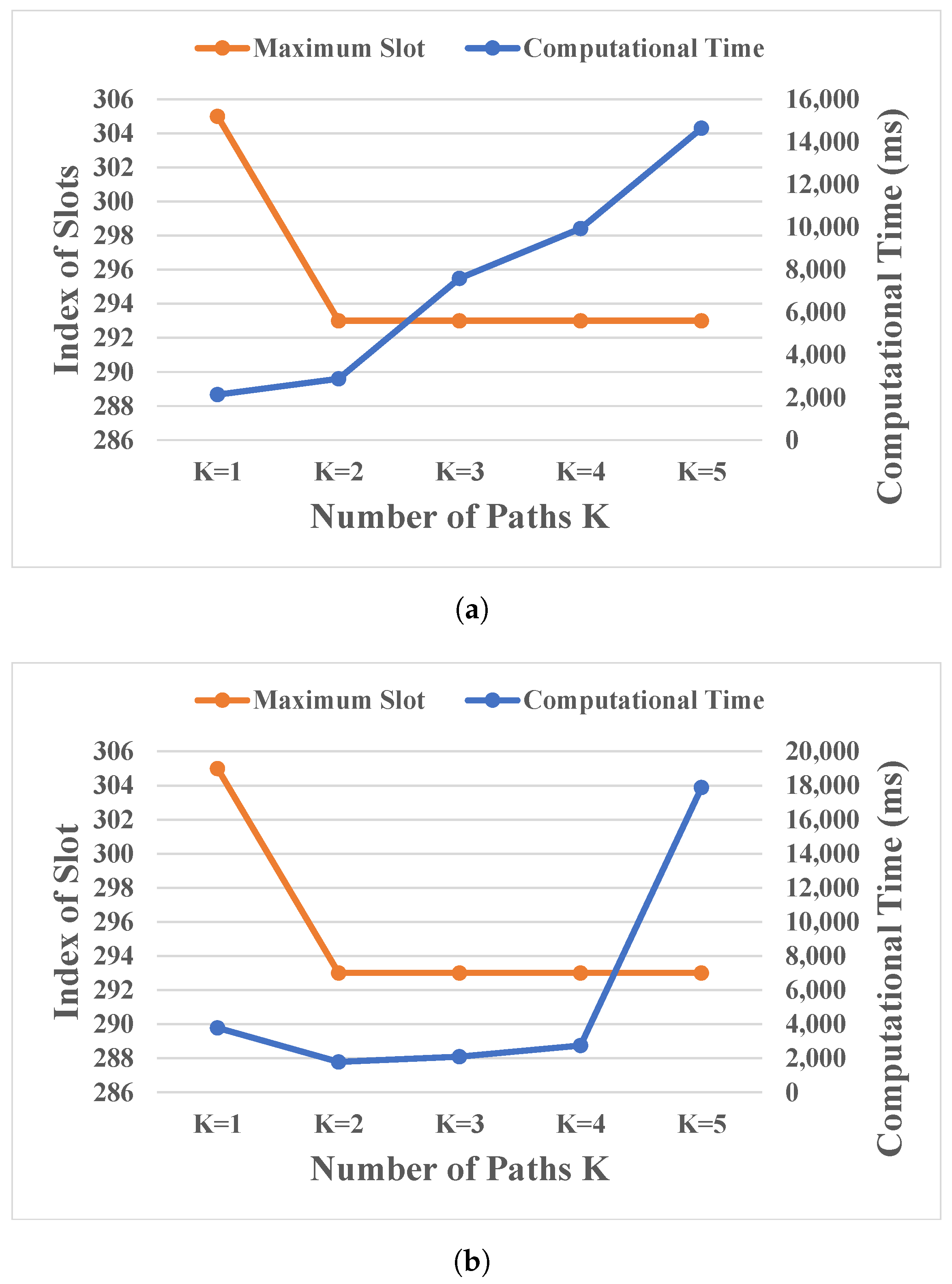
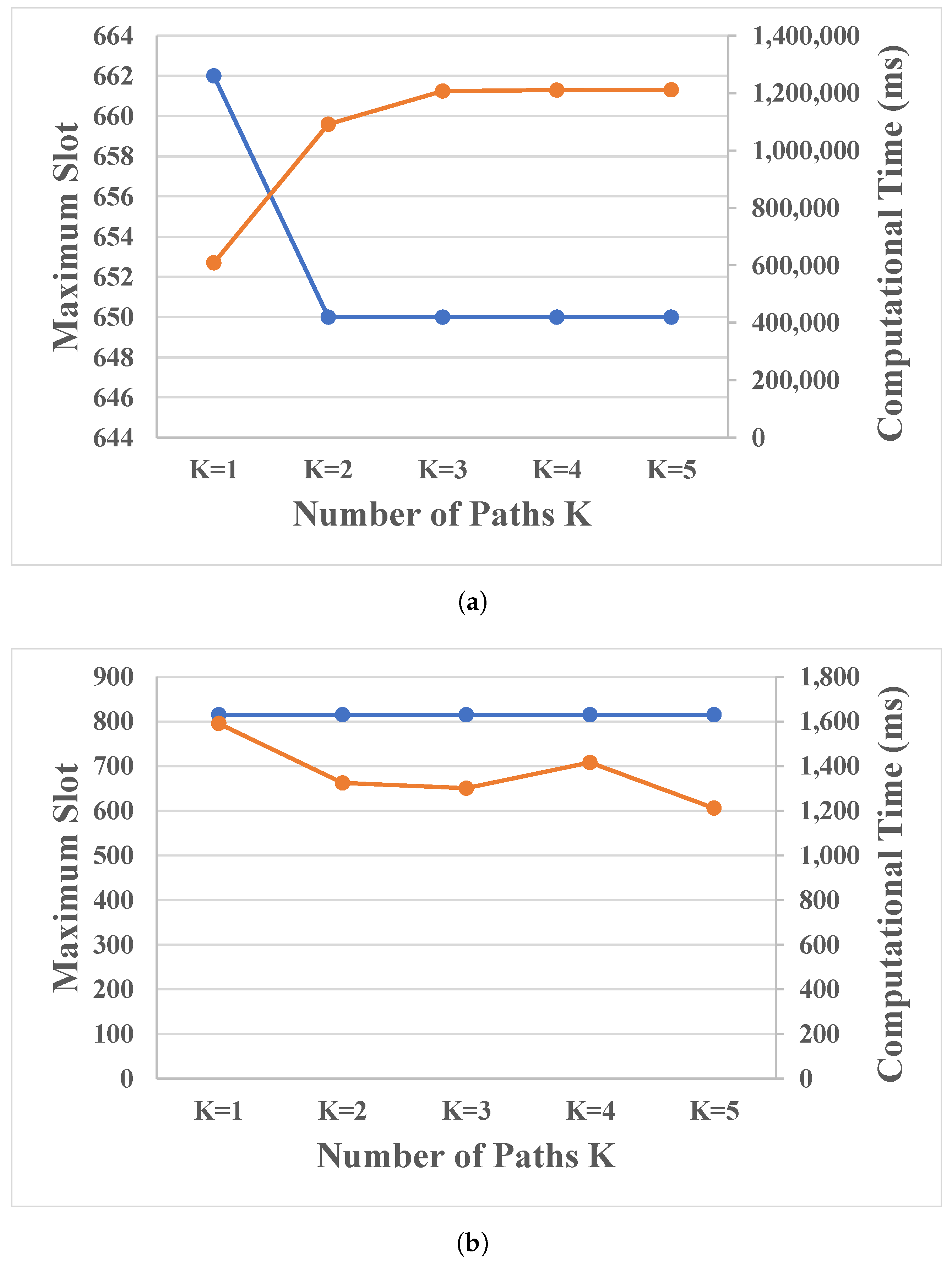
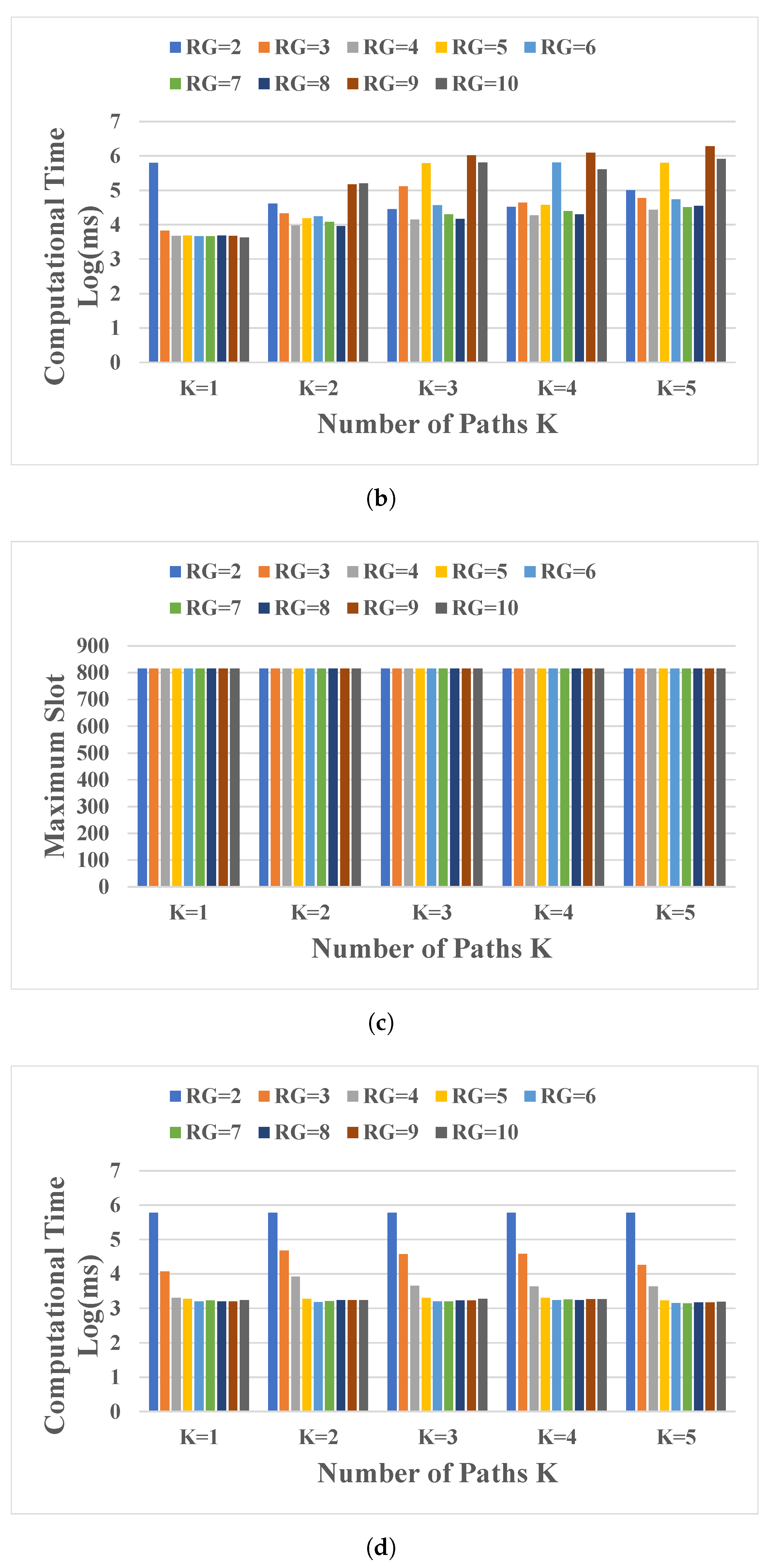
- Research Question 3: For path-oriented routing, how many available paths () are advisable to use to improve spectrum-usage efficiency without deteriorating computational time?As the available paths () increase, the spectrum efficiency should increase at the expense of computation time. To answer this question, the performance of solutions were averaged according to the path-oriented routing for the Abeline and Nobel-eu network topologies, considering the following parameters:
- -
- MP1
- -
- MPM
- -
- load (40 requests for Abeline and 80 requests for Nobel-eu).
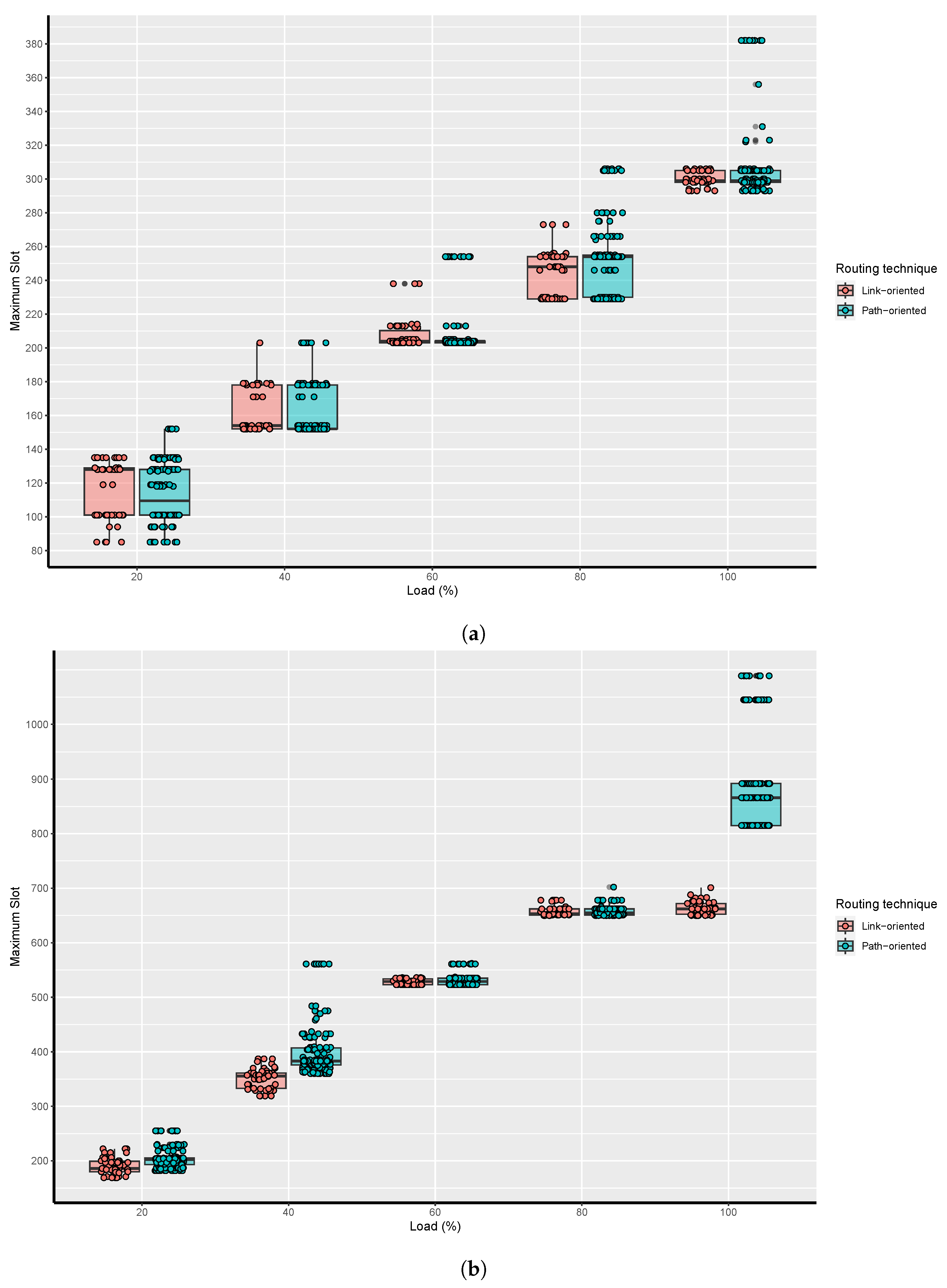
- Research Question 4: Between the path-oriented and link-oriented routing, which strategy would be the best in terms of used spectrum and computational time?Link-oriented routing could obtain better results than path-oriented routing in terms of spectrum efficiency at the cost of computational time. To answer this question, the following parameters were considered:
- -
- 1P1
- -
- MP1
- -
- 1PM
- -
- MPM
- -
- 1P1
- -
- ML1
- -
- 1LM
- -
- MLM
- -
- Loading percentage: (8, 16, 24, 32, 40 requests for Abeline and 16, 32, 48, 64, 80 requests for Nobel-eu).
Considering the complexity of the Nobel-eu network topology, the following parameters were also used:- -
- 1P1
- -
- MP1
- -
- 1PM
- -
- MPM
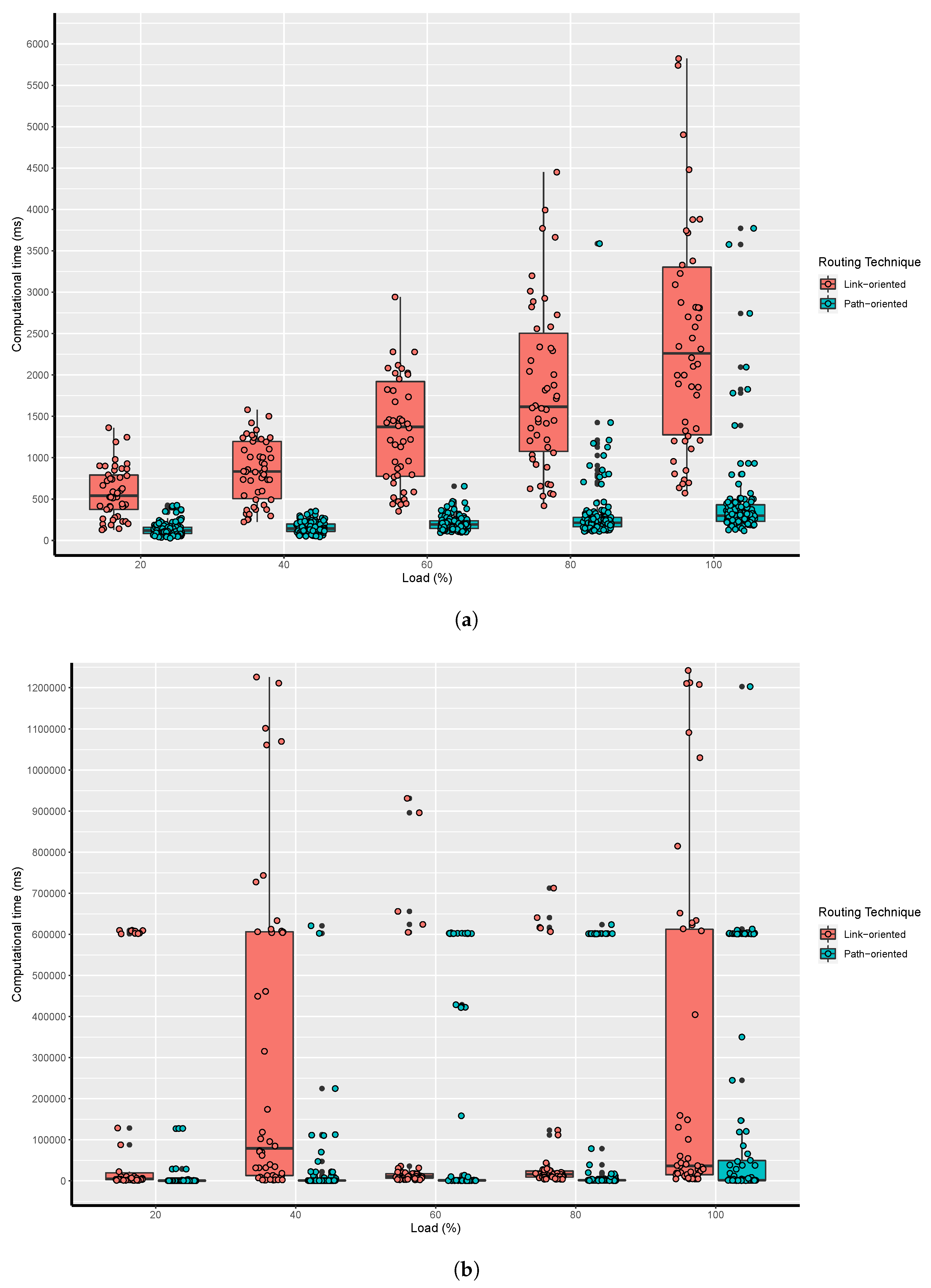
5. Results and Discussion
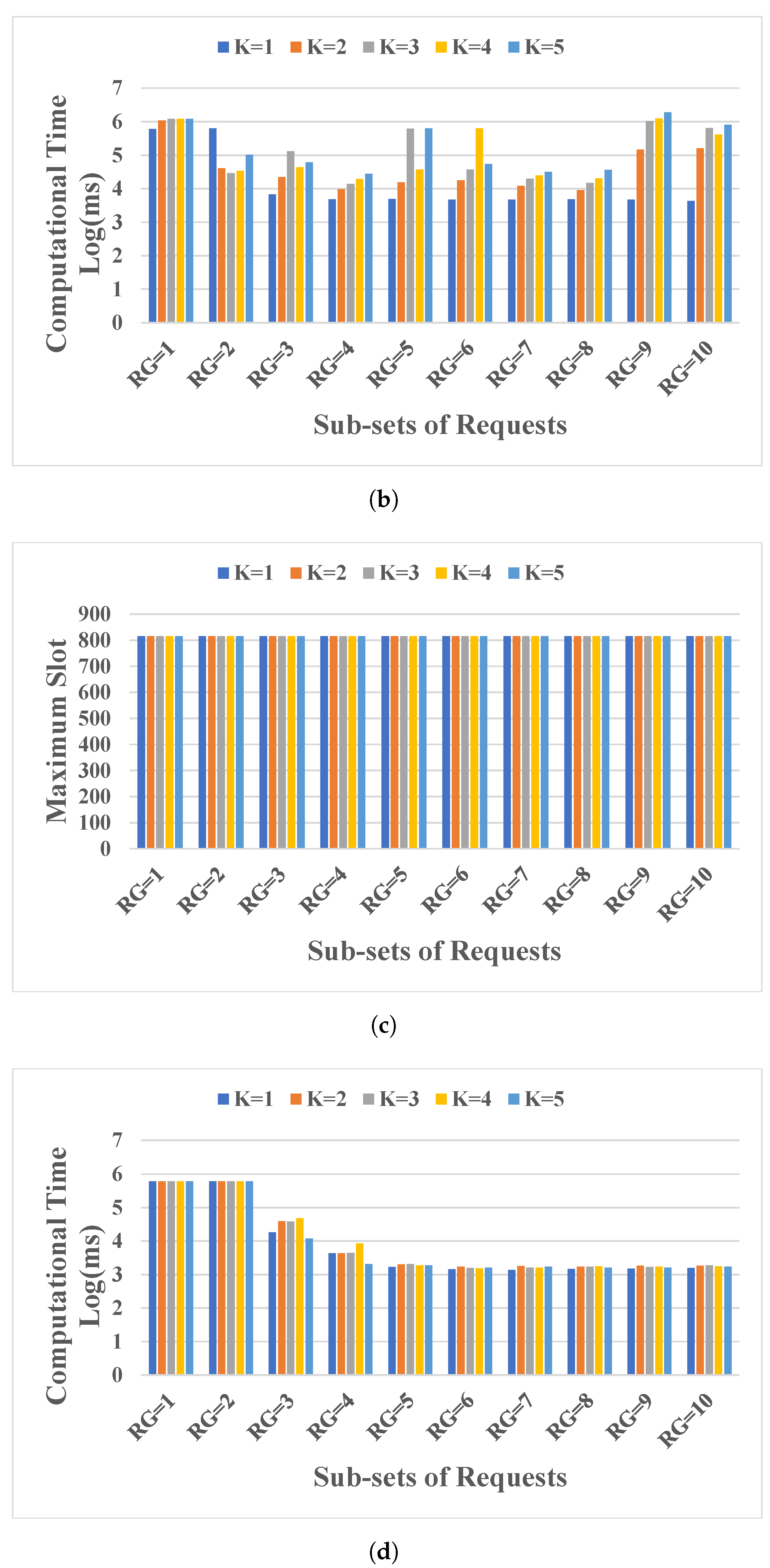
5.1. Results for Research Question 1
5.2. Results for Research Question 2
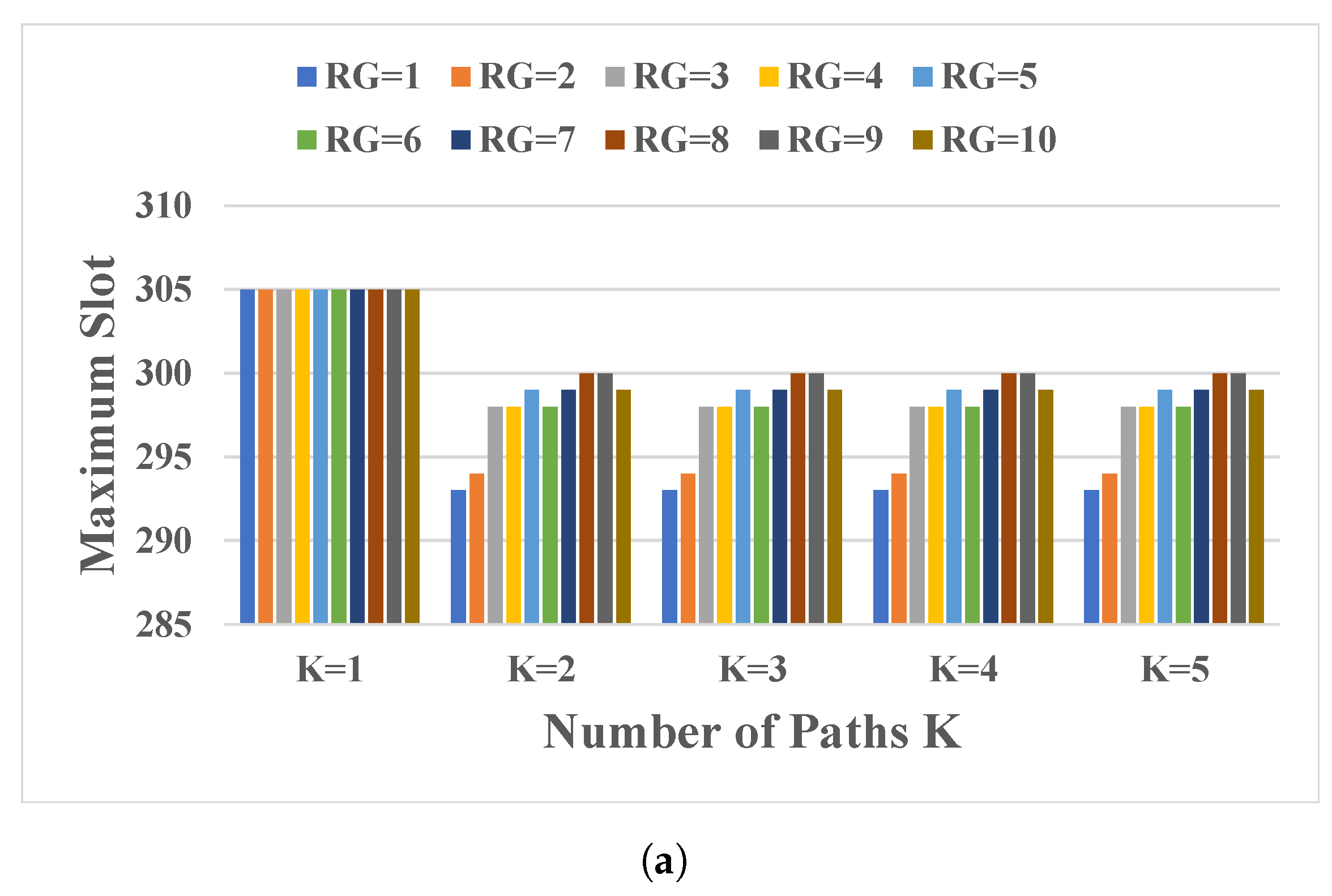
5.3. Results for Research Question 3
5.4. Results for Research Question 4
5.5. General Discussion
- Dividing the requests into multiple subsets up to a certain threshold reduces computation time. The threshold will vary according to the topology considered. Particularly, in both studied topologies, an RG between 3 and 5 is recommended.
- Splitting the traffic stream helps improve the used spectrum at the cost of increased computational time. We recommend splitting the traffic stream into no more than three sub-streams for the studied topologies and loads.
- The number of pre-computed shortest paths may help to improve the efficient use of spectrum and computation time. We observe that three-shortest paths are suitable in the topologies under study.
- Path-based models are more convenient compared to link-based models when the complexity of the problem increases. Determining the appropriate number of routes is necessary to perform simulations since it depends on optical resources and network structure.
6. Conclusions and Future Work
- use the multi-subset request scheme with different heuristics;
- extend this study to the Routing, Baud rate, Code, Modulation Level, and Spectrum Allocation (RBCMLSA) approach;
- use the multi-subset request scheme considering dynamic and reserved traffic; and
- consider other quality metrics such as requests blockage, power consumption, and optical channel impairments.
Author Contributions
Funding
Conflicts of Interest
Appendix A





References
- Patel, A.N.; Ji, P.N.; Jue, J.P.; Wang, T. Survivable transparent flexible optical WDM (FWDM) networks. In Proceedings of the Optical Fiber Communication Conference, Los Angeles, CA, USA, 6–10 March 2011; p. OTuI2. [Google Scholar]
- Jinno, M.; Takara, H.; Kozicki, B.; Tsukishima, Y.; Sone, Y.; Matsuoka, S. Spectrum-efficient and scalable elastic optical path network: Architecture, benefits, and enabling technologies. IEEE Commun. Mag. 2009, 47, 66–73. [Google Scholar] [CrossRef]
- Chatterjee, B.C.; Sarma, N.; Oki, E. Routing and Spectrum Allocation in Elastic Optical Networks: A Tutorial. IEEE Commun. Surv. Tutor. 2015, 17, 1776–1800. [Google Scholar] [CrossRef]
- Gerstel, O.; Jinno, M.; Lord, A.; Yoo, S.B. Elastic optical networking: A new dawn for the optical layer? IEEE Commun. Mag. 2012, 50, s12–s20. [Google Scholar] [CrossRef]
- Klinkowski, M.; Walkowiak, K.; Jaworski, M. Off-line algorithms for routing, modulation level, and spectrum assignment in elastic optical networks. In Proceedings of the 2011 13th International Conference on Transparent Optical Networks (ICTON), Stockholm, Sweden, 26–30 June 2011; pp. 1–6. [Google Scholar]
- Christodoulopoulos, K.; Tomkos, I.; Varvarigos, E. Elastic bandwidth allocation in flexible OFDM-based optical networks. J. Light. Technol. 2011, 29, 1354–1366. [Google Scholar] [CrossRef]
- Wang, Y.; Cao, X.; Pan, Y. A study of the routing and spectrum allocation in spectrum-sliced elastic optical path networks. In Proceedings of the 2011 IEEE INFOCOM, Shanghai, China, 10–15 April 2011; pp. 1503–1511. [Google Scholar]
- Ríos, I.; Bogado, C.M.; Pinto-Roa, D.P.; Barán, B. A Serial Optimization and Link-Oriented Based Routing Approach for RMLSA in Elastic Optical Networks: A Comparison Among ILP Based Solution Approaches. In Proceedings of the 10th Latin America Networking Conference, São Paulo, Brazil, 3–4 October 2018; pp. 48–55. [Google Scholar] [CrossRef]
- Zhou, X.; Lu, W.; Gong, L.; Zhu, Z. Dynamic RMSA in elastic optical networks with an adaptive genetic algorithm. In Proceedings of the 2012 IEEE Global Communications Conference (GLOBECOM), Anaheim, CA, USA, 3–7 December 2012; pp. 2912–2917. [Google Scholar] [CrossRef]
- Fernández-Martínez, S.; Barán, B.; Pinto-Roa, D.P. Spectrum defragmentation algorithms in elastic optical networks. Opt. Switch. Netw. 2019, 34, 10–22. [Google Scholar] [CrossRef]
- Martínez, S.F.; Pinto-Roa, D.P. Performance evaluation of non-hitless spectrum defragmentation algorithms in elastic optical networks. In Proceedings of the 2017 XLIII Latin American Computer Conference (CLEI), Cordoba, Argentina, 4–8 September 2017; pp. 1–8. [Google Scholar] [CrossRef]
- Pinto-Roa, D.P.; Brizuela, C.A.; Barán, B. Multi-objective routing and wavelength converter allocation under uncertain traffic. Opt. Switch. Netw. 2015, 16, 1–20. [Google Scholar] [CrossRef]
- Tanaka, T.; Inui, T.; Kadohata, A.; Imajuku, W.; Hirano, A. Multiperiod IP-over-elastic network reconfiguration with adaptive bandwidth resizing and modulation. IEEE/OSA J. Opt. Commun. Netw. 2016, 8, A180–A190. [Google Scholar] [CrossRef]
- Li, B.; Kim, Y.C. Efficient routing and spectrum allocation considering QoT in elastic optical networks. In Proceedings of the 2015 38th International Conference on Telecommunications and Signal Processing (TSP), Prague, Czech Republic, 9–11 July 2015; pp. 109–112. [Google Scholar]
- Assis, K.D.R.; Almeida, R.C.; Cartaxo, A.V.T.; dos Santos, A.F.; Waldman, H. Flexgrid optical networks design under multiple modulation formats. In Proceedings of the 2014 International Telecommunications Symposium (ITS), Sao Paulo, Brazil, 17–20 August 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Zhao, J.; Wymeersch, H.; Agrell, E. Nonlinear Impairment-Aware Static Resource Allocation in Elastic Optical Networks. In Proceedings of the Optical Fiber Communication Conference, OFC 2015, Los Angeles, CA, USA, 22–26 March 2015; Volume 33. [Google Scholar] [CrossRef]
- Velasco, L.; Vela, A.P.; Morales, F.T.; Ruiz, M. Designing, Operating, and Reoptimizing Elastic Optical Networks. J. Light. Technol. 2017, 35, 513–526. [Google Scholar] [CrossRef]
- Queiroz, I.M.; Assis, K.D.R. A MILP-based algorithm for energy saving in spectrum-sliced elastic optical networks. In Proceedings of the 2017 9th Computer Science and Electronic Engineering (CEEC), Colchester, UK, 27–29 September 2017; pp. 25–30. [Google Scholar] [CrossRef]
- Jia, X.; Ning, F.; Yin, S.; Wang, D.; Zhang, J.; Huang, S. An Integrated ILP Model for Routing, Modulation Level and Spectrum Allocation in the Next Generation DCN. In Proceedings of the Third International Conference on Cyberspace Technology (CCT 2015), Beijing, China, 17–18 October 2015; pp. 1–3. [Google Scholar] [CrossRef]
- Pagès, A.; Perelló, J.; Spadaro, S.; Comellas, J. Optimal route, spectrum, and modulation level assignment in split-spectrum-enabled dynamic elastic optical networks. IEEE/OSA J. Opt. Commun. Netw. 2014, 6, 114–126. [Google Scholar] [CrossRef]
- Dong, X.; El-Gorashi, T.E.H.; Elmirghani, J.M.H. Energy efficiency of optical OFDM-based networks. In Proceedings of the 2013 IEEE International Conference on Communications (ICC), Budapest, Hungary, 9–13 June 2013; pp. 4131–4136. [Google Scholar] [CrossRef]
- Goścień, R.; Walkowiak, K.; Klinkowski, M. Distance-adaptive transmission in cloud-ready elastic optical networks. IEEE/OSA J. Opt. Commun. Netw. 2014, 6, 816–828. [Google Scholar] [CrossRef]
- Goścień, R.; Walkowiak, K.; Klinkowski, M. Tabu Search algorithm for routing, modulation and spectrum allocation in elastic optical network with anycast and unicast traffic. Comput. Netw. 2015, 79, 148–165. [Google Scholar] [CrossRef]
- Tornatore, M.; Rottondi, C. Routing and spectrum assignment in metro optical ring networks with distance-adaptive transceivers. In Proceedings of the 2015 20th European Conference on Networks and Optical Communications—(NOC), London, UK, 30 June–2 July 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Christodoulopoulos, K.; Varvarigos, E. Static and dynamic spectrum allocation in flexi-grid optical networks. In Proceedings of the 2012 14th International Conference on Transparent Optical Networks (ICTON), Coventry, UK, 2–5 July 2012; pp. 1–5. [Google Scholar]
- Yaghubi-Namaad, M.; Rahbar, A.G.; Alizadeh, B. Adaptive modulation and flexible resource allocation in space-division-multiplexed elastic optical networks. IEEE/OSA J. Opt. Commun. Netw. 2018, 10, 240–251. [Google Scholar] [CrossRef]
- Din, D.R.; Zhan, M.X. The RBCMLSA problem on EONs with flexible transceivers. Photonic Netw. Commun. 2019, 38, 62–74. [Google Scholar] [CrossRef]
- Gong, L.; Zhou, X.; Liu, X.; Zhao, W.; Lu, W.; Zhu, Z. Efficient resource allocation for all-optical multicasting over spectrum-sliced elastic optical networks. IEEE/OSA J. Opt. Commun. Netw. 2013, 5, 836–847. [Google Scholar] [CrossRef]
- Takezaki, M.; Hirata, K. Static light-path establishment method with multi-path routing in elastic optical networks. In Proceedings of the 2017 International Conference on Information Networking (ICOIN), Da Nang, Vietnam, 11–13 January 2017; pp. 109–111. [Google Scholar] [CrossRef]
- Wang, R.; Mukherjee, B. Spectrum management in heterogeneous bandwidth optical networks. Opt. Switch. Netw. 2014, 11, 83–91. [Google Scholar] [CrossRef]
- Dinarte, H.A.; Correia, B.V.; Chaves, D.A.; Almeida, R.C. Routing and spectrum assignment: A metaheuristic for hybrid ordering selection in elastic optical networks. Comput. Netw. 2021, 197, 108287. [Google Scholar] [CrossRef]
- Talebi, S.; Alam, F.; Katib, I.; Khamis, M.; Salama, R.; Rouskas, G.N. Spectrum management techniques for elastic optical networks: A survey. Opt. Switch. Netw. 2014, 13, 34–48. [Google Scholar] [CrossRef]
- Popescu, I.; Cerutti, I.; Sambo, N.; Castoldi, P. On the optimal design of a spectrum-switched optical network with multiple modulation formats and rates. IEEE/OSA J. Opt. Commun. Netw. 2013, 5, 1275–1284. [Google Scholar] [CrossRef]
- Barán, B.; Pinto-Roa, D.P. Multiobjective Optimization in Optical Networks. In Bio-Inspired Computation in Telecommunications; Yang, X.S., Chien, S.F., Ting, T.O., Eds.; Morgan Kaufmann: Boston, MA, USA, 2015; pp. 205–244. [Google Scholar] [CrossRef]
- Cavalcante, M.; Pereira, H.; Chaves, D.; Almeida, R. Optimizing the cost function of power series routing algorithm for transparent elastic optical networks. Opt. Switch. Netw. 2018, 29, 57–64. [Google Scholar] [CrossRef]
- Lira, C.J.; Almeida, R.C.; Chaves, D.A. Spectrum allocation using multiparameter optimization in elastic optical networks. Comput. Netw. 2023, 220, 109478. [Google Scholar] [CrossRef]
- Tang, B.; Huang, Y.C.; Xue, Y.; Zhou, W. Deep Reinforcement Learning-Based RMSA Policy Distillation for Elastic Optical Networks. Mathematics 2022, 10, 3293. [Google Scholar] [CrossRef]
- Wan, X.; Hua, N.; Zheng, X. Dynamic routing and spectrum assignment in spectrum-flexible transparent optical networks. IEEE/OSA J. Opt. Commun. Netw. 2012, 4, 603–613. [Google Scholar] [CrossRef]
- Hai, D.T. Multi-objective genetic algorithm for solving routing and spectrum assignment problem. In Proceedings of the 2017 Seventh International Conference on Information Science and Technology (ICIST), Da Nang, Vietnam, 16–19 April 2017; pp. 177–180. [Google Scholar] [CrossRef]
- Fretes, C.; Pinto-Roa, D.P.; Ortiz, Y.M. A Multi-objective evolutionary algorithms study applied to routing and spectrum assignment in EON networks. In Proceedings of the XXIV Argentine Congress of Computer Science, Tandil, Argentina, 8–12 October 2018; pp. 735–744. [Google Scholar]
- Takeda, K.; Sato, T.; Shinkuma, R.; Oki, E. Multipath provisioning scheme for fault tolerance to minimize required spectrum resources in elastic optical networks. Comput. Netw. 2021, 188, 107895. [Google Scholar] [CrossRef]
- Assis, K.; Almeida, R.; Reed, M.; Santos, A.; Dinarte, H.; Chaves, D.; Li, H.; Yan, S.; Nejabati, R.; Simeonidou, D. Protection by diversity in elastic optical networks subject to single link failure. Opt. Fiber Technol. 2023, 75, 103208. [Google Scholar] [CrossRef]
- Villamayor-Paredes, M.M.R.; Maidana-Benítez, L.V.; Colbes, J.; Pinto-Roa, D.P. Routing, modulation level, and spectrum assignment in elastic optical networks. A route-permutation based genetic algorithms. Opt. Switch. Netw. 2023, 47, 100710. [Google Scholar] [CrossRef]
- Orlowski, S.; Wessäly, R.; Pióro, M.; Tomaszewski, A. SNDlib 1.0—Survivable Network Design Library. Networks 2010, 55, 276–286. [Google Scholar] [CrossRef]
| Optimization Approach | Request Management | Routing Strategies | Traffic Flow Division | Contributions Reported in the Literature | ||||
|---|---|---|---|---|---|---|---|---|
| One-stage RMLSA | Two-stage RML+SA | (1) One Set of Requests | (M)ultiple Subsets of Requests | (P)ath-oriented routing Pre-calculated Path Table | (L)ink-oriented routing All paths available | (1) One Traffic Flow | (M)ultiple Traffic sub-flows | |
| ✓ | ✓ | ✓ | ✓ | [13] | ||||
| ✓ | ✓ | ✓ | ✓ | [13,14,15,16,17,18,19] | ||||
| ✓ | ✓ | ✓ | ✓ | [20] | ||||
| ✓ | ✓ | ✓ | ✓ | [5,6,17,21,22,23,24,25,26,27] | ||||
| ✓ | ✓ | ✓ | ✓ | [16,28] | ||||
| ✓ | ✓ | ✓ | ✓ | 1L1 [8] | ||||
| ✓ | ✓ | ✓ | ✓ | 1PM [29] | ||||
| ✓ | ✓ | ✓ | ✓ | 1P1 [6] | ||||
| The proposed RML+SA models in this work | ||||||||
| ✓ | ✓ | ✓ | ✓ | 1LM | ||||
| ✓ | ✓ | ✓ | ✓ | MLM | ||||
| ✓ | ✓ | ✓ | ✓ | ML1 | ||||
| ✓ | ✓ | ✓ | ✓ | MPM | ||||
| ✓ | ✓ | ✓ | ✓ | MP1 | ||||
| Parameters | |
|---|---|
| : | Number of sub-set of requests, . |
| t: | Iterator of the global optimization process, . |
| : | Set of network nodes, . |
| : | Set of network links, where . |
| : | Status of slots at iteration t, , if the i-th slot of the link l is busy, then = 1, otherwise 0. |
| : | Number of slots available per link in the network. |
| : | Set of requests, where , is source node, is destination node, and is requested bandwidth. |
| : | Sub-set of requests to be installed at iteration t, . |
| : | Sub-set of requests already installed up to iteration , . |
| : | Set of available modulation format, where , T is the transmission range and R is the modulation rate. |
| : | Number of available paths per requests. |
| K: | Maximum number of traffic sub-flows allowed per request, 1 ≤ K ≤ . |
| : | Set of paths available for the request s, where . |
| : | Set of available paths of the request s that use the link , . |
| : | Number of slots for guard-band. |
| C: | Bandwidth of one slot with BPSK base modulation. |
| : | Length of a link l, . |
| : | Length of a path , . |
| : | Number of slots assigned to path , . |
| : | Number of slots assigned to request with modulation , . |
| : | Number of slots busy in the link l at the iteration t, . |
| : | Weight of the sum in objective function in RML phase, . |
| : | Set of outgoing links from node v, . |
| : | Set of incoming links to node v, . |
| : | Number of slots assigned to the already installed request in the , . |
| Variables | |
| : | Maximum slot obtained in the RML phase, . |
| : | Maximum slot obtained in SA phase, . |
| B: | Total number of slots used in the network, . |
| : | Number of slots used in the link l, |
| : | Traffic flow rate of request s on the path , . |
| : | Traffic flow rate of request s on the path with modulation format m, . |
| : | Binary variable, if the path is used, then = 1, otherwise 0. |
| : | Binary variable, if the path with modulation format m is used, then = 1, otherwise 0. |
| : | Binary variable, if the path with modulation format m uses the link l, then , otherwise 0. |
| : | Binary variable, if modulation format m is assigned to the path , then , otherwise 0. |
| : | Number of slots used by the path with modulation format m, . |
| : | Number of slots used by the link l of the path with modulation format m,. |
| : | First index of a slot block assigned to the path , . |
| : | Binary variable, if , then = 1, otherwise 0. |
| Phases | Models | |||
|---|---|---|---|---|
| MPM | 1PM | MP1 | 1P1 | |
| RML | (1)–(7) | (1)–(7) | (1)–(7) | (1)–(7) |
| SA | (26)–(38) | (26), (27), (29)–(33) | (26)–(38) | (26), (27), (29)–(33) |
| Model Parameters | ||||
| K | ||||
| Phases | MLM | 1LM | ML1 | 1L1 |
|---|---|---|---|---|
| RML | (8)–(24) | (8)–(24) | (8)–(24) | (8)–(24) |
| SA | (26)–(38) | (26), (27), (29)–(33) | (26)–(38) | (26), (27), (29)–(33) |
| Model Parameters | ||||
| K | ||||
| Setting | Variables and Constraints | Proportional Amount | Asymptotic Notation |
|---|---|---|---|
| RML-MPM | Integer Variables | ||
| Constraints | |||
| RML-MLM | Integer Variables | ||
| Constraints | |||
| SA | Integer Variables | ||
| Constraints |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maidana Benítez, L.V.; Villamayor Paredes, M.M.R.; Colbes, J.; Bogado-Martínez, C.F.; Barán, B.; Pinto-Roa, D.P. Routing, Modulation Level, and Spectrum Assignment in Elastic Optical Networks—A Serial Stage Approach with Multiple Sub-Sets of Requests Based on Integer Linear Programming. Math. Comput. Appl. 2023, 28, 67. https://doi.org/10.3390/mca28030067
Maidana Benítez LV, Villamayor Paredes MMR, Colbes J, Bogado-Martínez CF, Barán B, Pinto-Roa DP. Routing, Modulation Level, and Spectrum Assignment in Elastic Optical Networks—A Serial Stage Approach with Multiple Sub-Sets of Requests Based on Integer Linear Programming. Mathematical and Computational Applications. 2023; 28(3):67. https://doi.org/10.3390/mca28030067
Chicago/Turabian StyleMaidana Benítez, Luis Víctor, Melisa María Rosa Villamayor Paredes, José Colbes, César F. Bogado-Martínez, Benjamin Barán, and Diego P. Pinto-Roa. 2023. "Routing, Modulation Level, and Spectrum Assignment in Elastic Optical Networks—A Serial Stage Approach with Multiple Sub-Sets of Requests Based on Integer Linear Programming" Mathematical and Computational Applications 28, no. 3: 67. https://doi.org/10.3390/mca28030067
APA StyleMaidana Benítez, L. V., Villamayor Paredes, M. M. R., Colbes, J., Bogado-Martínez, C. F., Barán, B., & Pinto-Roa, D. P. (2023). Routing, Modulation Level, and Spectrum Assignment in Elastic Optical Networks—A Serial Stage Approach with Multiple Sub-Sets of Requests Based on Integer Linear Programming. Mathematical and Computational Applications, 28(3), 67. https://doi.org/10.3390/mca28030067







