Abstract
Simulated annealing is a metaheuristic that balances exploration and exploitation to solve global optimization problems. However, to deal with multi- and many-objective optimization problems, this balance needs to be improved due to diverse factors such as the number of objectives. To deal with this issue, this work proposes MOSA/D, a hybrid framework for multi-objective simulated annealing based on decomposition and evolutionary perturbation functions. According to the literature, the decomposition strategy allows diversity in a population while evolutionary perturbations add convergence toward the Pareto front; however, a question should be asked: What is the effect of such components when included as part of a multi-objective simulated annealing design? Hence, this work studies the performance of the MOSA/D framework considering in its implementation two widely used perturbation operators: classical genetic operators and differential evolution. The proposed algorithms are MOSA/D-CGO, based on classical genetic operators, and MOSA/D-DE, based on differential evolution operators. The main contribution of this work is the performance analysis of MOSA/D using both perturbation operators and identifying the one most suitable for the framework. The approaches were tested using DTLZ on two and three objectives and CEC2009 benchmarks on two, three, five, and ten objectives; the performance analysis considered diversity and convergence measured through the hypervolume (HV) and inverted generational distance (IGD) indicators. The results pointed out that there is a promising improvement in performance in favor of MOSA/D-DE.
1. Introduction
In the real world, optimization problems have multiple objectives that conflict. In other words, when we attempt to optimize one of these objectives, the rest is affected negatively. These problems are called Multi-Objective Optimization Problems (MOPs). A MOP is defined as follows:
where represents the decision space and represents the decision vector (solution). denotes the ith objective obtained from the decision vector . Evolutionary multi-objective optimization (EMO) is a research area concerned with ways to solve MOPs. The EMO algorithms perform well when the MOPs have two or three objectives. In EMO, the main algorithms proposed are based on Pareto dominance. In particular, these algorithms have been successfully detecting well-converged and well-diversified non-dominated solutions [1]. However, the number of real-world optimization problems is many times more than three. MOPs with four or more objectives are often referred to as many-objective optimization problems (MaOPs) [1,2]. Pareto dominance has been the key to the success of EMO algorithms in MOPs with two and three objectives, but the results are different in the case of MaOPs. The reason is that the selective pressure toward the Pareto front (PF) in MaOPs is insufficient using Pareto dominance. The use of EMOs based on Pareto dominance for MaOPs makes some issues evident, such as (i) deterioration of the searchability due to the increase in the number of objectives [3], (ii) exponential increase in the number of solutions required for approximation of the entire PF, and (iii) difficulty in visualizing the solutions. These issues are open areas of study and have led to new proposals for algorithms to solve MaOPs. Several algorithms that deal with MOPs and MaOPs in the literature use strategies such as the hybridization of heuristics and meta-heuristics strategies. When one algorithm approach is proposed as a strategy that combines a set of meta-heuristics, and these perform together, producing a profitable synergy, it is called Hybrid Meta-heuristic HM [4], HM also known as hybrid algorithm [5]. The hybrid algorithms have the advantage of dealing with complexity, noise, imprecision, uncertainty, and vagueness present in real-world optimization problems [4].
Strategies such as decomposition, simulated annealing and evolutionary genetic operators are approaches that together had produced profitable hybrid algorithms in recent years. Decomposition is an approach that has been applied to MaOPs with success. It is a strategy that divides a MOP into several single-objective sub-problems solved simultaneously. In addition, Bechikh et al. assert that decomposition is the most successful approach to solving MaOPs [6]. One algorithm based on decomposition is MOEA/D [7]. It is easy to apply the single-objective optimizer to the sub-problem associated with each solution while maintaining the solution dispersed [8]. Three advantages are obtained with the application of decomposition: it improves population diversity, allows for parallelism, and speeds up the solution [8]. Regularly, MOEA/D is the base of numerous new algorithms, though hybridized with other strategies. For example, Simulated Annealing (SA) obtained promising results in a new MOEA/D hybrid algorithm [9]. In the hybrid algorithm, SA worked as a Local Search (LS) strategy applied to the sub-problems. Simulated annealing (SA) is a probabilistic LS method for global optimization problems that allows gradual convergence to a near-optimal solution [10]. SA is a metaheuristic that adds exploration and exploitation to solve global optimization problems. SA is a well-known single-objective optimization algorithm that has been applied in hybrid algorithms such as LS strategy [9] and a selection mechanism [11] in other works. Differential evolution (DE) is a state-of-the-art global optimization technique [12]. This is an evolutionary algorithm (EA) with a classical EA framework, but it differs from other EAs in its mutation operator. It mutates the base vectors with scaled population-derived difference vectors and, as generations pass, these differences tend to adapt to the natural scaling of the problem [12]. Mutation in the DE context is interpreted as change or perturbation that involves random elements. Mutation in combination with the crossover (binomial or exponential crossover) is a strategy that improves the diversity and convergence of the population. As a mechanism of recombination, DE has shown promising results in hybrid algorithms [13,14,15].
A selection of relevant works related with the present work is described in the next lines. The adaptive evolutionary multi-objective approach based on decomposition (EMOSA) was presented by Li and Landa-Silva [9]. It combines SA with the MOEA/D algorithm [7]. EMOSA follows the concept of a population and external population (archive) of non-dominated solutions. Li and Landa-Silva mention that competition between individuals is essential to balance diversity and convergence. For this reason, when the current solution is updated, different criteria are used for population and external population. Dominance, the Tchebycheff aggregation function, and -dominance are used to update the neighborhood, the population, and the external population, respectively. MOEA/D-DE was proposed by Li and Zhang [13]. The algorithm is a combination of the MOEA/D framework and Differential Evolution operators. MOEA/D-DE and NSGA-II [16] were tested with complicated Pareto sets shapes. MOEA/D-DE showed much better results improving NSGA-II. Chen et al. [17] extended MOEA/D-DE, replaced the (1) DE operator with a guided mutation, and (2) implemented a new update mechanism. Various combinations of the mechanisms were proved using the instances of the CEC2009 benchmark [18]. In the work of Liu et al. [16], MOEA/D-DE was improved with two mechanisms: (1) using neighborhood information in the update strategy, and (2) adopting a random scale factor to improve the searchability of MOEA/D-DE. This approach was tested with instances from the CEC2009 benchmark and the real-world problem sizing of folded cascode amplifier. Mashwani et al. [14] suggested a strategy based on MOEA/D and using multiple crossover operators called HAEA/D. This strategy uses an adaptive operator of selection to apply different crossover operators (DE, CMX, PCX, TM, SPX, and SBX). HAEA/D was proved using the CEC2009 benchmark. Results showed that HAEAD performs better in most instances of CEC2009 regarding proximity and diversity. MODESA is a hybrid algorithm presented by Chen et al. [19]. DE algorithm is improving by using SA as a local search mechanism. The algorithm was proved using ZDT and DTLZ benchmarks. ESADE algorithm is the approach of Guo et al. [11]. In this approach, SA is used to improve the DE selection method. The primary strategy is replacing the DE greedy rule of selection with a SA rule of selection. CEC2005 benchmark was used to observe the performance of ESADE.
Focusing on some strategies that had good results in the related works, a hybrid framework called MOSA/D is proposed. According to the state-of-the-art research, the decomposition strategy allows diversity in a population [8] while evolutionary perturbations add convergence toward the Pareto front; however, a question should be considered: What is the effect of such components when included as part of a multi-objective simulated annealing design? Hence, this work studies the performance of MOSA/D considering two widely used perturbation operators in its implementation: classical genetic operators and differential evolution. The proposed algorithms are MOSA/D-CGO, based on classical genetic operators, and MOSA/D-DE, based on differential evolution operators. The main contribution of this work is the performance analysis of MOSA/D using both perturbations functions and identifying the one most suitable to the framework.
This paper is organized as follows. In Section 2, the primary strategies within the MOSA-D framework are provided. In addition, in this section, the proposed MOSA/D-CGO and MOSA/D-DE are described. Section 3 describes the experimental setup. Section 4 reports the experimental results. Finally, Section 5 concludes the paper with some future directions.
2. Materials and Methods
This section describes the main strategies used by the algorithms MOSA/D-CGO and MOSA/D-DE. Both algorithms are inspired by the works of Li and Landa-Silva [9] and Engrand [20]. Strategies such as decomposition, competition between individuals, and the logarithmic composite objective function are part of MOSA/D-CGO and MOSA/D-DE. However, the mentioned methods do not focus on the perturbation function as a strategy. For this reason, both algorithms implement perturbation functions to add convergence toward the PF. MOSA/D-CGO is based on classical genetic operators, while MOSA/D-DE is based on differential evolution operators. Maintaining a simple algorithm structure such as the classical SA is also considered (Algorithm 1).
The proposal to transform the classical SA framework into a multi-objective simulated annealing based on the decomposition framework has three main components:
- (1)
- decomposition strategy,
- (2)
- perturbation function, and
- (3)
- probability of acceptance.
2.1. Decomposition Strategy
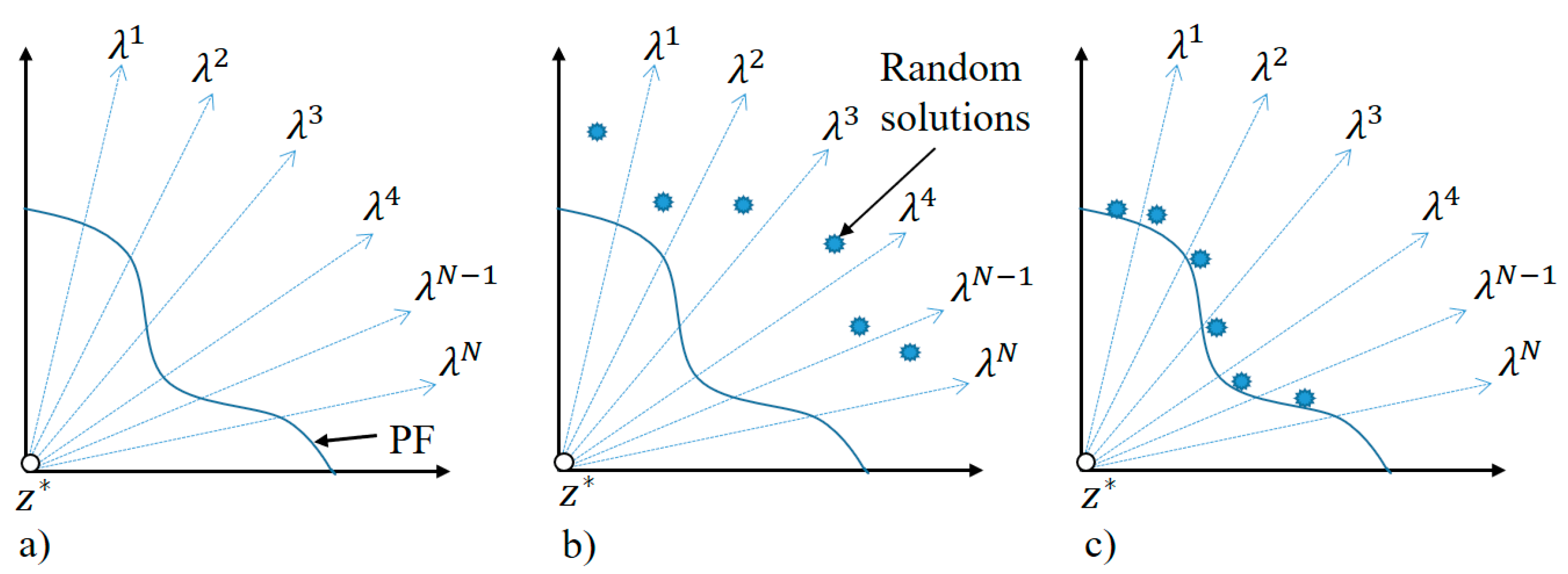
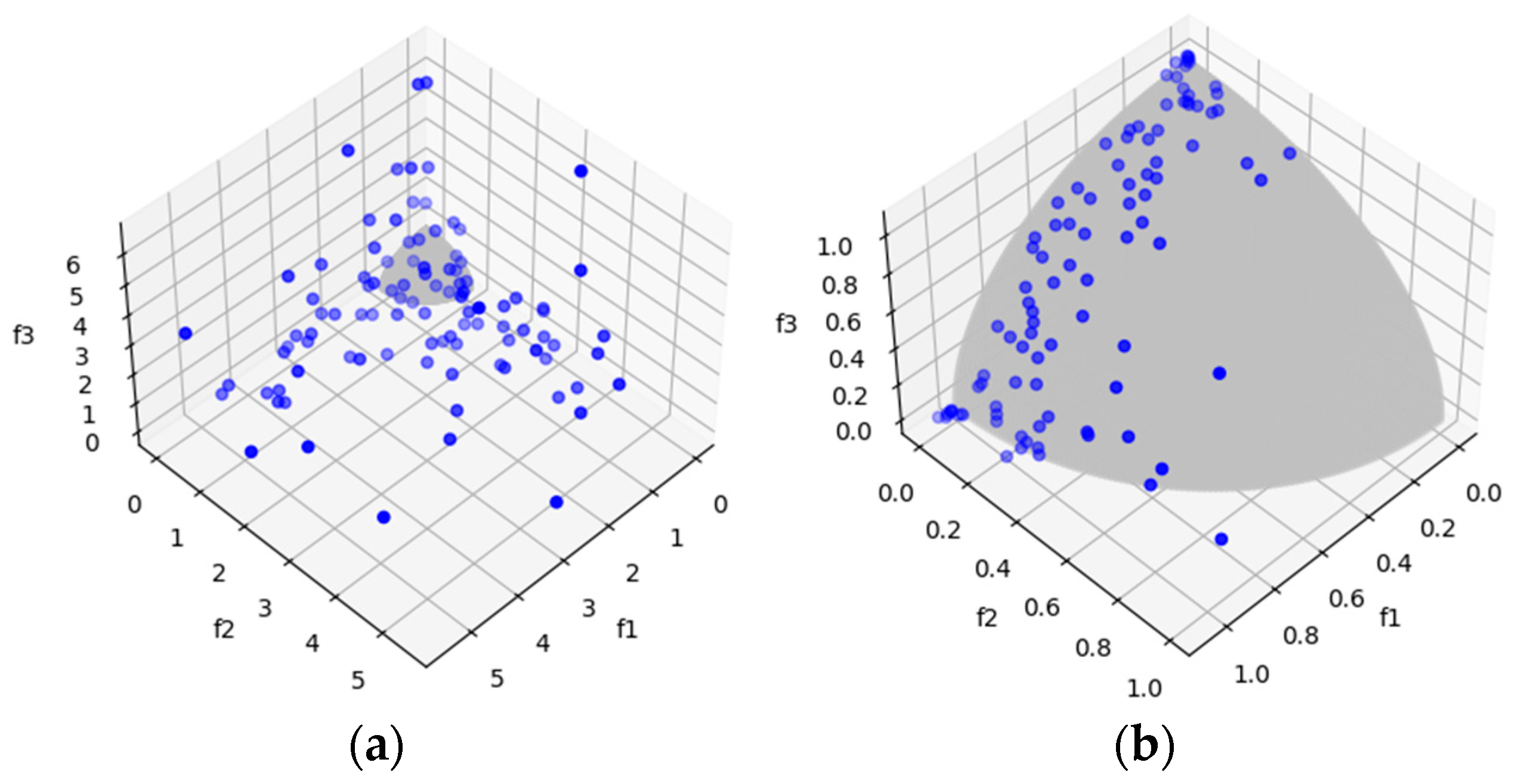
A strategy based on MOEA/D [7] is proposed to divide a MOP into N scalar sub-problems. To divide a MOP, a set of weight vectors (Figure 1) and an aggregation function (Equation (2)) are used.
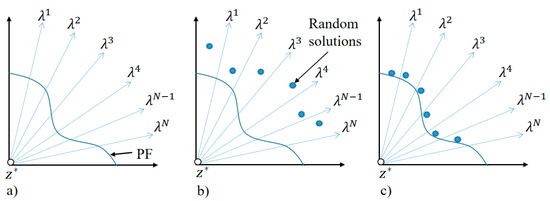
Figure 1.
Decomposition strategy. (a) A MOP is divided into N sub-problems ; (b) N random solutions are generated; (c) over a finite number of generations, solutions are simultaneously improved.
There are a number of aggregation functions; one of the most popular is the Tchebycheff function. Let be a weight vector, then the Tchebycheff approach is defined as
where m is the number of objectives, is the reference point, is the decision variable space, and is a solution for the ith sub-problem. To improve the solutions for ith sub-problem, a search method such as local search (simulated annealing) must be used and the candidate solutions compared in terms of the Tchebycheff function.
2.2. Perturbation Function
The perturbation function in simulated annealing explores the neighborhood of the current solution to determine a new candidate solution. Classically, the perturbation function uses a random exploration of the neighborhood [21,22,23]. Two approaches are chosen to create the perturbation function: classical genetic operators and differential evolution.
2.2.1. Classical Genetic Operators
Simulated binary crossover (SBX). SBX creates two-children solutions from two-parent solutions. To create the solutions, it is necessary to follow the procedure described below:
Step 1. Choose a uniform random number .
Step 2. Calculate spread factor using the equation
where is the distribution index, which is a non-negative real number.
Step 3. The children’s solutions can be computed using the following equations:
Polynomial mutation. The idea behind mutation operation is to restore unexpected genetic individuals to avoid local optimal solutions and thus enhance the exploration ability and population diversity. It operates as follows:
where is the child solution and is the parent solution, and are the upper and lower bounds of the parent component. Finally, is a function of (random number) and (mutation distribution index), as follows:
2.2.2. Differential Evolution Operators
This pair of operators is used in a different order from the previous operators. First, the mutation must be calculated; then, the crossover must be executed.
Rand/1 mutation. Rand/1 is a basic mutation of the most popular mutation strategies in differential evolution (DE) [24]. It operates as follows:
In Equation (8), , , represent three random solutions of the population at the generation G, and represents a new mutant solution. is a parameter called the scale factor.
Binomial crossover. After mutation, a crossover operation is performed between the target vector and the mutant vector to produce a trial vector . The binomial crossover operator is mainly used, and it is defined as
In Equation (9), represents the crossover rate, and represents the minimum difference between the target vector and the trial vector .
2.3. Probability of Acceptance
The Boltzmann probability in the classical SA is used to accept or refuse one solution. When the solution is accepted, it has a good probability of guiding new solutions and escaping from local optimal solutions. We propose the probability function in MOSA/D of the work of Engrand [20] that uses a multi-objective version of the Boltzmann probability. It uses a logarithm compositive function. According to Engrand, a new function G is defined as
The probability of acceptance p is defined by
Then, Equation (10) is added into Equation (11):
Using factoring and logarithm identities, the probability of acceptance is expressed in the following way:
where m is the number of objectives, Xn is the current solution, Xn+1 is the candidate solution, and Tk is the current temperature of the algorithm.
2.4. Multi-Objective Simulated Annealing Based on Decomposition Framework
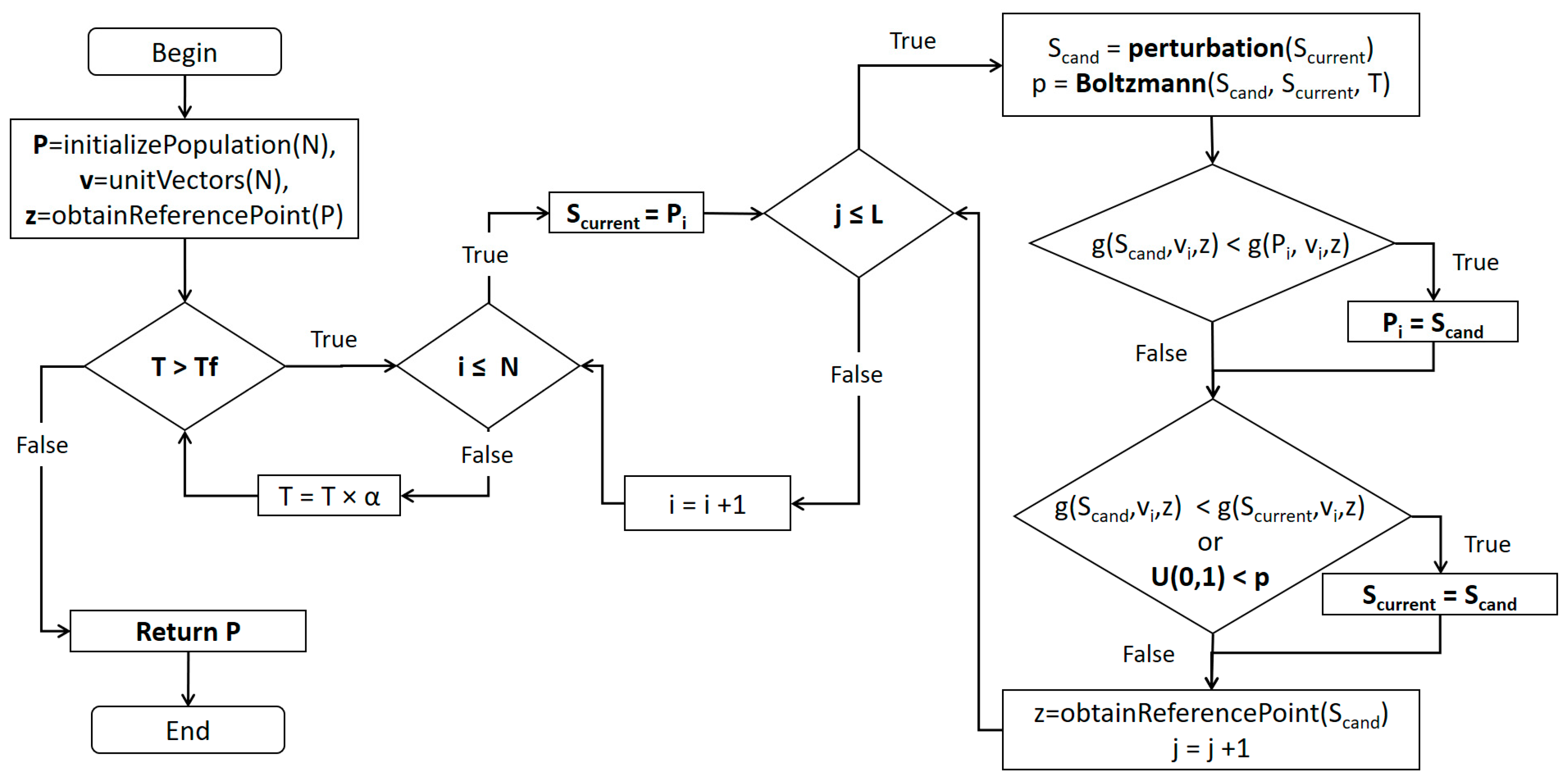
The multi-objective simulated annealing based on decomposition (MOSA/D) framework is based on simulated annealing, decomposition strategy from MOEA/D [7], and perturbation functions based on genetic operators (classical and DE operators). The MOSA/D framework (Figure 2) takes a multi-objective optimization problem (MOP) and decomposes it into a set of N sub-problems represented by a set of N weight vectors. Then, ith sub-problem is annealed by L executions at a temperature level of T, obtaining new solutions by a function of perturbation using crossover and mutation operations. The algorithm maintains a population of efficient solutions (P). When a new solution is obtained, it is evaluated to update the efficient solution (Pi) associated with the ith sub-problem. Additionally, the framework maintains a solution to explore the feasible surface of ith sub-problem. To update this solution, an evaluation is necessary with the new solution. Both evaluations of the new solution against the efficient and the exploring solution are conducted using the Tchebycheff approach. Tchebycheff approach avoids the use of Pareto dominance in the MOSA/D framework. Furthermore, the framework has a mechanism to escape from local optimums based on a logarithm compositive function. Finally, the perturbation functions are a novel part of the framework. Two algorithms are derived due to the perturbation functions: MOSA/D-CGO and MOSA/D-DE. We intend to observe the performance of both approaches in continuous multiple- and many-objective problems.
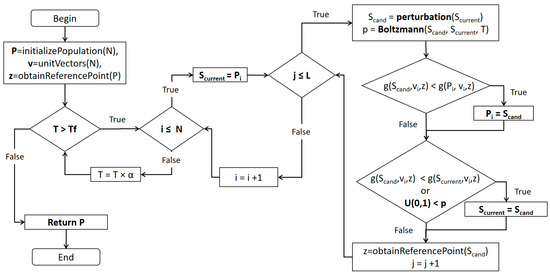
Figure 2.
MOSA/D framework flowchart.
2.4.1. MOSA/D-CGO Algorithm
The MOSA/D-CGO pseudocode is described by Algorithm 1. The algorithm receives as input the multi-objective problem to be solved, the initial temperature Ti, the final temperature Tf, the time factor α, the size of the population N, and the maximum number of MFE evaluations that it will carry out. The last generation of the population (P) represents the output. The algorithm initializes the random population P of size N, the sub-problems represented by weight vectors v of size N, the temperature T = Ti, the Scurrent solution serving as a guide in the search process, and the Scand solution, which is generated from disturbances on Scurrent, the calculation of z (reference point). FE = N is updated because it is the size of the initial population (Lines 1 and 2). From Line 3, Algorithm 1 has three loops: the first, second, and third (Lines 3, 4, and 6, respectively).
| Algorithm 1 MOSA/D-CGO | |
| Input: MOP, Initial temperature Ti, Factor α, Markov chain L, Final temperatura Tf, Size of population N, Maximal function evaluations MFE | |
| Output: Last generation of P | |
| 1 | To initialize: population P(N), weighted vectors v, solution Scurrent, solution Scand, reference point z, temperature T = Ti |
| 2 | FE = N |
| 3 | while (T ≥ Tf) y (FE ≤ MFE) |
| 4 | for i = 1 to N |
| 5 | Scurrent = Pi |
| 6 | for j = 1 to L |
| 7 | Scand = PerturbationCGO(Scurrent, P) |
| 8 | p = BoltzmannProbability(Scand, Scurrent, T) |
| 9 | if g(Scand, vi, z) < g(Pi, vi, z) |
| 10 | Pi = Scand |
| 11 | if g(Scand, vi, z) < g(Scurrent, vi, z) or U(0,1) < p |
| 12 | Scurrent = Scand |
| 13 | z = ObtainReferencePoint (Scand) |
| 14 | j = j +1 |
| 15 | i = i +1 |
| 16 | FE = N × L |
| 17 | T = T × α |
| 18 | return P |
The first loop (main loop) starts (Line 3). Then, while the temperature T is greater than Tf or the maximum number of evaluations is not reached, the main loop will perform the following:
- Start a second loop that proceeds through all the sub-problems (Line 4),
- Update FE = N × L as the multiplication of the number of sub-problems by the annealing cycles (Line 16),
- The temperature T is updated. It is multiplied by the temperature drop factor α (Line 17).
- The second loop (from 1 to N sub-problems) has the following tasks (Line 4):
- The Scurrent solution takes as its value the solution stored in Pi (Line 5),
- The ith sub-problem is annealed for L cycles (Lines 6–14) in the third loop,
- The sub-problem counter i is updated.
- The third loop (annealing process) works as follows (Lines 6–14):
- Scand is obtained by perturbation of Scurrent (Line 7),
- The Boltzmann probability p of Scand is computed based on Equation (6) (Line 8),
- The Tchebycheff function g is calculated for Scand and Pi. If g (Scand) is less than g (Pi), then Scand is a better solution than Pi. Then Pi takes the value of Scand (Lines 9–10).
- The Tchebycheff function g is calculated for Scand and Scurrent. If g (Scand) is less than g (Scurrent), then Scurrent takes the value of Scand (Lines 11–12).
- The reference point z is updated (Line 13).
- The Markov chain counter j is updated (Line 14)
- At the end of the main loop, the last generation of P is returned, and the algorithm ends (Line 18).
The MOSA/D-CGO implements a perturbation function based on simulated binary crossover (SBX) and polynomial mutation. The pseudocode of PerturbationCGO(Scurrent, P) is shown in Algorithm 2. The algorithm’s input is the current solution Scurrent and the population P. At Line 1, all solutions are initialized. Next, parent1 takes the value of Scurrent (Line 2). Next, a random solution is selected from P as parent2 (Line 3). Then the SBX is applied to parent1 and parent2, producing the new solution child (Line 4). Next, the mutation operator is applied to the solution child (Line 5), producing the candidate solution. Finally, the candidate solution is returned to the main algorithm.
| Algorithm 2 PerturbationCGO | |
| Input: Current solution Scurrent, population P | |
| Output: Candidate Solution Scand | |
| 1 | Initialize solutions: parent1, parent2, child |
| 2 | parent1 = Scurrent |
| 3 | parent2 = RandomSelection(P) |
| 4 | child = SBX(parent1, parent2) |
| 5 | Scand = PolynomialMutation(child) |
| 6 | return Scand |
2.4.2. MOSAD-DE Algorithm
Algorithm 3 is the main function of MOSA/D–DE. It is the same as the MOSA/D-CGO. The difference between MOSA/D-CGO and MOSA/D–DE is the perturbation function.
| Algorithm 3 MOSA/D-DE | |
| Input: MOP, Initial temperature Ti, Factor α, Markov chain L, Final temperatura Tf, Size of population N, Maximal function evaluations MFE | |
| Output: Last generation of P | |
| 1 | To initialize: population P(N), weighted vectors v, solution Scurrent, solution Scand, reference point z, temperature T = Ti |
| 2 | FE = N |
| 3 | while (T ≥ Tf) y (FE ≤ MFE) |
| 4 | for i = 1 to N |
| 5 | Scurrent = Pi |
| 6 | for j = 1 to L |
| 7 | Scand = PerturbationDE(Scurrent, P) |
| 8 | p = BoltzmannProbability(Scand, Scurrent, T) |
| 9 | if g(Scand, vi, z) < g(Pi, vi, z) |
| 10 | Pi = Scand |
| 11 | if g(Scand, vi, z) < g(Scurrent, vi, z) or U(0,1) < p |
| 12 | Scurrent = Scand |
| 13 | z = ObtainReferencePoint (Scand) |
| 14 | j = j +1 |
| 15 | i = i +1 |
| 16 | FE = N × L |
| 17 | T = T × α |
| 18 | return P |
In Algorithm 3, Line 7 references the function PerturbationDE(Scurrent, P). Its pseudocode is shown in Algorithm 4. The algorithm begins with the initialization of all solutions used in the algorithm (Line 1). Next, the solution target takes the values of Scurrent (Line 2). The next step is to select three random solutions from the population P (Lines 3, 4, and 5). In Line 6, RandOneMutation() (based on Equation (12)) produces the mutant solution. However, the mutant solution may exceed the limit values of its decision variables. For this reason, a repair operation is necessary over the mutant solution (Line 7). Then, the binomial crossover is executed to generate the candidate solution (Scand) (Line 8). Finally, the candidate solution (Scand) is returned to Algorithm 3.
| Algorithm 4 PerturbationDE | |
| Input: Current solution Scurrent, population P | |
| Output: Candidate Solution Scand | |
| 1 | Initialize solutions: target, mutant, sol1, sol2, sol3 |
| 2 | target = Scurrent |
| 3 | sol1 = RandomSelection(P) |
| 4 | sol2 = RandomSelection(P) |
| 5 | sol3 = RandomSelection(P) |
| 6 | mutant = RandOneMutation(ind1, ind2, ind3) |
| 7 | mutant = Repair(mutant) |
| 8 | Scand = BinomialCrossover (target, mutant) |
| 9 | return Scand |
3. Experimental Setup
This section presents the experimental setup to assess our proposed approaches: MOSA/D-CGO and MOSA/D-DE. Then, both algorithms are described to analyze their performance.
Benchmark problems. The experimental design used the DTLZ [25] and CEC2009 [18]. From DTLZ benchmark, DTLZ1 to DTLZ7 were selected with 3, 5, and 10 objectives for both algorithms MOSA/D-CGO and MOSA/D-DE. The number of variables of decision was calculated by , where is the number of objectives and is set to 5, 10, and 20 for DTLZ1, DTLZ2-6, and DTLZ7, respectively. The total number of experimental instances is 42 (7 problems 3 objective configurations 2 algorithms). From CEC2009 benchmark, UF1 to UF7 were selected with 2 objectives and UF8 to UF10 with 3 objectives. For all problems, the number of decision variables was 30. The total number of experimental instances was 20 (7 problems 1 objective configurations 2 algorithms + 3 problems 1 objective configurations 2 algorithms).
Parameter settings. In general, for both algorithms, the setting of the parameter is defined in Table 1. The parameter setting for the CGO perturbation function is defined in Table 2. Finally, the parameter setting for the DE perturbation function is defined in Table 3.

Table 1.
General parameter setting.

Table 2.
Parameter setting for MOSA/D.

Table 3.
Parameter setting for MOSA/D-DE.
Performance indicator. The indicators used to measure the performance of both algorithms were hypervolume (HV) and Inverted Generational Distance (IGD). HV allows measurement of convergence and diversity with a single value. Therefore, to calculate HV as a reference point is necessary. The reference points were obtained from determining both algorithms’ maximum objective value for DTLZ1 to DTLZ7 with 3, 5, and 10 objectives (Table 4). The reference points from UF1 to UF7 (2 objectives) and UF8 to UF10 (3 objectives) are shown in Table 5. IGD allows measurement of convergence and diversity with a single value. To calculated IGD is necessary set of points of the real Pareto front.

Table 4.
Reference points for DTLZ problems used by HV calculations.

Table 5.
Reference points for CEC2009 problems used by HV calculations.
4. Results
The experimental results are reported in Table 6, Table 7, Table 8 and Table 9, and expressed as the mean and standard deviation of the HV (Table 6 and Table 7) and IGD (Table 8 and Table 9). The best value of each configuration is highlighted in gray. To observe whether there is a significant difference between the MOSA/D-CGO and MOSA/D-DE results, we employ the Wilcoxon signed-rank test with (two tails). The symbols ↑, ↓, and --- represent a significant difference in favor of MOSA/D-DE, a significant difference in favor of MOSA/D-CGO, and no significant difference between MOSA/D-CGO and MOSA/D-DE, respectively.

Table 6.
Means and standard deviation of HV results of 42 instances.

Table 7.
Means and standard deviation of HV results of 20 instances.

Table 8.
Means and standard deviation of IGD results of 42 instances.

Table 9.
Means and standard deviation of IGD results of 20 instances.
The results of Table 6 show that MOSA/D-DE outperforms MOSA/D-CGO in six out of seven instances with three objectives. For five objectives, MOSA/D-DE outperforms MOSA/D-CGO in three out of seven instances (two instances without a significant difference). Finally, for 10 objectives, MOSA/D-DE outperforms MOSA/D-CGO in four out of seven instances.
The results of Table 7 show that MOSA/D-DE outperforms MOSA/D-CGO in all instances with two objectives. For three objectives, MOSA/D-DE outperforms MOSA/D-CGO in all instances.
The results of Table 8 show that MOSA/D-DE outperforms MOSA/D-CGO in six out of seven instances with three objectives. For five objectives, MOSA/D-DE outperforms MOSA/D-CGO in four out of seven instances. Finally, for 10 objectives, MOSA/D-DE and MOSA/D-CGO provide similar results in three out of seven (one instance without a significant difference).
The results of Table 9 show that MOSA/D-DE outperforms MOSA/D-CGO in six out seven instances with two objectives. For three objectives, MOSA/D-DE outperforms MOSA/D-CGO in all instances.
4.1. DTLZ Benchmark Analysis
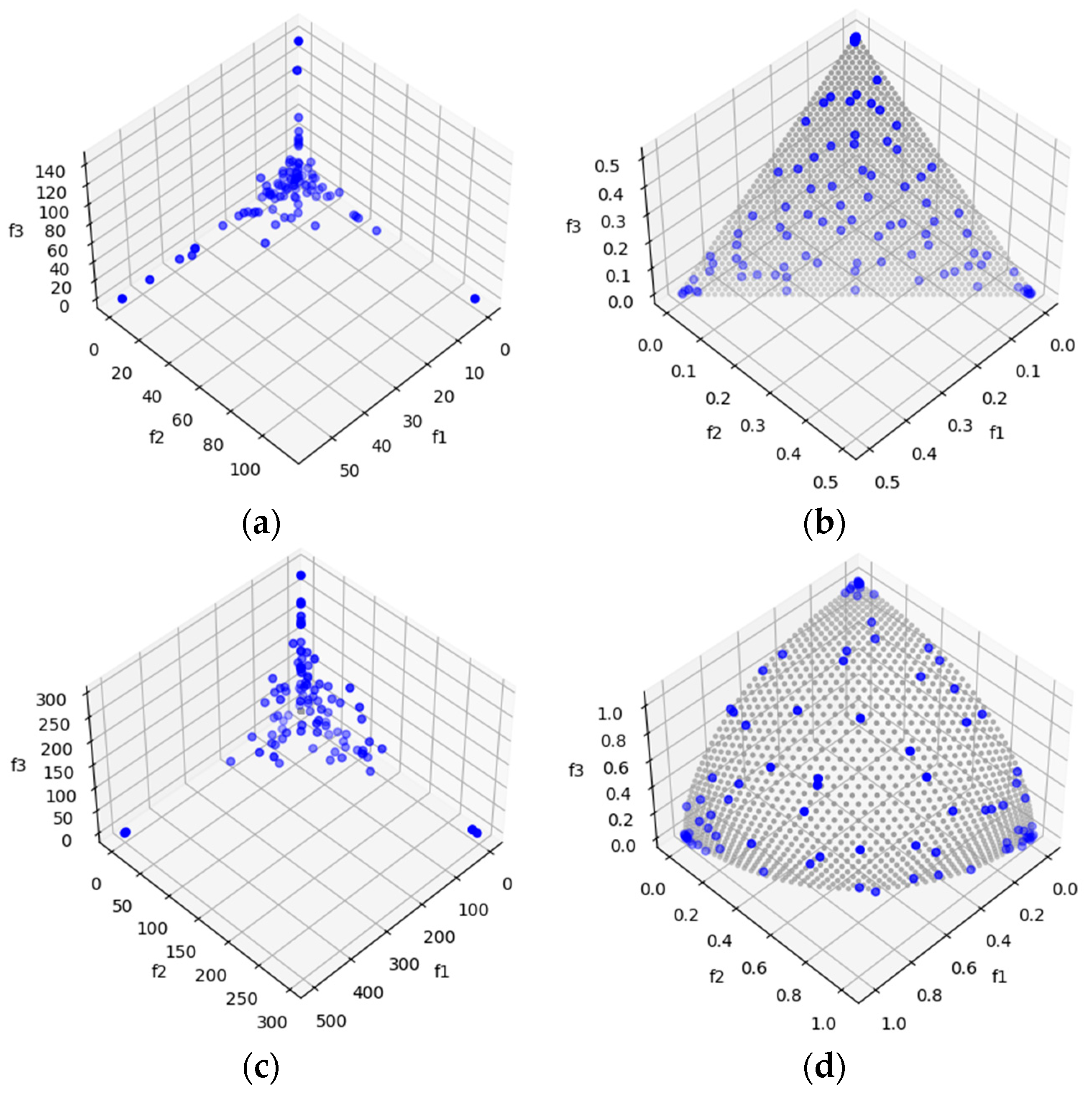
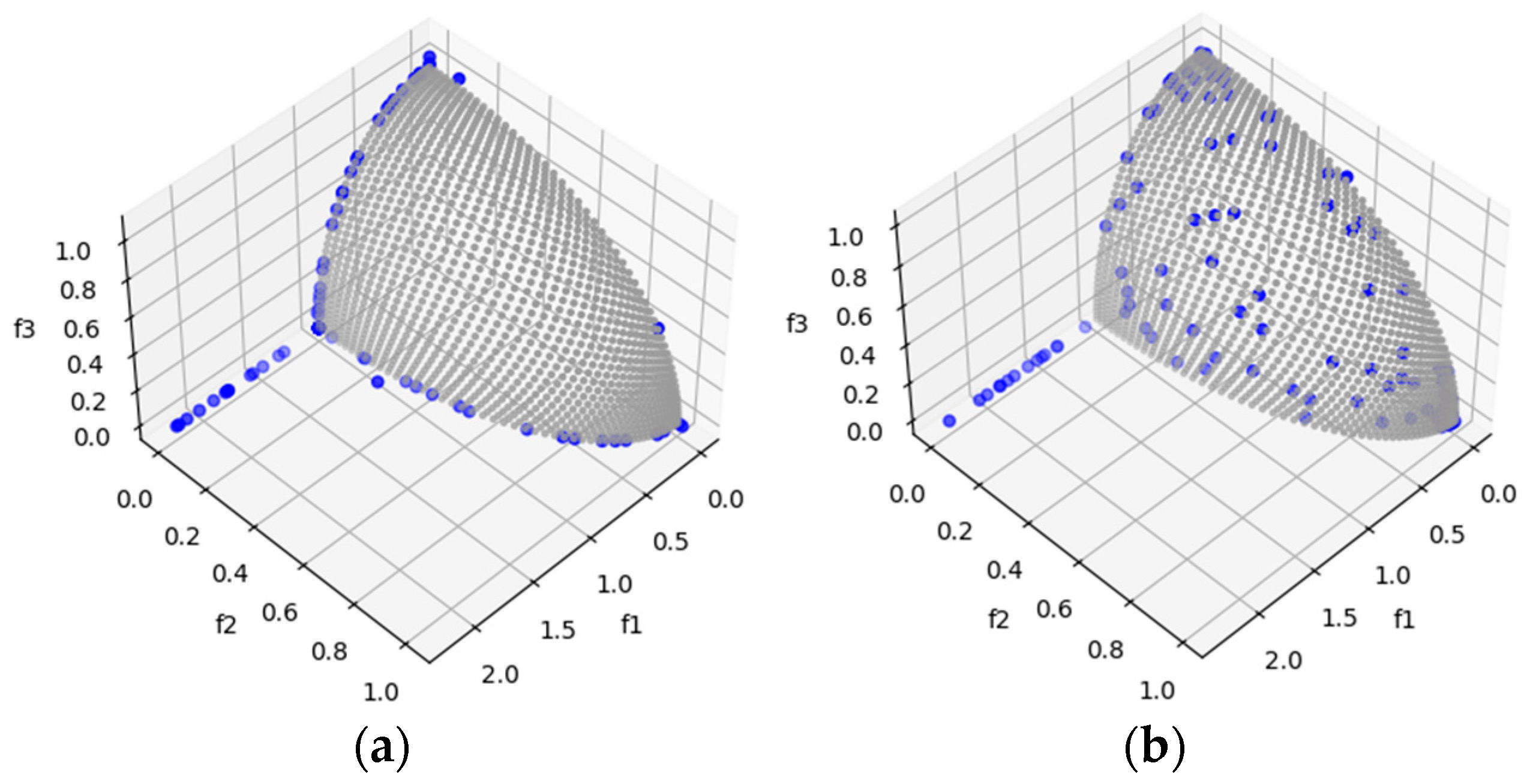
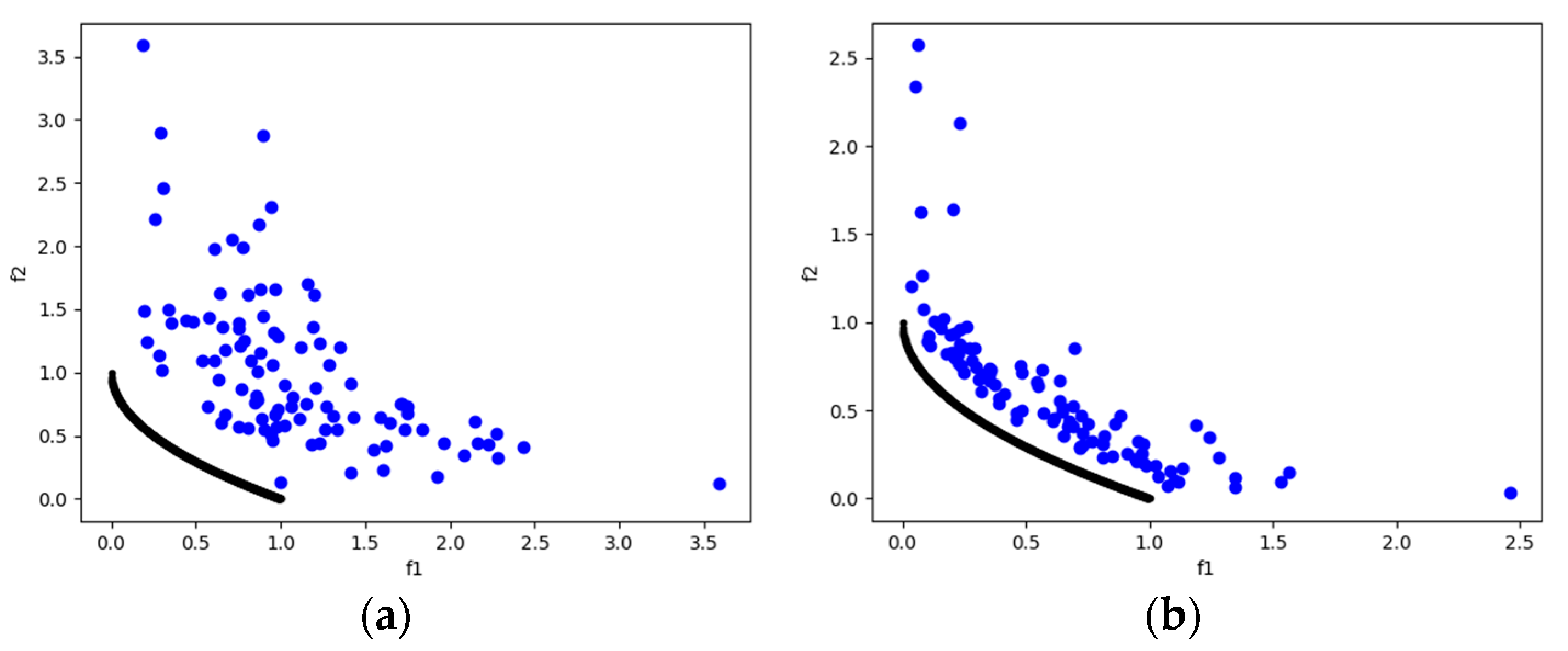
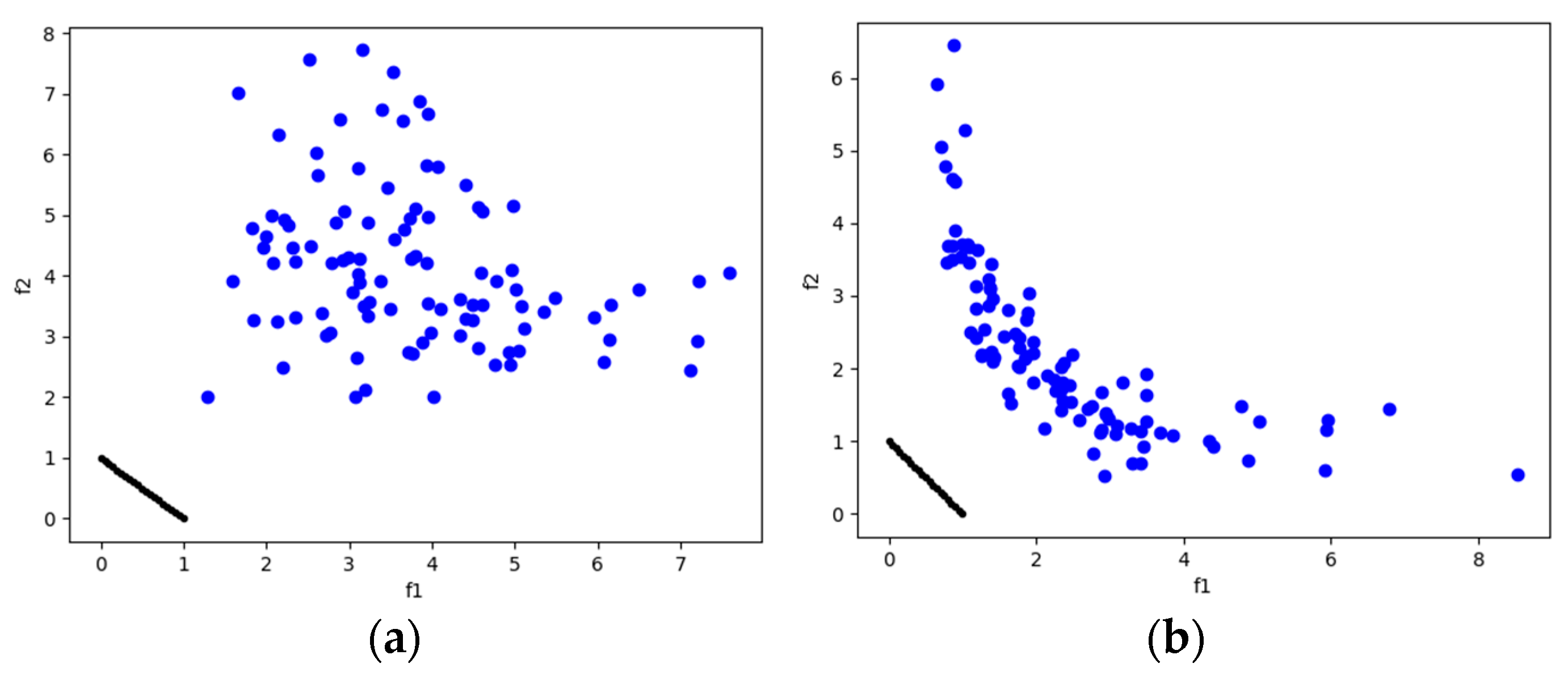
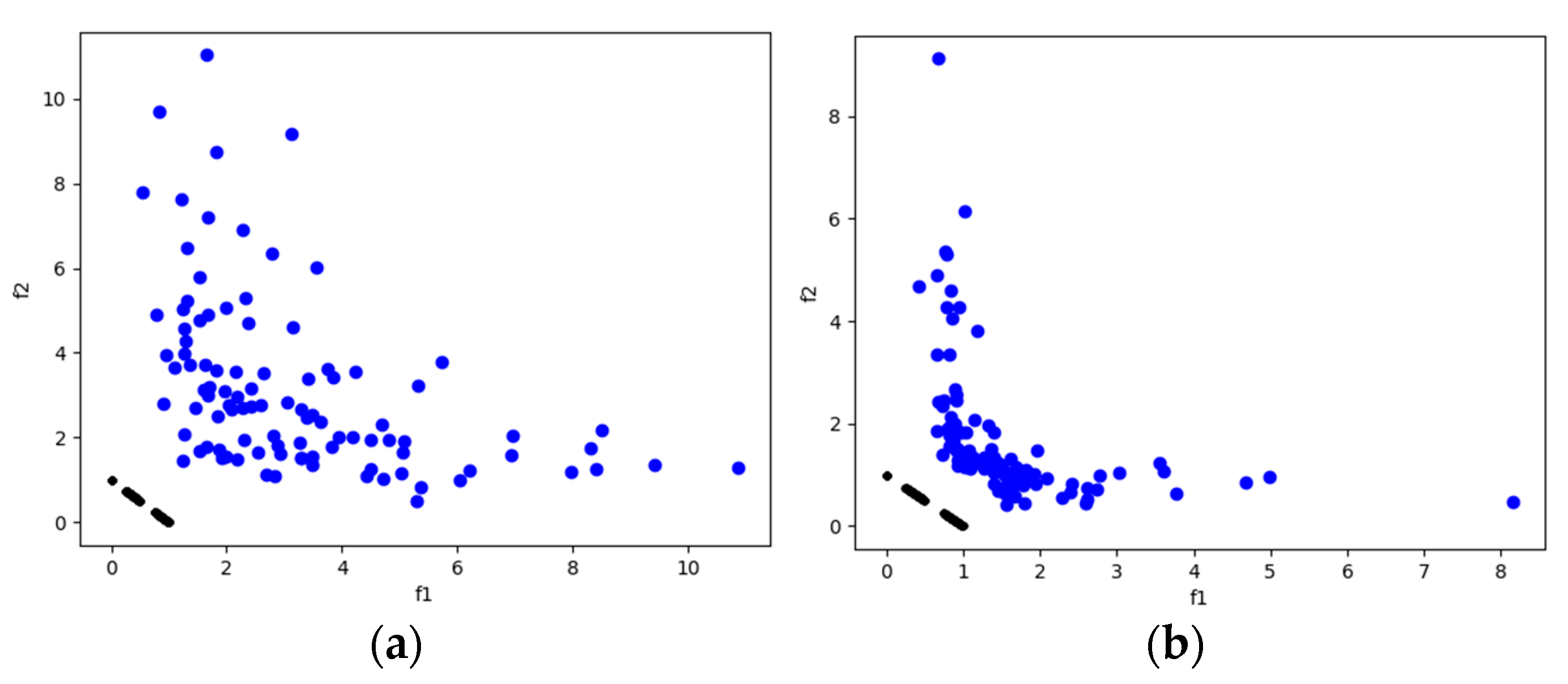
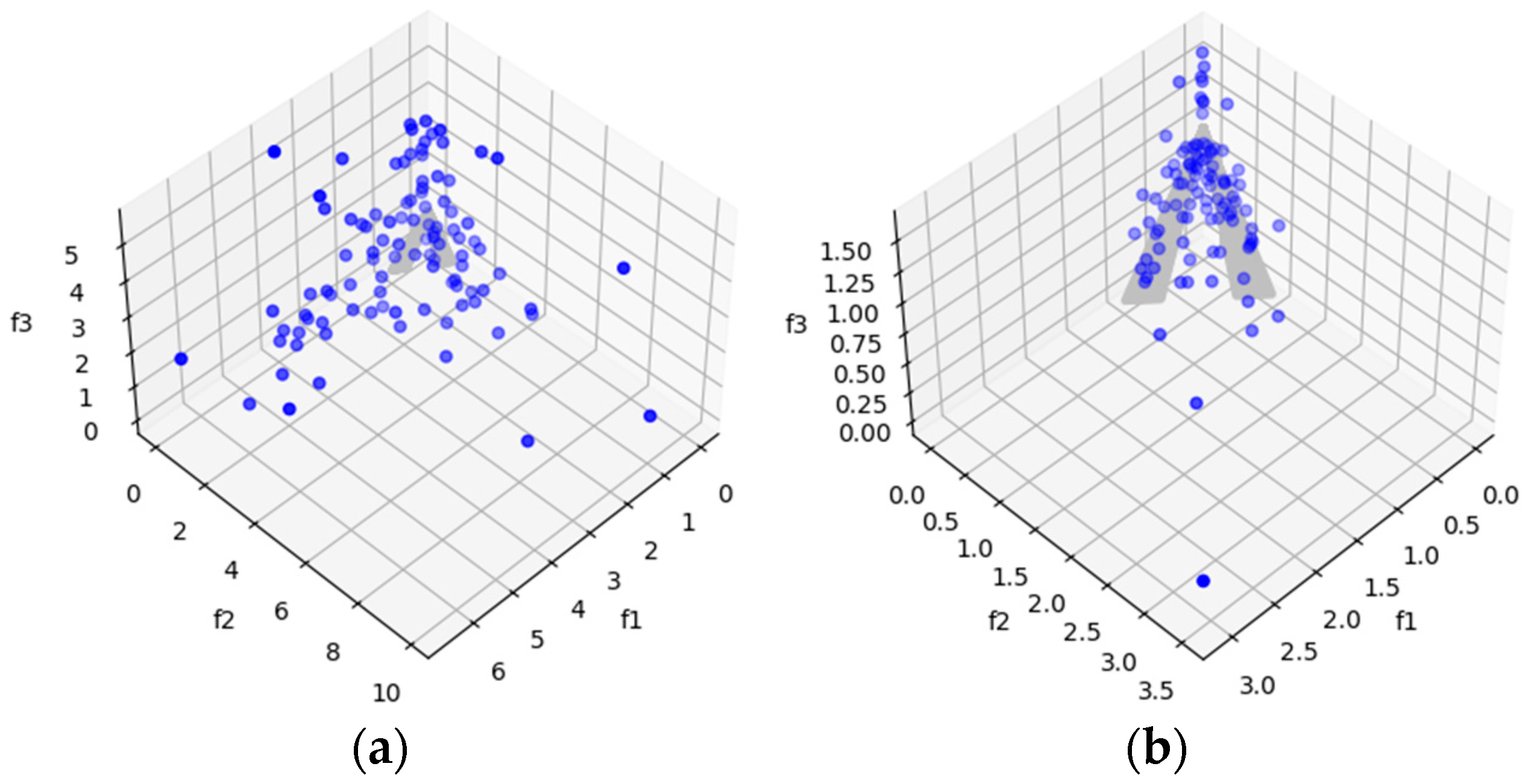
DTLZ1 and DTLZ3 are test problems with the difficulty of possessing local Pareto-optimal fronts. This allows us to observe the algorithms’ ability to escape local Pareto-optimal fronts. In this case, for both problems, MOSA/D-DE has promising HV (Table 6) and IGD (Table 8) results that outperform the MOSA/D-CGO results for three, five, and ten objectives. In Figure 3, it is possible to observe the Pareto front of DTLZ1 and DTLZ3 obtained by MOSA/D-CGO (left side) and MOSA/D-DE (right side) for three objectives. The contribution of DE allows the algorithm to escape from local Pareto-fronts better than the contribution of CGO.
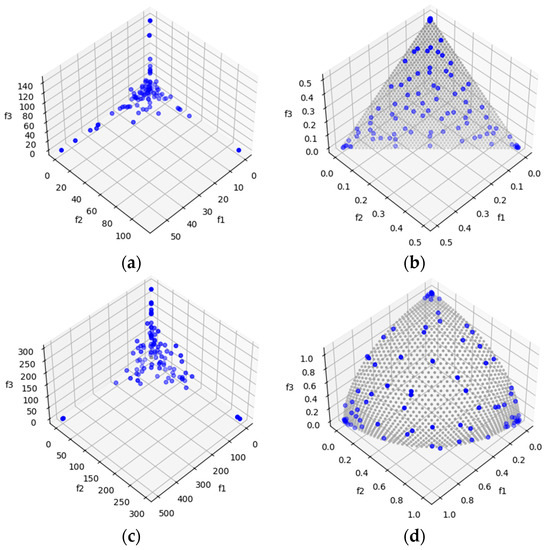
Figure 3.
The plots of the approximate PFs with the highest HV value against real PF. (a) DTLZ1 approximate PF using MOSA/D-CGO; (b) DTLZ1 approximate PF using MOSA/D-DE; (c) DTLZ3 approximate PF using MOSA/D-CGO; (d) DTLZ3 approximate PF using MOSA/D-DE.
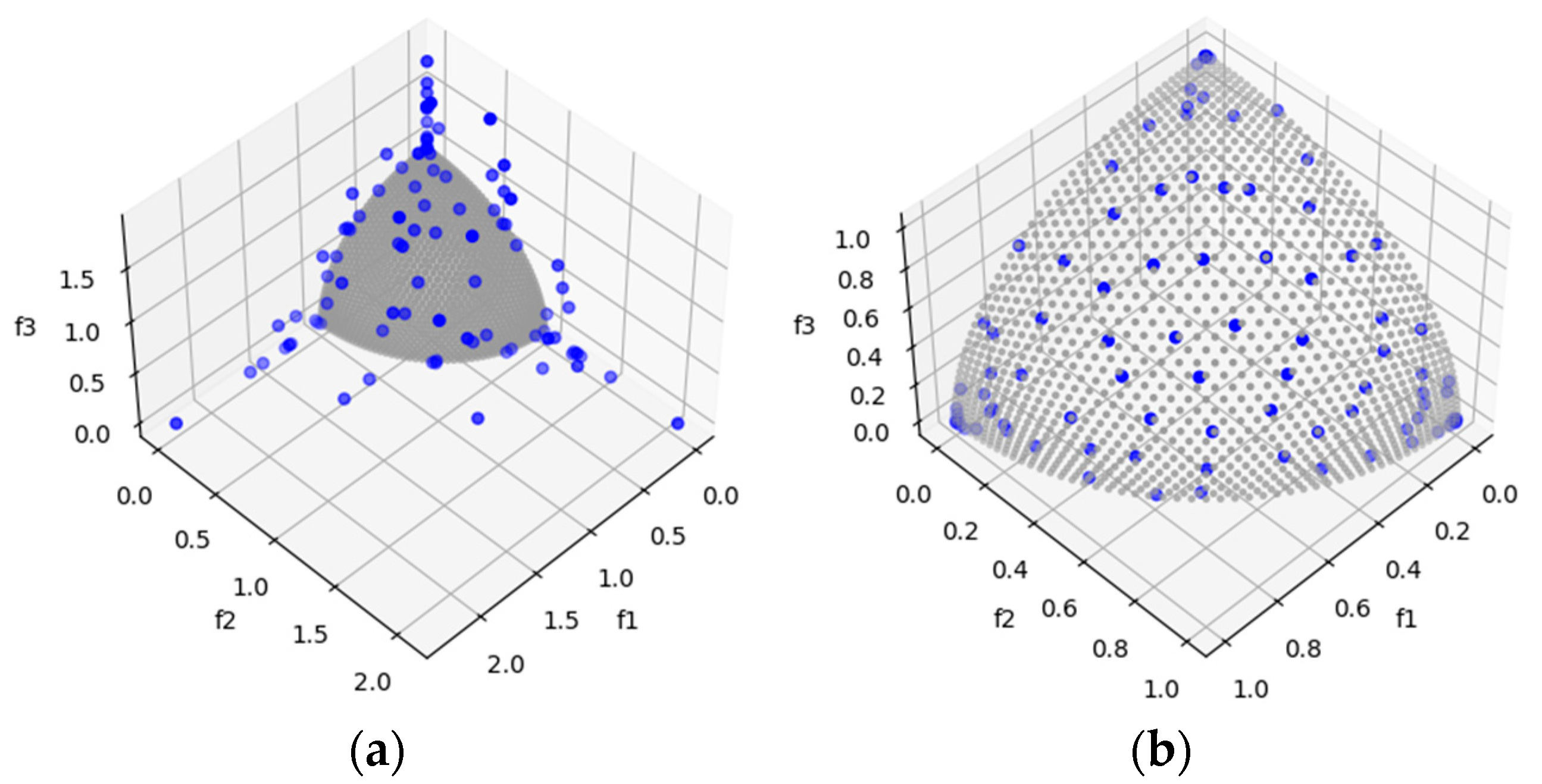
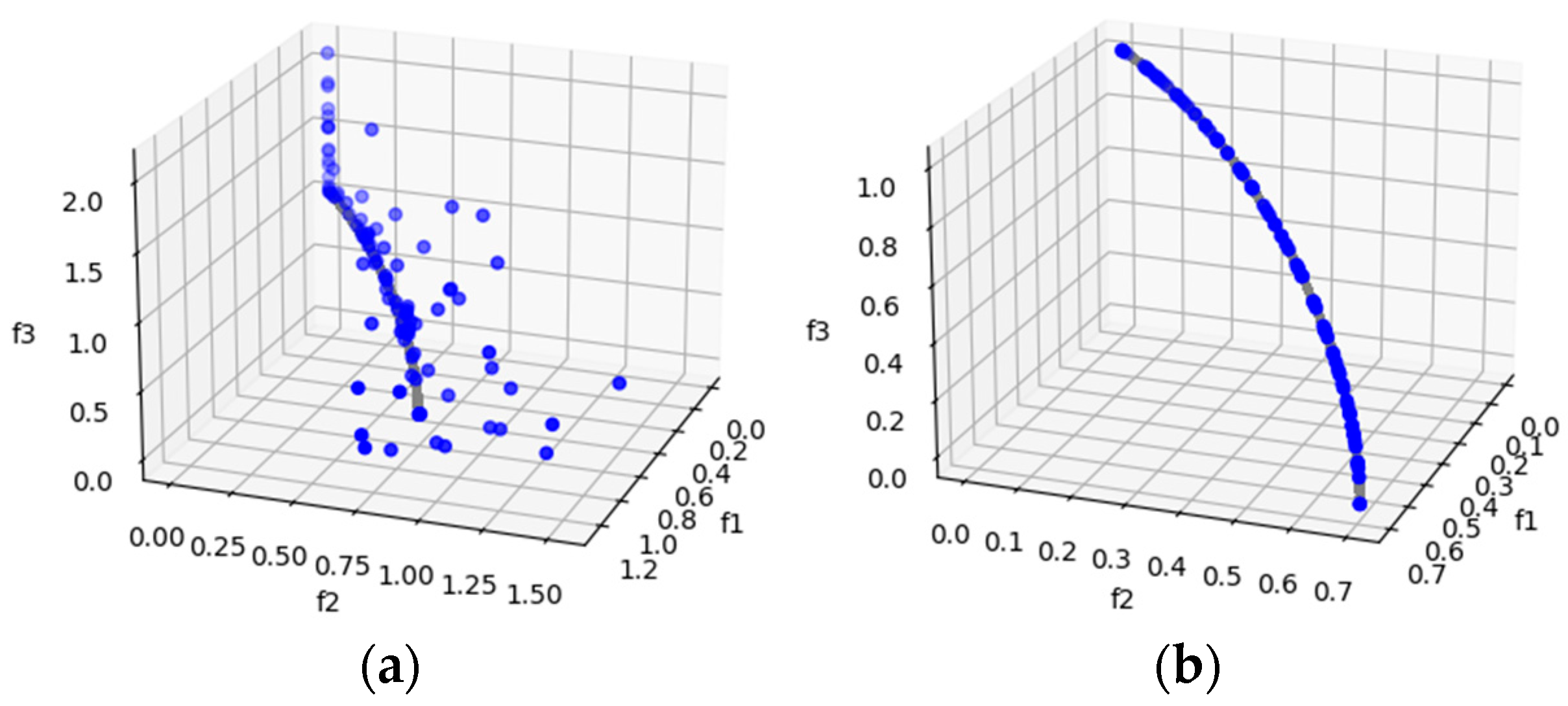
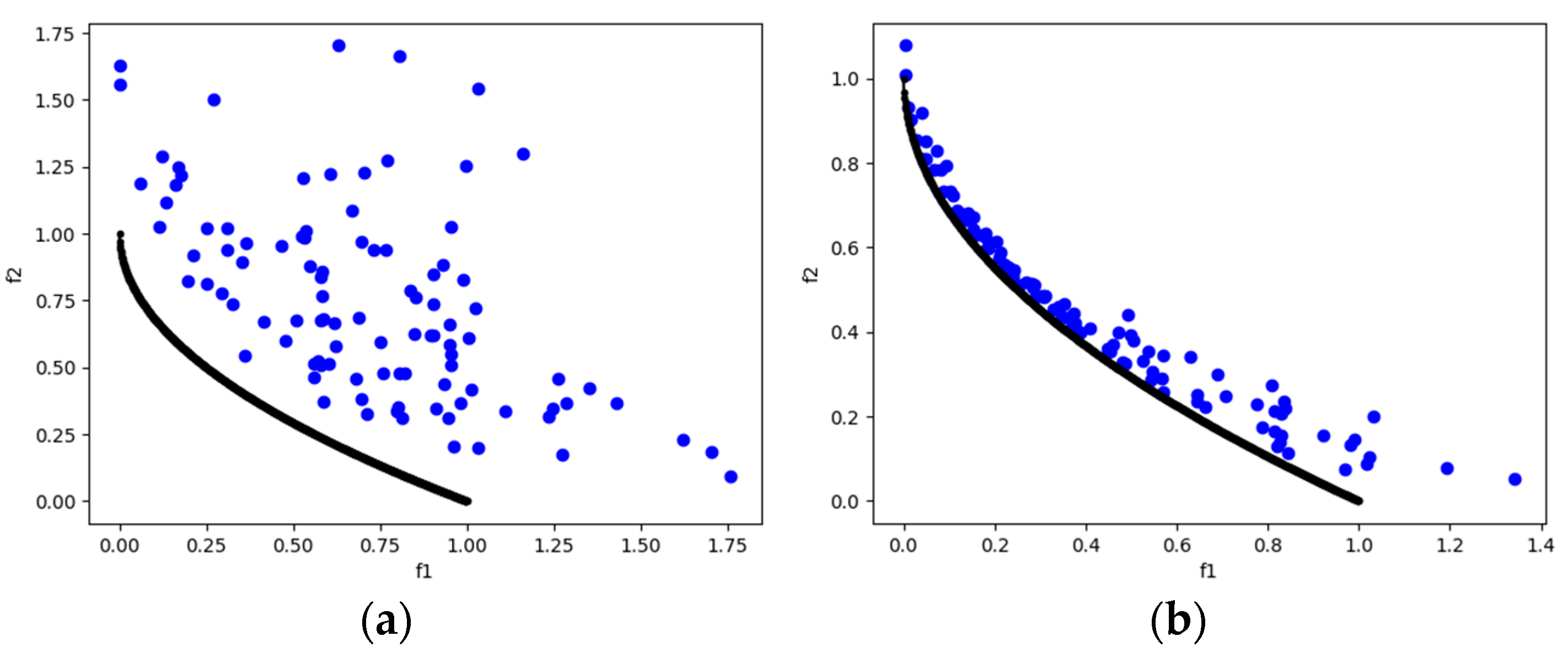
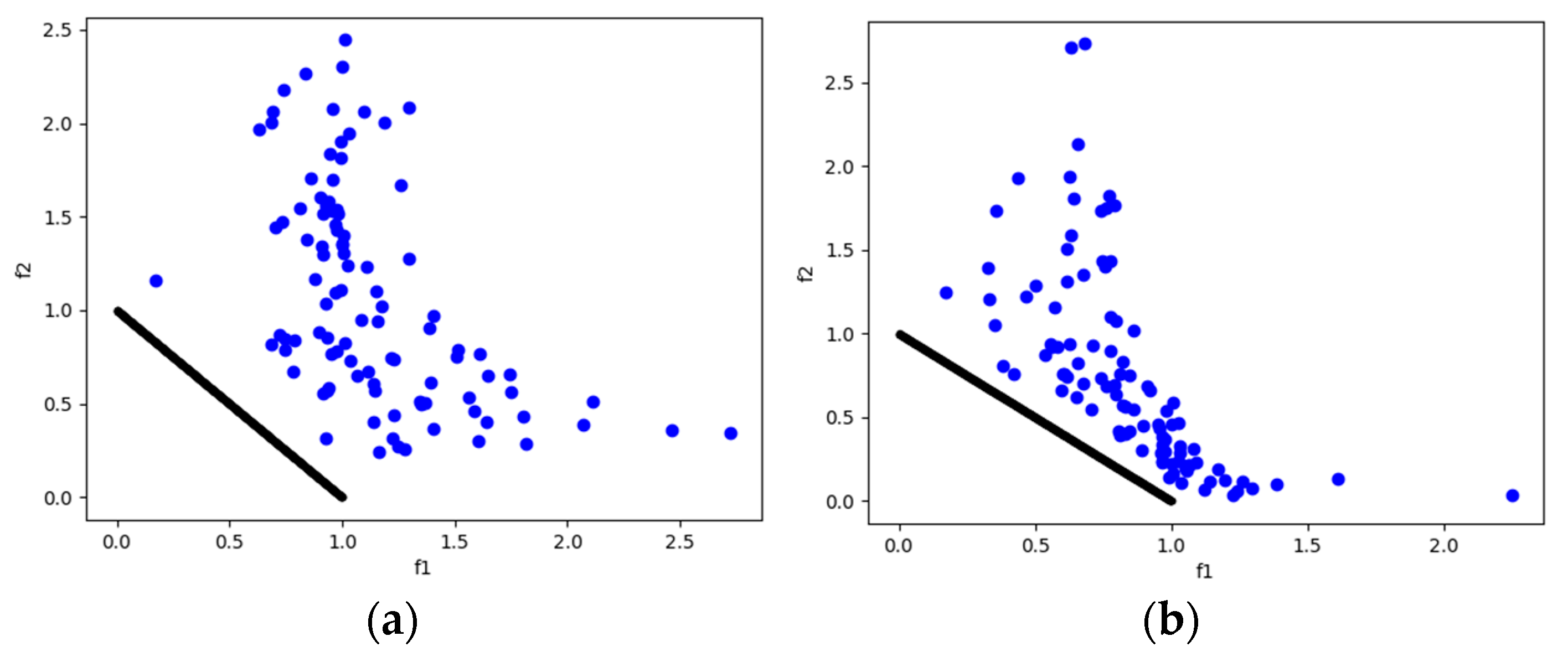
DTLZ2 is a test problem that allows us to observe the ability to converge to concave Pareto fronts. MOSA/D-DE outperforms MOSA/D-CGO in three and five objectives, but with ten objectives, the results favor MOSA/D-CGO in terms of HV results. The performance of differential evolution is promising for three and five objectives. The contribution of classical genetic operators improves the performance with 10 objectives. It is in concordance with IGD results where CGO outperforms DE in five and ten objectives. Figure 4 shows the convergence ability of MOSA/D-DE with three objectives.
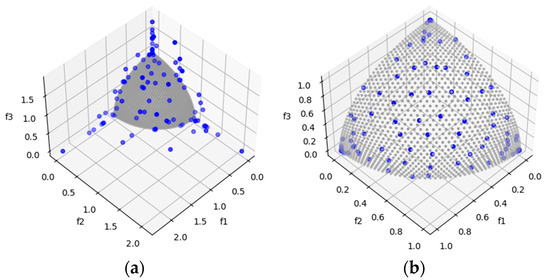
Figure 4.
The plots of the approximate PFs with the highest HV value against real PF. (a) DTLZ2 approximate PF using MOSA/D-CGO; (b) DTLZ2 approximate PF using MOSA/D-DE.
DTLZ4 is a test problem derived from DTLZ2 that allows observation of the algorithms capable of maintaining a good distribution of solutions. Based on the HV results of Table 6, MOSA/D-DE has a better distribution for three objectives (Figure 5). Moreover, for five and ten dimensions, the MOSA/D-CGO approach has a better distribution of solutions. In contrast, IGD (Table 8) shows results in favor of MOSA/D-DE with three and five objectives. It may be because MOSA/D-DE has more solutions near of the real Pareto front than MOSA/D-CGO.
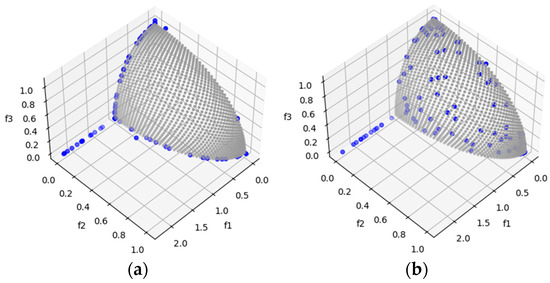
Figure 5.
The plots of the approximate PFs with the highest HV value against real PF. (a) DTLZ4 approximate PF using MOSA/D-CGO; (b) DTLZ4 approximate PF using MOSA/D-DE.
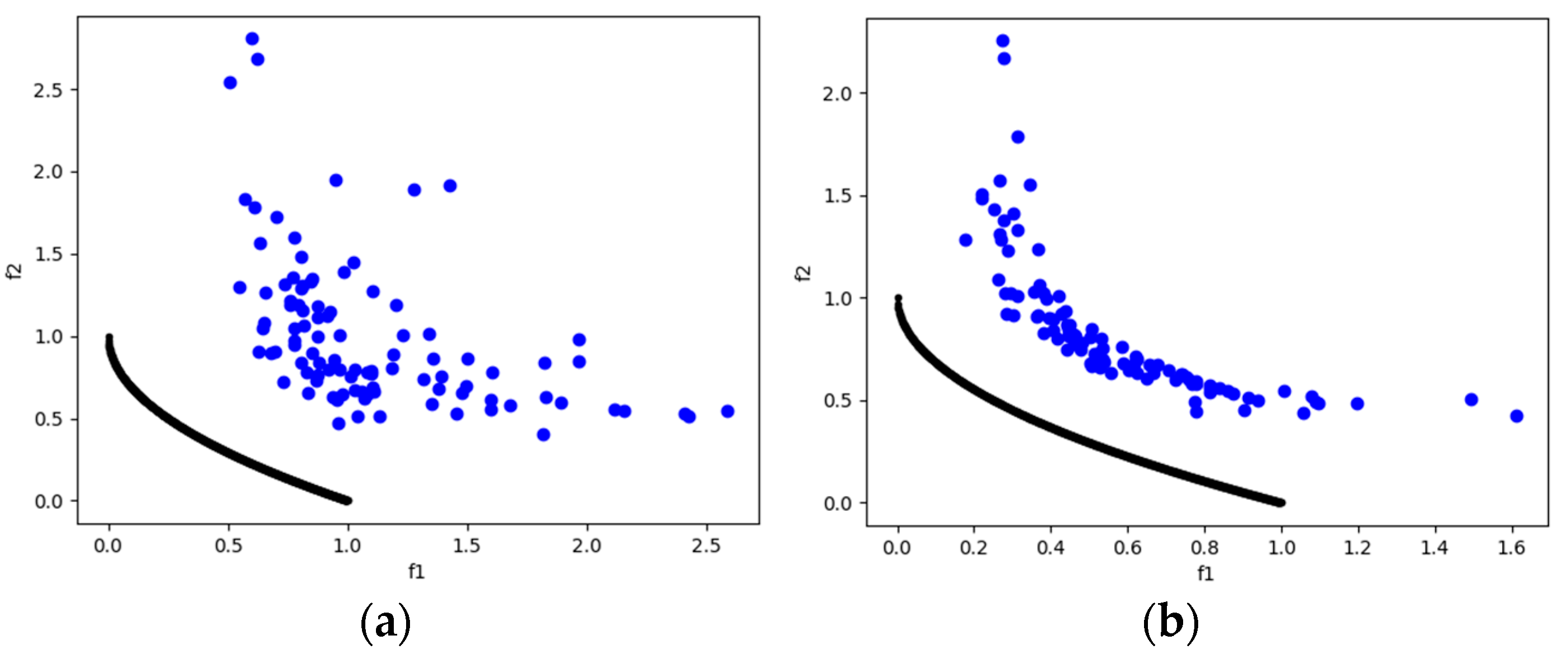
DTLZ5 is a test problem derived from DTLZ2 that allows us to observe whether the algorithms can converge to a curve. From the HV results (Table 6), MOSA/D-DE outperforms MOSA/D-CGO with three and ten objectives. For five objectives, the Wilcoxon signed-rank test indicates no significant difference between the MOSA/D-CGO and MOSA/D-DE results. In contrast, IGD results show that MOSA/D-CGO has a more solutions near of the real PF. Figure 6 shows the convergence toward the PF (curve) using MOSA/D-DE (right side).
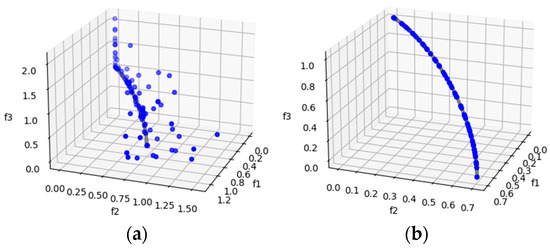
Figure 6.
The plots of the approximate PFs with the highest HV value against real PF. (a) DTLZ5 approximate PF using MOSA/D-CGO; (b) DTLZ5 approximate PF using MOSA/D-DE.
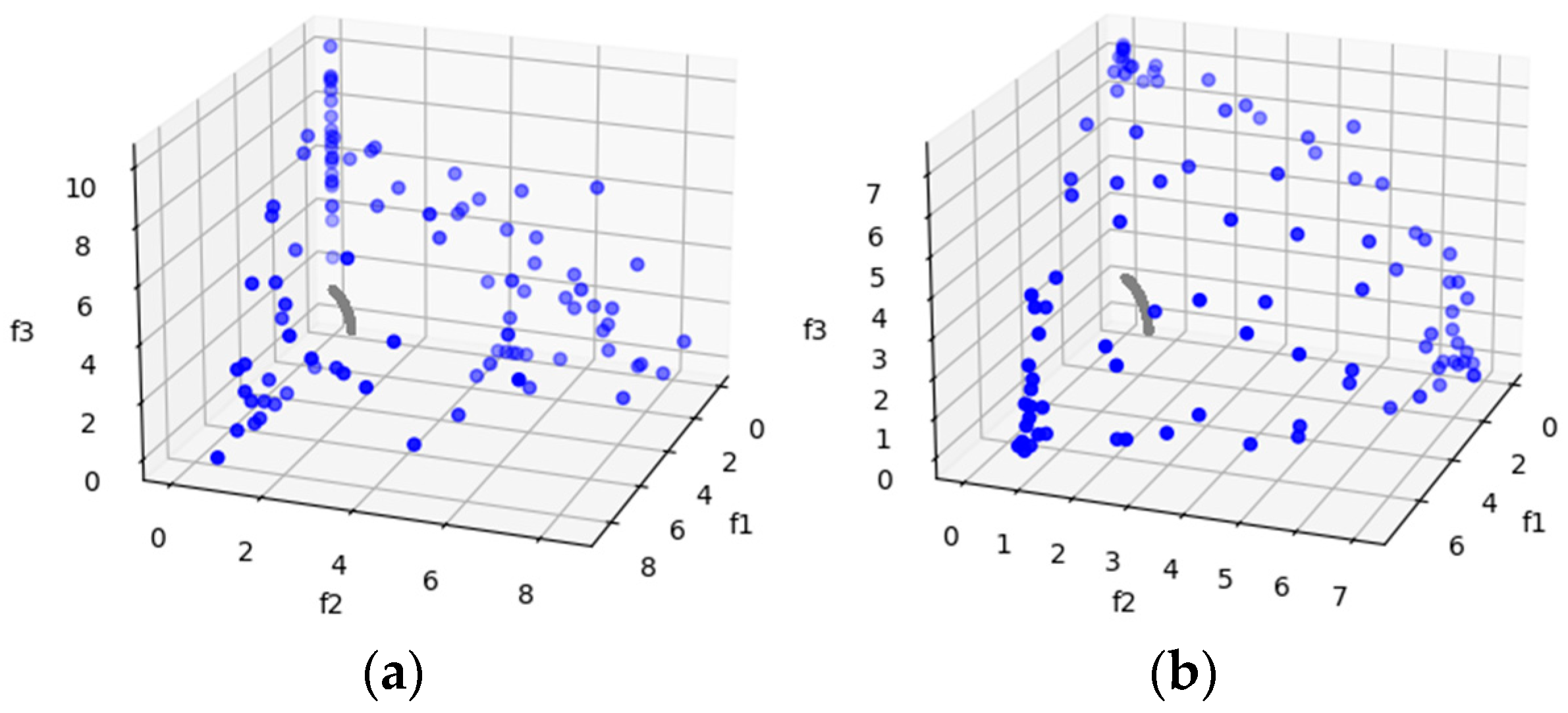
DTLZ6 is a more complex test problem derived from DTLZ5. It allows us to observe whether the algorithms are capable of converging to a curve. From the HV results, MOSA/D-CGO outperforms MOSA/D-DE for three, five and ten objectives. However, in this problem, the convergence of both algorithms deteriorates. For example, in Figure 7, both approaches fail to achieve convergence toward the PF. In results of HV and IGD, better performance of MOSA/D-DE over MOSA/D-CGO is displayed.
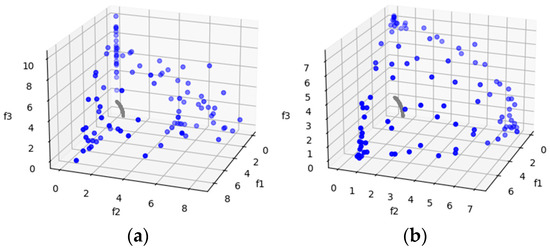
Figure 7.
The plots of the approximate PFs with the highest HV value against real PF. (a) DTLZ6 approximate PF using MOSA/D-CGO; (b) DTLZ6 approximate PF using MOSA/D-DE.
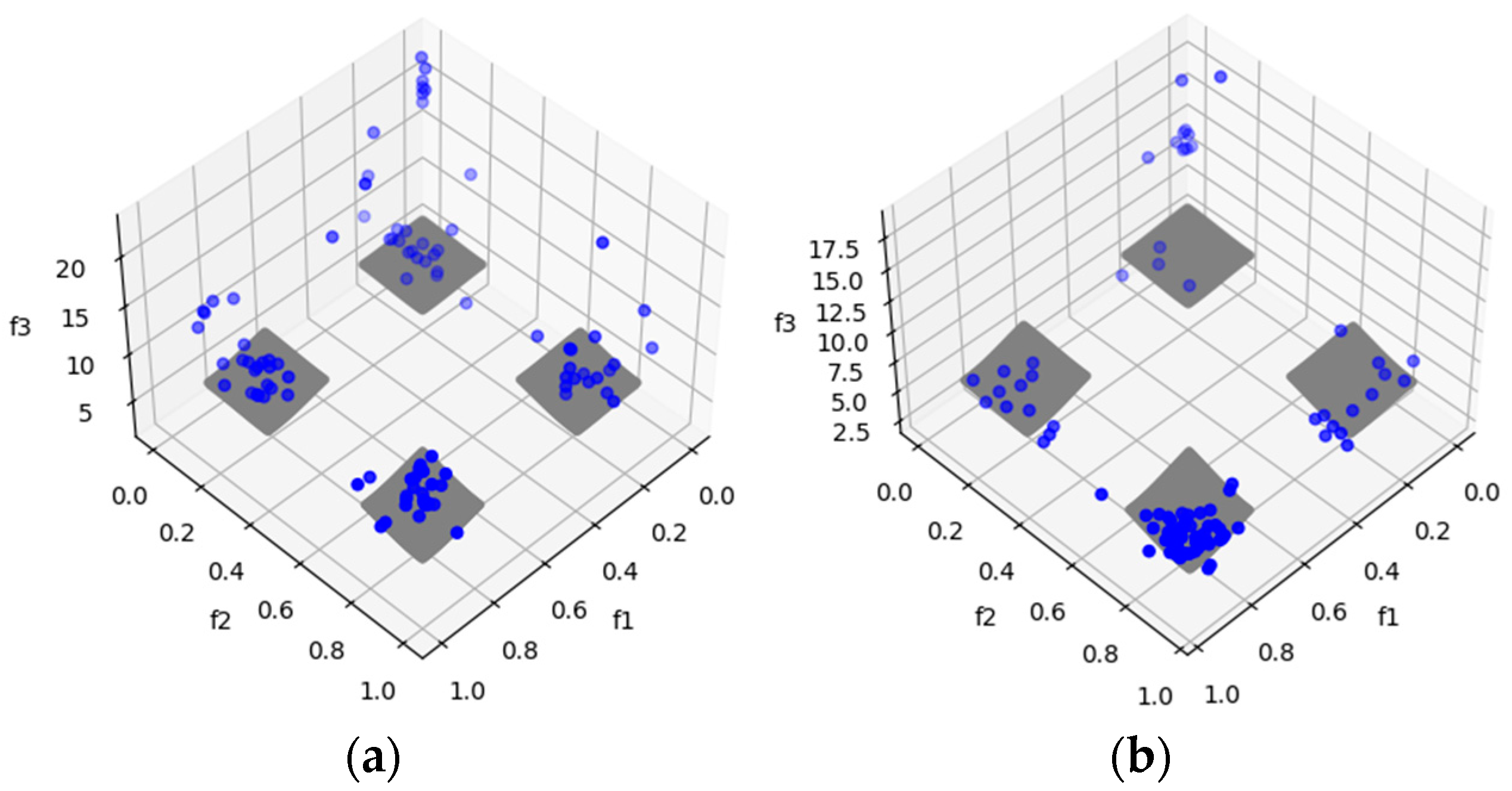
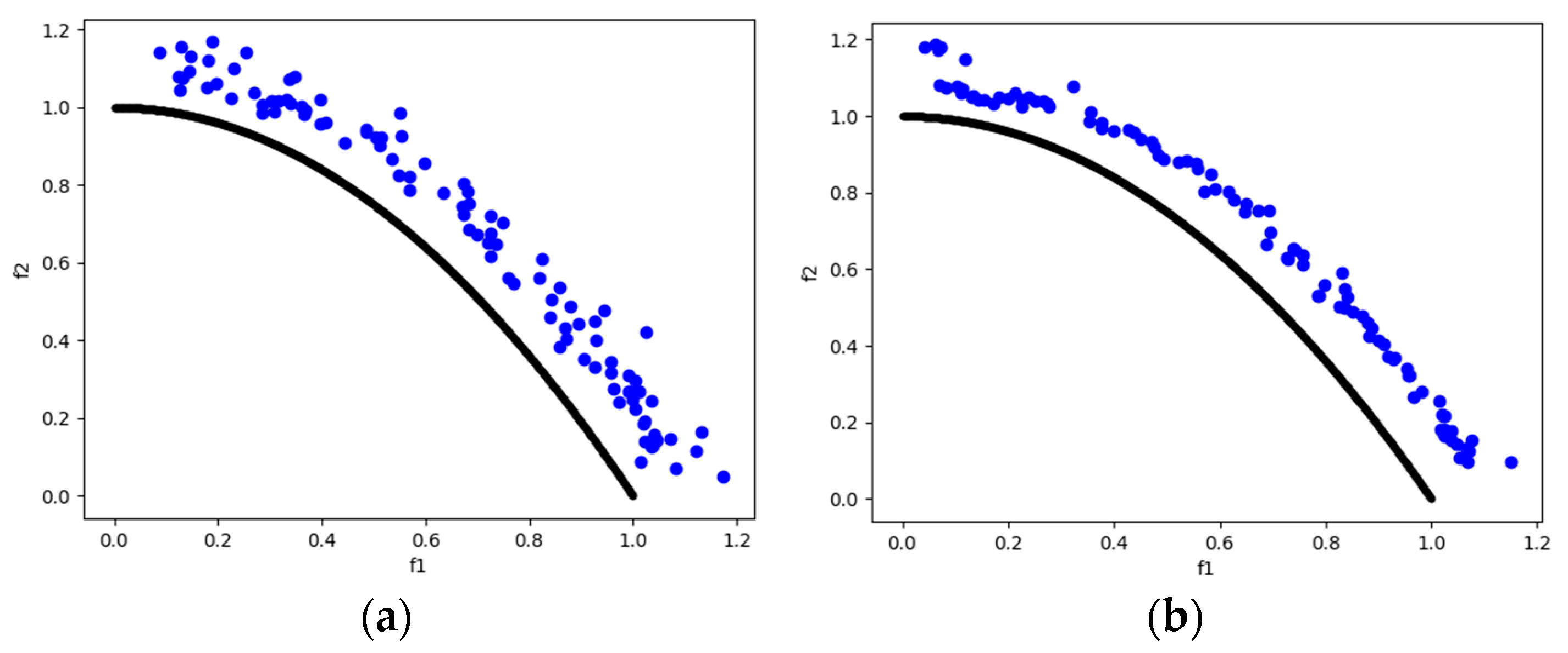
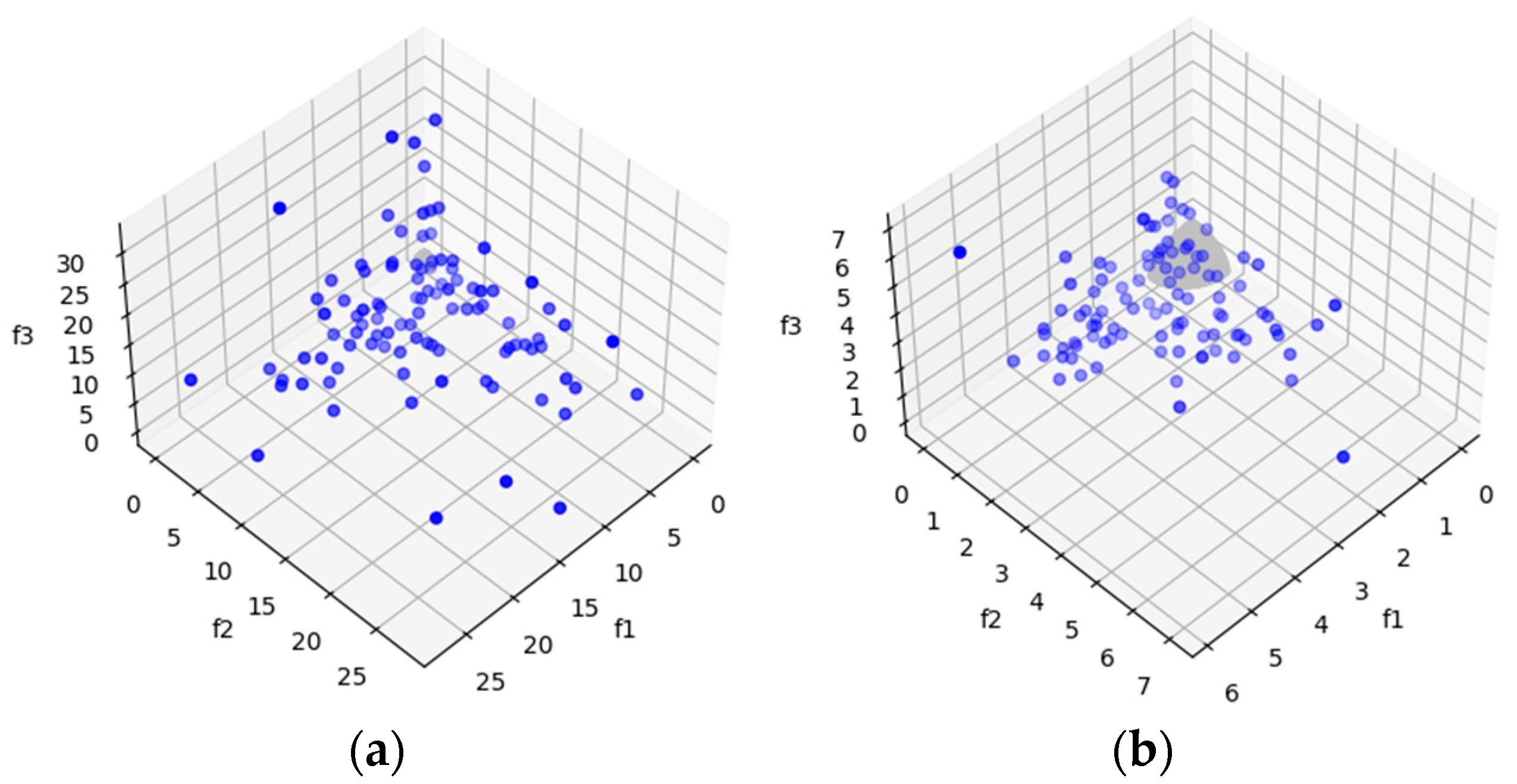
DTLZ7 is a test problem with disconnected Pareto-optimal regions in the search space. The purpose of this problem is to observe the algorithms’ ability to maintain sub-populations in different Pareto-optimal regions [25]. MOSA/D-DE outperforms MOSA/D-CGO for three and ten objectives based on the HV results (Table 6). For five objectives, the Wilcoxon signed-rank test indicates no significant difference between the MOSA/D-CGO and MOSA/D-DE results for DTLZ7. In addition, IGD (Table 8) results show that MOSA/D-DE outperform MOSA/D-CGO for three, five and ten objectives. However, in this problem, the convergence of the algorithms deteriorates although Figure 8 and shows that the four sub-populations of both approaches are necessary for more convergence toward the PF.
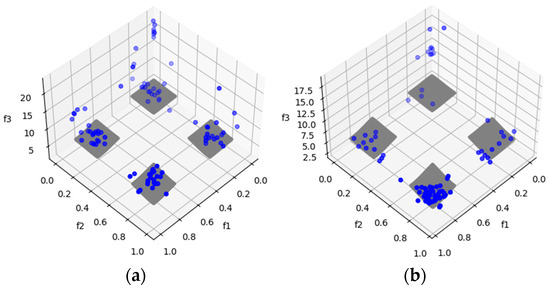
Figure 8.
The plots of the approximate PFs with the highest HV value against real PF. (a) DTLZ7 approximate PF using MOSA/D-CGO; (b) DTLZ7 approximate PF using MOSA/D-DE.
4.2. CEC2009 Benchmark Analysis
CEC2009 benchmark is a set of problems with complicated Pareto set shapes [18] to observe the searchability of multi-objective optimization algorithms. The HV results (Table 7) show that MOSA/D-DE outperforms MOSA/D-CGO in all instances. According to the IGD results (Table 9), MOSA/D-DE outperforms MOSA/D-CGO in experimental instances from UF1 to UF3 and UF5 to UF7 for 2 objectives, while MOSA/D-CGO outperforms MOSA/D-DE in UF4. The plots of approximate PFs for 2 objectives can be seen in Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15. On the other hand, according to the IGD results (Table 9), MOSA/D-DE outperforms MOSA/D-CGD in all instances of 3 objectives (UF8 to UF10). The plots of approximate PFs for 3 objectives can be seen in Figure 16, Figure 17 and Figure 18. Therefore, using the DE perturbation function has a better search ability contribution than the CGO perturbation function. MOSA/D-DE has promising results in the UF2 (Figure 10), UF4 (Figure 12), and UF8 (Figure 16) problems. However, the performance of both algorithms needs more search ability in seven out of ten problems of the benchmark. It shows a clear opportunity to improve the mechanism in future works.
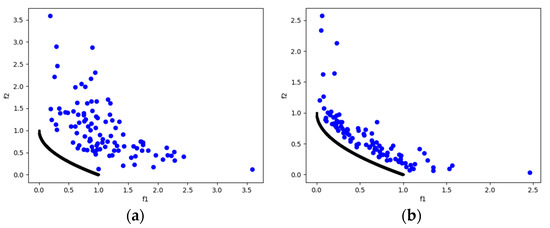
Figure 9.
The plots of the approximate PFs with the highest HV value against real PF. (a) UF1 approximate PF using MOSA/D-CGO; (b) UF1 approximate PF using MOSA/D-DE.
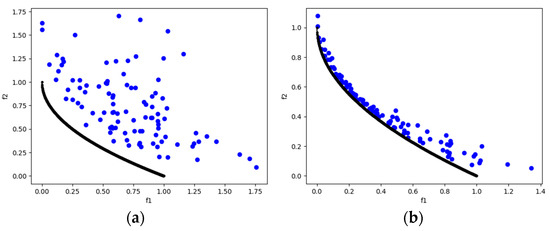
Figure 10.
The plots of the approximate PFs with the highest HV value against real PF. (a) UF2 approximate PF using MOSA/D-CGO; (b) UF2 approximate PF using MOSA/D-DE.
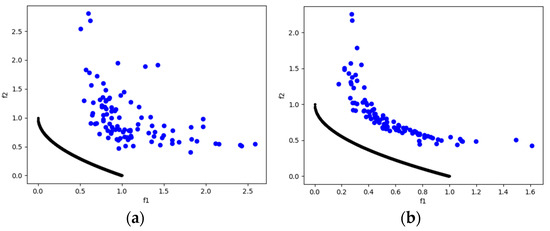
Figure 11.
The plots of the approximate PFs with the highest HV value against real PF. (a) UF3 approximate PF using MOSA/D-CGO; (b) UF3 approximate PF using MOSA/D-DE.
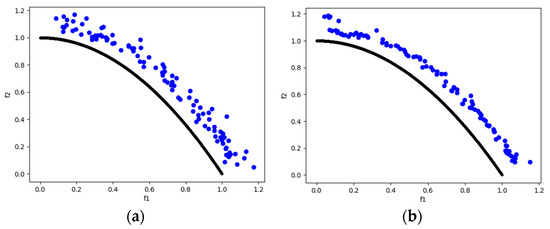
Figure 12.
The plots of the approximate PFs with the highest HV value against real PF. (a) UF4 approximate PF using MOSA/D-CGO; (b) UF4 approximate PF using MOSA/D-DE.
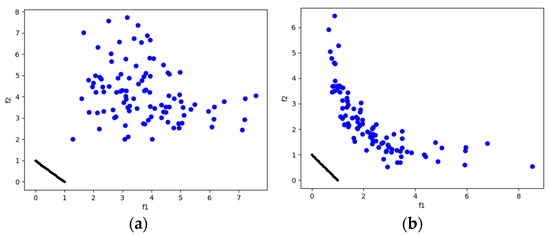
Figure 13.
The plots of the approximate PFs with the highest HV value against real PF. (a) UF5 approximate PF using MOSA/D-CGO; (b) UF5 approximate PF using MOSA/D-DE.
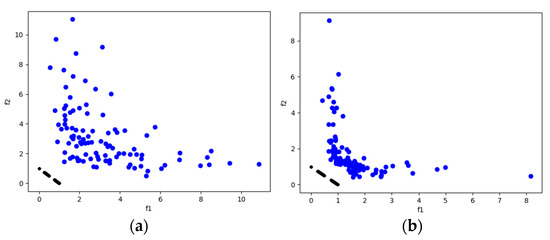
Figure 14.
The plots of the approximate PFs with the highest HV value against real PF. (a) UF6 approximate PF using MOSA/D-CGO; (b) UF6 approximate PF using MOSA/D-DE.
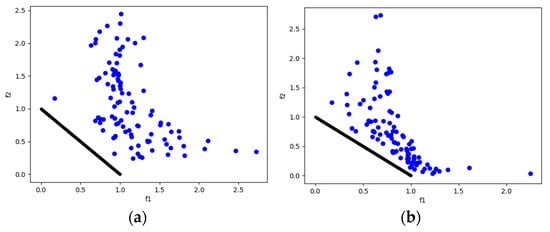
Figure 15.
The plots of the approximate PFs with the highest HV value against real PF. (a) UF7 approximate PF using MOSA/D-CGO; (b) UF7 approximate PF using MOSA/D-DE.
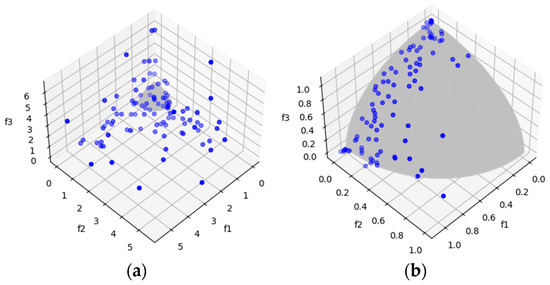
Figure 16.
The plots of the approximate PFs with the highest HV value against real PF. (a) UF8 approximate PF using MOSA/D-CGO; (b) UF8 approximate PF using MOSA/D-DE.
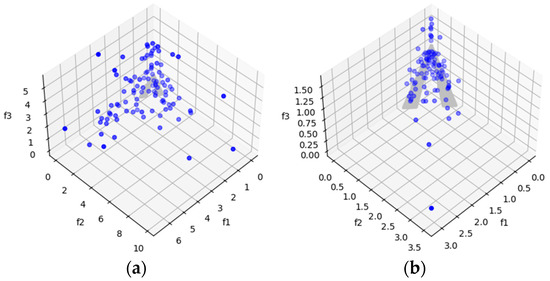
Figure 17.
The plots of the approximate PFs with the highest HV value against real PF. (a) UF9 approximate PF using MOSA/D-CGO; (b) UF9 approximate PF using MOSA/D-DE.
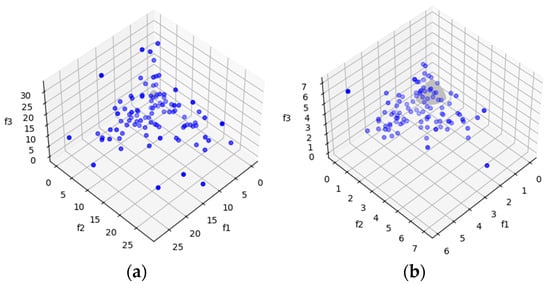
Figure 18.
The plots of the approximate PFs with the highest HV value against real PF. (a) UF10 approximate PF using MOSA/D-CGO; (b) UF10 approximate PF using MOSA/D-DE.
5. Conclusions
The MOSA/D-CGO and MOSA/D-DE approaches to deal with continuous multiple- and many-objective problems were introduced in this paper. Both algorithms harness the ability of convergence and diversity from simulated annealing and decomposition, respectively. MOSA/D-CGO adopts a perturbation function based on classical genetic operators. MOSA/D-DE adopts a perturbation function based on differential evolution. It is essential to point out that MOSA/D-DE shows some promising abilities: (i) its ability to escape from local Pareto-optimal sets in linear and concave problems, (ii) its ability to converge to concave and curved Pareto fronts. Furthermore, MOSA/D-CGO also shows promising abilities: (i) it obtains reasonably distributed solutions with five and ten objectives. MOSA/D-CGO and MOSA/D-DE show convergence to concave Pareto fronts. Both algorithms show the promising ability to converge to Pareto-optimal regions.
The MOSA/D-CGO and MOSA/D-DE algorithms show deterioration of convergence with complex problems with curved Pareto fronts. Both algorithms also show deterioration of convergence with solutions in separate Pareto regions. In conclusion, based on the experiments, the MOSA/D-DE algorithm has promising results. The results in almost all the experiments conducted for three, five, and ten objectives favor MOSA/D-DE. In addition, MOSAD-DE outperforms MOSA/D-CGO in two abilities: (i) the capacity to escape from local Pareto-optimal fronts and (ii) convergence to curved Pareto fronts. The other abilities as measured by the DTLZ benchmark show that both MOSA/D algorithms have mixed results. In addition, both algorithms were proved using problems with complicated Pareto set shapes. Both algorithms were proved using problems with complicated Pareto set shapes. The HV and IGD results show that MOSA/D-DE outperforms MOSA/D-CGO in almost all experimental instances. Furthermore, MOSA/D-DE has promising results in three out of ten problems. However, the mechanism needs more searchability with the complicated Pareto set shapes. Finally, using perturbation functions in multi-objective simulated annealing significantly impacts the convergence toward the PF. This impact can be improved in future work.
In future work, the aim is to determine another strategy to add convergence into complex problems with curved PF and separate Pareto regions. For example, to converge in a curved PF (DTLZ6), both MOSA fail, but, based on the HV results, MOSA/D-CGO has a slight advantage over MOSA/D-DE. Both algorithms indeed achieve solutions in separate Pareto regions (Figure 8), but there needs to be more convergence. It will be interesting to observe the performance of both algorithms with additional convergence. The search ability with the CEC2009 benchmark show deterioration; for this reason, an update of the mechanism is necessary. MOSA/D algorithms are the hybridized result of simulated annealing, decomposition, and special perturbation functions. This design allows a simple structure (Algorithm 1) that can be easily updated. For example, the algorithms can both use the concept of the neighborhood as in MOEA/D [7] and use a strategy based on preferences to deal with MaOPs. In addition, future work will aim to observe the performance of both MOSA/D with real world problems such as the portfolio selection problem (PSP), knapsack problem, and traveling salesman problem.
Author Contributions
The manuscript was written through the contributions of all authors. Conceptualization, M.V.-M. and N.R.-V.; methodology, M.V.-M., N.R.-V. and E.F.; software, M.V.-M. and N.R.-V.; validation, M.V.-M., N.R.-V. and E.F.; formal analysis, C.G.-S.; investigation, M.L.M.-R.; resources, C.G.-S.; data curation, N.R.-V.; writing—original draft preparation, M.V.-M.; writing—review and editing, M.V.-M. and N.R.-V.; visualization, C.G.-S.; supervision, E.F.; project administration, M.L.M.-R.; funding acquisition, M.L.M.-R., C.G.-S. and N.R.-V. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The files of the results produced by this work are available at https://www.dropbox.com/sh/fk8bt8v8gy6ghbz/AABaDrhbC2DKwkB_YH2L64xZa?dl=0, accessed on 29 January 2023.
Acknowledgments
José Manuel Vargas Martínez acknowledges CONACyT Ph.D. scholarship (Grant 788668). Also, the authors acknowledge the support obtained from: IxM CONACyT project 3058-“Optimización de Problemas Complejos”, Laboratorio Nacional de Tecnologías de Información (LaNTI) at TecNM/Instituto Tecnológico de Ciudad Madero, and TecNM research networks “Tecnologías Computacionales Aplicadas” and “Electromovilidad”.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chand, S.; Wagner, M. Evolutionary Many-Objective Optimization: A Quick-Start Guide. Surv. Oper. Res. Manag. Sci. 2015, 20, 35–42. [Google Scholar] [CrossRef]
- Ishibuchi, H.; Tsukamoto, N.; Nojima, Y. Evolutionary Many-Objective Optimization: A Short Review. In Proceedings of the 2008 IEEE Congress on Evolutionary Computation, Hong Kong, China, 1–6 June 2008; pp. 2424–2431. [Google Scholar]
- Falcón-Cardona, J.G.; Coello Coello, C.A. A new indicator-based many-objective ant colony optimizer for continuous search spaces. Swarm Intell. 2017, 11, 71–100. [Google Scholar] [CrossRef]
- Rodriguez, F.J.; García-Martinez, C.; Lozano, M. Hybrid Metaheuristics Based on Evolutionary Algorithms and Simulated Annealing: Taxonomy, Comparison, and Synergy Test. IEEE Trans. Evol. Comput. 2012, 16, 787–800. [Google Scholar] [CrossRef]
- Mashwani, W.K. Comprehensive Survey of the Hybrid Evolutionary Algorithms. Int. J. Appl. Evol. Comput. 2013, 4, 1–19. [Google Scholar] [CrossRef]
- Bechikh, S.; Elarbi, M.; Ben Said, L. Many-objective optimization using evolutionary algorithms: A survey. Adapt. Learn. Optim. 2017, 20, 105–137. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Xu, Q.; Xu, Z.; Ma, T. A short survey and challenges for multiobjective evolutionary algorithms based on decomposition. In Proceedings of the CITS 2019—International Conference on Computer, Information and Telecommunication Systems, Beijing, China, 28–31 August 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Li, H.; Landa-Silva, D. An adaptive evolutionary multi-objective approach based on simulated annealing. Evol. Comput. 2011, 19, 561–595. [Google Scholar] [CrossRef] [PubMed]
- Amine, K. Multiobjective Simulated Annealing: Principles and Algorithm Variants. Adv. Oper. Res. 2019, 2019, 8134674. [Google Scholar] [CrossRef]
- Guo, H.; Li, Y.; Li, J.; Sun, H.; Wang, D.; Chen, X. Differential Evolution Improved with Self-Adaptive Control Parameters Based on Simulated Annealing. Swarm Evol. Comput. 2014, 19, 52–67. [Google Scholar] [CrossRef]
- Opara, K.R.; Arabas, J. Differential Evolution: A survey of theoretical analyses. Swarm Evol. Comput. 2019, 44, 546–558. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Q. Multiobjective Optimization Problems With Complicated Pareto Sets, MOEA/D and NSGA-II. IEEE Trans. Evol. Comput. 2009, 13, 284–302. [Google Scholar] [CrossRef]
- Mashwani, W.K.; Salhi, A.; Yeniay, O.; Jan, M.A.; Khanum, R.A. Hybrid Adaptive Evolutionary Algorithm Based on Decomposition. Appl. Soft Comput. J. 2017, 57, 363–378. [Google Scholar] [CrossRef]
- Mashwani, W.; Salhi, A.; Jan, M.; Khanum, R.; Sulaiman, M. Impact Analysis of Crossovers in a Multi-Objective Evolutionary Algorithm. Sci. Int. 2015, 27, 4943–4956. [Google Scholar]
- Liu, B.; Fernández, F.V.; Zhang, Q.; Pak, M.; Sipahi, S.; Gielen, G. An Enhanced MOEA/D-DE and Its Application to Multiobjective Analog Cell Sizing. In Proceedings of the 2010 IEEE Congress on Evolutionary Computation CEC, Barcelona, Spain, 18–23 July 2010. [Google Scholar] [CrossRef]
- Chen, C.M.; Chen, Y.P.; Zhang, Q. Enhancing MOEA/D with Guided Mutation and Priority Update for Multi-Objective Optimization. In Proceedings of the 2009 IEEE Congress on Evolutionary Computation CEC, Trondheim, Norway, 18–21 May 2009; pp. 209–216. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhou, A.; Zhao, S.; Suganthan, P.N.; Liu, W. Multiobjective Optimization Test Instances for the CEC 2009 Special Session and Competition. In Proceedings of the 2009 IEEE Congress on Evolutionary Computation CEC, Trondheim, Norway, 18–21 May 2009; pp. 1–30. [Google Scholar]
- Chen, B.; Zeng, W.; Lin, Y.; Zhong, Q. An Enhanced Differential Evolution Based Algorithm with Simulated Annealing for Solving Multiobjective Optimization Problems. J. Appl. Math. 2014, 2014, 931630. [Google Scholar] [CrossRef]
- Engrand, P. Multi-objective optimization approach based on simulated annealing and its application to nuclear fuel management. In Proceedings of the 1997 ICONE International Conference on Nuclear Engineering, Nice, France, 25–29 May 1997; p. 477. [Google Scholar]
- Ulungu, E.L.; Teghem, J.; Fortemps, P.H.; Tuyttens, D. Heuristic for multi- objective combinatorial optimization problems by simulated annealing. In MCDM: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 1995; pp. 229–238. [Google Scholar]
- Ulungu, E.L.; Teghem, J.; Fortemps, P.H.; Tuyttens, D. MOSA method: A tool for solving multiobjective combinatorial optimization problems. J. Multi-Criteria Decis. Anal. 1999, 8, 221–236. [Google Scholar] [CrossRef]
- Czyzżak, P.; Jaszkiewicz, A. Pareto simulated annealing-a metaheuristic technique for multiple-objective combinatorial optimization. J. Multi-Criteria Decis. Anal. 1998, 7, 34–47. [Google Scholar] [CrossRef]
- Das, S.; Suganthan, P.N. Differential evolution: A survey of the state-of-the-art. IEEE Trans. Evol. Comput. 2011, 15, 4–31. [Google Scholar] [CrossRef]
- Deb, K.; Thiele, L.; Laumanns, M.; Zitzler, E. Scalable Test Problems for Evolutionary Multiobjective Optimization. In Evolutionary Multiobjective Optimization; Springer: London, UK, 2005; pp. 105–145. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).