Abstract
In this paper, we focus on investigating the performance of the mathematical software program Maple and the programming language MATLAB when using these respective platforms to compute the method of steps (MoS) and the Laplace transform (LT) solutions for neutral and retarded linear delay differential equations (DDEs). We computed the analytical solutions that are obtained by using the Laplace transform method and the method of steps. The accuracy of the Laplace method solutions was determined (or assessed) by comparing them with those obtained by the method of steps. The Laplace transform method requires, among other mathematical tools, the use of the Cauchy residue theorem and the computation of an infinite series. Symbolic computation facilitates the whole process, providing solutions that would be unmanageable by hand. The results obtained here emphasize the fact that symbolic computation is a powerful tool for computing analytical solutions for linear delay differential equations. From a computational viewpoint, we found that the computation time is dependent on the complexity of the history function, the number of terms used in the LT solution, the number of intervals used in the MoS solution, and the parameters of the DDE. Finally, we found that, for linear non-neutral DDEs, MATLAB symbolic computations were faster than Maple. However, for linear neutral DDEs, which are often more complex to solve, Maple was faster. Regarding the accuracy of the LT solutions, Maple was, in a few cases, slightly better than MATLAB, but both were highly reliable.
1. Introduction
Often, engineers and scientists may need to choose a software that is specific to their application or modeling purpose. Some software languages may have different features, speed/computational complexity, tolerances, architecture, libraries, ease of use, etc., that can affect the accuracy of the model. Here, we investigated the performance of the mathematical software program Maple and the programming language MATLAB when applying the method of steps (MoS) and the Laplace transform (LT) methods to solve linear delay differential equations (DDEs). To make the comparison fair, we used the benefits offered by these two programs for symbolic computation, which allows us to derive the solutions of these DDEs in the ways we would think about carrying them out by hand with variables, symbols, functions, and other mathematical formulas. An advantage of using symbolic computation is that it eliminates cases of roundoff errors in intermediate calculations since parameter variables are carried throughout the calculations using infinite precision arithmetic [1,2,3]. However, in some cases, using symbolic computations can lead to slower execution times depending on the program used and the process [4,5,6]. Symbolic computation has been used and proposed for solving many different problems [7,8,9,10,11].
In this paper, we focus on comparing the symbolic mathematical computations of Maple and MATLAB to obtain analytical solutions of linear neutral and non-neutral DDEs by using the LT method. The accuracy of the LT solutions may be determined by comparing them with the MoS solutions [12,13,14,15,16,17]. However, the MoS has a very important limitation since it is a stepwise process that requires solving the relevant differential equation in each respective time interval, which can be computationally expensive. Moreover, for many types of DDEs, we will often encounter the swelling phenomena, i.e., the complexity of the closed-form solution increases rapidly in each successive time interval, making the computations unfeasible [14,16]. On the other hand, the LT method produces a solution that can be evaluated at any particular value of time. Thus, we can compute the approximated solution by evaluating it at any point. Other advantages of the analytical solutions, such as the long-term behavior of the solution, can be seen in [14,15,18,19,20,21,22]. The errors of the LT solutions usually decrease as time increases. On the other hand, for classical numerical solutions, the computation increases as [14,23,24,25]. However, numerical schemes that solve linear and nonlinear DDEs are useful and, in some cases, are easy to implement. For instance, in [26], the authors developed a numerical scheme based on a fitted difference scheme with the use of exponential basis functions and interpolating quadrature rules to solve first order linear DDEs. Some researchers have proposed different collocation methods to solve linear and nonlinear DDEs [27,28]. For instance, in [29], the Haar wavelet collocation method was applied to obtain the numerical solution of a particular class of DDEs. The method is also applied to systems involving DDEs. In [30], the authors proposed a numerical method for solving linear fractional differential equations using discretization at the Jacobi–Gauss collocation points. Other methods that have been applied that involve more general DDEs can be found in [31,32]. In these works, the authors deal with the differential-difference equation in an infinite-dimensional space and with unbounded domains. Moreover, they consider mixed-type equations that include both forward and backward shifts of the argument. These forms are generated by different temporal and spatial discretizations. It is important to mention that one might expect that some of the techniques and results of retarded differential equations could be applied to mixed-type equations, but, given that the independent variable in this paper is strictly temporal, this may require one to introduce some modifications [32,33]. In addition, these last works deal with idealized nonlinearities in order to obtain a more tractable problem.
It is important to point out that, even for linear DDEs, it might be challenging to obtain an analytical solution. Moreover, in most cases, the neutral delay differential equations (NDDEs) are more difficult to solve due to the appearance of a time delay on the derivative of the state variable. Regarding solving ordinary differential equations (ODEs) and DDEs, the latter is usually more difficult to solve since the derivatives of the state variables depend on the values of the state variable from the past. The classic approach used to obtain the solutions of DDEs is the MoS, but, in many cases, it is unfeasible to advance further in time and obtain the solution in the long term [14,15,34,35,36]. In [14], the authors studied the accuracy of the LT for linear DDEs and, in particular, for NDDEs. In [20], the authors developed a method for solving linear and nonlinear DDEs with a proportional delay using a combination of the LT and the differential transformation method (DTM). The authors mentioned that the convergence rate can be improved by the combination of the two methods. The LT method has also been used to solve linear second order DDEs [37]. However, complex analytical computations and the use of the residue theorem are required [14,37]. Linear DDEs have different applications and have been applied in many problems [17,38,39].
In order to compare the symbolic computations involved in obtaining the solutions of neutral and non-neutral linear DDEs using the LT method, we selected Maple and MATLAB software since they are well-known in the scientific community [3,40]. In Maple, we made use of the symbolic functions diff, dsolve, fsolve, eval, and subs, to name a few, whereas, in MATLAB, we utilized functions from the symbolic math and optimization toolboxes such as fsolve, subs, vpa, and vpasolve. We explored several examples of DDEs of neutral and non-neutral type in order to compare the symbolic computation of Maple and MATLAB. For each example, we computed the solution over some finite time interval using the MoS briefly described in Section 2.1 and the LT method described in Section 3. First, we explored two examples of non-neutral DDEs and then we followed with several examples of neutral DDEs. For each example, we compared: (1) the solutions of the two methods from each program software, (2) the errors associated with each method and software, and (3) the computation times. DDEs have been used in many different fields, including astronomy and epidemiology [17,41,42,43]. For some applications, such as control or communication systems, the computation time may be a critical factor [44,45,46,47]. All computations were performed on a computer system with an Intel(R) Core(TM) i9-10900K CPU @ 3.70 GHz processor and 64 GB RAM.
The organization of this paper is as follows. In Section 2, preliminaries for DDEs, NDDEs, and the MoS for solving linear DDEs are presented. In Section 3, we briefly present the main aspects of the LT method with the relevant equations and formulas. In Section 4, we compare the symbolic computations to obtain the solution of linear DDEs using the LT method. We present several examples related to DDEs and their corresponding numerical solutions. In Section 5, conclusions regarding the symbolic computations required to obtain the solution of DDEs using the LT method are provided.
2. Preliminaries
In this section, we present some preliminary definitions that are needed to solve the different linear DDEs presented in this work. Some preliminaries include background concepts, the Lambert function, the residue theorem, and the MoS. Familiarity with the basic concepts of complex analysis is assumed.
2.1. Method of Steps (MoS)
The traditional method for solving DDEs is with an elementary method called the method of steps [17,34,35,48,49,50]. It is well-known for being a tedious process when being worked out by hand, but the complexity can be drastically simplified with symbolic toolboxes in computer programs [15]. Let us consider a NDDE with fixed delay :
where is the initial time value, is a constant/discrete delay, and is some constant. For DDE initial value problems (IVPs), we require a history function, , and an initial value, for , to solve the problem. This condition implies that DDEs are in fact infinite-dimensional problems since we define an infinite set of initial conditions between .
Using integration properties on the interval , the solution is then given by , which is a solution to the following NDDE:
Repeating this process for successive intervals and using the solution over the past interval, we find the following general derivative formula for the nth partition of the IVP ():
The solutions of form a piecewise solution of the original NDDE (1) on the interval .
Even though the MoS provides an analytical solution for DDEs, it has some drawbacks, including time consumption and the complexity of the integrals to be solved over each interval. This method also requires full knowledge of the history before the approach can be used. Since it is a successive process, it can be quite difficult to observe the behavior of the solution or to perform stability analysis of as .
2.2. Lambert W Function
From ODEs, the roots of the characteristic equation provide information about the solution of a linear ODE or system of linear ODEs. Often times, this equation is a simple polynomial that is easy to solve with algebraic operations or use of the quadratic formula. A linear DDE or system of linear DDEs can be characterized in a similar manner to ODEs by looking at the characteristic equation. Take, for example, the following linear DDE with discrete time delay :
where is the initial value. The characteristic polynomial of the above DDE takes the form of a quasi-polynomial due to the introduction of the exponential, i.e., . By setting , there could be an infinite number of poles. Through simplifying, we obtain , which takes the form of a Lambert W function with the equation form , where z is some complex number and is the multi-valued function solution of the equation.
Lambert functions are used when the unknown of an equation appears as both a base and exponent. Equations such as cannot be solved with algebraic, logarithmic, or exponential properties. For certain values of z, this equation can have an infinite number of solutions called branches of W, and are denoted by for . One of the branches, called the principal branch, is analytic at zero and is denoted by (). For real numbers, the branches and can be used to solve the equation with real numbers x and y if . The solution, y, can be found using the following conditions.
We note that the second condition implies that, in the interval , the equation has two real solutions.
In terms of our given problem, the poles of the quasi-polynomial are given by . The analytical solution to the DDE, then, can be expressed in terms of an infinite number of branches, given as
where the s are the coefficients determined from the history function, , and the initial value, . One can analyze how changes in the parameters c, , and affect the real part of the eigenvalues of the system and, in turn, how that impacts the stability of the solution. Further details and applications of the Lambert function can be found in literature such as [51,52].
2.3. Cauchy’s Residue Theorem
The LT method for solving DDEs requires the use of Cauchy’s residue theorem, which is a powerful tool discussed in complex analysis for evaluating complex real integrals or infinite series [53,54]. Here, it was used to find the solution of a DDE when converting from the s-space back to the t-domain.
Suppose is an analytic function in the complex region defined by , or the neighborhood of a point . Then, is an isolated singular point of . The function can be represented by the Laurent series expansion as [54]:
where
are the coefficients and C is a simple closed contour in . The principal part of the series is given by the negative portion, , where is called the residue of at . An isolated singularity is a pole if is of the form [53,54]:
where is the order of the pole, is an analytic function in , and .
Residues of Poles: If , then has a simple pole at . At a simple pole , the residue of is given by [54]:
If the limit does not exist, then there exists an essential singularity at . If the limit is zero, then is analytic at , or is a removable singularity. If the limit is infinity, then the order is greater than [53,54].
Now, suppose can be expressed as a rational function, , where and are analytic functions in and has a zero at . Let , where is analytic in and is nonzero. Using the Taylor series expansion of and , the residue is given as [53,54]:
Residue Theorem: Suppose C is a simple closed contour and let be an analytic function inside and on C, excluding a finite number (K) of isolated singularities inside C. Then,
The use of Cauchy’s residue theorem in the LT method comes from the definition of the inverse Laplace transform (ILT):
where the integration is over a vertical path in the complex plane defined at Re. From complex analysis, the function is entire and, thus, we require the vertical path to be to the right of all of the poles of . In other words, the real part of all of the poles needs to be to the left of c. Let us denote this vertical path shown in Figure 1. To use the residue theorem to evaluate the above integral, we construct a contour path, , enclosing all of the poles with radius R as shown in Figure 1 going in a CCW direction. From this contour and Cauchy’s residue theorem, we obtain
which implies that
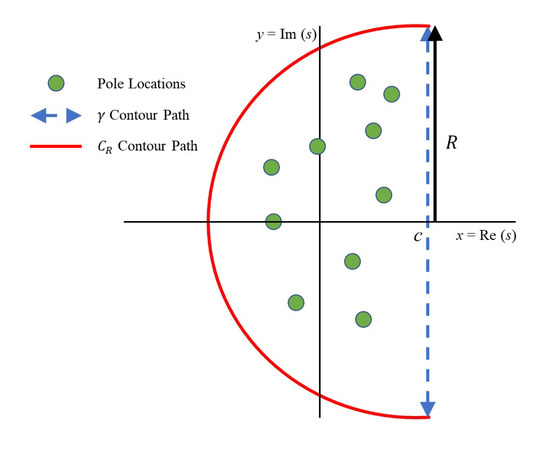
Figure 1.
Bromwich contour (interested readers are referred to [54]).
Let . We need to show that . Achieving this will give:
where c is a fixed real constant s.t. has a finite number of poles located to the left of the line .
Let . For , we enclosed in the left half plane where ,. Then, , and we obtain
We find that
and
for sufficiently large . Then, we have
In the integrand, we note that is negative for . Then, as , we can observe that , which implies that . Then, we have shown that the ILT of can be represented using residues and is given by
3. Laplace Transform (LT) Method
We denote the LT of the solution as . Then, for a given delay term in the state variable, the LT is given by (such that )
When the delay is present in the derivative of the state variable, the LT is given by (such that ):
The LT method uses Equations (9) and (10) as a part of the process to obtain the solutions of the linear NDDEs. For further details, interested readers are referred to [14,15].
3.1. Theory for Linear Non-Neutral DDE Case
First, we consider a simple linear non-neutral DDE case as shown below, where the solution is derived using the ILT and the residue formula as described in Section 2.3:
Considering the homogeneous case, and applying the LT to Equation (11) (using Equation (9)), we obtain the LT transform, , of :
Setting , we find that the poles of occur at for . Recall from the definition of the Lambert function that, if the argument , then we encounter a case where the real pole is of order (since by definition of the and Lambert branches). If , then the poles are of order . By applying the ILT, for , we obtain the solution
where the s are the computed residues. Further details can be found in [14].
If the linear non-neutral DDE is non-homogeneous, we obtain the LT:
where is the LT of the function . We denote the additional poles introduced by as for (assuming that , and are of order ) with corresponding residues . Applying the ILT and the residue theorem, we obtain the solution
where
For more details about the LT, the interested readers are referred to [14]. In Section 4.1, we will explore the solutions of both cases (homogeneous and non-homogeneous).
3.2. Theory for NDDE Case
Next, we consider a simple NDDE case as shown below, where the solution is derived using the residue formula as described in Section 2.3:
where , and , . Considering the homogeneous case, and applying the LT to Equation (16) (using Equations (9) and (10)), we obtain the LT transform, , of :
Setting , we can find the poles of . Under some general conditions, the poles are of order . Then, applying the ILT, we obtain the solution
where the s are the computed residues. We can analyze different cases depending on , and the signs and magnitudes of and for . For further details, interested readers are referred to [14].
If the NDDE is non-homogeneous, similar properties hold as in the non-neutral case. In Section 4.2, we explore the solution behavior of different delay cases. Further details and analysis can be found in [14].
4. Comparison of MoS and LT Methods Using Symbolic Computation
Here, we present and discuss different examples of non-neutral DDEs and NDDEs introduced in [14] and apply the MoS and LT methodologies to each example to find the solution of such equations using the Maple and MATLAB software. First, the solutions obtained by each method will be compared between programs to highlight the variances in program computations. Second, the accuracy of the LT method will be evaluated against the analytical solution obtained by the MoS for each program. For this section, we introduce the following notation:
- : Absolute error in the solution between Maple and MATLAB via the MoS.
- : Absolute error in the solution between Maple and MATLAB via the LT.
- : Absolute error in the solution between the MoS and LT via Maple.
- : Absolute error in the solution between the MoS and LT via MATLAB.
4.1. Linear Non-Neutral DDE Examples
The two examples presented in this section demonstrate solutions formed from poles of order . Figure 2 and Figure 3 and Table 1 summarize the solution results, error comparisons between MoS and LT in each programming language, and the computation times for the corresponding example.
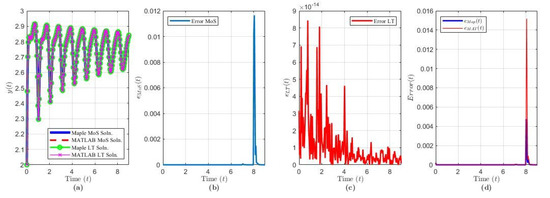
Figure 2.
Solution results of Equation (19) over ( terms): plot of (a) the solution via each method and software, (b) , (c) , (d) and .
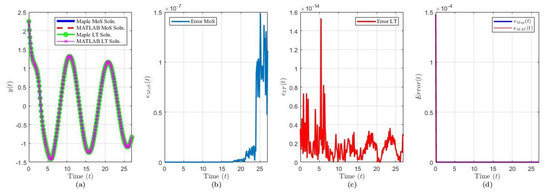
Figure 3.
Solution results of Equation (20) over ( terms): plot of (a) the solution via each method and software, (b) , (c) , (d) and .
Example 1.
Let us consider the following DDE:
where . Taking the LT of Equation (19), we obtain the quasi-polynomial , which has a real pole at with residue (from Equation (4)). The remaining poles and residues are given by: , , with property , and . Applying the ILT and Cauchy’s residue theorem, we obtain the LT solution of :
The solution of Example 1 via MoS (over intervals) and LT () and in each software program is shown in Figure 2a. We notice that, as , since , , and each Re for . Figure 2b,c demonstrate the variances between the software when evaluating the solution via MoS (blue curve) or the LT (red curve). Figure 2d demonstrates the accuracy of the LT compared to the analytical MoS via Maple (blue curve) and MATLAB (red curve). Upon analyzing Figure 2b,d, we note that the MATLAB MoS solution significantly deviates from its LT solution and the Maple MoS solution. In the MoS process, a piecewise function is produced for each interval and it becomes harder to integrate and solve the sub-IVPs as the functions become more complicated with each step. In the LT solution, we see that, as t progresses, the variance fluctuations in the solution between programs decrease. Each plot shows that error spikes occur every . The reason is that, around these points, the sines of the truncated non-harmonic series do not play any significant role, while the cosine and exponential terms are essentially equal to 1. Therefore, the approximated series solution loses the ability to approximate the solution close to . The spikes can be reduced if we include more terms in the truncated series [14].
The computation times via each method and software are shown in Table 1. Given the number of terms to compute for the LT solution, the computation time was higher for both programs compared to the MoS solutions. However, with the use of MATLAB’s symbolic toolbox functions, the computation time for the LT solution was reduced by a factor of four compared to Maple for this particular example.
Example 2.
Let us consider the following DDE:
where . Taking the LT of Equation (20), we obtained the quasi-polynomial , which has no real poles since (see [14]). The complex poles are given by: , , with property , and corresponding residues . Applying the ILT and Cauchy’s residue theorem, we obtained the LT solution of :
The solution of Example 2 via MoS (over intervals) and LT () and in each software program is shown in Figure 3a. We noticed that, as , since Re. Figure 3b,c demonstrates the variances between the software when evaluating the solution via MoS (blue curve) or the LT (red curve). Figure 3d demonstrates the accuracy of the LT compared to the analytical MoS via Maple (blue curve) and MATLAB (red curve).
Compared to Example 1, Figure 3b,d demonstrates that the performance error in MATLAB’s MoS solution, relative to the Maple MoS solution and the MATLAB LT solution, decreased. One notable difference between Examples 1 and 2 is the reduced complexity in the history function. In Example 1, the history function was a fifth-order polynomial, whereas, here, the history is a second-order polynomial. In both examples, the LT solution is truncated to 5000 terms. Note that truncation creates ringing in the solution near the history function endpoints. In Figure 3d, the LT error decreases exponentially for both software, while, in Figure 2d, we notice that the error has a maximum peak at around . In some cases, increasing the number of terms reduces the error further and improves the history function approximation, but at the cost of computational complexity and time.
The computation times via each method and software are shown in Table 1. We noticed that Examples 1 and 2 exhibit similar times since we used the same solution structure in both programs, compatible functions between programs, number of terms to be computed, and number of intervals to integrate over. Given the number of terms to be computed for the LT solution, the computation time was higher for both programs compared to the MoS solutions. However, with the use of MATLAB’s symbolic toolbox functions, the computation time for the LT solution was reduced by 4x compared to Maple for both examples.
4.2. Linear NDDE Examples
The NDDE examples to be discussed conform to the general form in Equation (16). These five examples demonstrate solutions formed from poles of order . Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 and Table 2 summarize the solution results, error comparisons between MoS and LT in each programming language, and the computation times for the corresponding example.
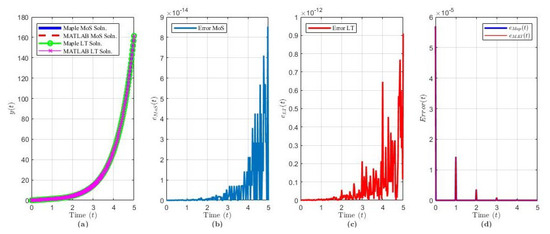
Figure 4.
Solution results of Equation (21) over ( terms): plot of (a) the solution via each method and software, (b) , (c) , (d) and .
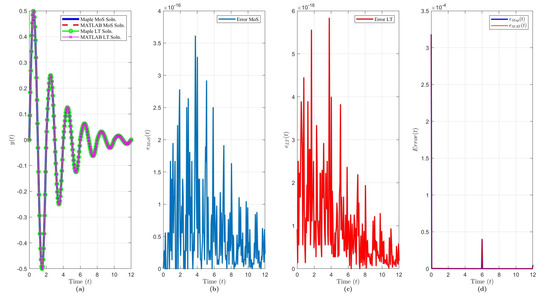
Figure 5.
Solution results of Equation (22) over ( terms): plot of (a) the solution via each method and software, (b) , (c) , (d) and .
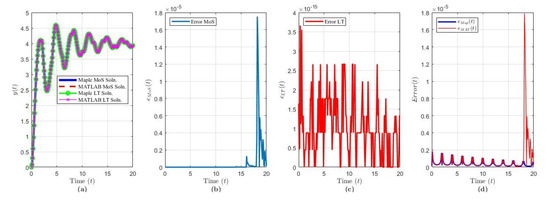
Figure 6.
Solution results of Equation (23) over ( terms): plot of (a) the solution via each method and software, (b) , (c) , (d) and .
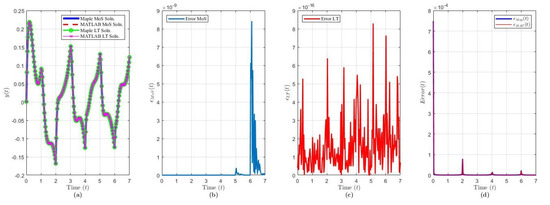
Figure 7.
Solution results of Equation (24) over ( terms): plot of (a) the solution via each method and software, (b) , (c) , (d) and .
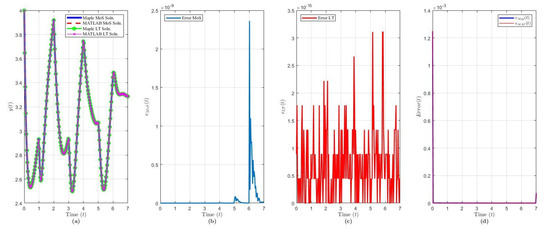
Figure 8.
Solution results of Equation (25) over ( terms): plot of (a) the solution via each method and software, (b) , (c) , (d) and .
Example 3.
Consider
where , , and . This example was utilized in [36] to evaluate the performance of a numerical method for solving linear NDDEs using the generalized Lambert W function [55,56]. Applying MoS for a few partitions, we obtained the following analytical solution:
Taking the LT of Equation (21), we obtained the quasi-polynomial , which has a real pole at with residue (from Equation (4)). The remaining poles and residues are given by the sequence for and , respectively. For large , these poles approach for (see [14]). Since , then, from the stability analysis, the solution will be unstable. Applying the ILT and Cauchy’s residue theorem, we obtained the LT solution of :
The solution of Example 3 via MoS (over intervals) and LT () and in each software program is shown in Figure 4a. Figure 4b,c shows that, as , the variance between each software increases exponentially. Figure 4d indicates that the accuracy of the LT solution improves exponentially as t increases for both programs, and with noticeable spikes every . Compared to the non-neutral examples, NDDE solutions have a higher complexity and, thus, one software may be more beneficial to use vs. another.
Example 4.
Consider
where , , and . This second example was first presented in [57] to study the superconvergence of continuous Galerkin finite element methods for linear NDDEs. Applying the MoS, the following analytical solution of over the interval was obtained, where m is the number of intervals:
The characteristic equation of the system is given by , which has a real pole at with residue . The remaining poles and residues are given by the sequence for and , respectively. These poles are exactly given by for (see [14]). Since and Re, then, from the stability analysis, the solution will be stable. Applying the ILT and Cauchy’s residue theorem, we obtained the LT solution of :
The solution of Example 4 via MoS (over intervals) and LT () and in each software program is shown in Figure 5a. Figure 5b,c shows that the variance between each software is of order and, as , the error decreases with peak errors every for . Figure 5d indicates that the accuracy of the LT solution improves as t increases for both programs, and has an interesting spike located around .
Example 5.
Let us consider
where and . The third example does not contain a state-dependent delay term. This equation is governed by the characteristic quasi-polynomial given by , which has a real pole at with residue . The other poles are given by the sequence . For large , these poles approach for (see [14]). The corresponding residues are given by . Applying the ILT and Cauchy’s residue theorem, we obtained the LT solution of :
The solution of Example 5 via MoS (over intervals) and LT () and in each software program is shown in Figure 6a. Figure 6b,c shows that the variance between each software is of order via MoS and order via LT. From Figure 6d, as , the error decreases with peak errors every for . This indicates that the accuracy of the LT solution improves as t increases for both programs, and has an interesting spike located around .
Example 6.
Let us consider
where , , and . The fourth example has the characteristic quasi-polynomial given by , which has no real poles. The complex poles are given by the sequence . For large , these poles approach for (see [14]). The corresponding residues are given by . Applying the ILT and Cauchy’s residue theorem, we obtained the LT solution of :
The solution of Example 6 via MoS (over intervals) and LT () and in each software program is shown in Figure 7a. Figure 7b,c shows that the variance between each software is of order via MoS and order via LT. We see similar deviances in the MoS solutions compared to Example 5 between each software. A larger timespan would be needed to deduce conclusions on the similarities of the LT solution between each software. From Figure 6d, as , the error decreases, with peak errors every for .
Example 7.
Let us consider
where , , and . The fifth example in Equation (25) has the characteristic quasi-polynomial given by , which has a real pole at with residue . The remaining poles are divided into two sequences (see [14]). One sequence of poles, , lies relatively close to the imaginary axis, which, for large , approaches for . The second sequence of poles, , is offset from the imaginary axis, which, for large , approaches for . The corresponding residues are given by . Then, the solution is of the form
The solution of Example 7 via MoS (over intervals) and LT () and in each software program is shown in Figure 8a. Figure 8b,c shows that the variance between each software is of order via MoS and order via LT. We see similar deviances in the MoS solutions near the boundary intervals compared to Example 5. Relative to previous NDDE examples, Example 7 has a larger error in the LT solution vs. the analytical MoS via both software, with an order of magnitude as shown in Figure 8d, despite the simplicity of the history function. Nevertheless, we can observe that, as , the error decreases.
The computation times via each method and software are shown in Table 2. We make the following notes regarding the time computation results:
- From Maple MoS solutions, the order of time computation is as follows:Example 5 > Example 6 > Example 7 > Example 4 > Example 3.
- From Maple LT solutions, the order of time computation is as follows:Example 7 > Example 3 > Example 6 > Example 5 > Example 4.
- From MATLAB MoS solutions, the order of time computation is as follows:Example 4 > Example 5 > Example 7 > Example 6 > Example 3.
- From MATLAB LT solutions, the order of time computation is as follows:Example 3 > Example 7 > Example 6 > Example 4 > Example 5.
From these results, we notice that the computation time is dependent on the complexity of the history function, the number of terms used in the LT solution, the number of intervals used in the MoS solution, and the magnitude of the parameters of the NDDE. Regarding MoS solutions, Examples 4 and 5 both have a complicated history function (one is a fourth-order polynomial and the other is periodic), and we observe that both programs took longer to compute the solutions. Regarding LT solutions, Examples 3 and 7 took the most time to compute via both software, even though Example 1 had the most terms. The differences between these examples is that Example 7 consisted of an extra sequence of poles due to the different delays in the state-dependent term and the derivative-of-state-dependent term. Nevertheless, Example 3 was found to be the quickest to compute via MoS for both softwares, whereas Examples 4 and 5 were found to be the quickest to compute via LT. We also note that, in all cases, Maple’s computation time was found to significantly outrank MATLAB’s computation time.
We notice that Examples 3 and 4 exhibit similar times since we used the same solution structure in both programs, compatible functions between programs, number of terms to be computed, and number of intervals to integrate over. Given the number of terms to be computed for the LT solution, the computation time was higher for both programs compared to the MoS solutions. However, with the use of MATLAB’s symbolic toolbox functions, the computation time for the LT solution was reduced by 4x compared to Maple for both examples.
5. Conclusions
In this paper, we investigated the symbolic mathematical computational performance of the software program Maple and the programming language MATLAB when applying the method of steps (MoS) and the Laplace transform (LT) methods to solve neutral and retarded linear DDEs. Of particular interest was comparing how these programs performed. The exact, analytic MoS solution was used to aid in this comparison. However, the main reason for why most of the graphs only include the first 5–10 time-intervals is due to the fact that the method of steps often could not compute the solution beyond these intervals. The Laplace solution is an infinite series, which requires one to compute the relevant poles along with their associated residues. We computed the analytical solutions using Maple and MATLAB in order to take advantage of their respective symbolic computation features. The accuracy of the Laplace method solutions were measured by comparing them with those obtained by the method of steps. The Laplace method produces an analytical solution that can be evaluated at any particular value of time. The results obtained emphasize that symbolic computational software is a powerful tool, capable of computing analytic solutions for linear delay differential equations, including neutral ones. From a computational viewpoint, we found that the computation time is dependent on the complexity of the history function, the number of terms used in the LT solution, the number of intervals used in the MoS solution, and the DDE parameters. We found that, for linear non-neutral DDEs, MATLAB symbolic computations were faster than the ones from Maple. However, for the linear neutral DDEs, which are often more difficult to solve, Maple was faster. Regarding accuracy, it is important to point out that we compared Maple and MATLAB via MoS and LT. The differences between both software were smaller for the LT in comparison to the MoS. In addition, the accuracy of the LT solutions using Maple were, in a few cases, slightly better than the ones generated by MATLAB. However, both were reliable, but we can mention that Maple lightly surpasses MATLAB in symbolic computation due to its symbolic capabilities/nature. Finally, we would like to mention some limitations of the LT irrespective of the software choice. The LT method is only applicable for linear DDEs due to the Laplace transform definition. Thus, nonlinear DDEs should be solved by other means. In addition, we implemented the LT for scalar linear DDEs with constant coefficients and a finite number of delays. However, the LT method can also be extended to solve first-order linear DDE systems. In this work, we applied the LT method to homogeneous and non-homogenous DDEs. Future works that are in progress include solving linear non-homogeneous DDEs with Dirac delta function inputs, with one related goal being to develop a Green’s function type kernel.
Author Contributions
Conceptualization, M.S. and G.G.-P.; methodology, M.S., G.K. and G.G.-P.; software, M.S., G.K. and G.G.-P.; validation, M.S., G.K. and G.G.-P.; formal analysis, M.S., G.K. and G.G.-P.; investigation, M.S., G.K. and G.G.-P.; resources, M.S., G.K. and G.G.-P.; writing—original draft preparation, M.S., G.K. and G.G.-P.; writing—review and editing, M.S., G.K. and G.G.-P.; visualization, M.S., G.K. and G.G.-P.; supervision, G.G.-P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Alnæs, M.S.; Mardal, K.A. On the efficiency of symbolic computations combined with code generation for finite element methods. ACM Trans. Math. Softw. TOMS 2010, 37, 1–26. [Google Scholar] [CrossRef]
- Chaparro, L.; Akan, A. Signals and Systems Using MATLAB; Academic Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Gander, W.; Gander, M.J.; Kwok, F. Scientific Computing-An Introduction Using Maple and MATLAB; Springer: Berlin/Heidelberg, Germany, 2014; Volume 11. [Google Scholar]
- Herber, D.R.; Sundarrajan, A.K. On the uses of linear-quadratic methods in solving nonlinear dynamic optimization problems with direct transcription. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Virtual, 16–19 November 2020; Volume 84546, p. V07AT07A003. [Google Scholar]
- Petcu, D.; Gheorghiu, D. PAVIS: A parallel virtual environment for solving large mathematical problems. In Parallel Computing: Advances and Current Issues; World Scientific: Singapore, 2002; pp. 490–497. [Google Scholar]
- Sam, P.; Nanakorn, P.; Theerakittayakorn, K.; Suttakul, P. Closed-form effective elastic constants of frame-like periodic cellular solids by a symbolic object-oriented finite element program. Int. J. Mech. Mater. Des. 2017, 13, 363–383. [Google Scholar] [CrossRef]
- Dorrah, H.T.; Gabr, W.I.; Elsayed, M.S. Generic symbolic parameters varying systems frameworks versus other techniques: Returning back to the roots. Alex. Eng. J. 2018, 57, 3577–3594. [Google Scholar] [CrossRef]
- Falcone, A.; Garro, A.; Mukhametzhanov, M.S.; Sergeyev, Y.D. A Simulink-based software solution using the Infinity Computer methodology for higher order differentiation. Appl. Math. Comput. 2021, 409, 125606. [Google Scholar] [CrossRef]
- Gama, S.M.; Chertovskih, R.; Zheligovsky, V. Computation of kinematic and magnetic α-effect and eddy diffusivity tensors by Padé approximation. Fluids 2019, 4, 110. [Google Scholar] [CrossRef]
- Kovács, Z. Real-time animated dynamic geometry in the classrooms by using fast Gröbner basis computations. Math. Comput. Sci. 2017, 11, 351–361. [Google Scholar] [CrossRef]
- Krämer, W. Computer-assisted proofs and symbolic computations. Serdica J. Comput. 2010, 4, 73–84. [Google Scholar]
- Erneux, T. Applied Delay Differential Equations; Springer: Berlin/Heidelberg, Germany, 2009; Volume 3. [Google Scholar]
- Ha, P.; Mehrmann, V. Analysis and numerical solution of linear delay differential-algebraic equations. BIT Numer. Math. 2016, 56, 633–657. [Google Scholar] [CrossRef]
- Kerr, G.; González-Parra, G. Accuracy of the Laplace transform method for linear neutral delay differential equations. Math. Comput. Simul. 2022, 197, 308–326. [Google Scholar] [CrossRef]
- Kerr, G.; González-Parra, G.; Sherman, M. A new method based on the Laplace transform and Fourier series for solving linear neutral delay differential equations. Appl. Math. Comput. 2022, 420, 126914. [Google Scholar] [CrossRef]
- Roussel, M.R. Delay-differential equations. In Nonlinear Dynamics: A Hands-on Introductory Survey; Morgan & Claypool Publishers: San Rafael, CA, USA, 2019. [Google Scholar]
- Smith, H.L. An Introduction to Delay Differential Equations with Applications to the Life Sciences; Springer: New York, NY, USA, 2011; Volume 57. [Google Scholar]
- Alfifi, H.Y. Feedback control for a diffusive and delayed Brusselator model: Semi-analytical solutions. Symmetry 2021, 13, 725. [Google Scholar] [CrossRef]
- Aljahdaly, N.H.; El-Tantawy, S. On the multistage differential transformation method for analyzing damping Duffing oscillator and its applications to plasma physics. Mathematics 2021, 9, 432. [Google Scholar] [CrossRef]
- Chamekh, M.; Elzaki, T.M.; Brik, N. Semi-analytical solution for some proportional delay differential equations. SN Appl. Sci. 2019, 1, 148. [Google Scholar] [CrossRef]
- González-Parra, G.; Arenas, A.J.; Jódar, L. Piecewise finite series solutions of seasonal diseases models using multistage Adomian method. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 3967–3977. [Google Scholar] [CrossRef]
- Shakeri, F.; Dehghan, M. Solution of delay differential equations via a homotopy perturbation method. Math. Comput. Model. 2008, 48, 486–498. [Google Scholar] [CrossRef]
- Faheem, M.; Raza, A.; Khan, A. Collocation methods based on Gegenbauer and Bernoulli wavelets for solving neutral delay differential equations. Math. Comput. Simul. 2021, 180, 72–92. [Google Scholar] [CrossRef]
- Faheem, M.; Raza, A.; Khan, A. Wavelet collocation methods for solving neutral delay differential equations. Int. J. Nonlinear Sci. Numer. Simul. 2021. [Google Scholar] [CrossRef]
- Mohamed, S.; Khader, M. Numerical treatment for first order neutral delay differential equations using spline functions. Eng. Math. Lett. 2012, 1, 32–43. [Google Scholar]
- Cimen, E.; Ekinci, Y. Numerical method for a neutral delay differential problem. Int. J. Math. Comput. Sci. 2017, 1, 1–11. [Google Scholar]
- Adel, W.; Sabir, Z. Solving a new design of nonlinear second-order Lane–Emden pantograph delay differential model via Bernoulli collocation method. Eur. Phys. J. Plus 2020, 135, 427. [Google Scholar] [CrossRef]
- Bellour, A.; Bousselsal, M.; Laib, H. Numerical Solution of Second-Order Linear Delay Differential and Integro-Differential Equations by Using Taylor Collocation Method. Int. J. Comput. Methods 2020, 17, 1950070. [Google Scholar] [CrossRef]
- Aziz, I.; Amin, R. Numerical solution of a class of delay differential and delay partial differential equations via Haar wavelet. Appl. Math. Model. 2016, 40, 10286–10299. [Google Scholar] [CrossRef]
- Peykrayegan, N.; Ghovatmand, M.; Noori Skandari, M. On the convergence of Jacobi-Gauss collocation method for linear fractional delay differential equations. Math. Methods Appl. Sci. 2021, 44, 2237–2253. [Google Scholar] [CrossRef]
- Elmer, C.E.; Van Vleck, E.S. Anisotropy, propagation failure, and wave speedup in traveling waves of discretizations of a Nagumo PDE. J. Comput. Phys. 2003, 185, 562–582. [Google Scholar] [CrossRef]
- Van Vleck, E.S.; Mallet-Paret, J.; Cahn, J.W. Traveling wave solutions for systems of ODEs on a two-dimensional spatial lattice. SIAM J. Appl. Math. 1998, 59, 455–493. [Google Scholar] [CrossRef]
- Hale, J.K.; Lunel, S.M.V. Introduction to Functional Differential Equations; Springer: Berlin/Heidelberg, Germany, 2013; Volume 99. [Google Scholar]
- Cooke, K.L. Differential—Difference equations. In International Symposium on Nonlinear Differential Equations and Nonlinear Mechanics; Elsevier: Amsterdam, The Netherlands, 1963; pp. 155–171. [Google Scholar]
- Heffernan, J.M.; Corless, R.M. Solving some delay differential equations with computer algebra. Math. Sci. 2006, 31, 21–34. [Google Scholar]
- Jamilla, C.; Mendoza, R.; Mezo, I. Solutions of neutral delay differential equations using a generalized Lambert W function. Appl. Math. Comput. 2020, 382, 125334. [Google Scholar] [CrossRef]
- Cimen, E.; Uncu, S. On the solution of the delay differential equation via Laplace transform. Commun. Math. Appl. 2020, 11, 379–387. [Google Scholar]
- Jamilla, C.U.; Mendoza, R.G.; Mendoza, V.M.P. Explicit solution of a Lotka-Sharpe-McKendrick system involving neutral delay differential equations using the r-Lambert W function. Math. Biosci. Eng. 2020, 17, 5686–5708. [Google Scholar] [CrossRef]
- Bellen, A.; Guglielmi, N.; Ruehli, A.E. Methods for linear systems of circuit delay differential equations of neutral type. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1999, 46, 212–215. [Google Scholar] [CrossRef]
- Shampine, L.F.; Thompson, S. Solving ddes in matlab. Appl. Numer. Math. 2001, 37, 441–458. [Google Scholar] [CrossRef]
- Ebaid, A.; Al-Enazi, A.; Albalawi, B.Z.; Aljoufi, M.D. Accurate approximate solution of Ambartsumian delay differential equation via decomposition method. Math. Comput. Appl. 2019, 24, 7. [Google Scholar] [CrossRef]
- González-Parra, G.; Sultana, S.; Arenas, A.J. Mathematical modeling of toxoplasmosis considering a time delay in the infectivity of oocysts. Mathematics 2022, 10, 354. [Google Scholar] [CrossRef]
- Rihan, F.A. Delay Differential Equations and Applications to Biology; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Alagoz, B.B.; Tepljakov, A.; Ates, A.; Petlenkov, E.; Yeroglu, C. Time-domain identification of one noninteger order plus time delay models from step response measurements. Int. J. Model. Simul. Sci. Comput. 2019, 10, 1941011. [Google Scholar] [CrossRef]
- Altosole, M.; Campora, U.; Figari, M.; Laviola, M.; Martelli, M. A diesel engine modelling approach for ship propulsion real-time simulators. J. Mar. Sci. Eng. 2019, 7, 138. [Google Scholar] [CrossRef]
- Krämer, M.; Rösmann, C.; Hoffmann, F.; Bertram, T. Model predictive control of a collaborative manipulator considering dynamic obstacles. Optim. Control. Appl. Methods 2020, 41, 1211–1232. [Google Scholar] [CrossRef]
- van den Berg, R.; Lefeber, E.; Rooda, K. Modeling and control of a manufacturing flow line using partial differential equations. IEEE Trans. Control Syst. Technol. 2007, 16, 130–136. [Google Scholar] [CrossRef]
- Bauer, R.J.; Mo, G.; Krzyzanski, W. Solving delay differential equations in S-ADAPT by method of steps. Comput. Methods Programs Biomed. 2013, 111, 715–734. [Google Scholar] [CrossRef]
- Kalmár-Nagy, T. Stability analysis of delay-differential equations by the method of steps and inverse Laplace transform. Differ. Equ. Dyn. Syst. 2009, 17, 185–200. [Google Scholar] [CrossRef]
- Kaslik, E.; Sivasundaram, S. Analytical and numerical methods for the stability analysis of linear fractional delay differential equations. J. Comput. Appl. Math. 2012, 236, 4027–4041. [Google Scholar] [CrossRef]
- Corless, R.M.; Gonnet, G.H.; Hare, D.E.; Jeffrey, D.J.; Knuth, D.E. On the LambertW function. Adv. Comput. Math. 1996, 5, 329–359. [Google Scholar] [CrossRef]
- Yi, S.; Duan, S.; Nelson, P.; Ulsoy, A. The Lambert W Function Approach to Time Delay Systems and the LambertW_DDE Toolbox. IFAC Proc. Vol. 2012, 45, 114–119. [Google Scholar] [CrossRef]
- Brown, J.W.; Churchill, R.V. Complex Variables and Applications, 8th ed.; McGraw-Hill: New York, NY, USA, 2009. [Google Scholar]
- Ablowitz, M.J.; Fokas, A.S. Complex Variables: Introduction and Applications, 2nd ed.; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar] [CrossRef]
- Mező, I.; Baricz, A. On the generalization of the Lambert function. Trans. Am. Math. Soc. 2017, 369, 7917–7934. [Google Scholar] [CrossRef]
- Scott, T.C.; Mann, R.; Martinez, R.E. General relativity and quantum mechanics: Towards a generalization of the Lambert W function A Generalization of the Lambert W Function. Appl. Algebra Eng. Commun. Comput. AAECC 2006, 17, 41–47. [Google Scholar] [CrossRef]
- Hongyu, Q.; Qifeng, Z.; Shaohua, W. The continuous Galerkin finite element methods for linear neutral delay differential equations. Appl. Math. Comput. 2019, 346, 76–85. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

