A Continuous Model of Marital Relations with Stochastic Differential Equations
Abstract
1. Introduction
1.1. Continuous Model
Deterministic Case
1.2. Stochastic Model
2. Analysis of the Deterministic Case
Qualitative Analysis for the Bilinear Influence Function
- (1)
- A saddle point if:
- (2)
- A node if:It will be stable if or unstable if .
- (3)
- A spiral if:it will be stable if and unstable if .
- (4)
- A center if:
- (5)
- A proper or improper node if:
- (i)
- Saddle points (and therefore unstable) if and only if , and or
- (ii)
- Stable nodes if and only if and .
3. Numerical Simulations
3.1. Single Individual with Validating Personality
3.2. Validating Wife and Husband with Bilinear Influence Function
3.3. Piece-Wise Influence Function
3.4. Piece-Wise Linear Influence Function
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Strogatz, S.H. Nonlinear Dynamics and Chaos with Student Solutions Manual: With Applications to Physics, Biology, Chemistry, and Engineering; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Elishakoff, I. Differential Equations of Love and Love of Differential Equations. J. Humanist. Math. 2019, 9, 226–246. [Google Scholar] [CrossRef]
- Ghosh, K. Love between Two Individuals in a Romantic Relationship: A Newly Proposed Mathematical Model. In Proceedings of the 7th IMT-GT International Conference on Mathematics, Statistics and Its Applications, Bangkok, Thailand, 21–23 July 2011; Volume 21. [Google Scholar]
- Rey, J.M. A mathematical model of sentimental dynamics accounting for marital dissolution. PLoS ONE 2010, 5, e9881. [Google Scholar] [CrossRef] [PubMed]
- Binder, P.M. Chaos and Love Affairs. Math. Mag. 2000, 73, 235–236. [Google Scholar] [CrossRef]
- Gragnini, A.; Rinaldi, S.; Feichtlinger, G. Cyclic Dynamics in Romantic Relationships. Int. J. Bifurc. Chaos 1997, 7, 2611–2619. [Google Scholar] [CrossRef]
- Gottman, J.M. The Mathematics of Marriage: Dynamic Nonlinear Models; MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Allen, L.J. Introduction to Mathematical Biology; Pearson/Prentice Hall: Upper Saddle River, NJ, USA, 2007. [Google Scholar]
- Evans, L.C. An Introduction to Stochastic Differential Equations; American Mathematical Society: Providence, RI, USA, 2012; Volume 82. [Google Scholar]
- Allen, E. Modeling with Itô Stochastic Differential Equations; Springer Science & Business Media: Berlin, Germany, 2007; Volume 22. [Google Scholar]
- Hindmarsh, A.C. Ordinary Differential Equation System Solver; Technical Report; Lawrence Livermore National Laboratory: Livermore, CA, USA, 1992. [Google Scholar]
- Kloeden, P.; Platen, E. Applications of mathematics. In Numerical Solution of Stochastic Differential Equations; Springer: Berlin, Germany, 1992; Volume 23. [Google Scholar]
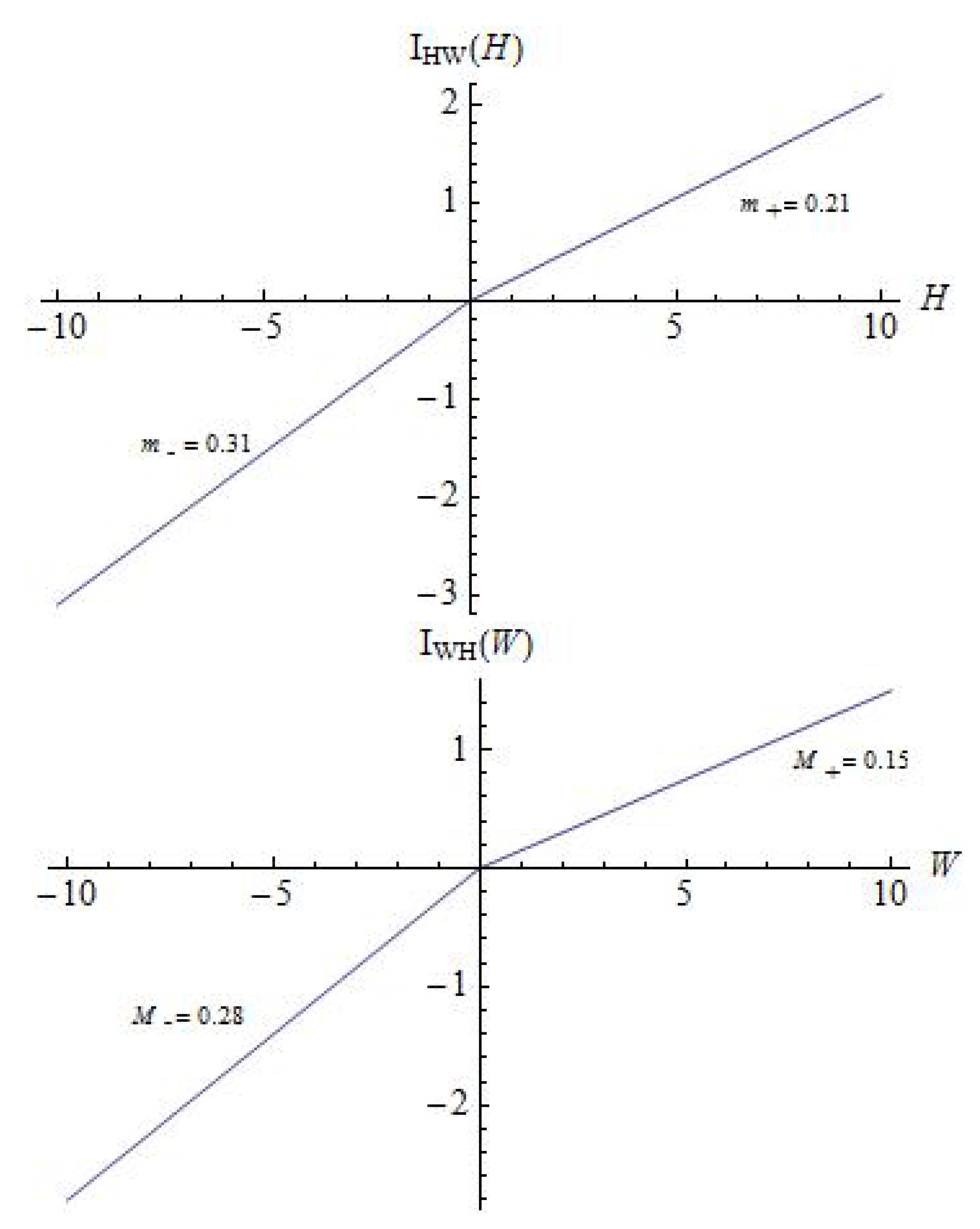
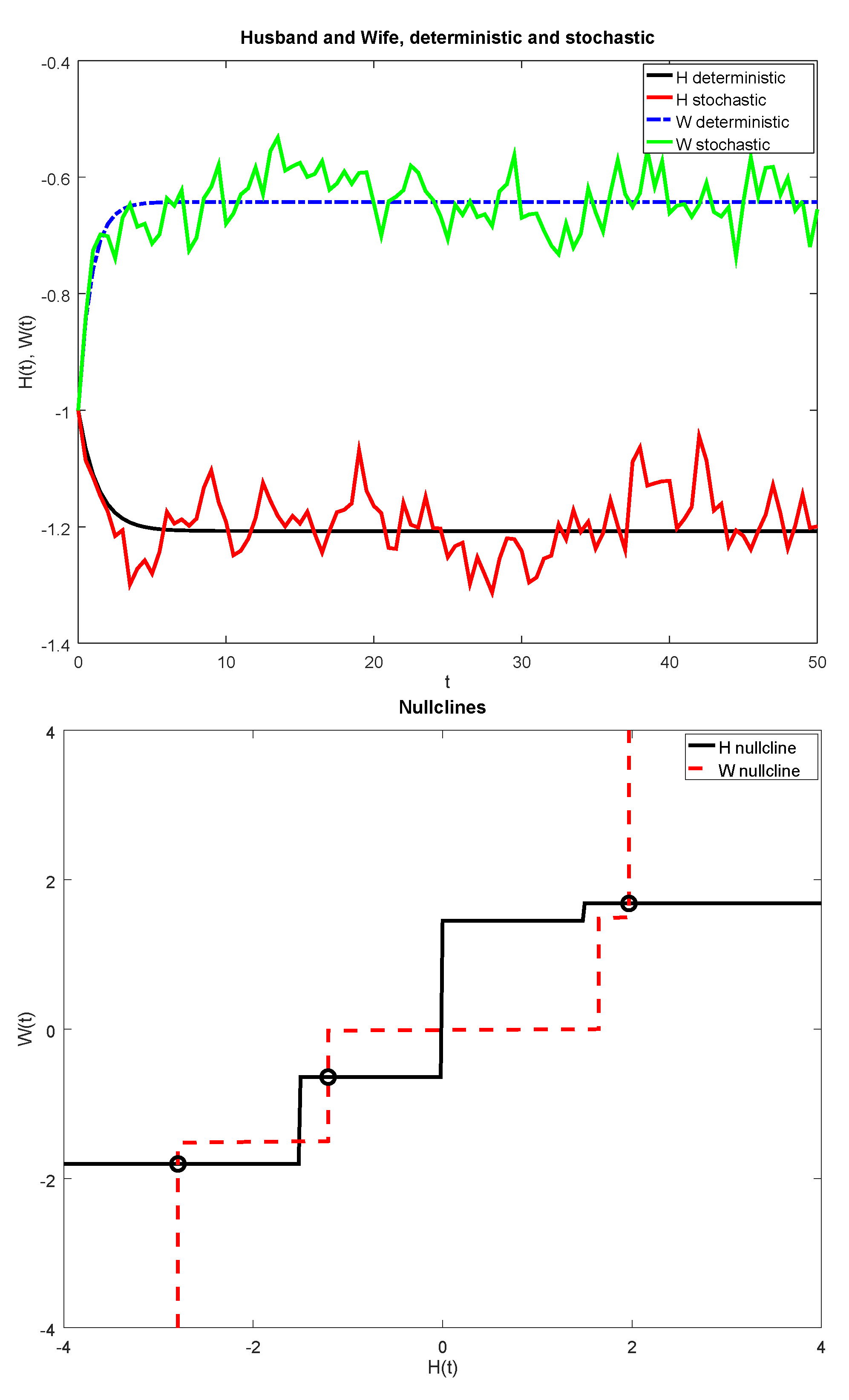

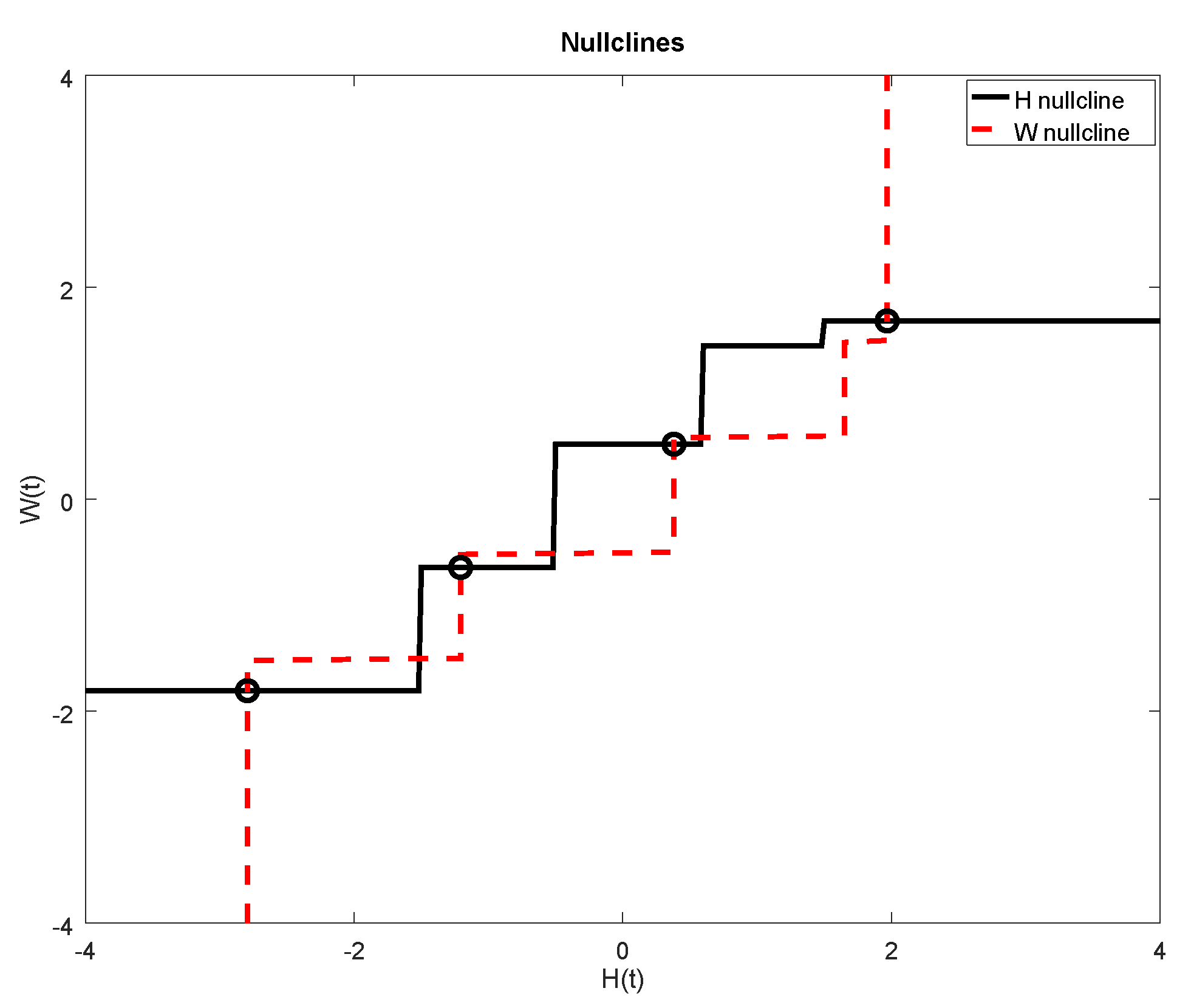
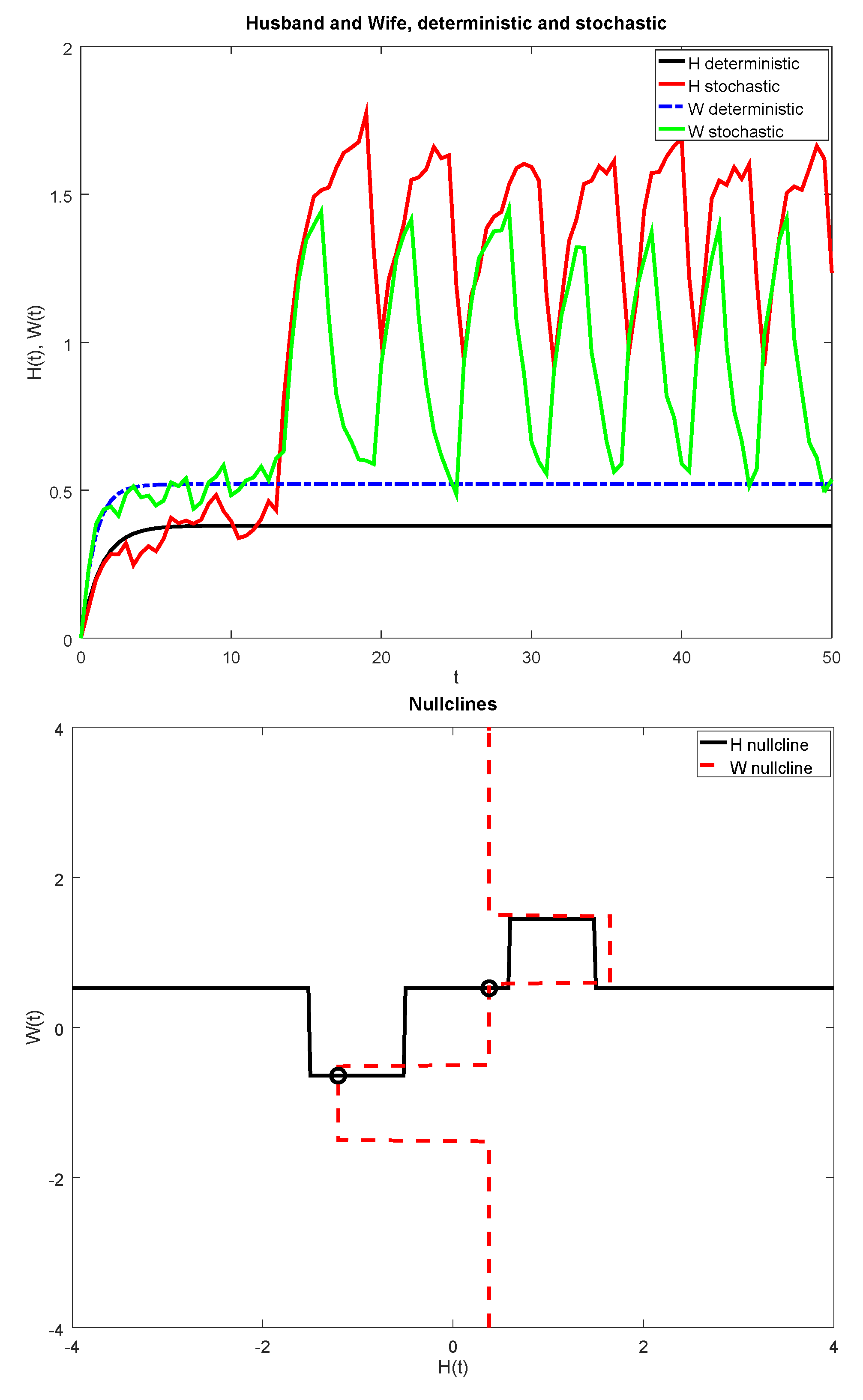
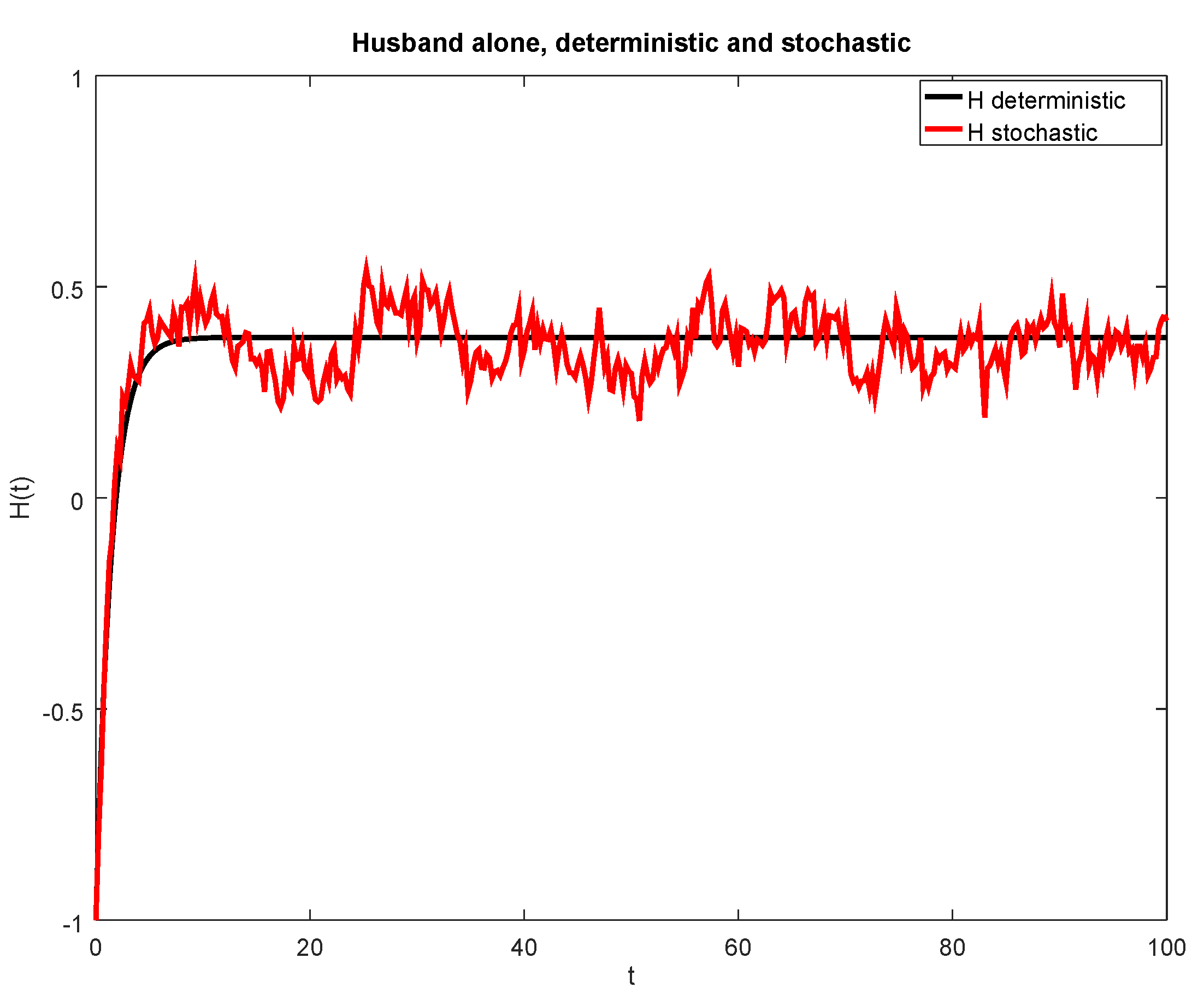
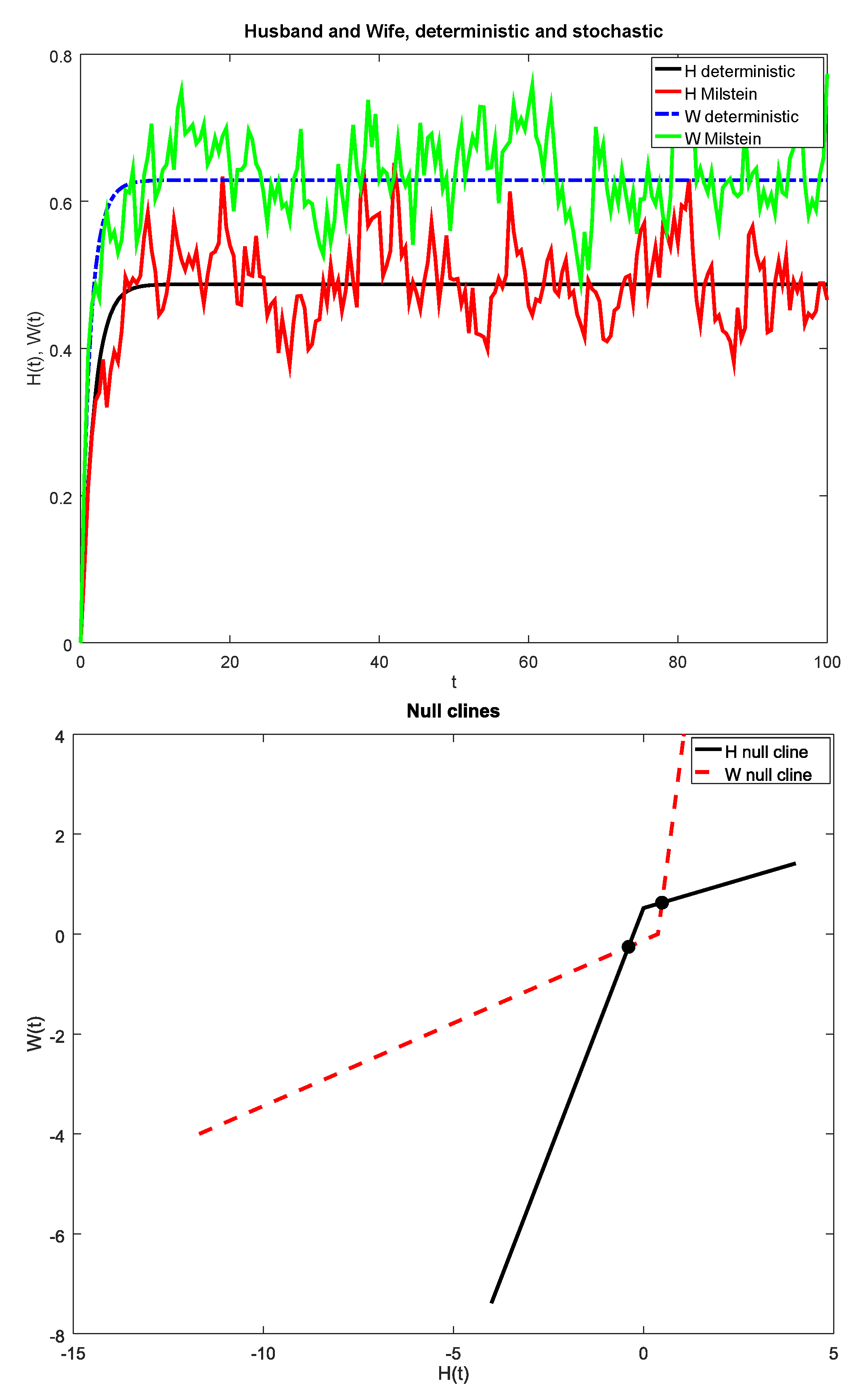

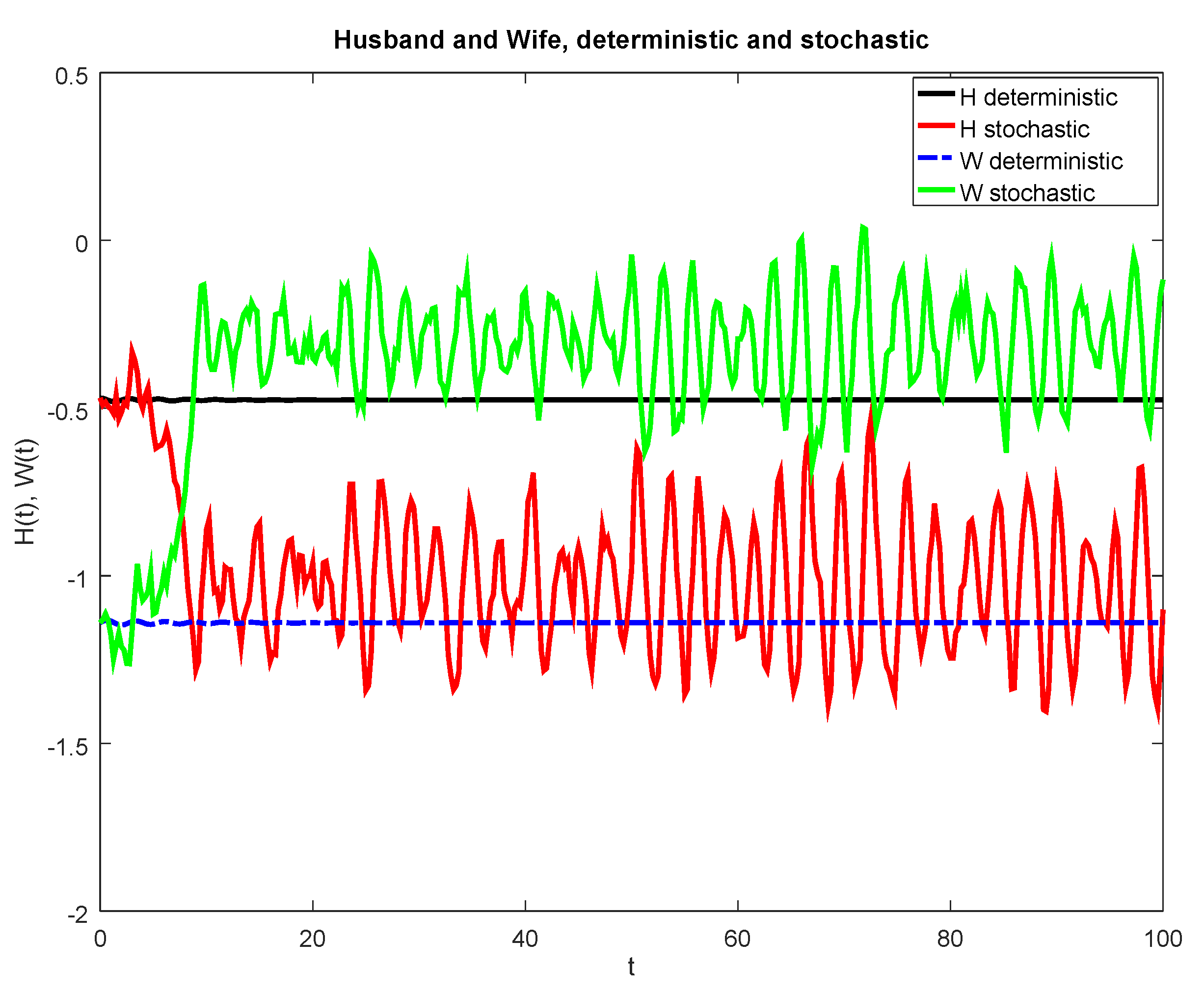
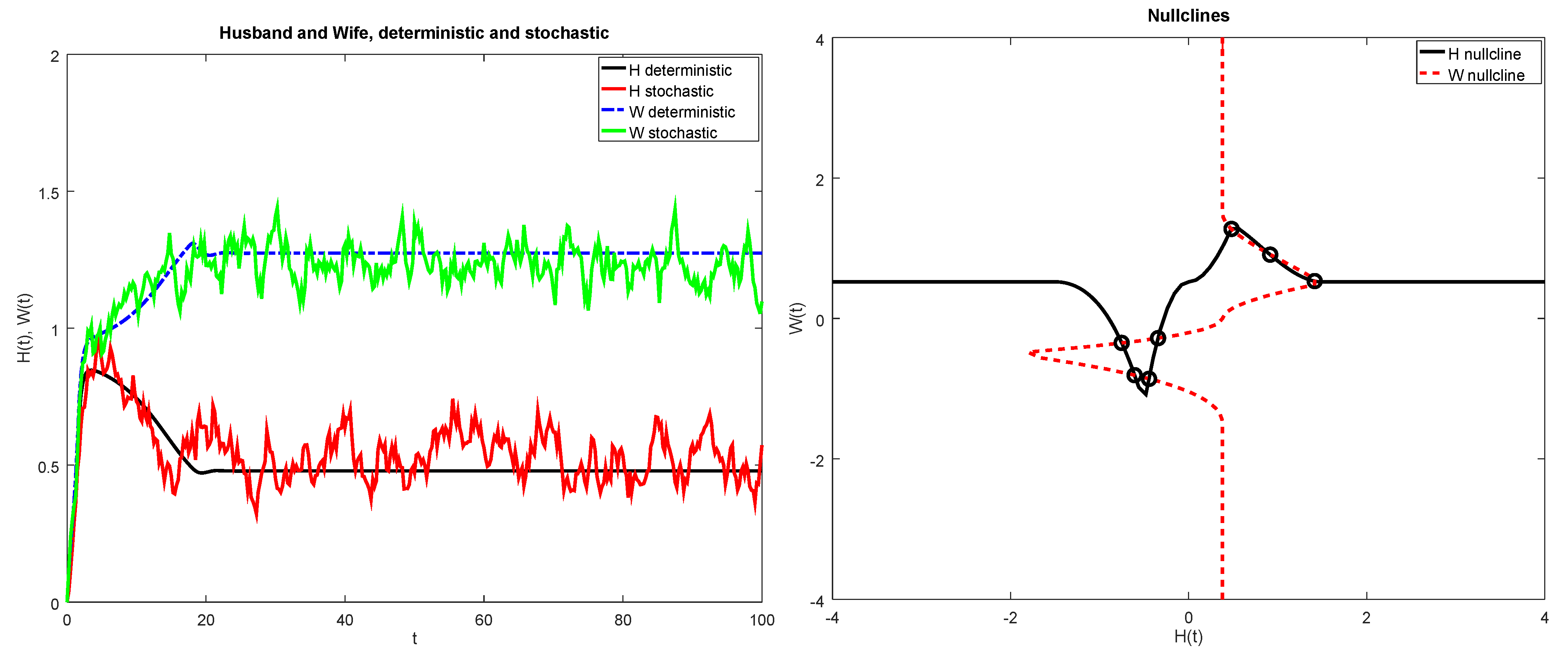

| Figure Number | Type of Influence Function | Parameters |
|---|---|---|
| 2 | Zero influence function | , . |
| 3 | Bilinear | , , , , ; , , . |
| 4 | Piece-wise constant | , , , , , , |
| 5 | Piece-wise constant | , , , , , , , |
| 6 | Piece-wise constant with saturation | , , , , , , , |
| 7 and 8 | Piece-wise linear | , , ; , , |
| 9 and 10 | Piece-wise cubic | , , ; , , |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen-Charpentier, B.; Garza-Hume, C.E.; Jorge, M.d.C. A Continuous Model of Marital Relations with Stochastic Differential Equations. Math. Comput. Appl. 2021, 26, 3. https://doi.org/10.3390/mca26010003
Chen-Charpentier B, Garza-Hume CE, Jorge MdC. A Continuous Model of Marital Relations with Stochastic Differential Equations. Mathematical and Computational Applications. 2021; 26(1):3. https://doi.org/10.3390/mca26010003
Chicago/Turabian StyleChen-Charpentier, Benito, Clara Eugenia Garza-Hume, and María del Carmen Jorge. 2021. "A Continuous Model of Marital Relations with Stochastic Differential Equations" Mathematical and Computational Applications 26, no. 1: 3. https://doi.org/10.3390/mca26010003
APA StyleChen-Charpentier, B., Garza-Hume, C. E., & Jorge, M. d. C. (2021). A Continuous Model of Marital Relations with Stochastic Differential Equations. Mathematical and Computational Applications, 26(1), 3. https://doi.org/10.3390/mca26010003






