A Saint-Venant Model for Overland Flows with Precipitation and Recharge
Abstract
:1. Introduction
2. Navier–Stokes Equations with Infiltration and Recharge
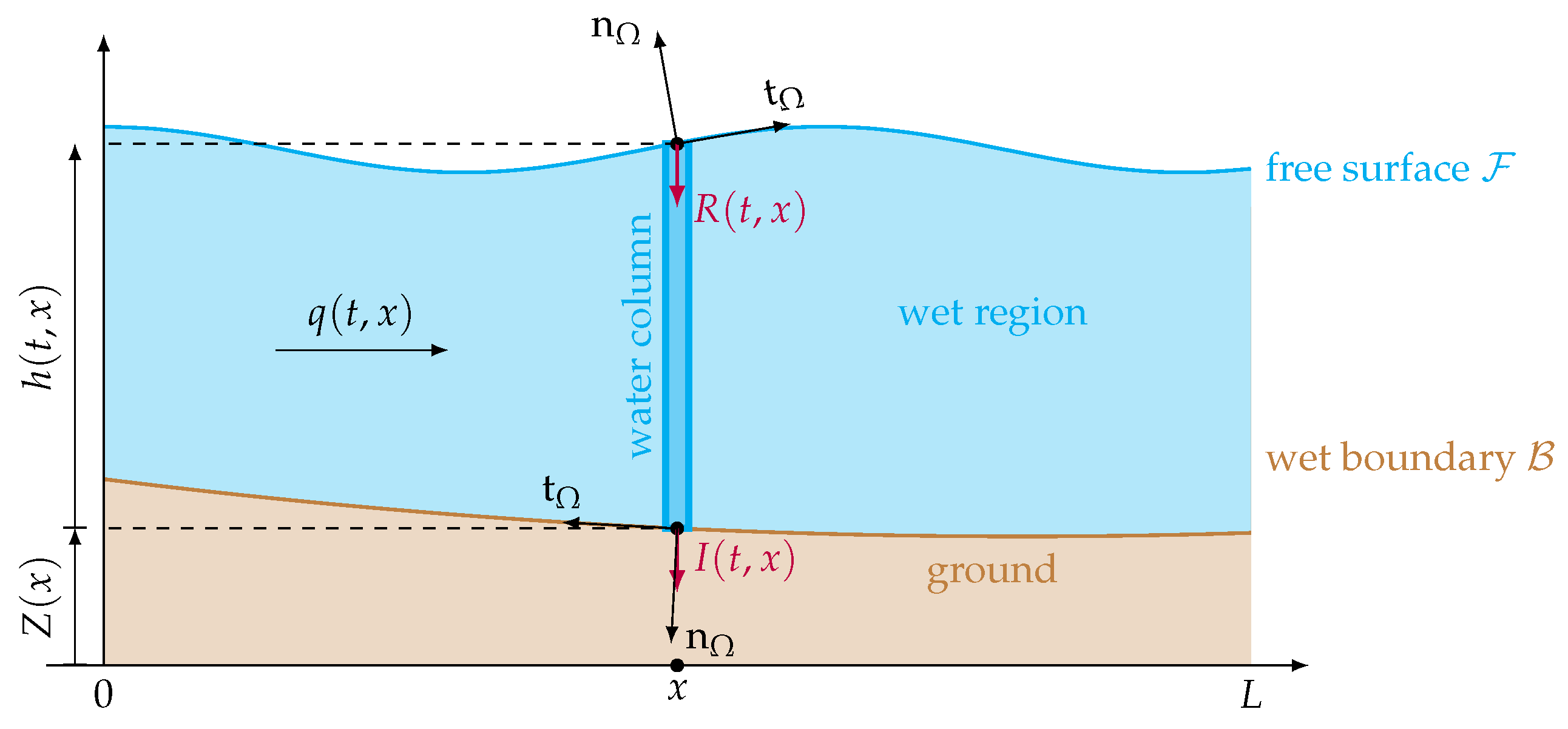
2.1. Geometric Set-Up and the Two-Dimensional Navier—Stokes Equations
2.2. The Wet Boundary
2.3. The Free Surface
2.4. Mixing Friction
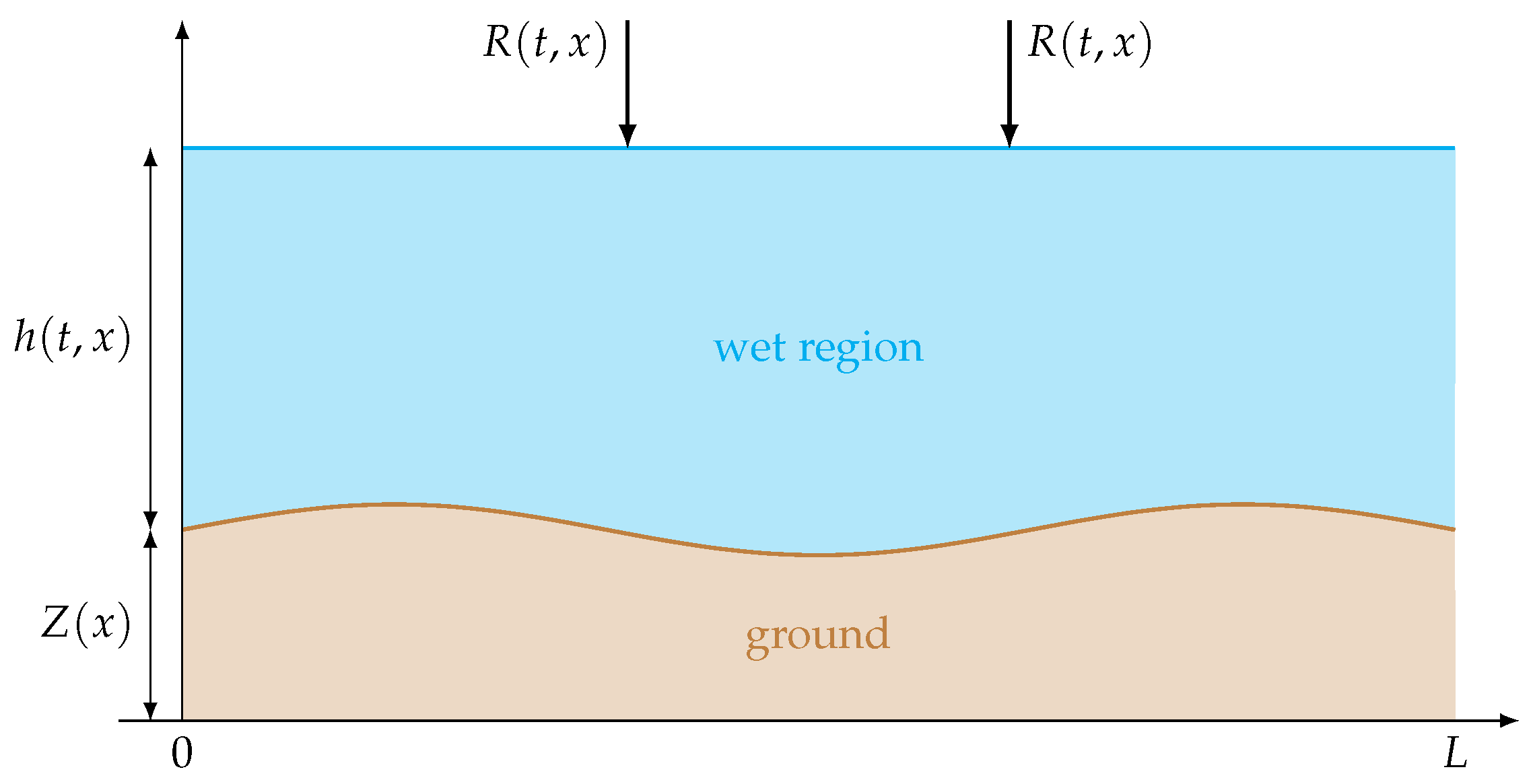
3. Saint-Venant System with Recharge via Vertical Averaging
3.1. Dimensionless Navier–Stokes Equations
3.2. Remark Slip vs. No-Slip Boundary Condition
3.3. First-Order Approximation of the Dimensionless Navier–Stokes Equations
3.4. The Saint-Venant System with Recharge
3.5. Example (Lake at Rest and Filling the Lake)
3.6. Why the Mixing Friction?
4. Entropy
4.1. Theorem (Hyperbolicity and Stability)
- (a)
- System (70) is strictly hyperbolic on the set .
- (b)
- If is smooth and , we have the velocity balance equation
- (a)
- The Jacobian of (70)’s flux function is given bywith eigenvaluesFor these eigenvalues to be real and distinct, we require that ; the Jacobian matrix is thus diagonalizable and system (70) is strictly hyperbolic on the set .
- (b)
- We rewrite the conservation of momentum equation in system (70) in terms of the unknowns , with , asApplying the product rule to the first term of (82) and substituting in the conservation of mass equation, we getfrom which we can cancel on both sides. Using the product rule again, we have thatwhich can be substituted into (83) to giveenabling us to now cancel . We note thatSubstituting this into (85) and dividing by h throughout, we getMaking the further substitutionand grouping derivatives of x, we have
4.2. Remark (Friction Effects)
4.3. Theorem (Entropy Production)
4.4. Remark (Entropy–Entropy-Flux Pairs and Entropy Production)
4.5. Remark (Discontinuous Solutions)
5. The Numerical Model
5.1. Well-Balanced Schemes
5.2. Kinetic Function
5.3. Proposition (Macroscopic–Microscopic Relations)
5.4. Kinetic Connection to Saint-Venant
5.5. Remark (Advantages of the Kinetic Formulation)
- (i)
- In contrast to previous work (e.g., [19]), the kinetic Equation (113) contains an extra term accounting for precipitation and infiltration effects. This departure is crucial for the derivation of the fluxes that lead to a well-balanced scheme in the presence of such terms.
- (ii)
- We also note that, even though the Maxellian M is constructed for still water steady states, where , we can still use it here to ensure a well-balanced scheme.
- (iii)
- In general, it is easier to find a numerical scheme to solve Equation (113) for M that has the properties we desire, such as entropy stability, than to solve the full Saint-Venant system for h and u. However, in finding M, we can calculate h and by virtue of the macro-/microscopic relations (Proposition 5.3). In fact, M is never calculated explicitly; rather, the functionis used to build the fluxes appearing in a finite volume method, as we shall explain in Section 5.6.
- (iv)
- As shown and fixed by Xia et al. [48], Buttinger-Kreuzhuber et al. [49], and Taccone et al. [50], some other well-balanced numerical methods fail to correctly represent the effect of the topography, especially when the water height h is close to zero, while the kinetic approach used herein supports arbitrarily small h.
5.6. Discretization and Kinetic Fluxes
- (i)
- : movement of water with positive velocity () from within cell to cell ;
- (ii)
- : movement of water with negative velocity () from within cell to cell . This term is decomposed a second time into components reflecting whether the water has enough energy to overcome the topography and friction to enter or leave the cell.
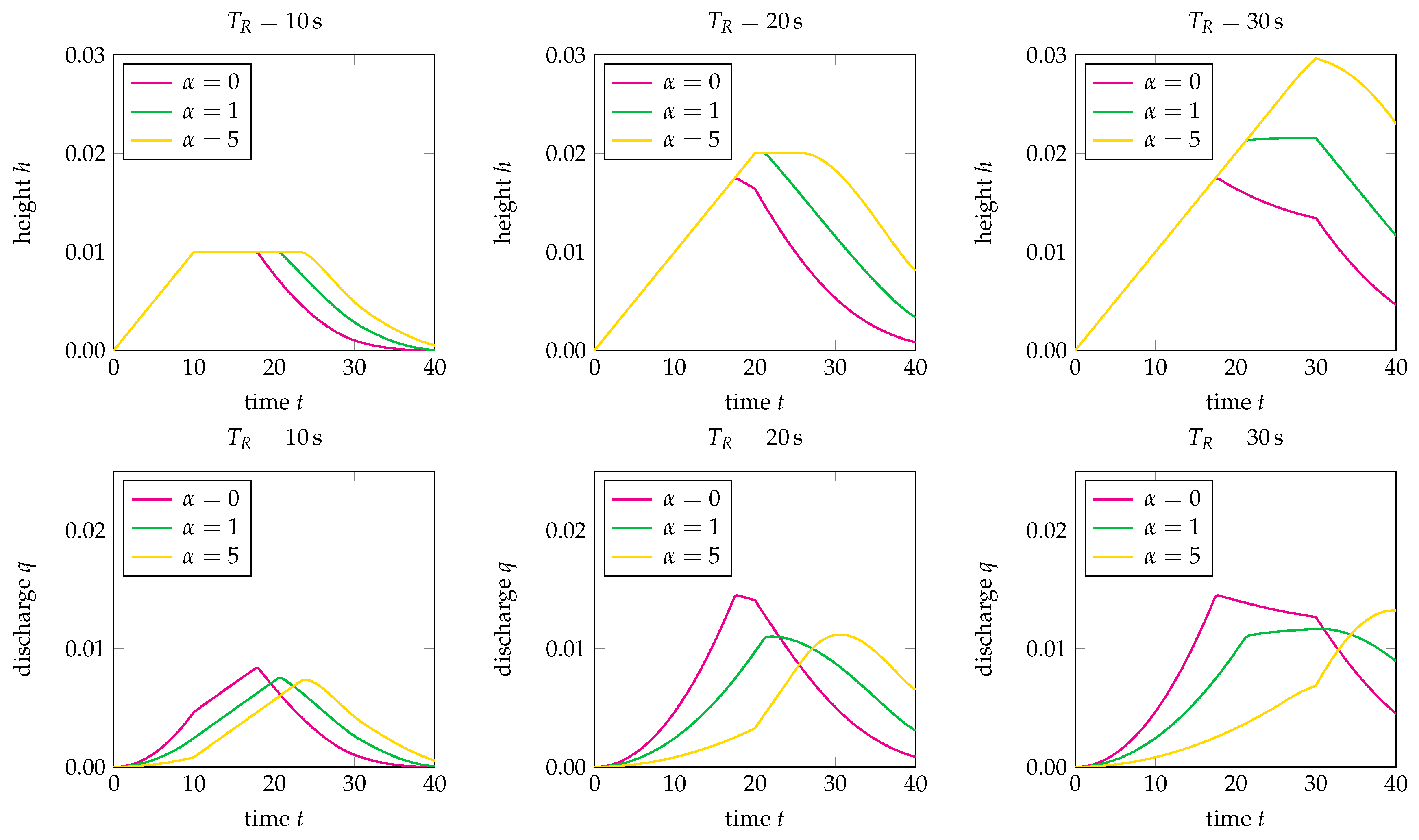
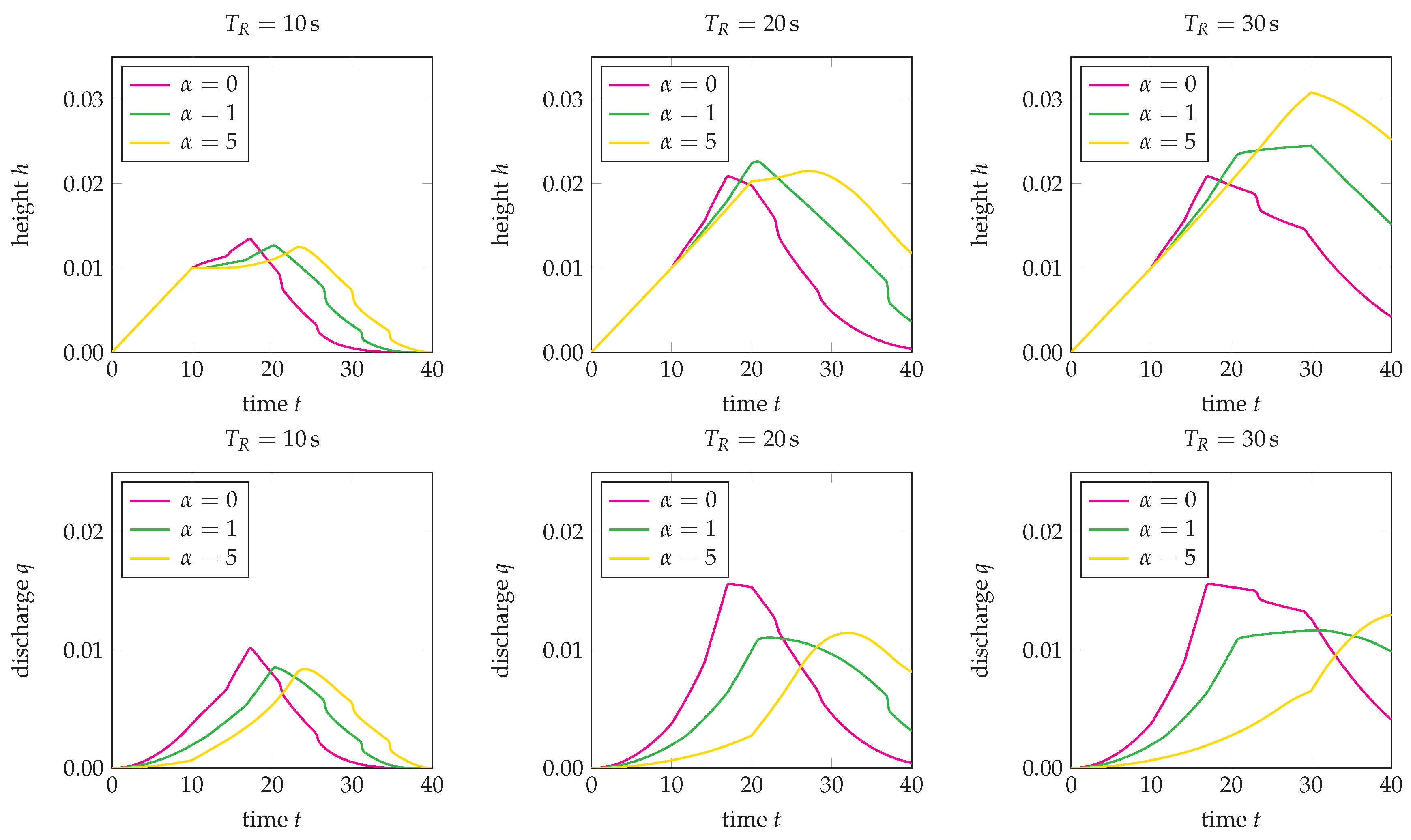
6. Numerical Tests
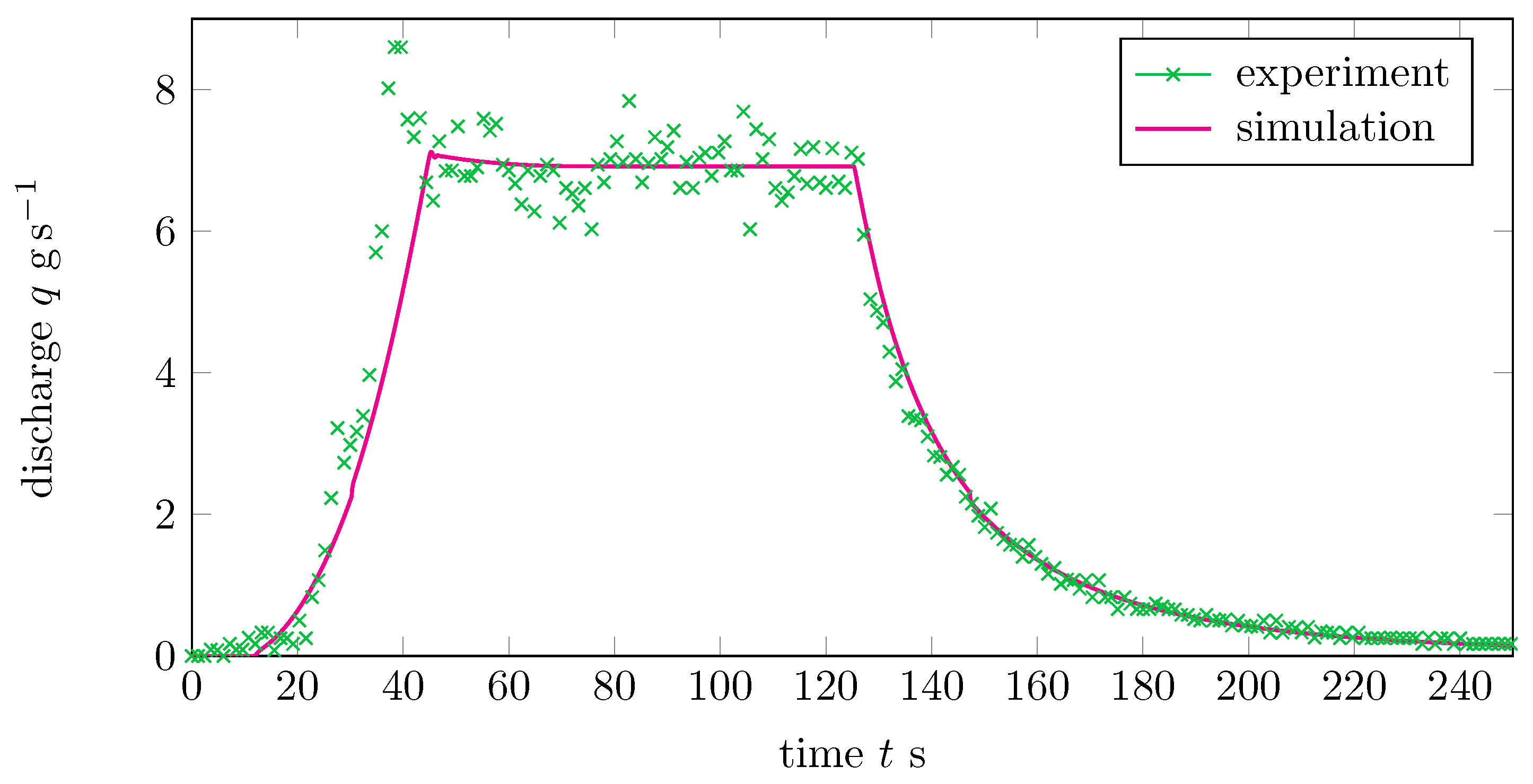
6.1. Comparison with Real-World Data
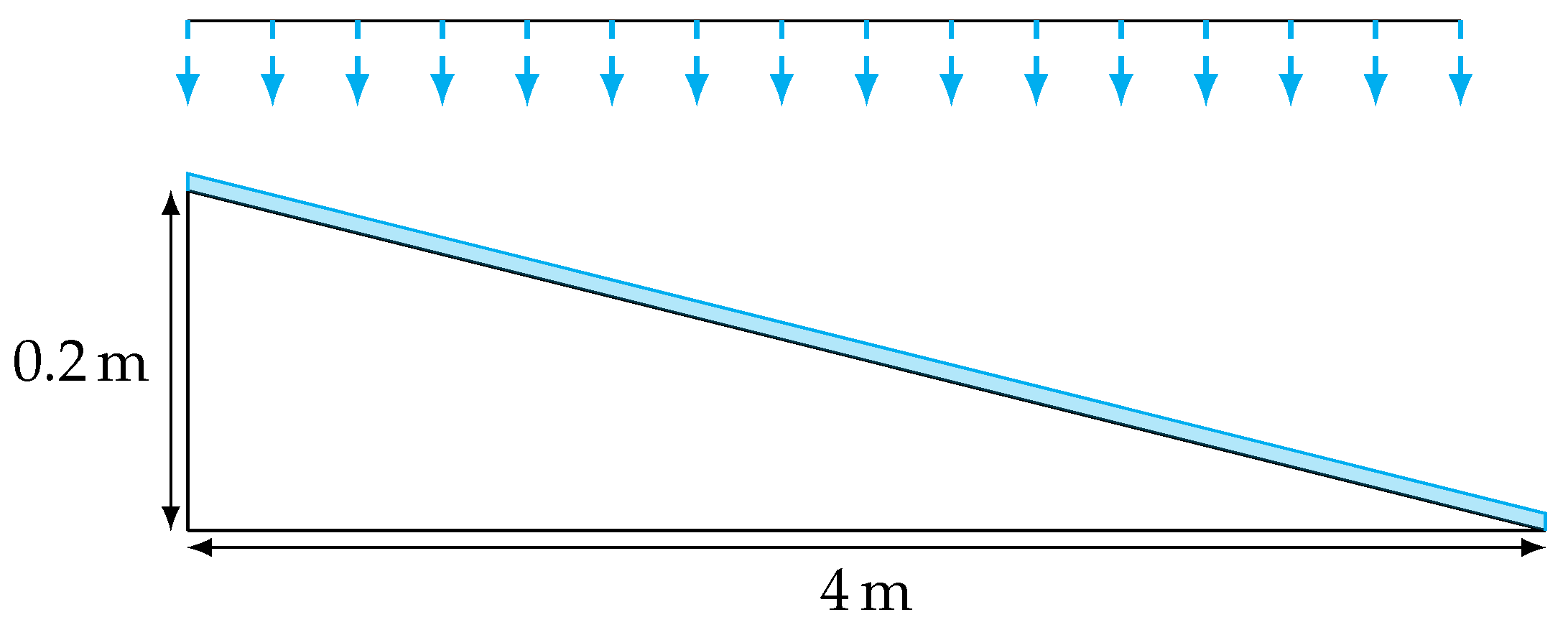
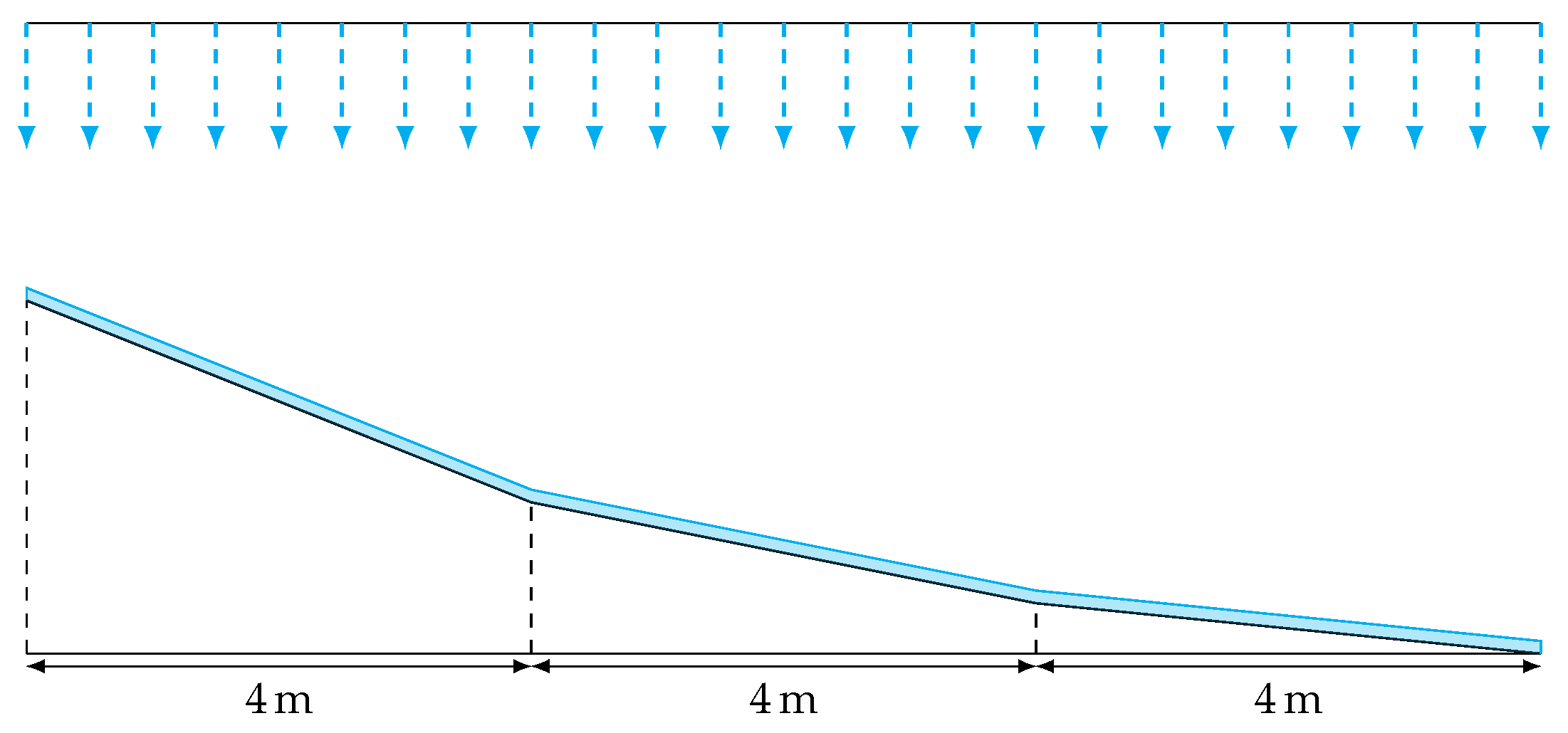
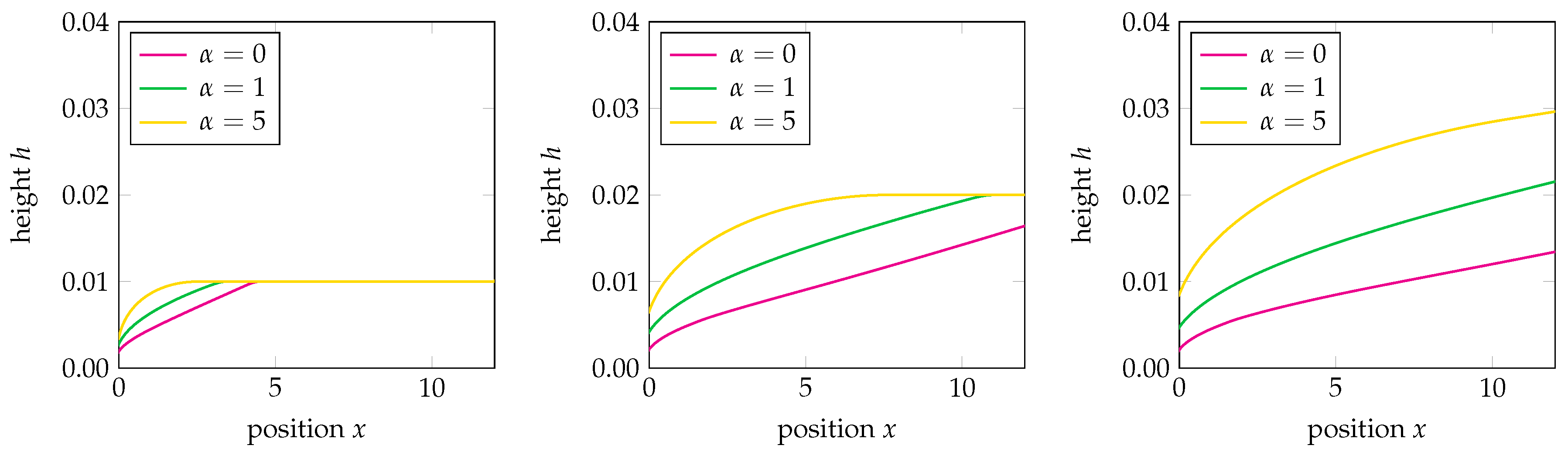
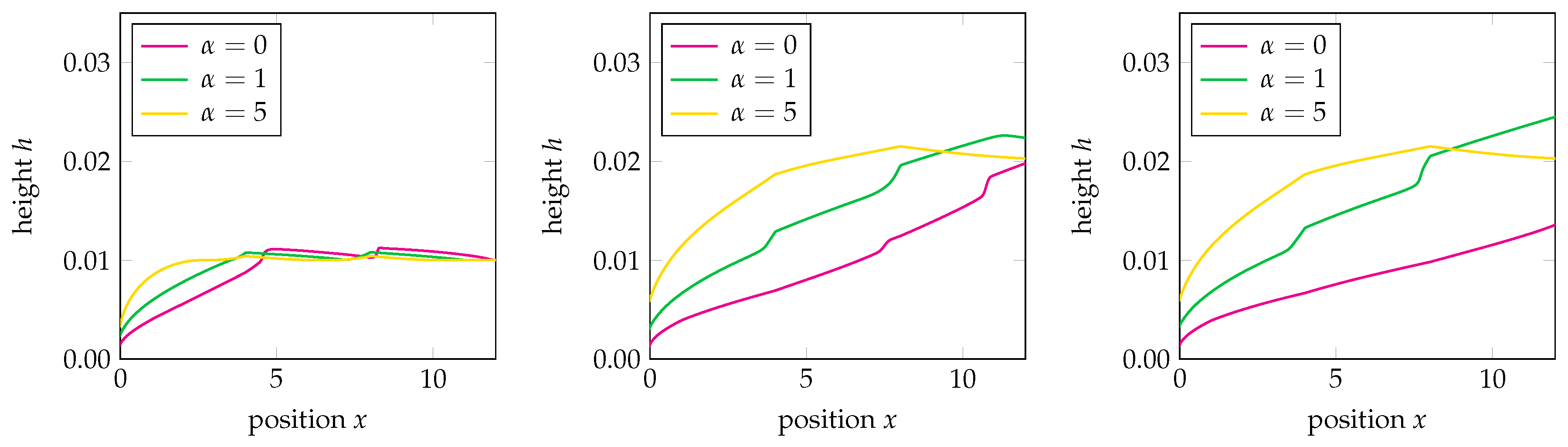
6.2. Single-Level and Three-Level Cascades
- (1)
- The total length of the rainfall process ,
- (2)
- The topography of the slope onto which the rain falls, for which we consider a constant slope (the single cascade) with and a decreasing slope (the three-level cascade, see Figure 6) with
- (3)
- The rain-induced friction level , for which we take and 5 for both the single cascade and the three-level cascade.
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Grace, R.; Eagleson, P.S. Modeling of Overland Flow. Water Resour. Res. 1966, 2, 393–403. [Google Scholar] [CrossRef]
- Woolhiser, D.A.; Liggett, J.A. Unsteady, one-dimensional flow over a plane—The rising hydrograph. Water Resour. Res. 1967, 3, 753–771. [Google Scholar] [CrossRef]
- Zhang, W.; Cundy, T.W. Modeling of two-dimensional overland flow. Water Resour. Res. 1989, 25, 2019–2035. [Google Scholar] [CrossRef]
- Esteves, M.; Faucher, X.; Galle, S.; Vauclin, M. Overland flow and infiltration modelling for small plots during unsteady rain: Numerical results versus observed values. J. Hydrol. 2000, 228, 265–282. [Google Scholar] [CrossRef]
- Weill, S.; Mouche, E.; Patin, J. A generalized Richards equation for surface/subsurface flow modelling. J. Hydrol. 2009, 366, 9–20. [Google Scholar] [CrossRef]
- Rousseau, M.; Cerdan, O.; Ern, A.; Le Maître, O.; Sochala, P. Study of overland flow with uncertain infiltration using stochastic tools. Adv. Water Resour. 2012, 38, 1–12. [Google Scholar] [CrossRef] [Green Version]
- de Saint-Venant, A.J.C.B. Théorie du mouvement non-permanent des eaux, avec application aux crues des rivières at à l’introduction des marées dans leur lit. C. R. Hebd. SéAnces L’AcadéMie Sci. 1871, 73, 147–154. [Google Scholar]
- Fiedler, F.R.; Ramirez, J.A. A numerical method for simulating discontinuous shallow flow over an infiltrating surface. Int. J. Numer. Methods Fluids 2000, 32, 219–239. [Google Scholar] [CrossRef]
- Sochala, P. Numerical Methods for Subsurface Flows and Coupling with Surface Runoff. Ph.D. Thesis, Ecole des Ponts ParisTech, Champs-sur-Marne, France, 2008. [Google Scholar]
- Delestre, O.; James, F. Simulation of rainfall events and overland flow. In Proceedings of the X International Conference Zaragoza-Pau on Applied Mathematics and Statistics, Jaca, Spain, 15–17 September 2008; Volume 35, pp. 125–135. [Google Scholar]
- Costabile, P.; Costanzo, C.; Macchione, F. Two-dimensional numerical models for overland flow simulations. In River Basin Management V; WIT Press: Southampton, UK, 2009; pp. 137–148. [Google Scholar] [CrossRef] [Green Version]
- Fernández-Pato, J.; Caviedes-Voullième, D.; García-Navarro, P. Rainfall/runoff simulation with 2D full shallow water equations: Sensitivity analysis and calibration of infiltration parameters. J. Hydrol. 2016, 536, 496–513. [Google Scholar] [CrossRef]
- Cea, L.; Bladé, E. A simple and efficient unstructured finite volume scheme for solving the shallow water equations in overland flow applications. Water Resour. Res. 2015, 51, 5464–5486. [Google Scholar] [CrossRef] [Green Version]
- Kirstetter, G.; Hu, J.; Delestre, O.; Darboux, F.; Lagrée, P.Y.; Popinet, S.; Fullana, J.M.; Josserand, C. Modeling rain-driven overland flow: Empirical versus analytical friction terms in the shallow water approximation. J. Hydrol. 2016, 536, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Costabile, P.; Costanzo, C.; Ferraro, D.; Macchione, F.; Petaccia, G. Performances of the New HEC-RAS Version 5 for 2-D Hydrodynamic-Based Rainfall-Runoff Simulations at Basin Scale: Comparison with a State-of-the Art Model. Water 2020, 12, 2326. [Google Scholar] [CrossRef]
- Wenzel, H.G.J. The Effect of Raindrop Impact and Surface Roughness on Sheet Flow; Research Report 34; FINAL REPORT Project No. B-018-ILL; Water Rresearch Centre University of Illinois: Urbana-Champaign, IL, USA, 1970. [Google Scholar]
- Yoon, Y.N.; Wenzel, H.G. Mechanics of sheet flow under simulated rainfall. J. Hydraul. Div. 1971, 97, 1367–1386. [Google Scholar]
- Audusse, E.; Bristeau, M.O.; Perthame, B. Kinetic Schemes for Saint-Venant Equations with Source Terms on Unstructured Grids; Research Report RR-3989; Projet M3N; INRIA: Le Chesnay-Rocquencourt, French, 2000. [Google Scholar]
- Perthame, B.; Simeoni, C. A kinetic scheme for the Saint-Venant system with a source term. Calcolo 2001, 38, 201–231. [Google Scholar] [CrossRef]
- Besson, M.; Lakkis, O.; Townsend, P. Finite Volume Code 1D Saint Venant. Available online: https://sourceforge.net/projects/finitevolumecode1dsaintvenant/ (accessed on 29 December 2020).
- Wylie, E.B.; Streeter, V.L. Fluid transients; McGraw-Hill International Book Co.: New York, NY, USA, 1978. [Google Scholar]
- Streeter, V.L.; Wylie, E.B.; Bedford, K.W. Fluid Mech.; OCLC: 37475163; WCB/McGraw Hill: Boston, MA, USA, 1998. [Google Scholar]
- Gerbeau, J.F.; Perthame, B. Derivation of viscous Saint-Venant system for laminar shallow water; numerical validation. Discret. Contin. Dyn. Syst. Ser. B 2001, 1, 89–102. [Google Scholar] [CrossRef]
- Levermore, C.D.; Sammartino, M. A shallow water model with eddy viscosity for basins with varying bottom topography. Nonlinearity 2001, 14, 1493. [Google Scholar] [CrossRef]
- Marche, F. Derivation of a new two-dimensional viscous shallow water model with varying topography, bottom friction and capillary effects. Eur. J. Mech. B Fluids 2007, 26, 49–63. [Google Scholar] [CrossRef]
- Beavers, G.S.; Joseph, D.D. Boundary conditions at a naturally permeable wall. J. Fluid Mech. 1967, 30, 197–207. [Google Scholar] [CrossRef]
- Saffman, P.G. On the Boundary Condition at the Surface of a Porous Medium. Stud. Appl. Math. 1971, 50, 93–101. [Google Scholar] [CrossRef]
- Jäger, W.; Mikelić, A. On the interface boundary condition of Beavers, Joseph, and Saffman. SIAM J. Appl. Math. 2000, 60, 1111–1127. [Google Scholar] [CrossRef]
- Badea, L.; Discacciati, M.; Quarteroni, A. Numerical analysis of the Navier–Stokes/Darcy coupling. Numer. Math. 2010, 115, 195–227. [Google Scholar] [CrossRef] [Green Version]
- Shen, H.W.; Li, R. Rainfall effect on sheet flow over smooth surface. J. Hydraul. Div. 1973, 99, 771–792. [Google Scholar]
- Lu, J.Y.; Chen, J.Y.; Chang, F.H.; Lu, T.F. Characteristics of Shallow Rain-Impacted Flow over Smooth Bed. J. Hydraul. Eng. 1998, 124, 1242–1252. [Google Scholar] [CrossRef]
- Ersoy, M. Dimension reduction for incompressible pipe and open channel flow including friction. In Proceedings of the International Conference Applications of Mathematics 2015, in Honor of the Birthday Anniversaries of Ivo Babuška (90) and Milan Práger (85) and Emil Vitásek(85); Brandts, J., Korotov, S., Křížek, M., Segeth, K., Šístek, J., Vejchodský, T., Eds.; Czech Academy of Sciences: Staré Město, Czech Republic, 2015; pp. 17–33. [Google Scholar]
- De Vita, F.; Lagrée, P.Y.; Chibbaro, S.; Popinet, S. Beyond Shallow Water: Appraisal of a numerical approach to hydraulic jumps based upon the Boundary Layer theory. Eur. J. Mech. B Fluids 2020, 79, 233–246. [Google Scholar] [CrossRef]
- Yang, F.; Liang, D.; Xiao, Y. Influence of Boussinesq coefficient on depth-averaged modelling of rapid flows. J. Hydrol. 2018, 559, 909–919. [Google Scholar] [CrossRef]
- Serre, D. Systems of Conservation Laws 1: Hyperbolicity, Entropies, Shock Waves; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Bouchut, F. Nonlinear Stability of Finite Volume Methods for Hyperbolic Conservation Laws: And Well-Balanced Schemes for Sources; Frontiers in Mathematics, Birkhäuser Basel: Basel, Switzerland, 2004. [Google Scholar]
- Dafermos, C.M. Hyperbolic Conservation Laws in Continuum Physics, 3rd ed.; Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences]; Springer: Berlin/Heidelberg, Germany, 2010; Volume 325, p. xxxvi+708. [Google Scholar]
- Bouchut, F.; Morales de Luna, T. A subsonic-well-balanced reconstruction scheme for shallow water flows. SIAM J. Numer. Anal. 2010, 48, 1733–1758. [Google Scholar] [CrossRef] [Green Version]
- Evans, L.C. Entropy and Partial Differential Equations; Online Lecture Notes; Department of Mathematics, UC Berkeley: Berkeley, CA, USA, 2013. [Google Scholar]
- Bouchut, F.; Lhébrard, X. A multi well-balanced scheme for the shallow water MHD system with topography. Numer. Math. 2017, 136, 875–905. [Google Scholar] [CrossRef] [Green Version]
- Kröner, D. Numerical Schemes for Conservation Laws; Chichester, B., Teubner Stuttgart, G., Eds.; Wiley-Teubner Series Advances in Numerical Mathematics; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 1997; p. viii+508. [Google Scholar]
- LeVeque, R.J. Numerical Methods for Conservation Laws, 2nd ed.; Lectures in Mathematics ETH Zürich, Birkhäuser Verlag: Basel, Switerland, 1992; p. x+214. [Google Scholar] [CrossRef]
- LeVeque, R.J. Finite Volume Methods for Hyperbolic Problems; Cambridge Texts in Applied Mathematics; Cambridge University Press: Cambridge, UK, 2002; p. xx+558. [Google Scholar] [CrossRef]
- Toro, E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics, 3rd ed.; A Practical Introduction; Springer: Berlin/Heidelberg, Germany, 2009; p. xxiv+724. [Google Scholar] [CrossRef]
- Kurganov, A. Finite-volume schemes for shallow-water equations. Acta Numer. 2018, 27, 289–351. [Google Scholar] [CrossRef] [Green Version]
- Bourdarias, C.; Ersoy, M.; Gerbi, S. Unsteady mixed flows in non uniform closed water pipes: A full kinetic approach. Numer. Math. 2014, 128, 217–263. [Google Scholar] [CrossRef] [Green Version]
- Bourdarias, C.; Ersoy, M.; Gerbi, S. A kinetic scheme for transient mixed flows in non uniform closed pipes: A global manner to upwind all the source terms. J. Sci. Comput. 2011, 48, 89–104. [Google Scholar] [CrossRef] [Green Version]
- Xia, X.; Liang, Q.; Ming, X.; Hou, J. An efficient and stable hydrodynamic model with novel source term discretization schemes for overland flow and flood simulations. Water Resour. Res. 2017, 53, 3730–3759. [Google Scholar] [CrossRef]
- Buttinger-Kreuzhuber, A.; Horváth, Z.; Noelle, S.; Blöschl, G.; Waser, J. A fast second-order shallow water scheme on two-dimensional structured grids over abrupt topography. Adv. Water Resour. 2019, 127, 89–108. [Google Scholar] [CrossRef]
- Taccone, F.; Antoine, G.; Delestre, O.; Goutal, N. A new criterion for the evaluation of the velocity field for rainfall-runoff modelling using a shallow-water model. Adv. Water Resour. 2020, 140, 103581. [Google Scholar] [CrossRef]
- Iwagaki, Y. Fundamental Studies on the Runoff Analysis by Characteristics; Disaster Prevention Research Institute, Kyoto University: Kyoto, Japan, 1955; Volume 10. [Google Scholar]
- Ambiental. Ambiental Environmental Assessment a Company of Royal HaskoningDHV; Brighton UK and Royal HaskoningDHV: Nijmegen, The Netherlands, 2020; Available online: https://www.ambiental.co.uk/ (accessed on 29 December 2020).
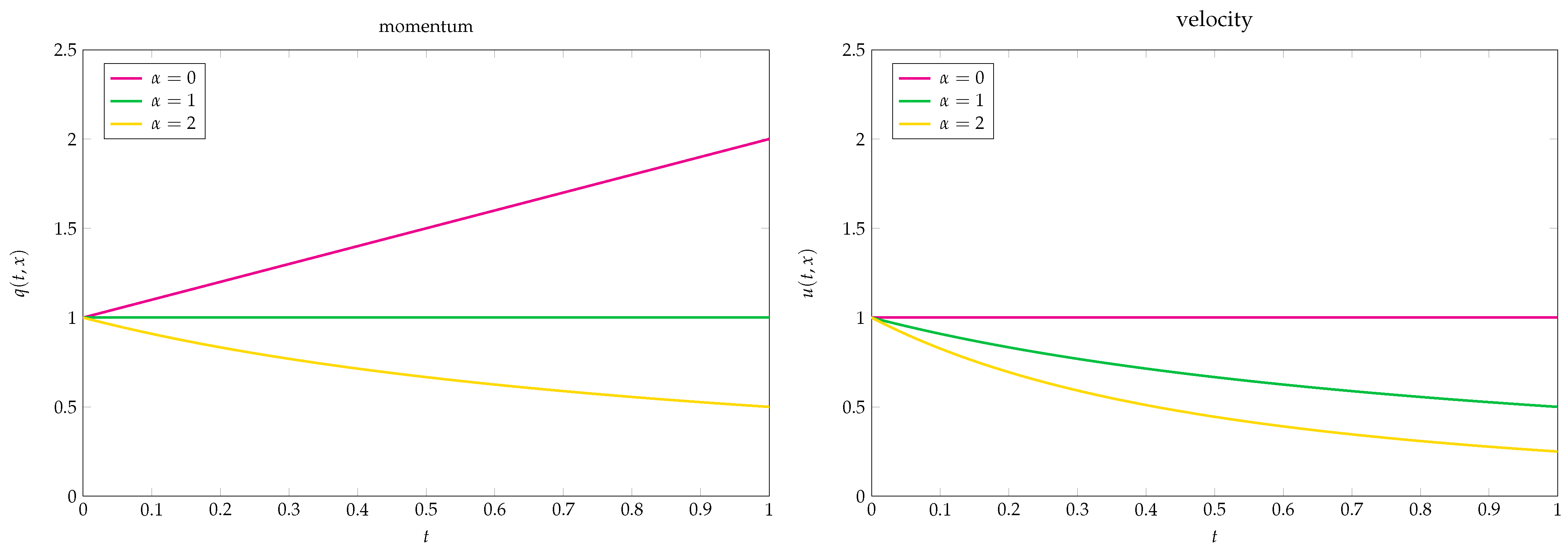
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ersoy, M.; Lakkis, O.; Townsend, P. A Saint-Venant Model for Overland Flows with Precipitation and Recharge. Math. Comput. Appl. 2021, 26, 1. https://doi.org/10.3390/mca26010001
Ersoy M, Lakkis O, Townsend P. A Saint-Venant Model for Overland Flows with Precipitation and Recharge. Mathematical and Computational Applications. 2021; 26(1):1. https://doi.org/10.3390/mca26010001
Chicago/Turabian StyleErsoy, Mehmet, Omar Lakkis, and Philip Townsend. 2021. "A Saint-Venant Model for Overland Flows with Precipitation and Recharge" Mathematical and Computational Applications 26, no. 1: 1. https://doi.org/10.3390/mca26010001
APA StyleErsoy, M., Lakkis, O., & Townsend, P. (2021). A Saint-Venant Model for Overland Flows with Precipitation and Recharge. Mathematical and Computational Applications, 26(1), 1. https://doi.org/10.3390/mca26010001





