Half-Space Relaxation Projection Method for Solving Multiple-Set Split Feasibility Problem
Abstract
1. Introduction
1.1. Split Inverse Problem
1.2. Split Feasibility Problem and Multiple-Set Split Feasibility Problem
2. Preliminary
- (i)
- The function f is convex and weakly lower semi-continuous on ;
- (ii)
- for ;
- (iii)
- is -Lipschitz, i.e.,
- (i)
- The point solves the SFP (3), i.e., ;
- (ii)
- The point is the fixed point of the mapping , i.e.,
- (i)
- (ii)
- (iii)
3. Half-Space Relaxation Projection Algorithm
- (i)
- For each and , define
- (ii)
- and are defined as and so where such that for each ,
- (iii)
- For each and , define
| Algorithm 1: Half-Space Relaxation Projection Algorithm (HSRPA). |
| Initialization: Choose u, . Let the positive real constants , and (), and the real sequences , and satisfy the following conditions:
Iterative Step: Proceed with the following computations: |
- i.
- When the point u in HSRPA is taken to be 0, from Theorem 1, we see that the limit point of the sequence is the unique minimum norm solution of the MSSFP, i.e.,
- ii.
- In the algorithm (HSRPA), the stepsize can also be replaced bywhere
| Algorithm 2: Algorithm for solving the SFP. |
| Initialization: Choose u, . Let the positive real constants and , and the real sequences , and satisfy the following conditions:
Iterative Step: Proceed with the following computations: |
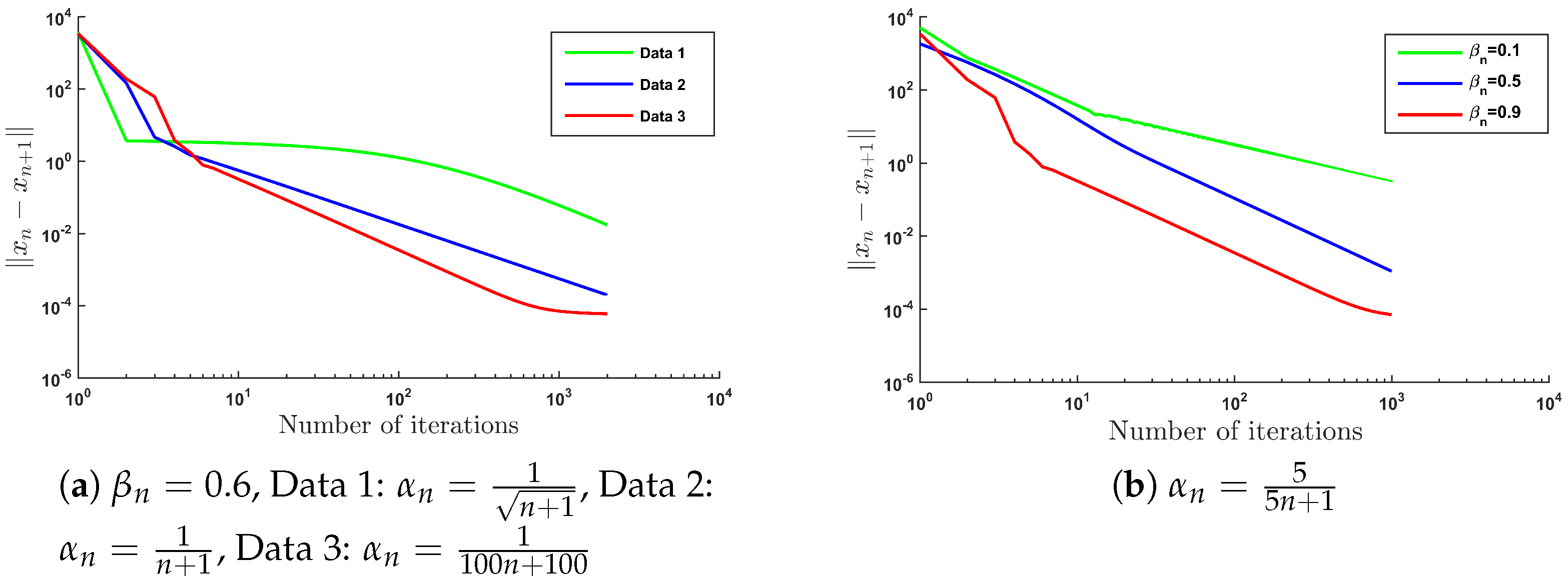
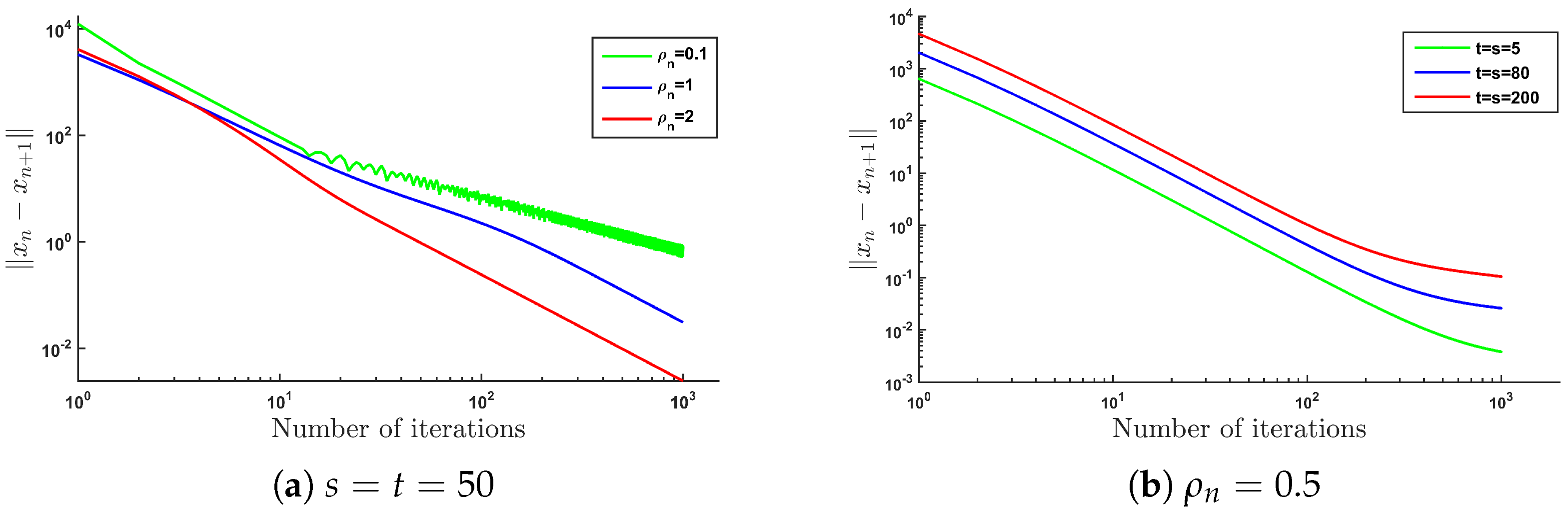
4. Preliminary Numerical Results and Applications
- •
- for all , where r is a positive real number,
- •
- for each ,
- •
- ,
- •
- ,
- •
- , and , where θ is a nonzero real number.
- (i)
- A sequence in which the terms are very close to zero;
- (ii)
- A sequence in which terms are very close to 1;
- (iii)
- A sequence in which terms are larger but not exceeding 4.
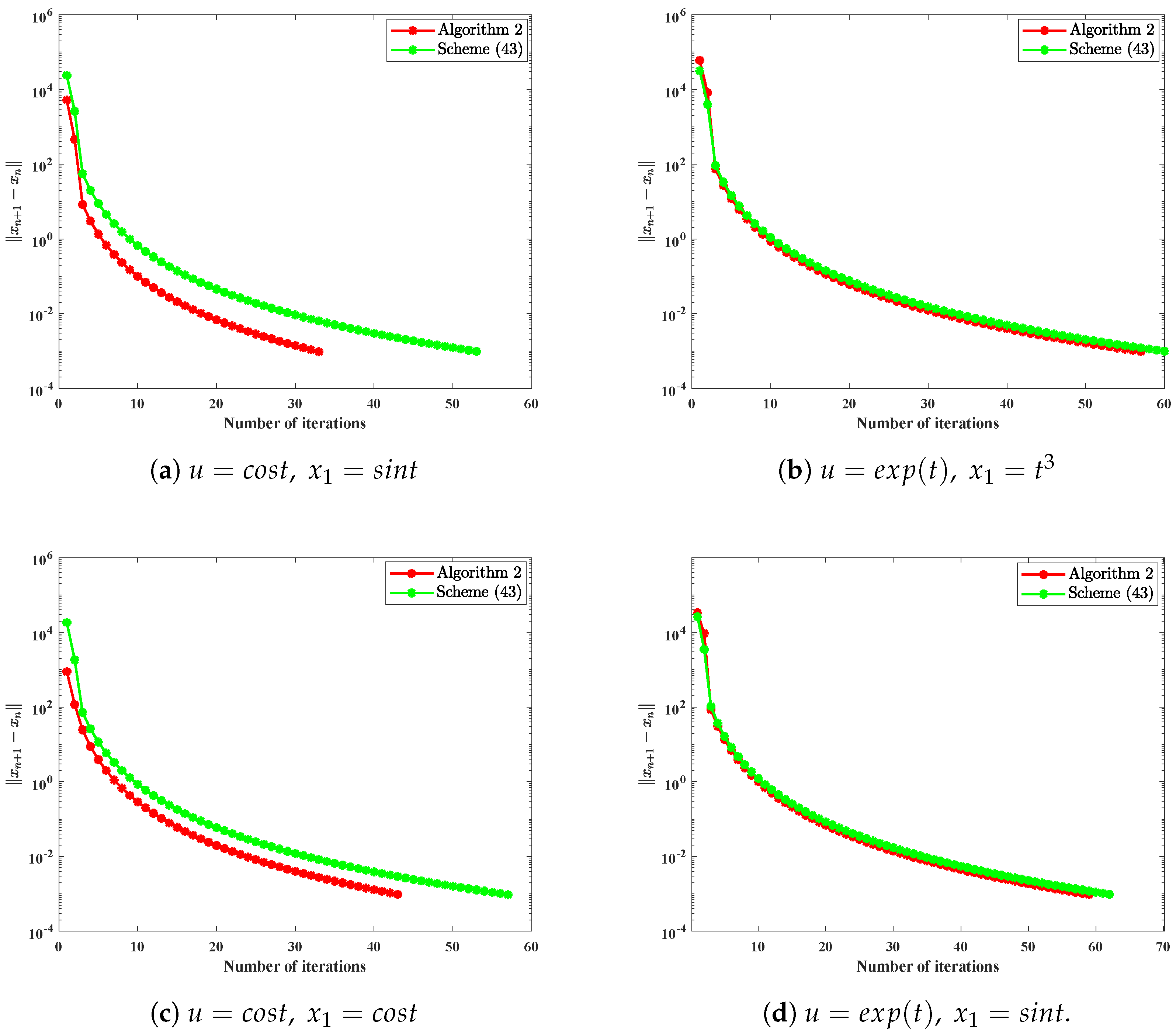
4.1. Application to Signal Recovery
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Censor, Y.; Gibali, A.; Reich, S. Algorithms for the split variational inequality problem. Numer. Algorithms 2012, 59, 301–323. [Google Scholar] [CrossRef]
- López, G.; Martín-Márquez, V.; Wang, F.; Xu, H.K. Solving the split feasibility problem without prior knowledge of matrix norms. Inverse Probl. 2012, 28, 085004. [Google Scholar] [CrossRef]
- Byrne, C. A unified treatment of some iterative algorithms in signal processing and image reconstruction. Inverse Probl. 2003, 20, 103. [Google Scholar] [CrossRef]
- Combettes, P. The convex feasibility problem in image recovery. In Advances in Imaging and Electron Physics; Elsevier: Amsterdam, The Netherlands, 1996; Volume 95, pp. 155–270. [Google Scholar]
- Qu, B.; Xiu, N. A note on the CQ algorithm for the split feasibility problem. Inverse Probl. 2005, 21, 1655. [Google Scholar] [CrossRef]
- Censor, Y.; Elfving, T. A multiprojection algorithm using Bregman projections in a product space. Numer. Algorithms 1994, 8, 221–239. [Google Scholar] [CrossRef]
- Censor, Y.; Elfving, T.; Kopf, N.; Bortfeld, T. The multiple-sets split feasibility problem and its applications for inverse problems. Inverse Probl. 2005, 21, 2071. [Google Scholar] [CrossRef]
- Censor, Y.; Lent, A. Cyclic subgradient projections. Math. Program. 1982, 24, 233–235. [Google Scholar] [CrossRef]
- Byrne, C.; Censor, Y.; Gibali, A.; Reich, S. The split common null point problem. arXiv 2011, arXiv:1108.5953. [Google Scholar]
- Censor, Y.; Segal, A. The split common fixed point problem for directed operators. J. Convex Anal. 2009, 16, 587–600. [Google Scholar]
- Dang, Y.; Gao, Y.; Li, L. Inertial projection algorithms for convex feasibility problem. J. Syst. Eng. Electron. 2012, 23, 734–740. [Google Scholar] [CrossRef]
- He, Z. The split equilibrium problem and its convergence algorithms. J. Inequalities Appl. 2012, 2012, 162. [Google Scholar] [CrossRef]
- Taiwo, A.; Jolaoso, L.O.; Mewomo, O.T. Viscosity approximation method for solving the multiple-set split equality common fixed-point problems for quasi-pseudocontractive mappings in Hilbert spaces. J. Ind. Manag. Optim. 2017, 13. [Google Scholar] [CrossRef]
- Aremu, K.O.; Izuchukwu, C.; Ogwo, G.N.; Mewomo, O.T. Multi-step iterative algorithm for minimization and fixed point problems in p-uniformly convex metric spaces. J. Manag. Optim. 2017, 13. [Google Scholar] [CrossRef]
- Oyewole, O.K.; Abass, H.A.; Mewomo, O.T. A strong convergence algorithm for a fixed point constrained split null point problem. Rend. Circ. Mat. Palermo Ser. 2 2020, 13, 1–20. [Google Scholar]
- Izuchukwu, C.; Ugwunnadi, G.C.; Mewomo, O.T.; Khan, A.R.; Abbas, M. Proximal-type algorithms for split minimization problem in P-uniformly convex metric spaces. Numer. Algorithms 2019, 82, 909–935. [Google Scholar] [CrossRef]
- Jolaoso, L.O.; Alakoya, T.O.; Taiwo, A.; Mewomo, O.T. Inertial extragradient method via viscosity approximation approach for solving equilibrium problem in Hilbert space. Optimization 2020, 1–20. [Google Scholar] [CrossRef]
- He, S.; Wu, T.; Cho, Y.J.; Rassias, T.M. Optimal parameter selections for a general Halpern iteration. Numer. Algorithms 2019, 82, 1171–1188. [Google Scholar] [CrossRef]
- Dadashi, V.; Postolache, M. Forward–backward splitting algorithm for fixed point problems and zeros of the sum of monotone operators. Arab. J. Math. 2020, 9, 89–99. [Google Scholar] [CrossRef]
- Yao, Y.; Leng, L.; Postolache, M.; Zheng, X. Mann-type iteration method for solving the split common fixed point problem. J. Nonlinear Convex Anal. 2017, 18, 875–882. [Google Scholar]
- Byrne, C. Iterative oblique projection onto convex sets and the split feasibility problem. Inverse Probl. 2002, 18, 441. [Google Scholar] [CrossRef]
- Dang, Y.; Gao, Y. The strong convergence of a KM–CQ-like algorithm for a split feasibility problem. Inverse Probl. 2010, 27, 015007. [Google Scholar] [CrossRef]
- Jung, J.S. Iterative algorithms based on the hybrid steepest descent method for the split feasibility problem. J. Nonlinear Sci. Appl. 2016, 9, 4214–4225. [Google Scholar] [CrossRef]
- Wang, F.; Xu, H.K. Cyclic algorithms for split feasibility problems in Hilbert spaces. Nonlinear Anal. Theory Methods Appl. 2011, 74, 4105–4111. [Google Scholar] [CrossRef]
- Xu, H.K. An iterative approach to quadratic optimization. J. Optim. Theory Appl. 2003, 116, 659–678. [Google Scholar] [CrossRef]
- Xu, H.K. A variable Krasnosel’skii–Mann algorithm and the multiple-set split feasibility problem. Inverse Probl. 2006, 22, 2021. [Google Scholar] [CrossRef]
- Xu, H.K. Iterative methods for the split feasibility problem in infinite-dimensional Hilbert spaces. Inverse Probl. 2010, 26, 105018. [Google Scholar] [CrossRef]
- Yu, X.; Shahzad, N.; Yao, Y. Implicit and explicit algorithms for solving the split feasibility problem. Optim. Lett. 2012, 6, 1447–1462. [Google Scholar] [CrossRef]
- Shehu, Y.; Mewomo, O.T.; Ogbuisi, F.U. Further investigation into approximation of a common solution of fixed point problems and split feasibility problems. Acta Math. Sci. 2016, 36, 913–930. [Google Scholar] [CrossRef]
- Shehu, Y.; Mewomo, O.T. Further investigation into split common fixed point problem for demicontractive operators. Acta Math. Sin. Engl. Ser. 2016, 32, 1357–1376. [Google Scholar] [CrossRef]
- Mewomo, O.T.; Ogbuisi, F.U. Convergence analysis of an iterative method for solving multiple-set split feasibility problems in certain Banach spaces. Quaest. Math. 2018, 41, 129–148. [Google Scholar] [CrossRef]
- Dong, Q.L.; Tang, Y.C.; Cho, Y.J.; Rassias, T.M. “Optimal” choice of the step length of the projection and contraction methods for solving the split feasibility problem. J. Glob. Optim. 2018, 71, 341–360. [Google Scholar] [CrossRef]
- Cegielski, A. Landweber-type operator and its properties. Contemp. Math. 2016, 658, 139–148. [Google Scholar]
- Cegielski, A. General method for solving the split common fixed point problem. J. Optim. Theory Appl. 2015, 165, 385–404. [Google Scholar] [CrossRef]
- Cegielski, A.; Reich, S.; Zalas, R. Weak, strong and linear convergence of the CQ-method via the regularity of Landweber operators. Optimization 2020, 69, 605–636. [Google Scholar] [CrossRef]
- Hendrickx, J.M.; Olshevsky, A. Matrix p-norms are NP-hard to approximate if p ≠ 1,2,∞. SIAM J. Matrix Anal. Appl. 2010, 31, 2802–2812. [Google Scholar] [CrossRef]
- Yang, Q. The relaxed CQ algorithm solving the split feasibility problem. Inverse Probl. 2004, 20, 1261. [Google Scholar] [CrossRef]
- Bauschke, H.H.; Borwein, J.M. On projection algorithms for solving convex feasibility problems. SIAM Rev. 1996, 38, 367–426. [Google Scholar] [CrossRef]
- Fukushima, M. A relaxed projection method for variational inequalities. Math. Program. 1986, 35, 58–70. [Google Scholar] [CrossRef]
- Alakoya, T.O.; Jolaoso, L.O.; Mewomo, O.T. Modified inertial subgradient extragradient method with self adaptive stepsize for solving monotone variational inequality and fixed point problems. Optimization 2020, 1–30. [Google Scholar] [CrossRef]
- Jolaoso, L.O.; Taiwo, A.; Alakoya, T.O.; Mewomo, O.T. A unified algorithm for solving variational inequality and fixed point problems with application to the split equality problem. Comput. Appl. Math. 2020, 39, 38. [Google Scholar] [CrossRef]
- Buong, N. Iterative algorithms for the multiple-sets split feasibility problem in Hilbert spaces. Numer. Algorithms 2017, 76, 783–798. [Google Scholar] [CrossRef]
- Censor, Y.; Motova, A.; Segal, A. Perturbed projections and subgradient projections for the multiple-sets split feasibility problem. J. Math. Anal. Appl. 2007, 327, 1244–1256. [Google Scholar] [CrossRef]
- Latif, A.; Vahidi, J.; Eslamian, M. Strong convergence for generalized multiple-set split feasibility problem. Filomat 2016, 30, 459–467. [Google Scholar] [CrossRef]
- Masad, E.; Reich, S. A note on the multiple-set split convex feasibility problem in Hilbert space. J. Nonlinear Convex Anal. 2007, 8, 367. [Google Scholar]
- Zhao, J.; Yang, Q. Self-adaptive projection methods for the multiple-sets split feasibility problem. Inverse Probl. 2011, 27, 035009. [Google Scholar] [CrossRef]
- Zhao, J.; Yang, Q. Several acceleration schemes for solving the multiple-sets split feasibility problem. Linear Algebra Appl. 2012, 437, 1648–1657. [Google Scholar] [CrossRef][Green Version]
- Zhao, J.; Yang, Q. A simple projection method for solving the multiple-sets split feasibility problem. Inverse Probl. Sci. Eng. 2013, 21, 3537–3546. [Google Scholar] [CrossRef]
- Yao, Y.; Postolache, M.; Zhu, Z. Gradient methods with selection technique for the multiple-sets split feasibility problem. Optimization 2019, 69, 269–281. [Google Scholar] [CrossRef]
- Osilike, M.O.; Isiogugu, F.O. Weak and strong convergence theorems for nonspreading-type mappings in Hilbert spaces. Nonlinear Anal. Theory Methods Appl. 2011, 74, 1814–1822. [Google Scholar] [CrossRef]
- Aubin, J.P. Optima and Equilibria: An Introduction to Nonlinear Analysis; Springer Science & Business Media: Berlin, Germany, 2013; Volume 140. [Google Scholar]
- Ceng, L.C.; Ansari, Q.H.; Yao, J.C. An extragradient method for solving split feasibility and fixed point problems. Comput. Math. Appl. 2012, 64, 633–642. [Google Scholar] [CrossRef]
- Bauschke, H.H.; Combettes, P.L. Convex Analysis and Monotone Operator Theory in Hilbert Spaces; Springer: Berlin/Heidelberg, Germany, 2011; Volume 408. [Google Scholar]
- Maingé, P.E.; Măruşter, Ş. Convergence in norm of modified Krasnoselski–Mann iterations for fixed points of demicontractive mappings. Appl. Math. Comput. 2011, 217, 9864–9874. [Google Scholar] [CrossRef]
- He, B. Inexact implicit methods for monotone general variational inequalities. Math. Program. 1999, 86, 199–217. [Google Scholar] [CrossRef]
- Shehu, Y. Strong convergence result of split feasibility problems in Banach spaces. Filomat 2017, 31, 1559–1571. [Google Scholar] [CrossRef][Green Version]
- Cegielski, A. Iterative Methods for Fixed Point Problems in Hilbert Spaces; Springer: Berlin/Heidelberg, Germany, 2012; Volume 2057. [Google Scholar]
- Gibali, A.; Liu, L.W.; Tang, Y.C. Note on the modified relaxation CQ algorithm for the split feasibility problem. Optim. Lett. 2018, 12, 817–830. [Google Scholar] [CrossRef]
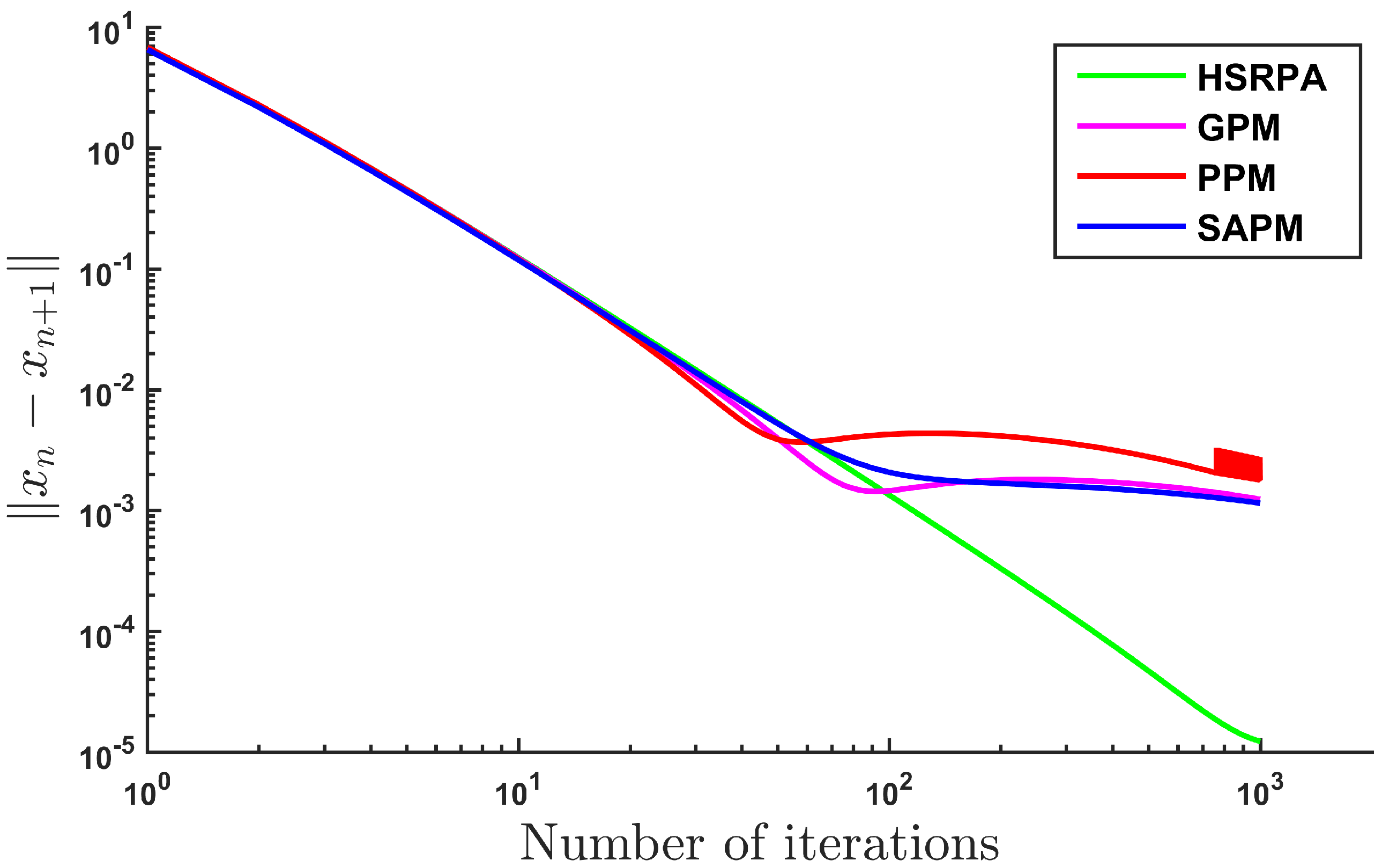
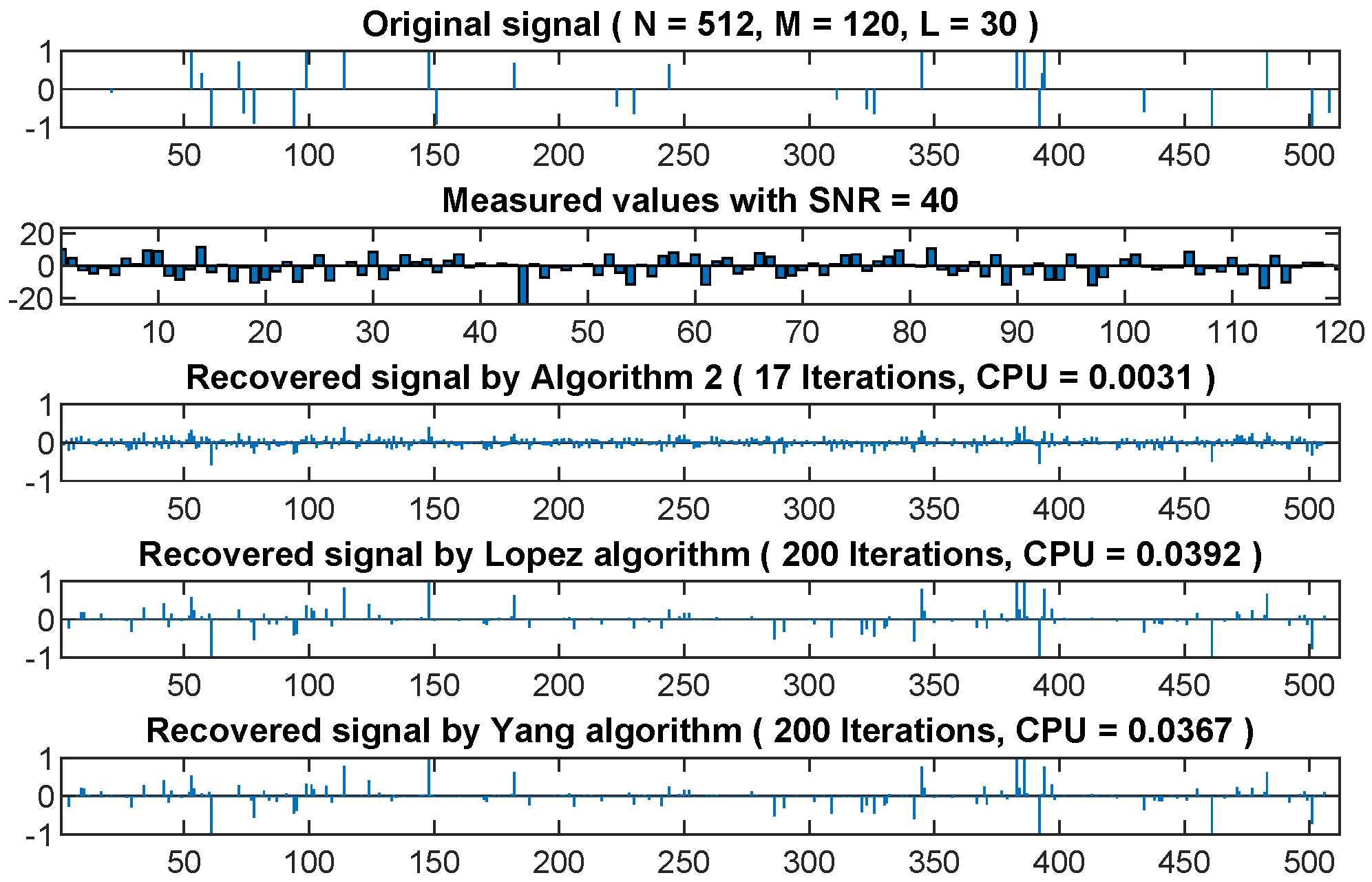
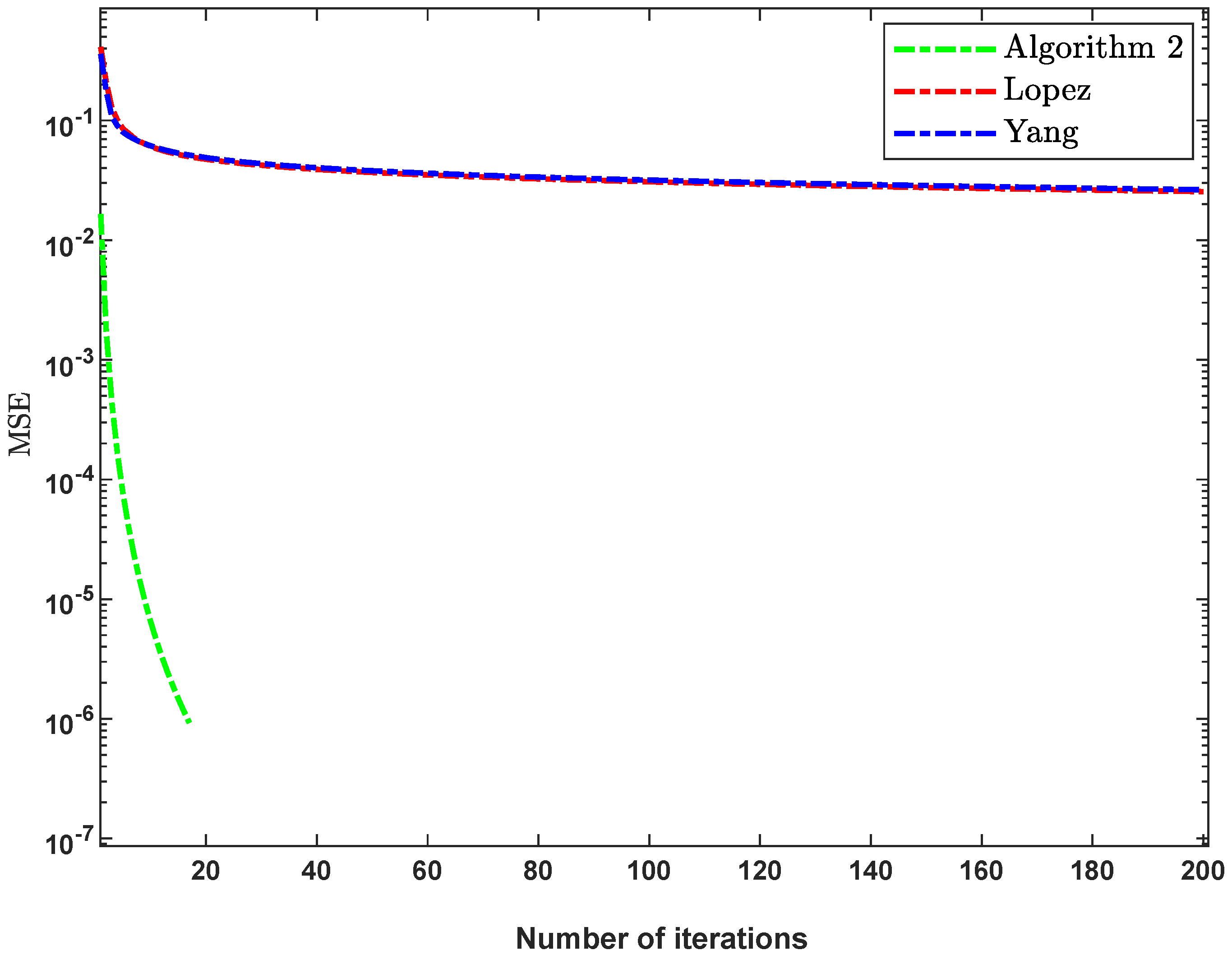
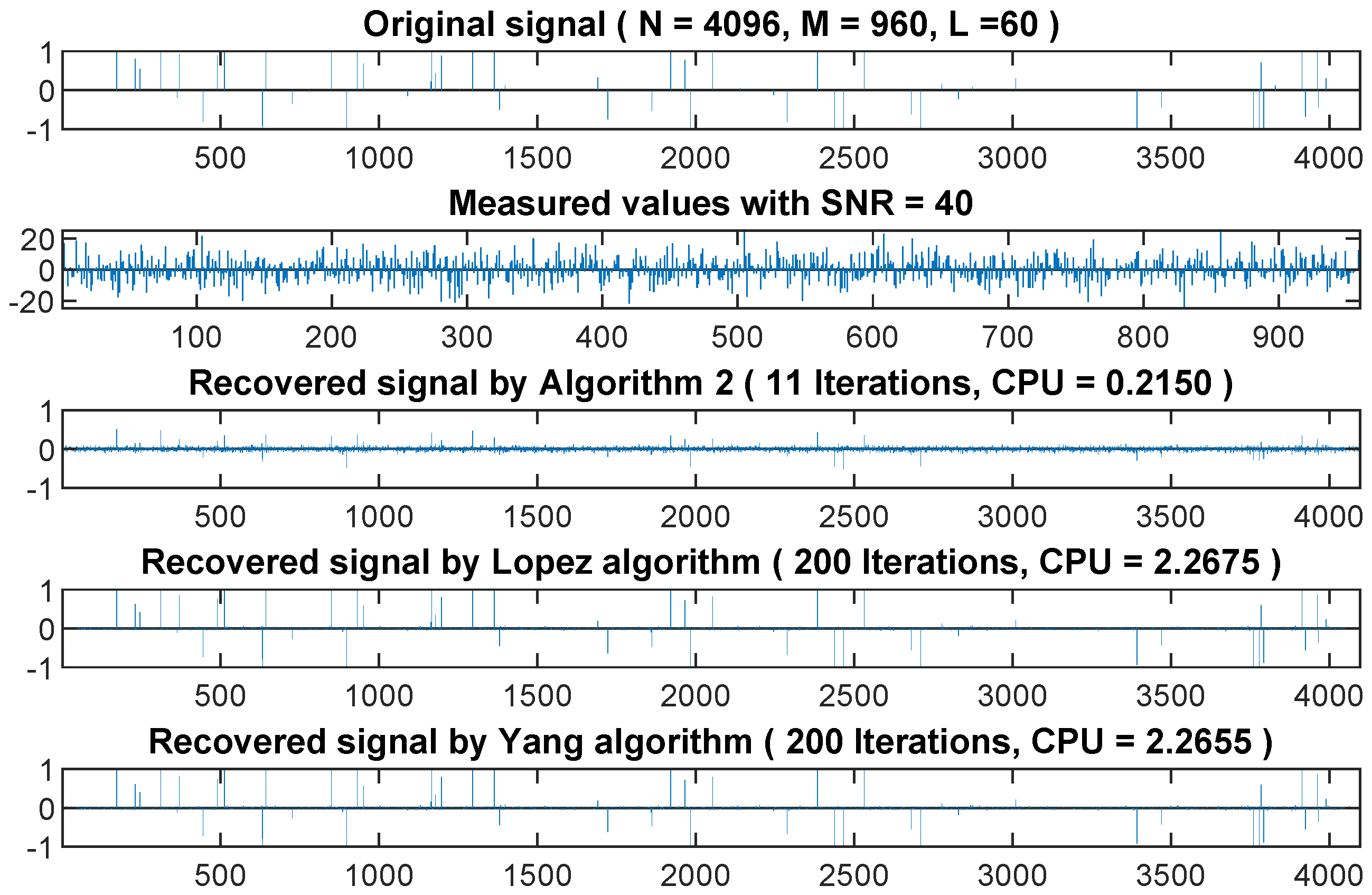
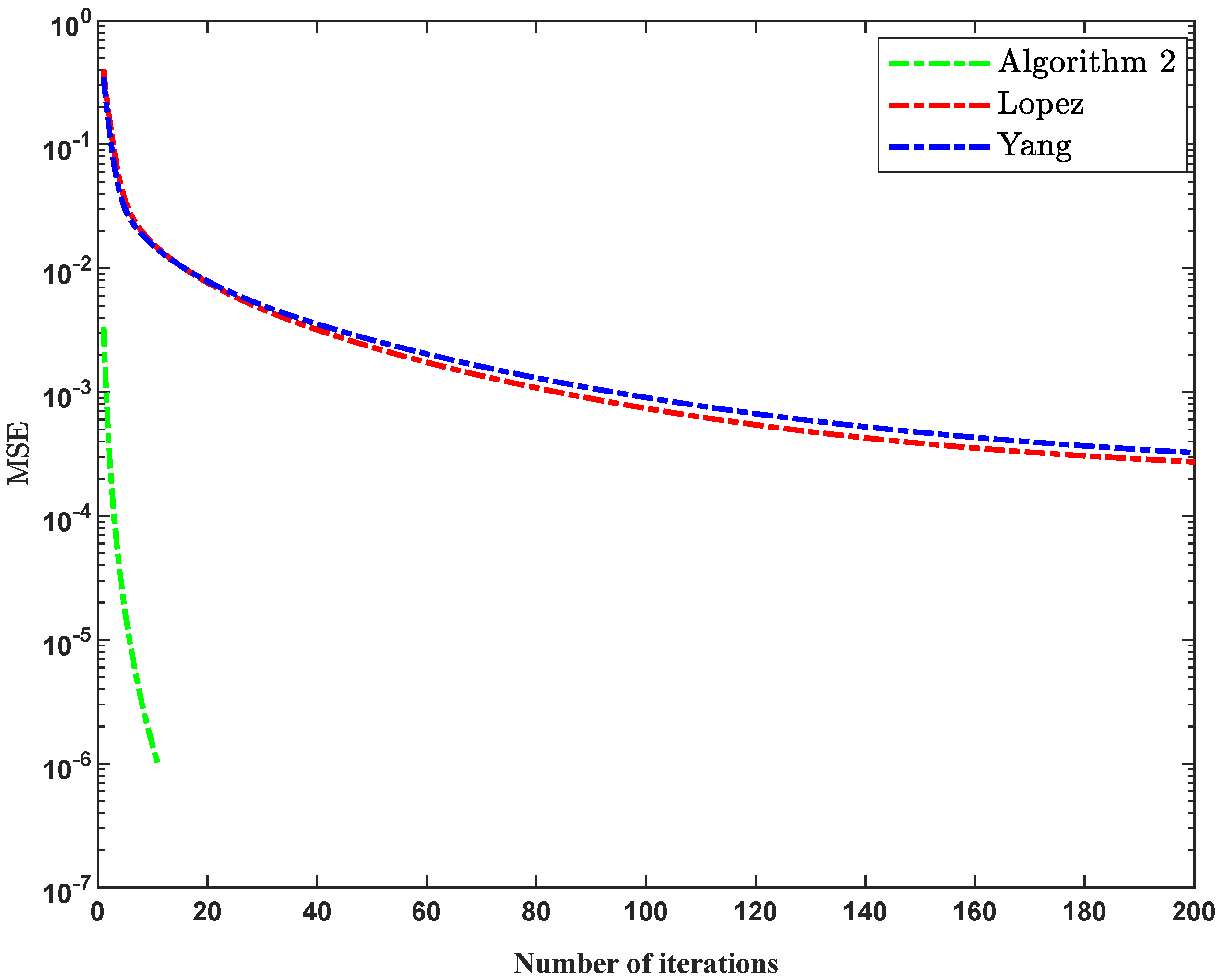
| ,, | , | ||||
|---|---|---|---|---|---|
| Iter(n) | 271 | 359 | |||
| HSRPA | CPUt(s) | ||||
| Iter(n) | 286 | 421 | |||
| GPM | CPUt(s) | ||||
| Iter(n) | 293 | 368 | |||
| PPM | CPUt(s) | ||||
| Iter(n) | 277 | 397 | |||
| SAPM | CPUt(s) | ||||
| Choices of | HSRPA () | HSRPA () | Algorithm 2.1 | |||
|---|---|---|---|---|---|---|
| Ite. | CPUt(s) | Ite. | CPUt(s) | Ite. | CPUt(s) | |
| 56 | 8.9971 | 51 | 7.3628 | 235 | 28.7590 | |
| 55 | 5.8883 | 37 | 3.7528 | |||
| 45 | 4.7402 | 39 | 3.9150 | |||
| 42 | 4.6510 | 38 | 3.9080 | |||
| 38 | 3.9295 | 45 | 4.5573 | |||
| 36 | 3.1803 | 44 | 4.4400 | |||
| 42 | 4.3067 | 50 | 5.0784 | |||
| 29 | 3.4536 | 36 | 3.8640 | |||
| 32 | 3.3220 | 38 | 4.1409 | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taddele, G.H.; Kumam, P.; Gebrie, A.G.; Sitthithakerngkiet, K. Half-Space Relaxation Projection Method for Solving Multiple-Set Split Feasibility Problem. Math. Comput. Appl. 2020, 25, 47. https://doi.org/10.3390/mca25030047
Taddele GH, Kumam P, Gebrie AG, Sitthithakerngkiet K. Half-Space Relaxation Projection Method for Solving Multiple-Set Split Feasibility Problem. Mathematical and Computational Applications. 2020; 25(3):47. https://doi.org/10.3390/mca25030047
Chicago/Turabian StyleTaddele, Guash Haile, Poom Kumam, Anteneh Getachew Gebrie, and Kanokwan Sitthithakerngkiet. 2020. "Half-Space Relaxation Projection Method for Solving Multiple-Set Split Feasibility Problem" Mathematical and Computational Applications 25, no. 3: 47. https://doi.org/10.3390/mca25030047
APA StyleTaddele, G. H., Kumam, P., Gebrie, A. G., & Sitthithakerngkiet, K. (2020). Half-Space Relaxation Projection Method for Solving Multiple-Set Split Feasibility Problem. Mathematical and Computational Applications, 25(3), 47. https://doi.org/10.3390/mca25030047







