Effect of Thrust on the Structural Vibrations of a Nonuniform Slender Rocket
Abstract
1. Introduction
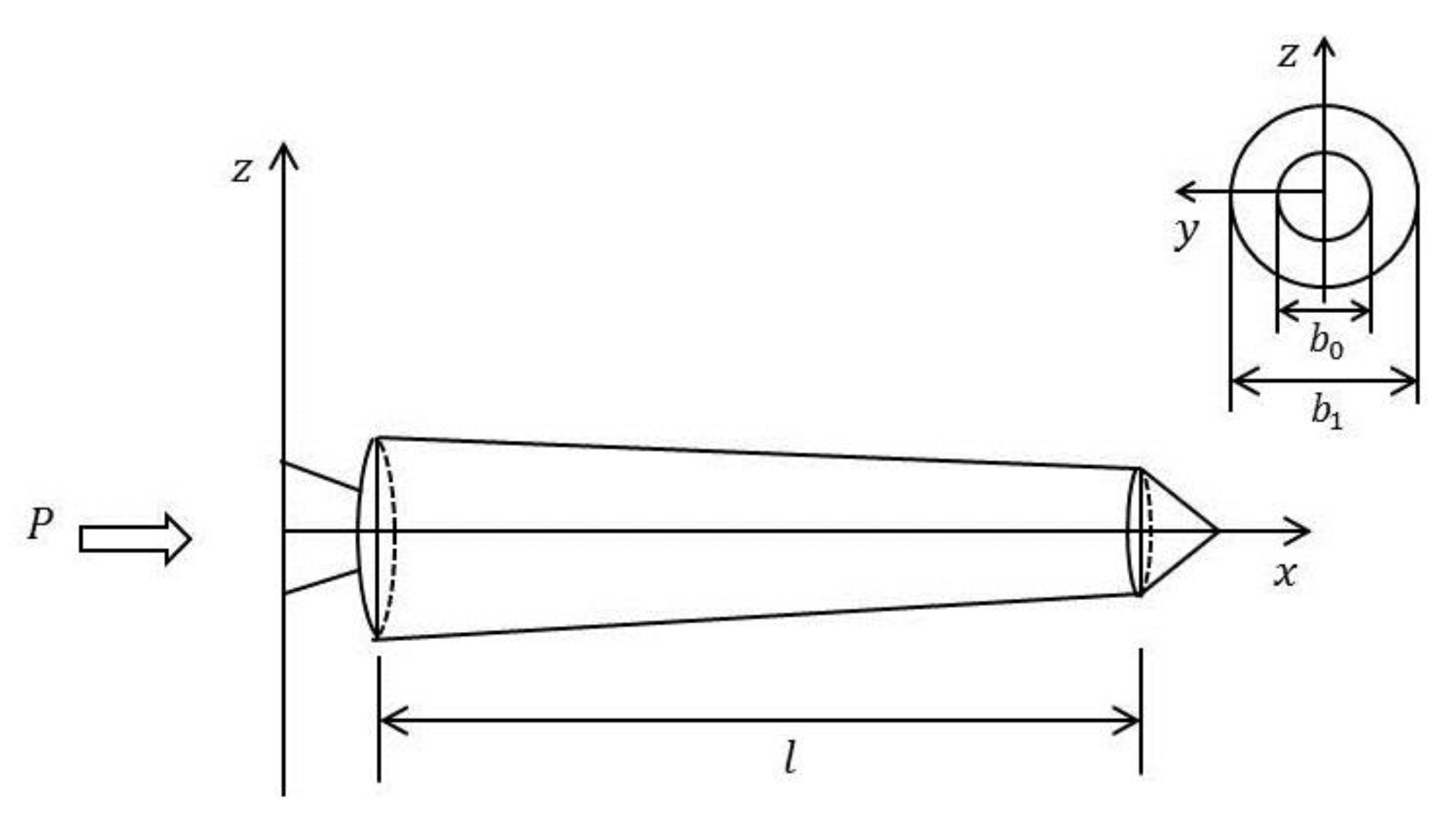
2. Structural Modeling
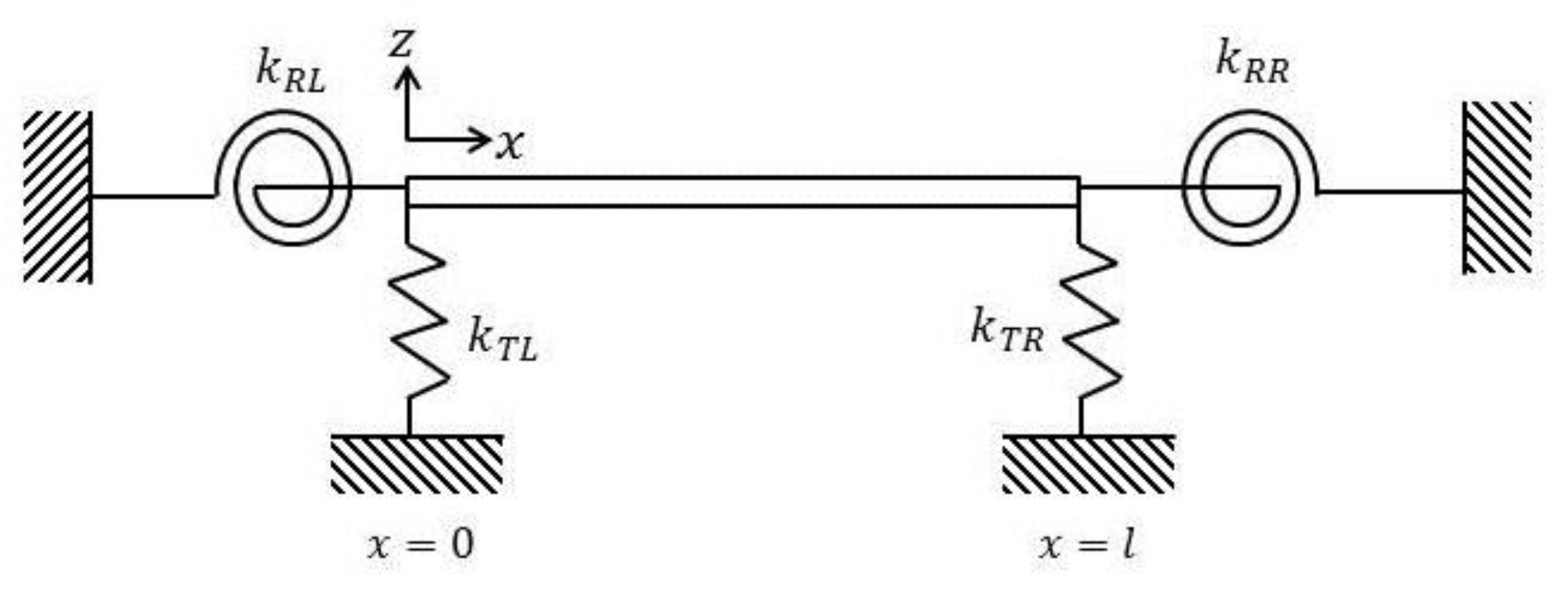
3. Boundary Conditions
4. Application of AMDM
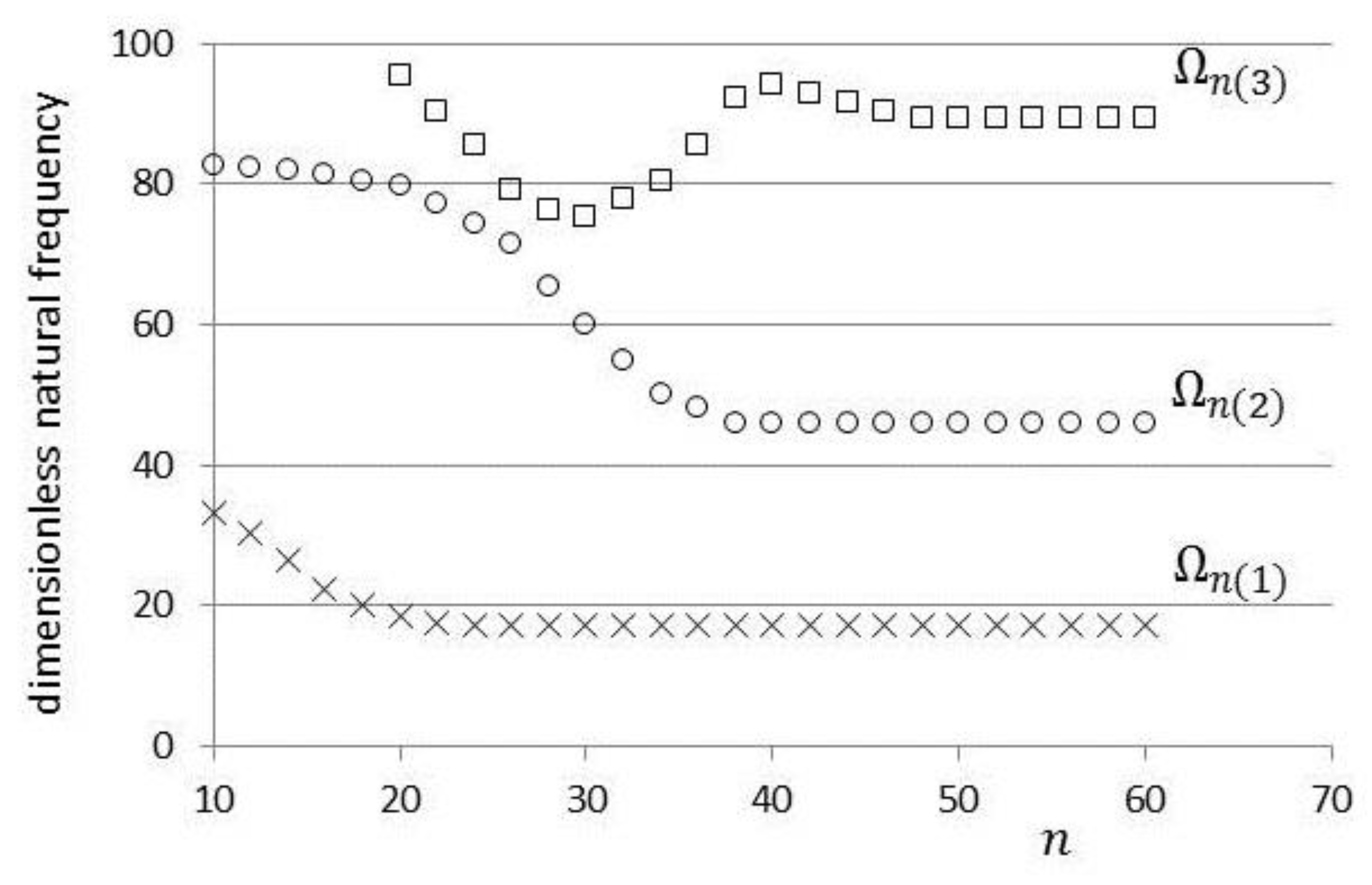
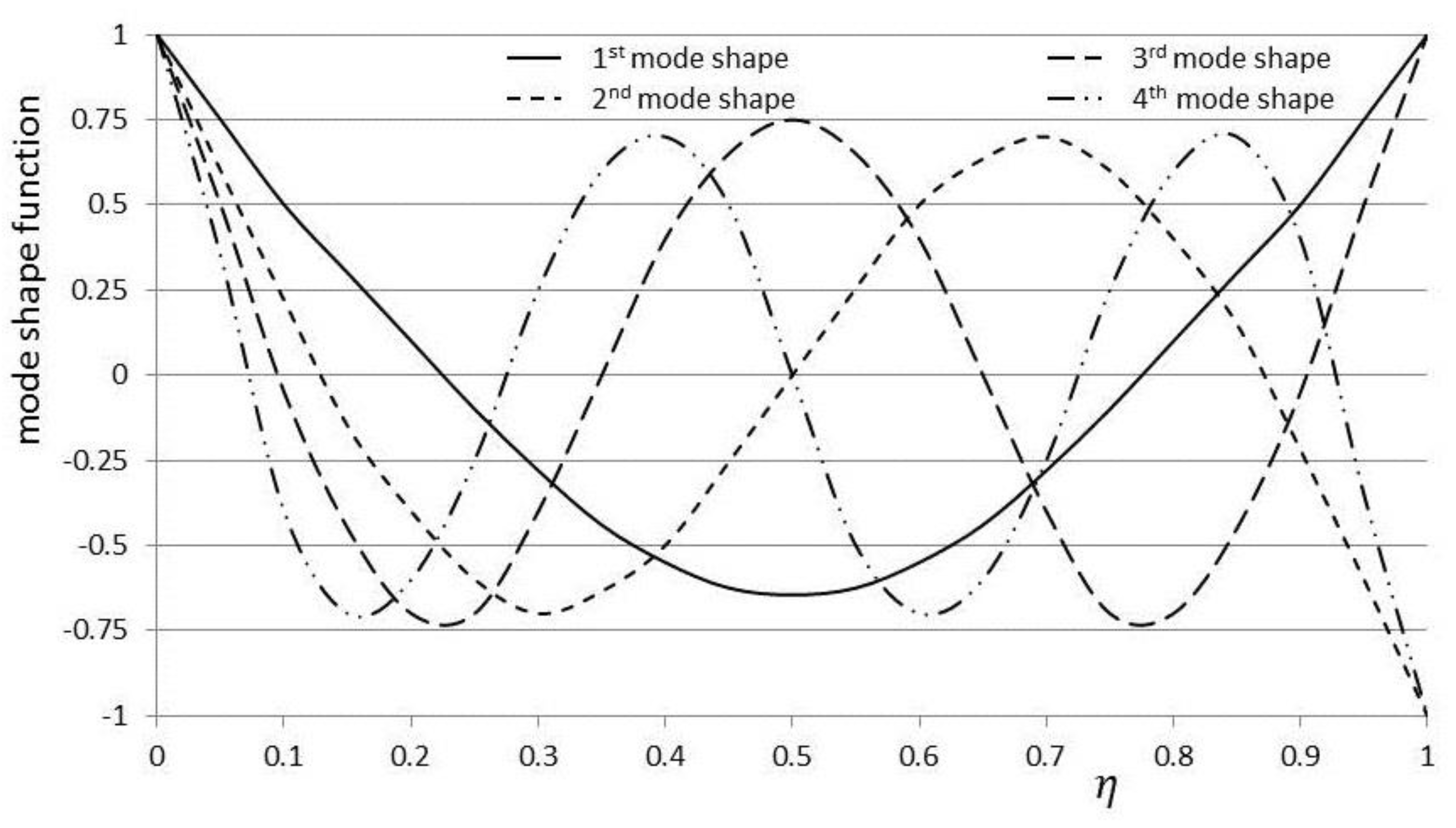
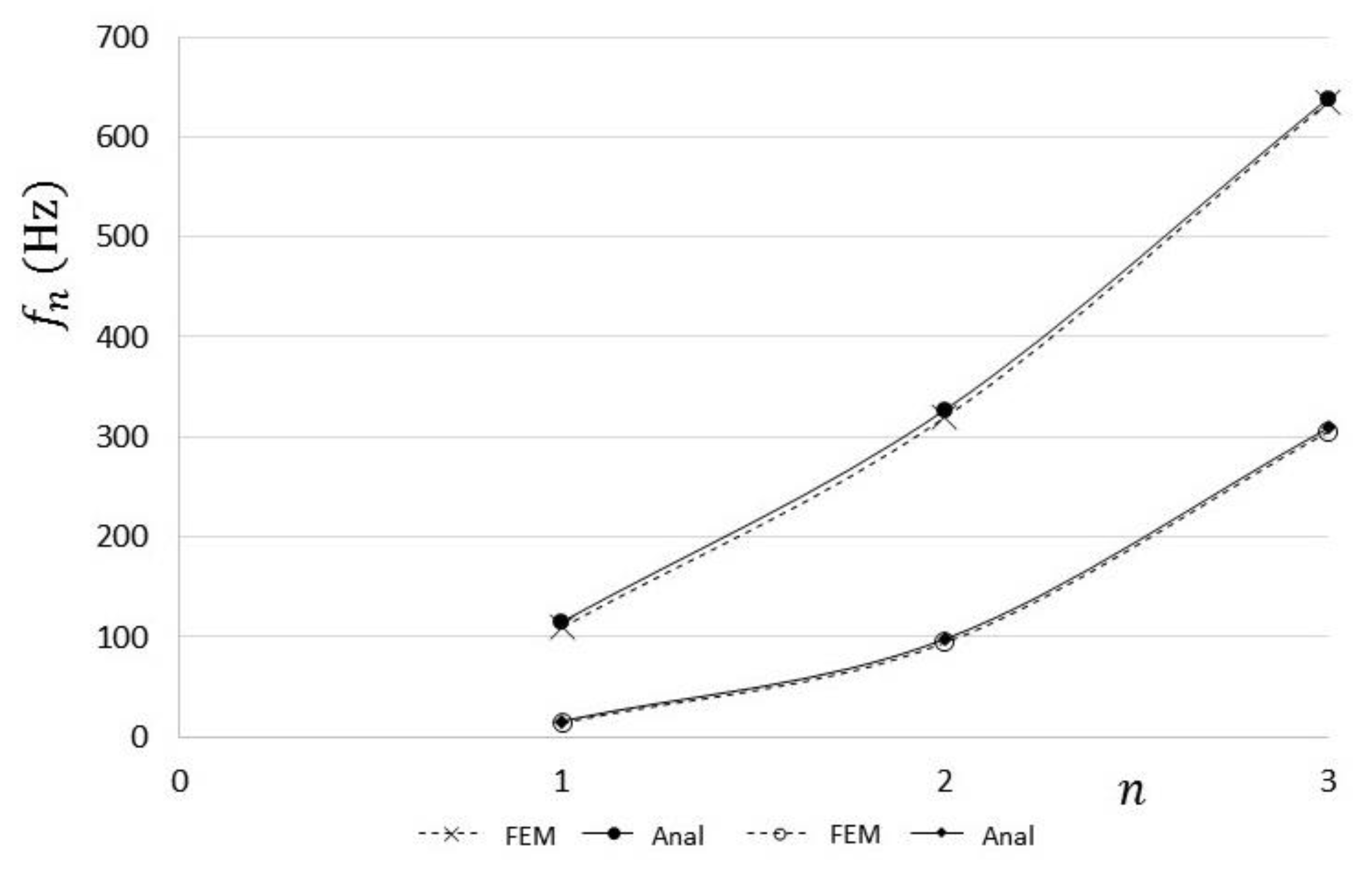
5. Numerical Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Pourtakdoust, S.H.; Assadian, N. Investigation of thrust effect on the vibrational characteristics of flexible guided missiles. J. Sound Vib. 2004, 272, 287–299. [Google Scholar] [CrossRef]
- Kim, J.H.; Choo, Y.-S. Dynamic stability of a free-free Timoshenko beam subjected to a pulsating follower force. J. Sound Vib. 1998, 216, 623–636. [Google Scholar] [CrossRef]
- Bolotin, V.V. Nonconservative Problem of the Theory of Elastic Stability; Pergamon Press: New York, NY, USA, 1963. [Google Scholar]
- Yun, X.; Changchuan, X.; Chao, Y. Effect of thrust on aeroelastic stability of a slender missile. In Proceedings of the 49th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Schaumburg, IL, USA, 7–10 April 2008. [Google Scholar]
- Beal, T.R. Dynamic stability of a flexible missile under constant and pulsating thrust. J. Aircraft. 1965, 3, 486–494. [Google Scholar] [CrossRef]
- Wu, J.J. On the stability of a free-free beam under axial thrust subjected to directional control. J. Sound Vib. 1975, 43, 45–52. [Google Scholar] [CrossRef]
- Wu, J.J. Missile stability using finite elements-An unconstrained variational approach. AIAA J. 1976, 14, 313–319. [Google Scholar] [CrossRef]
- Yoon, S.H.; Kim, J.H. A concentrated mass on the spinning unconstrained beam subjected to a thrust. J. Sound Vib. 2002, 254, 621–634. [Google Scholar] [CrossRef]
- Trikha, M.; Roy Mahapatra, D.; Gopalakrishnan, S.; Pandivan, R. Structural stability of slender aerospace vehicles: Part 1 Mathematical Modeling. Int. J. Mech. Sci. 2010, 52, 937–951. [Google Scholar] [CrossRef]
- Hodges, D.H. A New Approach to Aeroelastic Response, Stability and Loads of Missiles and Projectiles. Available online: https://pdfs.semanticscholar.org/82dc/e823900602140105fff85506f1727271c10f.pdf (accessed on 29 April 2020).
- Ohshima, T.; Sugiyama, Y. Effect of Aerodynamic Loads on Dynamic Stability of Slender Launch Vehicle Subjected to An End Rocket Thrust; American Society of Mechanical Engineers: New York, NY, USA; New Orleans, LA, USA, 2002. [Google Scholar]
- Lamorte, N.; Friedmann, P.P. Hypersonic aeroelastic and aerothermoelastic studies using computational fluid dynamics. AIAA J. 2014, 52, 2062–2078. [Google Scholar] [CrossRef]
- Adomain, G. A review of the decomposition method in applied mathematics. J. Math. Anal. Appl. 1988, 135, 501–544. [Google Scholar] [CrossRef]
- Adomian, G. On the solution of algebraic equations by the decomposition method. J. Math. Anal. Appl. 1985, 105, 141–166. [Google Scholar] [CrossRef]
- Adomian, G. Nonlinear Stochastic System Theory and Application to Physics, Kluwer Academic; Springer: New York, USA, 1988. [Google Scholar]
- Adomian, G.; Rach, R. On composite nonlinearities and the decomposition method. J. Math. Anal. Appl. 1986, 113, 504–509. [Google Scholar] [CrossRef][Green Version]
- Wazwaz, A.M. Analytic treatment for variable coefficient fourth-order parabolic partial differential equations. Appl. Math. Comput. 2001, 123, 219–227. [Google Scholar] [CrossRef]
- Mao, Q. Application of adomain modified decomposition method to free vibration analysis of rotating beams. Math. Probl. Eng. 2013. [Google Scholar] [CrossRef]
- Adair, D.; Jaeger, M. Simulation of tapered rotating beams with centrifugal stiffening using the Adomian decomposition method. Appl. Math. Model. 2016, 40, 3230–3241. [Google Scholar] [CrossRef]
- Hsu, J.-C.; Lai, H.-Y.; Chen, C.-K. An innovative eigenvalue problem solver for free vibration of uniform Timoshenko beams using the Adomian modified decomposition method. J. Sound Vib. 2009, 325, 451–470. [Google Scholar] [CrossRef]
- Lai, H.-Y.; Chen, C.-K.; Hsu, J.-C. Free vibration of non-uniform Euler-Bernoulli beams by the Adomian modified decomposition method. CMES Comput. Model. Eng. Sci. 2008, 34, 87–113. [Google Scholar]
- Lai, H.-Y.; Hsu, J.-C.; Chen, C.-K. An innovative eigenvalue problem solver for free vibration of Euler-Bernoulli beam by using the Adomian decomposition method. Comput. Math. Appl. 2008, 56, 3204–3220. [Google Scholar] [CrossRef]
- Yaman, Y. Adomian decomposition method for solving a cantilever beam of varying orientation with tip mass. J. Comput. Nonlinear Dyn. 2007, 2, 52–57. [Google Scholar] [CrossRef]
- Adair, D.; Jaeger, M. Simulation of the vibrations of a non-uniform beam loaded with both transversely and axially eccentric tip mass. Int. J. Comput. Methods Exp. Meas. 2018, 6, 679–690. [Google Scholar] [CrossRef][Green Version]
- Sugiyama, Y.; Oshima, T. Effect of Aerodynamic Loads on Dynamic Stability of Slender Launch Vehicle Subjected to An End Rocket Thrust; Paper IMECE 2002-33034, FSI, AE & FIV + N Symposium; ASME: New Orleans, LA, USA; New York, NY, USA, 2002. [Google Scholar]
- Krynicki, E.; Mazurkiewicz, Z. Free vibration of a simply supported bar with a linearly variable height of cross section. Trans. Am. Soc. Mech. Eng. J. Appl. Mech. (Series E) 1962, 29, 497–501. [Google Scholar] [CrossRef]
- Naguleswaran, S. A direct solution for the transverse vibration of Euler-Bernoulli wedge and cone beams. J. Sound Vib. 1994, 172, 289–304. [Google Scholar] [CrossRef]
- Pourtakdoust, S.H.; Assadian, N. Aeroelastic Simulation of Guided Missiles; M. S. Project; Sharif University of Technology: Tehran, Iran, 2001. [Google Scholar]
- ANSYS. Academic Research; Ansys Inc.: Canonsburg, PA, USA, 2014. [Google Scholar]
- Avcar, M. Free vibration analysis of beams considering different geometric characteristics and boundary conditions. Int. J. Mech. Appl. 2014, 4, 94–100. [Google Scholar] [CrossRef]

| Uniform Cylinder, | |||
|---|---|---|---|
| Current | 22.3745 | 61.6912 | 121.0452 |
| Ref. [26] | 22.3733 | 61.6728 | 120.9030 |
| ‘Complete’ Rocket, | ||||
|---|---|---|---|---|
| Current | 17.4195 | 35.0436 | 57.4867 | 84.8549 |
| Ref. [27] | 17.4164 | 35.0270 | 57.3796 | 84.6028 |
| Truncated Cone | ||||
|---|---|---|---|---|
| 0.05 | Current | 15.9551 | 33.1259 | 56.5495 |
| Ref. [27] | 15.9543 | 33.1251 | 56.5484 | |
| 0.15 | Current | 14.9399 | 34.8542 | 63.8621 |
| Ref. [27] | 14.9381 | 34.8535 | 63.8434 | |
| 0.25 | Current | 15.1278 | 37.8976 | 71.5367 |
| Ref. [27] | 15.1266 | 37.8972 | 71.5171 | |
| 0.35 | Current | 15.7681 | 41.1205 | 78.8673 |
| Ref. [27] | 15.7674 | 41.1193 | 78.8259 | |
| 0.45 | Current | 16.6135 | 44.3543 | 86.0330 |
| Ref. [27] | 16.6130 | 44.3537 | 85.8162 | |
| 0.55 | Current | 17.5662 | 47.5667 | 90.2381 |
| Ref. [27] | 17.5653 | 47.5650 | - | |
| 0.65 | Current | 18.5803 | 50.6751 | 93.7655 |
| Ref. [27] | 18.5794 | - | - | |
| Truncated Cone | ||||
|---|---|---|---|---|
| 0.05 | 15.9551 | 33.1259 | 56.5495 | |
| 11.9663 | 22.7243 | 35.3434 | ||
| 7.6451 | 14.2773 | 22.9732 | ||
| 5.9561 | 10.2790 | 16.7838 | ||
| 0.25 | 15.1278 | 37.8976 | 71.5367 | |
| 11.0306 | 25.7700 | 44.7104 | ||
| 6.9336 | 16.3336 | 29.0618 | ||
| 5.9881 | 11.7861 | 21.2321 | ||
| 0.65 | 18.5803 | 50.6751 | 93.7655 | |
| 13.1610 | 34.9608 | 60.9476 | ||
| 8.1289 | 22.2970 | 39.3815 | ||
| 6.5804 | 16.2160 | 28.1300 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adair, D.; Nagimova, A.; Jaeger, M. Effect of Thrust on the Structural Vibrations of a Nonuniform Slender Rocket. Math. Comput. Appl. 2020, 25, 29. https://doi.org/10.3390/mca25020029
Adair D, Nagimova A, Jaeger M. Effect of Thrust on the Structural Vibrations of a Nonuniform Slender Rocket. Mathematical and Computational Applications. 2020; 25(2):29. https://doi.org/10.3390/mca25020029
Chicago/Turabian StyleAdair, Desmond, Aigul Nagimova, and Martin Jaeger. 2020. "Effect of Thrust on the Structural Vibrations of a Nonuniform Slender Rocket" Mathematical and Computational Applications 25, no. 2: 29. https://doi.org/10.3390/mca25020029
APA StyleAdair, D., Nagimova, A., & Jaeger, M. (2020). Effect of Thrust on the Structural Vibrations of a Nonuniform Slender Rocket. Mathematical and Computational Applications, 25(2), 29. https://doi.org/10.3390/mca25020029




