Abstract
Prime numbers are one of the most intriguing figures in mathematics. Despite centuries of research, many questions remain still unsolved. In recent years, computer simulations are playing a fundamental role in the study of an immense variety of problems. In this work, we present a simple representation of prime numbers in two dimensions that allows us to formulate a number of conjectures that may lead to important avenues in the field of research on prime numbers. In particular, although the zeroes in our representation grow in a somewhat erratic, hardly predictable way, the gaps between them present a remarkable and intriguing property: a clear exponential decay in the frequency of gaps vs. gap size. The smaller the gaps, the more frequently they appear. Additionally, the sequence of zeroes, despite being non-consecutive numbers, contains a number of primes approximately equal to , n being the number of terms in the sequence.
1. Introduction
Prime numbers have fascinated mathematicians since the beginnings of Mathematics [1,2,3,4]. Their distribution is intriguing and mysterious to some extent, despite being non-chaotic. After centuries of research, there are still many open problems to be solved, and the exact details of the prime numbers distribution are yet to be understood [5,6]. Today, the interest in prime numbers has received a new impulse after their unexpected appearance in different contexts ranging from cryptology [7] or quantum chaos [8,9] to biology [10,11]. Furthermore, with the advent of more and more powerful computers, different studies are being undertaken where methods traditionally used by physicists are being applied to the study of primes. For example, in [12], the multifractality of primes was investigated, whereas some appropriately defined Lyapunov exponents for the distribution of primes were calculated numerically in [13]. Additionally, one of the most studied problems in number theory, the Goldbach conjecture, first formulated around 1740, has been being continuously studied with the help of computers [14,15,16] (Its weaker version, called the ternary Goldbach conjecture, was finally proven to be true in 2013 [17]). More examples can be found in [18].
2. Jacob’s Ladder
One can argue that prime numbers present perplexing features, somewhat of a hybrid of local unpredictability and global regular behavior. It is this interplay between randomness and regularity that motivated searches for local and global patterns that could perhaps be signatures of more fundamental mathematical properties.
Our work is concerned with the long standing question of the prime numbers distribution, or more precisely with the gaps between primes [19,20], a topic that has attracted much attention recently [16,21,22] after some massive advances [23]. Some problems related to prime gaps are well known, for instance, Legendre’s conjecture states that there is a prime number between and for every positive integer n. This conjecture is one of Landau’s problems on prime numbers [24] and, up to the current date (2018), it is still waiting to be proved or disproved. Another example would be the famous twin primes conjecture [25]. Proving this conjecture seemed to be far out of reach until just recently. In 2013, Zhang demonstrated the existence of a finite bound 70,000,000, such that there are infinitely many pairs of distinct primes which differ by no more than B [23]. After such an important breakthrough, proving the twin prime conjecture looked much more plausible. Immediately after, a cooperative team led by Terence Tao, building upon Zhang’s techniques, was able to lower that bound down to 4680. Then, in the same year, Maynard slashed the value of B down to 600, and finally the Polymath project further reduced it to 246 [26,27,28].
Displaying numbers in two dimensions has been a traditional approach toward primes visualization [29,30]. Here, we propose an original way of number arrangement yielding an appealing visual structure: an oscillating plot that increases and decreases according to the prime number distribution. We plot the integers from 1 to n in 2D (x, y) starting with 1 and (hence, the first point will be (1, 0)), moving to 2 the plot moves up on the y-axis, so that the next point in terms of coordinates is (2, 1). In the next step, it goes up or down depending on whether the number n is a prime number or not. Number 2 is prime, so it flips in such a way that it goes down next, and hence the third point is (3, 0). Now, 3 is prime so the next step goes up again, and we move up to (4, 1). The number 4 is not a prime so it continues moving up, and so on. We used our own code but different codes to produce Jacob’s ladder can be found in the On-Line Encyclopedia of Integer Sequences [31].
In Figure 1, the sequence produced by the algorithm is shown up to . The blue dashed line stands for the line (or x axis), which will be central to our study. We will refer to the points (x, 0) as zeroes from now on. Because of the resemblance of this numerical structure to a ladder, we refer to this set of points in the 2D plane as Jacob’s Ladder, for short hereafter. The points in the ladder (the y values) can be written as:
where denotes the number of primes .
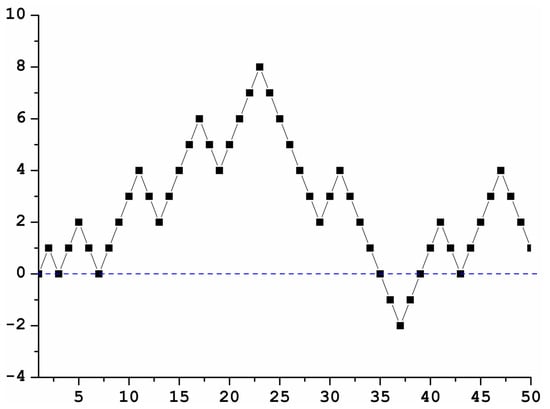
Figure 1.
Illustrative plot of the first 50 points of the Jacob’s Ladder sequence. The blue dashed line stands for .
3. Results
The next figures show the numerical results, which inspired the ideas and conjectures we will present in the next section. Figure 2(Top) shows Jacob’s Ladder from 1 to 100. The blue dashed line signals the x-axis for clarity’s sake. As can be seen, up to 100, the Ladder is almost positive, most of its points being above the x-axis. This is misleading, though, as we can see from looking at the behavior of Jacob’s Ladder from 1 to 10,000 (Figure 2(Bottom)).
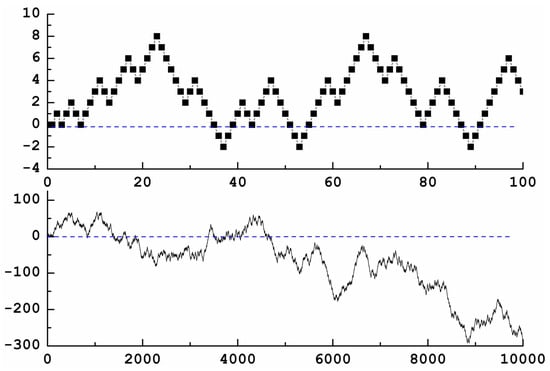
Figure 2.
Top: Jacob’s Ladder from 1 to 100. Bottom: Jacob’s Ladder from 1 to 10,000. The blue dashed line stands for .
Figure 2(Bottom) shows Jacob’s Ladder from 1 to 10,000. As can be seen, now most of the Ladder is negative except for two regions. However, this fact changes again if we move to higher values. Figure 3(Top) shows Jacob’s Ladder from 1 to 100,000 and here we see, as said before, that, after 50,000, most of the Ladder is again positive. Figure 3(Bottom) shows Jacob’s Ladder from 1 to 1,000,000. Note that the Ladder presents a big region of negative values after 150,000. After this, no more zeroes are present up until 16,500,000 (see Figure 4(Top)). Afterwards, the Ladder is mostly negative again.
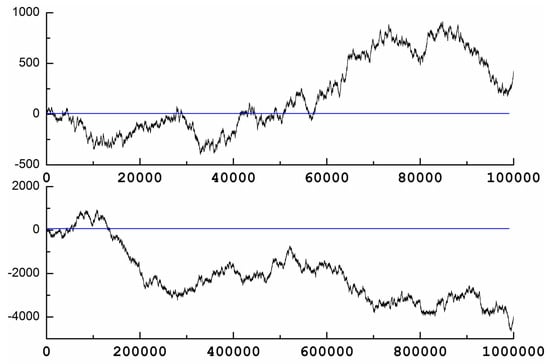
Figure 3.
Jacob’s Ladder from 1 to 100,000 (Top) and from 1 to 1,000,000 (Bottom). The blue line stands for .
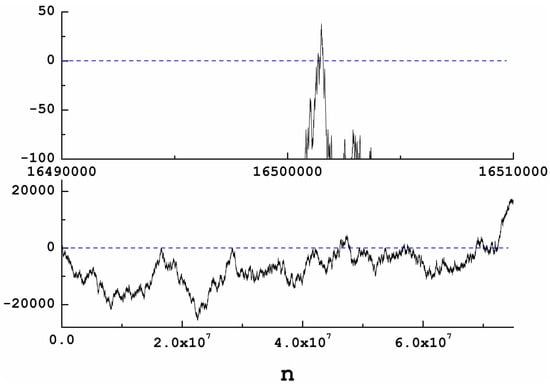
Figure 4.
Top: Jacob’s Ladder goes up again at ∼ 16,000,000. Bottom: Jacob’s Ladder shows a big positive peak and hundreds of zeroes around 44 million (and around 70 million). The blue dashed line stands for .
Around 45 million, hundreds of zeroes are found (Figure 4(Bottom)). Going up to 100 million, more zeroes appear, totaling 2415. The next crossing appears for 202,640,007. Larger gaps appear in the sequence at this point. For instance, no zeroes are found between 6,572,751,127 and 9,107,331,715.
Much larger is the gap found at 9,169,470,319. The next zero is 222,564,950,675. In addition, an even larger is the one from 225,888,362,295 to 676,924,242,679 (which are consecutive zeroes as well).
Jacob’s ladder resembles what in probability theory is called a Wiener process, so the probability distributions could be studied as well. It is quite clear that points very far from the x-axis will be less abundant when compared to the number of points close to it, above, or below the axis, so, renormalizing the number of points in the Ladder up to a given point, it seems natural to expect some version of an inverse arcsine law (centered around the x-axis) in the distribution of these points. Despite the large interval explored, the data are not enough to plot a convincing graph due to the ladder’s noticeable asymmetry, so we prefer to leave this point as an open question.
Building from the figures presented above, this simple representation of prime numbers in two dimensions brings about many interesting questions and allows us to arrive at a list of conjectures, which, despite their simplicity, will unfortunately be very difficult to prove or disprove. The most natural one is discussed below. Two additional ones are presented and analyzed in Appendix A. The continuous appearance of an increasing number of zeroes, although sparse, points towards all of them holding true in the limit of large numbers.
Conjecture I:
The number of cuts (zeroes) on the x-axis tends to infinity. In mathematical language, being the number of zeroes in the Ladder,
Discussion:
Proving this conjecture is beyond the scope of this article, but, in the following, we describe the empirical motivation behind it. This is the main idea in our study and the basis of the conjectures that follow. Figure 5 presents the number of zeroes vs. n, in Jacob’s Ladder, from 1 to (logarithmic scale on both axes). Notice that the number of zeroes increases (by construction, it cannot decrease) with n in an apparently chaotic or unpredictable way. In some intervals of n, the number of zeroes is constant, meaning that the ladder is entirely above or below . After those plateaus, it increases again and again. If our conjecture is true, it will increase forever as we move towards increasingly bigger values of n. However, we conjecture as well that the slope dictating this increase will be lower and lower as n goes to infinity. The fact that the prime numbers become increasingly separated seems to indicate so: since the prime numbers are more and more separated, the ladder will present a smaller amount of zigzagging.
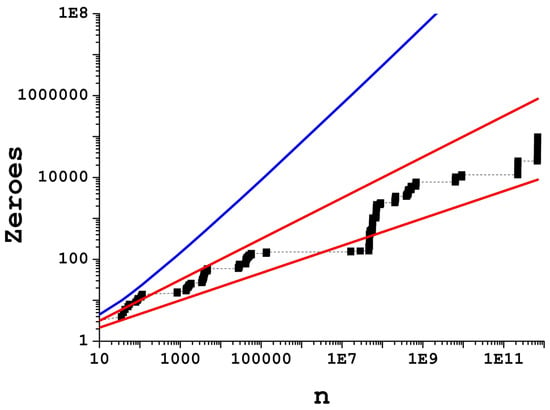
Figure 5.
(Color online) , the number of zeroes in Jacob’s Ladder from 1 to . Note the logarithmic scale on both axes. Number of zeroes = 194,531. Red lines stand for the and functions. In blue, we plotted the counting function, , for the sake of comparison.
The sequence of cuts, or zeroes, can be denoted as and in the same way infinitely many successions can be defined: being the number of cuts on the line up to n, being the number of cuts in up to n, and so on. In other words, we conjecture that contains infinitely many elements, and, if Conjecture I is true, then it is likely that any other will contain infinitely many terms when n tends to infinity. Thus, the Ladder allows for non-trivially defining infinitely many successions with infinitely many terms (and without repetitions), whose cardinal will be and the sum of all of them is again .
It is to be noted that the ladder cannot be constrained between two y-values, since the gaps between primes can be arbitrarily large. A lower or upper limit could exist, but not both.
An interesting question can be formulated here: how does grow? What would be a good approximation for the number of zeroes given a value of n? The answer is not trivial, since the function is neither multiplicative nor additive. In Figure 5, we present two simple functions that operate as approximate upper and lower limits of the function, namely and , represented by red lines. The number of zeroes is not strictly confined between these two curves; however, the agreement is fair enough for the purposes of this paper. We also plotted the counting function in blue, for the sake of comparison.
The idea here is not to extract accurate upper and lower bounds with these functions, but to simply offer a qualitative approximation. The reason why such a qualitative conclusion is relevant lies on the geometrical insight that can be extracted from these simple approximations. If the numbers from 1 to were to be plotted within a square (for instance forming a spiral, like in [29]), then having approximately n zeroes (or any other selection of numbers used as tracking mechanism) would mean that the amount of zeroes we have is approximately given by the length of the side of the square. In an analogous way, if we display the numbers from 1 to within a cube of side n, then the side of the cube would give us that information. Therefore, having a number of zeroes constrained between and seems to point towards some kind of fractality for the number of zeroes present in the sequence .
4. Discussion
While completing this paper, we found similar studies, like those presented in [32,33,34]. For instance, in [34], a one-dimensional random walk (RW), where steps up and down are performed according to the occurrence of special primes (twins and cousins), was defined. If there are infinitely many twins and cousins (as suggested by the Hardy–Littlewood conjecture), then the RW defined there will continue to perform steps forever, in contrast to the RW considered in [32] or [33], where random walks were finite. In our case, we prefer not to talk about random walks since the distribution of primes, despite mysterious, is not random. On the other side, the idea of Jacob’s ladder is simple and beautiful given that, due to the infinitude of prime numbers, its intrinsic complexity and zigzagging must continue indefinitely. Now, its properties, by definition, depend both on the number of primes in a given interval and on the separation between them. It is known that the gaps between consecutive prime numbers cluster on multiples of 6. Because of this fact, 6 is sometimes called the jumping champion, and it is conjectured that it stays the champion all the way up to about [35,36].
Beyond , and until , the jumping champion becomes 30 (), and, beyond that point, the most frequent gap is 210 () [36]. It is a natural conjecture that, after some large number, the jumping champion will be 2310 () and so on. Further interesting results on some statistical properties between gaps have been recently found [37,38]. However, all of the aforementioned numerical observations, despite revealing intriguing properties of the primes sequence, are not easily put into our problem in order to know whether or not the Ladder will have infinitely many zeroes or not. On the other side, according to Ares et al. [39], the apparent regularities observed in some works [34,40,41] reveal no structure in the sequence of primes, and that is precisely a consequence of its randomness [42]. However, this is a controversial topic. Recent computational work points that “after appropriate rescaling, the statistics of spacings between adjacent prime numbers follows the Poisson distribution”. See [43,44] and references therein for more on the statistics of the gaps between consecutive prime numbers.
The question at hand is encapsulated by whether, after a given number, all turns in the Ladder will have an “order”. By order, we mean that will go up (or down) after the next prime, and then down (or up) and so on but always keeping a property: that an “averaged” curve will continue asymptotically along one particular direction of the plane without ever going back to the x-axis—or, in other words, is it possible that, after an unknown number X, the sum of all intervals between primes “up” minus the sum of all intervals “down” (or the other way around) will be positive (or negative) for all possible values as ?
where () stands for the interval between two primes [] which make the Ladder go up (down) (Sensu stricto this could be true for a number and the sum represented by Equation (3) could be (or ) without crossing the x-axis because we start from some point up (or down) the axis.). This looks unlikely and would be some interesting order property if it turned out to be the case (and it would prove Conjecture I to be false). If so, it would be interesting to find that number X distinctly.
This is related to the question of whether the zeroes are randomly distributed, or follow some kind of ordered distribution. For instance, do the terms in follow Benford’s law [45]? In many different natural datasets and mathematical sequences, the leading digit d is found to be non-uniformly distributed as opposed to naive expectations (The leading digit of a number is its non-zero leftmost digit. For example, the leading digits of 2018 and 994,455 are 2 and 9, respectively). Instead, it presents a biased probability given by where . While this empirical law was indeed first discovered by the Canadian–American astronomer, applied mathematician and autodidactic polymath Simon Newcomb [46] in 1881, it is popularly known as Benford’s law, and also as the law of anomalous numbers [45]. Up to date, many mathematical sequences such as and [47], binomial arrays [48], geometric sequences, or sequences generated by recurrence relations [49,50], to cite a few, have been proved to conform to Benford.
Figure 6 shows the proportion of the different leading digits found in the different intervals , up to 194,531 zeroes, and the expected values according to Benford’s law. Note that intervals have been chosen such that , with D a natural integer, in order to ensure an unbiased sample where all possible first digits are a priori equiprobable. With that in mind, however, the results for the interval are also presented because the number of zeroes are many times more than those found up to . Obviously, the curve is likely to change as more and more zeroes are counted (it changes when fewer zeroes are counted). A straightforward calculation demonstrates that, in the best of cases, one should count up to five (or six) times the current number of zeroes before having a distribution in fair agreement with Benford’s law. Note that, in order to obtain such a large amount of zeroes, according to Figure 5, it is likely that one should explore the Ladder in a 25 (36) or 125 (216) times larger interval, i.e., up to ().
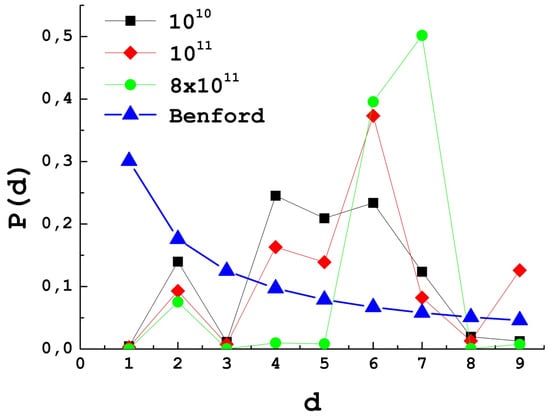
Figure 6.
(Color online) Leading digit histogram of the zeroes sequence . The proportion of the different leading digits found in the intervals, , and in is shown in black squares, red diamonds, and green circles as labeled. The expected values according to Benford’s law are shown in blue triangles.
On the other hand, it is natural to assume that the distribution presented by will be the same for all values of y. Thus, while being aware that the numbers are still very small from a statistical point of view, the analysis of the terms in more crowded sequences can provide further evidence for the random distribution (or better said, non-Benford-like distribution) of for all y.
Another point to be noticed is that all of the zeroes can be written as . This is not a surprise—in fact, it can be easily proved that it must be this way: after 3, which is the first zero excluding 1, all zeroes must be separated by a number twice the sum of the number of gaps between primes (every pair of primes is separated by an even number); therefore, the gaps between zeroes will always be a multiple of 4.
For one more test about some possible unexpected non-random properties of the zeroes in the Ladder, we can check the number of zeroes ending in a given odd digit (since all the even ones will not be in ). Doing so, we observe that they change depending on the explored interval, so there is no clear evidence of any trend (The terms ending in 1, 3, 5, 7, and 9 amount to 38,835, 38,905, 38,799, 38,898, and 39,093, respectively, in the first 194,530 zeroes, thus showing a uniform distribution ( each). A linear fit () to the data (in probabilities, given as %) provides the following result: (0.04315) and (0.00751). The slope is small, and just twice the error of the linear fit, so it is quite unsafe to assume a trend on this).
However, going back to the zeroes as a whole, we can observe the two most important results found in our study. First, it is natural to wonder: how many of these zeroes are primes? Is this number somewhere predictable? Since in an interval we find primes, should we expect, in a set of X consecutive zeroes (but not consecutive numbers!), an amount of primes approximately equal to ? Interestingly, it seems to be the case if we count a few thousands of zeroes when looking at Figure 7, but it is not really the case from looking at the differences in percentage (see Table 1). The prime zeroes found are nevertheless in remarkable agreement with this simple assumption. As we see in Figure 7, for , the prime numbers found in depart steadily from , the latter being an overestimate of the actual number of primes.
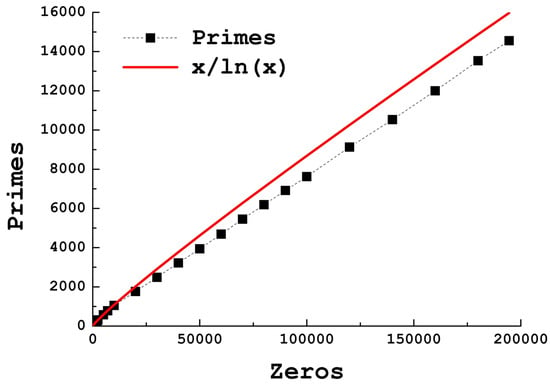
Figure 7.
(Color online) Number of primes as a function of the number of terms (zeroes) in the sequence . The red line stands for the plausible similitude with the counting function .

Table 1.
Summary of the results insofar. The first column is the interval of , the second is the number of zeroes found in it, the third is the number of primes in the sequence, the fourth is —n being the number of zeroes, the fifth shows the difference in percentage, and the sixth the average gap between zeroes.
As mentioned before, all zeroes can be written as . However, is the same as . It is a well known result that all primes (except 2) can be written as or —the first ones allowing to be expressed as the sum of two perfect squares , while the second ones can never be expressed in such a way. Therefore, in our results, those zeroes which are prime always belong to the second subgroup. Furthermore, the arithmetic progressions , (and ) are of particular interest because the primes in the progression (and ) are known to be “denser” than in the progression (and ); a result conjectured in 1853 by Tschebyschef [51,52] and proved by Phragmen [53] and Landau [54]. However, the problem is, as is usually the case in number theory, far from being simple. A famous result by Littlewood [2] showed that there are infinitely many integers x such that there are more prime numbers in the progression than in the , up to that number x (Using formal mathematical notation, it is said that for infinitely many x, where denotes the number of positive primes which are equal to c (mod b)).
It is easy to see that every sequence (or zeroes in the lines ) will contain primes (that is, reversals of the ladder) if and only if b is even. In particular, if , with a an integer number or zero, then those primes will belong to the arithmetic progression . In addition, those sequences where will contain primes belonging to the arithmetic progression (with the exception of 2, there are no primes in the sequences when b is odd). Thus, it is clear that the problem of how to demonstrate the existence of an infinite number of zeroes in Jacob’s Ladder is related with previous important results regarding primes in arithmetic progressions. However, it is not enough to know how many primes are found in a particular progression: the gaps between primes are equally important, and this is a more mysterious problem.
Now, we will see what can be said about gaps: how are the zeroes separated? As we have seen in Figure 1, Figure 2, Figure 3 and Figure 4, the Ladder goes up and down in an erratic way, resulting in a rather capricious distribution of the zeroes. Nevertheless, counting the number of times that a given gap between zeroes appears within a given number of zeroes, and the result is clearly non-arbitrary. Figure 8 shows the result after analyzing the gaps in up to . It can be seen that a clear exponential decay is found. Note as well that all gaps are multiples of 4, except 2, which only appears once (The demonstration of the fact that all gaps are multiples of 4 is trivial).
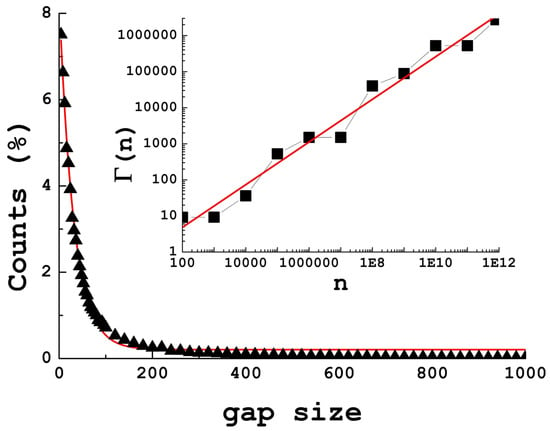
Figure 8.
Number of times that a gap appears depending on the the gap size, only up to 1000 for clarity’s sake. The red line presents the exponential decay fit. The inset shows the averaged gap vs. the interval size.
The inset shows the averaged gap, , vs. the interval size. is calculated as the sum of gaps divided by the number of gaps. Another possible definition, , would be the interval size divided by the number of zeroes. The plateaus are due to intervals (from to for instance) where no more zeroes are found, so the number of gaps is constant. Using the definition, the averaged gap would be 10 times larger.
Figure 8, showing the distribution of gaps, is a remarkable result, and it may lead to a number of interesting observations. Note that almost 25% of the gaps are 4, 8, 12, or 16, and more than 53% of the gaps are smaller than 60. Gaps represent more than 63% of the gaps found; however, as mentioned before, very large gaps are found as well as large as 451,035,880,384 (about half the interval explored).
In the intervals explored up to now, 4 is always the most frequent gap, referred to as hereafter, followed by , (i.e., the second most frequent gap is 8, the third most frequent is 12, etc.). Immediately, a legitimate and important question would be to inquire about the behavior of the distribution of gaps for large values of n. Will be 4 for any interval, no matter how large—or is it possible that, from a very large interval onwards, it shifts to 8, and later on to 12, and so on? Furthermore, it could be reasonable as well to expect an equiprobable distribution of gaps in the limit .
However, it has been shown that 4 is the most probable gap size (Figure 8). If the exponential decay of vs. n hypothesis were finally confirmed , such result would represent an attribute of the Ladder of fundamental importance, meaning that, every time that the ladder crosses the x axis, it is close to a prime number. This observation can be misleading, though because, at the same time, the average gap clearly seems to increase with n (Inset in Figure 8). Thus, these results do not mean that all of the zeroes are primes. In fact, as showed before (See Figure 7 and Table 1), out of n zeroes, about are actually primes.
The percentage of gaps of length 4 decreases with n faster than exponentially, in the same way as those of length 8 or 12, and likely for all gap values (in small intervals, some variations may occur, but we are interested in properties appearing in the limit of large intervals), as shown in Figure 9. This result can be easily explained since, the larger the interval is, the more gaps enter into the list of gaps, so it is natural that the percentage would decrease.
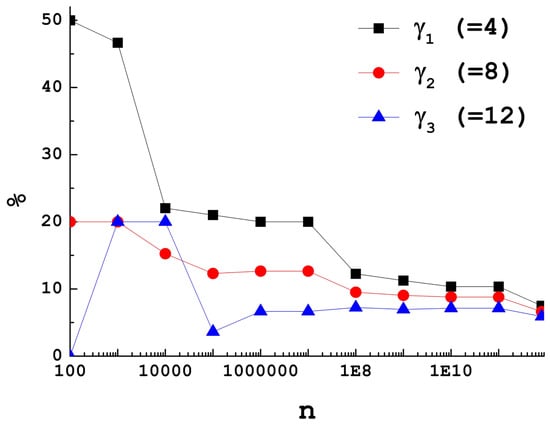
Figure 9.
Percentage of the total gaps of value 4, 8 and 12 (colors black, red and blue respectively) vs. number of zeroes, in log scale. As can be seen the percentage, decreases for all these three cases, with the order remaining as = 4, = 8, = 12.
At the same time, since the average gap increases, it could be natural to expect an increase in the percentage of larger gaps. However, this is not the case—only for small intervals do we observe an increase with n of the percentage of large gaps because, for small intervals, large gaps are rare, yet it seems that the percentage of large gaps is always below that of 4, 8, etc.
A final important remark: we started this work without knowing any previous studies on this topic—only while writing the paper did we check if the sequence of zeroes appeared in the On-Line Encyclopedia of Integer Sequences [31], and then we found it was first studied in 2001 by Jason Earls and subsequently by Hans Havermann within a different context (See full sequence in http://chesswanks.com/num/a064940.txt) and Don Reble (See full sequence in https://oeis.org/A064940/a064940.txt).
5. Conclusions
In this paper, an original idea has been proposed with the aim of arranging integers in 2D according to the occurrence of primality. This arrangement of numbers resembles a ‘ladder’ and displays peaks and valleys at the positions of the primes. Numerical studies have been undertaken in order to extract qualitative information from such a representation. As a result of those studies, it is possible to promote four observations in the category of conjectures. One may easily state that the ladder, from its own construction, will cross the horizontal axis an indefinite number of times; namely, the ladder will have infinitely many zeroes.
The number of zeroes grows in a hardly predictable way, somewhere between and , but the number of primes in is very well fitted by for small numbers (up to 10,000 zeroes). However, for larger numbers, the fit is just fair. Interestingly, this sequence of zeroes does not seem to follow Benford’s Law, at least up to the range of .
Furthermore, no trend is apparent looking at the last digit of the zeroes, all digits (1, 3, 5, 7, and 9 only) being equiprobable. Thus, we have shown that the distribution of zeroes is, if not “random” (How random are the zeroes in the sequence? Naively, one would assume them to be as random as the prime number distribution. It is beyond the scope of this work to answer this question, but it would worthy studying the randomness of this sequence (or any other created with this scheme) by using advanced randomness tests [55,56,57,58]), at least rather capricious. On the other hand, the gaps between zeroes present a remarkably well defined trend, displaying an exponential decay according to the size, the length of the gap, and the frequency with which it appears. This important result echoes previous studies regarding gaps between primes, such as those presented in [34,37,38,39,40,41,43,44]. Whether or not this will be true for any given interval is another open question.
Our theoretical predictions are largely based on intuition, but we provide qualitative support from our preliminary results. Although the behaviors reported here have been validated only for n as large as , it is reasonable to expect that they would be observed for any arbitrary n. However, mathematical proofs for our conjectures are likely to be extremely difficult since they are inextricably intertwined with the still mysterious distribution of prime numbers.
To conclude, the algorithm (The program is available under request) of Jacob’s Ladder exhibits a remarkable feature despite its simplicity: Most of the zeroes are close to prime numbers since the smaller the gaps are, the more frequently they appear. This important result represents an unexpected correlation between the apparently chaotic sequence, the zeroes in , and the prime numbers distribution.
Author Contributions
Conceptualization, A.F. and R.M.; methodology, R.M. and D.F.; software, R.M. and D.F.; validation, A.F., R.M., and D.F.; formal analysis, A.F.; investigation, A.F.; writing—original draft preparation, A.F.; writing—review and editing, D.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Ministry of Education, Youth and Sport of the Czech Republic under project CZ.02.1.01/0.0/0.0/15_003/0000464, and by the Icelandic Research Fund, under contract 163419-051. A.F. acknowledges the use of the Anselm and Salomon HPC clusters administered by the IT4Innovations National Supercomputing Center, University of Ostrava. D.F. is grateful for the hospitality of the Technical University of Vienna.
Conflicts of Interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Appendix A. Additional Conjectures
Conjecture II:
The slope of the Ladder is zero in the limit when n goes to infinity.
Discussion:
The Ladder could have a finite (although we conjecture this not to be case) amount of zeroes, so that, after a certain number X, all points would be either above or below the x-axis, and hence the slope would be positive or negative in consequence. Note that, even if Conjecture I is false, the slope could decrease continuously when n increases. In addition, obviously if Conjecture I is true, then Conjecture II is more likely, but still not necessarily true.
It is important to note that an arbitrarily large amount of zeroes does not imply . This can be proved with a simple counterexample, as shown in Figure A1 (Upper Panel), where a simple ladder is constructed by stacking triangles, each one three times higher than the previous one. This ladder will have an infinite number of zeroes by construction, but, as can be easily seen, the slope is not zero (The Lower Panel in Figure A1 shows the values of vs the number of points).
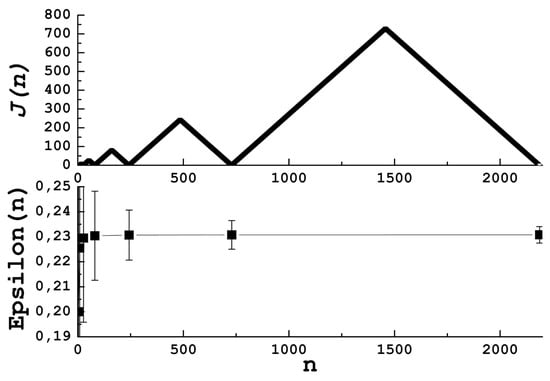
Figure A1.
Upper Panel: A counterexample of a ladder presenting infinitely many zeroes, but where . Lower Panel: vs. the number of points in the ladder.
A clearer picture of the late behavior of Jacob’s ladder can be ascertained from an analysis of the gaps and the frequency with which they appear, as we discuss in Section 4. Under closer inspection, a pattern with signs of predictability arises, allowing us to get an intuition on how the ladder is likely to extend towards infinity, much in the same way that a physicist would extrapolate statistically. To which extent one should trust that intuition is not a matter of debate for the present paper.
For these reasons, we argue that Conjecture II is true even if Conjecture I is not. Now a different, more complex question, is how fast . The value of is obtained by fitting the Ladder to following a least squares approach
Whether the slope b tends to zero or not depends on the difference between the terms of the numerator, which is where the prime numbers define the Ladder through the , which are unknown a priori (the values are known for all i). Many important papers have been published in the last decades— see [12,13,19,20,21,22,23,24,25,26,27,28,29,34,35,36,37,38,39,40,41,43,44] to name a few—some of which could help or show the way to calculate certain upper (and/or lower) limits for in the limit when n tends to infinity. It seems to be a problem that could be attacked using methods of probabilistic number theory [59,60]; however, it is beyond the scope of this paper to prove this conjecture.
A first naive idea could be to assume that the slope is of the same order of magnitude as , that is to say, , where is the prime-counting function as usual (see Figure A2). It is to be mentioned that Figure A2 plots the absolute value of b, but this value can be positive or negative. It goes without saying that the slope will depend not only on the number of primes, but also on their order, which is unknown a priori. (The slope is plotted up to due to computational limitations. A way of calculating the slope of billions of points would be to “sift” or “filter” them that is to say, to take only 1 every 100 or every 1000, etc. The error, however, is rather difficult to determine). The model seems, however, to be an underestimate of , suggesting that could be a better approximation. Obviously, one can always obtain a better fit by adding one more parameter to some function, in this case, a power to .
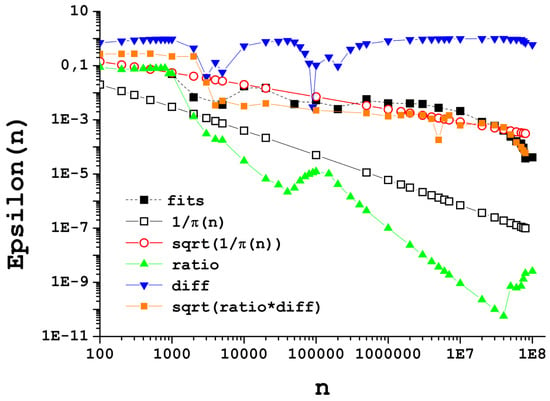
Figure A2.
(Color online) Slope of Jacob’s Ladder from 100 to 100,000,000 in logarithmic scale. Black full squares are the numerical values (obtained by fitting the Ladder to ), while red empty circles, black empty squares and blue/green triangles are simple models. Orange squares are the values obtained averaging both green and blue points (see text).
In any case, this simple expression fits reasonably well the values for 10,000 (See Figure A2, red open circles). It is also instructive to consider two very simple models, which are presented in blue (green) triangles. These are two clearly crude estimates, obtained by dividing the difference (ratio) between points up and down over n. We conjecture that the ratio p will tend to 1 (see next section), so the slope calculated this way will tend to 0. It can be seen that the models badly over- and underestimate the value of almost in the whole range, but, interestingly, the geometric average (i.e., the square root of the product) of both functions seems to be a valid ballpark estimate.
Conjecture III-A
If Conjecture I is true, then the area below the upper part of the Ladder is equal to the area above the lower part of the Ladder when , or, more precisely, the ratio between both areas tends to 1 in that limit:
Discussion:
It is natural to think that, if no particular order is found, then the ratio of both areas in the limit will be 1. This is similar, but not equivalent to say that the number of points above and below (positive and negative respectively, or just and ) will be the same for , so that their ratio will tend to 1. Thus, a similar conjecture can be formulated:
Conjecture III-B
If Conjecture I is true, the ratio between numbers of points above and below will tend to 1:
Discussion:
The area depends not only on the number of points up or down, but also on the ordinates of those points, so it is straightforward to see that Conjecture III-A can be true and Conjecture III-B false, or the other way around. However, we presume that in the limit both the area and the ratio will tend to 1. Figure A3 (bottom) shows the number of positive (black) and negative (red) points in Jacob’s Ladder up to (plotted against the number of zeroes to show it as a continuum). It is to be mentioned as well that there is a strong possibility that these limits do not exist.
Importantly, note that Conjecture III (A or B) is not equivalent to Conjecture I. If Conjecture III (A or B) is true, then Conjecture I is true, but it could be that Conjecture I is true and Conjecture III (A or B) is not (Conjecture III (A and B) could be stated as Conjecture I, and hence we could talk of Conjecture I (infinitely many zeroes) as a corollary, given that Conjecture III (A, B or both) demonstrates that the number of zeroes tends to infinity, the result being a corollary of Conjecture I. However, we consider it more natural, at a first glance at Jacob’s ladder, to think of the number of possible cuts (zeroes) when , so we decided to keep them in this order).
Figure A3 (Top) shows the ratio between the number of positive and negative points in Jacob’s Ladder (presented in Figure A2) up to 100 million. As can be seen, some approximate periodicity over a decreasing behaviour seems apparent. Nonetheless, we believe this to be a misleading result so that the ratio, whenever n is sufficiently large, will tend to 1, and the approximate periodicity in Figure A3 (Top) will disappear.
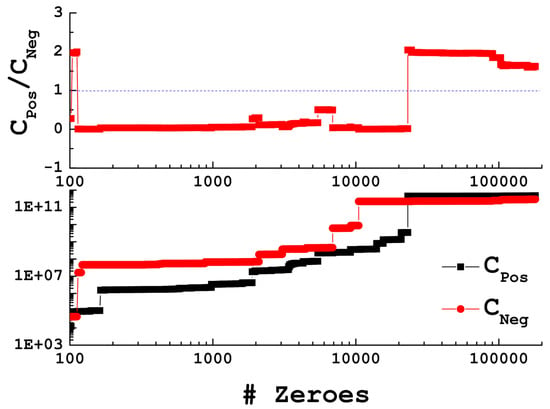
Figure A3.
(Color online) Bottom: Number of positive (black squares) and negative (red circles) points in Jacob’s Ladder up to . Top: Ratio between the number of positive and negative points up to . The blue dashed line marks , the conjectured asymptotic ratio. Note the logarithmic scale on both axes.
References
- Ingham, A.E. The Distribution of Prime Numbers. In Cambridge Mathematical Tracts; Cambridge University Press: Cambridge, UK, 1932. [Google Scholar]
- Littlewood, J.E. Sur la distribution des nombres premiers. Comptes Rendus Acad. Sci. Paris 1914, 158, 1869–1872. [Google Scholar]
- Anglin, W.S. The Queen of Mathematics: An Introduction to Number Theory; Kluwer: Dordrecht, The Netherlands, 1995. [Google Scholar]
- Apostol, T.M. Introduction to Analytic Number Theory; Springer: New York, NY, USA, 1976. [Google Scholar]
- Hardy, G.H.; Wright, W.M. Unsolved Problems Concerning Primes. In An Introduction to the Theory of Numbers, 5th ed.; Oxford University Press: Oxford, UK, 1979; pp. 19 and 415–416. [Google Scholar]
- Shanks, D. Solved and Unsolved Problems in Number Theory; Chelsea: New York, NY, USA, 1985; pp. 30–31 and 222. [Google Scholar]
- Stallings, M. Cryptography and Network Security: Principles and Practice; Prentice-Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Goles, E.; Schulz, O.; Markus, M. Prime number selection of cycles in a predator–prey model. Complexity 2001, 6, 33–38. [Google Scholar] [CrossRef]
- Toha, J.; Soto, M.A. Biochemical identification of prime numbers. Med. Hypothesis 1999, 53, 361. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Berry, M.V. Quantum chaology, prime numbers and Riemann’s zeta function. Inst. Phys. Conf. Ser. 1993, 133, 133–134. [Google Scholar]
- Sakhr, J.; Bhaduri, R.K.; van Zyl, B.P. Zeta function zeros, powers of primes, and quantum chaos. Phys. Rev. E 2003, 68, 026206. [Google Scholar] [CrossRef]
- Wolf, M. Multifractality of prime numbers. Phys. A 1989, 160, 24. [Google Scholar] [CrossRef]
- Gamba, Z.; Hernando, J.; Romanelli, L. Are prime numbers regularly ordered? Phys. Lett. A 1990, 145, 106. [Google Scholar] [CrossRef]
- Saouter, Y. Checking the odd Goldbach conjecture up to 1020. Math. Comput. 1998, 67, 863–866. [Google Scholar] [CrossRef]
- Richstein, J. Verifying the Goldbach conjecture up to 4·1014. Math. Comput. 2001, 70, 1745–1750. [Google Scholar] [CrossRef]
- Granville, A.; van de Lune, J.; Te Riele, H.J.J. Checking the Goldbach conjecture on a vector computer. Proc. NATO Adv. Study Inst. 1989, 1988, 423–433. [Google Scholar]
- Helfgott, H.A. The ternary Goldbach conjecture is true. arXiv 2013, arXiv:1312.7748. [Google Scholar]
- Borwein, J.; Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century; A. K. Peters Co.: Wellesley, MA, USA, 2003; p. 64. [Google Scholar]
- Cramér, H. On the order of magnitude of the difference between consecutive prime numbers. Acta Arith. 1936, 2, 23–46. [Google Scholar] [CrossRef]
- Erdós, P. On the difference of consecutive primes. Q. J. Math. Oxf. Ser. 1935, 6, 124–128. [Google Scholar] [CrossRef]
- Maynard, J. Large gaps between primes. Ann. Math. 2016, 183, 915–933. [Google Scholar] [CrossRef][Green Version]
- Maynard, J. Dense clusters of primes in subsets. Compos. Math. 2016, 152, 1517–1554. [Google Scholar] [CrossRef]
- Zhang, Y. Bounded gaps between primes. Ann. Math. 2014, 179, 1121–1174. [Google Scholar] [CrossRef]
- Guy, R. Unsolved Problems in Number Theory, 2nd ed.; Springer: Berlin, Germany, 1994; p. vii. [Google Scholar]
- Hardy, G.H.; Littlewood, J.E. Some problems of ’Partitio numerorum’ III: On the expression of a number as a sum of primes. Acta Math. 1923, 44, 1–70. [Google Scholar] [CrossRef]
- Polymath, D.H.J. New equidistribution estimates of Zhang type, and bounded gaps between primes. Algebra Number Theory 2014, 8, 2067–2199. [Google Scholar]
- Polymath, D.H.J. Variants of the Selberg sieve, and bounded intervals containing many primes. Res. Math. Sci. 2014, 1, 12. [Google Scholar] [CrossRef]
- Maynard, J. Small gaps between primes. Ann. Math. 2015, 181, 383–413. [Google Scholar] [CrossRef]
- Stein, M.L.; Ulam, S.M.; Wells, M.B. A visual display of some properties of the distribution of primes. Am. Math. Mon. 1964, 71, 516–520. [Google Scholar] [CrossRef]
- Chmielewski, L.J.; Orlowski, A. Finding Line Segments in the Ulam Square with the Hough Transform. In Proceedings of the International Conference on Computer Vision and Graphics, Warsaw, Poland, 19–21 September 2016; pp. 617–626. [Google Scholar]
- Entry in the On-Line Encyclopedia of Integer Sequences. Available online: https://oeis.org/A065358 (accessed on 10 January 2020).
- Billingsley, P. Prime numbers and Brownian motion. Am. Math. Mon. 1973, 80, 1099–1115. [Google Scholar] [CrossRef]
- Peng, C.-K.; Buldyrev, S.V.; Goldberger, A.L.; Havlin, S.; Sciortino, F.; Simons, M.; Stanley, H.E. Long-range correlations in nucleotide sequences. Nature 1992, 356, 168. [Google Scholar] [CrossRef] [PubMed]
- Wolf, M. Random walk on the prime numbers. Phys. A 1998, 250, 335–344. [Google Scholar] [CrossRef]
- Wolf, M. Unexpected regularities in the distribution of prime numbers. In Proceedings of the 8th Joint EPS-APS International Conference, Krakow, Poland, 17–21 September 1996; pp. 361–367. [Google Scholar]
- Odlyzko, A.; Rubinsten, M.; Wolf, M. Jumping champions. Exp. Math. 1999, 8, 107–118. [Google Scholar] [CrossRef]
- Szpiro, G.G. The gaps between the gaps: Some patterns in the prime number sequence. Phys. A 2004, 341, 607–617. [Google Scholar] [CrossRef]
- Szpiro, G.G. Peaks and gaps: Spectral analysis of the intervals between prime numbers. Phys. A 2007, 384, 291–296. [Google Scholar] [CrossRef]
- Ares, S.; Castro, M. Hidden structure in the randomness of the prime number sequence? Phys. A 2006, 360, 285–296. [Google Scholar] [CrossRef]
- Wolf, M. 1/f noise in the distribution of primes. Phys. A 1997, 241, 439–499. [Google Scholar] [CrossRef]
- Ball, P. Prime numbers not so random? Nature 2003. [Google Scholar] [CrossRef]
- Hull, T.E.; Dobell, A.R. Random Number Generators. SIAM Rev. 1962, 4, 230–254. [Google Scholar] [CrossRef]
- Wolf, M. Nearest-neighbor-spacing distribution of prime numbers and quantum chaos. Phys. Rev. E 2014, 89, 022922. [Google Scholar] [CrossRef] [PubMed]
- García-Perez, G.; Serrano, M.A.; Boguña, M. Complex architecture of primes and natural numbers. Phys. Rev. E 2014, 90, 022806. [Google Scholar] [CrossRef] [PubMed]
- Benford, F. The law of anomalous numbers. Proc. Am. Philos. Soc. 1938, 78, 551–572. [Google Scholar]
- Newcomb, S. Note on the frequency of use of the different digits in natural numbers. Am. J. Math. 1881, 4, 39–40. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Diaconis, P. The distribution of leading digits and uniform distribution mod 1. Ann. Probab. 1977, 5, 72–81. [Google Scholar] [CrossRef]
- Raimi, R.A. The first digit problem. Am. Math. Mon. 1976, 83, 521–538. [Google Scholar] [CrossRef]
- Miller, S.J.; Takloo-Bighash, R. An Invitation to Modern Number Theory; Princeton University Press: Princeton, NJ, USA, 2006. [Google Scholar]
- Dickson, L.E. History of the Theory of Numbers; Carnegie Institution of Washington: Washington, DC, USA, 1919. [Google Scholar]
- Tschebyschef, P.L. Lettre de M. le Professeur Tchebychev à M. Fuss, sur un nouveau théorème relatif aux nombres premiers contenus dans les formes 4n ± 1 et 4n ± 3. Bulletin de l’Académie impériale des sciences de Saint-Pétersbourg 1853, 11, 208. [Google Scholar]
- Phragmen, E. Sur le logarithme integral et la fonction f(x) de Riemann. Ofversigt af Kongl. Vetenskaps-Akademiens Forhandlingar 1891, 48, 559–616. [Google Scholar]
- Landau, E. Handbuch der Lehre von der Verteilung der Primzahlen; Chelsea: New York, NY, USA, 1953. [Google Scholar]
- Cacert Research Lab. Available online: http://www.cacert.at/random/ (accessed on 10 January 2020).
- The ENT Program. Available online: http://www.fourmilab.ch/random/ (accessed on 10 January 2020).
- Marsaglia, G. The Marsaglia Random Number CDROM, with The Diehard Battery of Tests of Randomness. Available online: http://www.cs.hku.hk/diehard/ (accessed on 10 January 2020).
- Marsaglia, G.; Tsang, W.W. Some difficult-to-pass tests of randomness. J. Stat. Softw. 2002, 7, 1–9. [Google Scholar] [CrossRef]
- Kubilius, J. Probabilistic Methods in the Theory of Numbers (Translations of Mathematical Monographs); American Mathematical Society: Providence, RI, USA, 1962. [Google Scholar]
- Kowalski, E. Arithmetic Randonnée: An Introduction to Probabilistic Number Theory. ETH Zürich Lecture Notes 2019. Available online: www.math.ethz.ch/kowalski/probabilistic-number-theory.pdf (accessed on 10 January 2020).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).