1. Introduction
The use of educational software has been increasingly recognized as a useful tool to promote students’ motivation to deal with, and understand, new concepts in different study fields (see, for instance, [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10,
11,
12]). In fact, educational software tools have a great potential of applicability, particularly at the university level, where the knowledge of various areas by different careers is required [
8]. Current digital technology allows students to work with a large number and variety of graphics, in an interactive way, complementing the theoretical results and the so often used paper and pencil calculations. Obviously, calculations with this kind of support do not replace paper and pencil calculations, and they should be properly combined with other methods of calculation, including mental calculation. Some studies conclude that students using computer algebra systems are at least as good in “pencil and paper” skills as their traditional counterparts [
13]. This aspect is not of minor relevance. Although the “pencil and paper” work can be done by computers, students should learn how calculations are made and also should learn how the computer algebra systems work [
14] (we thank an anonymous referee for this observation). Also, the use of technology in the classroom can lead to advances in conceptualization, contributing thereby to students’ engagements and motivation [
15]. According to [
16], one of the reasons for students to use computer algebra systems is their belief that these tools help their understanding of new concepts.
The computer algebra system
Mathematica, conceived by Stephen Wolfram, and developed by Wolfram Research, is a very powerful software that allows the implementation of many interactive visual applications. Thanks to the symbolic and numerical capabilities of Mathematica, these applications are eminently dynamic tools, where the user can interact with the graphical and analytical information in real time. More importantly, the graphics are taken out of the textbook and they are placed under the user’s control, where the user can manipulate, investigate, and explore their characteristics. Students who have used
Mathematica for at least one year identified this kind of visualization as one of the significant benefits they found with the use of
Mathematica [
16].
Graphics are always helpful in the learning process, but [
16] states that it makes a difference whether the students’ interaction with graphic visualization is active or passive. As reported by [
17], academics in higher education institutions should not only worry about the contents, but also give attention to the learning environment as they face students with different motivations and different levels of involvement. Such differences will likely affect the teaching and learning process. Moreover, teachers can expect that, in any classroom, some students prefer to be receivers (observers or listeners), while others prefer to be active participants. In fact, there are students with a more active attitude, who, even in a more traditional class, theorize, apply and relate, and there are those who exhibit more passive behavior. Clearly, these students require different orientation and teaching methods so that they are able to fully engage in the classroom activities as agents of a truly active learning process. This type of learning denotes a style of teaching that provides opportunities for students to talk, to listen to, and to reflect on what they have learned, as they participate in a variety of learning activities [
18,
19]. We should note that teachers who employ active learning strategies in their classrooms are unlikely to please all students all the time [
20], but neither is a teacher who relies regularly on traditional lectures. The active learning also aims to improve the students’ performance and develop the skills they need, for example, to obtain a better grade in a specific curricular unit [
19]. In many cases, active learning can be employed without increased costs and with only a modest change in current teaching practices with a reduced risk and a high return [
20]. Unfortunately, there are gaps between teaching and learning, between teaching and testing, and between educational research and practice in higher education institutions [
21]. A serious gap also exists between how faculty members typically teach (i.e., relying largely on the “lecture method”) and how they know they should teach (i.e., employing active learning strategies to develop intellectual skills, and to shape personal attitudes and values). Moreover, teachers see few incentives to change mainly because the use of educational software in classrooms is time-consuming. In fact, any faculty member who has ever attempted to lead a true one hour class discussion, in which students talk and respond to one another, knows how difficult it is to have control over the discussion.
Notwithstanding the above, the importance of using educational software in mathematics, as an efficient tool to help students grasp with hard-to-understand concepts and to more quickly gain a deeper understanding of the materials being taught firsthand, is acknowledged (see, for instance, [
1,
2,
10,
16,
22]) and thereby such software can help to promote an active learning environment inside the classroom.
Although it is recognized that some economic concepts can be more easily understood when the students work with a large number and variety of graphics in an interactive way, with the support of the appropriate technology, the use of computer algebra systems is rare and under-studied in economics education (we thank an anonymous referee for this observation). In fact, the use of educational software in economics has been limited to some specific economic concepts (see, for instance, [
23,
24,
25]). According to [
23,
24], there are automatic algebraic simplifiers, but simplicity is often in the eye of the beholder and such tools are sparingly used by economic theorists. Furthermore, computers have already been used to generate numerical examples, providing only approximate, rather than exact, results. This gap opens a window of opportunity for the development of new educational tools directed to socio-economic science students. In a previous work [
26], it was shown how some dynamic and interactive mathematical tools, created with
Mathematica, can be used to promote better student activity and engagement in the learning process. Another work [
27] discusses some teaching possibilities offered by the F-Tool concept that can provide an active learning environment in socio-economic science subjects.
The current paper intends to present a new interactive and dynamic mathematical tool for the study of the price elasticity of supply concept, the new PES(Linear)-Tool (see
Supplementary Materials), which allows students to change a function’s parameter values and get the analytical and graphical results in real time. Furthermore, the interactive and dynamic features of this tool make it suitable to promote an active learning environment and it is available, at no cost, in the Computable Document Format. This format allows the use of the PES(Linear)-Tool, even without an active Wolfram
Mathematica license (additional information about how to work with the CDF format can be found at
http://www.wolfram.com/cdf-player/). The potentialities of the PES(Linear)-Tool will be exhaustively explored to introduce and deal with multiple features of the price elasticity of supply, a central concept in economics. In our opinion, its use in classrooms can promote better student activity and engagement in the learning process, among students enrolled in socio-economic programs.
This paper is structured as follows. After this brief introduction section,
Section 2 introduces some basic economic concepts which frame the application of the new tool.
Section 3 details the F-tool concept and its application.
Section 4 presents the design of the PES(Linear)-Tool.
Section 5 is dedicated to some final remarks.
3. Dynamic and Interactive Tools
Faculty members who regularly use strategies to promote active learning typically find several ways to ensure that students learn the assigned content: promoting the dialog and reflection, promoting the acquisition of new knowledge and the transmission of the acquired knowledge, and doing short-assessments every week.
Currently, several software applications can be (free of charge or for a cost) downloaded from the World Wide Web. In particular, there are many dynamic and interactive tools dealing with some specific economic concepts implemented with the computer algebra system
Mathematica, which is already available in the Wolfram Demonstrations Project website. In this project (
http://demonstrations.wolfram.com) the creators of
Mathematica promote and divulge globally the innovations designed by its users. Some of these applications provide only analytical information (the
Inflation-Adjusted Yield tool, available at
http://demonstrations.wolfram.com/InflationAdjustedYield/, illustrates how one’s investment life planning turns on the net of nominal investment yield and inflation, according to its author). Several other tools provide only graphical information (the
Short-Run Cost Curves tool, available at
http://demonstrations.wolfram.com/ShortRunCostCurves/, provides graphical information about the cubic cost function and its average and marginal cost curves; the
Monopoly Profit and Loss tool, available at
http://demonstrations.wolfram.com/MonopolyProfitAndLoss/, provides graphical information about the marginal cost and the average cost curves). In particular, for the elasticity of demand concept there are tools that provide non-rigorous analytical information such as
The Price Elasticity of Demand tool (available at
http://demonstrations.wolfram.com/ThePriceElasticityOfDemand/) which shows two ways to calculate the price elasticity of demand), and tools that provide only graphical information (the
Constant Price Elasticity of Demand tool, available at
http://demonstrations.wolfram.com/ThePriceElasticityOfDemand/ illustrates the price elasticity of demand for a specific inverse demand function). However, none of these applications provide all rigorous and exhaustive required information for a global and deep understanding of economic concepts introduced at undergraduate levels, in higher education institutions. Furthermore, these existing materials can hardly be adapted to explain specific concepts in socio-economic sciences or they would require additional resources from both the teacher and the students. This is a gap that the new educational tool described in this paper intends to fulfill since it is adapted to specific training programs to meet educational goals. It allows the design of tasks for independent work and the analysis of individual special cases that are important to recent graduate economists.
3.1. The F-Tool Concept
The F-Tool concept, which was first presented in the 1st National Conference on Symbolic Computation in Education and Research (Portugal 2012), where it was distinguished with the
Timberlake Award for Best Article by a Young Researcher, was created as an interactive
Mathematica notebook, specifically to explore the concept of real functions and their graphics, by analyzing the effects caused by changing the values of the parameters of general analytical expressions [
28]. Each F-Tool allows the study of a typical class of functions. For each class, a set of parameters is considered such that the class is fully determined by the corresponding analytical expression. This means that each F-Tool provides graphical and rigorous analytical information for all the functions within the corresponding class. In fact, unlike the other tools available in the
Wolfram Demonstrations Project website, all the tools created under the F-Tool concept provide all the graphical and analytical information desired by the user. Additionally, the user can get exact or approximate analytical results. Finally, the new PES(Linear)-Tool has a very intuitive interface that allows even the most inexperienced user, with no previous knowledge in educational software, to start using all its features in an efficient and autonomous way.
The existing F-Tool are available, free of charge, in the Computable Document Format and the corresponding CDF files can be downloaded for free at
https://sapientia.ualg.pt. This format allows anyone with a computer to fully use it, even without an active Wolfram
Mathematica license.
The F-Tool’s framework is composed by three main panels (see
Figure 1):
In the left panel, the user can set the parameters’ values, and choose which functions related with the main function are to be displayed.
In the middle panel, all the functions are plotted, according to the options defined in the left panel.
In the right panel, all the analytical information is displayed in accordance with the options chosen by the user in the left panel.
In summary, all the controls and options for all functionalities are located in the left panel. As the user interacts dynamically with the tool, all the graphical and analytical results are displayed in real time in the middle and right panels, respectively. When choosing the option ▸, the user will then see the corresponding graphics moving continuously and the analytical information changing accordingly. It is through this kind of dynamic interaction that “computer algebra systems present new opportunities for teaching and learning” [
29].
The use of the F-Tool concept in the classroom allows a dynamic approach to various concepts related to the study of functions and promotes new ways of reasoning/thinking, evaluating, teaching, and learning. The F-Tool concept was conceived as an active learning tool, that is, its adequate use provides a context of teaching and learning where students and teachers are both invited to fully participate [
30]. Through dynamic changes of the parameters values, it is possible to obtain rigorous analytical information, presented in exact or approximate arithmetic, as well as static and non-static visual information [
22]. Although it is a dynamic and interactive educational software, the F-Tool can also be used in the construction of multiple choice and open response evaluation questions [
1].
3.2. The F-Tool Concept Adapted to the Socio-economic Sciences
Taking into account our experience of using dynamic and interactive mathematical tools [
1] as active learning tools in natural science courses, we decided to adapt this type of approach to some economic concepts. The idea is to focus the teaching process on the students, stimulating their participation and motivating those with a level of math knowledge, often insufficient, to obtain new knowledge in a solid way. In this way, it becomes possible to teach new concepts in a solid and consistent way.
The most common way for faculty members to engage students in active learning is by stimulating the discussion [
20]. A variety of materials and techniques can be used to trigger the discussion and each teacher can provide several experiences that will stimulate the discussion among students. Demonstrations during a lecture can be used to stimulate the students’ curiosity and to improve their understanding of conceptual material and processes [
31], particularly when the demonstration invites students to participate in research activities through the use of questions such as “What would happen if we change dynamically the parameter
b? Would the price elasticity of supply change? And what would happen if the parameter
a changes dynamically?” (see Figures 8–10). So, the faculty member can encourage the discussion, dialogue, and reflection in the classroom, proposing stimulating exercises that lead to a supervised constructive debate among the students.
In
Section 4 we present the new dynamic and interactive economic tool, called the PES(Linear)-Tool, created under the F-Tool concept. The usefulness of this tool is illustrated by introducing the price elasticity of supply concept in a microeconomics class, as well as all the analytical and graphical information involved with the analysis of this concept.
4. Designing the New PES(Linear)-Tool
The use of the symbolic computation capabilities of Mathematica, and its own programming language (along with the pretty-print functionality that allows one to write mathematical expressions on the computer using the traditional notation, as on paper), enables us to implement on a computer, and in a rather straightforward manner, all the ideas that go into the F-Tool concept.
The PES(Linear)-Tool was created as an interactive
Mathematica notebook and it is available online, in the Computable Document Format, as a supplement to this article. It allows the exploration of concepts related to a market supply function (
3), where
,
and
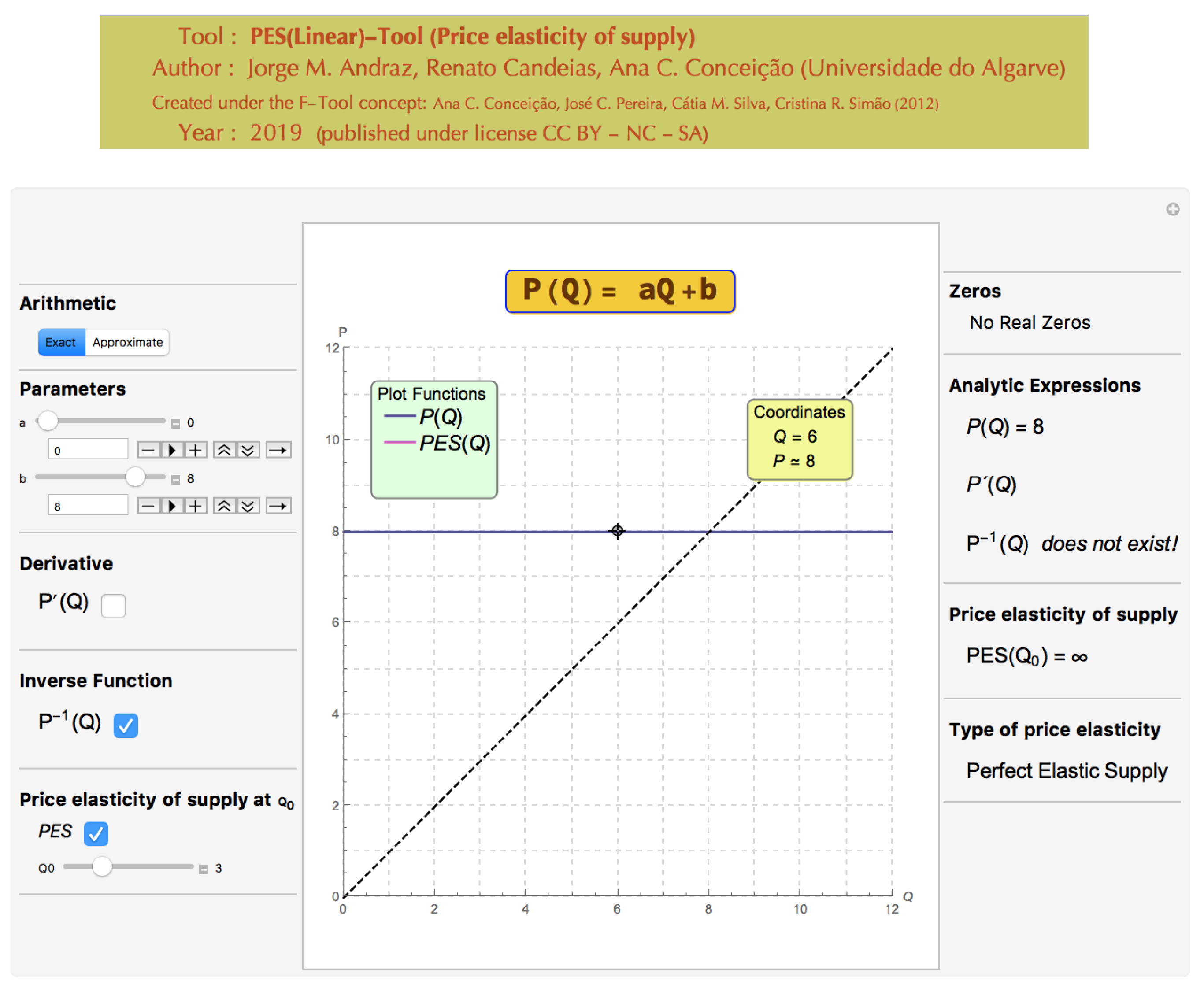
It should be noted that the particular case of
was also included to exemplify the perfectly elastic supply (when
) (see Figure 7). In terms of implementation and in spite of their mathematic simplicity, constant functions should be dealt with separately because they have no inverse function (see Figure 7). This means that the constant case has to be coded separately, in order to generate the correct analytical information for those functions. The PES(Linear)-Tool provides all graphical and analytical information of the inverse function of
(that is, the market supply function). As students often confuse the concepts of elasticity and derivative, the tool provides the option “Derivative” on the left panel (see Figures 10–12). The PES(Linear)-Tool displays graphical information on the value of the PES(
) whenever this option is selected. This allows the user to visualize the change from an economic model with an elastic supply to a model with an inelastic supply (going through a unitary elastic supply). As in the F-Tool, the user can interact with this information in real time.
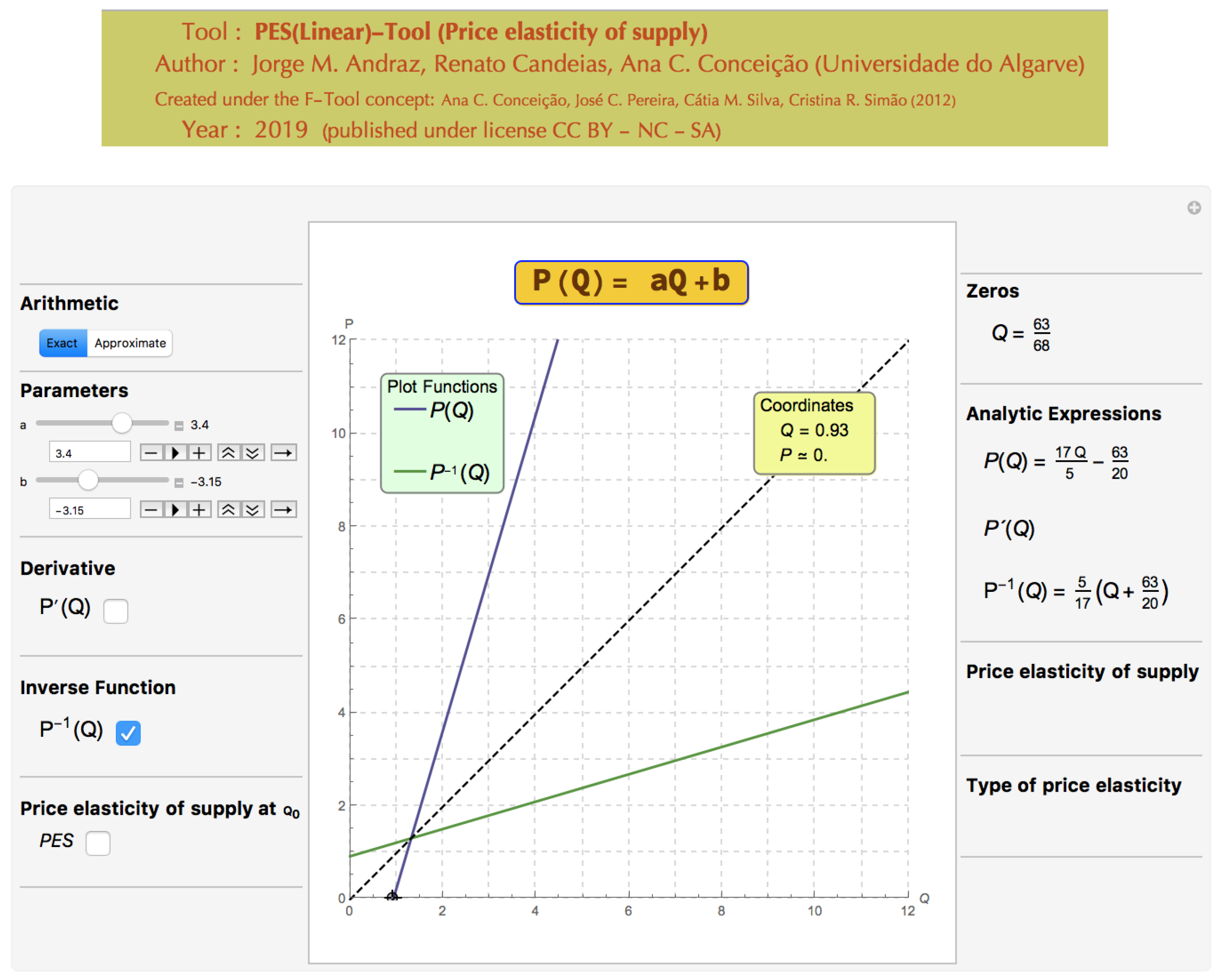
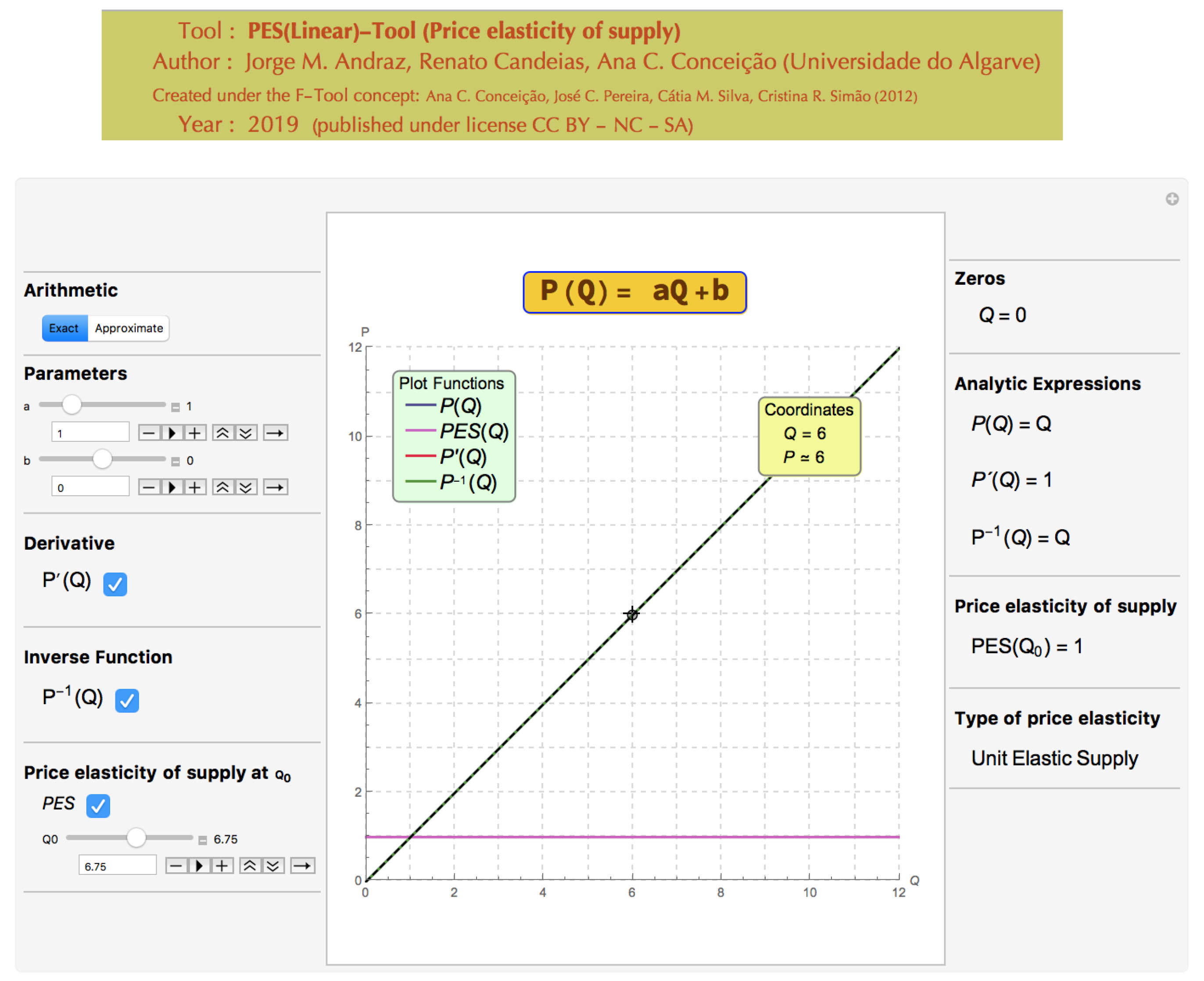
As an illustration of this tool, let us to consider the plot of the inverse function (
3) as depicted in
Figure 1, and the market supply function (in terms of the variable
Q). In this case, the exact analytical expressions of the function and its inverse are displayed, once the exact arithmetic option has been selected. The dashed line displayed on the plot is described by the equation
and corresponds to the symmetry axis of the inverse transformation.
The PES(Linear)-Tool is essentially created by a single
Manipulate command (see
Figure 2), whose output is not just a static result but a running program that we can interact with. In fact, the code consists of some initial definitions followed by the single command
Manipulate. This command is responsible for creating the interactive object that contains the three panels. In particular, the command
Manipulate generates all the functional controls, such as the sliders for the parameters’ values and checkboxes for the plots’ options. Through dynamic changes of the parameters’ values, it is possible to obtain approximate or exact analytical information, as well as static and non-static visual information [
28].
To create the PES(Linear)-Tool we used part of the code of the educational software F-Tool. Obviously, to provide all the graphical and analytical information for the price elasticity of supply, several adaptations were performed and new fields related to this socio-economic concept were added.
Figure 3 displays the code block that generates the value of the price elasticity of supply at a given quantity
. It should be noticed that the cases of
and/or
(see Figures 5, 6, 13) should be considered separately.
4.1. Parameters a and b
In order to create a consistent tool that considers all the mathematical possibilities for which the economic model makes sense, several situations concerning the values of the parameters
a and
b should be implemented. Given the function (
3), only non-negative values for the parameter
a are considered in the code (the range of values that run through the slider, see
Figure 4).
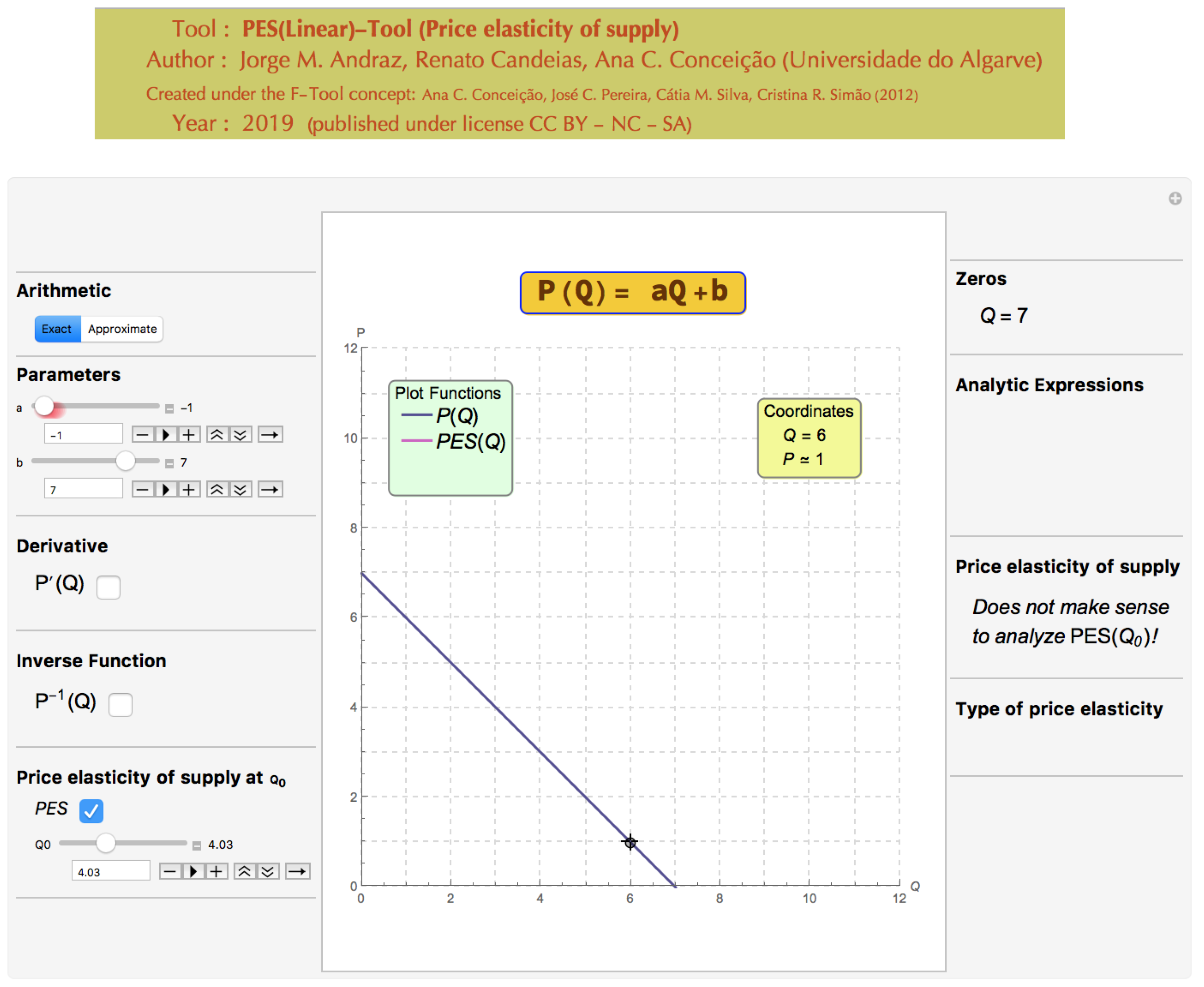
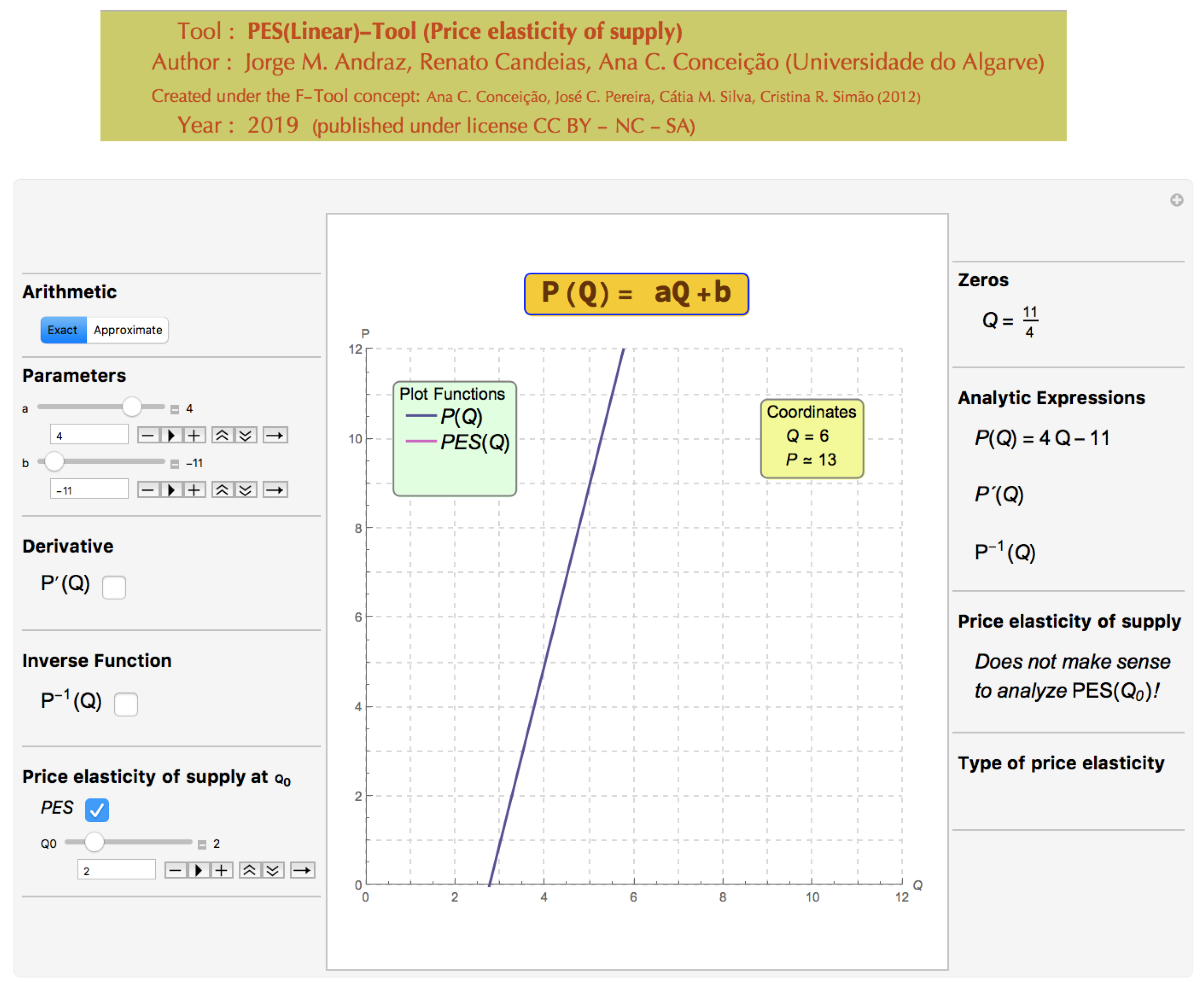
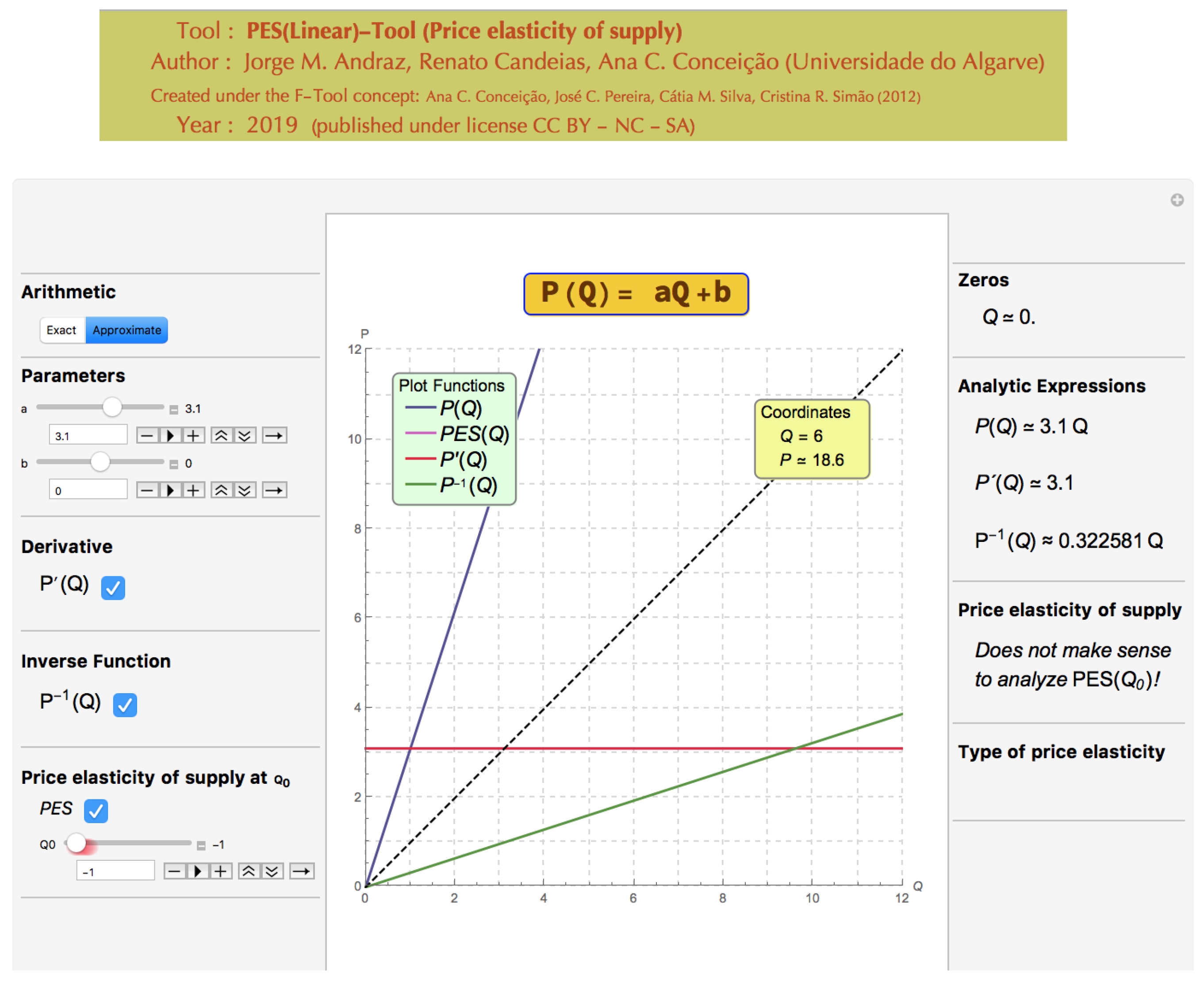
The user can also introduce directly the parameters’ values. However, for certain values of the parameters, the correspondent market supply function is not defined and therefore, the PES(Linear)-Tool will exhibit the following message: “Does not make sense to analyze PES(Q0)!”, whenever the PES button is selected (see
Figure 5). Consequently, all options will be unavailable until acceptable parameter values are considered. This situation occurs when the user chooses a non-positive value for the parameter
a, and/or the user chooses a non-positive value for the variable
Q (see
Figure 6 and Figure 13).
Depending on the values considered for the parameters
a and/or
b,
Q can assume values in different numeric sets. So, the values of
that can be considered depend on the values of
a and
b. The PES(Linear)-Tool can be used to improve the students’ understanding of this conceptualization because it enables students to analyze the relationship between the null value of the function
and the range of acceptable values for
(see
Figure 6).
4.2. Perfectly Elastic Supply
This subsection illustrates how the PES(Linear)-Tool can be used to improve the students’ understanding of the price elasticity of supply concept (see
Figure 7). In the classroom the faculty can explain that this is a limit case that occurs when the market supply function is not defined. The teacher may ask the students if a change in the parameter
b causes any change in the type of price elasticity. Then it can be asked about the effects of a possible change in parameter
a.
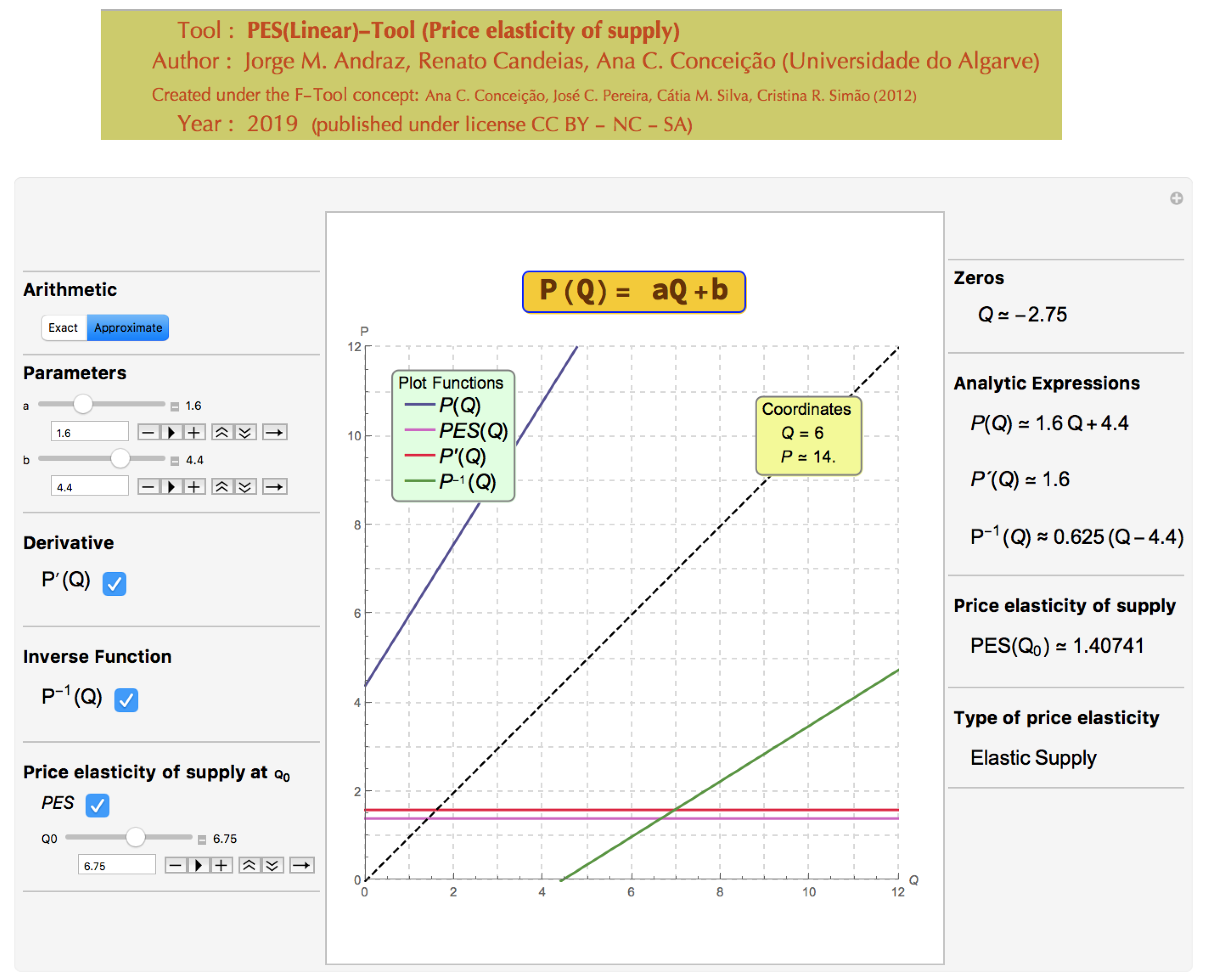
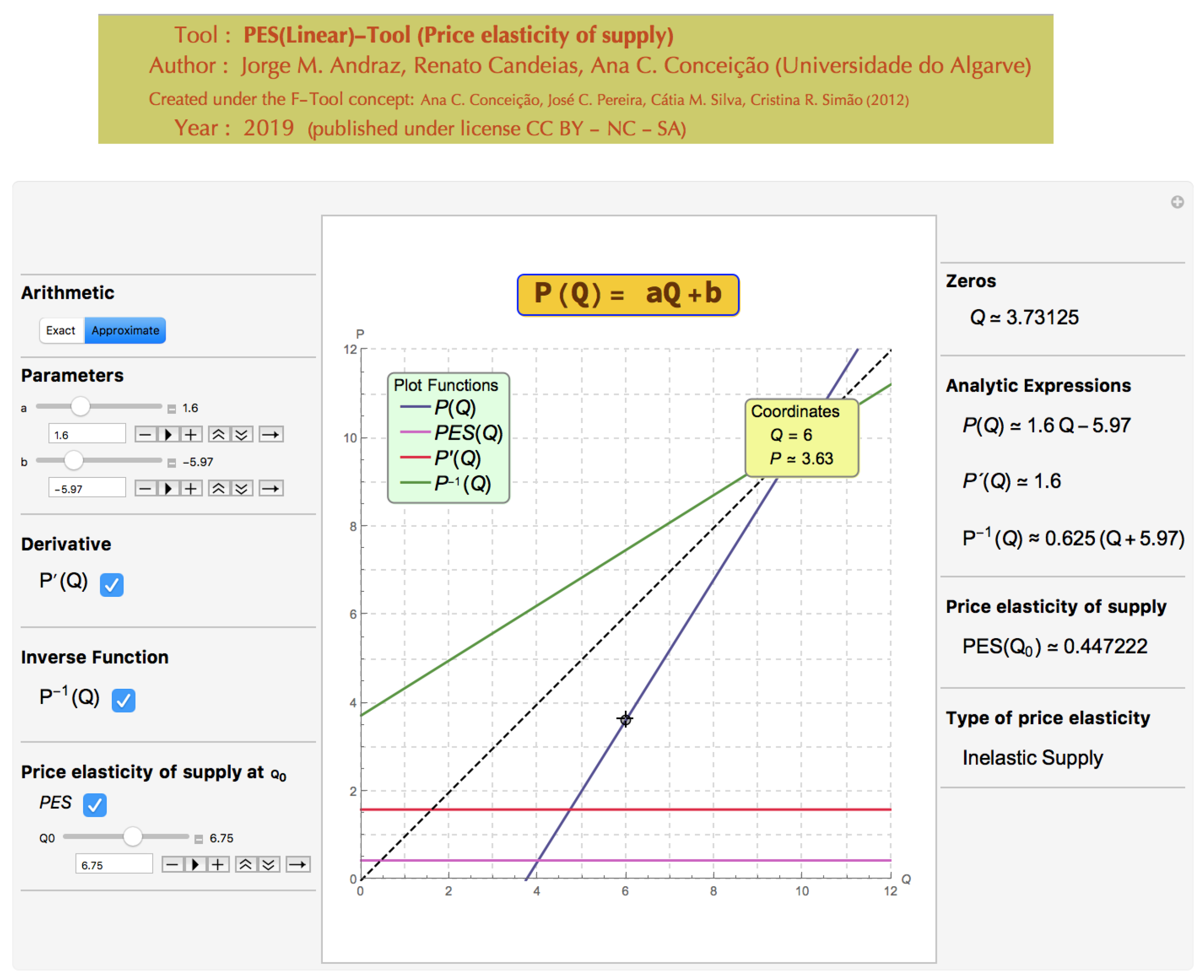
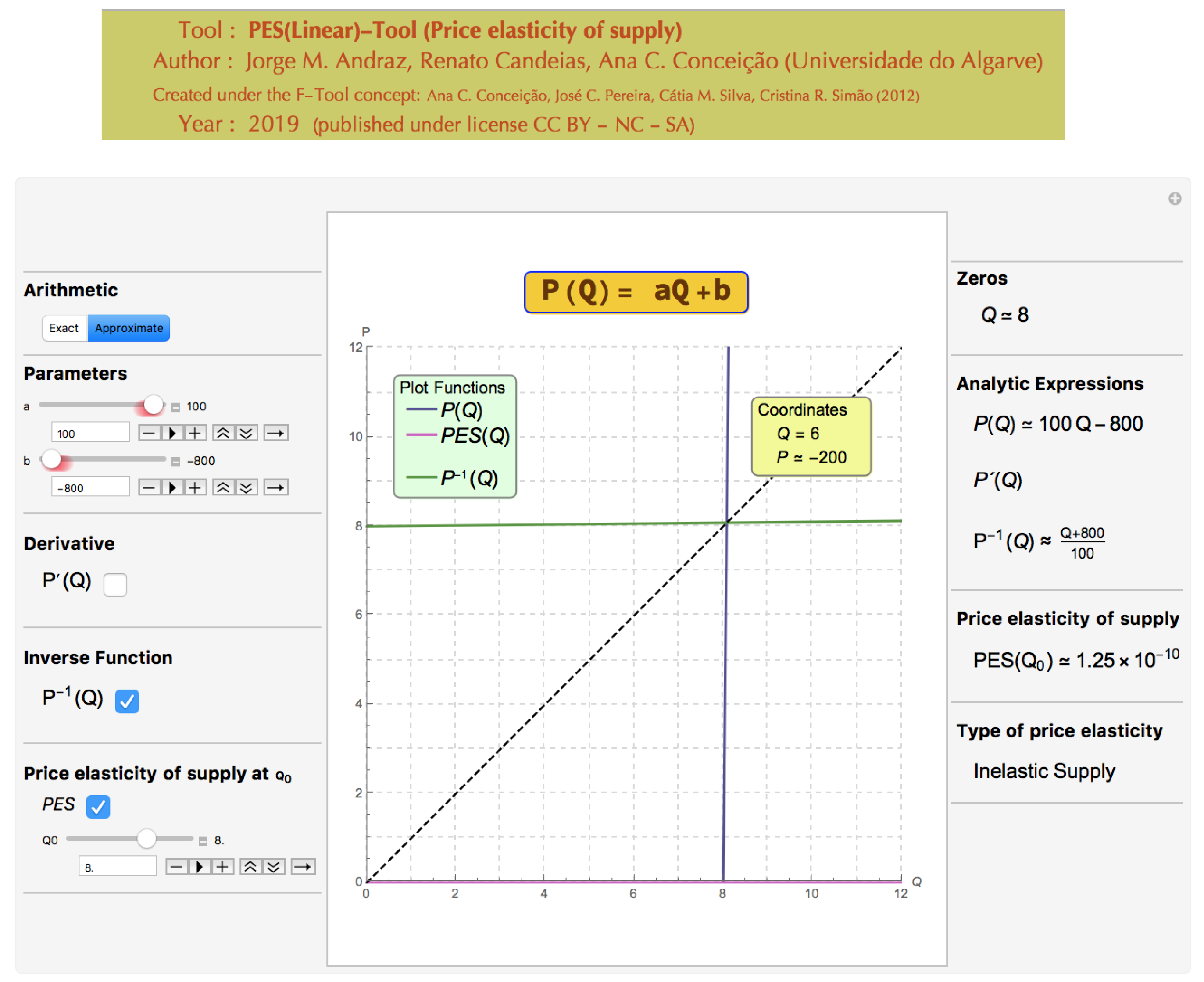
4.3. Elastic and Inelastic Supplies
This subsection describes how the PES(Linear)-Tool can be used to improve the students’ understanding of the price elasticity of supply concept.
By using the PES(Linear)-Tool the faculty can ask the students to interpret the value PES
depending on the values of
a,
b, and
. The faculty can start with an example of an elastic supply and ask the students to identify the parameter to be changed in order to get an inelastic supply and how the value of
affects the elasticity’s value (see
Figure 8,
Figure 9 and
Figure 10).
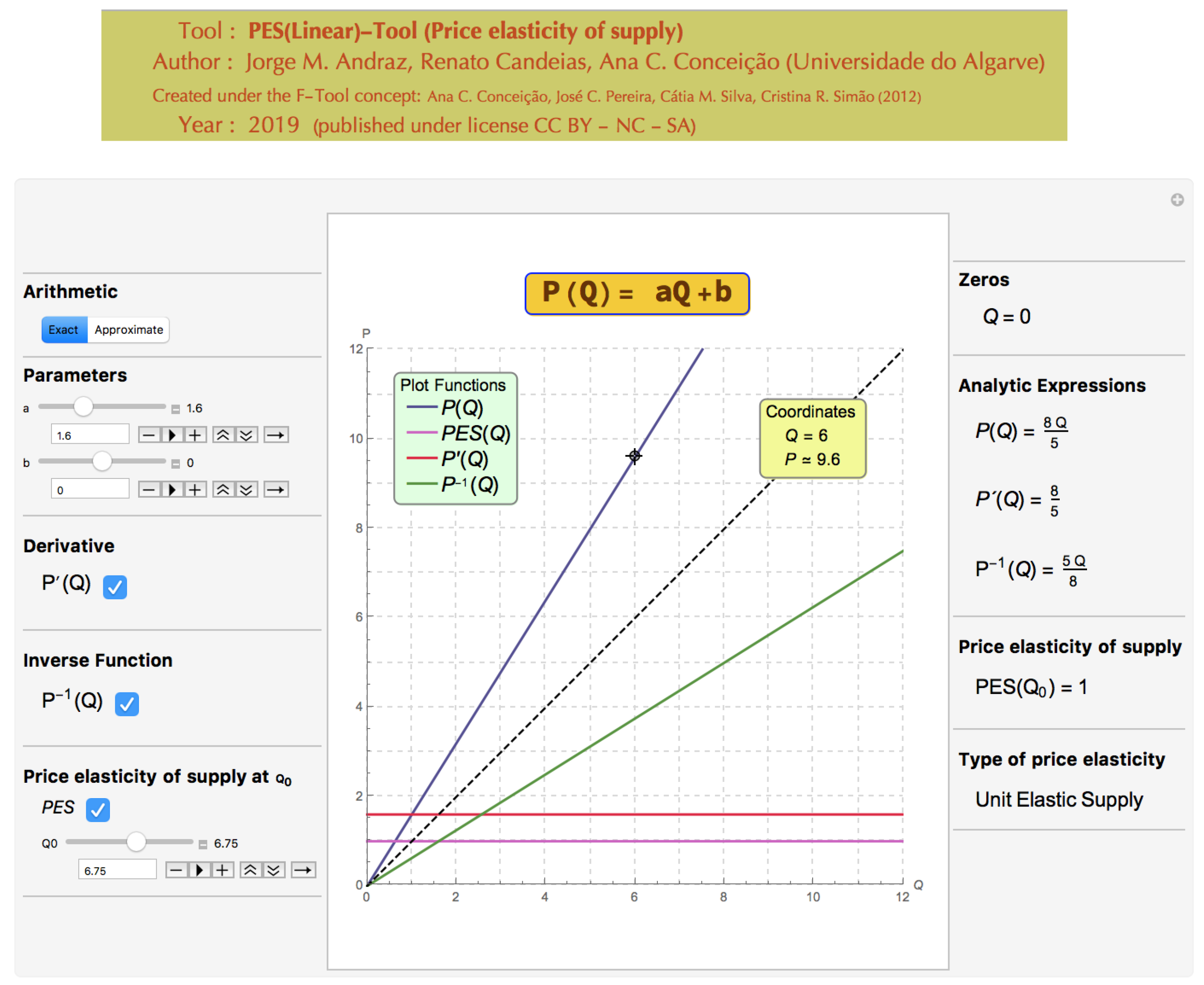
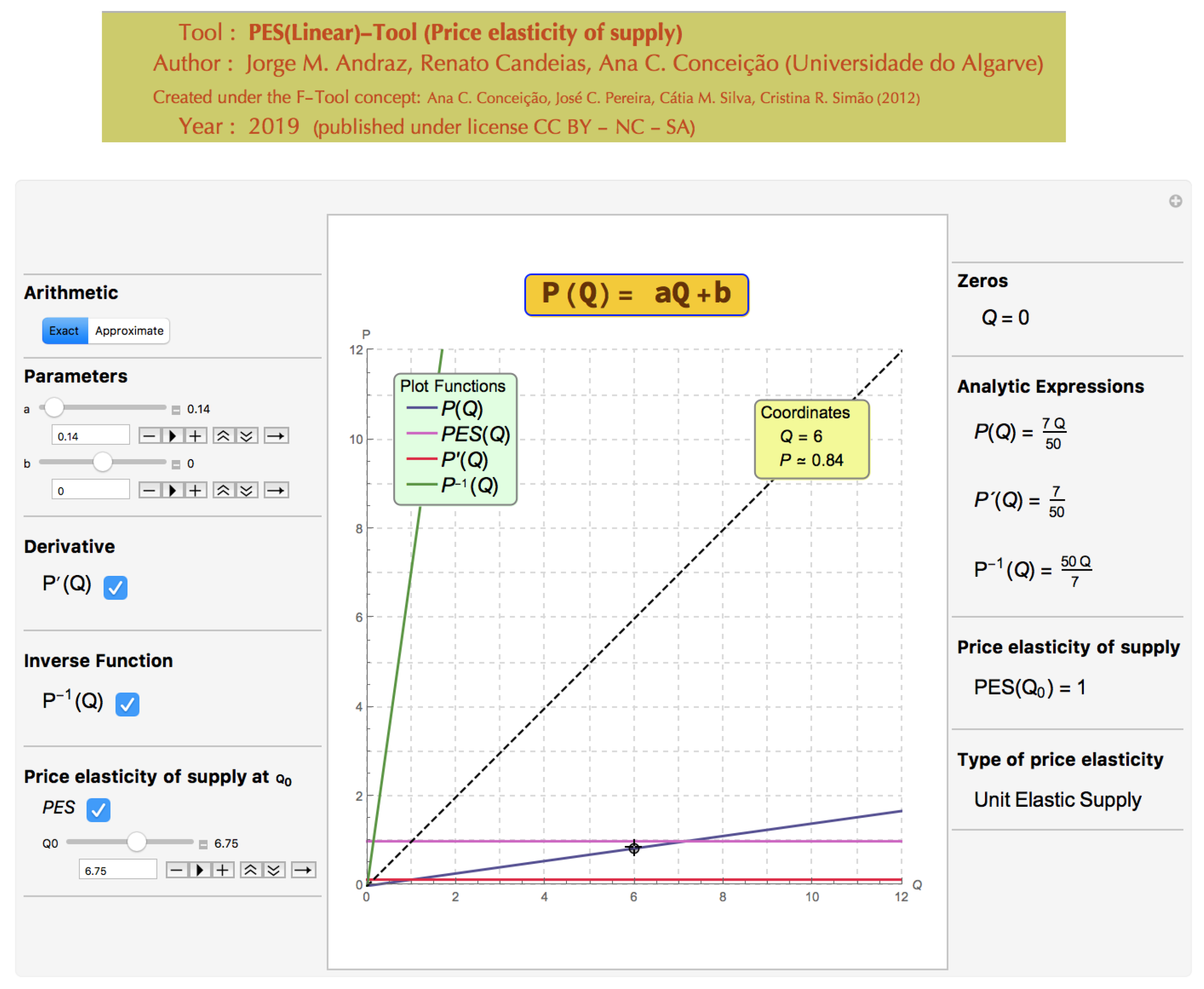
4.4. Unit Elastic Supply
It is generally acknowledged that there is often a confusion between the concepts of elasticity and derivative among students. In order to illustrate the contribution of the PES(Linear)-Tool to distinguish such concepts, this subsection presents some examples of unit elastic supply functions associated to different derivatives’ values.
Figure 10,
Figure 11 and
Figure 12 present examples of unitary elasticity supply functions associated to derivatives’ values above, below and equal to 1, respectively.
The graphical and analytical information, reported by the tool, confirm that despite the existence of a relationship between the two concepts (elasticity and derivative), their values are not directly connected.
Finally,
Figure 13 exhibits a non economic model in which
(if any positive value of
is considered, the economic model would have a unitary elasticity).
4.5. Perfectly Inelastic Supply
Although the PES(Linear)-Tool cannot fully illustrate the perfectly inelastic supply case, it can be used to make this case easier for students to understand. Once the information that this limit case occurs when
has been transmitted to the students, the immediate conclusion is that the corresponding PES is zero. In this case, the teacher should state that
, in (2), is also null (or question why) and therefore (2) is not an invertible function. This case is depicted in
Figure 14.
5. Final Remarks
This paper presents a new dynamic and interactive tool created with the computer algebra system Mathematica, the PES(Linear)-Tool, designed to be applied in economics education, a domain where the use of computer algebra has been particularly limited. Although there are several free of charge applications available at the Wolfram Demonstrations Project website, none of those provide all the graphical and analytical information necessary for a good understanding of the concepts introduced in socio-economic undergraduate courses in universities. Moreover, these applications provide either graphical or analytical information, but not both, and/or only for some particular cases, and they can hardly be adapted to explain specific concepts in social economic sciences, or that adaptation would require additional resources from both the teacher and the students.
The above mentioned issues constitute several gaps which the new tool intends to fulfill. The PES(Linear)-Tool is a computer algebra tool directed to the study of one of the most widely used concepts in socio-economics courses—the price elasticity of supply. Starting with the specification of the market supply function, the design, functionalities and capabilities of the PES(Linear)-Tool are exhaustively explored in this paper to analyze the price elasticity of supply, accounting for all the mathematical possibilities for which the economic model makes sense. This tool also differs from other existing tools in that it can be downloaded at no cost and allows the complete analysis of multiple situations involving the study of the price elasticity supply in a dynamic and interactive way. Specifically, the tool offers the students the possibility of changing the parameters’ values in the economic model and getting both the analytical and graphical effects in real time. The new PES(Linear)-Tool has a very intuitive interface that allows even the most inexperienced user, with no previous knowledge in educational software, to start using all the features in an efficient and autonomous way.
Given the recognition in the literature that some economic concepts can be more easily understood when students work with a large number and variety of graphics in an interactive way, with the support of the appropriate technology, we believe that the use of the PES(Linear)-Tool in the classroom can promote new ways of reasoning/thinking, evaluating, teaching, and learning in a context where students and teachers are invited to contribute. In this way, this tool promotes the active learning in classrooms and simultaneously students’ autonomous work, by allowing the design of challenging problems based on dynamic and interactive exercises using the CDF format, which students can work on and then send in their results to the faculty by email.
The design of the PES(Linear)-Tool can be generalized to other economic models that can be studied through other classes of functions, and also opens the possibility for the development of other interactive tools associated with other economic concepts.
Going forward, a statistically rigorous study in loco to assess the students’ perception when using the PES(Linear)-Tool, and therefore to estimate the tool’s pedagogical value is of extremely importance. We believe that this study can be an important help for the future development of these kind of educational tools.