Mathematical Models for Simulation and Optimization of High-Flux Solar Furnaces
Abstract
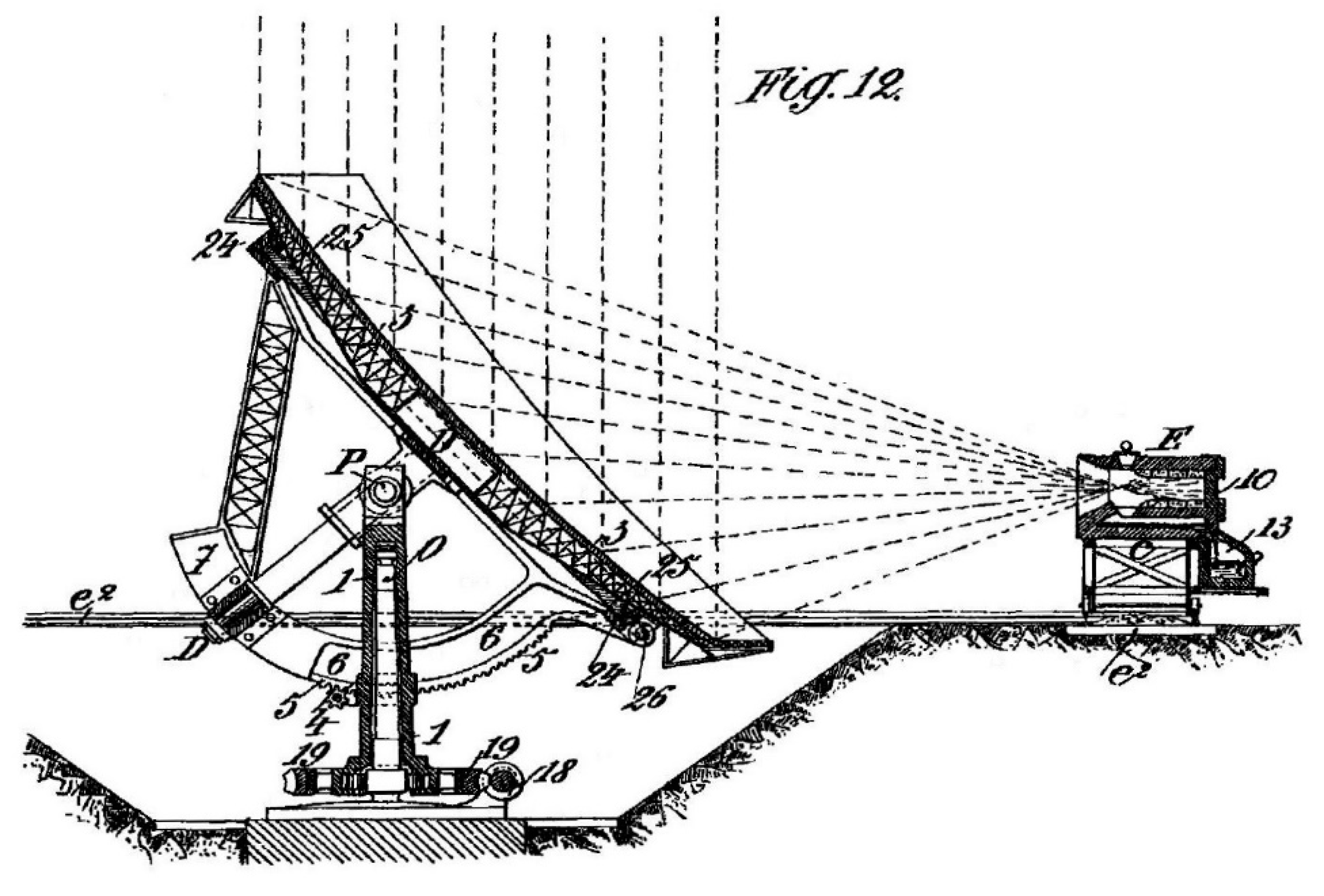
1. Introduction
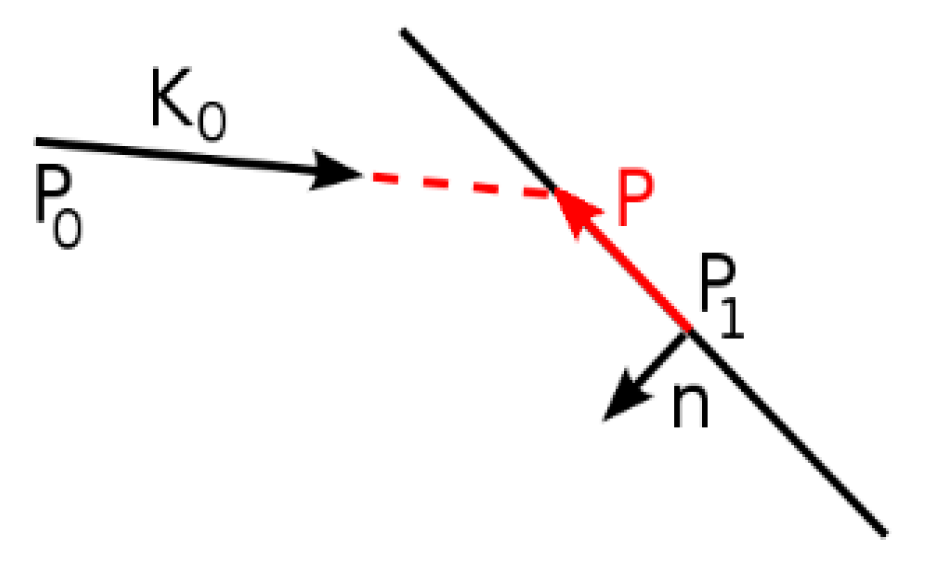
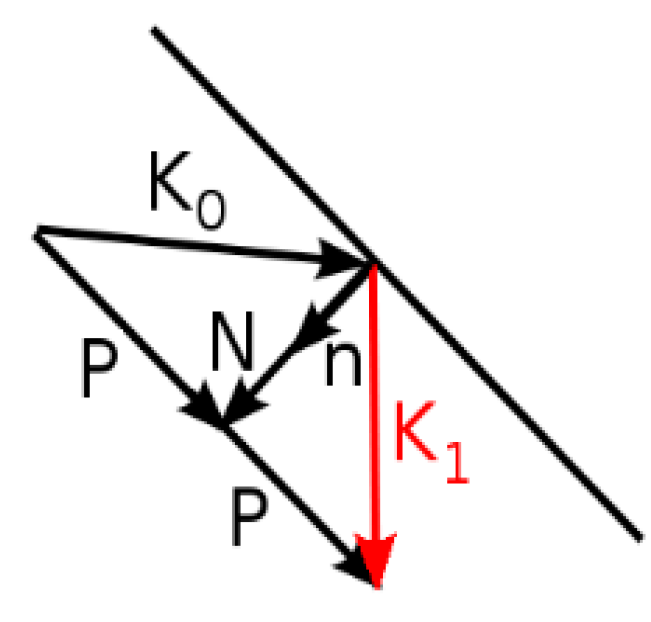
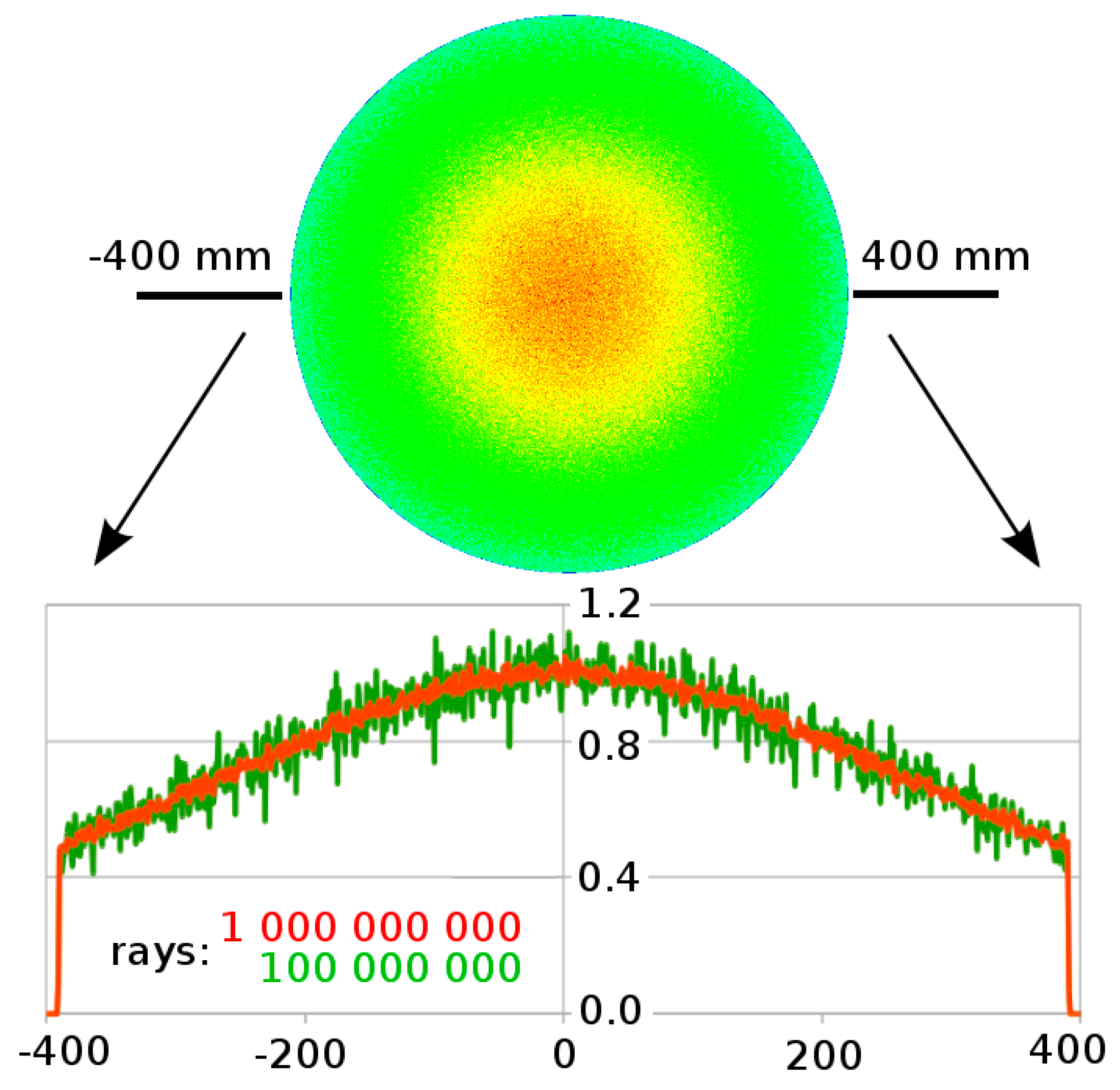
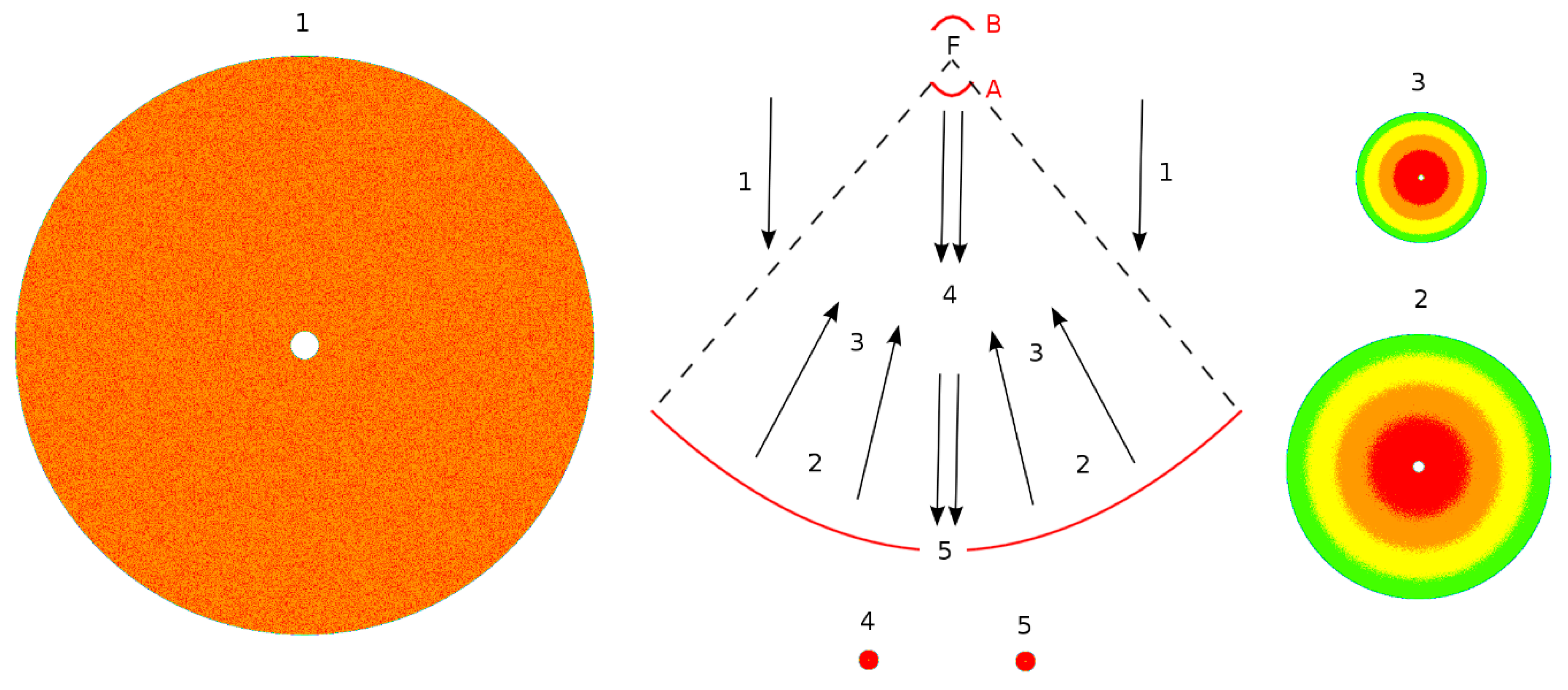
2. Ray Tracing Simulation
3. Models and Simulations
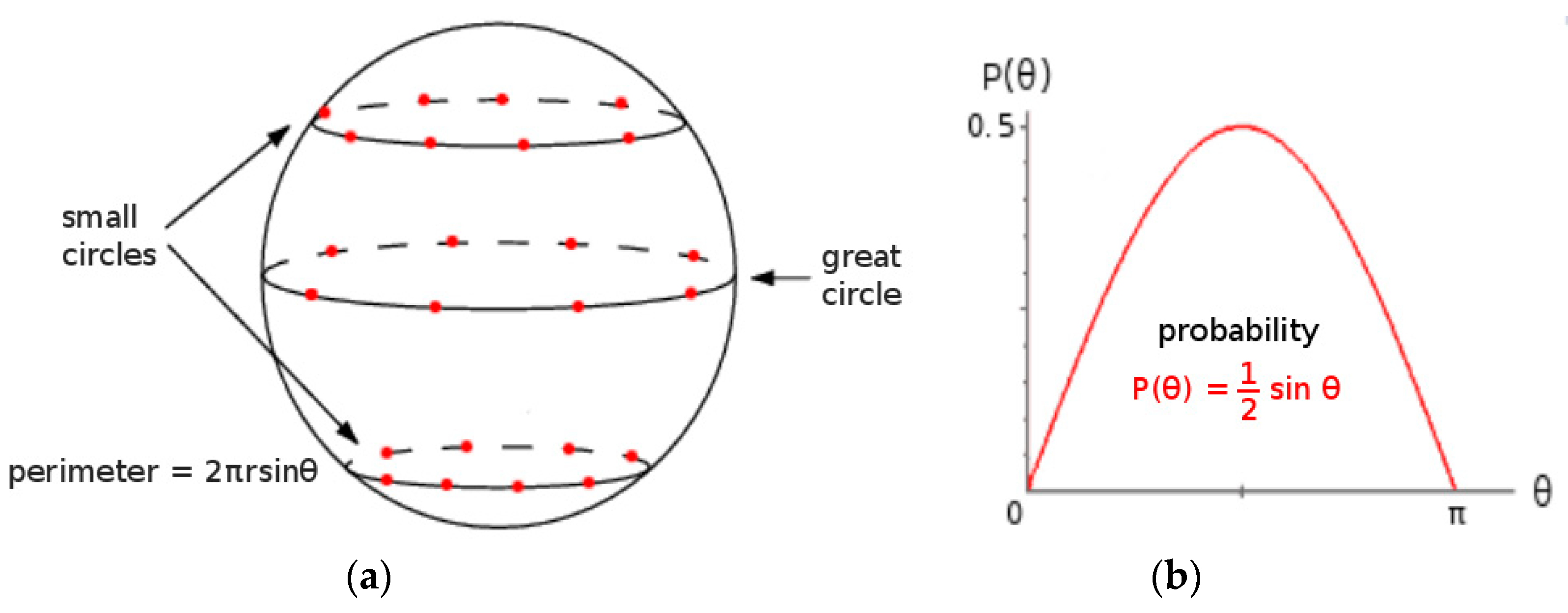
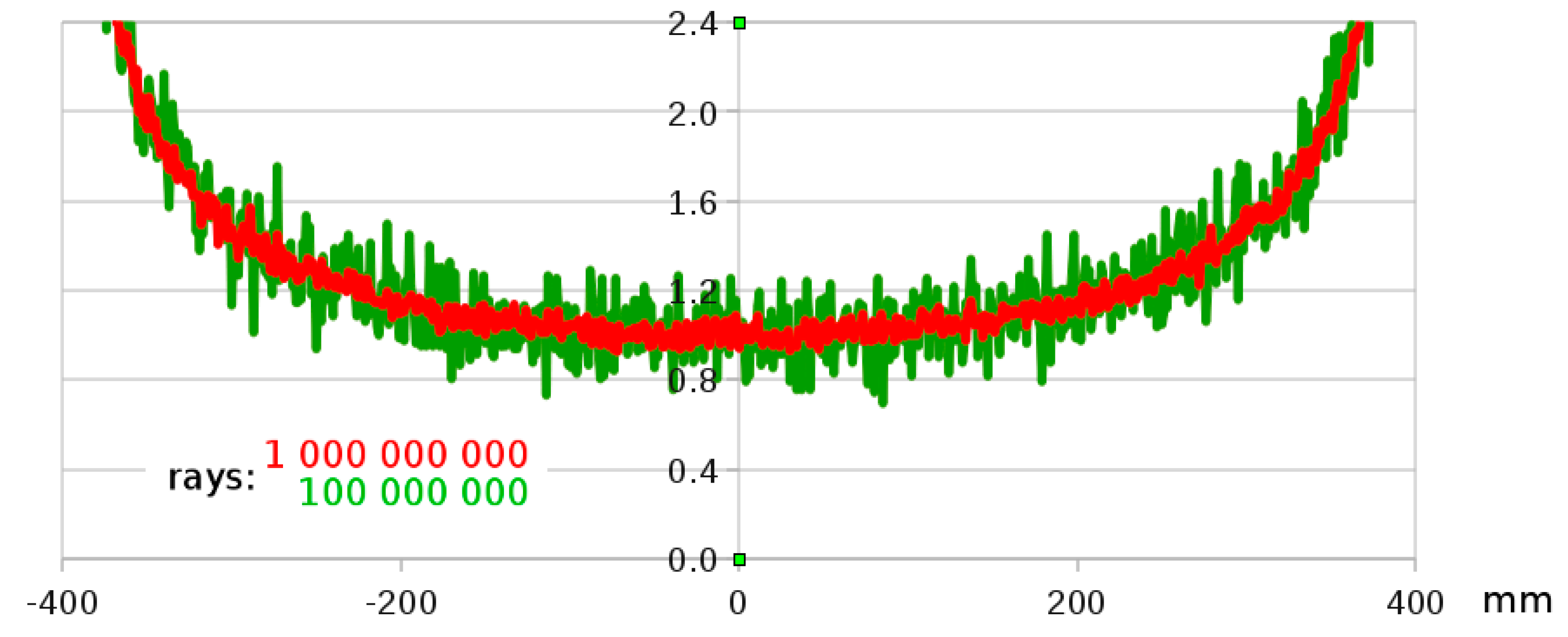
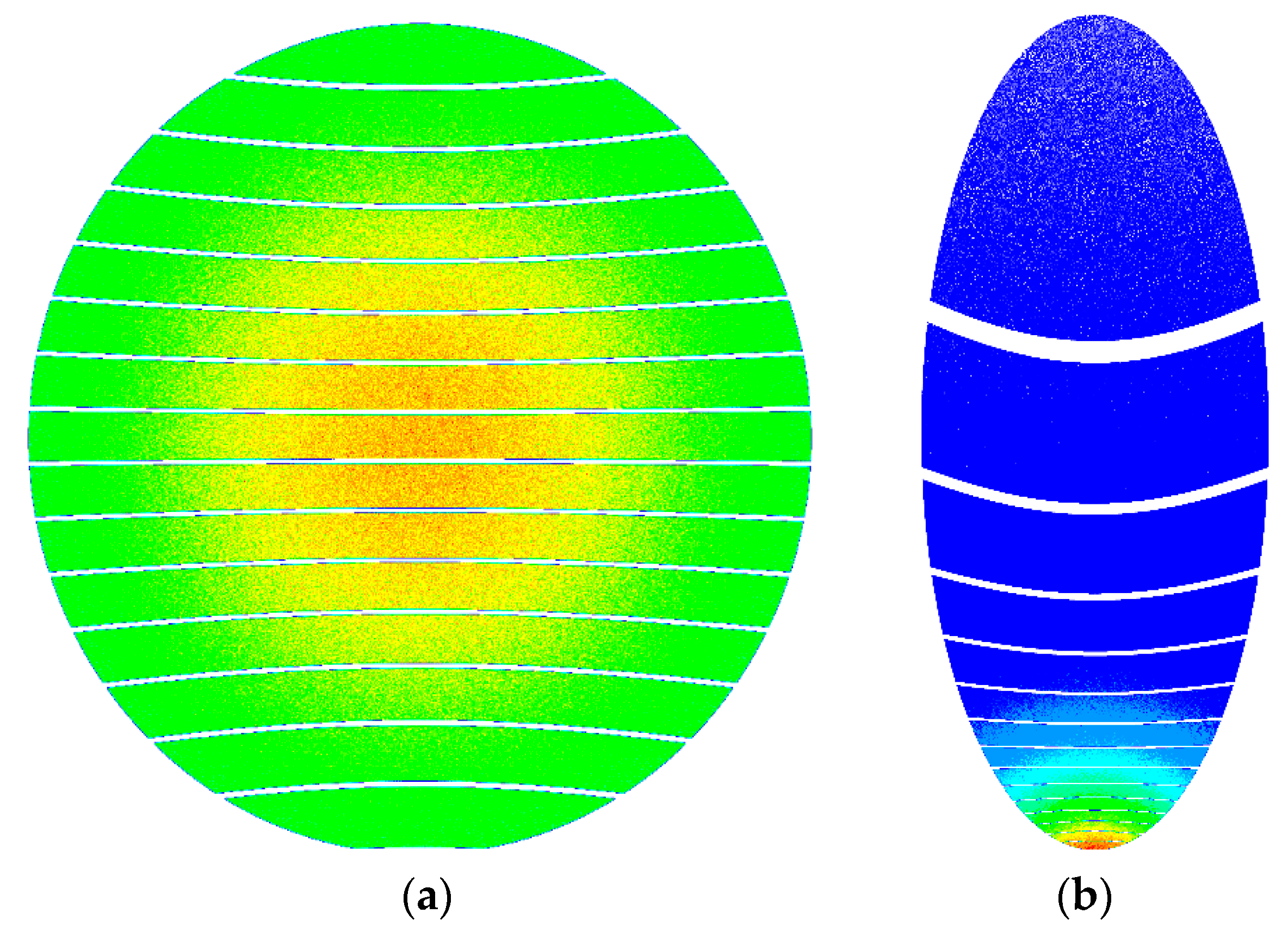
3.1. Spherical Emission Model
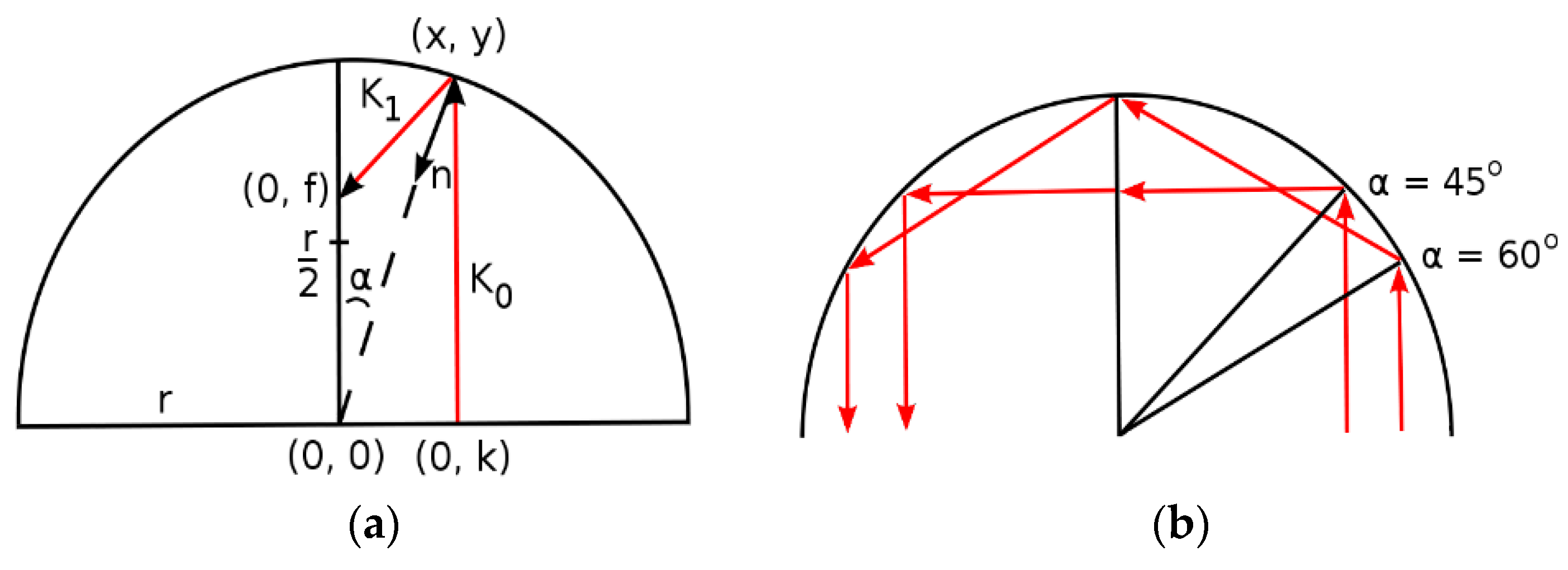
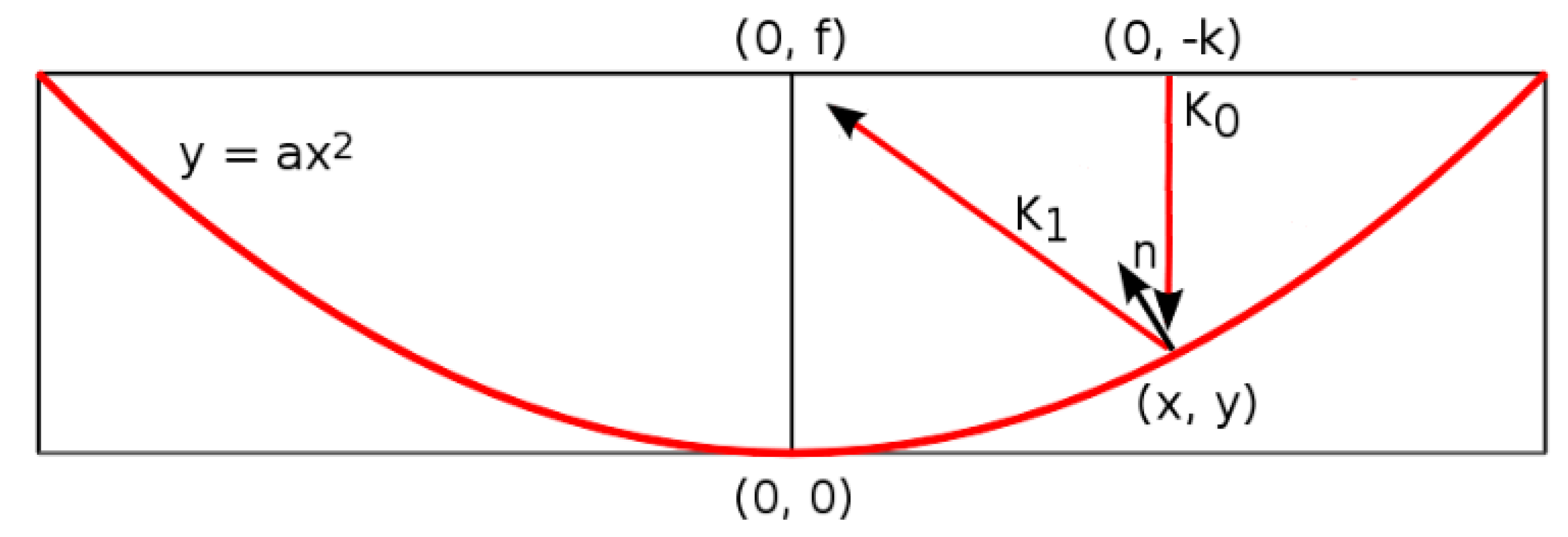
3.2. Spherical Reflection Model
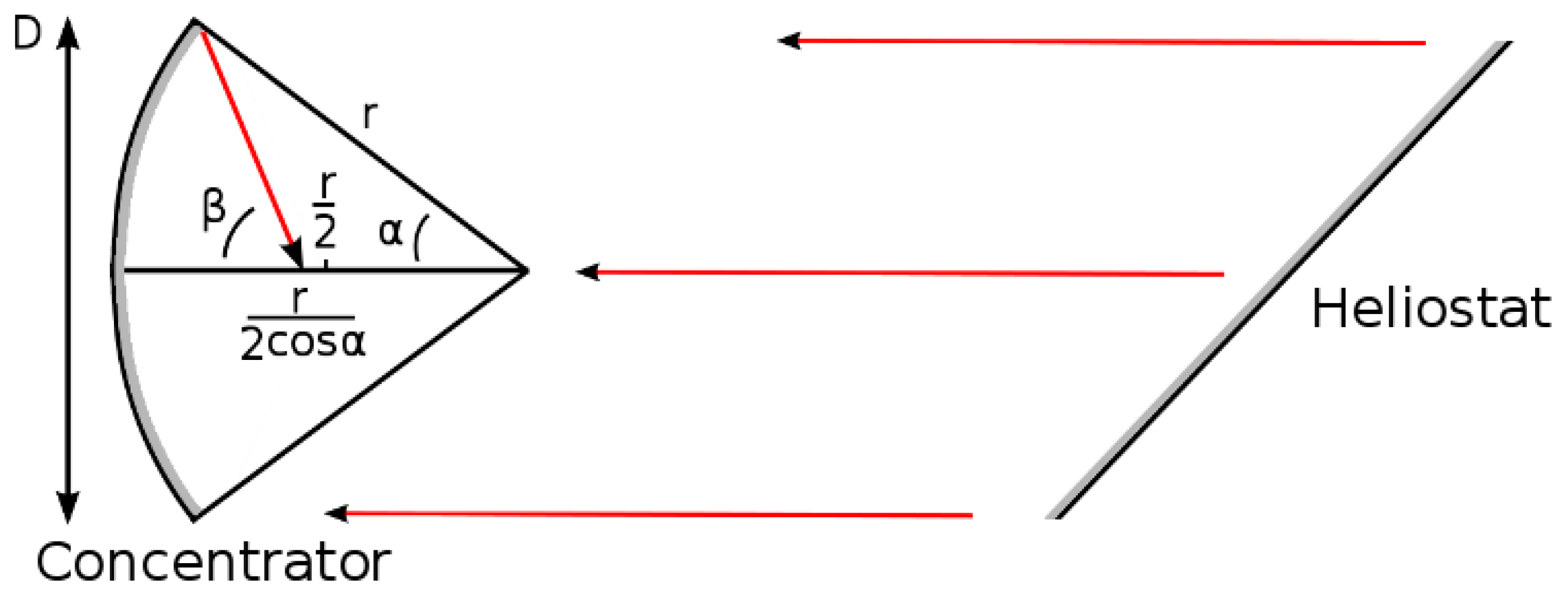
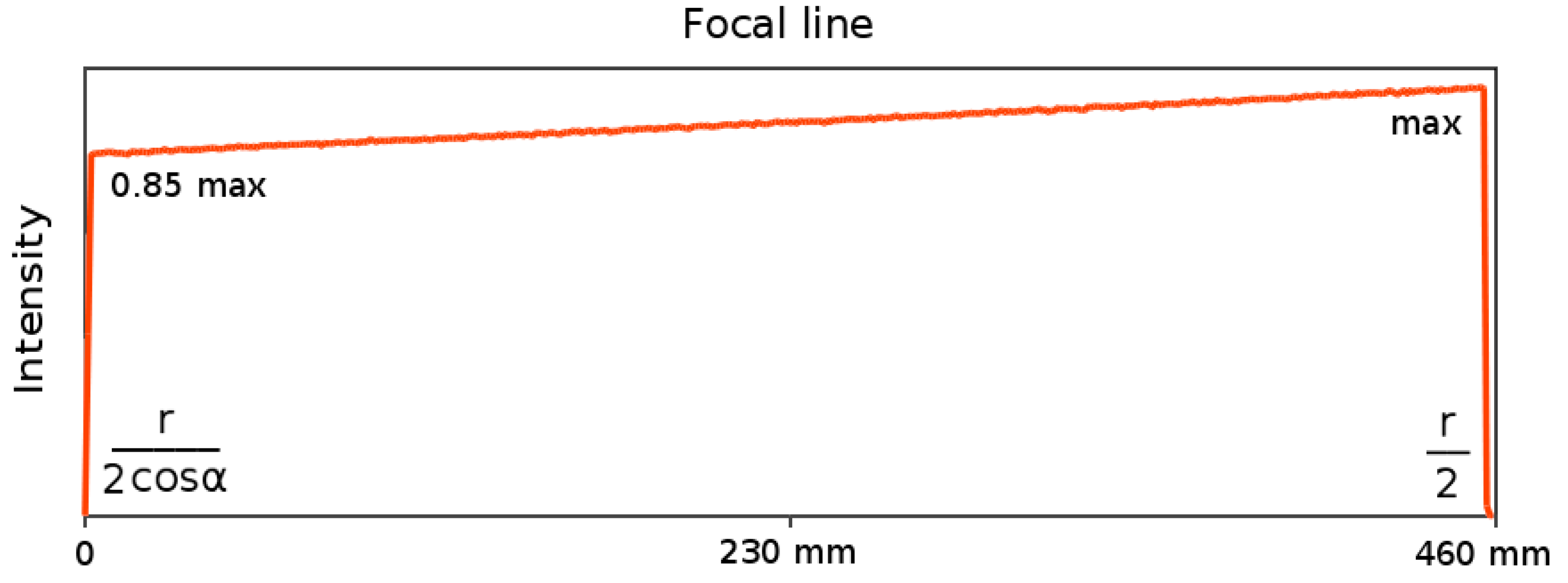
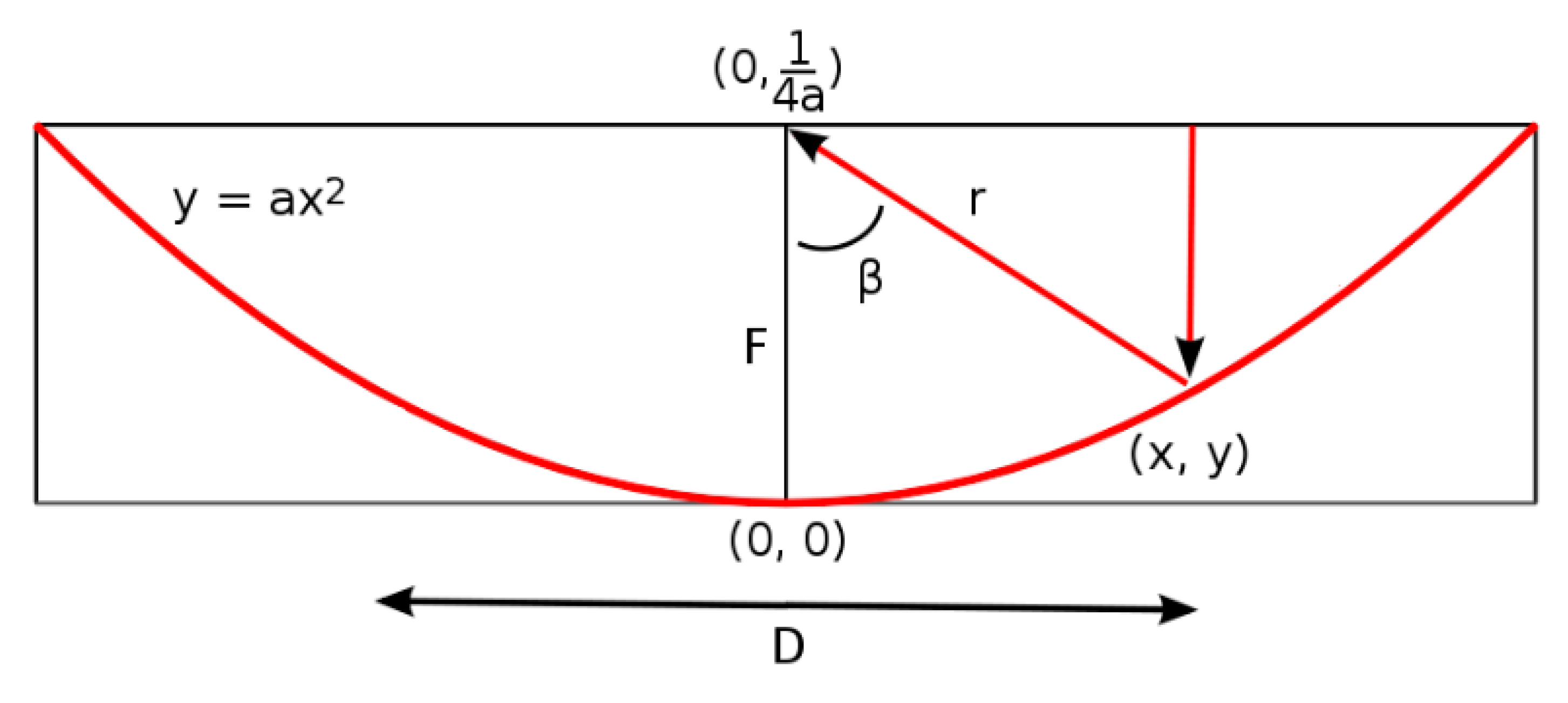
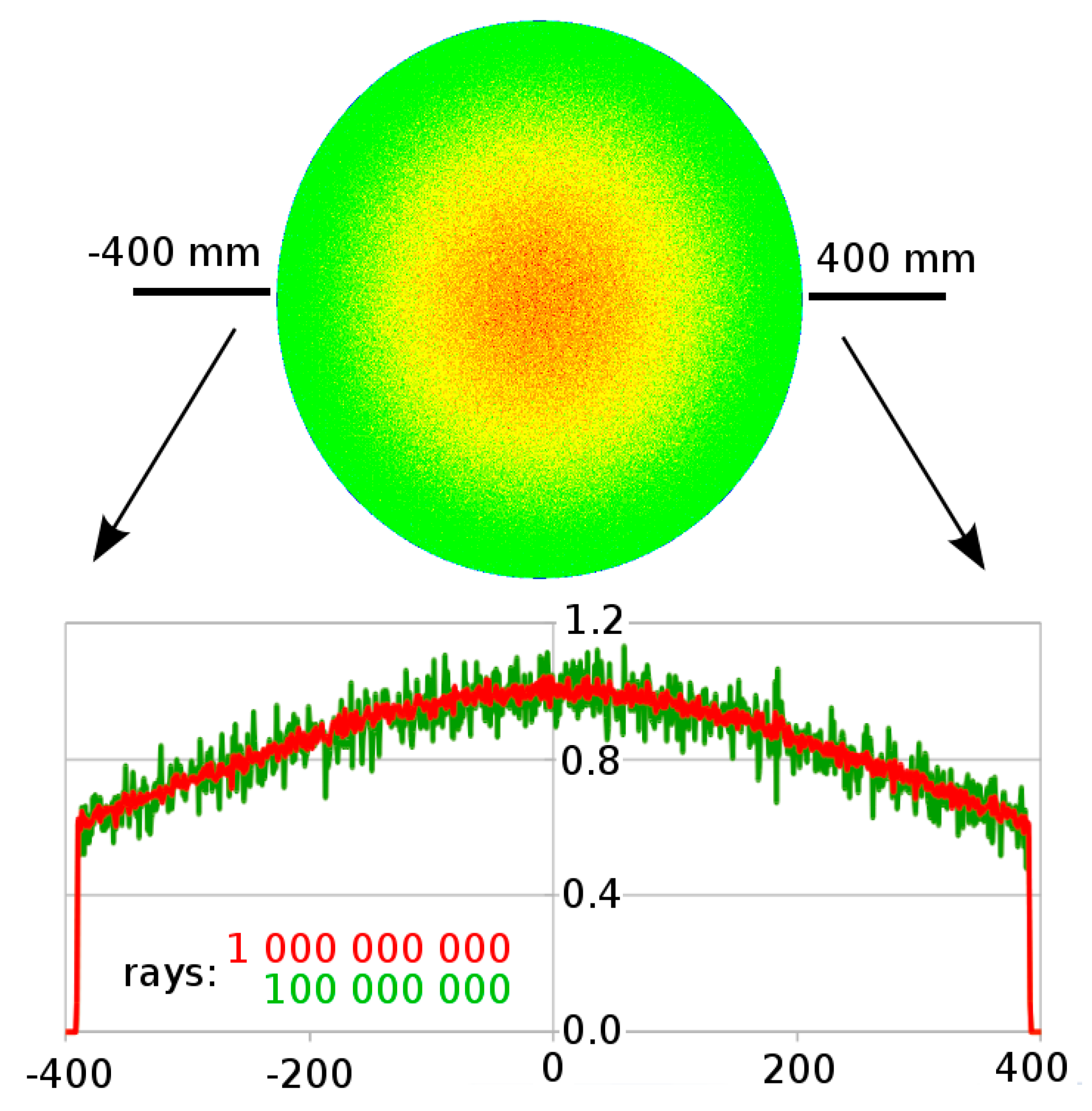
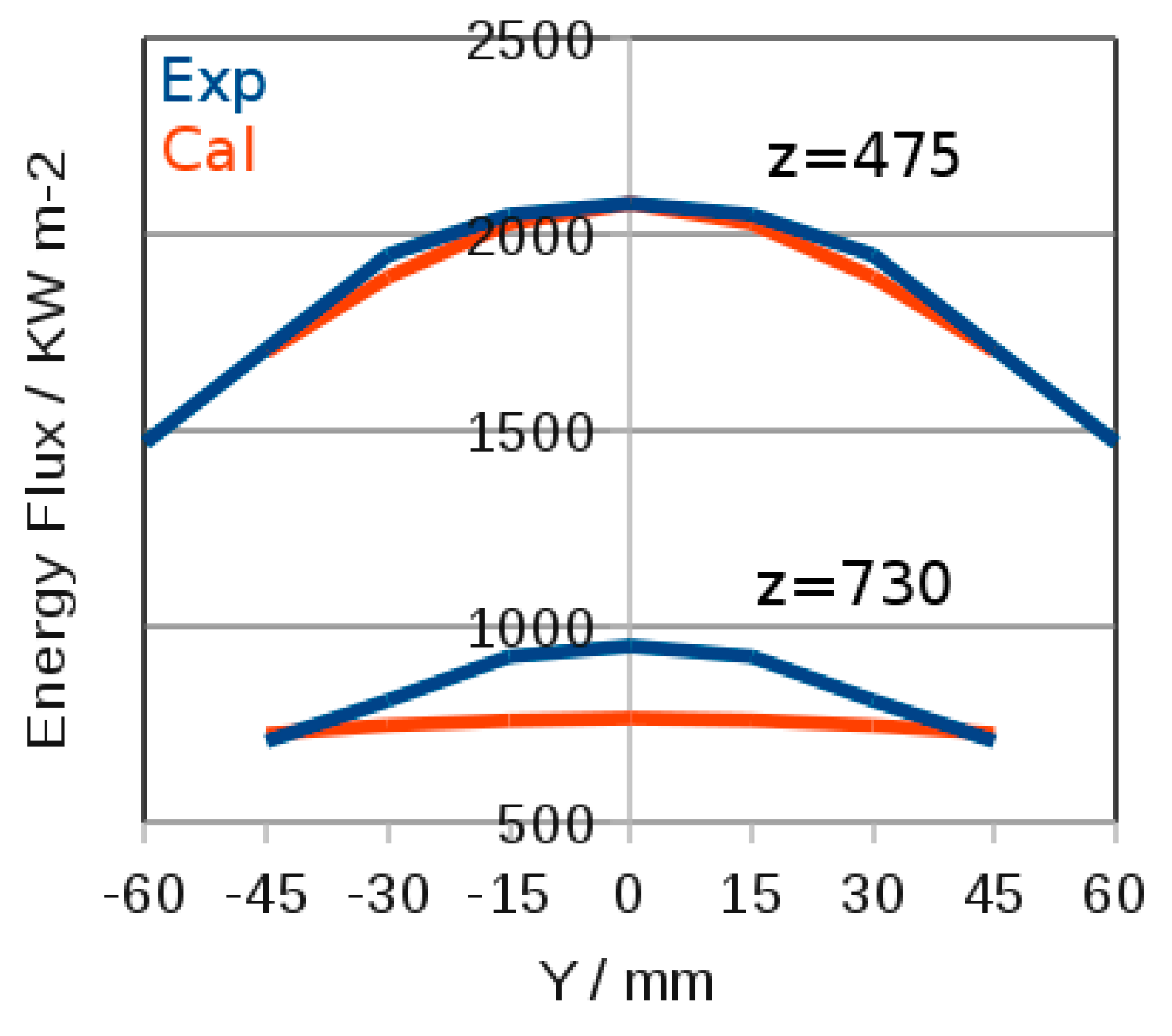
3.3. Paraboloid Reflection Model
4. Conclusions and Prospects for Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Rashed, R. A Pioneer in Anaclastics: Ibn Sahl on burning mirrors and lenses. Isis 1990, 81, 464–491. [Google Scholar] [CrossRef]
- Dijksterhuis, F.J. Christiaan Huygens and the Mathematical Science of Optics in the Seventeenth Century; Springer: Berlin/Heidelberg, Germany, 2004; ISBN 978-1-4020-2697-3. [Google Scholar]
- Young, T. The Bakerian Lecture. Experiments and calculations relative to physical optics. Philos. Trans. R. Soc. Lond. 1804, 94, 1–16. [Google Scholar] [CrossRef][Green Version]
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light, 7th ed.; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Hecht, E. Optics, 5th ed.; Pearson: London, UK, 2016. [Google Scholar]
- Himalaya, M.A.G. Improved Apparatus for Making Industrial Use of the Heat of the Sun and Obtaining High Temperatures. Patent GB190116181, 26 October 1901. Available online: https://worldwide.espacenet.com/publicationDetails/biblio?FT=D&date=19011026&DB=EPODOC&locale=en_EP&CC=GB&NR=190116181A&KC=A&ND=2# (accessed on 20 June 2019).
- Himalaya, M.A.G. Solar Apparatus for Producing High Temperatures. U.S. Patent 797,891, 22 August 1905. Available online: https://patents.google.com/patent/US797891 (accessed on 20 June 2019).
- Rodrigues, J. A conspiração solar do Padre Himalaya—Esboço biográfico dum português pioneiro da Ecologia (The Solar Conspiration of Father Himalaya—Biographic Outline of a Portuguese Pioneer in Ecology); Árvore—Cooperativa de Actividades Artísticas: Porto, Portugal, 1999; ISBN 972-9089-44-2. [Google Scholar]
- Tinoco, A. Portugal na Exposição Universal de 1904: O Padre Himalaia e o Pirelióforo. Cadernos de Sociomuseologia 2012, 42, 113–127, Edições Universitárias Lusófonas. Available online: http://hdl.handle.net/10437/4545 (accessed on 20 June 2019).
- Trombe, F.; Le Phat Vinh, A. Thousand kW solar furnace, built by the National Center of Scientific Research, in Odeillo (France). Sol. Energy 1973, 15, 57–61. [Google Scholar] [CrossRef]
- Levêque, G.; Bader, R.; Lipinski, W.; Haussener, S. High-flux optical systems for solar thermochemistry. Sol. Energy 2017, 156, 133–148. [Google Scholar] [CrossRef]
- Fernández-González, D.; Ruiz-Bustinza, I.; González-Gasca, C.; Piñuela-Noval, J.; Mochón-Csataños, J.; Sancho-Gorostiaga, J.; Verdeja, L.F. Concentrated solar energy applications in materials science and metallurgy. Sol. Energy 2018, 170, 520–540. [Google Scholar] [CrossRef]
- Riveros-Rosas, D.; Herrera-Vázquez, J.; Pérez-Rábago, C.A.; Arancibia-Bulnes, C.A.; Vázquez-Montiel, S.; Sánchez-González, M.; Granados-Agustín, F.; Jaramillo, O.A.; Estrada, C.A. Optical design of a high radiative flux solar furnace for Mexico. Sol. Energy 2010, 84, 792–800. [Google Scholar] [CrossRef]
- Llorente, J.; Ballestrín, J.; Vásques, A.J. A new solar concentrating system: Description, characterization and applications. Sol. Energy 2011, 85, 1000–1006. [Google Scholar] [CrossRef]
- Luque, S.; González-Aguilar, J.; Romero, M. Design of a calorimetric facility to assess volumetric receivers employing a 42 kW high flux solar simulator. In Proceedings of the ISES Solar World Conference 2017 and the IEA SHC Solar Heating and Cooling Conference for Buildings and Industry, Abu Dhabi, UAE, 29 October–2 November 2017; International Solar Energy Society: Breisgau, Germany, 2017. [Google Scholar] [CrossRef]
- Welford, W.T.; Winston, R. The Optics of Nonimaging Concentrators: Light and Solar Energy, 1st ed.; Academic Press: Cambridge, MA, USA, 1978. [Google Scholar]
- Spencer, G.H.; Murty, M.V.R. General ray-tracing procedure. J. Opt. Soc. Am. 1962, 52, 672–678. [Google Scholar] [CrossRef]
- Freniere, E.R.; Tourtellott, J. A brief history of generalized ray tracing. Proc. SPIE 1997, 3130, 170–178. [Google Scholar] [CrossRef]
- Howell, B.J.; Wilson, M.E. Automatic ray-surface intersection method. Appl. Opt. 1982, 21, 2184–2188. [Google Scholar] [CrossRef]
- Kerisit, S.; Rosso, K.M.; Cannon, B.D.; Gao, F.; Xie, Y.L. Computer simulation of the light yield nonlinearity of inorganic scintillators. J. Appl. Phys. 2009, 105, 114915. [Google Scholar] [CrossRef]
- Dlugach, J.; Mishchenko, M.I.; Liu, L.; Mackowski, D.W. Numerically exact computer simulations of light scattering by densely packed, random particulate media. J. Quant. Spectrosc. Radiat. Transf. 2011, 112, 2068–2078. [Google Scholar] [CrossRef][Green Version]
- Jafrancesco, D.; Sansoni, P.; Francini, F.; Contento, G.; Privato, C.; Graditi, G.; Ferruzzi, D.; Mercatelli, L.; Sani, E.; Fontani, D. Mirrors array for a solar furnace: Optical analysis and simulation results. Renew. Energy 2014, 63, 263–271. [Google Scholar] [CrossRef]
- Bader, R.; Haussener, S.; Lipinski, W. Optical design of multisource high-flux solar simulators. J. Sol. Energy Eng. 2015, 137, 021012. [Google Scholar] [CrossRef]
- Danko, O.; Danko, V.; Kovalenko, A. Light focusing through a multiple scattering medium: Ab initio computer simulation. Proc. SPIE 2017, 10612, 1061216. [Google Scholar] [CrossRef]
- Jin, J.; Liu, M.K.; Lin, P.Z.; Fu, T.R.; Hao, Y.; Jin, H.G. Ultrahigh temperature processing by concentrated solar energy with accurate temperature measurement. Appl. Therm. Eng. 2019, 150, 1337–1344. [Google Scholar] [CrossRef]
- CUtrace. Available online: https://www.mathworks.com/matlabcentral/fileexchange/52820-cutrace (accessed on 8 May 2019).
- OpenRayTrace. Available online: http://openraytrace.sourceforge.net/ (accessed on 8 May 2019).
- Pujol-Nadal, R.; Martínez-Moll, V.; Moià-Pol, A.; Cardona, G.; Hertel, J.D.; Bonnín, F. OTSun Project: Development of a Computational Tool for High-resolution Optical Analysis of Solar Collectors. In Proceedings of the 11th ISES EUROSUN 2016 Conference, Palma, Spain, 11–14 October 2016; Martinez, V., Gonzalez, J., Eds.; International Solar Energy Society: Freiburg, Germany, 2017; pp. 989–999. [Google Scholar] [CrossRef]
- Ray Optics Module. Available online: https://www.comsol.com/ray-optics-module#cmm-optical-ray-tracing-software (accessed on 8 May 2019).
- Ray Optics Simulation, Developed by Rick Tu. Available online: https://ricktu288.github.io/ray-optics/simulator/ (accessed on 8 May 2019).
- Solstice—The Solar Plant Simulation Tool. Available online: https://www.meso-star.com/projects/solstice/solstice.html (accessed on 8 May 2019).
- SolTrace. Available online: https://www.nrel.gov/csp/soltrace.html (accessed on 8 May 2019).
- Stellar Software. Available online: https://www.stellarsoftware.com/ (accessed on 8 May 2019).
- Tonatiuh. Available online: http://iat-cener.github.io/tonatiuh/ (accessed on 8 May 2019).
- Zemax’ OpticStudio. Available online: https://customers.zemax.com/os/resources/learn/tutorials (accessed on 8 May 2019).
- Li, B.; Oliveira, F.A.C.; Rodríguez, J.; Fernandes, J.C.; Rosa, L.G. Numerical and experimental study on improving temperature uniformity of solar furnaces for materials processing. Sol. Energy 2015, 115, 95–108. [Google Scholar] [CrossRef]
- Oliveira, F.A.C.; Fernandes, J.C.; Rodríguez, J.; Cañadas, I.; Galindo, J.; Rosa, L.G. Temperature uniformity improvement in a solar furnace by indirect heating. Sol. Energy 2016, 140, 141–150. [Google Scholar] [CrossRef]
- Martins, C.A.B. Aparelho Concentrador e Estabilizador de Raios Solares e Sistema de Transmissão de um Feixe de Raios Solares Concentrados e Estabilizados que o Contém. Portuguese Patent Pending Request No. PT20160109071, 4 January 2016. Available online: https://pt.espacenet.com/searchResults?CY=pt&DB=EPODOC&F=0&FIRST=1&LG=pt&PN=PT109071&Submit=PESQUISAR&bookmarkedResults=true&locale=pt_pt&sf=n (accessed on 20 June 2019).




© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pereira, J.C.G.; Fernandes, J.C.; Guerra Rosa, L. Mathematical Models for Simulation and Optimization of High-Flux Solar Furnaces. Math. Comput. Appl. 2019, 24, 65. https://doi.org/10.3390/mca24020065
Pereira JCG, Fernandes JC, Guerra Rosa L. Mathematical Models for Simulation and Optimization of High-Flux Solar Furnaces. Mathematical and Computational Applications. 2019; 24(2):65. https://doi.org/10.3390/mca24020065
Chicago/Turabian StylePereira, José Carlos Garcia, Jorge Cruz Fernandes, and Luís Guerra Rosa. 2019. "Mathematical Models for Simulation and Optimization of High-Flux Solar Furnaces" Mathematical and Computational Applications 24, no. 2: 65. https://doi.org/10.3390/mca24020065
APA StylePereira, J. C. G., Fernandes, J. C., & Guerra Rosa, L. (2019). Mathematical Models for Simulation and Optimization of High-Flux Solar Furnaces. Mathematical and Computational Applications, 24(2), 65. https://doi.org/10.3390/mca24020065






