Bisimulation for Secure Information Flow Analysis of Multi-Threaded Programs
Abstract
1. Introduction
2. Preliminaries and Assumptions
2.1. Program Model
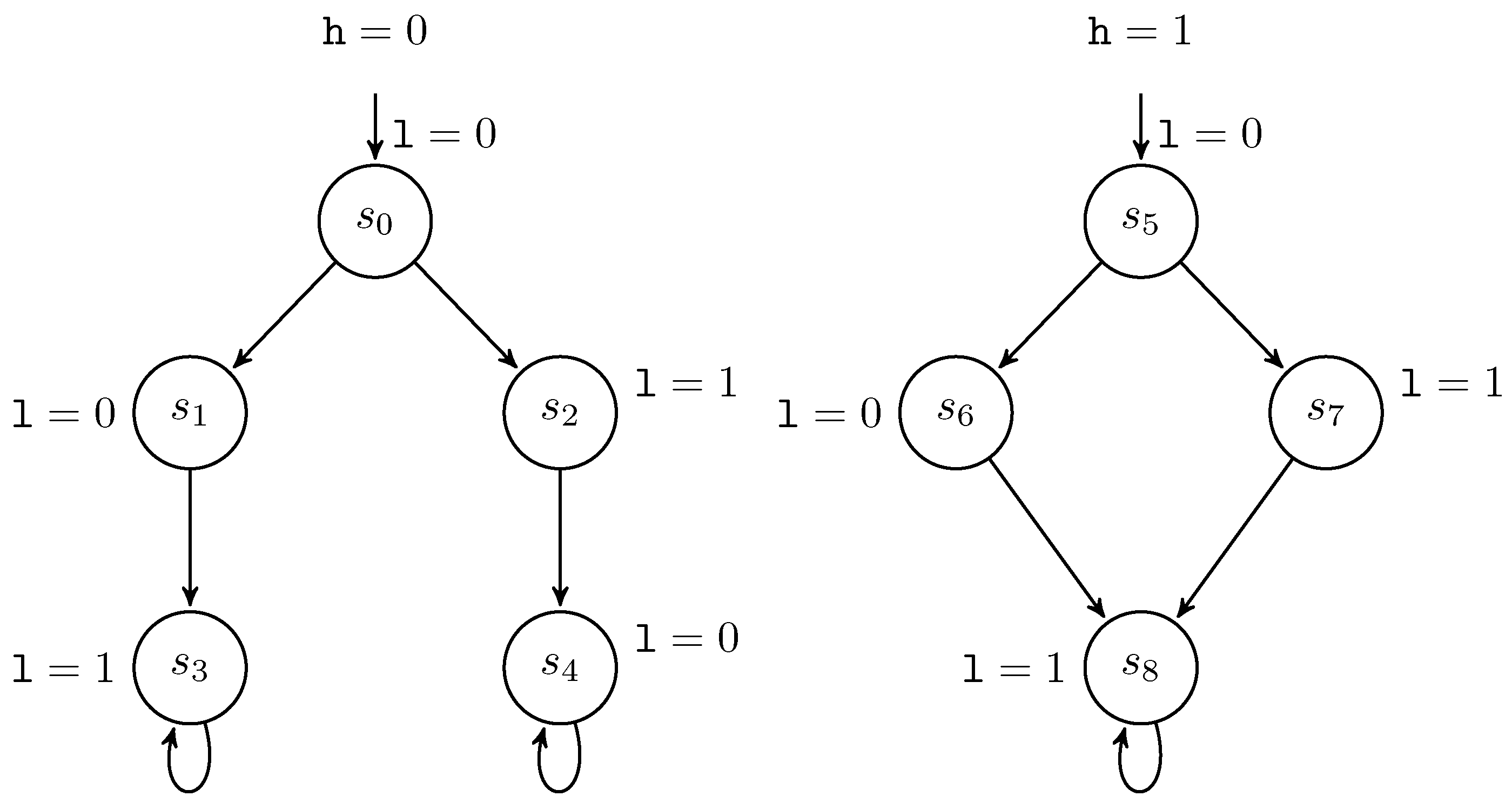
l:=0; l:=1 || if l=1 then l:=h (P1)
2.2. Attacker Model
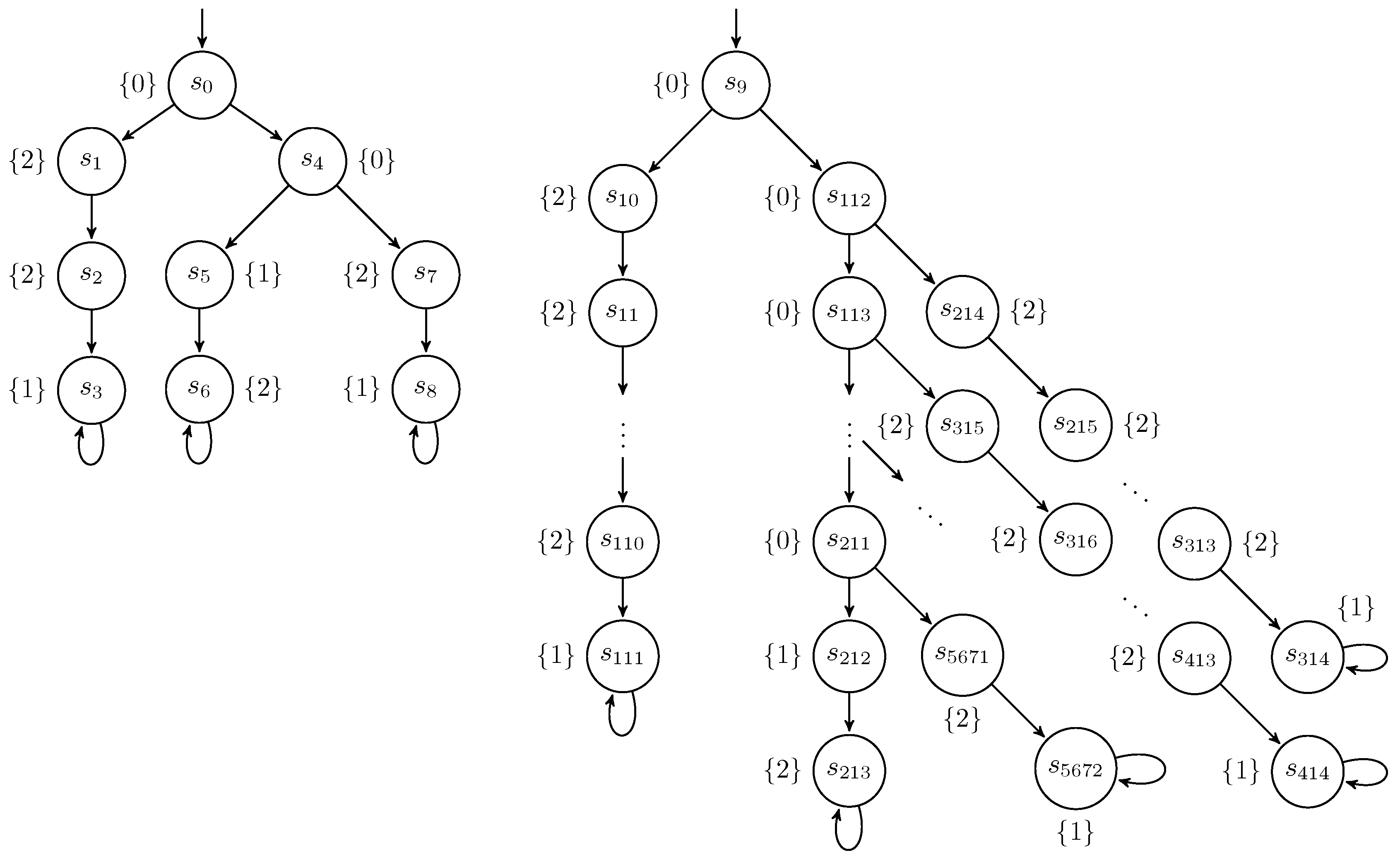
2.3. Low-Bisimulation
- 1.
- .
- 2.
- If with , then there exists a finite path fragment with and , and .
- 3.
- If with , then there exists a finite path fragment with and , and .
3. Related Work
4. The Proposed Approach
4.1. Bisimulation-Based Observational Determinism
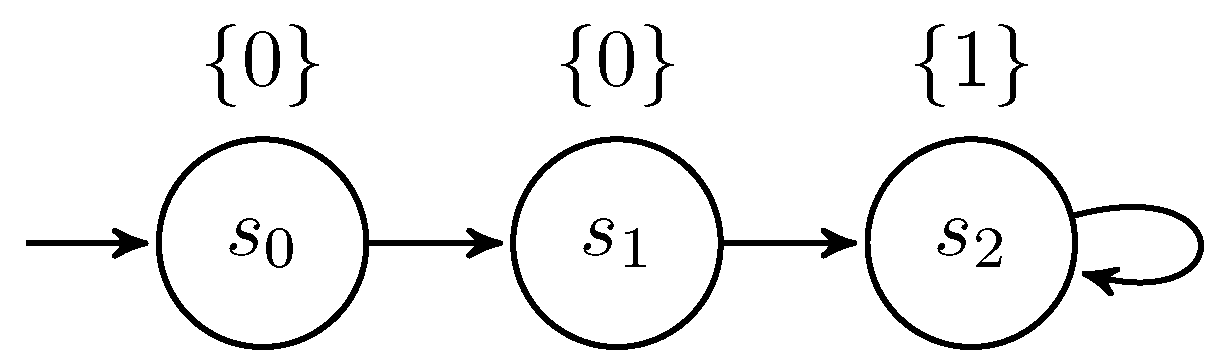
l:=0; h:=l+3; l:=l+1 (P2)
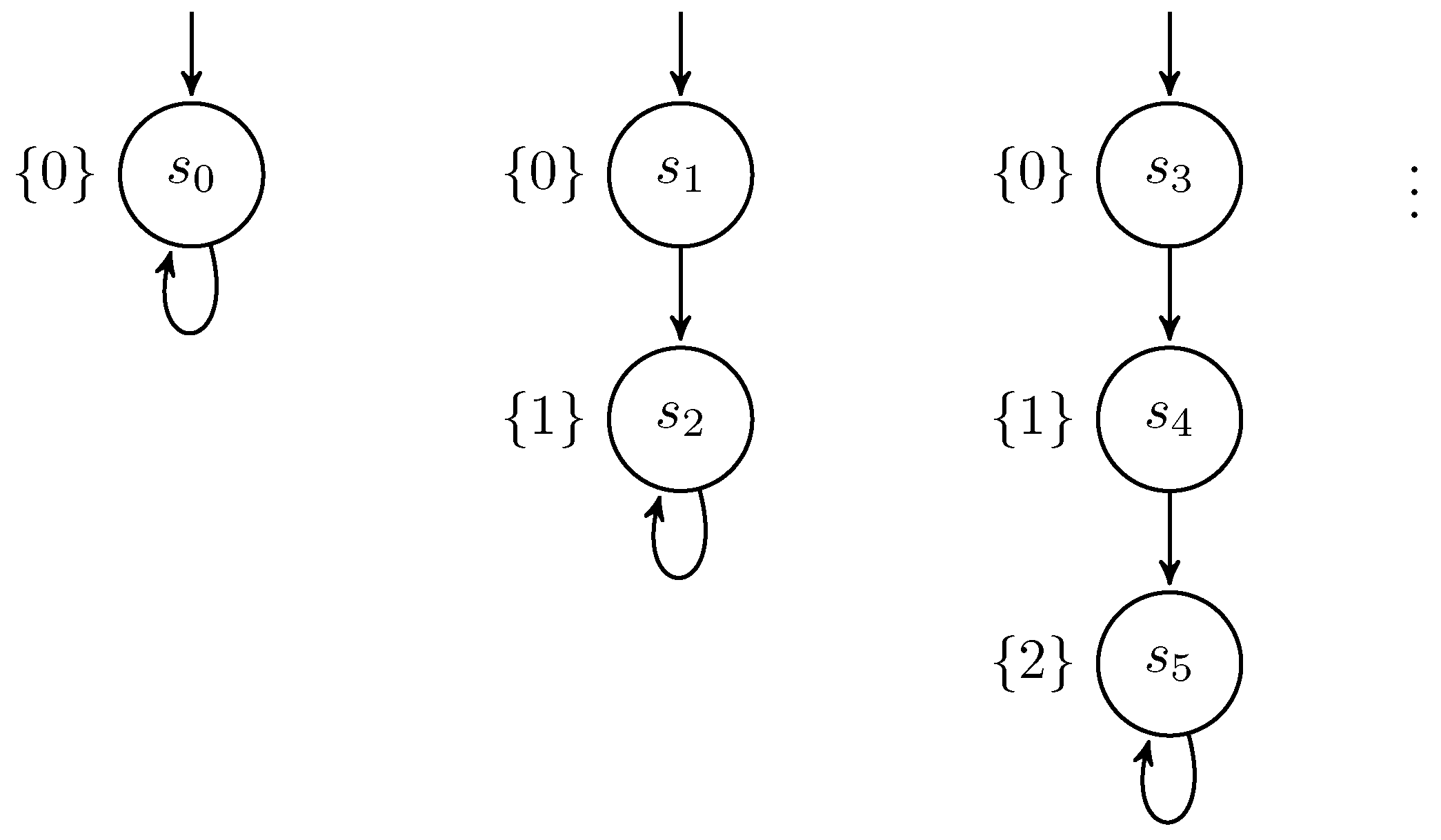
if l>0 then h:=h+1
else h:=0 (P3)
l:=0; while h>0 do {l++; h--} (P4)
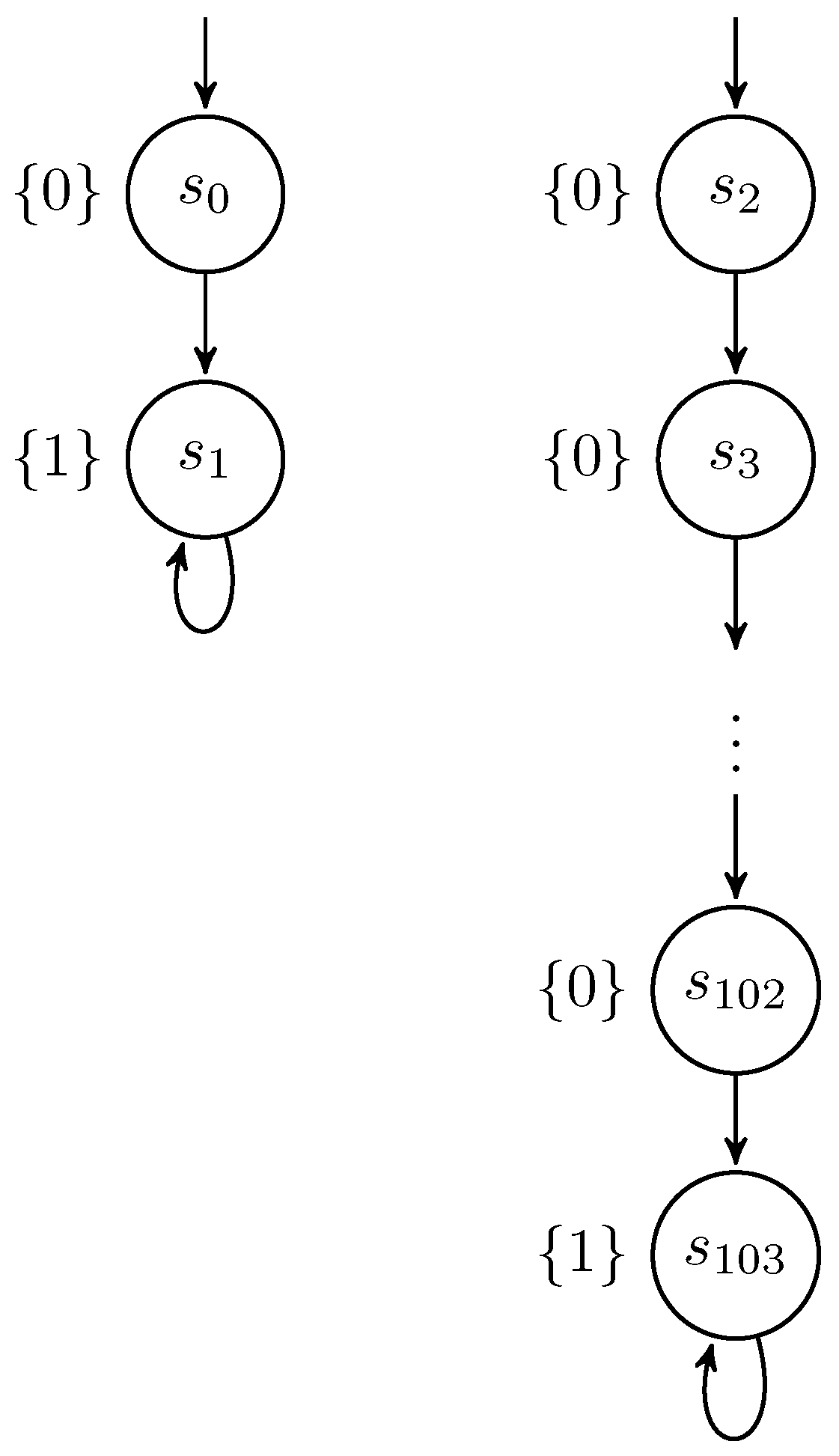
l:=0; if h>0 then l:=1
else {sleep 100; l:=1} (P5)
where sleep 100 means 100 consecutive skip commands. The Kripke structure of the program is depicted in Figure 4.l:=0 l:=2 || (if h=1 then sleep 100); l:=1 (P6)
4.2. Verifying BOD
4.2.1. The Algorithm
| Algorithm 1 Verification of BOD |
|
4.2.2. Correctness of the Algorithm
4.2.3. Complexity of the Algorithm
4.2.4. Implementation and Case Study
Thread α: while mask != 0 do while trigger0 = 0 do; /* busy waiting */ result := result | mask ; /* bitwise ‘or’ */ trigger0 := 0; maintrigger := maintrigger + 1; if maintrigger = 1 then trigger1 := 1 Thread β: while mask != 0 do while trigger1 = 0 do; /* busy waiting */ result := result & ~ mask ; /* bitwise ‘and’ with the complement of mask */ trigger1 := 0; maintrigger := maintrigger + 1; if maintrigger = 1 then trigger0 := 1 Thread γ: while mask != 0 do maintrigger := 0; if (PIN & mask ) = 0 then trigger0 := 1 else trigger1 := 1; while maintrigger != 2 do; /* busy waiting */ mask := mask / 2; trigger0 := 1; trigger1 := 1
5. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Appendix A
dtmc const int n = 3; // num of bits of the pin variable global result : [0.. pow (2, n) -1]; global mask : [0.. pow (2, n) -1]; global pin : [0.. pow (2, n) -1]; global trigger0 : [0..1]; global trigger1 : [0..1]; global maintrigger : [0..2]; global turn : [1..3]; module Alpha c1 : [0..5]; [] turn =1 & c1 =0 & mask !=0 -> (c1 ’=1); [] turn =1 & c1 =1 & trigger0 =0 & trigger1 =1 -> (turn ’=2); [] turn =1 & c1 =1 & trigger0 =0 & trigger1 !=1 -> (turn ’=3); [] turn =1 & c1 =1 & trigger0 !=0 -> (c1 ’=2); [] turn =1 & c1 =2 & mod( floor ( result / mask ) ,2)=0 & result +mask <= pow (2,n)-1 -> ( result ’= result + mask ) & (c1 ’=3); [] turn =1 & c1 =2 & mod( floor ( result / mask ) ,2)=1 -> (c1 ’=3); [] turn =1 & c1 =3 -> ( trigger0 ’=0) & (c1 ’=4); [] turn =1 & c1 =4 & maintrigger <2 -> ( maintrigger ’= maintrigger +1) & (c1 ’=5); [] turn =1 & c1 =5 & maintrigger =1 -> ( trigger1 ’=1) & (c1 ’=0); [] turn =1 & c1 =5 & maintrigger !=1 -> (c1 ’=0); endmodule module Beta c2 : [0..5]; [] turn =2 & c2 =0 & mask !=0 -> (c2 ’=1); [] turn =2 & c2 =1 & trigger1 =0 & trigger0 =1 -> (turn ’=1); [] turn =2 & c2 =1 & trigger1 =0 & trigger0 !=1 -> (turn ’=3); [] turn =2 & c2 =1 & trigger1 !=0 -> (c2 ’=2); [] turn =2 & c2 =2 & mod( floor ( result / mask ) ,2)=1 -> (result ’= result - mask ) & (c2 ’=3); [] turn =2 & c2 =2 & mod( floor ( result / mask ) ,2)=0 -> (c2 ’=3); [] turn =2 & c2 =3 -> ( trigger1 ’=0) & (c2 ’=4); [] turn =2 & c2 =4 & maintrigger <2 -> ( maintrigger ’= maintrigger +1) & (c2 ’=5); [] turn =2 & c2 =5 & maintrigger =1 -> ( trigger0 ’=1) & (c2 ’=0); [] turn =2 & c2 =5 & maintrigger !=1 -> (c2 ’=0); endmodule module Gamma c3 : [0..6]; [] turn =3 & mask !=0 & c3 =0 -> (c3 ’=1); [] turn =3 & mask =0 & c3 =0 -> (c3 ’=5); [] turn =3 & c3 =1 -> ( maintrigger ’=0) & (c3 ’=2); [] turn =3 & c3 =2 & mod( floor ( pin / mask ) ,2)=0 -> ( trigger0 ’=1) & (c3 ’=3); [] turn =3 & c3 =2 & mod( floor ( pin / mask ) ,2)=1 -> ( trigger1 ’=1) & (c3 ’=3); [] turn =3 & c3 =3 & maintrigger =2 -> (c3 ’=4); [] turn =3 & c3 =3 & maintrigger !=2 -> 0.5:( turn ’=1) + 0.5:( turn ’=2); [] turn =3 & c3 =4 -> (mask ’= floor ( mask /2)) & (c3 ’=0); [] turn =3 & c3 =5 -> ( trigger0 ’=1) & (c3 ’=6); [] turn =3 & c3 =6 -> ( trigger1 ’=1) ; endmodule init mask =2 & result =0 & maintrigger =0 & trigger0 =0 & trigger1 =0 & c1 =0 & c2 =0 & c3 =0 & turn =3 endinit
References
- Mastroeni, I.; Pasqua, M. Statically Analyzing Information Flows: An Abstract Interpretation-based Hyperanalysis for Non-interference. In Proceedings of the 34th ACM/SIGAPP Symposium on Applied Computing, SAC ’19, Limassol, Cyprus, 8–12 April 2019; pp. 2215–2223. [Google Scholar] [CrossRef]
- Smith, G. Principles of secure information flow analysis. In Malware Detection; Springer: Berlin/Heidelberg, Germany, 2007; pp. 291–307. [Google Scholar]
- Sabelfeld, A.; Myers, A.C. Language-based information-flow security. IEEE J. Sel. Areas Commun. 2003, 21, 5–19. [Google Scholar] [CrossRef]
- McLean, J. Proving noninterference and functional correctness using traces. J. Comput. Secur. 1992, 1, 37–57. [Google Scholar] [CrossRef]
- Roscoe, A.W. CSP and determinism in security modelling. In Proceedings of the 1995 IEEE Symposium on Security and Privacy, Oakland, CA, USA, 8–10 May 1995; pp. 114–127. [Google Scholar]
- Zdancewic, S.; Myers, A.C. Observational determinism for concurrent program security. In Proceedings of the 16th IEEE Computer Security Foundations Workshop, CSFW’03, Pacific Grove, CA, USA, 30 June–2 July 2003; pp. 29–43. [Google Scholar]
- Huisman, M.; Worah, P.; Sunesen, K. A temporal logic characterisation of observational determinism. In Proceedings of the 19th IEEE workshop on Computer Security Foundations, CSFW’06, Venice, Italy, 5–7 July 2006. [Google Scholar]
- Terauchi, T. A type system for observational determinism. In Proceedings of the 21st IEEE Computer Security Foundations Symposium, CSF’08, Pittsburgh, PA, USA, 23–25 June 2008; pp. 287–300. [Google Scholar]
- Huisman, M.; Blondeel, H.C. Model-checking secure information flow for multi-threaded programs. In Proceedings of the Joint Workshop on Theory of Security and Applications, TOSCA’11, Saarbrücken, Germany, 31 March–1 April 2011; Springer: Berlin/Heidelberg, Germany, 2012; pp. 148–165. [Google Scholar]
- Ngo, T.M.; Stoelinga, M.; Huisman, M. Effective verification of confidentiality for multi-threaded programs. J. Comput. Secur. 2014, 22, 269–300. [Google Scholar] [CrossRef]
- Bischof, S.; Breitner, J.; Graf, J.; Hecker, M.; Mohr, M.; Snelting, G. Low-deterministic security for low-nondeterministic programs. J. Comput. Secur. 2018, 1–32. [Google Scholar]
- Datta, A.; Franklin, J.; Garg, D.; Jia, L.; Kaynar, D. On Adversary Models and Compositional Security. IEEE Secur. Priv. 2011, 9, 26–32. [Google Scholar] [CrossRef]
- Sabelfeld, A.; Sands, D. Probabilistic noninterference for multi-threaded programs. In Proceedings of the 13th IEEE Workshop on Computer Security Foundations, CSFW’00, Cambridge, UK, 3–5 July 2000; pp. 200–214. [Google Scholar]
- Balliu, M. Logics for Information Flow Security: From Specification to Verification. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2014. [Google Scholar]
- Russo, A.; Hughes, J.; Naumann, D.; Sabelfeld, A. Closing internal timing channels by transformation. In Proceedings of the Annual Asian Computing Science Conference, Doha, Qatar, 9–11 December 2006; pp. 120–135. [Google Scholar]
- Mantel, H.; Sudbrock, H. Flexible scheduler-independent security. In Proceedings of the 15th European Conference on Research in Computer Security, ESORICS’10, Athens, Greece, 20–22 September 2010; pp. 116–133. [Google Scholar]
- Boudol, G.; Castellani, I. Noninterference for concurrent programs and thread systems. Theor. Comput. Sci. 2002, 281, 109–130. [Google Scholar] [CrossRef]
- Smith, G. Probabilistic noninterference through weak probabilistic bisimulation. In Proceedings of the 16th IEEE Workshop on Computer Security Foundations, CSFW’03, Pacific Grove, CA, USA, 30 June–2 July 2003; pp. 3–13. [Google Scholar]
- Baier, C.; Katoen, J.P. Principles of Model Checking; MIT Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Dabaghchian, M.; Abdollahi Azgomi, M. Model checking the observational determinism security property using PROMELA and SPIN. Form. Asp. Comput. 2015, 27, 789–804. [Google Scholar] [CrossRef]
- Giffhorn, D.; Snelting, G. A new algorithm for low-deterministic security. Int. J. Inf. Secur. 2015, 14, 263–287. [Google Scholar] [CrossRef]
- Volpano, D.; Irvine, C.; Smith, G. A sound type system for secure flow analysis. J. Comput. Secur. 1996, 4, 167–187. [Google Scholar] [CrossRef]
- Smith, G.; Volpano, D. Secure information flow in a multi-threaded imperative language. In Proceedings of the 25th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL’98, San Diego, CA, USA, 19–21 January 1998; pp. 355–364. [Google Scholar]
- Volpano, D.; Smith, G. Probabilistic noninterference in a concurrent language. J. Comput. Secur. 1999, 7, 231–253. [Google Scholar] [CrossRef]
- Barthe, G.; D’Argenio, P.R.; Rezk, T. Secure information flow by self-composition. In Proceedings of the 17th IEEE Workshop on Computer Security Foundations, CSFW’04, Washington, DC, USA, 28–30 June 2004; pp. 100–114. [Google Scholar]
- Clarkson, M.R.; Finkbeiner, B.; Koleini, M.; Micinski, K.K.; Rabe, M.N.; Sánchez, C. Temporal logics for hyperproperties. In Proceedings of the Third International Conference on Principles of Security and Trust, POST’14, Grenoble, France, 5–13 April 2014; pp. 265–284. [Google Scholar]
- Pnueli, A. The temporal logic of programs. In Proceedings of the 18th Annual Symposium on Foundations of Computer Science (SFCS 1977), Providence, RI, USA, 30 September–31 October 1977; pp. 46–57. [Google Scholar] [CrossRef]
- Finkbeiner, B.; Hahn, C.; Stenger, M.; Tentrup, L. Monitoring Hyperproperties. In Runtime Verification; Lahiri, S., Reger, G., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 190–207. [Google Scholar]
- Hahn, C.; Stenger, M.; Tentrup, L. Constraint-Based Monitoring of Hyperproperties. In Tools and Algorithms for the Construction and Analysis of Systems; Vojnar, T., Zhang, L., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 115–131. [Google Scholar]
- Groote, J.F.; Vaandrager, F. An efficient algorithm for branching bisimulation and stuttering equivalence. In Proceedings of the 17th International Colloquium on Automata, Languages and Programming, Coventry, UK, 16–20 July 1990; pp. 626–638. [Google Scholar]
- Kwiatkowska, M.; Norman, G.; Parker, D. PRISM 4.0: Verification of Probabilistic Real-time Systems. In Proceedings of the 23rd International Conference on Computer Aided Verification, CAV’11, Snowbird, UT, USA, 14–20 July 2011; Gopalakrishnan, G., Qadeer, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6806, pp. 585–591. [Google Scholar]
- Ngo, T.M. Qualitative and Quantitative Information Flow Analysis for Multi-Thread Programs. Ph.D Thesis, University of Twente, Enschede, The Netherlands, 2014. [Google Scholar]
- Blom, S.; van de Pol, J.; Weber, M. LTSmin: Distributed and Symbolic Reachability. In Computer Aided Verification; Touili, T., Cook, B., Jackson, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 354–359. [Google Scholar]
- Flanagan, C.; Freund, S.N.; Qadeer, S. Thread-modular verification for shared-memory programs. In Proceedings of the 11th European Symposium on Programming Languages and Systems, ESOP’02, Grenoble, France, 8–12 April 2002; Springer: Berlin/Heidelberg, Germany, 2002; pp. 262–277. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noroozi, A.A.; Karimpour, J.; Isazadeh, A. Bisimulation for Secure Information Flow Analysis of Multi-Threaded Programs. Math. Comput. Appl. 2019, 24, 64. https://doi.org/10.3390/mca24020064
Noroozi AA, Karimpour J, Isazadeh A. Bisimulation for Secure Information Flow Analysis of Multi-Threaded Programs. Mathematical and Computational Applications. 2019; 24(2):64. https://doi.org/10.3390/mca24020064
Chicago/Turabian StyleNoroozi, Ali A., Jaber Karimpour, and Ayaz Isazadeh. 2019. "Bisimulation for Secure Information Flow Analysis of Multi-Threaded Programs" Mathematical and Computational Applications 24, no. 2: 64. https://doi.org/10.3390/mca24020064
APA StyleNoroozi, A. A., Karimpour, J., & Isazadeh, A. (2019). Bisimulation for Secure Information Flow Analysis of Multi-Threaded Programs. Mathematical and Computational Applications, 24(2), 64. https://doi.org/10.3390/mca24020064




