1. Introduction
This paper concerns the numerical solution of nonlinear equations of the general form . Such equations appear in real world problems frequently while there is no closed form solution for them. That is why the numerical solution of these types of equations draws much attention nowadays. One of the common problems encountered in science and engineering is: given a single variable function , find the values of x for which . The root of such nonlinear equations may be real or complex. There are two general types of methods available to find the roots of algebraic and transcendental equations. One of them is the direct methods which are not always applicable to find the roots and the other one is iterative methods based on the concept of successive approximation. In the second type, the general procedure for solving is to start with some initial approximation near to the root and attain a sequence of iterates which in the limit converges to the true solution. The most efficient existing root-solvers are based on multi-point iterations since they overcome theoretical limits of one-point methods concerning the convergence order and computational efficiency.
To determine the solution of nonlinear equations, many iterative methods have been proposed in [
1,
2,
3] and the references therein. Construction of iterative methods for nonlinear equations is one of the vital area of research in numerical analysis. Among them, the most familiar iterative without memory method is the Newton–Raphson method which is given by
This method is an optimal method with efficiency index (EI) 1.414. Another well known method is the Halley’s iteration method given by
To accelerate the convergence of Newton’s method, many authors have modified it as we can see in [
4,
5]. Significant among them is the Arithmetic mean Newton’s method (
) [
5] and the other one is the Harmonic mean Newton’s method both having cubic convergence. These two-step methods are respectively given as follows:
The efficiency index of the methods (
3) and (
4) is 1.442 with three function evaluations per iteration.
Recently, some fourth and eighth order optimal iterative methods have been developed in [
6,
7]. A more extensive list of references as well as a survey on the progress made in the class of multi-point methods is found in the recent book by Petkovic et al. [
8]. In the recent past, many higher order optimal and non-optimal iterative methods have been developed using the idea of weight functions (see [
7,
9,
10,
11,
12,
13]).
The main objective of this paper is to construct multi-step iterative formula without memory with improved convergence and better efficiency index. Therefore, we have presented three new Newton-type iterative methods having fifth, eighth and fourth order convergence whose efficiency indices are 1.495, 1.516 and 1.587 respectively. Among these three methods, fourth order method is a class of optimal method.
Section 2 discusses the preliminaries and
Section 3 presents the construction of new methods.
Section 4 analyses the convergence order of the proposed methods. In
Section 5, the performances of new methods are compared with some well known equivalent methods. Seven real life application problems are taken in
Section 6, where all the listed methods and the proposed methods are numerically verified. Finally, conclusions are given in
Section 7.
5. Numerical Examples
In this section, several numerical examples are considered to confirm the convergence order and to illustrate the performance of the new methods
,
and
. The new methods are compared with some existing methods such as
,
,
,
,
,
,
and
which are given below. Note that all computations are carried out using variable precision arithmetic that uses floating point representation with 500 decimal accuracy using the
Matlab software. The number of iterations
,
and cpu time in seconds are listed under the condition that
, where
. In addition, to testify the theoretical order of convergence, we calculate the computational order of convergence
defined by
For demonstrating numerical results of equivalent methods, we have given below a few methods from literature:
A fourth order optimal method proposed by Sharifi–Babajee–Soleymani (
) [
19] is given by
Another fourth order optimal method proposed by Chun et al. (
) [
20] is given by
A fifth order method proposed by Liang Fang et al. (
) [
21] is given by
An optimal eighth order method proposed by Petkovic et al. (8
thPNPDM) [
8] is given by
A non-optimal eighth order method proposed by Parimala et al. (8
thPKJ) [
22] is given by
The following examples are used for numerical verification:
Table 1 shows the efficiency index of the new methods with some known methods.
Table 2 and
Table 3 display initial value
, number of iteration (N), computational order of convergence (
),
and CPU time (in seconds) for all the listed methods. From the computational results, we observe that all the proposed methods
,
and
have a lower number of iterations when compared to the other equivalent methods for most of the test functions. In addition, it can be seen that the computational order of convergence perfectly coincides with the theoretical results. Based on the numerical results, it is observed that the presented methods produce converging roots for all the functions, whereas
method and
method diverge for the functions
,
,
and
,
,
respectively.
6. Some Real Life Applications
In this section we give some applications and compare the proposed methods to other well known methods:
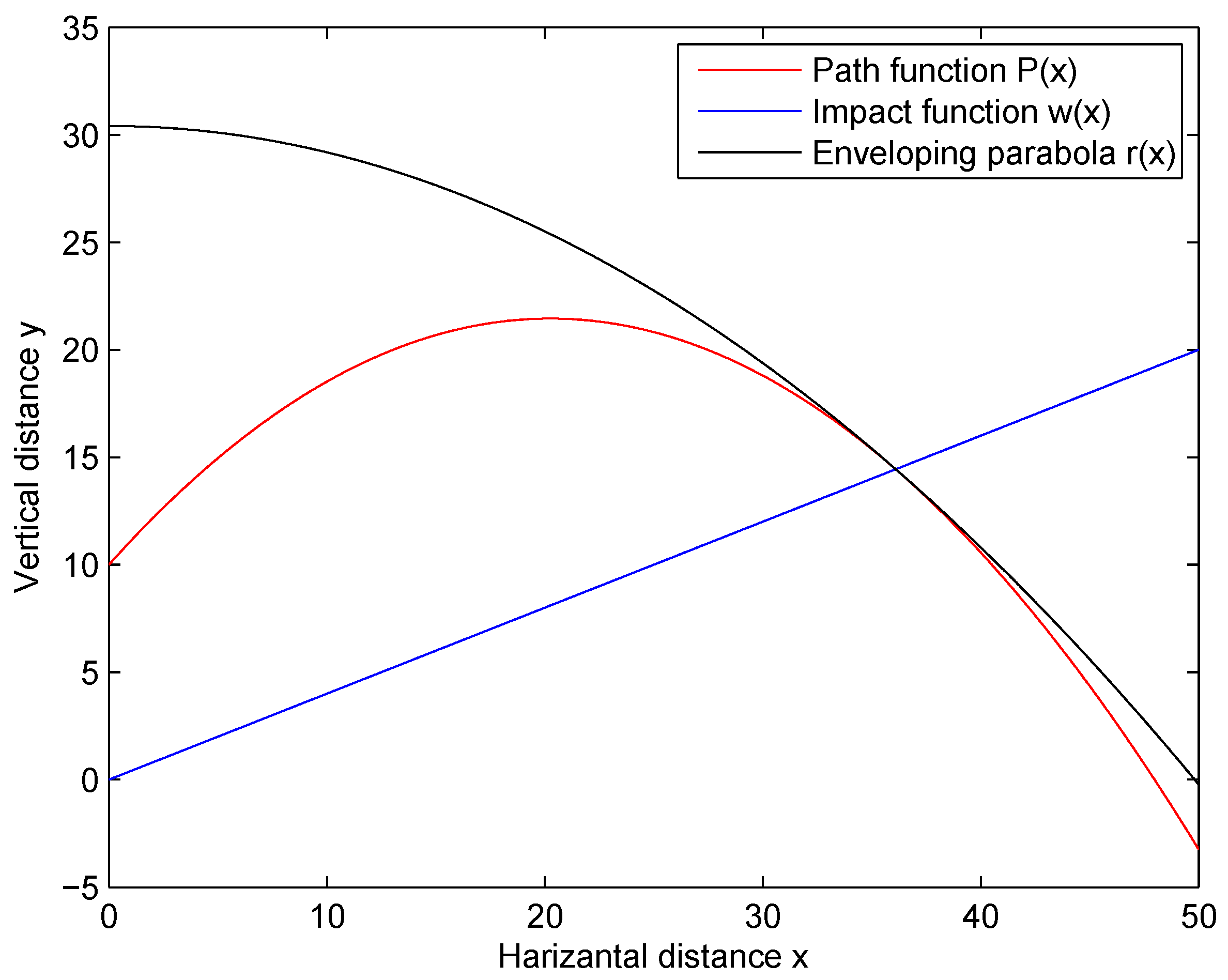
Application 1: We consider the classical projectile problem [
23] in which a projectile is launched from a tower of height
, with initial speed
v and at an angle
with respect to the horizontal distance onto a hill, which is defined by the function
, called the impact function which is dependent on the horizontal distance,
x. We wish to find the optimal launch angle
which maximizes the horizontal distance. In our calculations, we neglect air resistance.
The path function
that describes the motion of the projectile is given by
When the projectile hits the hill, there is a value of
x for which
for each value of
x. We wish to find the value of
that maximizes
x.
Differentiating Equation (
29) implicitly w.r.t.
, we have
Setting
in Equation (
30), we have
or
An enveloping parabola is a path that encloses and intersects all possible paths. This enveloping parabola is obtained by maximizing the height of the projectile for a given horizontal distance
x which will give the path that encloses all possible paths. Let
, then Equation (
28) becomes
Differentiating Equation (
33) w.r.t.
w and setting
, Henelsmith obtained
so that the enveloping parabola is defined by
.
The solution to the projectile problem requires first finding
which satisfies
and solving for
in Equation (
32) because we want to find the point at which the enveloping parabola
intersects the impact function
, and then find
that corresponds to this point on the enveloping parabola. We choose a linear impact function
with
and
. We let
. Then we apply our I.F.s starting from
to solve the non-linear equation
whose root is given by
and
.
Figure 1 shows the intersection of the path function, the enveloping parabola and the linear impact function for this application when
method is applied.
Application 2: The depth of embedment
x if a sheet-pile wall is governed by the equation [
24]:
An engineer has estimated the depth to be . Here we find the root of the equation with initial guess 2.5 and compare some well known methods to our methods.
Application 3: The vertical stress
generated at point in an elastic continuum under the edge of a strip footing supporting a uniform pressure
q is given by Boussinesq’s formula [
24] to be:
A scientist is interested to estimate the value of
x at which the vertical stress
will be 25 percent of the footing stress
q. Initially it is estimated that
. The above can be rewritten for
being equal to 25 percent of the footing stress
q:
Now we find the root of the equation with initial guess 0.4 and compare some well known methods to our methods.
Application 4: Generally, many problems in scientific and engineering which involve determination of any unknown appearing implicitly give rise to a root-finding problem. The Planck’s radiation law problem appearing in [
25,
26] is one among them and it is given by
which calculates the energy density within an isothermal blackbody. Here,
is the wavelength of the radiation;
T is the absolute temperature of the blackbody;
k is Boltzmann’s constant;
h is the Planck’s constant; and
c is the speed of light. Suppose we would like to determine wavelength
, which corresponds to maximum energy density
. From Equation (
35), we get
It can be checked that a maxima for occurs when , that is when
Here, taking
, the above equation becomes
The aim is to find a root of the equation
. Obviously, one of the root
is not taken for discussion. As argued in [
25], the left-hand side of Equation (
36) is zero for
and
. Hence, it is expected that another root of the equation
might occur near
. The approximate root of the Equation (
37) is given by
. Consequently, the wavelength of radiation (
) corresponding to which the energy density is maximum is approximated as
.
Application 5: Study of the multipactor effect [
27]:
The trajectory of an electron in the air gap between two parallel plates is given by
where
is the
electric field between plates at time
,
and
are the position and velocity of the electron,
e and
m are the charge and mass of the electron at rest respectively. For the particular parameters, one can deal with a simpler expression as follows:
The required zero of the above function is .
Application 6: Van der Waals equation representing a real gas is given by [
28]:
Here,
a and
b are parameters specific for each gas. This equation reduces to a nonlinear equation given by
By using the particular values for unknown constants, one can obtain the following nonlinear function
having three zeros. Out of them, two are complex zeros and the third one is a real zero. However, our desired root is
Application 7: Fractional conversion in a chemical reactor [
29]: In the following expression
x represents the fractional conversion of species A in a chemical reactor. Our required zero to this problem is
.
Table 4,
Table 5,
Table 6,
Table 7,
Table 8,
Table 9 and
Table 10 display the numerical results with respect to number of iterations (
N),
, order of convergence
and CPU time (in seconds). The numerical experiments of the above real life problems demonstrate the validity and applicability of the proposed methods. It is observed that the presented methods take less CPU time and equal number of iterations among the equivalent compared methods. This shows that the proposed methods are very much suitable for all the application problems. In most of the cases, the proposed methods show better performance in comparison to the existing methods.