Data-Driven Microstructure Property Relations
Abstract
1. Introduction
2. Materials and Methods
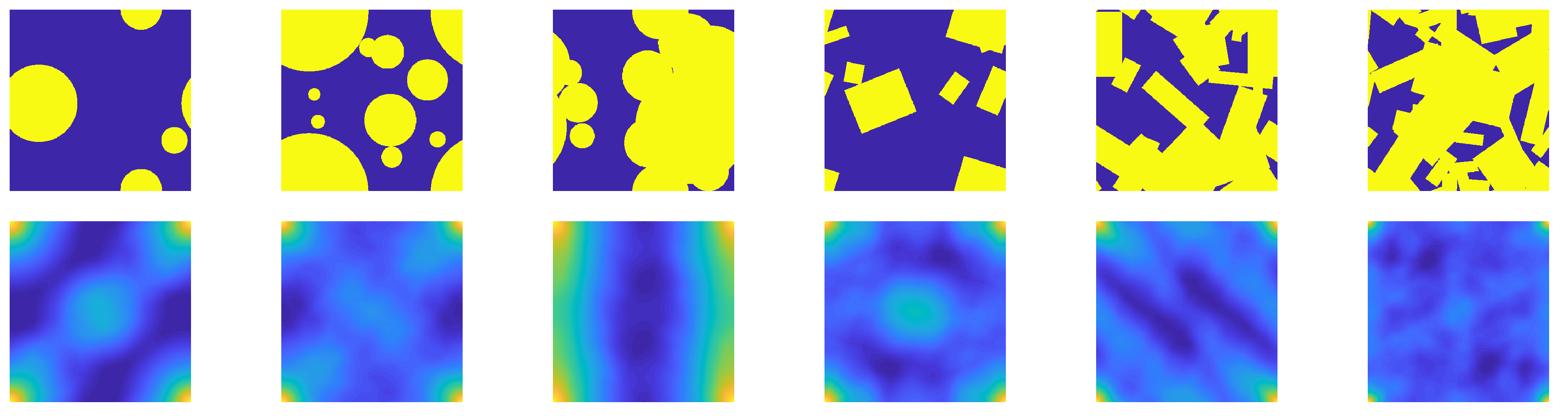
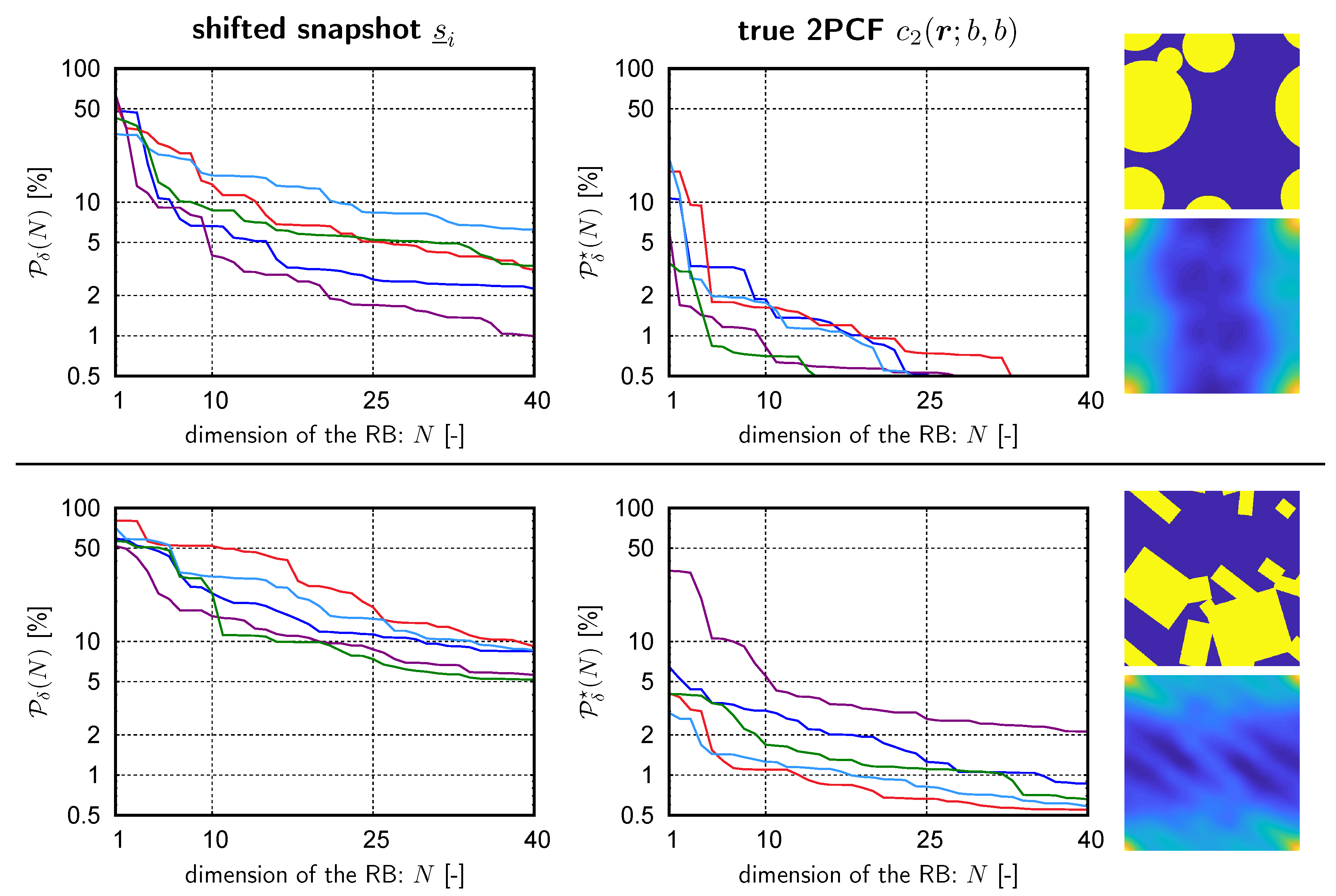
2.1. Microstructure Classification
- The maximum of occurs at the corners of the domain (corresponding to );
- Preferred directions of the inclusion placement and/or orientation correspond to laminate-like images (best seen in the third microstructure from the left);
- The domain around partially reflects the average inclusion shape;
- Some similarities are found, particularly with respect to shape of the 2PCF at the corners and in the center.
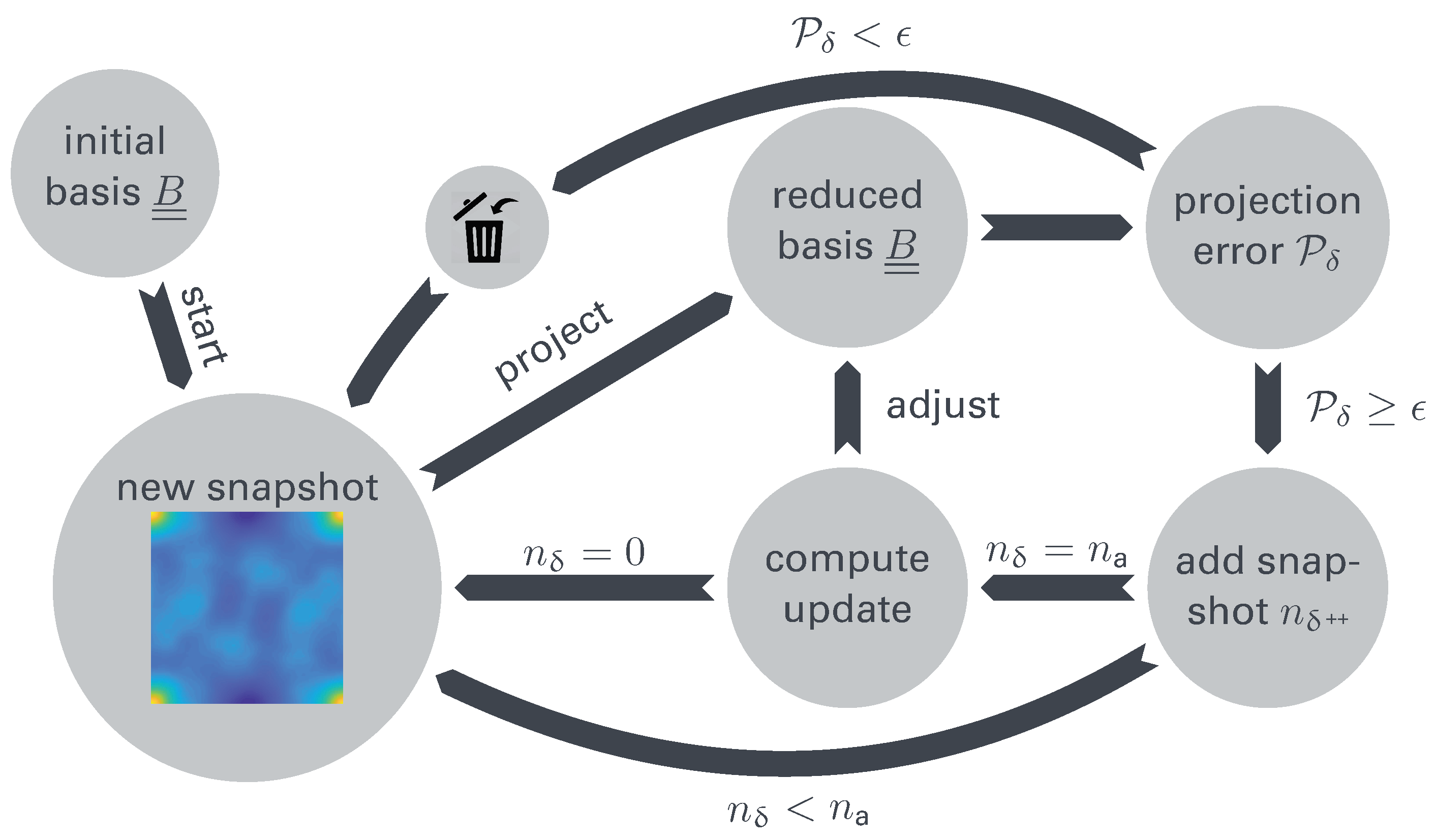
2.2. Unsupervised Learning via Snapshot Proper Orthogonal Decomposition
2.3. Incremental Generation of the Reduced Basis
2.3.1. Method A: Append Eigenmodes to
Remarks on Method A
- A.1
- The truncation parameter must be chosen carefully such thatIn particular, the normalization with respect to the original data prior to projection onto the existing RB must be taken.
- A.2
- By appending orthonormal modes to the existing basis it is a priori guaranteed that the accuracy of previously considered snapshots cannot worsen, i.e., an upper bound for the relative projection error of all snapshots considered until termination of the algorithm is given by the truncation parameter and :This estimate is, however, overly pessimistic and it must be noted that the enrichment will guarantee a drop in the residual for all snapshots contained in
2.3.2. Method B: Approximate Reconstruction of the Snapshot Correlation Matrix
Remarks on Method B
- B.1
- The existing RB is not preserved but it is updated using the newly available information. Thereby, the accuracy of the RB for the approximation of the previous snapshots is not guaranteed a priori. However, numerical experiments have shown no increase in the approximation errors of previously well-approximated snapshots.
- B.2
- In contrast to Method A the dimension of the RB can remain constant, i.e., a mere adjustment of existing modes is possible. The average number of added modes per enrichment is well below that of Method A.
- B.3
- The additional storage requirements are tolerable and the additional computations are of low algorithmic complexity. In particular, the correlation matrix consists of a diagonal block complemented by a dense rectangular block, rendering the eigenvalue decomposition more affordable.
2.3.3. Method C: Incremental SVD
Remarks on Method C
- C.1
- As highlighted for Method B (see remark B.1), the existing RB is not preserved but adjusted by considering the newly added information. A priori guarantees regarding the subset approximation accuracy can not be made, i.e., the approximation error of the previous snapshots could theoretically worsen. However, our numerical experiments did not exhibit such behavior at any point.
- C.2
- In contrast to Method A the dimension of the RB can remain constant, i.e., a mere adjustment of existing modes is possible. The average number of added modes per enrichment is well below that of Method A.
- C.3
- Each update step in (38) is computed separately and, consequently, storing is not required since only the RB is of interest.
- C.4
- The diagonal matrix has low storage requirements corresponding to that of a vector in .
3. Supervised Learning Using Feed Forward Neural Network
4. Results
4.1. Generation of Synthetic Microstructures
- M.1
- The phase volume fraction of the inclusions (0.2–0.8);
- M.2
- The size of each inclusion (0.0–1.0);
- M.3
- For rectangles: The orientation (0–) and the aspect ratio (1.0–10.0);
- M.4
- The admissible relative overlap for each inclusion (0.0–1.0).
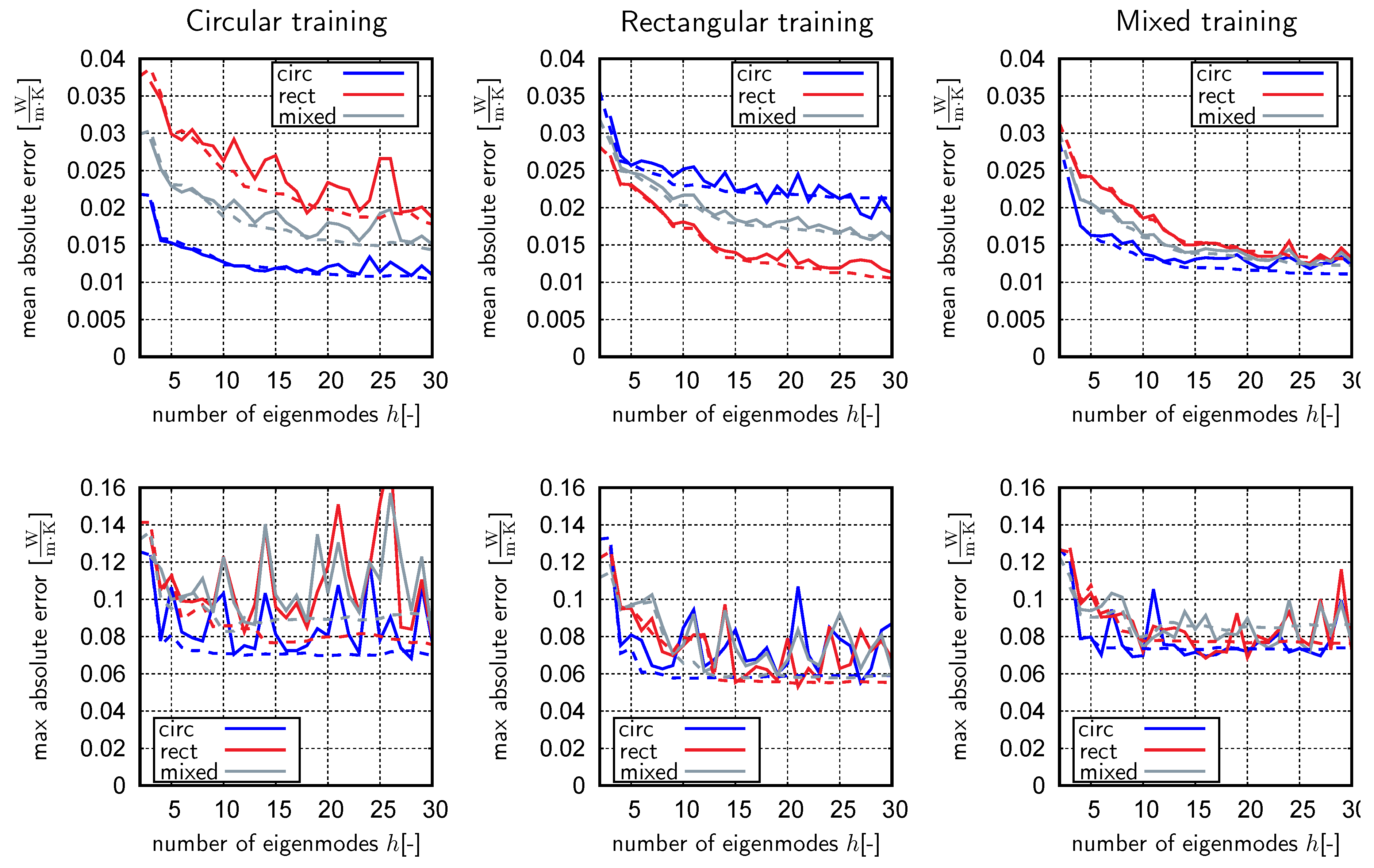
4.2. Unsupervised Learning
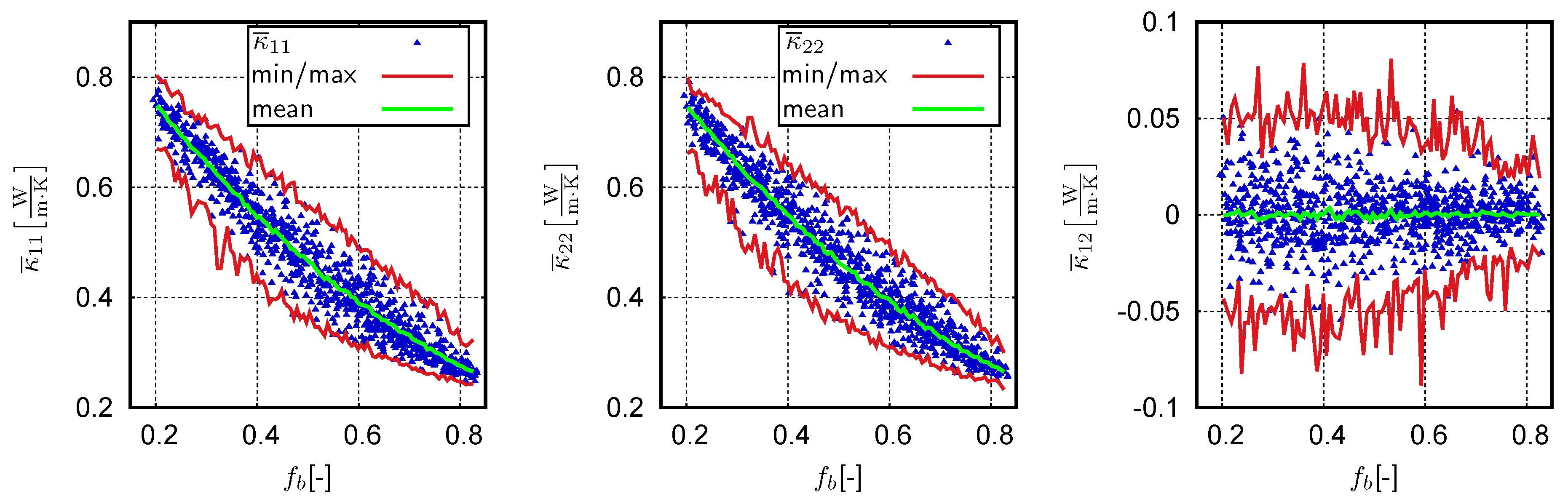
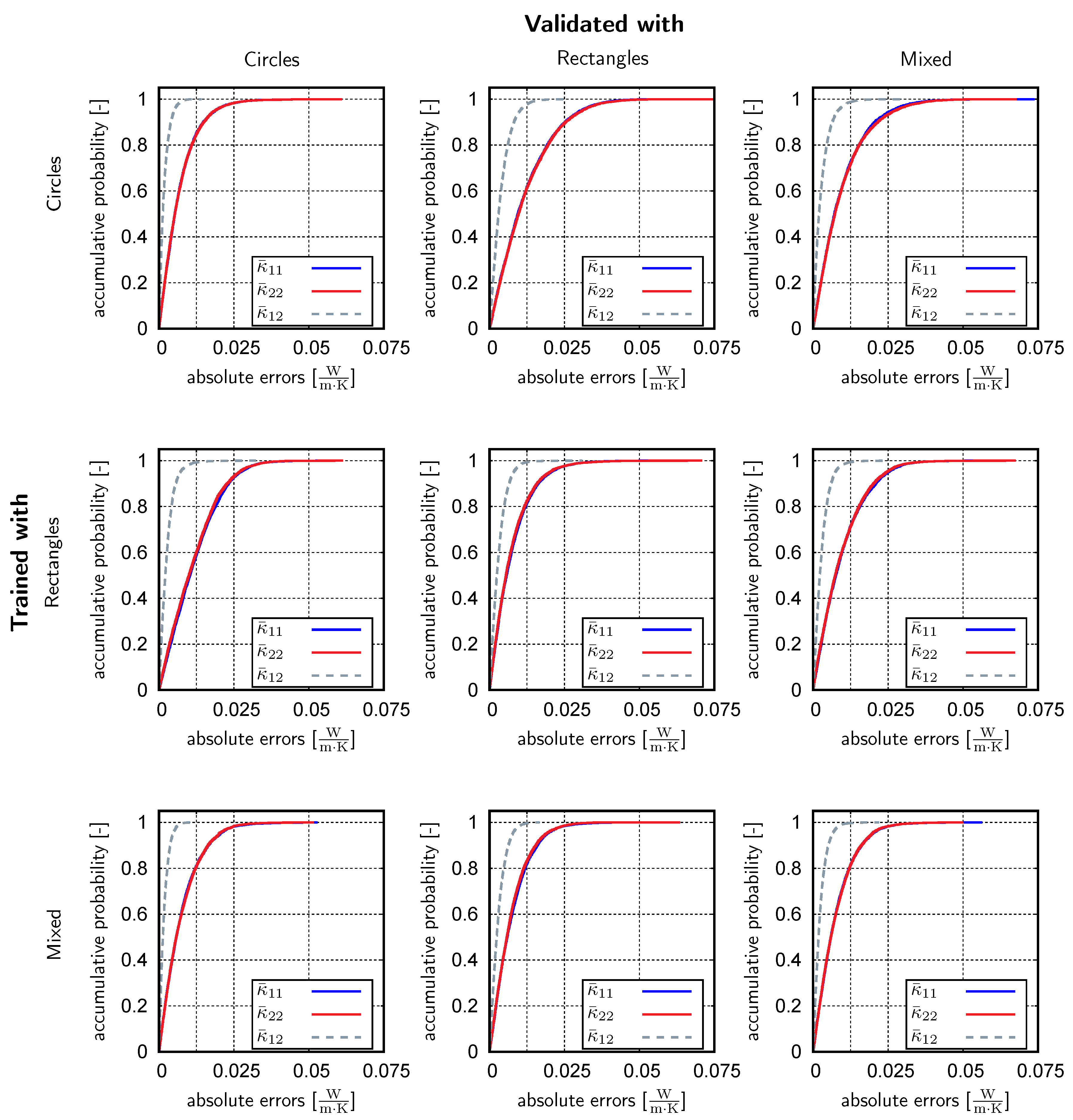
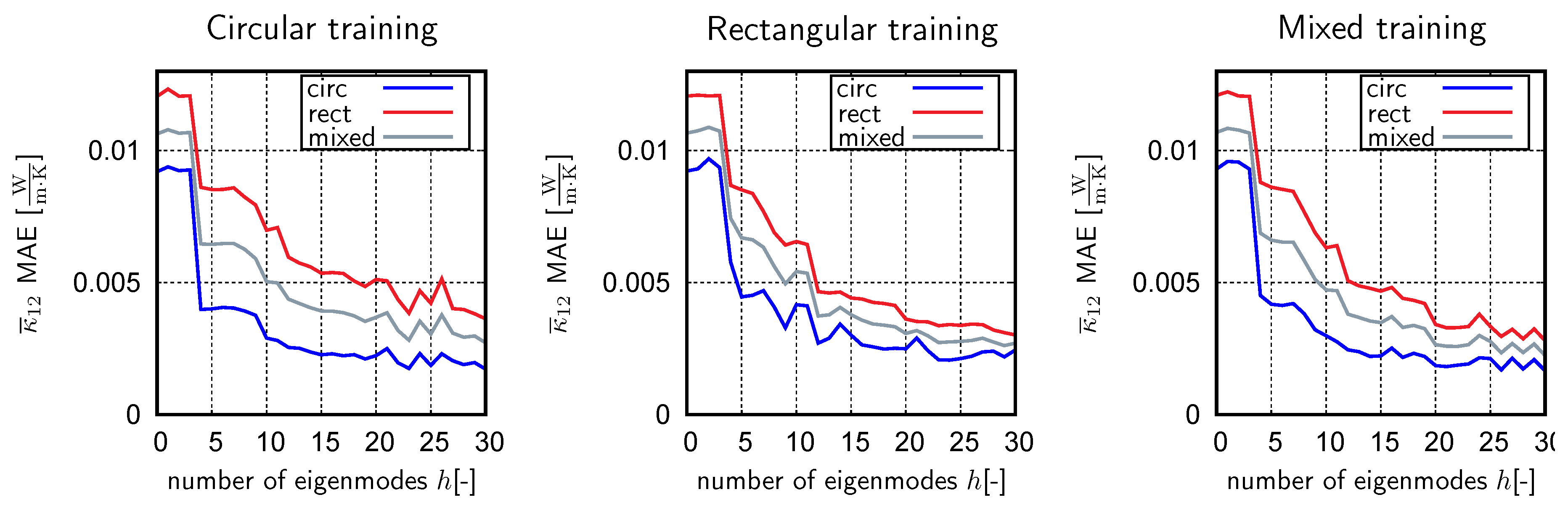
4.3. Supervised Learning
5. Computational Effort
6. Conclusions
6.1. Summary and Concluding Remarks
6.2. Discussion and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ghosh, S.; Lee, K.; Moorthy, S. Multiple scale analysis of heterogeneous elastic structures using homogenization theory and Voronoi cell finite element method. Int. J. Solids Struct. 1995, 32, 27–62. [Google Scholar] [CrossRef]
- Dhatt, G.; Lefrançois, E.; Touzot, G. Finite Element Method; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Leuschner, M.; Fritzen, F. Fourier-Accelerated Nodal Solvers (FANS) for homogenization problems. Comput. Mech. 2018, 62, 359–392. [Google Scholar] [CrossRef]
- Torquato, S. Random Heterogeneous Materials: Microstructure and Macroscopic Properties; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Jiang, M.; Alzebdeh, K.; Jasiuk, I.; Ostoja-Starzewski, M. Scale and boundary condition effects in elastic properties of random composites. Acta Mech. 2001, 148, 63–78. [Google Scholar] [CrossRef]
- Feyel, F. Multiscale FE2 elastoviscoplastic analysis of composite structures. Comput. Mater. Sci. 1999, 16, 344–354. [Google Scholar] [CrossRef]
- Miehe, C. Strain-driven homogenization of inelastic microstructures and composites based on an incremental variational formulation. Int. J. Numer. Methods Eng. 2002, 55, 1285–1322. [Google Scholar] [CrossRef]
- Beyerlein, I.; Tomé, C. A dislocation-based constitutive law for pure Zr including temperature effects. Int. J. Plast. 2008, 24, 867–895. [Google Scholar] [CrossRef]
- Ryckelynck, D. Hyper-reduction of mechanical models involving internal variables. Int. J. Numer. Methods Eng. 2009, 77, 75–89. [Google Scholar] [CrossRef]
- Hernández, J.; Oliver, J.; Huespe, A.; Caicedo, M.; Cante, J. High-performance model reduction techniques in computational multiscale homogenization. Comput. Methods Appl. Mech. Eng. 2014, 276, 149–189. [Google Scholar] [CrossRef]
- Fritzen, F.; Hodapp, M. The Finite Element Square Reduced (FE2R) method with GPU acceleration: Towards three-dimensional two-scale simulations. Int. J. Numer. Methods Eng. 2016, 107, 853–881. [Google Scholar] [CrossRef]
- Leuschner, M.; Fritzen, F. Reduced order homogenization for viscoplastic composite materials including dissipative imperfect interfaces. Mech. Mater. 2017, 104, 121–138. [Google Scholar] [CrossRef]
- Yvonnet, J.; He, Q.C. The reduced model multiscale method (R3M) for the non-linear homogenization of hyperelastic media at finite strains. J. Comput. Phys. 2007, 223, 341–368. [Google Scholar] [CrossRef]
- Kunc, O.; Fritzen, F. Finite strain homogenization using a reduced basis and efficient sampling. Math. Comput. Appl. 2019, 24, 56. [Google Scholar] [CrossRef]
- Kanouté, P.; Boso, D.; Chaboche, J.; Schrefler, B. Multiscale Methods For Composites: A Review. Arch. Comput. Methods Eng. 2009, 16, 31–75. [Google Scholar] [CrossRef]
- Matouš, K.; Geers, M.G.; Kouznetsova, V.G.; Gillman, A. A review of predictive nonlinear theories for multiscale modeling of heterogeneous materials. J. Comput. Phys. 2017, 330, 192–220. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Brough, D.B.; Wheeler, D.; Kalidindi, S.R. Materials knowledge systems in python—A data science framework for accelerated development of hierarchical materials. Integr. Mater. Manuf. Innov. 2017, 6, 36–53. [Google Scholar] [CrossRef] [PubMed]
- Paulson, N.H.; Priddy, M.W.; McDowell, D.L.; Kalidindi, S.R. Reduced-order structure-property linkages for polycrystalline microstructures based on 2-point statistics. Acta Mater. 2017, 129, 428–438. [Google Scholar] [CrossRef]
- Gupta, A.; Cecen, A.; Goyal, S.; Singh, A.K.; Kalidindi, S.R. Structure–property linkages using a data science approach: Application to a non-metallic inclusion/steel composite system. Acta Mater. 2015, 91, 239–254. [Google Scholar] [CrossRef]
- Kalidindi, S.R. Computationally efficient, fully coupled multiscale modeling of materials phenomena using calibrated localization linkages. ISRN Mater. Sci. 2012, 2012, 1–13. [Google Scholar] [CrossRef]
- Bostanabad, R.; Bui, A.T.; Xie, W.; Apley, D.W.; Chen, W. Stochastic microstructure characterization and reconstruction via supervised learning. Acta Mater. 2016, 103, 89–102. [Google Scholar] [CrossRef]
- Kumar, A.; Nguyen, L.; DeGraef, M.; Sundararaghavan, V. A Markov random field approach for microstructure synthesis. Model. Simul. Mater. Sci. Eng. 2016, 24, 035015. [Google Scholar] [CrossRef]
- Xu, H.; Liu, R.; Choudhary, A.; Chen, W. A machine learning-based design representation method for designing heterogeneous microstructures. J. Mech. Des. 2015, 137, 051403. [Google Scholar] [CrossRef]
- Xu, H.; Li, Y.; Brinson, C.; Chen, W. A descriptor-based design methodology for developing heterogeneous microstructural materials system. J. Mech. Des. 2014, 136, 051007. [Google Scholar] [CrossRef]
- Bessa, M.; Bostanabad, R.; Liu, Z.; Hu, A.; Apley, D.W.; Brinson, C.; Chen, W.; Liu, W.K. A framework for data-driven analysis of materials under uncertainty: Countering the curse of dimensionality. Comput. Methods Appl. Mech. Eng. 2017, 320, 633–667. [Google Scholar] [CrossRef]
- Basheer, I.A.; Hajmeer, M. Artificial neural networks: Fundamentals, computing, design, and application. J. Microbiol. Methods 2000, 43, 3–31. [Google Scholar] [CrossRef]
- Torquato, S.; Stell, G. Microstructure of two-phase random media. I. The n-point probability functions. J. Chem. Phys. 1982, 77, 2071–2077. [Google Scholar] [CrossRef]
- Berryman, J.G. Measurement of spatial correlation functions using image processing techniques. J. Appl. Phys. 1985, 57, 2374–2384. [Google Scholar] [CrossRef]
- Cooley, J.W.; Tukey, J.W. An Algorithm for the Machine Calculation of Complex Fourier Series. AMS Math. Comput. 1965, 19, 297–301. [Google Scholar] [CrossRef]
- Frigo, M.; Johnson, S.G. FFTW: An adaptive software architecture for the FFT. In Proceedings of the 1998 IEEE International Conference on Acoustics, Speech and Signal Processing, Seattle, WA, USA, 15 May 1998; Volume 3, pp. 1381–1384. [Google Scholar] [CrossRef]
- Fast, T.; Kalidindi, S.R. Formulation and calibration of higher-order elastic localization relationships using the MKS approach. Acta Mater. 2011, 59, 4595–4605. [Google Scholar] [CrossRef]
- Fullwood, D.T.; Niezgoda, S.R.; Kalidindi, S.R. Microstructure reconstructions from 2-point statistics using phase-recovery algorithms. Acta Mater. 2008, 56, 942–948. [Google Scholar] [CrossRef]
- Sirovich, L. Turbulence and the Dynamics of Coherent Structures. Part 1: Coherent Structures. Q. Appl. Math. 1987, 45, 561–571. [Google Scholar] [CrossRef]
- Liang, Y.; Lee, H.; Lim, S.; Lin, W.; Lee, K.; Wu, C. Proper Orthogonal Decomposition and Its Applications—Part I: Theory. J. Sound Vib. 2002, 252, 527–544. [Google Scholar] [CrossRef]
- Camphouse, R.C.; Myatt, J.; Schmit, R.; Glauser, M.; Ausseur, J.; Andino, M.; Wallace, R. A snapshot decomposition method for reduced order modeling and boundary feedback control. In Proceedings of the 4th Flow Control Conference, Seattle, WA, USA, 23–26 June 2008; p. 4195. [Google Scholar] [CrossRef][Green Version]
- Quarteroni, A.; Manzoni, A.; Negri, F. Reduced Basis Methods for Partial Differential Equations: An Introduction; Springer: Berlin, Germany, 2016. [Google Scholar]
- Klema, V.; Laub, A. The singular value decomposition: Its computation and some applications. IEEE Trans. Autom. Control 1980, 25, 164–176. [Google Scholar] [CrossRef]
- Gu, M.; Eisenstat, S.C. A Stable and Fast Algorithm for Updating the Singular Value Decomposition. Available online: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.46.9767 (accessed on 30 May 2019).
- Fareed, H.; Singler, J.; Zhang, Y.; Shen, J. Incremental proper orthogonal decomposition for PDE simulation data. Comput. Math. Appl. 2018, 75, 1942–1960. [Google Scholar] [CrossRef]
- Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Widrow, B.; Lehr, M.A. 30 years of adaptive neural networks: Perceptron, madaline, and backpropagation. Proc. IEEE 1990, 78, 1415–1442. [Google Scholar] [CrossRef]
- Kimoto, T.; Asakawa, K.; Yoda, M.; Takeoka, M. Stock market prediction system with modular neural networks. In Proceedings of the 1990 IJCNN International Joint Conference on Neural Networks, San Diego, CA, USA, 17–21 June 1990; pp. 1–6. [Google Scholar] [CrossRef]
- Sundermeyer, M.; Schlüter, R.; Ney, H. LSTM neural networks for language modeling. In Proceedings of the Thirteenth Annual Conference of the International Speech Communication Association, Portland, OR, USA, 9–13 September 2012; pp. 194–197. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Angermueller, C.; Pärnamaa, T.; Parts, L.; Stegle, O. Deep learning for computational biology. Mol. Syst. Biol. 2016, 12, 878. [Google Scholar] [CrossRef]
- Hecht-Nielsen, R. Theory of the backpropagation neural network. In Neural Networks for Perception; Elsevier: Cambridge, MA, USA, 1992; pp. 65–93. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. Tensorflow: A system for large-scale machine learning. OSDI 2016, 16, 265–283. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Bostanabad, R.; Kearney, T.; Tao, S.; Apley, D.W.; Chen, W. Leveraging the nugget parameter for efficient Gaussian process modeling. Int. J. Numer. Methods Eng. 2018, 114, 501–516. [Google Scholar] [CrossRef]
- An, S.; Kim, T.; James, D.L. Optimizing cubature for efficient integration of subspace deformations. ACM Trans. Graph. 2009, 27, 165. [Google Scholar] [CrossRef] [PubMed]
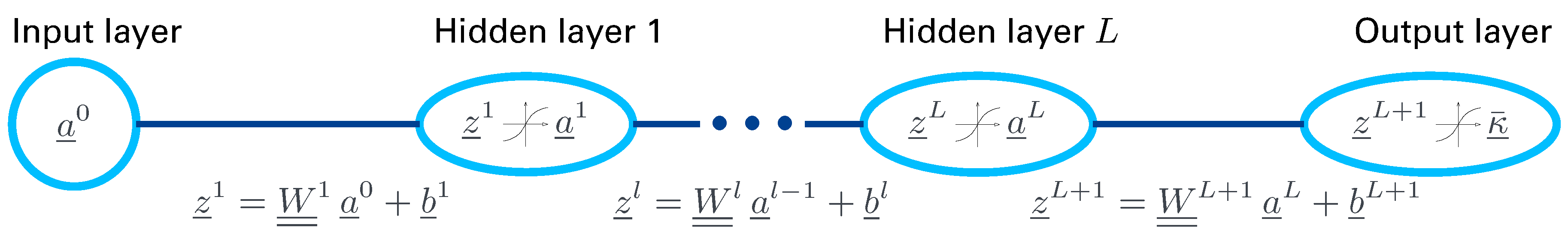





| Method | Final Basis Size | Snapshots with | Snapshots with | Enrichment Steps | Time [s] | Used Microstructures |
|---|---|---|---|---|---|---|
| A | 143 | 150 | 730 | 4 | 20 |  |
| B | 80 | 400 | 2400 | 7 | 70 | |
| C | 96 | 800 | 7700 | 12 | 200 | |
| A | 596 | 670 | 4500 | 11 | 150 |  |
| B | 294 | 2400 | 12,700 | 34 | 500 | |
| C | 312 | 2600 | 16,500 | 37 | 550 | |
| A | 464 | 560 | 2900 | 9 | 150 |  |
| B | 274 | 2000 | 16,100 | 29 | 500 | |
| C | 244 | 1540 | 8000 | 22 | 280 |
| Validated with | |||||||
|---|---|---|---|---|---|---|---|
| Circles | Rectangles | Mixed | |||||
| Trained with | Error Measures | ||||||
| Circles | Mean [%] | 1.58 | 1.57 | 2.60 | 2.62 | 2.11 | 2.14 |
| Max [%] | 12.8 | 12.5 | 13.9 | 13.0 | 14.7 | 11.7 | |
| Rectangles | Mean [%] | 2.68 | 2.57 | 1.60 | 1.58 | 2.14 | 2.09 |
| Max [%] | 12.9 | 11.7 | 12.5 | 12.0 | 13.8 | 13.0 | |
| Mixed | Mean [%] | 1.77 | 1.76 | 1.65 | 1.60 | 1.72 | 1.71 |
| Max [%] | 11.7 | 14.1 | 11.6 | 10.5 | 10.4 | 12.4 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lißner, J.; Fritzen, F. Data-Driven Microstructure Property Relations. Math. Comput. Appl. 2019, 24, 57. https://doi.org/10.3390/mca24020057
Lißner J, Fritzen F. Data-Driven Microstructure Property Relations. Mathematical and Computational Applications. 2019; 24(2):57. https://doi.org/10.3390/mca24020057
Chicago/Turabian StyleLißner, Julian, and Felix Fritzen. 2019. "Data-Driven Microstructure Property Relations" Mathematical and Computational Applications 24, no. 2: 57. https://doi.org/10.3390/mca24020057
APA StyleLißner, J., & Fritzen, F. (2019). Data-Driven Microstructure Property Relations. Mathematical and Computational Applications, 24(2), 57. https://doi.org/10.3390/mca24020057





