1. Introduction
There are two aspects of implementation of an algorithm. One is the illustration for the validity of the algorithm, and the other for the efficient exploitation of its steps thanks to the choice of suitable tools.
Remez’s minimax algorithm is well established (see Section 3.5 in [
1]), but all the steps to proceed it contain the two main obstacles when being performed in practice:
As a warning to experienced users, they should have close control of the evaluation error at almost every calculation for the above steps. Therefore, it could be difficult to effectively implement this algorithm for approximating the trigonometric functions themselves.
Here, we choose
Algorithm 2 in [
2] to be implemented with MAPLE (or any of Computer Algebra Systems (CAS), if possible), because it has the great advantage: only using arithmetic calculations on finite rational numbers and comparisons. The choice of MAPLE is due to its powerfulness of symbolic computation and its ability to display exact number of significant digits for the obtained numerical results. The description of
Algorithm 2 is clear, but examples on numerical integration and graphical plots in [
2] seem to be as of the first kind of implementation as mentioned above. Therefore, we come back to the article [
2] with aspiration to provide the beginners or occasional users with a complete MAPLE procedure, the output of which being easy and convenient to exploit when implementing
Algorithm 2.
From [
2], we have that the function
is piecewise approximated on an interval
by the polynomials
on the subintervals
,
, such that
, where
and
and
or
These approximations all have the accuracy of in absolute value for a given arbitrary positive integer r. The main purpose of Algorithm 2 is to give the pairs of , , and, as a convention, the notations of this output is used in the next sections.
The paper is organized as follows. In
Section 2, we construct a complete MAPLE procedure by blocks of commands so that we can modify them easily. These blocks whose purpose is clearly explained may be useful to design other procedures.
Section 3 is for exploitation of the obtained results from the output of the procedure.
Section 3 is the detailed discussion on how to find a desired estimate
p for the best
-approximation
of the sine function in the vector space
. In particular, it is possible to make a complete MAPLE procedure to find
p’s with different values of
ℓ from the existing materials, and we let the reader do it with his or her close control of evaluation error for the steps containing norms of vectors. Moreover, the crucial components of a procedure that computes approximate values of integration with integrands of the form
(
) are also provided.
Section 4 is the conclusion.
2. Implementation by MAPLE Procedures
We list here the MAPLE commands that appear in our procedures. They are all very important and frequently used in MAPLE programming:
add,
coeff,
Digits,
ERROR,
evalf,
floor,
for,
irem,
int,
nops,
op,
piecewise,
RETURN,
seq,
sort, and
while. A declaration to create a function, e.g.,
f, such as
f:=x->F(x) or
f:=unapply(F(x),x), where
F(x) is an expression in
x, is a very useful and convenient tool in MAPLE procedures for doing calculations. In addition, the conditional structure
if–
then is indispensable in branch programming, whereas the type
list is a flexible ordered arrangement of operands (or things and elements). See [
3,
4] and MAPLE help pages in each session to know more details about meaning, syntax and usage of these commands, structures and types.
In the following, we consider in succession the steps to perform
Algorithm 2 in [
2] with their content and corresponding MAPLE codes. However, we modify some steps in
Algorithm 2 to get the extraction results conveniently from its output. Firstly, we recall the two blocks of commands (inside steps) for getting the degree
n of the approximate polynomial
of the function
(Block 1), which satisfies the accuracy of
, and for finding the approximate values of
, which appear in
.
| Block 1 |
| n:=0: d:=1: |
| while (d>0) do |
| n:=n+1: |
| d:=(0.8)^(n+1)*10^(r+1)-(n+1)!; |
| end do: |
Block 2 is nothing but the full content of
FindPoint, a procedure to determine nodes of the form
, where
and
is an approximate value of
(see [
2]). These nodes are ending points of subintervals in the partition of an arbitrary interval
. The output of
FindPoint from its argument
y also gives the approximate polynomial
F. Moreover, we have them all together,
k,
and
F from a list of three components; that is, we may write
yk,
p’,
P] with
,
for all
and
.
| Block 2 |
| m:=r+2: |
| while ((b+3.2)*10^(r+3)-10^m>0) do |
| m:=m+1: |
| end do: |
| Digits:=m+4: |
| q:=evalf[m+3](Pi/2): |
| T:=x/q-floor(x/q): |
| if (T=0.5) then |
| k0:=floor(x/q): |
| else |
| while (2.4*10^m*min(T,0.5-T)-abs(x)<0) and |
| (2.4*10^m*min(1-T,T-0.5)-abs(x)<0) do |
| m:=m+1: Digits:=m+4: |
| q:=evalf[m+3](Pi/2): |
| T:=x/q-floor(x/q): |
| end do: |
| end if: |
| if (0.5<T) then |
| k0:=floor(x/q)+1: |
| else |
| k0:=floor(x/q): |
| end if: |
| if (irem(k0-1,2)=0) then |
| F:=unapply((-1)^((k0-1)/2)*add((-1)^s*(t-k0*q)^(2*s)/((2*s)!), |
| s=0..floor(n/2)),t): |
| else |
| F:=unapply((-1)^(k0/2)*add((-1)^s*(t-k0*q)^(2*s+1)/((2*s+1)!), |
| s=0..floor((n-1)/2)),t): |
| end if: |
| [k0,q,F]; |
Next, Block 3 that may be the most important one is designed to find approximate polynomials
, corresponding to intervals
, where
,
, are the nodes mentioned above. This block gives a so-called spreading technique that takes nodes together with the polynomials
, by using Block 2 successively, as clearly described in [
2]. We choose the output of Block 3 as a function of a finite sequence of lists given in the form of
This output has the advantages of a function itself or a sequence of terms, because we can take its values
and
, or its components (or operands)
as we want.
We design a MAPLE procedure named
ApproxFunct to give the approximate function
P for the sine function on an interval
for
. In the cases of
and
, we may set
on
and
on
, respectively, where
and
n is determined by Block 1. Before giving the MAPLE codes of Block 3 chosen as the full content of
TempApproxFunct, the procedure to give the approximation to the sine function on
only for
, we recall here (from [
2]) the important remark: if
are numbers such that
with
p’ =
FindPoint()[2],
p” =
FindPoint()[2], then we have |
α −
kp”| < 0.8 and |
β −
kp’| < 0.8.
| Block 3 |
| n0:=FindPoint(b)[1]: |
| p0:=FindPoint(b)[2]: |
| B0:=FindPoint(b)[3]: |
| i:=0: |
| k[i]:=FindPoint(a)[1]: |
| p[i]:=FindPoint(a)[2]: |
| A[i]:=FindPoint(a)[3]: |
| u:=k[i]: |
| if n0<=u then |
| H:=x->[[a,b],A[0](x)]: |
| RETURN(H); |
| end if: |
| while u<n0 do |
| i:=i+1: |
| k[i]:=FindPoint(k[i-1]*p[i-1]+p[i-1])[1]: |
| p[i]:=FindPoint(k[i-1]*p[i-1]+p[i-1])[2]: |
| A[i]:=FindPoint(k[i-1]*p[i-1]+p[i-1])[3]: |
| u:=k[i]: |
| end do: |
| if i=1 then |
| if b<=k[0]*p[0]+p[0]/2 then |
| H:=x->[[a,b],A[0](x)]: |
| RETURN(H); |
| elif b<=k[0]*p[0]+p[0] then |
| H:=x->([[a,k[0]*p[0]+p[0]/2],A[0](x)],[[k[0]*p[0]+p[0]/2,b],A[1](x)]): |
| RETURN(H); |
| else |
| H:=x->([[a,k[0]*p[0]+p[0]/2],A[0](x)],[[k[0]*p[0]+p[0]/2,k[0]*p[0]+p[0]], |
| A[1](x)],[[k[0]*p[0]+p[0],b],B0(x)]): |
| RETURN(H); |
| end if: |
| elif i=2 then |
| if b<=k[1]*p[1]+p[1]/2 then |
| H:=x->([[a,k[0]*p[0]+p[0]/2],A[0](x)],[[k[0]*p[0]+p[0]/2,b],A[1](x)]): |
| RETURN(H); |
| elif b<=k[1]*p[1]+p[1] then |
| H:=x->([[a,k[0]*p[0]+p[0]/2],A[0](x)],[[k[0]*p[0]+p[0]/2,k[1]*p[1]+p[1]/2], |
| A[1](x)],[[k[1]*p[1]+p[1]/2,b],A[2](x)]): |
| RETURN(H); |
| else |
| H:=x->([[a,k[0]*p[0]+p[0]/2],A[0](x)],[[k[0]*p[0]+p[0]/2,k[1]*p[1]+p[1]/2], |
| A[1](x)],[[k[1]*p[1]+p[1]/2,k[1]*p[1]+p[1]],A[2](x)],[[k[1]*p[1]+p[1],b],B0(x)]): |
| RETURN(H); |
| end if: |
| else |
| if b<=k[i-1]*p[i-1]+p[i-1]/2 then |
| H:=x->([[a,k[0]*p[0]+p[0]/2],A[0](x)],seq([[k[m-1]*p[m-1]+p[m-1]/2, |
| k[m]*p[m]+p[m]/2],A[m](x)],m=1..i-2),[[k[i-2]*p[i-2]+p[i-2]/2,b],A[i-1](x)]): |
| RETURN(H); |
| elif b<=k[i-1]*p[i-1]+p[i-1] then |
| H:=x->([[a,k[0]*p[0]+p[0]/2],A[0](x)],seq([[k[m-1]*p[m-1]+p[m-1]/2, |
| k[m]*p[m]+p[m]/2],A[m](x)],m=1..i-1),[[k[i-1]*p[i-1]+p[i-1]/2,b],A[i](x)]): |
| RETURN(H); |
| else |
| H:=x->([[a,k[0]*p[0]+p[0]/2],A[0](x)],seq([[k[m-1]*p[m-1]+p[m-1]/2, |
| k[m]*p[m]+p[m]/2],A[m](x)],m=1..i-1),[[k[i-1]*p[i-1]+p[i-1]/2,k[i]*p[i-1]], |
| A[i](x)],[[k[i]*p[i-1],b],B0(x)]): |
| RETURN(H); |
| end if: |
| end if: |
Note that TempApproxFunct takes three arguments in order as a, b and r. Next, we combine Block 1 and Block 3 with some conditional commands to form Block 4, which is the content of the ApproxFunct.
| Block 4 |
| G:=unapply(add((-1)^s*t^(2*s+1)/((2*s+1)!),s=0..floor((n-1)/2)),t): |
| if (a<0) then ERROR(‘1st argument must be nonegative’); |
| elif (a<0.8) then |
| if (b<=0.8) then |
| [[a,b],G]; |
| else |
| ([[a,0.8],G],TempApproxFunct(0.8,b,r)); |
| end if: |
| else |
| TempApproxFunct(a,b,r); |
| end if: |
Now, we may call ApproxFunct(a,b,r) to fully access all subintervals together with approximate polynomials for the accuracy of on an interval , . In particular, if we want to extract the jth interval and its corresponding approximate polynomial, use the calling sequence ApproxFunct(a,b,r)(x)[j], where j is chosen from the output ApproxFunct(a,b,r)(x).
Finally, from the above analysis, we obtain the desired procedure named
PiecewiseFunct (see the
supplementary material accompanying this paper for MAPLE codes), which gives a special partition of an arbitrary interval
into subintervals
[,] together with corresponding approximate polynomials
, where
with
. Here, there is a warning that, in MAPLE, if
A:=a,b,c,d or
A:=(a,b,c,d), we cannot determine
nops(A); however, we can if
A:=[a,b,c,d], so
. To all three settings for
A, we can select ordered elements of
A, namely
, for example.
Thus, a complete MAPLE procedure to perform
Algorithm 2 in [
2] is suggested to be
| The PiecewiseFunct procedure |
| PiecewiseFunct:=proc(a::realcons,b::realcons,r::posint) |
| local ApproxFunct,j,n,d,G,num,funct,intrv; |
| ApproxFunct:=proc(a::realcons,b::realcons,r::posint) |
| local TempApproxFunct,n,d,G;option remember; |
| TempApproxFunct:=proc(a::realcons,b::realcons,r::posint) |
| local i,p0,n0,B0,u,p,k,A,H,FindPoint;option remember; |
| FindPoint:=proc(x::realcons) |
| local m,q,n,d,k0,F,T;option remember; |
| Block 1 |
| Block 2 |
| end proc: |
| Block 3 |
| end proc: |
| Block 1 |
| Block 4 |
| end proc: |
| Block 1 |
| G:=unapply(add((-1)^s*t^(2*s+1)/((2*s+1)!),s=0..floor((n-1)/2)),t): |
| if (0<=a) then |
| ApproxFunct(a,b,r)(x); |
| elif (-0.8<=a) then |
| if (b<=0) then |
| [[a,b],G(x)]; |
| else |
| ([[a,0],G(x)],ApproxFunct(0,b,r)(x)); |
| end if: |
| else |
| if (b<=0) then |
| num:=nops([ApproxFunct(-b,-a,r)(-x)]): |
| for j from 1 to num do |
| funct[j]:=op(2,(-1)*ApproxFunct(-b,-a,r)(-x)[j]): |
| intrv[j]:=sort(op(1,(-1)*ApproxFunct(-b,-a,r)(-x)[j])): |
| end do: |
| seq([intrv[num+1-i],funct[num+1-i]],i=1..num); |
| else |
| num:=nops([ApproxFunct(0,-a,r)(-x)]): |
| for j from 1 to num do |
| funct[j]:=op(2,(-1)*ApproxFunct(0,-a,r)(-x)[j]): |
| intrv[j]:=sort(op(1,(-1)*ApproxFunct(0,-a,r)(-x)[j])): |
| end do: |
| (seq([intrv[num+1-i],funct[num+1-i]],i=1..num),ApproxFunct(0,b,r)(x)); |
| end if: |
| end if: |
| end proc: |
The last part of the
PiecewiseFunct procedure might need to be explained in more detail. In the case
, we make a partition first for the interval
; then, from the result of the partition, we take a sample of the form
and convert it into its symmetric part in the partition of
:
. Such a sample in MAPLE language is given by the declaration:
[intrv[j],funct[j]], where
Because the converted intervals should be arranged in the correct order on the real axis, we use the calling sequence seq([intrv[num+1-i],funct[num+1-i]],i=1..num).
In fact,
PiecewiseFunct contains a technique that indirectly solves a difficult problem “How to reduce values of arguments when doing calculations with the trigonometric functions”. There was a great attempt to solve the problem and perhaps [
1] would be one of the best reference books on this fact. However, this technique is only a suitable remedy for applying Taylor’s Theorem, which has not been considered a good way in approximation theory.
PiecewiseFunct can be also used to give pointwise approximate values of the sine function, so we do not need to recall here
Algorithm 1 (see [
2]). A hint: Combine Block 1, Block 2 and the illustrated MAPLE codes for the distinction between “
r-th decimal digit” and “
r significant digits” on [
2] to make a procedure, e.g.,
Sine, to implement
Algorithm 1.
3. Exploitation of the Output of the PiecewiseFunct Procedure
Firstly, we save the result from performing
PiecewiseFunct in a variable chosen as a list of lists
A:=[PiecewiseFunct(a,b,r)], then put
num:=nops(A). Now, we number the ending points of subintervals and corresponding approximate polynomials, for instance, by a
for-loop:
For a given number
, we can choose the index
i such that the interval
contains
, hence we put
. Note that
F[i] is still an expression in
x as default, not a function; besides, we cannot set
because
x here and
x in
F[i] are not the same by MAPLE’s rule. Then,
with the accuracy of
. In MAPLE, we can use the command
piecewise for a sequence of conditional settings to get the piecewise polynomial approximation to the sine function on
by putting
Now, we have for all with the accuracy of .
In the following, we take examples on approximating values of the sine function at rational and irrational arguments and getting the graph of approximate functions on an arbitrary intervals with various accuracy. Moreover, the approximation of integration on with integrands of the form () is considered in both theoretical and practical aspects.
To find the approximate value of
with the accuracy of
, we put
123,124,20
. Then,
A and the interval
is partitioned into the subintervals
and
. Thus, we take
A and obtain
where
. Hence, we have the desired approximation
Now, with an irrational number
x, how do we approximate the value of
with the accuracy of
? In principle, we can find a rational number
such that
and use the
PiecewiseFunct procedure to determine a polynomial
P that satisfies
. Then, we have the estimate
. For example, we approximate the value of
with the accuracy of
by first taking
Since
A, with
1.73,2,51
, we set
A. Then, we have the needed estimate
There are many algorithms in the literature to find rational approximations to an irrational number with the desired accuracy, mostly using continued fractions. The theoretical basis of this classic problem can be found in the two great books [
5] and [
6]. CAS of course have their built-in commands to compute such approximations. Here, we may take
by the calling sequence
evalf[51](sqrt(3)).
Besides, from Equation (
1) with the declaration in Equation (
2), we derive the graph of piecewise polynomial approximation to the sine function by the command
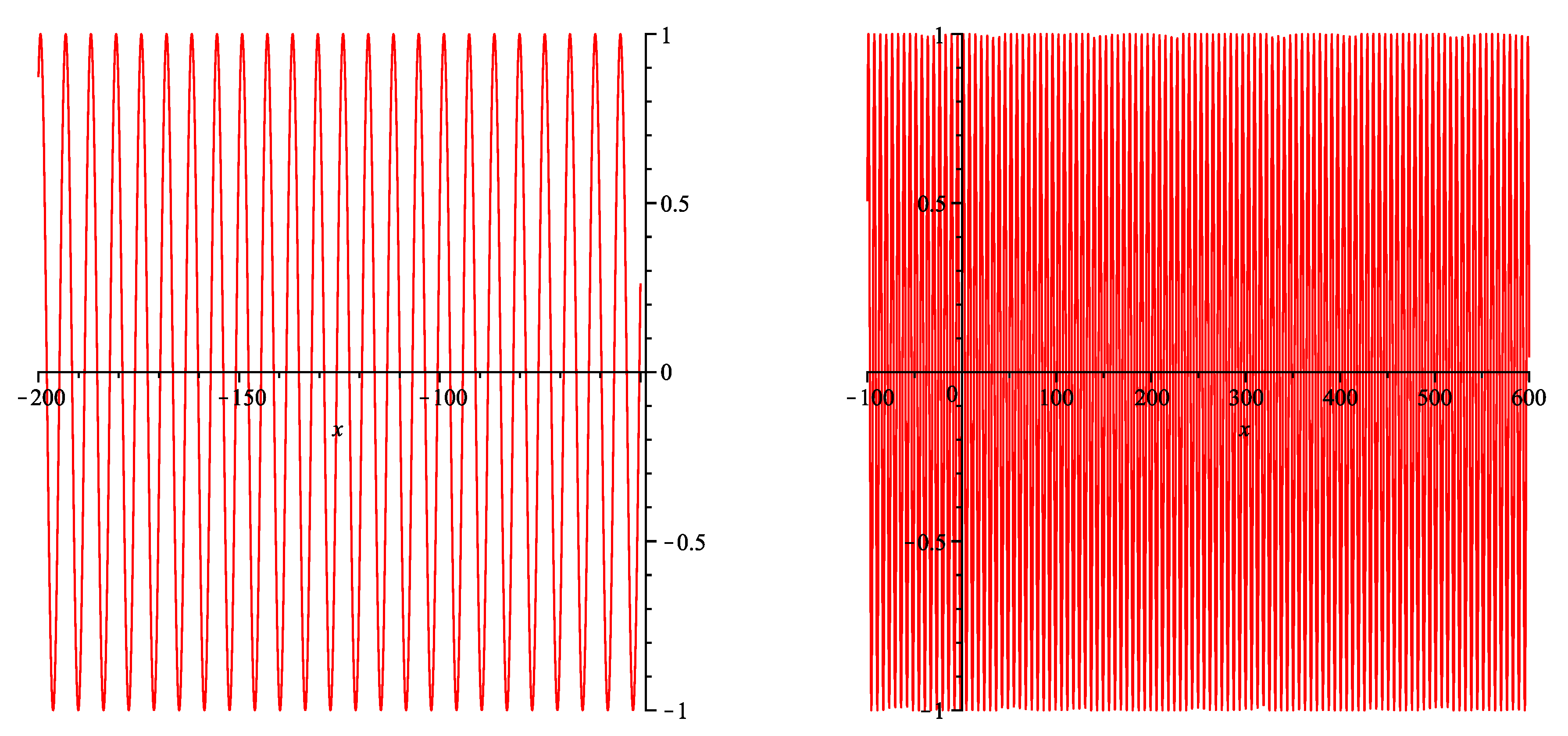
. We choose the large values
and
for the intervals
and
, respectively. Let us try the case
to see the display of 448 pairs of interval–polynomial with the accuracy of
. The corresponding graphs are depicted in
Figure 1.
We may also exploit
PiecewiseFunct from the other side of our approximation. We have used Taylor polynomials with larger degrees when higher accuracy is required thus far. If we want to confine approximate polynomials to a fixed degree, we might relate this determination to the vector space
, a subspace of
. We know that in
there is the best polynomial approximation
of the sine function in
-norm
of
, which is endowed with the inner product
Now, we use the Gram–Schmidt procedure to find an orthonormal basis
for
from the basis
, according to the recursion
Once the orthonormal basis has been found, we obtain
To give an estimate for
, where
F is our piecewise polynomial approximation to the sine function on
, we first approximate
by
These estimates have the absolute error
where
Therefore, we may choose
as an approximation of
. Then, we have the following estimation for the error norm
Hence, we may take
to obtain the estimate
To determine
with MAPLE, it would be better to write the polynomial
in the form of
, hence we have
According to the initial settings in Equation (
1), the coefficients
and the inner products
can be computed by the following commands
We can make a procedure named
PowerIntApprox only to compute
,
. This procedure, which has one more argument, e.g., “
deg”, for the chosen degree of
, may take all the blocks of
PiecewiseFunct, but replacing the output of Block 3, Block 4 and the last part of
PiecewiseFunct with the commands recapped in the following. For the output
RETURN of Block 3, we take the sum of integrals of
on
, instead of giving the sequence of
; and we do similarly for the output of Block 4. The last part of
PiecewiseFunct may be replaced with the commands
and the reason we do so can be easily recognized. Here,
ApproxInt has a similar role as
ApproxFunct, but is simpler to use.
Now, we have enough materials derived from Equations (
3)–(
6) to make a procedure for finding a desired approximation on
in
-norm to the best approximation
of the sine function in
with a given positive integer
ℓ. The procedure takes four arguments,
a,
b,
ℓ and
u, to give
as its output such that
. As mentioned above, if we named the procedure
BestApprox, hence it takes
PowerIntApprox as its local variable, then it would be interesting to run
BestApprox with different values of its input. However, as warned in
Section 1, we should pay much attention to the cases of large values of
ℓ and
u to take an appropriate regulation.