An Analytical Expression for Magnet Shape Optimization in Surface-Mounted Permanent Magnet Machines
Abstract
1. Introduction
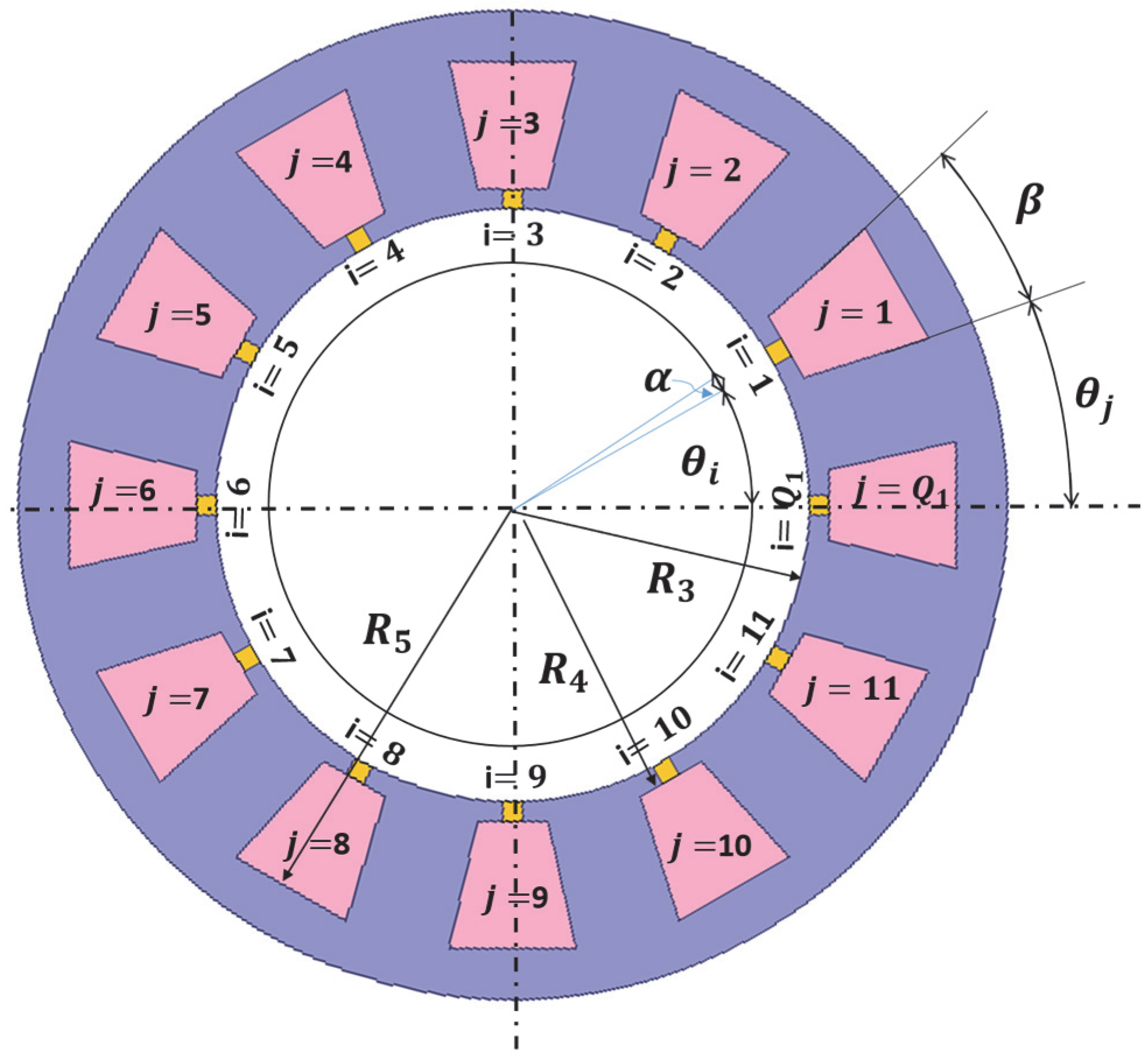
2. Subdomain Definition
3. Magnetic Vector Potential Computation
- The end effects are neglected (i.e., the machine is infinitely long: the magnetic variables are independent of z).
- The stator is assumed to be infinitely permeable (i.e., the saturation effect is neglected) with zero electrical conductivity.
- The relative magnetic permeability and electrical conductivity of the solid rotor and shaft are assumed to be constant.
- The current density in the slots has only one component along the z-axis.
3.1. Magnetic Vector Potential in the Stator Slot Subdomain (Region j)
3.2. Magnetic Vector Potential in the Stator Slot Opening Subdomain (Region i)
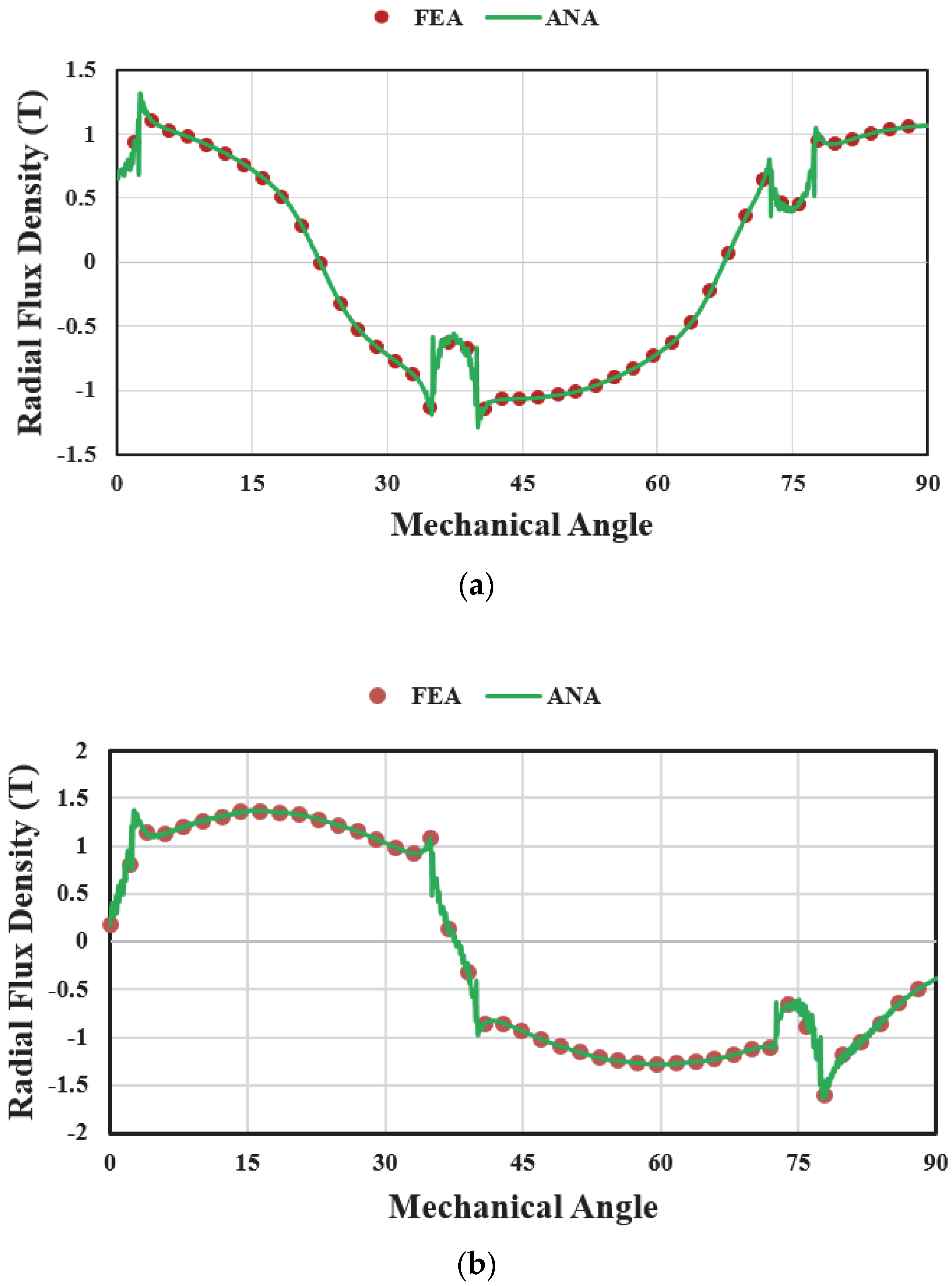
3.3. Magnetic Vector Potential in the Air-Gap Subdomain (Region II)
3.4. Magnetic Vector Potential in the Rotor Permanent Magnet Subdomain (Region I)
3.4.1. Radial Magnetization
3.4.2. Parallel Magnetization
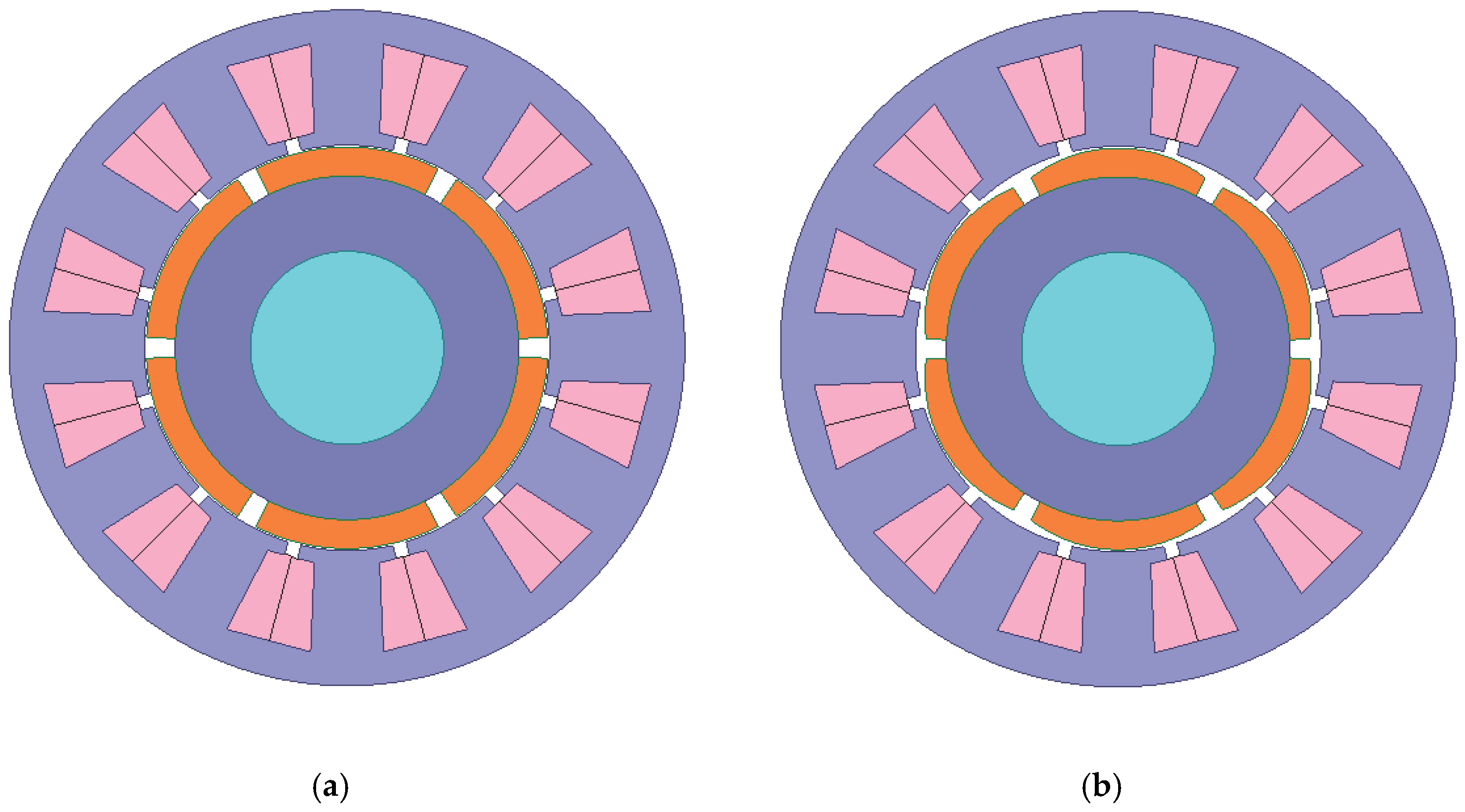
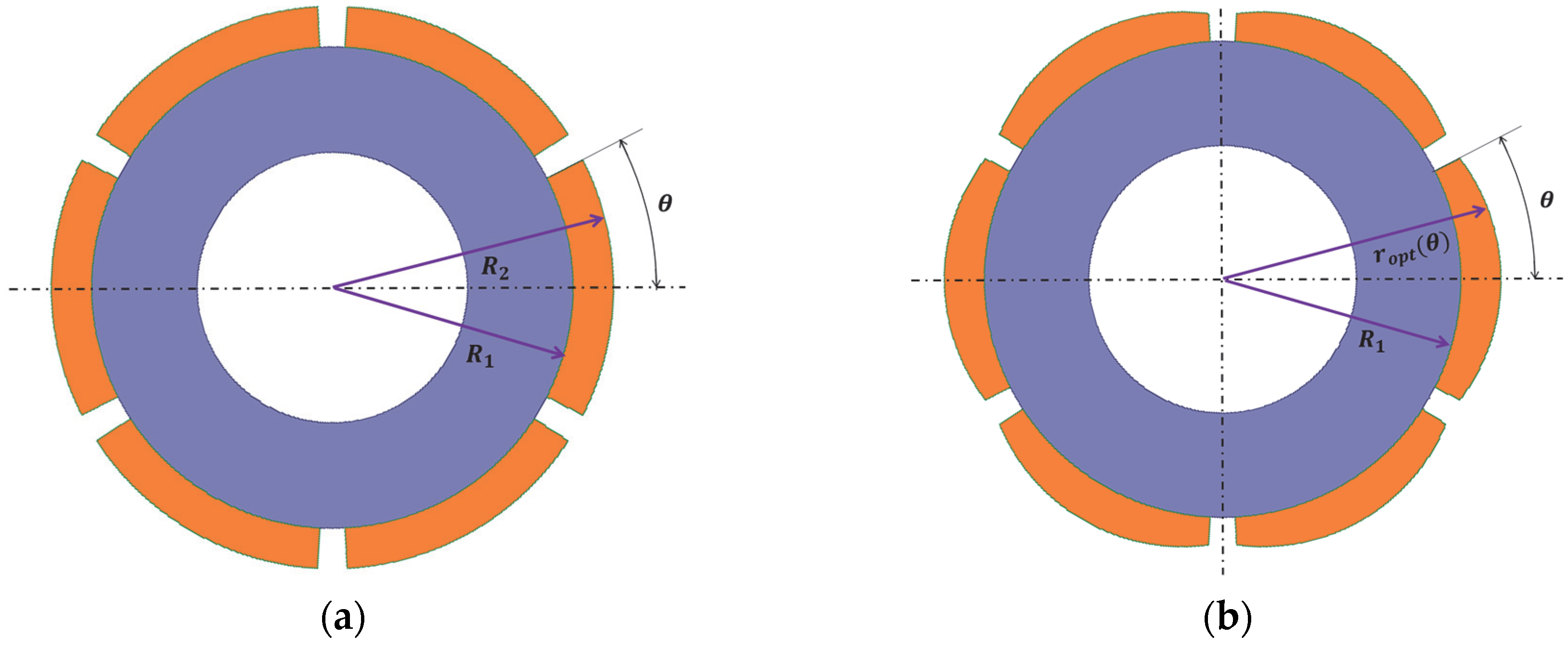
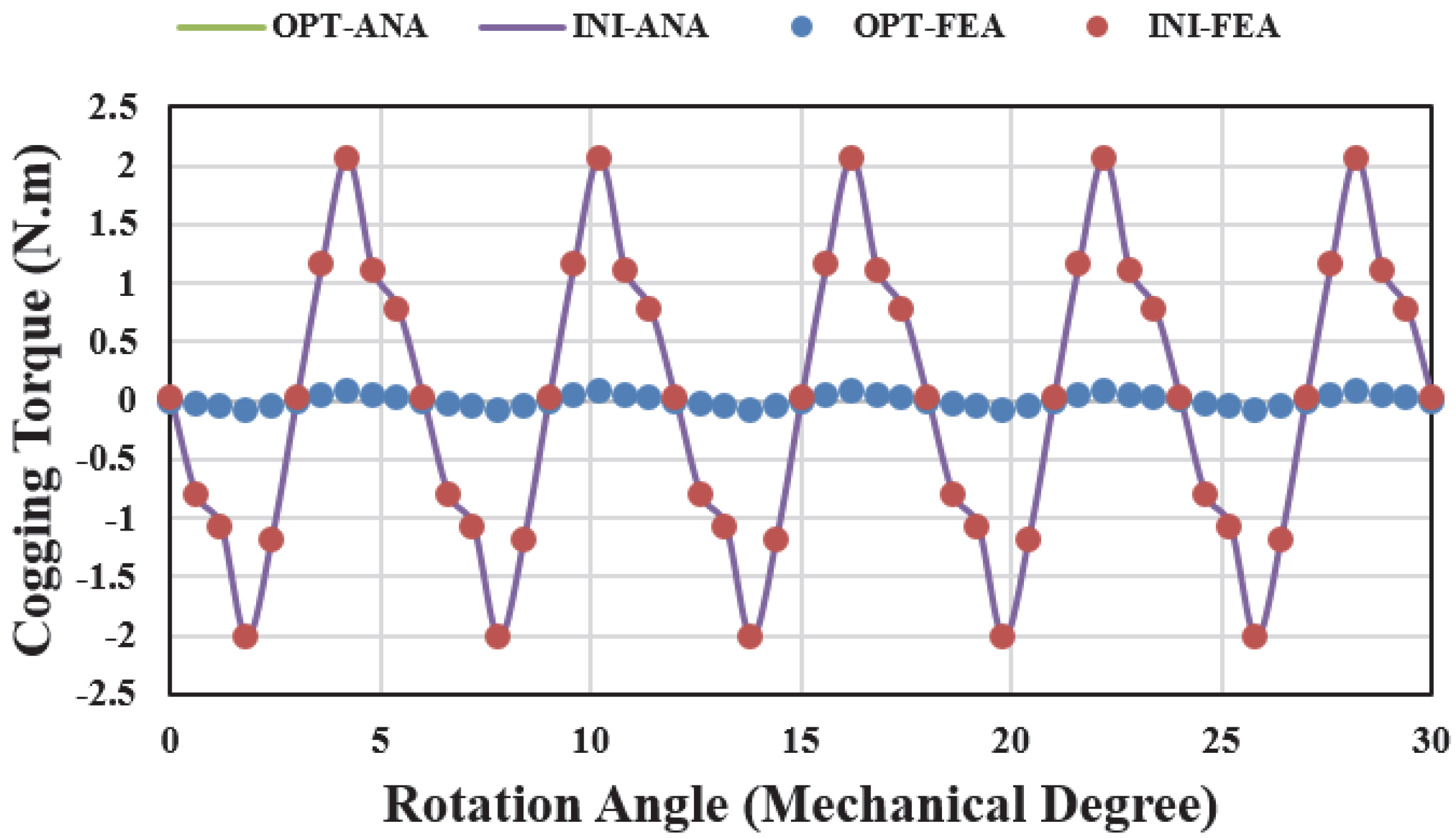
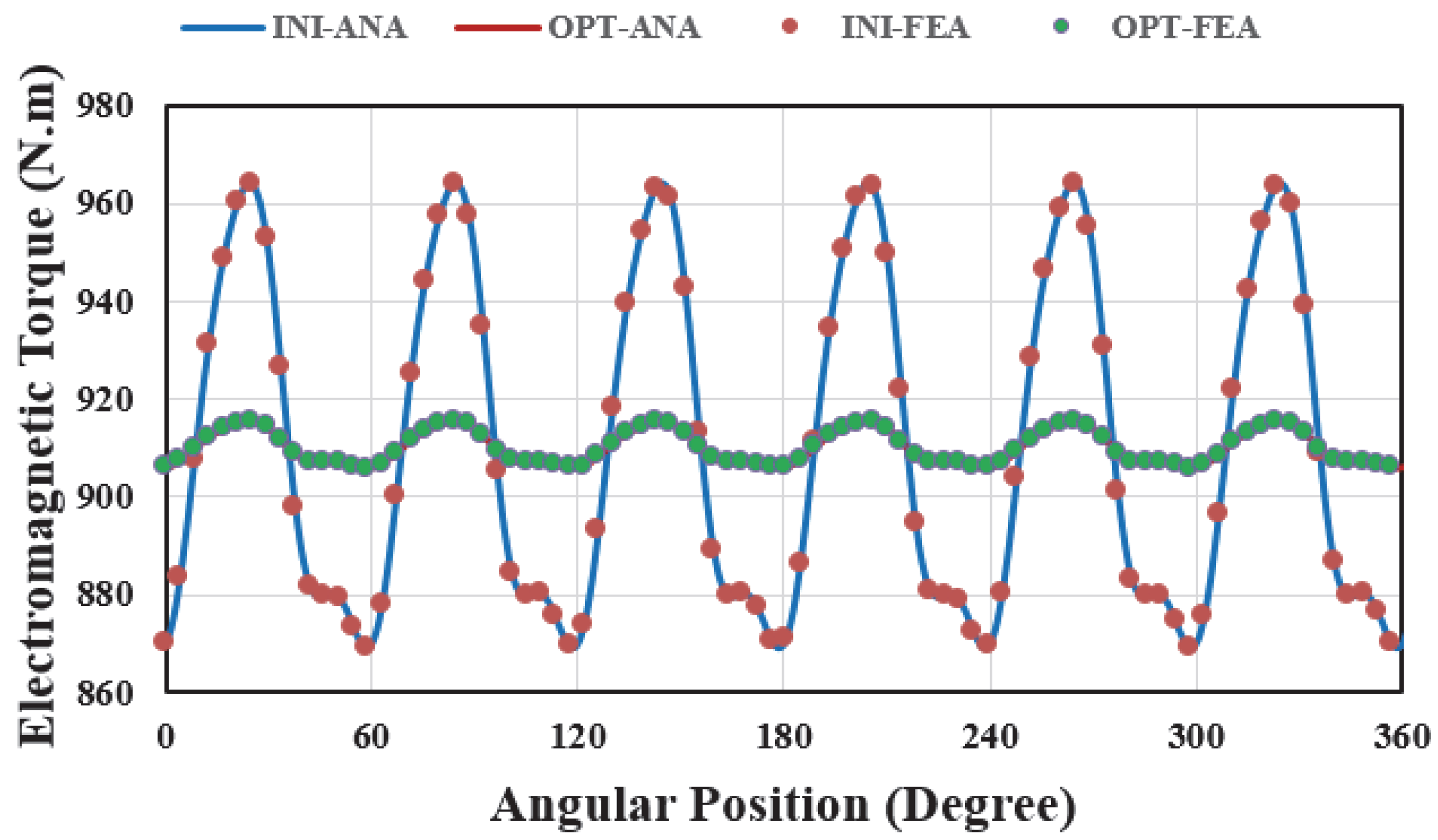
4. Magnet Pole Shape Optimization
- The scalar magnetic potential is expressed as in the inner stator surfaceor
- The normal flux density waveforms is sinusoidal in the inner stator surface and expressed as . Therefore,or
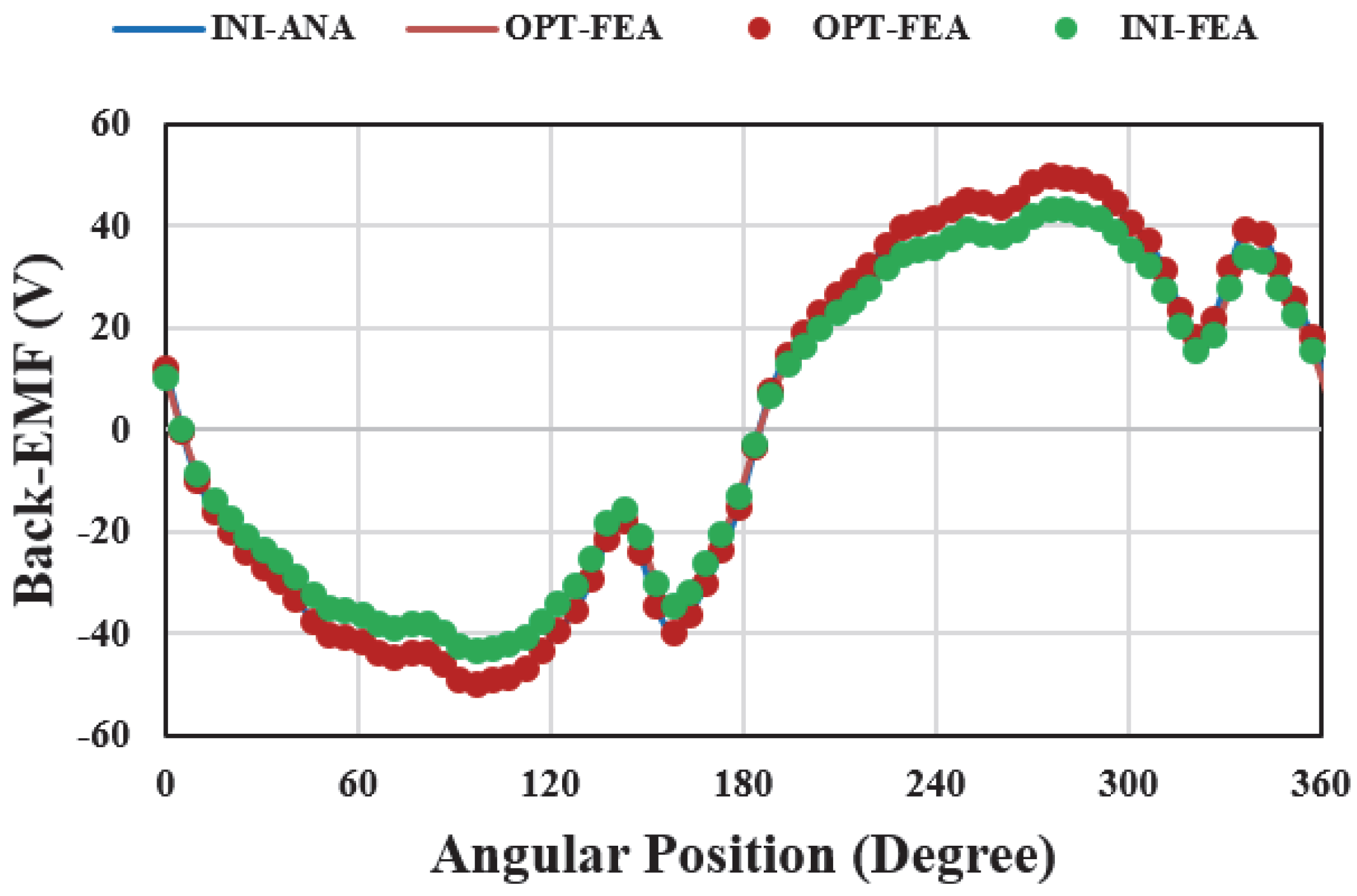
5. Performance Calculation
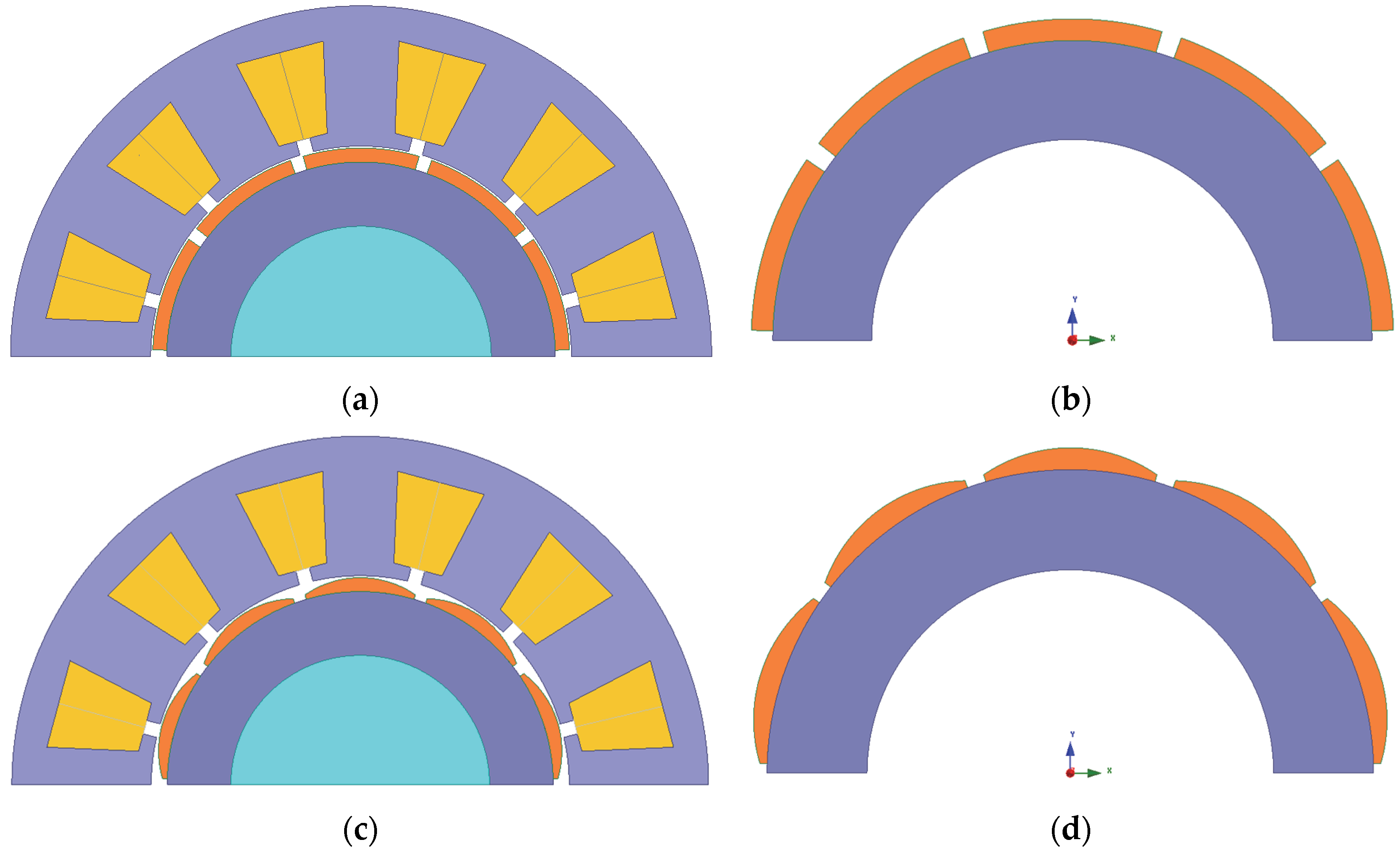
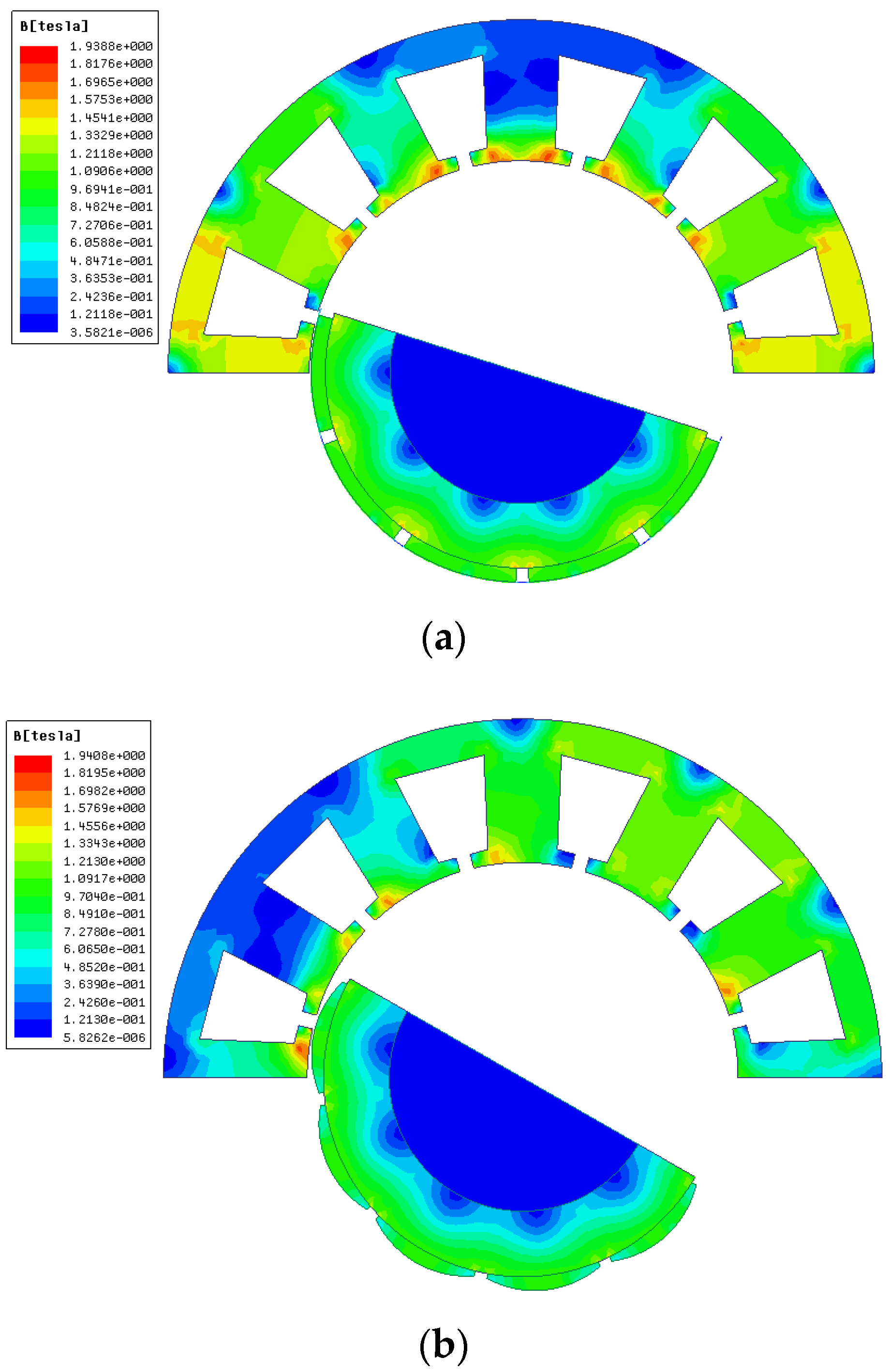
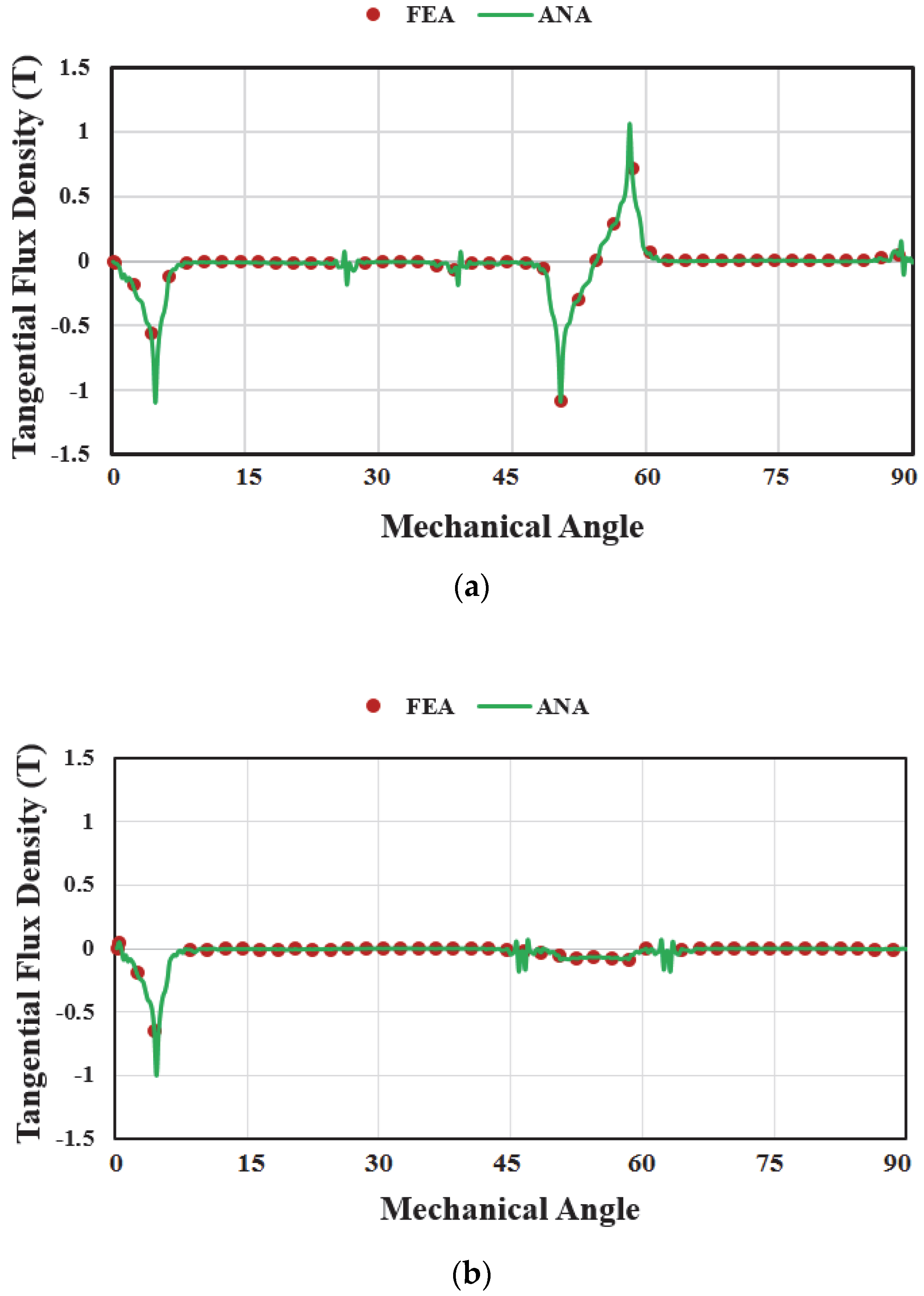
6. Model Evaluation
7. Conclusions
Conflicts of Interest
References
- Jahns, T.M.; Soong, W.L. Pulsating torque minimization techniques for permanent magnet AC motor drives—A review. IEEE Trans. Ind. Electron. 1996, 43, 321–330. [Google Scholar] [CrossRef]
- Bianchi, N.; Bolognani, S. Design techniques for reducing the cogging torque in surface-mounted PM motors. IEEE Trans. Ind. Appl. 2002, 38, 1259–1265. [Google Scholar] [CrossRef]
- Lukaniszyn, M.; Jagiela, M.; Wrobel, R. Optimization of permanent magnet shape for minimum cogging torque using a genetic algorithm. IEEE Trans. Magn. 2004, 40, 1228–1231. [Google Scholar] [CrossRef]
- Lateb, R.; Takorabet, N.; Meibody-Tabar, F. Effect of magnet segmentation on the cogging torque in surface-mounted permanent-magnet motors. IEEE Trans. Magn. 2006, 42, 442–445. [Google Scholar] [CrossRef]
- Ackermann, B.; Sottek, R.; Janssen, J.H.H.; van Steen, R.I. New technique for reducing cogging torque in a class of brushless DC motors. IEE Proc. B Electric Power Appl. 1992, 139, 315–320. [Google Scholar] [CrossRef]
- Ishikawa, T.; Slemon, G.R. A method of reducing ripple torque in permanent magnet motors without skewing. IEEE Trans. Magn. 1993, 29, 2028–2031. [Google Scholar] [CrossRef]
- Keyhani, C.B.; Studer, T.; Sebastian, S.K.; Murthy, A. Study of cogging torque in permanent magnet machines. Electric Mach. Power Syst. 1999, 27, 665–678. [Google Scholar] [CrossRef]
- Li, T.; Slemon, G. Reduction of cogging torque in permanent magnet motors. IEEE Trans. Magn. 1988, 24, 2901–2903. [Google Scholar]
- Hwang, C.C.; John, S.B.; Wu, S.S. Reduction of cogging torque in spindle motors for CD-ROM drive. IEEE Trans. Magn. 1998, 34, 468–470. [Google Scholar] [CrossRef]
- Jabbari, A.; Shakeri, M.; Nabavi Niaki, S.A. Pole shape optimization of permanent magnet synchronous motors using the reduced basis technique. Iran. J. Electr. Electron. Eng. 2010, 6, 48–55. [Google Scholar]
- Markovic, M.; Jufer, M.; Perriard, Y. Reducing the cogging torque in brushless DC motors by using conformal mappings. IEEE Trans. Magn. 2004, 40, 451–455. [Google Scholar] [CrossRef]
- Zarko, D.; Ban, D.; Lipo, T.A. Analytical calculation of magnetic field distribution in the slotted air gap of a surface permanent-magnet motor using complex relative air-gap permeance. IEEE Trans. Magn. 2006, 42, 1828–1837. [Google Scholar] [CrossRef]
- Boughrara, K.; Zarko, D.; Ibtiouen, R.; Touhami, O.; Rezzoug, A. Magnetic field analysis of inset and surface-mounted permanent-magnet synchronous motors using Schwarz–Christoffel transformation. IEEE Trans. Magn. 2009, 45, 3166–3178. [Google Scholar] [CrossRef]
- Ilhan, E.; Gysen, B.L.J.; Paulides, J.J.H.; Lomonova, E.A. Analytical hybrid model for flux switching permanent magnet machines. IEEE Trans. Magn. 2010, 46, 1762–1765. [Google Scholar] [CrossRef]
- Tang, Y.; Motoasca, T.E.; Paulides, J.J.H.; Lomonova, E.A. Analytical modeling of flux-switching machines using variable global reluctance networks. In Proceedings of the 2012 XXth International Conference on Electrical Machines, Marseille, France, 2–5 September 2012; pp. 2792–2798. [Google Scholar]
- Hua, W.; Zhang, G.; Cheng, M.; Dong, J. Electromagnetic performance analysis of hybrid-excited flux-switching machines by a nonlinear magnetic network model. IEEE Trans. Magn. 2011, 47, 3216–3219. [Google Scholar] [CrossRef]
- Gu, Q.; Gao, H. Effect of slotting in PM electric machines. Electric Mach. Power Syst. 1985, 10, 273–284. [Google Scholar]
- Boules, N. Prediction of no-load flux density distribution in permanent magnet machines. IEEE Trans. Ind. Appl. 1985, 3, 633–643. [Google Scholar] [CrossRef]
- Ackermann, B.; Sottek, R. Analytical modeling of the cogging torque in permanent magnet motors. Electr. Eng. Archiv fur Elektrotechnik 1995, 78, 117–125. [Google Scholar] [CrossRef]
- Radun, A. Analytical calculation of the switched reluctance motor’s unaligned inductance. IEEE Trans. Magn. 1999, 35, 4473–4481. [Google Scholar] [CrossRef]
- Rasmussen, K.F.; Davies, J.H.; Miller, T.J.E.; McGelp, M.I.; Olaru, M. Analytical and numerical computation of air-gap magnetic fields in brushless motors with surface permanent magnets. IEEE Trans. Ind. Appl. 2000, 36, 1547–1554. [Google Scholar]
- Wang, X.; Li, Q.; Wang, S.; Li, Q. Analytical calculation of air-gap magnetic field distribution and instantaneous characteristics of brushless DC motors. IEEE Trans. Energy Convers. 2003, 18, 424–432. [Google Scholar] [CrossRef]
- Liu, Z.J.; Li, J.T. Analytical solution of air-gap field in permanent-magnet motors taking into account the effect of pole transition over slots. IEEE Trans. Magn. 2007, 43, 3872–3883. [Google Scholar] [CrossRef]
- Liu, Z.J.; Li, J.T.; Jiang, Q. An improved analytical solution for predicting magnetic forces in permanent magnet motors. J. Appl. Phys. 2008, 103, 07F135. [Google Scholar] [CrossRef]
- Liu, Z.J.; Li, J.T. Accurate prediction of magnetic field and magnetic forces in permanent magnet motors using an analytical solution. IEEE Trans. Energy Convers. 2008, 23, 717–726. [Google Scholar] [CrossRef]
- Kumar, P.; Bauer, P. Improved analytical model of a permanent-magnet brushless DC motor. IEEE Trans. Magn. 2008, 44, 2299–2309. [Google Scholar] [CrossRef]
- Lubin, T.; Mezani, S.; Rezzoug, A. Exact analytical method for magnetic field computation in the air gap of cylindrical electrical machines considering slotting effects. IEEE Trans. Magn. 2010, 46, 1092–1099. [Google Scholar] [CrossRef]
- Gysen, B.L.; Ilhan, E.; Meessen, K.J.; Paulides, J.J.; Lomonova, E.A. Modeling of flux switching permanent magnet machines with fourier analysis. IEEE Trans. Magn. 2010, 46, 1499–1502. [Google Scholar] [CrossRef]
- Boughrara, K.; Ibtiouen, R.; Lubin, T. Analytical prediction of magnetic field in parallel double excitation and spoke-type permanent-magnet machines accounting for tooth-tips and shape of polar pieces. IEEE Trans. Magn. 2012, 48, 2121–2137. [Google Scholar] [CrossRef]
- Boughrara, K.; Lubin, T.; Ibtiouen, R. General subdomain model for predicting magnetic field in internal and external rotor multiphase flux-switching machines topologies. IEEE Trans. Magn. 2013, 49, 5310–5325. [Google Scholar] [CrossRef]
- Tiang, T.L.; Ishak, D.; Jamil, M.K.M. Complete subdomain model for surface-mounted permanent magnet machines. In Proceedings of the 2014 IEEE Conference on Energy Conversion, Johor Bahru, Malaysia, 11–13 October 2014; pp. 140–145. [Google Scholar]
- Liu, X.; Hu, H.; Zhao, J.; Belahcen, A.; Tang, L.; Yang, L. Analytical solution of the magnetic field and EMF calculation in ironless BLDC motor. IEEE Trans. Magn. 2016, 52, 1–10. [Google Scholar] [CrossRef]
- Dubas, F.; Espanet, C. Analytical solution of the magnetic field in permanent-magnet motors taking into account slotting effect: No-load vector potential and flux density calculation. IEEE Trans. Magn. 2009, 45, 2097. [Google Scholar] [CrossRef]
- Roubache, L.; Boughrara, K.; Dubas, F.; Ibtiouen, R. New subdomain technique for electromagnetic performances calculation in radial-flux electrical machines considering finite soft-magnetic material permeability. IEEE Trans. Magn. 2018. [Google Scholar] [CrossRef]
- Dubas, F.; Boughrara, K. New scientific contribution on the 2-D subdomain technique in Cartesian coordinates: Taking into account of iron parts. Math. Comput. Appl. 2017, 22, 17. [Google Scholar]
- Dubas, F.; Boughrara, K. New scientific contribution on the 2-D subdomain technique in polar coordinates: Taking into account of iron parts. Math. Comput. Appl. 2017, 22, 42. [Google Scholar]
- Hannon, B.; Sergeant, P.; Dupré, L. Two-dimensional Fourier-based modeling of electric machines. In Proceedings of the 2017 IEEE International Electric Machines and Drives Conference, Miami, FL, USA, 21–24 May 2017; pp. 1–8. [Google Scholar]
- Jabbari, A. 2D Analytical Modeling of Magnetic Vector Potential in Surface Mounted and Surface Inset Permanent Magnet Machines. Iran. J. Electr. Electron. Eng. 2017, 13, 362–373. [Google Scholar]
- Jabbari, A. Exact analytical modeling of magnetic vector potential in surface inset permanent magnet DC machines considering magnet segmentation. J. Electr. Eng. 2018, 69, 39–45. [Google Scholar] [CrossRef]
- Jabbari, A. Analytical Modeling of Magnetic Field Distribution in Inner Rotor Brushless Magnet Segmented Surface Inset Permanent Magnet Machines. Iran. J. Electr. Electron. Eng. 2018, 14, 259–269. [Google Scholar]
- Jabbari, A. Analytical Modeling of Magnetic Field Distribution in Multiphase H-Type Stator Core Permanent Magnet Flux Switching Machines. Iran. J. Sci. Tech. Trans. Electr. Eng. 2018, 3, 1–13. [Google Scholar] [CrossRef]
| Parameter | Value |
|---|---|
| Rotor Outer Diameter | 208 mm |
| Rotor Inner Diameter | 130 mm |
| Number of poles | 10 |
| Pole Arc | 35° |
| Pole Thickness | 20 mm |
| Magnet material | NEO-39SH |
| Stator Outer Diameter | 350 mm |
| Stator Inner Diameter | 210 mm |
| Number of Slots | 12 |
| Stator Tooth Width | 30 mm |
| Stator Yoke Width | 26 mm |
| Slot Open | 7 mm |
| Tip Thickness | 2.5 mm |
| Slot Skew | 0° |
| Stator Length | 100 mm |
| Lamination material | M 19–0.5 mm |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jabbari, A. An Analytical Expression for Magnet Shape Optimization in Surface-Mounted Permanent Magnet Machines. Math. Comput. Appl. 2018, 23, 57. https://doi.org/10.3390/mca23040057
Jabbari A. An Analytical Expression for Magnet Shape Optimization in Surface-Mounted Permanent Magnet Machines. Mathematical and Computational Applications. 2018; 23(4):57. https://doi.org/10.3390/mca23040057
Chicago/Turabian StyleJabbari, Ali. 2018. "An Analytical Expression for Magnet Shape Optimization in Surface-Mounted Permanent Magnet Machines" Mathematical and Computational Applications 23, no. 4: 57. https://doi.org/10.3390/mca23040057
APA StyleJabbari, A. (2018). An Analytical Expression for Magnet Shape Optimization in Surface-Mounted Permanent Magnet Machines. Mathematical and Computational Applications, 23(4), 57. https://doi.org/10.3390/mca23040057





