Holographic Tachyon in Fractal Geometry
Abstract
:1. Introduction
2. Preliminaries
3. Tachyonic Reconstruction of Holographic Energy
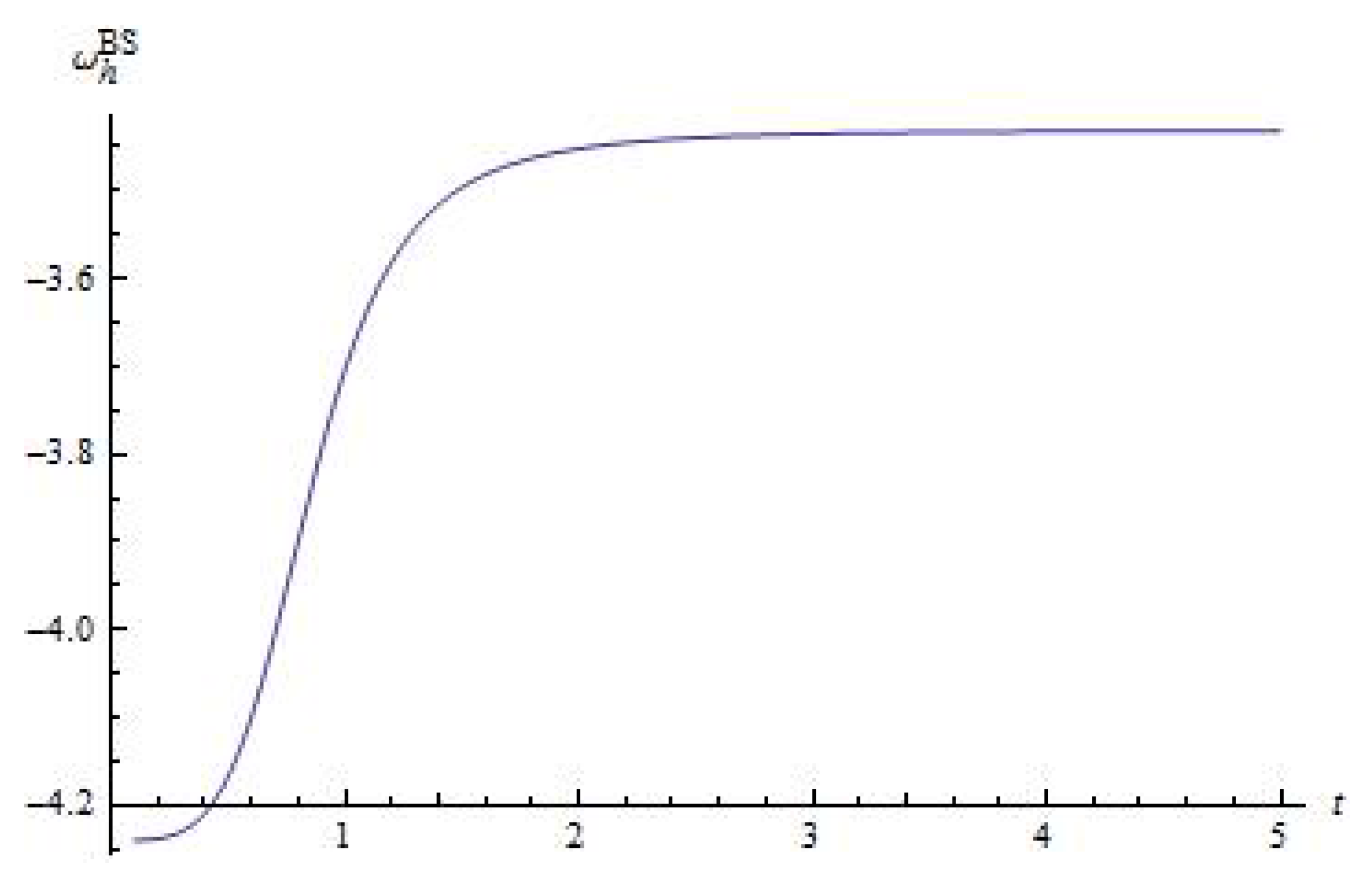
3.1. The Basic Scenario
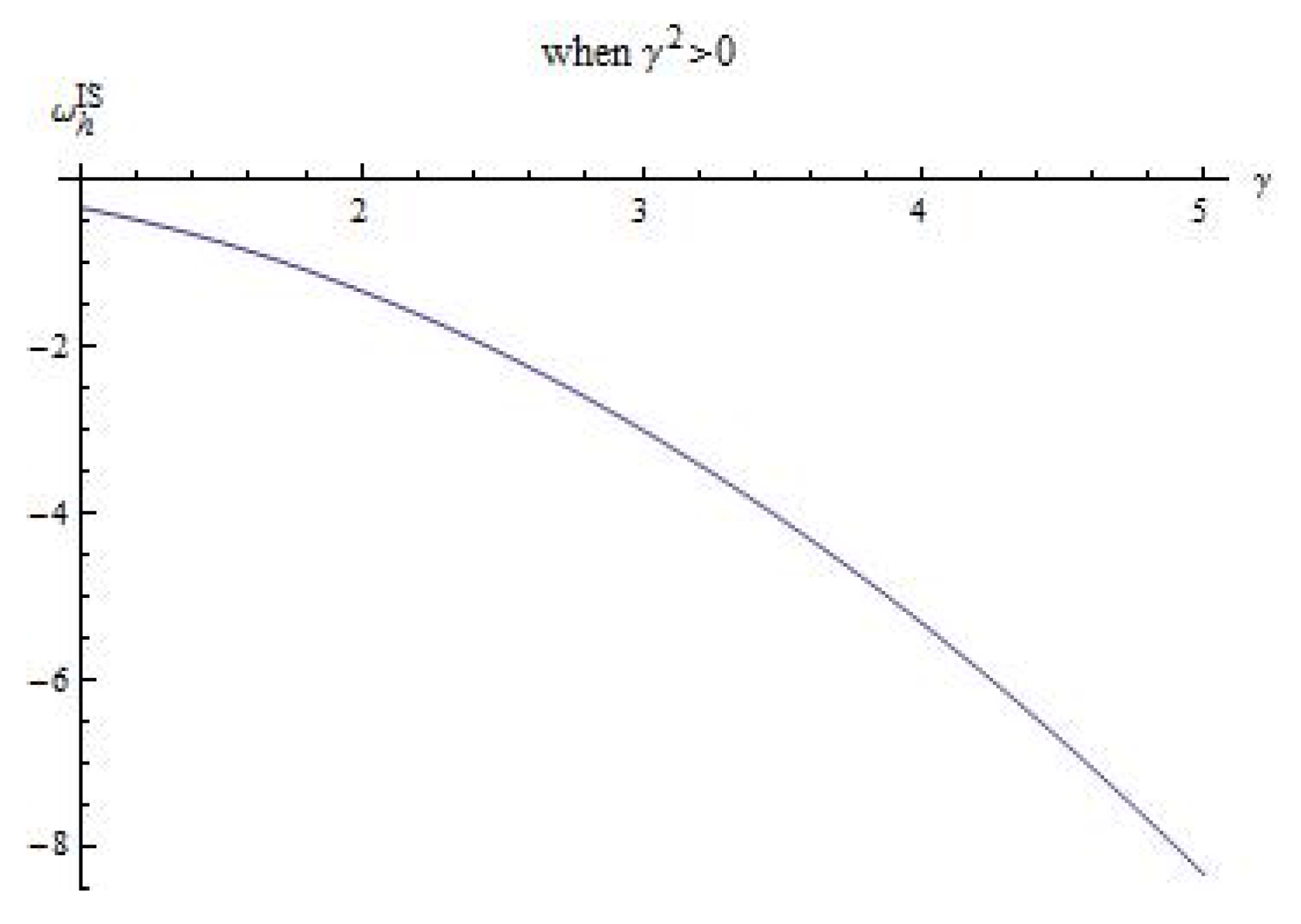
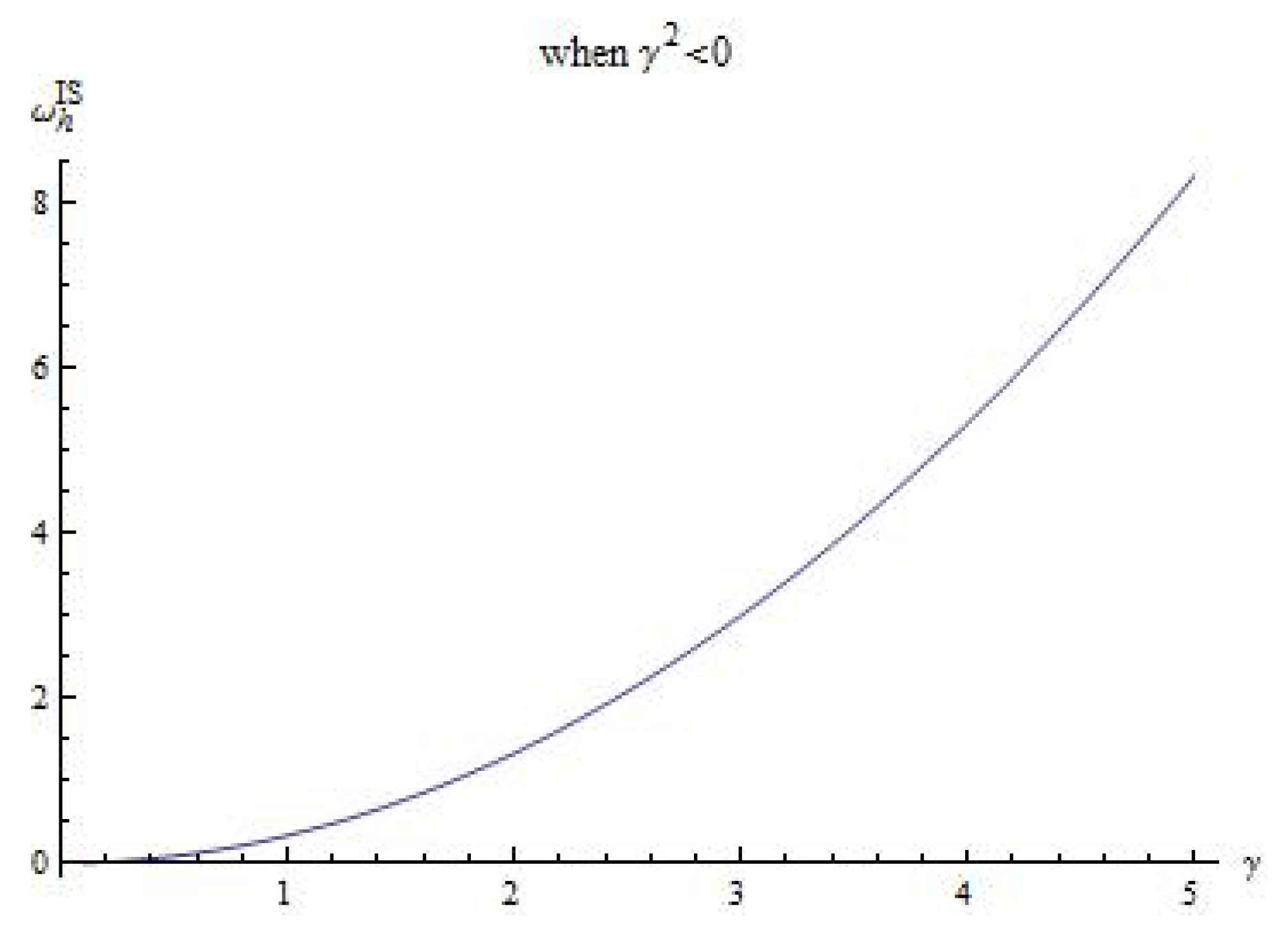
3.2. The Interacting Scenario
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 2. [Google Scholar] [CrossRef]
- Bennet, C.L.; Halpern, M.; Hinshaw, G.; Jarosik, N.; Kogut, A.; Limon, M.; Meyer, S.S.; Page, L.; Spergel, D.N.; Tucker, G.S.; et al. First Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Preliminary Maps and Basic Results. Astrophys. J. Suppl. 2003, 148, 1. [Google Scholar] [CrossRef]
- Tegmark, M.; Strauss, M.; Blanton, M.; Abazajian, K.; Dodelson, S.; Sandvik, H.; Wang, X.; Weinberg, D.; Zehavi, I.; Bahcall, N.; et al. Cosmological parameters from SDSS and WMAP. Phys. Rev. D 2004, 69, 103501. [Google Scholar] [CrossRef]
- Allen, A.W.; Schmidt, R.W.; Ebeling, H.; Fabian, A.C.; van Speybroeck, L. Constraints on dark energy from Chandra observations of the largest relaxed galaxy clusters. Mon. Not. Roy. Astron. Soc. 2004, 353, 457. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Armitage-Caplan, C.; Arnaud, M.; Ashdown, M.; Atrio-Barandela, F.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; et al. Planck 2013 results. XVI. Cosmological parameters. Astron. Astrophys. 2014, 571, A16. [Google Scholar]
- Ng, Y.J. From Computation to Black Holes and Space-Time Foam. Phys. Rev. Lett. 2001, 86, 2946. [Google Scholar] [CrossRef] [PubMed]
- Arzano, M.; Kephart, T.W.; Ng, Y.J. From spacetime foam to holographic foam cosmology. Phys. Lett. B 2007, 649, 243. [Google Scholar] [CrossRef]
- Duran, I.; Pavon, D. Holographic dark energy at the Ricci scale. J. Phys. Conf. Ser. 2011, 314, 012058. [Google Scholar] [CrossRef]
- del Campo, S.; Fabris, J.C.; Herrera, R.; Zimdahl, W. Holographic dark-energy models. Phys. Rev. D 2011, 83, 123006. [Google Scholar] [CrossRef]
- Sheykhi, A. Holographic scalar field models of dark energy. Phys. Rev. D 2011, 84, 107302. [Google Scholar] [CrossRef]
- Li, M.; Li, X.D.; Wang, S.; Wang, Y. Dark Energy. Commun. Theor. Phys. 2011, 56, 525. [Google Scholar] [CrossRef]
- Sheykhi, A.; Bagheri, A. Quintessence Ghost Dark Energy Model. Europhys. Lett. 2011, 95, 39001. [Google Scholar] [CrossRef]
- Pasqua, A.; Khodam-Mohammadi, A.; Jamil, M.; Myrzakulov, R. Interacting Ricci Dark Energy with Logarithmic Correction. Astrophys. Space Sci. 2012, 340, 199. [Google Scholar] [CrossRef]
- Komatsu, E.; Smith, K.M.; Dunkley, J.; Bennett, C.L.; Gold, B.; Hinshaw, G.; Jarosik, N.; Larson, D.; Nolta, M.R.; Page, L.; et al. Seven-year Wilkinson microwave anisotropy probe (wmap) observations: cosmological interpretation. Astrophys. J. Suppl. 2011, 192, 18. [Google Scholar] [CrossRef]
- Hinshaw, G.; Larson, D.; Komatsu, E.; Spergel, D.N.; Bennett, C.L.; Dunkley, J.; Nolta, M.R.; Halpern, M.; Hill, R.S.; Odegard, N.; et al. Nine-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Parameter Results. Astrophys. J. Suppl. 2013, 208, 19. [Google Scholar] [CrossRef]
- Calcagni, G. Fractal Universe and Quantum Gravity. Phys. Rev. Lett. 2010, 104, 251301. [Google Scholar] [CrossRef] [PubMed]
- Calcagni, G. Quantum field theory, gravity and cosmology in a fractal universe. JHEP 2010, 03, 120. [Google Scholar] [CrossRef]
- Karami, K.; Jamil, M.; Ghaffari, S.; Fahimi, K. Holographic, new agegraphic and ghost dark energy models in fractal cosmology. Can. J. Phys. 2013, 91, 770. [Google Scholar] [CrossRef]
- Radicella, N.; Pavon, D. On the c2 term in the holographic formula for dark energy. JCAP 2010, 1010:005. [Google Scholar]
- Wolfram Research. Wolfram Mathematica 8.0; Wolfram Research Inc.: Long Hanborough Oxfordshire OX29 8FD, UK, 2010. [Google Scholar]
- Gibbons, G.W. Cosmological evolution of the rolling tachyon. Phys. Lett. B 2002, 537, 1. [Google Scholar] [CrossRef]
- Mazumdar, A.; Panda, S.; Perez-Lorenzana, A. Assisted inflation via tachyon condensation. Nucl. Phys. B 2001, 614, 101. [Google Scholar] [CrossRef]
- Padmanabhan, T. Accelerated expansion of the universe driven by tachyonic matter. Phys. Rev. D 2002, 66, 021301. [Google Scholar] [CrossRef]
- Jamil, M.; Karami, K.; Sheykhi, A. Restoring New Agegraphic Dark Energy in RS II Braneworld. Int. J. Theor. Phys. 2011, 50, 3069. [Google Scholar] [CrossRef]
- Sheykhi, A.; Movahed, M.S.; Ebrahimi, E. Tachyon Reconstruction of Ghost Dark Energy. Astrophys. Space Sci. 2012, 339, 93. [Google Scholar] [CrossRef]
- Jamil, M.; Saridakis, E.N.; Setare, M.R. Thermodynamics of dark energy interacting with dark matter and radiation. Phys. Rev. D 2010, 81, 023007. [Google Scholar] [CrossRef]
- Wetterich, C. The cosmon model for an asymptotically vanishing time-dependent cosmological constant. Astron. Astrophys. 1995, 301, 321. [Google Scholar]
- Amendola, L. Scaling solutions in general nonminimal coupling theories. Phys. Rev. D 1999, 60, 043501. [Google Scholar] [CrossRef]
- Zhang, X. Coupled Quintessence in a Power-Law Case and The Cosmic Coincidence Problem. Mod. Phys. Lett. A 2005, 20, 2575. [Google Scholar] [CrossRef]
- Gonzalez, T.; Leon, G.; Quiros, I. Dynamics of quintessence models of dark energy with exponential coupling to dark matter. Class. Quant. Grav. 2006, 23, 3165. [Google Scholar] [CrossRef]
- Bertolami, O.; Gil Pedro, F.; Le Delliou, M. Dark energy–dark matter interaction and putative violation of the equivalence principle from the Abell cluster A586. Phys. Lett. B 2007, 654, 165. [Google Scholar] [CrossRef]
- Jamil, M.; Rashid, M.A. Constraints on Coupling Constant Between Chaplygin Gas and Dark Matter. Eur. Phys. J. C 2008, 58, 111. [Google Scholar] [CrossRef]
- Sola, J.; Stefancic, H. Effective equation of state for dark energy: Mimicking quintessence and phantom energy through a variable Λ. Phys. Lett. B 2005, 624, 147. [Google Scholar] [CrossRef]
- Shapiro, I.L.; Sola, J. On the possible running of the cosmological constant. Phys. Lett. B 2009, 682, 105. [Google Scholar] [CrossRef]
- Grande, J.; Sola, J.; Stefancic, H. LXCDM: A Cosmon model solution to the cosmological coincidence problem? JCAP 2006, 011, 0608. [Google Scholar]
- Feng, C.; Wang, B.; Gong, Y.; Su, R.-K. Testing the viability of the interacting holographic dark energy model by using combined observational constraints. J. Cosmol. Astropart. Phys. 2007, 9, 5. [Google Scholar] [CrossRef]
- Amendola, L.; Tocchini-Valetini, D. Stationary dark energy: The present universe as a global attractor. Phys. Rev. D 2001, 64, 043509. [Google Scholar] [CrossRef]
- Setare, M.R.; Jamil, M. Correspondence between entropy-corrected holographic and Gauss-Bonnet dark-energy models. Phys. Lett. B 2010, 690, 1. [Google Scholar] [CrossRef]
- Zhang, H.; Zhu, Z.H. Interacting Chaplygin gas. Phys. Rev. D 2006, 73, 043518. [Google Scholar] [CrossRef]
- Ichiki, K.; Keum, Y.Y. Primordial Neutrinos, Cosmological Perturbations in Interacting Dark-Energy Model: CMB and LSS. J. Cosmol. Astropart. Phys. 2008, 6, 5. [Google Scholar] [CrossRef]
- Amendola, L.; Campos, G.C.; Rosenfeld, R. Consequences of dark matter-dark energy interaction on cosmological parameters derived from type Ia supernova data. Phys. Rev. D 2007, 75, 083506. [Google Scholar] [CrossRef]
- Wang, B.; Gong, Y.; Abdalla, E. Transition of the dark energy equation of state in an interacting holographic dark energy model. Phys. Lett. B 2005, 624, 141. [Google Scholar] [CrossRef]
- Wang, B.; Lin, C.Y.; Abdalla, E. Constraints on the interacting holographic dark energy model. Phys. Lett. B 2005, 637, 357. [Google Scholar] [CrossRef]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753. [Google Scholar] [CrossRef]
- Copeland, E.J.; Garousi, M.R.; Sam, M.; Tsujikawa, S. What is needed of a tachyon if it is to be the dark energy? Phys. Rev. D 2005, 71, 043003. [Google Scholar] [CrossRef]
- Aguirregabiria, J.M.; Lazkoz, R. Tracking solutions in tachyon cosmology. Phys. Rev. D 2004, 69, 123502. [Google Scholar] [CrossRef]
- Salti, M.; Korunur, M.; Acikgoz, I. Extended Ricci and holographic dark energy models in fractal cosmology. Eur. Phys. J. Plus 2014, 129, 95. [Google Scholar] [CrossRef]
- Chattopadhyay, S.; Pasqua, A.; Roy, S. A Study on Some Special Forms of Holographic Ricci Dark Energy in Fractal Universe. ISRN High Energy Physics 2013, 2013, 251498. [Google Scholar] [CrossRef] [PubMed]
- Abedi, H.; Salti, M. Ghost quintessence in fractal gravity. Pramana-J. Phys. 2015, 84, 503. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salti, M.; Aydogdu, O. Holographic Tachyon in Fractal Geometry. Math. Comput. Appl. 2016, 21, 21. https://doi.org/10.3390/mca21020021
Salti M, Aydogdu O. Holographic Tachyon in Fractal Geometry. Mathematical and Computational Applications. 2016; 21(2):21. https://doi.org/10.3390/mca21020021
Chicago/Turabian StyleSalti, Mustafa, and Oktay Aydogdu. 2016. "Holographic Tachyon in Fractal Geometry" Mathematical and Computational Applications 21, no. 2: 21. https://doi.org/10.3390/mca21020021
APA StyleSalti, M., & Aydogdu, O. (2016). Holographic Tachyon in Fractal Geometry. Mathematical and Computational Applications, 21(2), 21. https://doi.org/10.3390/mca21020021





