Hydrodynamic Analysis of a Multibody Wave Energy Converter in Regular Waves
Abstract
:1. Introduction
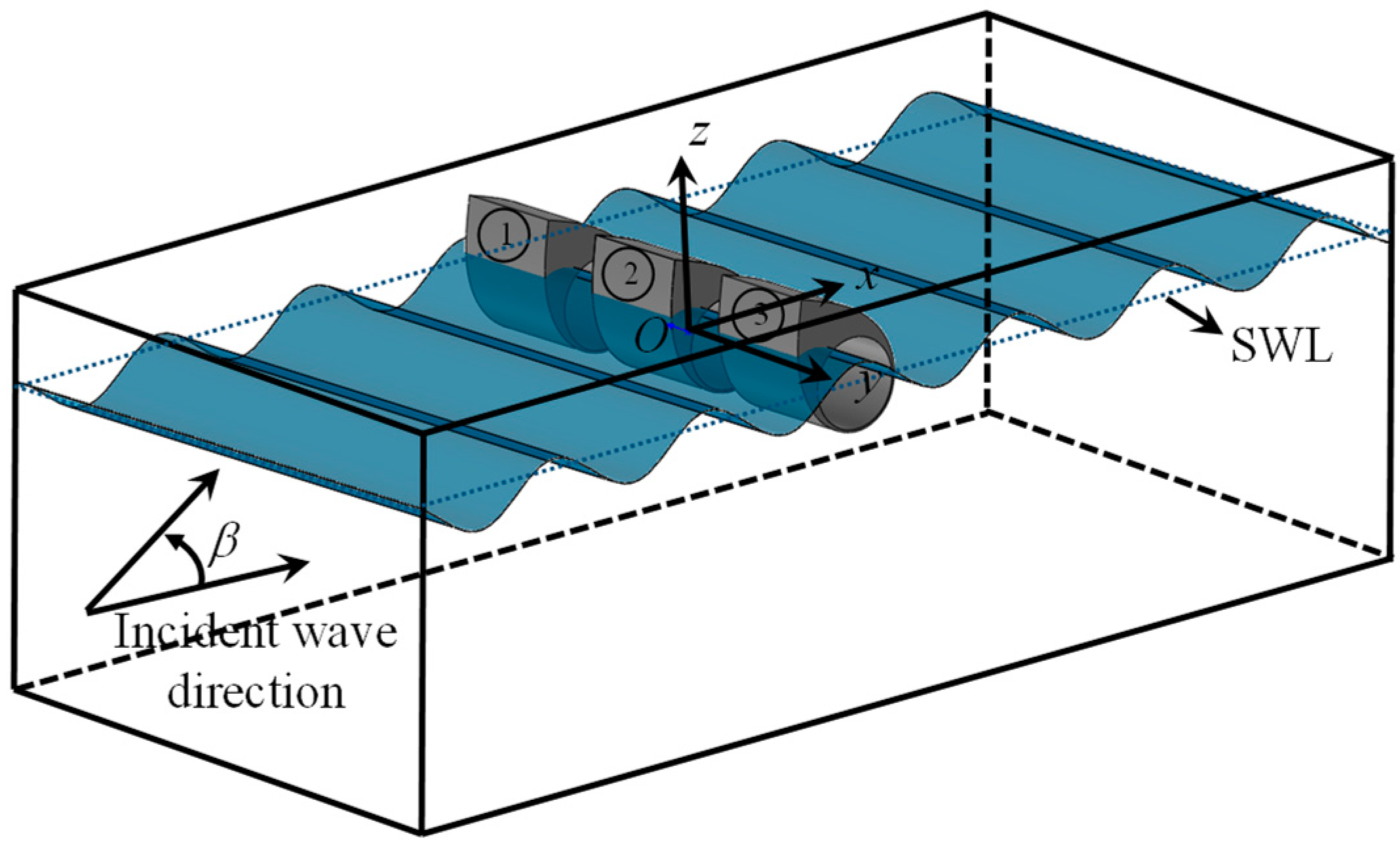
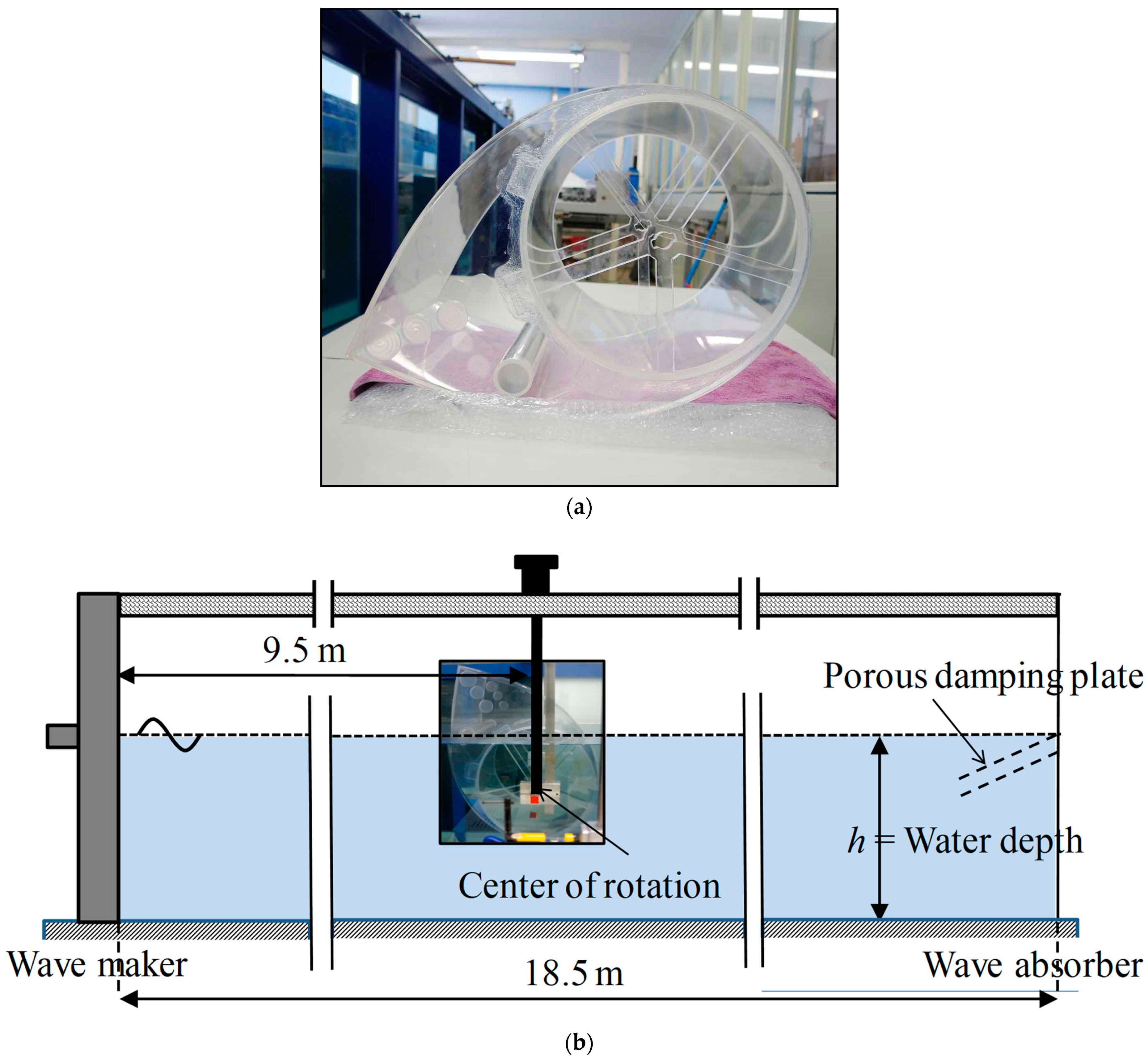
2. Mathematical Model and Experimental Setup
- n is the total number of WECs (n = 3 in the present study),
- is the mass moment of inertia of the Mth WEC in the pitch direction,
- is the hydrodynamic-added mass inertia of the Mth WEC in the pitch direction induced by the Sth motion of the Nth WEC,
- is the hydrodynamic radiation damping of the Mth WEC in the pitch direction induced by the Sth motion of the Nth WEC,
- is the viscous damping of the Mth WEC in the pitch direction,
- is the power take-off (PTO) damping of the Mth WEC in the pitch direction,
- is the hydrostatic stiffness moment of the Mth WEC in the pitch direction, and
- is the wave excitation moment acting on the Mth WEC in the pitch direction.
- The wave tank is equipped with a hydraulic piston-type wave maker at one end to generate waves and a wave absorber at the other end.
- The WEC rotates due to wave excitation around a fixed-axis shaft (y-direction) located below the waterline, and both ends of the shaft are connected to vertical rods, which are supported from the fixed frame along the wave flume.
- A ball bearing mechanism is provided for smooth rotation in the pitch motion.
- An image processing technique is used to measure the pitch motion of the WEC rotor.
3. Computational Fluid Dynamics
4. Results and Discussion
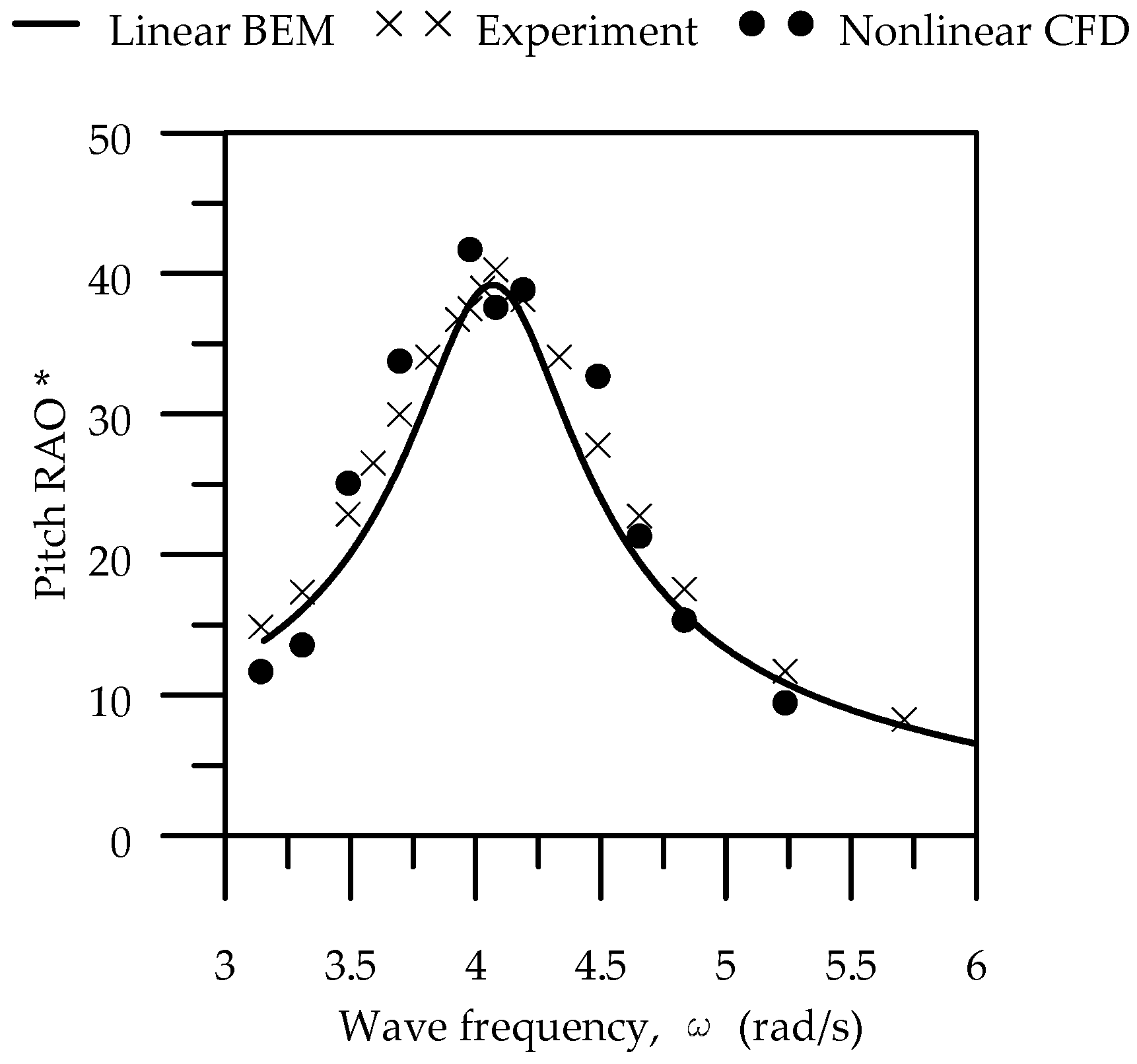
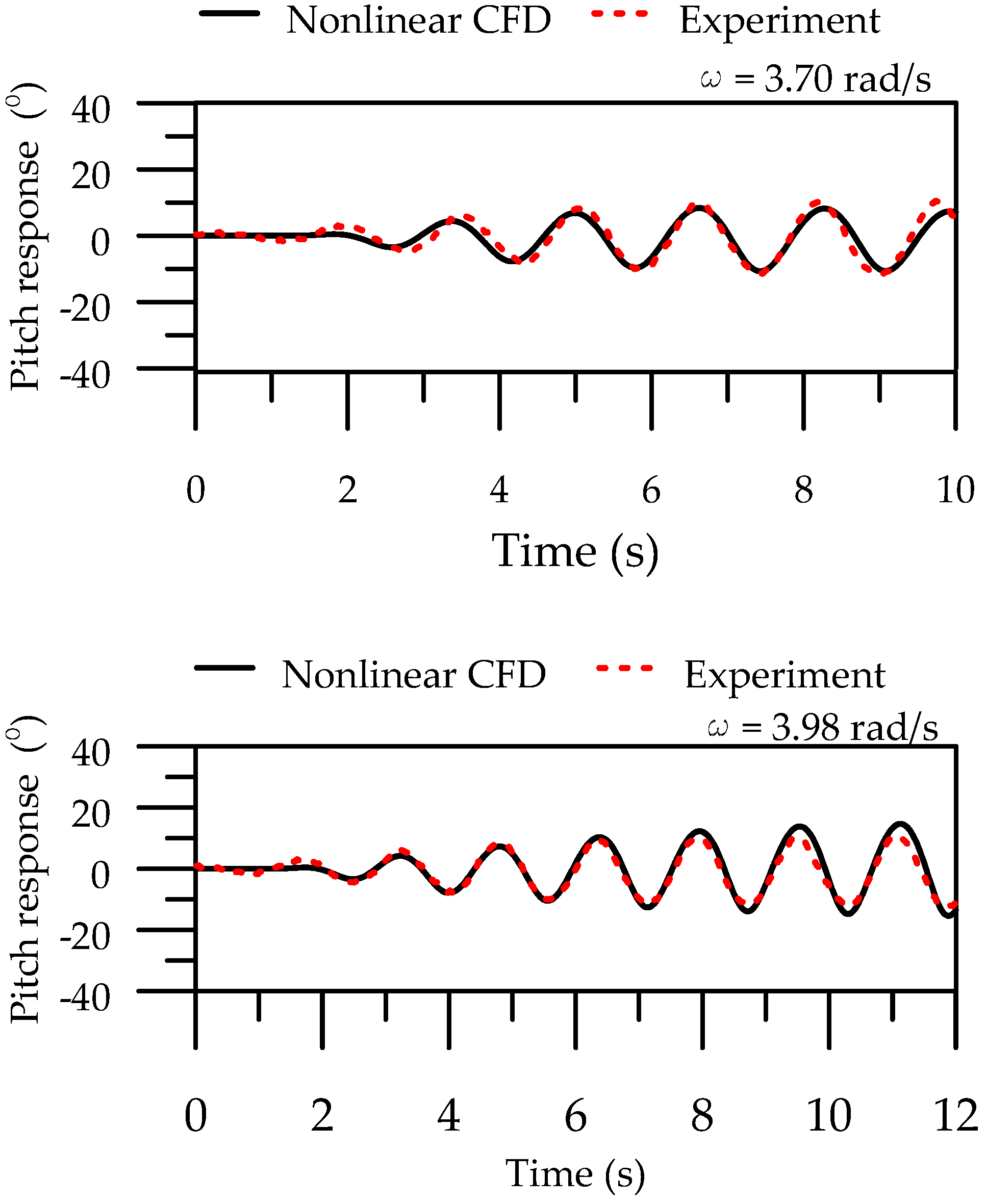
4.1. Validation
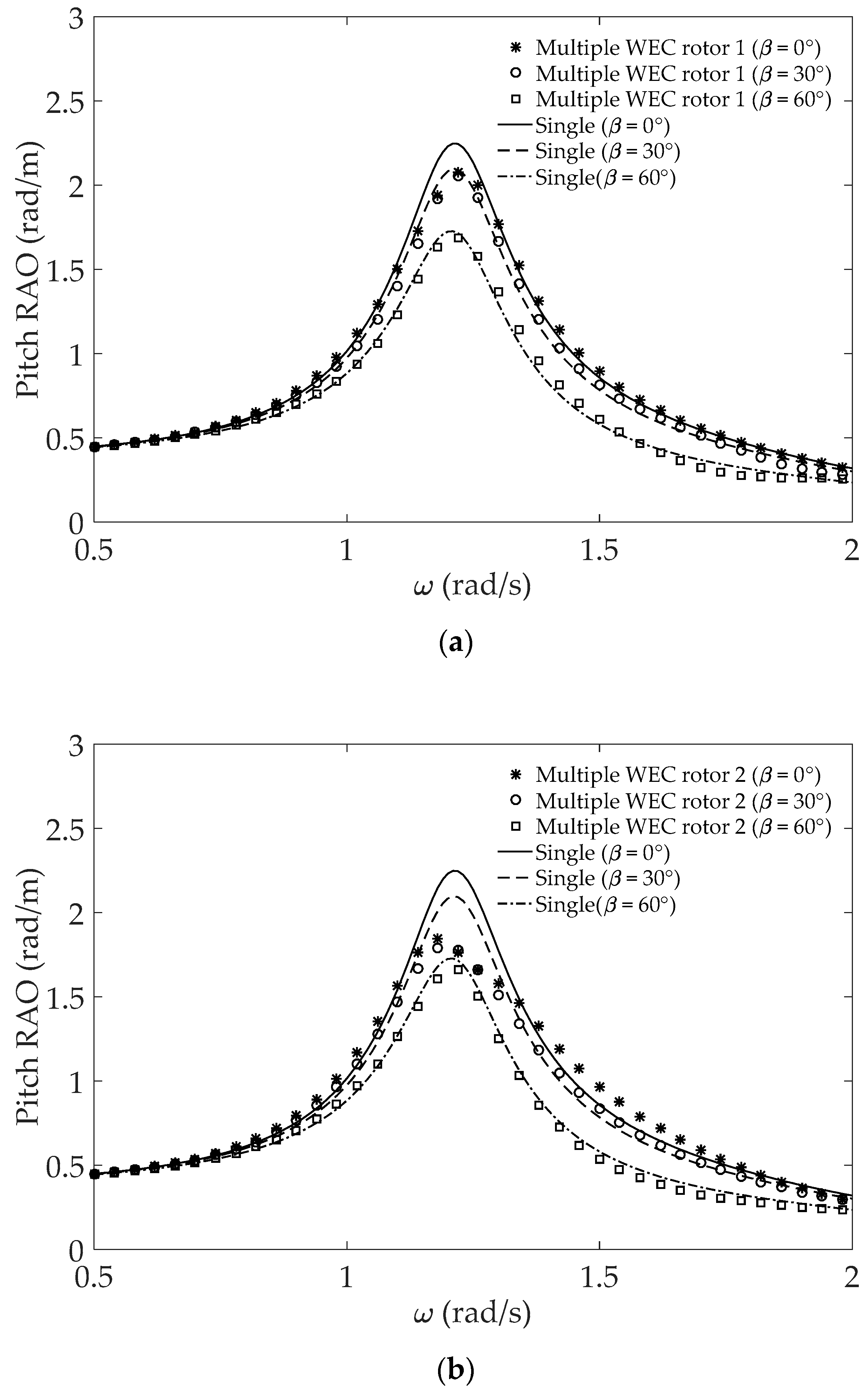
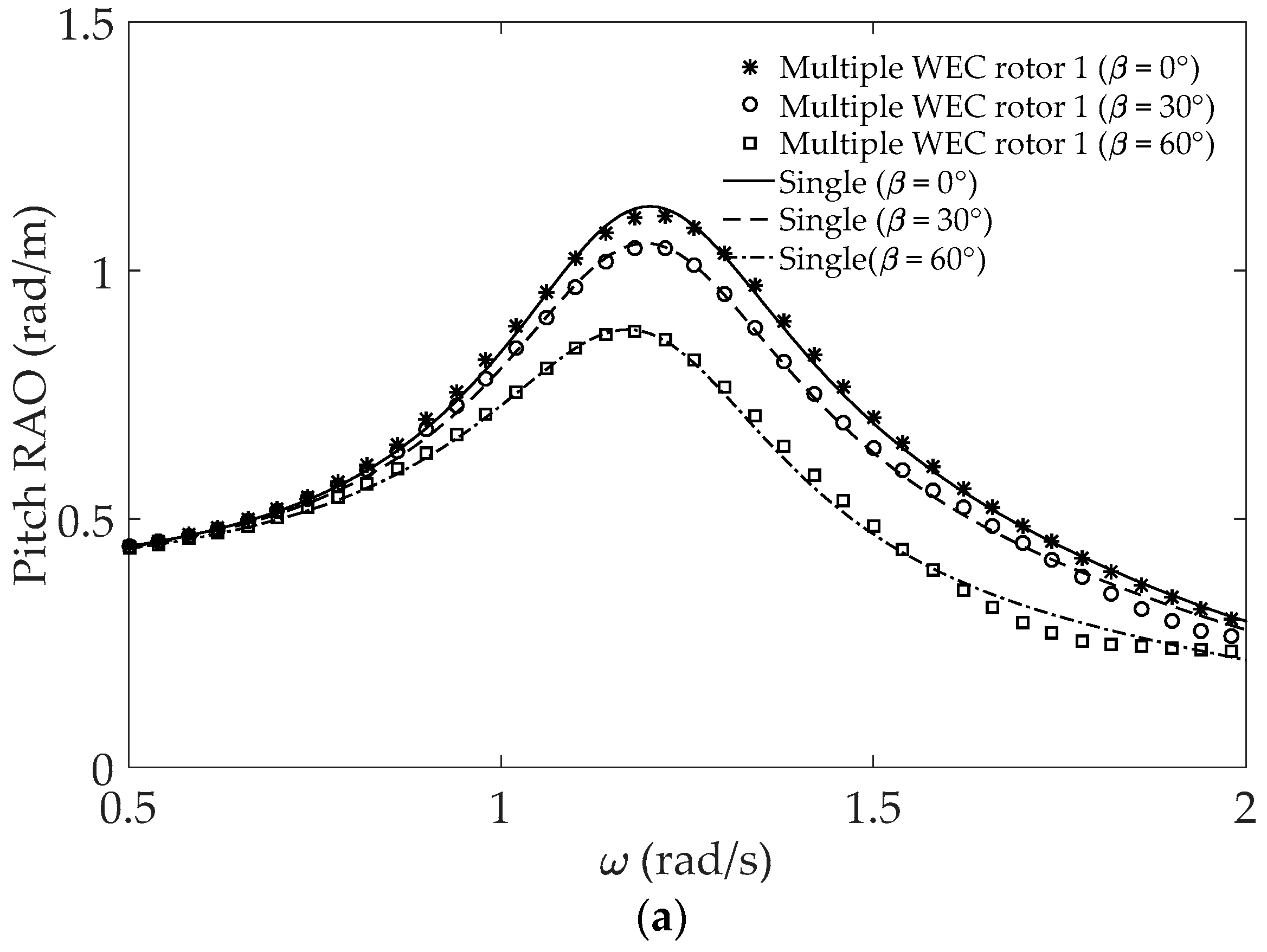
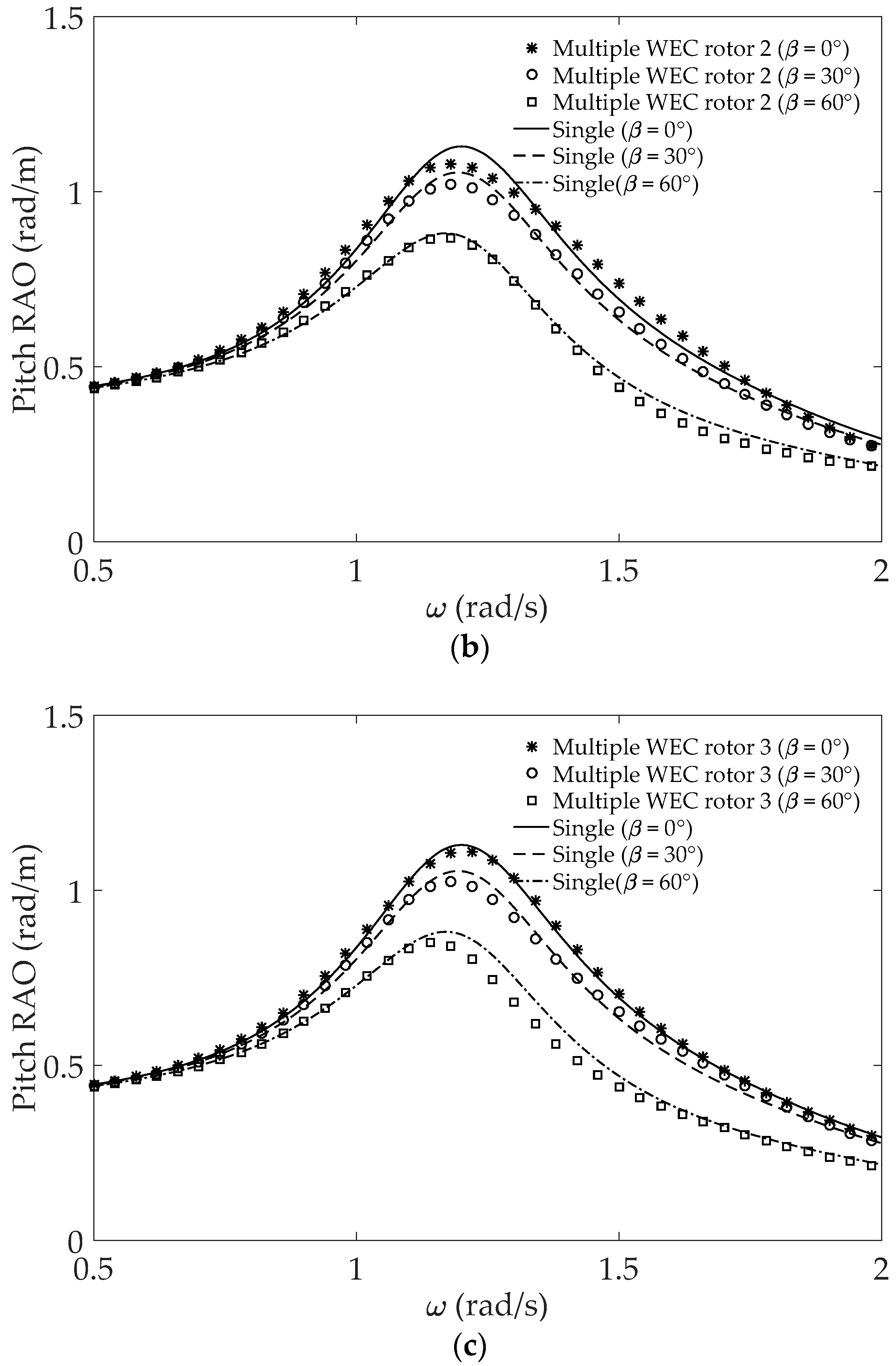
4.2. Multiple WEC Rotors
4.2.1. Linear BEM Results
- Each cell represents (peak frequency (rad/s), peak pitch RAO(rad/m)).
- First row: β = 0°, Second row: β = 30°, and Third row: β = 60°.
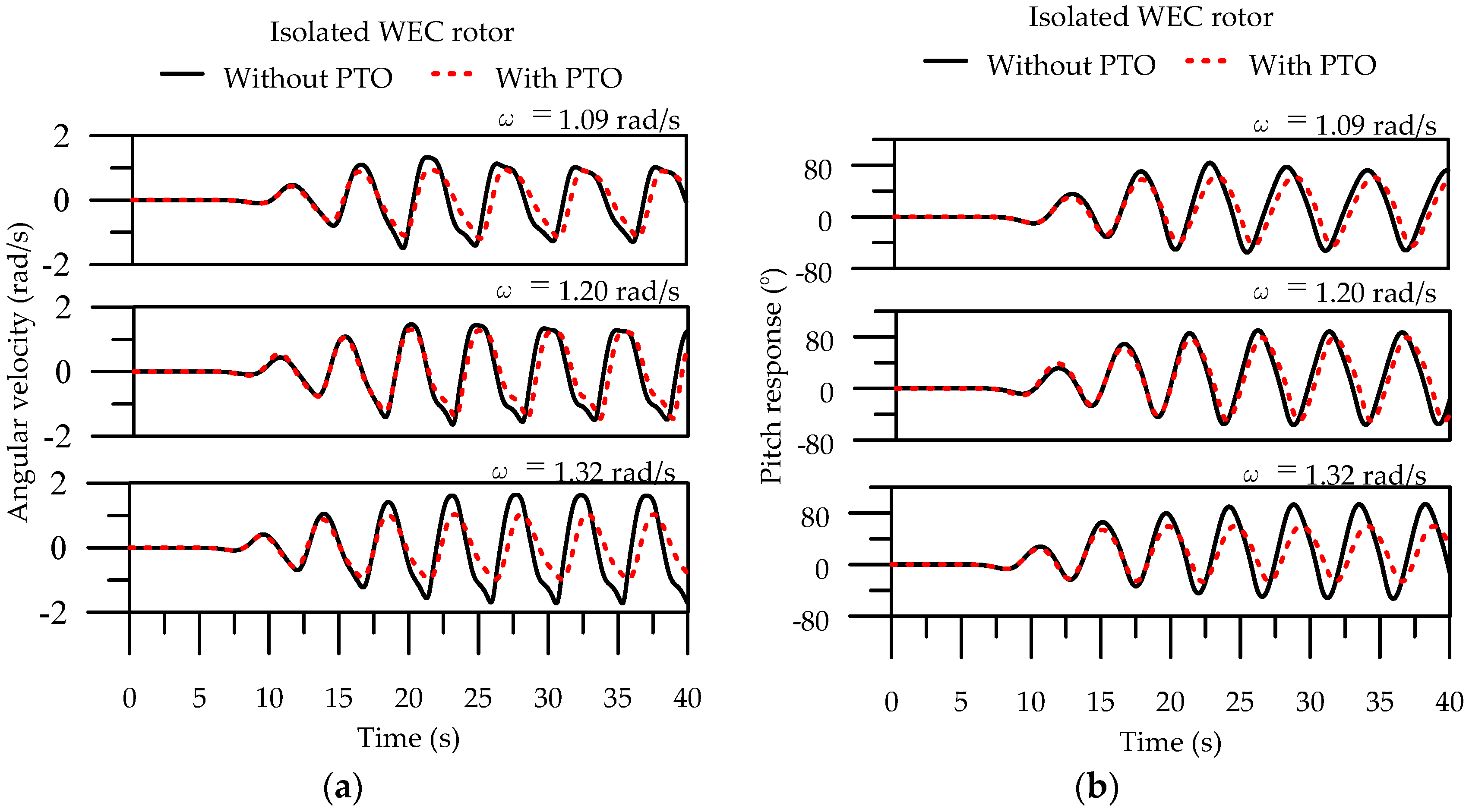
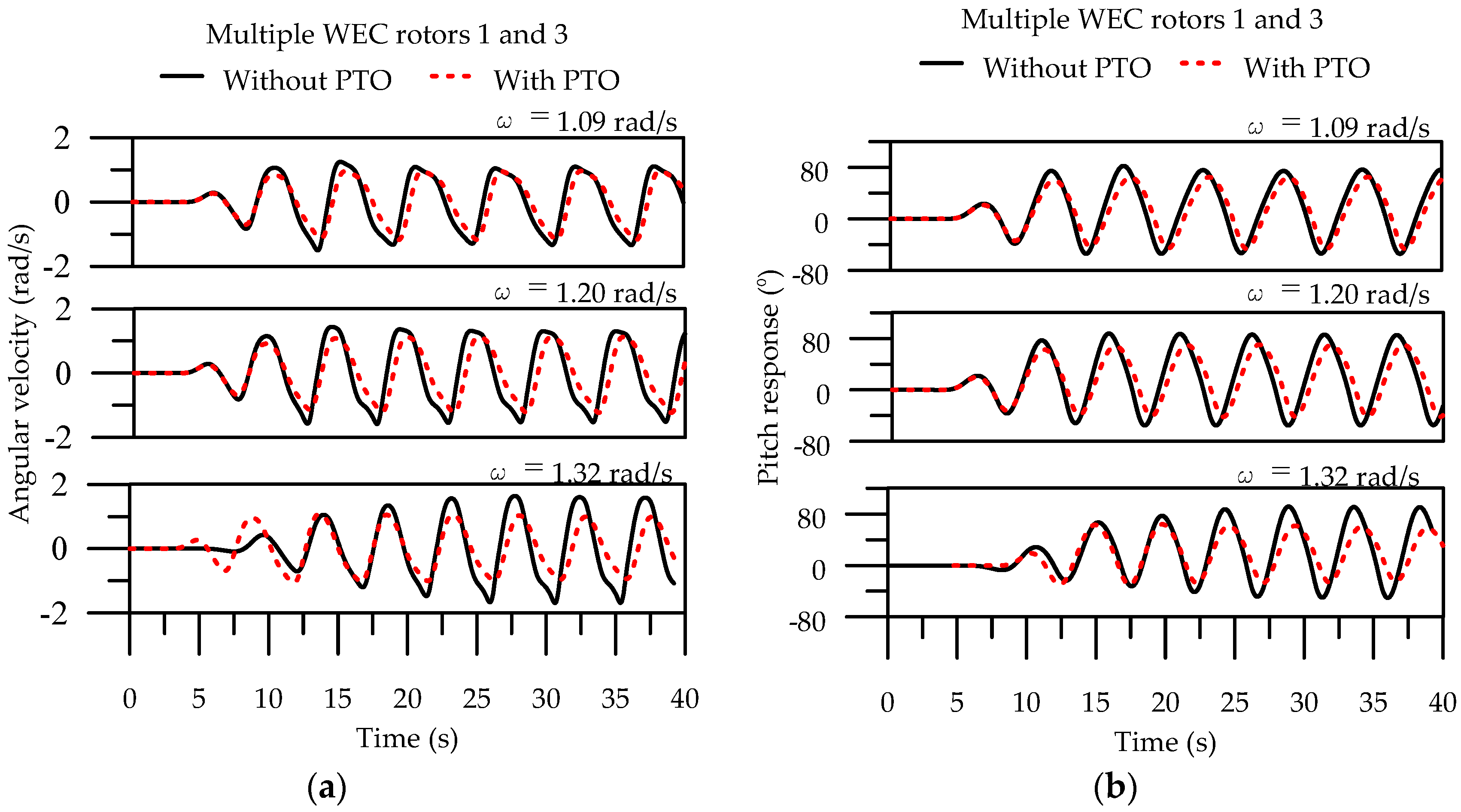
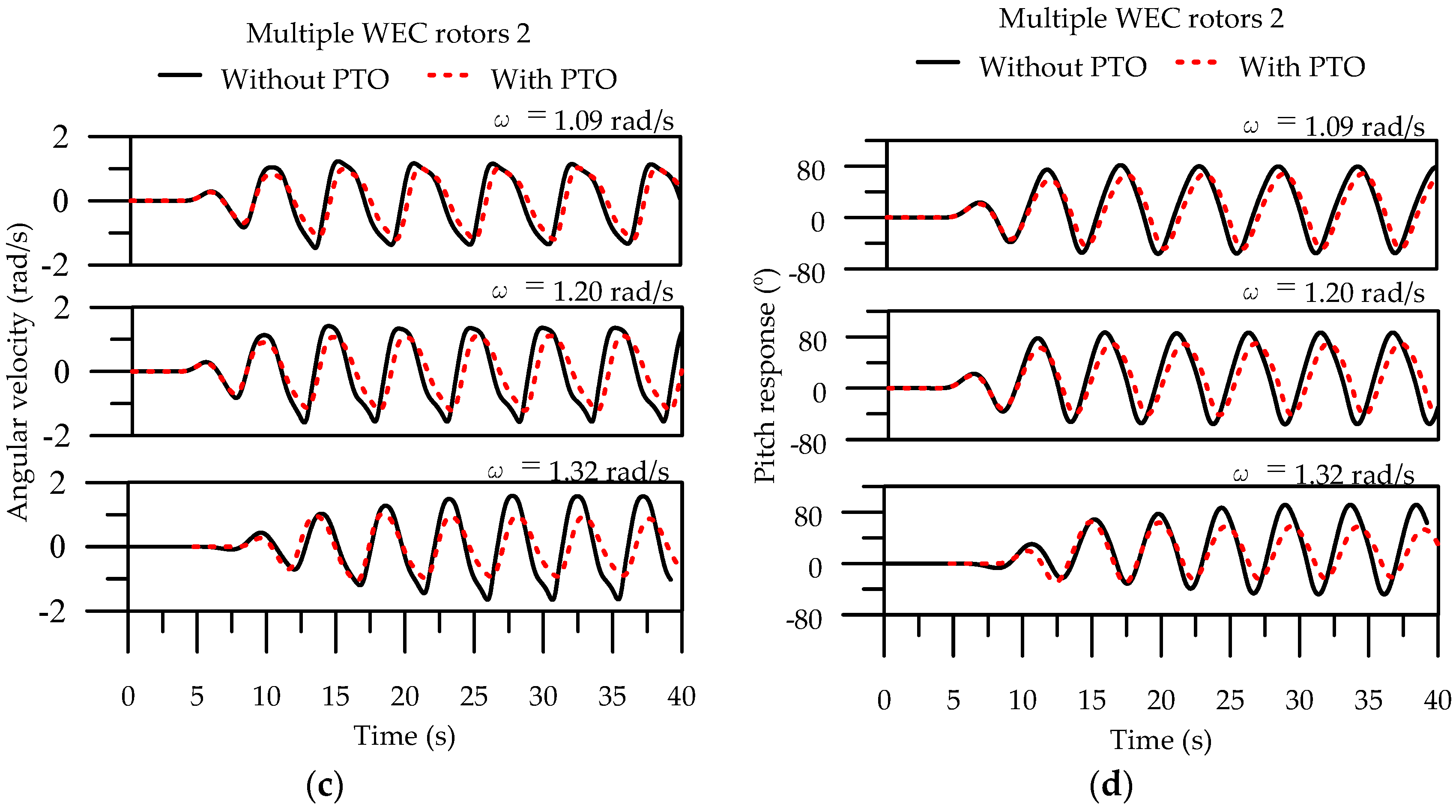
4.2.2. Nonlinear CFD Results
- First row: ω = 1.09 rad/s, Second row: ω = 1.2 rad/s, and Third row: 1.32 rad/s.
4.3. Optimal Time-Averaged Extracted Power
- First row: β = 0°, Second row: β = 30°, and Third row: β = 60°.
- First row: ω = 1.09 rad/s, Second row: ω = 1.2 rad/s, and Third row: 1.32 rad/s.
5. Conclusions
- The range of tested wave frequencies showed that the small wave-heading angle of the isolated WEC rotor increases the RAO while peak amplitudes are slightly affected in multiple WEC rotors with the linear BEM.
- The maximum reduction of the pitch RAO is focused around the peak frequency but insignificant elsewhere with the application of the PTO damping system.
- The q-factor demonstrated a constructive interaction in the range of (0.5 < ω < 1.08 and β ≤ 60°) and (1.34 < ω < 1.82 and β < 30°) for without PTO and (0.52 < ω < 1.1 and β ≤ 60°) and (1.33 < ω < 1.77 and β < 30°) for with PTO but destructive otherwise with the linear BEM.
- Investigation based on the prototype isolated and multiple WEC rotors, the pitch RAO, and the q-factor with without PTO at chosen wave frequencies demonstrated satisfactory overall consistency between the linear BEM and nonlinear CFD results, except for significant differences at 1.20 rad/s without PTO and 1.32 rad/s with PTO. These differences were qualified by nonlinear CFD simulations because the violent liquid motion at the center of the rotation leaves large slamming forces on the WEC rotor and leads to reduced and distinct responses from other wave frequencies.
- The estimated maximum time-averaged optimal power is distributed close to zero-heading angles around the resonance frequency and continuously decreases as the wave-heading angle increases.
- The linear BEM results showed overestimated extracted power compared with the nonlinear CFD due to the absence of nonlinear effects.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mclver, P. Wave Forces on Arrays of Floating Bodies. J. Eng. Math. 1984, 18, 273–285. [Google Scholar] [CrossRef]
- Kagemoto, H.; Yue, D.K. Interactions among multiple three-dimensional bodies in water waves: An exact algebraic method. J. Fluid Mech. 1986, 166, 189–209. [Google Scholar] [CrossRef]
- Mavrakos, S.A. Hydrodynamic coefficients for groups of interacting vertical axisymmetric bodies. Ocean Eng. 1991, 18, 485–515. [Google Scholar] [CrossRef]
- Pecher, A.; Kofoed, J.P.; Larsen, T.; Marchalot, T. Experimental study of the Weptos wave energy converter. In Proceedings of the ASME 2012 31st International Conference on Ocean, Offshore and Arctic Engineering (ASME 2012), Rio de Janeiro, Brazil, 1–6 July 2012; pp. 525–534. [Google Scholar]
- Pecher, A.; Kofoed, J.P.; Larsen, T. The extensive R&D behind the Weptos WEC. Renew. Energ. Offshore 2015, 351–358. [Google Scholar]
- Windt, C.; Davidson, J.; Ringwood, J.V. High-fidelity numerical modelling of ocean wave energy systems: A review of computational fluid dynamics-based numerical wave tanks. Renew. Sustain. Energy Rev. 2018, 93, 610–630. [Google Scholar] [CrossRef] [Green Version]
- Newman, J.N. Wave effects on multiple bodies. Hydrodyn. Ship Ocean Eng. 2001, 3, 3–26. [Google Scholar]
- Folley, M.; Babarit, A.; Child, B.; Forehand, D.; O’Boyle, L.; Silverthorne, K.; Spinneken, J.; Stratigaki, V.; Troch, P. A review of numerical modelling of wave energy converter arrays. In Proceedings of the ASME 2012 31st International Conference on Ocean, Offshore and Arctic Engineering 2012, American Society of Mechanical Engineers Digital Collection, Rio de Janeiro, Brazil, 1–6 July 2012; pp. 535–545. [Google Scholar]
- Folley, M. Numerical Modelling of Wave Energy Converters: State-of-the-Art Techniques for Single Devices and Arrays; Academic Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Ogden, D. Numerical Modelling Tool for Multibody Wave Energy Converters; University of Edinburgh: Edinburgh, Scotland, 2019. [Google Scholar]
- Taghipour, R.; Moan, T. Efficient frequency-domain analysis of dynamic response for the multi-buoy wave energy converter in multi-directional waves. In Proceedings of the 18th International Offshore and Polar Engineering Conference, Vancouver, WA, Canada, 6–11 July 2008. [Google Scholar]
- Thomas, S.; Weller, S.; Stallard, T.J. Float response within an array: Numerical and experimental comparison. In Proceedings of the 2nd International Conference on Ocean Energy (ICOE), Brest, France, 15–17 October 2008; Volume 1517. [Google Scholar]
- Folley, M.; Whittaker, T.J.T. The effect of sub-optimal control and the spectral wave climate on the performance of wave energy converter arrays. Appl. Ocean Res. 2009, 31, 260–266. [Google Scholar] [CrossRef]
- Bellew, S.; Stallard, T.; Stansby, P. Optimisation of a heterogeneous array of heaving bodies. In Proceedings of the 8th European Wave and Tidal Energy Conference 2009, Uppsala, Sweden, 7–11 September 2009; pp. 519–527. [Google Scholar]
- Cruz, J.; Sykes, R.; Siddorn, P.; Taylor, R.E. Estimating the loads and energy yield of arrays of wave energy converters under realistic seas. IET Renew. Power Gener. 2010, 4, 488–497. [Google Scholar] [CrossRef]
- Borgarino, B.; Babarit, A.; Ferrant, P. Impact of wave interactions effects on energy absorption in large arrays of wave energy converters. Ocean Eng. 2012, 41, 79–88. [Google Scholar] [CrossRef] [Green Version]
- Flavia, F.F. A Numerical Tool for the Frequency Domain Simulation of Large Clusters of Wave Energy Converters. Ph.D. Thesis, Ecole Centrale de Nantes, Nantes, France, 2017. [Google Scholar]
- Babarit, A.; Borgarino, B.; Ferrant, P.; Clément, A. Assessment of the influence of the distance between two wave energy converters on energy production. IET Renew. Power Gener. 2010, 4, 592–601. [Google Scholar] [CrossRef] [Green Version]
- Hansen, R.H.; Kramer, M.M. Modelling and control of the wavestar prototype. In Proceedings of the 9th European Wave and Tidal Energy Conference (EWTEC 2011), Southampton, UK, 5–9 September 2021. [Google Scholar]
- Nambiar, A.J.; Forehand, D.I.; Kramer, M.M.; Hansen, R.H.; Ingram, D.M. Effects of hydrodynamic interactions and control within a point absorber array on electrical output. Int. J. Mar. Energy 2015, 9, 20–40. [Google Scholar] [CrossRef]
- Forehand, D.I.; Kiprakis, A.E.; Nambiar, A.J.; Wallace, A.R. A fully coupled wave-to-wire model of an array of wave energy converters. IEEE Trans. Sustain. Energy 2015, 7, 118–128. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.; Gao, F.; Meng, X.; Fu, J. Design of the wave energy converter array to achieve constructive effects. Ocean Eng. 2016, 124, 13–20. [Google Scholar] [CrossRef]
- Agamloh, E.B.; Wallace, A.K.; Von Jouanne, A. Application of fluid–structure interaction simulation of an ocean wave energy extraction device. Renew. Energy 2008, 33, 748–757. [Google Scholar] [CrossRef]
- Westphalen, J.; Greaves, D.; Williams, C.; Taylor, P.; Causon, D.; Mingham, C.; Hu, Z.; Stansby, P.B.R.; Omidvar, P. Extreme Wave Loading on Offshore Wave Energy Devices Using CFD: A Hierarchical Team Approach. In Proceedings of the 8th European Wave and Tidal Energy Conference Uppsala, Uppsala, Sweden, 7–10 September 2009. [Google Scholar]
- Windt, C.; Davidson, J.; Ransley, E.J.; Greaves, D.; Jakobsen, M.; Kramer, M.; Ringwood, J.V. Validation of a CFD-based numerical wave tank model for the power production assessment of the wavestar ocean wave energy converter. Renew. Energy 2020, 146, 2499–2516. [Google Scholar] [CrossRef]
- Salter, S.H. Wave power. Nature 1974, 249, 720–724. [Google Scholar] [CrossRef]
- Poguluri, S.K.; Bae, Y.H. A study on performance assessment of WEC rotor in the Jeju western waters. Ocean. Syst. Eng. 2018, 8, 361–380. [Google Scholar]
- Poguluri, S.K.; Ko, H.S.; Bae, Y.H. CFD Investigation of Pitch-Type Wave Energy Converter-Rotor Based on RANS Simulations; Ships and Offshore Structures: Cambridge, UK, 2019; pp. 1–13. [Google Scholar]
- Kim, D.; Sik, K.H.; Bae, Y.H. Performance Analysis of Multiple Wave Energy Converters due to Rotor Spacing. J. Ocean. Eng. Technol. 2021, 35, 229–237. [Google Scholar]
- Poguluri, S.K.; Cho, I.H.; Bae, Y.H. A Study of the Hydrodynamic Performance of a Pitch-type Wave Energy Converter–Rotor. Energies 2019, 12, 842. [Google Scholar] [CrossRef] [Green Version]
- Kim, D.; Poguluri, S.K.; Ko, H.S.; Lee, H.; Bae, Y.H. Numerical and Experimental Study on Linear Behavior of Salter’s Duck Wave Energy Converter. J. Ocean. Eng. Technol. 2019, 33, 116–122. [Google Scholar] [CrossRef] [Green Version]
- Hadzic, H. Development and Application of Finite Volume Method for the Computation of Flows Around Moving Bodies on Unstructured, Overlapping Grids; Technische Universität Hamburg: Hamburg, Germany, 2006. [Google Scholar]








| Description | Prototype | Model (1:11) |
|---|---|---|
| Stern diameter, 2r (m) | 4 | 0.364 |
| Depth of submergence, d (m) | 3.6 | 0.3275 |
| Beak angle, α (°) | 60 | 60 |
| Width, W (m) | 5 | 0.455 |
| Total mass (kg) | 21,327.686 | 13.65 |
| Pitch moment of inertia around the center of rotation, COR (kg⋅m2) | 117,132.05 | 0.7479 |
| Hydrostatic coefficient, K55/ρg | 22.52 | 0.16398 × 10−2 |
| Horizontal center of gravity w.r.t. COR (m) | −0.8934 | −0.0931 |
| Vertical center of gravity w.r.t. COR (m) | 1.0189 | 0.0998 |
| Pitch natural frequency, ω (rad/s) | 1.22 | 4.08 |
| Isolated | Multiple | |||
|---|---|---|---|---|
| Rotor 1 | Rotor 2 | Rotor 3 | ||
| Without PTO | 1.21, 2.248 | 1.23, 2.078 | 1.18, 1.844 | 1.23, 2.078 |
| 1.21, 2.096 | 1.22, 2.053 | 1.20, 1.803 | 1.19, 1.859 | |
| 1.21, 1.727 | 1.21, 1.690 | 1.21, 1.664 | 1.18, 1.659 | |
| With PTO | 1.20, 1.130 | 1.20, 1.113 | 1.18, 1.081 | 1.20, 1.113 |
| 1.19, 1.055 | 1.20, 1.050 | 1.18, 1.021 | 1.18, 1.025 | |
| 1.17, 0.881 | 1.17, 0.880 | 1.17, 0.870 | 1.15, 0.852 | |
| Solution | PTO Damping | Isolated WEC Rotor | Multiple | q-factor | ||
|---|---|---|---|---|---|---|
| WEC Rotor 1 | WEC Rotor 2 | WEC Rotor 3 | ||||
| Linear BEM | Without | 1.473 | 1.446 | 1.513 | 1.446 | 0.997 |
| 2.231 | 2.027 | 1.816 | 2.027 | 0.877 | ||
| 1.627 | 1.645 | 1.526 | 1.645 | 0.987 | ||
| With | 1.344 | 1.343 | 1.359 | 1.343 | 1.003 | |
| 1.506 | 1.484 | 1.435 | 1.484 | 0.975 | ||
| 1.326 | 1.337 | 1.300 | 1.337 | 0.999 | ||
| Nonlinear CFD | Without | 1.525 | 1.509 | 1.575 | 1.509 | 1.004 |
| 1.674 | 1.645 | 1.656 | 1.645 | 0.985 | ||
| 1.651 | 1.601 | 1.574 | 1.601 | 0.964 | ||
| With | 1.242 | 1.299 | 1.361 | 1.299 | 1.063 | |
| 1.501 | 1.289 | 1.285 | 1.289 | 0.858 | ||
| 1.000 | 0.997 | 0.916 | 0.997 | 0.970 | ||
| Solution | Isolated WEC Rotor | Multiple | ||
|---|---|---|---|---|
| WEC Rotor 1 | WEC Rotor 2 | WEC Rotor 3 | ||
| Linear | 32.834 | 32.375 | 29.577 | 32.375 |
| 28.364 | 28.303 | 26.370 | 26.350 | |
| 19.043 | 19.094 | 18.563 | 17.082 | |
| Solution | Isolated | Multiple | ||
|---|---|---|---|---|
| WEC Rotor 1 | WEC Rotor 2 | WEC Rotor 3 | ||
| Linear | 20.908 | 20.879 | 21.360 | 20.879 |
| 31.791 | 30.874 | 28.885 | 30.874 | |
| 29.800 | 30.347 | 28.658 | 30.348 | |
| Nonlinear | 17.836 | 19.521 | 21.440 | 19.521 |
| 26.054 | 19.209 | 19.109 | 19.209 | |
| 11.570 | 11.494 | 9.716 | 11.494 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Poguluri, S.K.; Kim, D.; Bae, Y.H. Hydrodynamic Analysis of a Multibody Wave Energy Converter in Regular Waves. Processes 2021, 9, 1233. https://doi.org/10.3390/pr9071233
Poguluri SK, Kim D, Bae YH. Hydrodynamic Analysis of a Multibody Wave Energy Converter in Regular Waves. Processes. 2021; 9(7):1233. https://doi.org/10.3390/pr9071233
Chicago/Turabian StylePoguluri, Sunny Kumar, Dongeun Kim, and Yoon Hyeok Bae. 2021. "Hydrodynamic Analysis of a Multibody Wave Energy Converter in Regular Waves" Processes 9, no. 7: 1233. https://doi.org/10.3390/pr9071233
APA StylePoguluri, S. K., Kim, D., & Bae, Y. H. (2021). Hydrodynamic Analysis of a Multibody Wave Energy Converter in Regular Waves. Processes, 9(7), 1233. https://doi.org/10.3390/pr9071233






