Thermodynamic Analysis of Brownian Motion-Induced Particle Agglomeration Using the Taylor-Series Expansion Method of Moments
Abstract
:1. Introduction
2. Theory and Model
2.1. Brownian Agglomeration
2.2. Taylor Series Expansion Method of Moments
2.3. Principle of Maximum Entropy
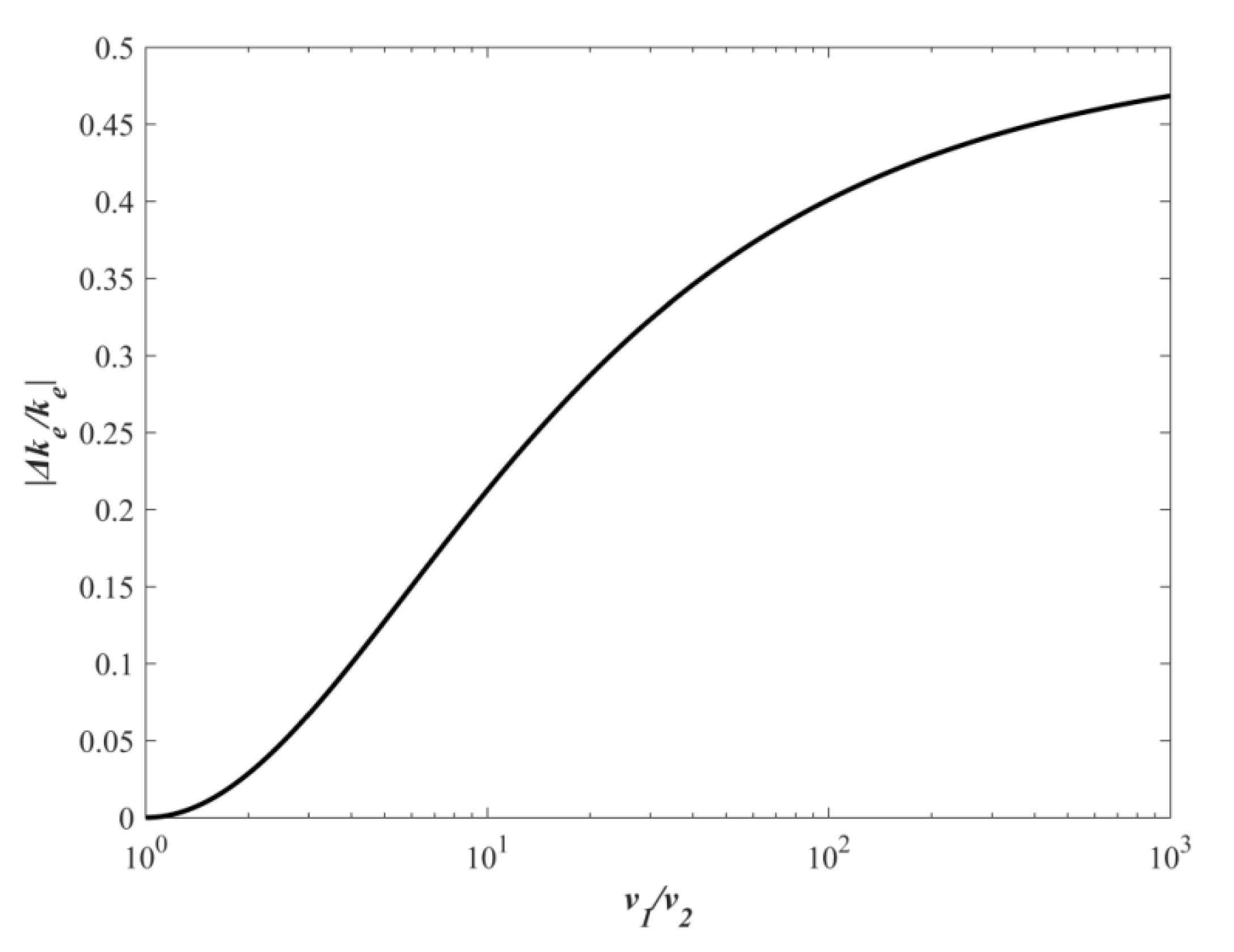
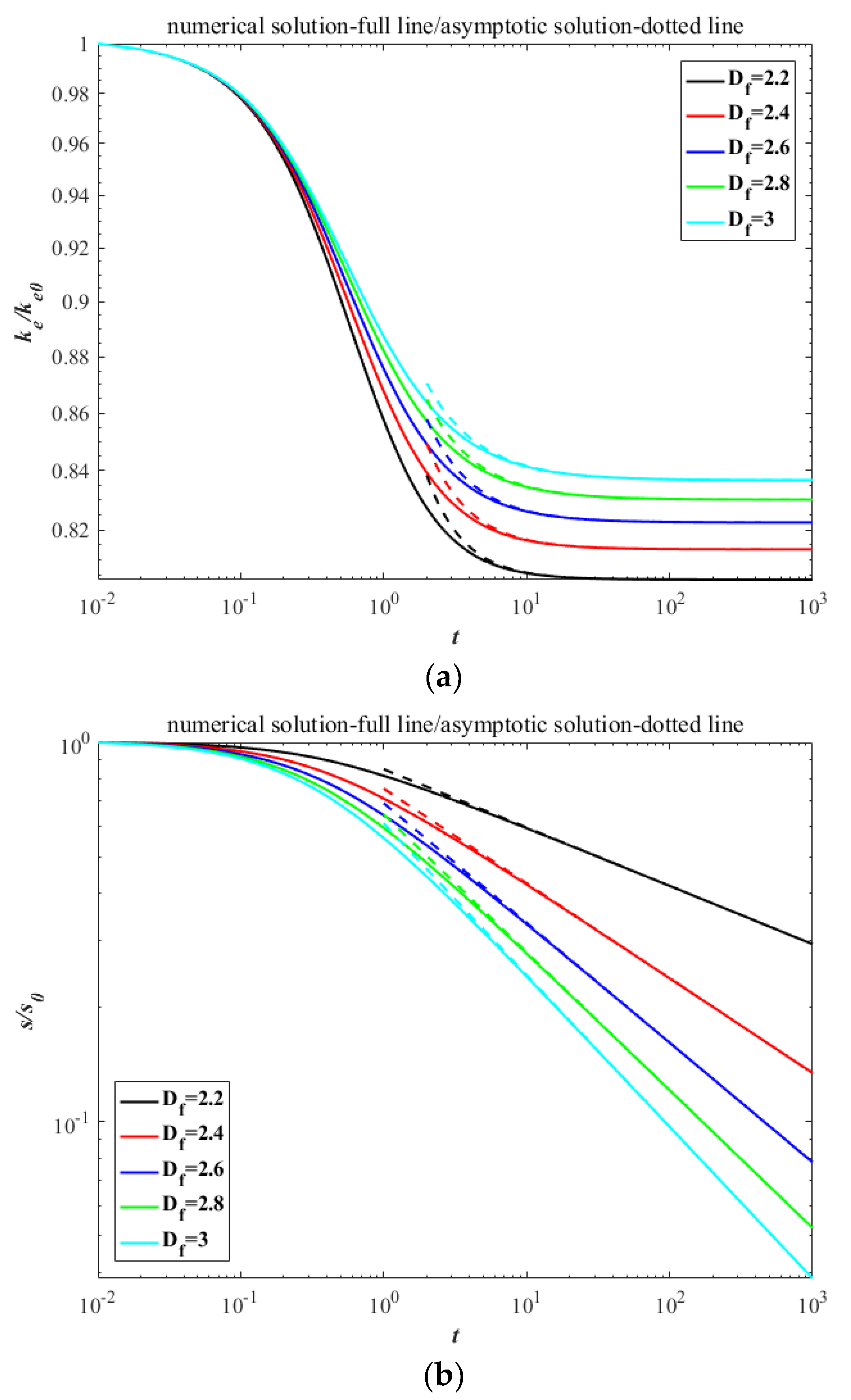
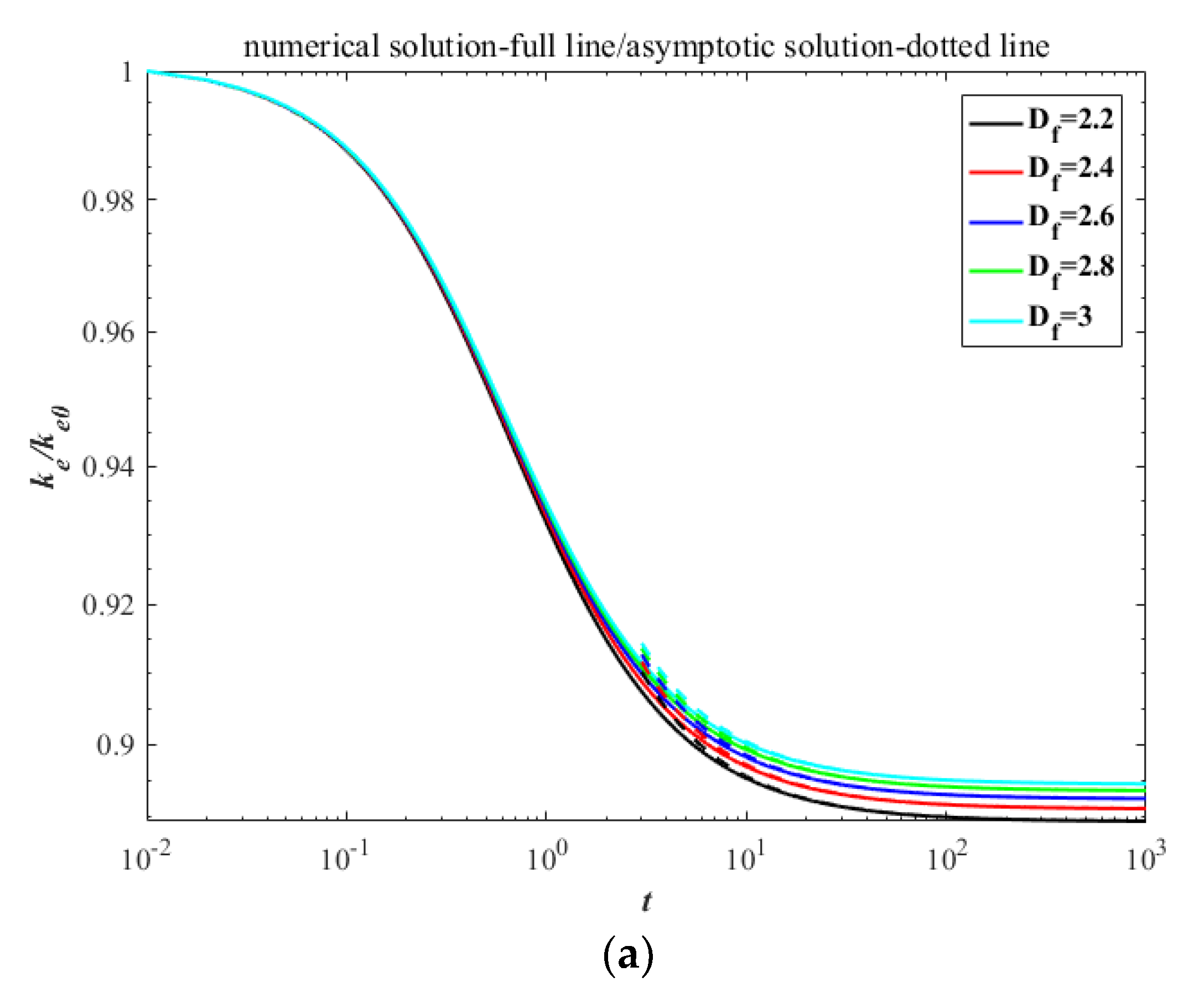
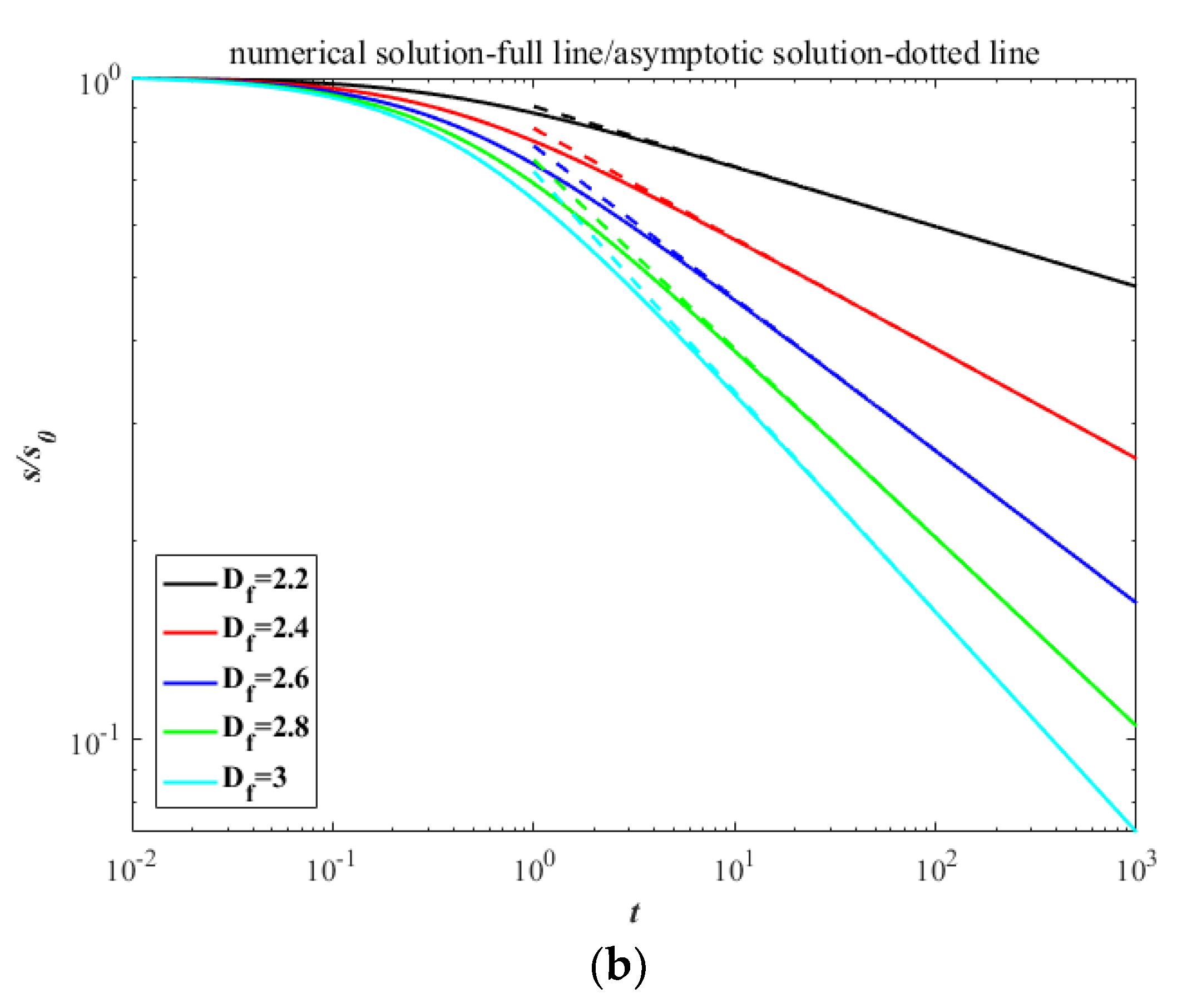
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Appendix A. The Asymptotic Solutions of TEMOM Model for Brownian Agglomeration
References
- Friedlander, S.K. Smoke, Dust and Haze: Fundamentals of Aerosol Dynamics, 2nd ed.; Oxford University Press: London, UK, 2000. [Google Scholar]
- Hu, B.; Yi, Y.; Liang, C.; Yuan, Z.L.; Szczepan, R.; Yang, L.J. Experimental study on particles agglomeration by chemical and turbulent agglomeration before electrostatic precipitators. Powder Technol. 2018, 335, 186–194. [Google Scholar]
- Yan, J.P.; Chen, L.Q.; Lin, Q. Removal of fine particles in WFGD system using the simultaneous acoustic agglomeration and supersaturated vapor condensation. Powder Technol. 2017, 315, 106–113. [Google Scholar] [CrossRef]
- Müller, H. Zur allgemeinen theorie ser raschen koagulation. Kolloidchem. Beih. 1928, 27, 223–250. [Google Scholar] [CrossRef]
- Dürr, R.; Bück, A. Approximate moment methods for population balance equations in particulate and bioengineering processes. Processes 2020, 8, 414. [Google Scholar] [CrossRef] [Green Version]
- Pratsinis, S.E. Simultaneous nucleation, condensation and coagulation in aerosol reactors. J. Colloid Interface Sci. 1988, 124, 416–427. [Google Scholar] [CrossRef]
- Gelbard, F.; Tambour, Y.; Seinfeld, J.H. Sectional representations for simulating aerosol dynamics. J. Colloid Interface Sci. 1980, 76, 541–556. [Google Scholar] [CrossRef]
- Tandon, P.; Rosner, D.E. Monte Carlo simulation of particle aggregation and simultaneous restructuring. J. Colloid Interface Sci. 1999, 213, 273–286. [Google Scholar] [CrossRef] [PubMed]
- Yu, M.Z.; Lin, J.Z.; Chan, T. A new moment method for solving the coagulation equation for particles in Brownian motion. Aerosol Sci. Technol. 2008, 42, 705–713. [Google Scholar] [CrossRef]
- Xie, M.L. Asymptotic behavior of TEMOM model for particle population balance equation over the entire particle size regimes. J. Aerosol Sci. 2014, 67, 157–165. [Google Scholar] [CrossRef]
- Xie, M.L. Asymptotic solution of moment approximation of the particle population balance equation for Brownian agglomeration. Aerosol Sci. Technol. 2015, 49, 109–114. [Google Scholar] [CrossRef]
- Chen, Z.L.; Lin, J.Z.; Yu, M.Z. Asymptotic behavior of the Taylor-expansion method of moments for solving a coagulation equation for Brownian particles. Particuology 2014, 14, 124–129. [Google Scholar] [CrossRef]
- Xie, M.L.; Wang, L.P. Asymptotic solution of population balance equation based on TEMOM model. Chem. Eng. Sci. 2013, 94, 79–83. [Google Scholar]
- Xie, M.L.; He, Q. Analytical solution of TEMOM model for particle population balance equation due to Brownian coagulation. J. Aerosol Sci. 2013, 66, 24–30. [Google Scholar]
- Friedlander, S.; Wang, C. The self-preserving particle size distribution for coagulation by Brownian motion. J. Colloid Interface Sci. 1966, 22, 126–132. [Google Scholar] [CrossRef]
- Trizac, E.; Krapivsky, P.L. Correlations in Ballistic Processes. Phys. Rev. Lett. 2003, 91, 218–302. [Google Scholar] [CrossRef] [Green Version]
- Xie, M.L. On the growth rate of particle surface area for Brownian coagulation. J. Aerosol Sci. 2017, 113, 36–39. [Google Scholar]
- Xie, M.L.; Yu, M.Z. Thermodynamic analysis of Brownian coagulation based on moment method. Int. J. Heat Mass Transf. 2018, 122, 922–928. [Google Scholar] [CrossRef]
- Yu, M.Z.; Lin, J.Z. Taylor series expansion scheme applied for solving population balance equation. Rev. Chem. Eng. 2017, 34, 561–594. [Google Scholar] [CrossRef]
- Cao, L.N.Y.; Chen, S.C.; Fissan, H.; Asbach, C.; Pui, D.Y.H. Development of a geometric surface area monitor (GSAM) for aerosol nanoparticles. J. Aerosol Sci. 2017, 114, 118–129. [Google Scholar] [CrossRef]
- He, Q.; Shchekin, A.K.; Xie, M.L. New analytical TEMOM solutions for a class of collision kernels in the theory of Brownian coagulation. Phys. A 2015, 428, 435–442. [Google Scholar] [CrossRef]
- Wu, M.; Friedlander, S. Enhanced power law agglomerate growth in the free molecule regime. J. Aerosol Sci. 1993, 24, 273–282. [Google Scholar] [CrossRef]
- Legrand, D.G.; Gaines, G.L. The molecular weight dependence of polymer surface tension. J. Colloid Interface Sci. 1969, 31, 162–167. [Google Scholar] [CrossRef]
- Legrand, D.G.; Gaines, G.L. Surface Tension of Homologous Series of Liquids. J. Colloid Interface Sci. 1973, 42, 181–184. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Q.; Xie, M. Thermodynamic Analysis of Brownian Motion-Induced Particle Agglomeration Using the Taylor-Series Expansion Method of Moments. Processes 2021, 9, 1218. https://doi.org/10.3390/pr9071218
He Q, Xie M. Thermodynamic Analysis of Brownian Motion-Induced Particle Agglomeration Using the Taylor-Series Expansion Method of Moments. Processes. 2021; 9(7):1218. https://doi.org/10.3390/pr9071218
Chicago/Turabian StyleHe, Qing, and Mingliang Xie. 2021. "Thermodynamic Analysis of Brownian Motion-Induced Particle Agglomeration Using the Taylor-Series Expansion Method of Moments" Processes 9, no. 7: 1218. https://doi.org/10.3390/pr9071218
APA StyleHe, Q., & Xie, M. (2021). Thermodynamic Analysis of Brownian Motion-Induced Particle Agglomeration Using the Taylor-Series Expansion Method of Moments. Processes, 9(7), 1218. https://doi.org/10.3390/pr9071218




