Abstract
In systems biology, biological phenomena are often modeled by Ordinary Differential Equations (ODEs) and distributed in the de facto standard file format SBML. The primary analyses performed with such models are dynamic simulation, steady-state analysis, and parameter estimation. These methodologies are mathematically formalized, and libraries for such analyses have been published. Several tools exist to create, simulate, or visualize models encoded in SBML. However, setting up and establishing analysis environments is a crucial hurdle for non-modelers. Therefore, easy access to perform fundamental analyses of ODE models is a significant challenge. We developed SBMLWebApp, a web-based service to execute SBML-based simulation, steady-state analysis, and parameter estimation directly in the browser without the need for any setup or prior knowledge to address this issue. SBMLWebApp visualizes the result and numerical table of each analysis and provides a download of the results. SBMLWebApp allows users to select and analyze SBML models directly from the BioModels Database. Taken together, SBMLWebApp provides barrier-free access to an SBML analysis environment for simulation, steady-state analysis, and parameter estimation for SBML models. SBMLWebApp is implemented in Java™ based on an Apache Tomcat® web server using COPASI, the Systems Biology Simulation Core Library (SBSCL), and LibSBMLSim as simulation engines. SBMLWebApp is licensed under MIT with source code freely available. At the end of this article, the Data Availability Statement gives the internet links to the two websites to find the source code and run the program online.
1. Introduction
An enormous intrinsic complexity characterizes biological systems from their smallest independently functioning unit, the individual cell, to entire organ systems and beyond. This complexity can be attributed to emergent characteristics of the individual components of biological systems and their interactions [1]. Consequently, any attempt to fully grasp the functions and simultaneously operating processes within a living organism nowadays heavily relies on computational tools and simulation. Building computer models in biology has already demonstrated its potential in many application areas, such as the contextualization and visualization of high-throughput data, e.g., [2], guiding metabolic engineering in biotechnology, e.g., [3], the directed search for potential antiviral targets, e.g., [4,5], or to mathematically describe measures to effectively control the spread of infections, e.g., [6]. Since computational modeling of biological systems remains a challenging task, several different approaches exist to derive model representations with varying simplifying assumptions, each of which tackles the underlying complexities in many ways. Examples of popular modeling strategies include:
- agent-based models, e.g., [7] which prove fruitful for non-linear interactions among entities of a biological system [8].
- qualitative models, e.g., [9,10], which offer a flexible framework to delineate the main properties of complex biological regulatory networks [11].
- statistical models, e.g., [12] and modeling approaches that are based on machine learning, e.g., [13], both of which provide probabilities of observed events.
- constraint-based models, e.g., [14] that predict metabolic and adjoint cellular functions based on the distribution of metabolic fluxes.
- stochastic kinetic models [15], which take random fluctuations of the amounts of individual molecules into account.
- deterministic kinetic models, e.g., [16], which will be explained in detail below.
- multi-paradigm models that try to bridge two or more of these approaches, e.g., [17].
The present study focuses on kinetic models. Kinetic models allow capturing the complex relationships of biological systems, e.g., between enzyme expression, metabolite levels, reaction fluxes, and regulatory processes [18]. Kinetic models are of particular interest when exploring dynamic effects [19]. The mathematical description of kinetic models can be formalized using a system of coupled nonlinear ODEs [20], which defines the state variables of the model and their possible evolution. These ODEs quantitatively describe the dynamics of kinetic systems and facilitate predicting the response of the model state to various perturbations, i.e., different inputs, altered kinetic parameters, or changing initial conditions [21]. The theory of creating kinetic models is generally established, and simplifying assumptions for the choice of particular equations have been proposed [22]. Their predictive power has turned kinetic models into a valuable resource for understanding biological systems. This, in turn, helped to excel advances in, e.g., biotechnological fields such as improving microbial strain design [23].
Kinetic modeling typically comprises the following three primary kinds of analyses:
- time-course simulation.
- steady-state analysis.
- parameter estimation.
The objective behind the time-course simulation is to mathematically describe the evolution of the investigated ODE system from given initial conditions. Thereby, the dynamics of the biological system can be investigated, e.g., the model’s behavior in response to varying inputs or other perturbations. Biological systems often reach a steady state after a long enough time, i.e., a state in which the metabolic concentrations remain constant. For some systems, multiple steady states may exist, and transitions between them may take place. Steady-state analysis numerically calculates possible steady states and evaluates likely transitions into a particular system’s state under the given conditions. Parameter estimation is a method to determine plausible values of the model’s parameters based on experimental data, e.g., reaction rate constants. For this reason, this procedure is sometimes called model calibration because data from laboratory experiments are compared to the output of model simulations aiming to fit the model to the data. Consequently, parameter estimation is often a prerequisite step for subsequent analyses, and it uses repeated time-course simulations. In other words, parameter estimation uses an optimization method whose objective is to identify the most plausible parameter values that calibrate a model towards the experimentally observed behavior of the corresponding biological system [24].
SBML is the de facto standard file format for computational models of biological systems [25,26]. For the analysis of kinetic models in SBML, several tools are available, e.g., the COmplex PAthway SImulator (COPASI) [27], the Systems Biology Toolbox for Matlab™ [28], libRoadRunner [29], or SBMLsimulator [30]. Many of these tools may cause difficulties to inexperienced users during installation or use of their algorithms and conventions. Some tools focus on a limited set of highly specialized functions, while others overwhelm their users with a large variety of features. Often, the users are indirectly assumed to understand the internal structures of systems biology model formats. In addition, many scientific software tools require a profound computational background or even coding skills to interact with the software. Installing these applications may not always be allowable if it requires administrator rights which are not always granted to every user in a research environment. These points might represent a considerable challenge for novice modelers or collaborators with an experimental background. A practical solution to these problems is to provide user-friendly and barrier-free access to a web application that can execute all the above mentioned analyses without requiring coding skills or admin setup rights.
A few freely available web applications for working with models in SBML format exist. APMonitor [31] supports simulation and parameter estimation but does not support steady-state analysis. One of the available standalone tools for simulation and parameter estimation is SBMLsimulator [30], which can be used via command-line or its Java™-based Graphical User Interface (GUI), but does not run online. Cycsim [32] supports visualization and time-course simulation of metabolic networks but not parameter estimation. The Systems BiologyWorkbench (SBW) [33] supports time course simulation and steady-state analysis but not parameter estimation. JWS Online [34] supports time course simulation and steady-state analysis but does not support parameter estimation. The tool suite RunBioSimulations [35] offers time course simulation and steady-state analysis but lacks support for parameter estimation. Additionally, RunBioSimulations offers many third-party analysis tools with many options and is hence most suitable for experienced users.
This article presents the user-friendly web application SBMLWebApp which allows the integrated analysis of kinetic models using time-course simulation, steady-state analysis, and parameter estimation. To the authors’ best knowledge, currently, no other web application exists besides the SBMLWebApp, with which novice users can effortlessly conduct all three analysis steps described above within a single framework. The SBMLWebApp, therefore, drastically expedites a profound and detailed analysis of kinetic models since all three steps are deeply intertwined, and the knowledge gained from a previous analysis step is often essential for following analyses. For example, time-course simulations with varying inputs are often executed after an initial system steady-state has been reached, i.e., first, a steady-state analysis is performed following by time-course simulations with varying inputs. For example, parameters determined via its parameter estimation features are subsequently used in time course and steady-state simulations to analyze the system’s behavior.
Providing a directly accessible web application with an intuitive user interface that combines services for time-course simulation, steady-state analysis, and parameter estimation makes a large portion of typical analyses within systems biology research accessible to less experienced users. In this way, the SBMLWebApp supports interdisciplinary collaboration as it allows experimentalists to effortlessly try out in-silico models from their dry-lab collaborators, which may help to accelerate the iterative cycles of alternating model development and wet-lab experimentation towards scientific progress.
2. Implementation
SBMLWebApp is implemented in Apache Tomcat® (https://tomcat.apache.org, accessed on 13 October 2021), and all servlets were written in Java™. The app uses the Bootstrap framework and is deployed on a Java application server using JQuery. SBMLWebApp uses AJAX software within the communication configuration between frontend and backend (GWT, http://www.gwtproject.org, accessed on 13 October 2021). The time course simulation servlet is executed using COPASI [27], SBSCL [36,37] with JSBML [38] as its internal data structure, and LibSBMLSim [39] that is based on libSBML [40]. The steady-state analysis servlet and parameter estimation servlet use COPASI [27]. The SBMLWebApp is accessible at http://simulate-biology.org. Our app uses the standard file format for computational models, SBML [25,26], and is compatible with SBML Level 3 Version 1 core [41].
3. Using the SBMLWebApp
Either a local SBML model or models from the BioModels Database [42] can be selected on the front page. BioModels is a highly curated database for computational biological models, currently containing 1017 manually curated SBML models (August 2021).
After selecting the SBML model, the relationships between species and reactions (stoichiometric network) are visualized (Figure 1) based on cytoscape.js [43].
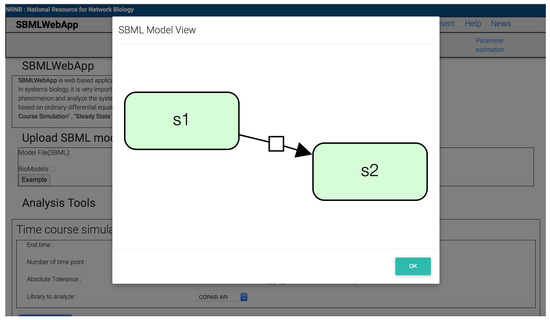
Figure 1.
SBML graph visualization of a simple example model consisting of the species s1 and s2. The graph shows the relationships between species and reactions in the SBML model. Species with a reactant role have no arrow (s1), whereas species with a product role have an arrow (s2).
To run a time course simulation with the model, the user can specify the end time, the number of time points, the absolute tolerance, and the simulation library to use as a solver backend. After setting these parameters and pressing the execute button, the simulation result is visualized as a graph (Figure 2), and the numerical results are provided in a table. Via the window on the right side, the initial amount of each species, the size of compartments, and values of kinetic parameters in the model can be edited. The respective simulation is executed on the fly.
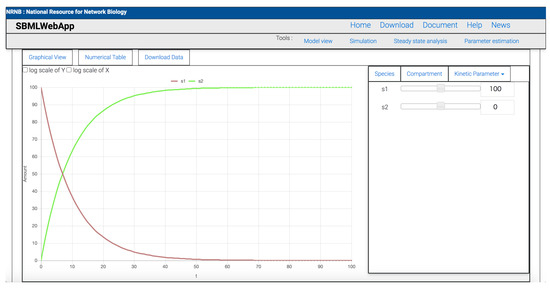
Figure 2.
Results of time-course simulation analysis. The x-axis shows the time, and the y-axis indicates amounts or concentrations of species depending on which of either the SBML model defines for the respective species. Each line in the graph corresponds to the time course of a single species. The check box of “log scale of Y” and “log scale of X” allows switching between linear and logarithmic axis scales. The initial values of species, compartment sizes, and kinetic parameters can be changed via the window on the right side. When a value is changed, the simulation is executed on the fly.
To run a steady-state analysis with the model, the available parameters that the user can specify include the resolution, derivation factor, and iteration limit to search steady states. After steady-state analysis, a single steady-state point of given initial expression for each species and the corresponding Jacobian matrix of this point is visualized as a numerical table (Figure 3).
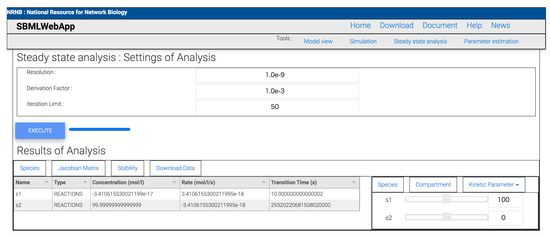
Figure 3.
The result of a steady-state analysis. The result shows the type of species, concentration in the steady-state point, the rate at this point, and transition time to reach this point from the initial value of each species.
To run a parameter estimation with the model, the algorithm, iteration limit to search fitted parameters, and fitting tolerance can be set. Available algorithms include the Levenberg-Marquardt algorithm [44,45], the Nelder Mead-algorithm [46], the particle swarm optimization method [47], and the differential evolution method [48]. The two latter optimization methods had been found to be particularly promising for the task of dynamic model calibration in systems biology applications [49]. The execution of a parameter estimation leads to a visualization of the simulation result with calibrated parameters and experimental results in Figure 4 and fitted parameters as a numerical table. The range of search parameters can be set in the window on the right side, and an analysis based on it can be executed after pressing return.
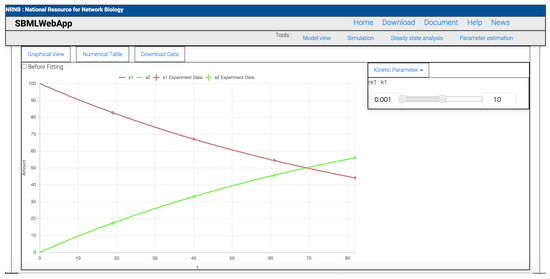
Figure 4.
The result of parameter estimation. The x- and y-axis in the graph show time vs. amount or concentration in the SBML model. Each line shows the simulation result with a fitted parameter of each species. Each plot shows the experimental value of each species. The check box of “Before Fitting” can visualize the simulation result with the original parameter value. The range searching proper parameter can be set using the slider on the window’s right side.
All result data can be downloaded via the “Download” tab. The graphs and tables are downloaded as PNG and CSV file, respectively. In parameter estimation, the model with calibrated parameters can be downloaded in SBML format.
4. Real-World Example and Applications
In the following section, one working example is provided, which demonstrates the functionality of the SBMLWebApp. This example is based on the work by Perelson et al. [50] and can be found on the BioModels database https://identifiers.org/biomodels.db/BIOMD0000000874, accessed on 13 October 2021. The SBMLWebApp provides three different methods for further analyses of kinetic models (time-course simulation, steady-state analysis, and parameter estimation). First, we have shown that the SBMLWebApp can reproduce the results of the simulations performed by Perelson et al. [50] on the population changes of T cells, latently infected T cells, actively infected T cells, and free viruses under various conditions (Supplementary Figures S1–S4). We have also shown that their theoretically derived unstable fixed points, stable fixed points, and unstable fixed points with oscillations for these populations can be analyzed numerically equivalent by the SBMLWebApp (Supplementary Figures S5–S7). Furthermore, in the parameter estimation for the time-series change of free virus in 10 HIV-infected patients by Stafford et al. [51], we showed that the SBMLWebApp could estimate parameters in good agreement with the measured results (Supplementary Figure S8). Table 1 provides an overview of the model and compares the outcomes of their analyses based on the model created as part of the study at hand.

Table 1.
Use case for a kinetic model analyzed with the SBMLWebApp (TCS: time-course simulation, SSA: steady-state analysis, PE: parameter estimation). All measurement results were the median of 10 measurements. The analysis conditions were the default settings of SBMLWebApp. The results in this table were achieved using a server with 16 CPUs of type AMD Ryzen 7 2700X Eight-Core Processor, each of which had 1882.649 MHz and a cache size of 512 kB.
5. Limitations of the Application
The app is developed using the most recent standards from the systems biology community, see also [52]. It currently only supports models in the format SBML Level 3 Version 1 [53]. Model calibration was performed using CellDesigner [54,55]. As such, the SBMLWebApp is bound by the features of CellDesigner. Some features of the SBMLWebApp are based on COPASI [27], which belongs to the leading simulation tools in the field of computational biology. However, this dependency also brings with it the application’s limitation to the features of this third-party software, see also [56]. This is also the reason why the SBMLWebApp is not able to estimate parameters using log-transformed loss functions. Kinetic models in biology often grow in size and thus in complexity. It is recommendable to use small or medium-sized models to allow the best possible functionality of the features provided by the SBMLWebApp. As such, computation times for individual analysis steps will differ, depending upon the size of the model. For data security reasons, the application does not store any user information. As such, any data that is not downloaded after running the analysis steps will be lost. At the moment, the SBMLWebApp is restricted to a selection of fundamental analyses in kinetic modeling. Future versions of SBMLWebApp will also include an easily accessible flux balance analysis tool because of the growing importance of this method.
6. Conclusions
SBMLWebApp is a user-friendly, web-based and freely available application to execute time course simulation, steady-state analysis, and parameter estimation for models in SBML. As open-source software, SBMLWebApp can be used as an example implementation of such a service and allows contributions and feature requests from the scientific community. It was developed to provide novice modelers and other non-specialist intuitive access to the core analyses for kinetic SBML models.
Supplementary Materials
The following materials are available online: at https://www.mdpi.com/article/10.3390/pr9101830/s1, S1–S8: Supplementary Figures, S9: ReproductionSummary.pdf, a collection of figures demonstrating the reproduction of simulation results; S10: PerelsonModel_Calibrated ForReproductionOfFigure8.xml, and S11: Perelson2000Model_ForParameterEstimation.xml, model files based on BIOMD0000000874 (https://identifiers.org/biomodels.db/BIOMD0000000874, accessed on 13 October 2021).
Author Contributions
Conceptualization, T.G.Y., A.F., M.K. and A.D.; methodology, T.G.Y.; software, T.G.Y. and M.F. mentored by M.K., K.I. and A.D.; validation, M.K. and A.D.; writing—original draft preparation, T.G.Y.; writing—review and editing, T.G.Y., K.I., M.F., A.F., M.K. and A.D.; supervision, A.F., M.K. and A.D.; project administration, A.D.; funding acquisition, T.G.Y., M.K. and A.D. All authors have read and agreed to the published version of the manuscript.
Funding
We thank all organizers of Google Summer of Code, National Resource for Network Biology (NRNB) in particular, and Google Inc. for allowing us to start this project. M.K. is supported by the Federal Ministry of Education and Research (BMBF, Germany) within the research network Systems Medicine of the Liver (LiSyM, grant No. 031L0054) and by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) within the Research Unit Programme FOR 5151 “QuaLiPerF (Quantifying Liver Perfusion–Function Relationship in Complex Resection––A Systems Medicine Approach)” by grant No. 436883643. A.D. was funded by the German Center for Infection Research (DZIF) within the Deutsche Zentren der Gesundheitsforschung (BMBF-DZG, German Centers for Health Research of the Federal Ministry of Education and Research), grant No. 8020708703. M.F. is funded by the DFG under Germany’s Excellence Strategy – EXC 2124 – 390838134 and supported by the Cluster of Excellence Controling Microbes to Fight Infections (CMFI) (grant No. EXC-2124/05.037_0 to AD). The authors acknowledge support from the Open Access Publishing Fund of the University of Tübingen (https://uni-tuebingen.de/en/58988, accessed on 13 October 2021).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The SBMLWebAPP is accessible from http://simulate-biology.org, and all source code of the project is available from https://github.com/TakahiroYamada/SBMLWebApp.
Acknowledgments
The authors are grateful to Theresa Anisja Harbig and Martin Lang for their support in administrating the compute server.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CSV | Comma-Separated Values |
| COPASI | COmplex PAthway SImulator |
| GUI | Graphical User Interface |
| GWT | Google Web Toolkit |
| ODE | Ordinary Differential Equation |
| PE | Parameter Estimation |
| PNG | Portable Network Graphics |
| TCS | Time-Course Simulation |
| SBML | Systems Biology Markup Language |
| SBSCL | Systems Biology Simulation Core Library |
| SBW | Systems Biology Workbench |
| SSA | Steady-State Analysis |
References
- Kitano, H. Computational systems biology. Nature 2002, 420, 206–210. [Google Scholar] [CrossRef]
- Buchweitz, L.F.; Yurkovich, J.T.; Blessing, C.; Kohler, V.; Schwarzkopf, F.; King, Z.A.; Yang, L.; Jóhannsson, F.; Sigurjónsson, O.E.; Rolfsson, O.; et al. Visualizing metabolic network dynamics through time-series metabolomic data. BMC Bioinform. 2020, 21, 130. [Google Scholar] [CrossRef]
- Mienda, B.S.; Dräger, A. Genome-Scale Metabolic Modeling of Escherichia coli and Its Chassis Design for Synthetic Biology Applications. In Computational Methods in Synthetic Biology; Marchisio, M.A., Ed.; Humana Press: New York, NY, USA, 2020; Volume 2189, pp. 217–229. [Google Scholar] [CrossRef]
- Renz, A.; Widerspick, L.; Dräger, A. Genome-Scale Metabolic Model of Infection with SARS-CoV-2 Mutants Confirms Guanylate Kinase as Robust Potential Antiviral Target. Genes 2021, 12, 796. [Google Scholar] [CrossRef]
- Renz, A.; Widerspick, L.; Dräger, A. FBA reveals guanylate kinase as a potential target for antiviral therapies against SARS-CoV-2. Bioinformatics 2020, 36, i813–i821. [Google Scholar] [CrossRef]
- Mostolizadeh, R.; Dräger, A. Computational Model Informs Effective Control Interventions against Y. enterocolitica Co-Infection. Biology 2020, 9, 431. [Google Scholar] [CrossRef]
- Bauer, A.L.; Beauchemin, C.A.; Perelson, A.S. Agent-based modeling of host–pathogen systems: The successes and challenges. Inf. Sci. 2009, 179, 1379–1389. [Google Scholar] [CrossRef]
- Shinde, S.B.; Kurhekar, M.P. Review of the systems biology of the immune system using agent-based models. IET Syst. Biol. 2018, 12, 83–92. [Google Scholar] [CrossRef]
- Li, F.; Long, T.; Lu, Y.; Ouyang, Q.; Tang, C. The yeast cell-cycle network is robustly designed. Proc. Natl. Acad. Sci. USA 2004, 101, 4781–4786. [Google Scholar] [CrossRef] [PubMed]
- Chaouiya, C.; Bérenguier, D.; Keating, S.M.; Naldi, A.; van Iersel, M.P.; Rodriguez, N.; Dräger, A.; Büchel, F.; Cokelaer, T.; Kowal, B.; et al. SBML Qualitative Models: A model representation format and infrastructure to foster interactions between qualitative modelling formalisms and tools. BMC Syst. Biol. 2013, 7, 135. [Google Scholar] [CrossRef] [PubMed]
- Traynard, P.; Fauré, A.; Fages, F.; Thieffry, D. Logical model specification aided by model-checking techniques: Application to the mammalian cell cycle regulation. Bioinformatics 2016, 32, i772–i780. [Google Scholar] [CrossRef] [PubMed]
- Khatri, P.; Draghici, S.; Ostermeier, G.C.; Krawetz, S.A. Profiling gene expression using onto-express. Genomics 2002, 79, 266–270. [Google Scholar] [CrossRef]
- Supper, J.; Fröhlich, H.; Spieth, C.; Dräger, A.; Zell, A. Inferring Gene Regulatory Networks by Machine Learning Methods. In Proceedings of the 5th Asia-Pacific Bioinformatics Conference (APBC 2007), Hong Kong, China, 15–17 January 2007; Sankoff, D., Wang, L., Chin, F., Eds.; Series on Advances in Bioinformatics and Computational Biology. Imperial College Press: London, UK, 2007; Volume 5, pp. 247–256. [Google Scholar] [CrossRef]
- Renz, A.; Widerspick, L.; Dräger, A. First Genome-Scale Metabolic Model of Dolosigranulum pigrum Confirms Multiple Auxotrophies. Metabolites 2021, 11, 232. [Google Scholar] [CrossRef]
- Erhard, F.; Friedel, C.C.; Zimmer, R. FERN – a Java framework for stochastic simulation and evaluation of reaction networks. BMC Bioinform. 2008, 9, 356. [Google Scholar] [CrossRef]
- Smallbone, K.; Simeonidis, E.; Swainston, N.; Mendes, P. Towards a genome-scale kinetic model of cellular metabolism. BMC Syst. Biol. 2010, 4, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Karr, J.R.; Sanghvi, J.C.; Macklin, D.N.; Gutschow, M.V.; Jacobs, J.M.; Bolival, B., Jr.; Assad-Garcia, N.; Glass, J.I.; Covert, M.W. A whole-cell computational model predicts phenotype from genotype. Cell 2012, 150, 389–401. [Google Scholar] [CrossRef] [PubMed]
- Strutz, J.; Martin, J.; Greene, J.; Broadbelt, L.; Tyo, K. Metabolic kinetic modeling provides insight into complex biological questions, but hurdles remain. Curr. Opin. Biotechnol. 2019, 59, 24–30. [Google Scholar] [CrossRef] [PubMed]
- Tummler, K.; Klipp, E. The discrepancy between data for and expectations on metabolic models: How to match experiments and computational efforts to arrive at quantitative predictions? Curr. Opin. Syst. Biol. 2018, 8, 1–6. [Google Scholar] [CrossRef]
- Resat, H.; Petzold, L.; Pettigrew, M.F. Kinetic modeling of biological systems. Comput. Syst. Biol. 2009, 311–335. [Google Scholar] [CrossRef]
- Klipp, E.; Nordlander, B.; Krüger, R.; Gennemark, P.; Hohmann, S. Integrative model of the response of yeast to osmotic shock. Nat. Biotechnol. 2005, 23, 975–982. [Google Scholar] [CrossRef]
- Du, B.; Zielinski, D.; Dräger, A.; Tan, J.; Zhang, Z.; Ruggiero, K.; Arzumanyan, G.; Palsson, B.O. Evaluation of Rate Law Approximations in Bottom-up Kinetic Models of Metabolism. BMC Syst. Biol. 2016, 10, 1–15. [Google Scholar] [CrossRef]
- Chowdhury, A.; Khodayari, A.; Maranas, C.D. Improving prediction fidelity of cellular metabolism with kinetic descriptions. Curr. Opin. Biotechnol. 2015, 36, 57–64. [Google Scholar] [CrossRef]
- Mendes, P.; Kell, D. Non-linear optimization of biochemical pathways: Applications to metabolic engineering and parameter estimation. Bioinformatics 1998, 14, 869–883. [Google Scholar] [CrossRef]
- Renz, A.; Mostolizadeh, R.; Dräger, A. Clinical Applications of Metabolic Models in SBML Format. In Systems Medicine; Wolkenhauer, O., Ed.; Academic Press: Oxford, UK, 2020; Volume 3, pp. 362–371. [Google Scholar] [CrossRef]
- Keating, S.M.; Waltemath, D.; König, M.; Zhang, F.; Dräger, A.; Chaouiya, C.; Bergmann, F.T.; Finney, A.; Gillespie, C.S.; Helikar, T.; et al. SBML Level 3: An extensible format for the exchange and reuse of biological models. Mol. Syst. Biol. 2020, 16, e9110. [Google Scholar] [CrossRef]
- Hoops, S.; Sahle, S.; Gauges, R.; Lee, C.; Pahle, J.; Simus, N.; Kummer, U. COPASI—a complex pathway simulator. Bioinformatics 2006, 22, 3067–3074. [Google Scholar] [CrossRef]
- Schmidt, H.; Jirstrand, M. Systems Biology Toolbox for MATLAB: A computational platform for research in systems biology. Bioinformatics 2006, 22, 514–515. [Google Scholar] [CrossRef]
- Somogyi, E.T.; Bouteiller, J.M.; Glazier, J.A.; König, M.; Medley, J.K.; Swat, M.H.; Sauro, H.M. libRoadRunner: A high performance SBML simulation and analysis library. Bioinformatics 2015, 31, 3315–3321. [Google Scholar] [CrossRef]
- Dörr, A.; Keller, R.; Zell, A.; Dräger, A. SBMLsimulator: A Java tool for model simulation and parameter estimation in systems biology. Computation 2014, 2, 246–257. [Google Scholar] [CrossRef] [PubMed]
- Hedengren, J.D.; Shishavan, R.A.; Powell, K.M.; Edgar, T.F. Nonlinear modeling, estimation and predictive control in APMonitor. Comput. Chem. Eng. 2014, 70, 133–148. [Google Scholar] [CrossRef]
- Le Fèvre, F.; Smidtas, S.; Combe, C.; Durot, M.; d’Alché-Buc, F.; Schachter, V. CycSim—An online tool for exploring and experimenting with genome-scale metabolic models. Bioinformatics 2009, 25, 1987–1988. [Google Scholar] [CrossRef] [PubMed]
- Bergmann, F.T.; Sauro, H.M. SBW-a modular framework for systems biology. In Proceedings of the 2006 Winter Simulation Conference, Monterey, CA, USA, 3–6 December 2006; pp. 1637–1645. [Google Scholar]
- Olivier, B.G.; Snoep, J.L. Web-based kinetic modelling using JWS Online. Bioinformatics 2004, 20, 2143–2144. [Google Scholar] [CrossRef] [PubMed]
- Shaikh, B.; Marupilla, G.; Wilson, M.; Blinov, M.L.; Moraru, I.I.; Karr, J.R. RunBioSimulations: An extensible web application that simulates a wide range of computational modeling frameworks, algorithms, and formats. Nucleic Acids Res. 2021, 49, W597–W602. [Google Scholar] [CrossRef]
- Keller, R.; Dörr, A.; Tabira, A.; Funahashi, A.; Ziller, M.J.; Adams, R.; Rodriguez, N.; Le Novère, N.; Hiroi, N.; Planatscher, H.; et al. The systems biology simulation core algorithm. BMC Syst. Biol. 2013, 7, 55. [Google Scholar] [CrossRef]
- Panchiwala, H.; Shah, S.; Planatscher, H.; Zakharchuk, M.; König, M.; Dräger, A. The Systems Biology Simulation Core Library. Bioinformatics 2021, btab669. [Google Scholar] [CrossRef]
- Rodriguez, N.; Thomas, A.; Watanabe, L.; Vazirabad, I.Y.; Kofia, V.; Gómez, H.F.; Mittag, F.; Matthes, J.; Rudolph, J.D.; Wrzodek, F.; et al. JSBML 1.0: Providing a smorgasbord of options to encode systems biology models. Bioinformatics 2015, 31, 3383–3386. [Google Scholar] [CrossRef]
- Takizawa, H.; Nakamura, K.; Tabira, A.; Chikahara, Y.; Matsui, T.; Hiroi, N.; Funahashi, A. LibSBMLSim: A reference implementation of fully functional SBML simulator. Bioinformatics 2013, 29, 1474–1476. [Google Scholar] [CrossRef][Green Version]
- Bornstein, B.J.; Keating, S.M.; Jouraku, A.; Hucka, M. LibSBML: An API Library for SBML. Bioinformatics 2008, 24, 880–881. [Google Scholar] [CrossRef] [PubMed]
- Hucka, M.; Bergmann, F.T.; Dräger, A.; Hoops, S.; Keating, S.M.; Le Novère, N.; Myers, C.J.; Olivier, B.G.; Sahle, S.; Schaff, J.C.; et al. Systems Biology Markup Language (SBML) Level 3 Version 1 Core. J. Integr. Bioinform. 2018, 15, 1. [Google Scholar] [CrossRef]
- Malik-Sheriff, R.S.; Glont, M.; Nguyen, T.V.N.; Tiwari, K.; Roberts, M.G.; Xavier, A.; Vu, M.T.; Men, J.; Maire, M.; Kananathan, S.; et al. BioModels—15 years of sharing computational models in life science. Nucleic Acids Res. 2020, 48, D407–D415. [Google Scholar] [CrossRef]
- Franz, M.; Lopes, C.T.; Huck, G.; Dong, Y.; Sumer, O.; Bader, G.D. Cytoscape. js: A graph theory library for visualisation and analysis. Bioinformatics 2015, 32, 309–311. [Google Scholar]
- Levenberg, K. A method for the solution of certain non-linear problems in least squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Marquardt, D.W. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–27 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Dräger, A.; Kronfeld, M.; Ziller, M.J.; Supper, J.; Planatscher, H.; Magnus, J.B.; Oldiges, M.; Kohlbacher, O.; Zell, A. Modeling metabolic networks in C. glutamicum: A comparison of rate laws in combination with various parameter optimization strategies. BMC Syst. Biol. 2009, 3, 5. [Google Scholar] [CrossRef]
- Perelson, A.S.; Kirschner, D.E.; De Boer, R. Dynamics of HIV infection of CD4+ T cells. Math. Biosci. 1993, 114, 81–125. [Google Scholar] [CrossRef]
- Stafford, M.A.; Corey, L.; Cao, Y.; Daar, E.S.; Ho, D.D.; Perelson, A.S. Modeling Plasma Virus Concentration during Primary HIV Infection. J. Theor. Biol. 2000, 203, 285–301. [Google Scholar] [CrossRef] [PubMed]
- Carey, M.A.; Dräger, A.; Beber, M.E.; Papin, J.A.; Yurkovich, J.T. Community standards to facilitate development and address challenges in metabolic modeling. Mol. Syst. Biol. 2020, 16, e9235. [Google Scholar] [CrossRef] [PubMed]
- Hucka, M.; Bergmann, F.T.; Hoops, S.; Keating, S.M.; Sahle, S.; Schaff, J.C.; Smith, L.P.; Wilkinson, D.J. The Systems Biology Markup Language (SBML): Language specification for level 3 version 1 core. J. Integr. Bioinform. 2015, 12, 382–549. [Google Scholar] [CrossRef]
- Funahashi, A.; Morohashi, M.; Kitano, H.; Tanimura, N. CellDesigner: A process diagram editor for gene-regulatory and biochemical networks. Biosilico 2003, 1, 159–162. [Google Scholar] [CrossRef]
- Funahashi, A.; Matsuoka, Y.; Jouraku, A.; Morohashi, M.; Kikuchi, N.; Kitano, H. CellDesigner 3.5: A versatile modeling tool for biochemical networks. Proc. IEEE 2008, 96, 1254–1265. [Google Scholar] [CrossRef]
- Bergmann, F.T.; Hoops, S.; Klahn, B.; Kummer, U.; Mendes, P.; Pahle, J.; Sahle, S. COPASI and its applications in biotechnology. J. Biotechnol. 2017, 261, 215–220. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).