5.3.1. Establishing Simulation Data
The simulation data of the production operations in the body shop and paint shop of the bus manufacturer were established as follows.
1. Parameters in the shop model
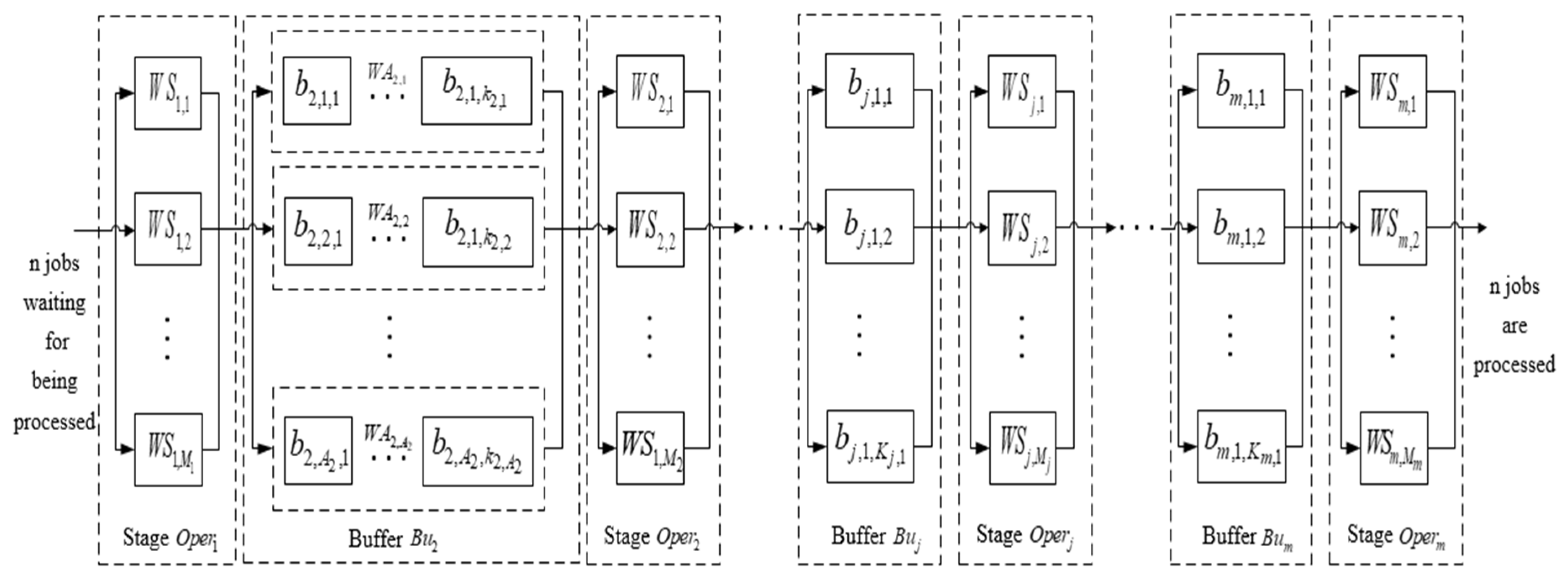
The body shop of the bus manufacturer is a rigid flow shop with multiple production lines, which can be simplified into one production stage. The production of the paint shop is simplified to three stages [
27]. The simulation data for scheduling include four stages, namely
, whose parallel machine
is
. The buffer between the body shop and the paint shop is a multi-queue limited buffer. As such, the buffer of stage
in the scheduling simulation data is set to the multi-queue limited buffer. The number of lanes in buffer
of stage
is equal to 2, namely
= 2. The number of spaces in lane
is 2, namely
= 2, and that of buffer
is 2, namely
= 2. That is to say, the multi-queue limited buffers have two lanes and each lane has two spaces.
In the production of the paint shop, it is necessary to clean the machine and adjust production equipment if the model and color of the buses that are successively processed on the machine are different. Therefore, the simulation process uses the changes in the model and color as the basis for calculating setup times.
Table 4 shows that the setup times parameters are set when the model and color of the buses that are processed successively on the machine changed. When the bus is assigned to the machine of the next stage from the buffer, the setup times of the machine is calculated using Equation (16).
2. Parameters of processing the object
The information of the bus model and color properties is shown in
Table 5. The sum of bus properties is 2, namely
.
represented the model property of the bus, while
denoted the color property of the bus. The value of model property (
) is
, and the value of color property (
) is
. It is assumed that two successively processed buses on machine of stage
are buses
and
. If model properties were as follows:
=
and
=
, and color properties are as follows:
=
and
=
, then
=
,
. Hence,
. Using Equation (16), the setup time can be obtained as follows:
=
= 4. And the
Table 6 shows the standard processing time for bus production.
5.3.3. Simulation Results and Analysis
1. Evaluation index of scheduling results
In the optimization process, makespan was used as the fitness function value of the global optimization algorithm. Meanwhile, a number of evaluation indexes related to the actual production line were established, including , , , , and . Except , the smaller the values, the better the remaining evaluation indexes.
Eight sets of simulation schemes were run 30 times. The average of 30 simulation results is presented in
Table 8. As shown in the table, under the principle of adopting the same global optimization algorithm, compared with schemes 1–4, each metric of schemes 5–8 has been improved to some extent, except the
. Among the metrics, the optimization improvement of
,
and
is obvious. This is mainly because schemes 5–8 adopted RCMQB rules when entering multi-queue limited buffers, which can allocate resources of multi-queue limited buffers more reasonably and reduce the occurrence of blocking. The SST rule, the FAM rule and the FCFS rule were adopted when leaving the buffer, which can more effectively control the jobs to select the machine with the least change of properties among multiple machines for processing. This was beneficial to reduce the setup times. Further,
is equal to the sum of the time for the job staying on the buffer, the blocking time of the job and setup times, so these three evaluation indexes were significantly improved. The reduction in blocking time and setup times will lead to the reduction in the makespan of the whole process and the reduction of the idle time for machines. Therefore,
,
and
of schemes 5–8 were also optimized to some extent. From the table we can also see that compared with the schemes 1–4, although the
of the schemes 5–8 had all increased, the rate of increase was small. This indicates that the complicated local rules adopted in schemes 5–8 can made full use of the capacity of the multi-queue limited buffers and effectively reduced the blocking time and setup times. At the same time, the running time costs were small and did not have much impact on the speed of the algorithm.
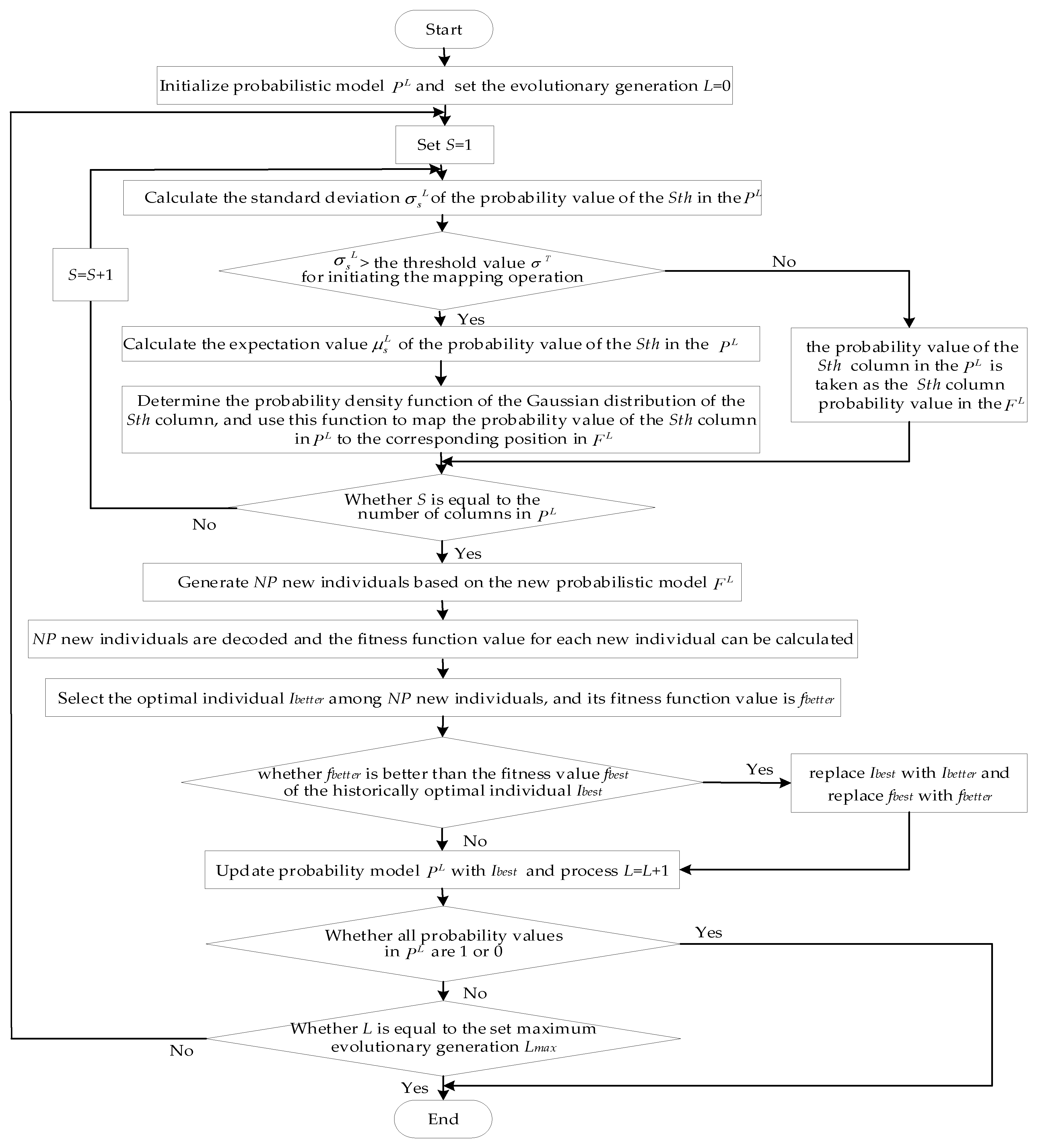
The comparison among schemes 1–4 or schemes 5–8 show that the running speed of the CGA and ICGA was significantly faster than that of the BA and WOA. The average running time of the BA reached 555.56 s, which is obviously not suitable for solving practical problems. In terms of optimization performance, under two different local dispatching rules, the optimization effect of ICGA for was the best among the four algorithms. Specially, compared with the CGA, the optimization effect of the ICGA was significantly improved. The above results show that the ICGA, to some extent, overcame the problem that the CGA was easy to prematurely converge while maintaining the fast running speed of the CGA. This is mainly because in the early stage of evolution, there is no large probability value in the probabilistic model. Thus, the ICGA was still evolving as the procedure of the CGA. In this way, the ICGA maintained the advantage that the CGA can converge quickly in the early stage of evolution. In the later stage of evolution, when falling into the local extremum, the ICGA mapped the original probabilistic model to the new probabilistic model through the probability density function of the Gaussian distribution. In this way, while keeping probability values’ distribution of the original probabilistic model unchanged, ICGA’s searching ability of feasible solutions was expanded, and the diversity of population individuals was improved. Therefore, the algorithm could jump out of the local extremum and continued to evolve.
Through the above analysis, it can be concluded that compared with the other seven schemes, the combination of the ICGA and local dispatching rules adopted in scheme 8 was the best for reducing setup times of the machine, and it effectively decreased the blocking effect of the limited buffers, more reasonably arranged the jobs in and out of the multi-queue limited buffer, and orderly assigned the processing tasks. Various evaluation metrics were improved, and the problem of multi-queue limited buffers scheduling problems in a flexible flow shop with setup times was more effectively solved.
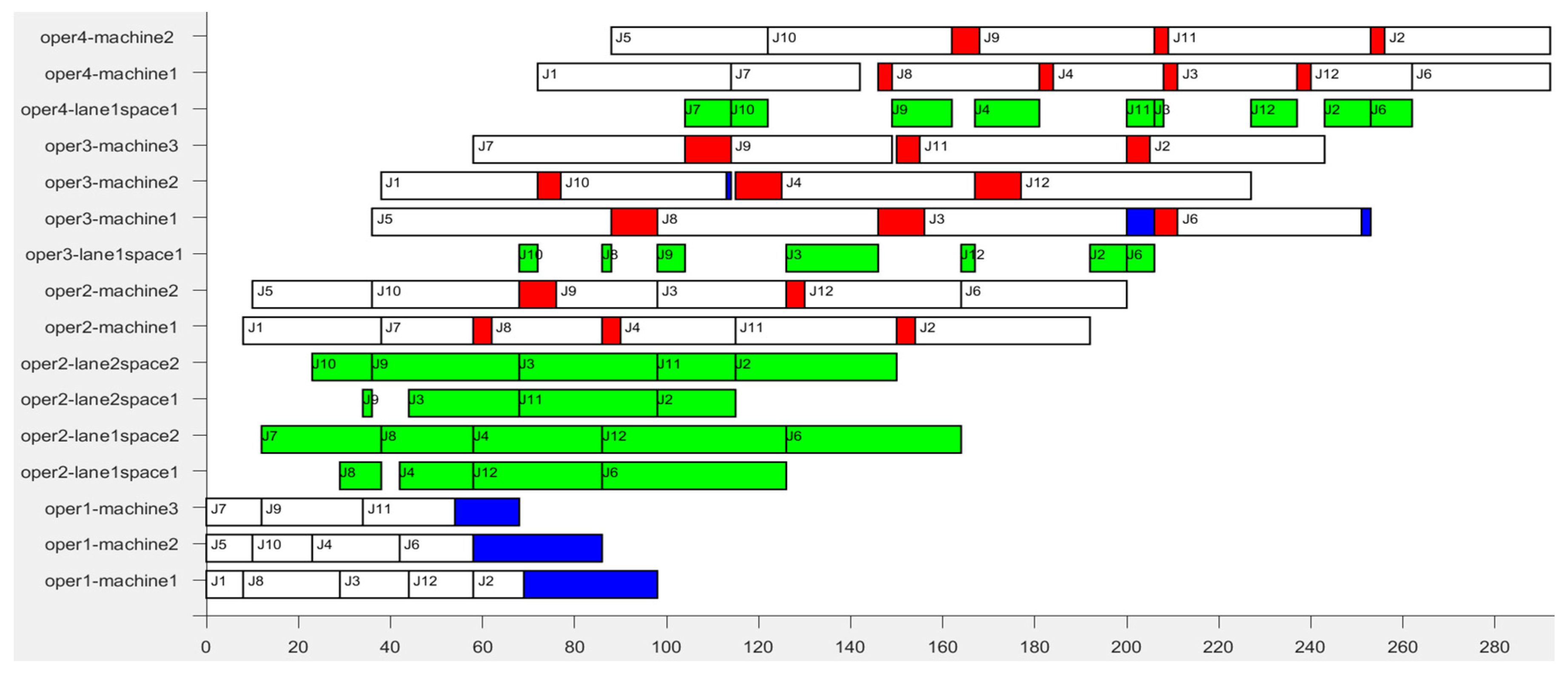
2. Gantt chart analysis of scheduling result
Figure 4 is the Gantt chart of the scheduling result of scheme 8, with time axis as the abscissa and machine of each stage as the ordinate. The green part indicates the residence time of the bus in the buffer. The red part indicates the setup times when the successively-processed buses are with different properties. The blue part denotes the blocking time of the bus on the machine after the completion of the process. The processing route of
was
. In
Figure 4, we can see that at time
= 44,
completed the processing on machine
of stage
(the competition time of
was 44, namely
= 44). At this time, the first lane
of buffer
had two jobs waiting to be processed (
and
), that is to say,
,
= 2. The second lane
of buffer
had one job waiting to be processed (
), that is to say,
,
= 1. The capacity of lane
was 2 (
= 2),
. And the capacity of lane
was 2 (
= 2),
. Both of them satisfy the constraint of Equation (10) of the limited buffers. At this time, based on the RCMQB rule which regulates the job’s access to the buffer, we can obtain
from Equation (26). The
was assigned to space
in lane
of stage
, waiting to be processed at stage
. The entry time of the bus into the buffer (
) was equal to
, which satisfied the constraint of Equation (8) of limited buffers.
At time = 68, left the space in lane , and the departure time out of the buffer () was 68. At the same time, was assigned to the space , waiting to be processed on the machine of stage . At time = 98, = 98, also departed from the buffer, and , satisfying the constraint of Equation (13). From the Gantt chart drawn from scheduling results, it can be seen that the constraint of Equation (12) was always met during the use of multi-queue limited buffers.
Further analysis of the process that
left the buffer is as follows. When
= 98, machine
completed the processing of
, so that machine
was available. At this time,
on space
in lane
was waiting for processing, and
on space
was also waiting for processing. According to the bus’s property information in
Table 3, in regard to machine
, if we choose to process
, the setup time (
) will be equal to
, namely
=
= 4; if we choose to process
, the setup time (
) will be 0, namely
= 0. In accordance with the SST rule that controls the job leaving the buffer,
was chosen to process.
3. Analysis of scheduling evolution
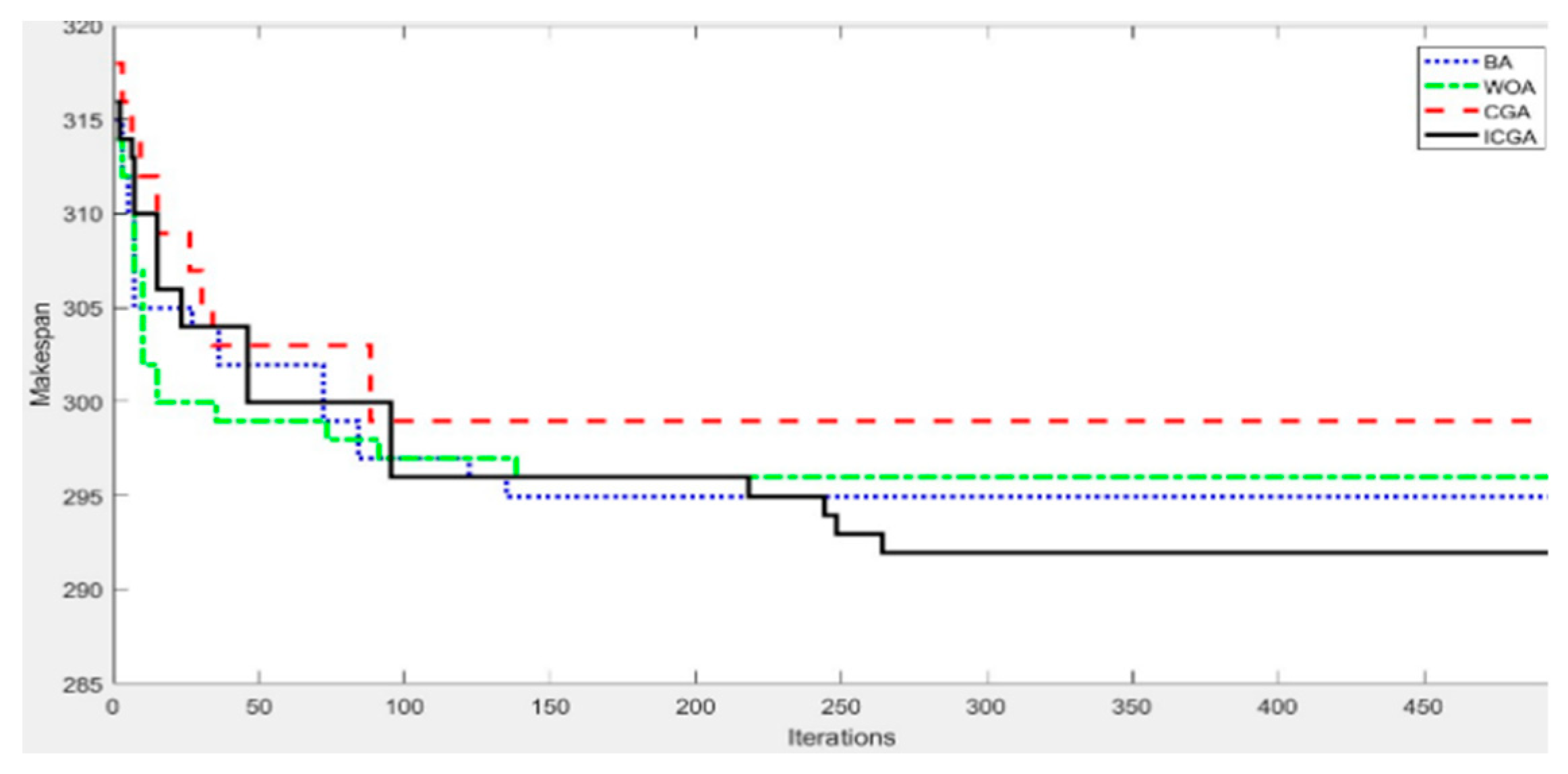
Figure 5 shows the relationship between fitness value and training iterations of schemes 5–8. As can be seen, the BA and WOA converged quickly at the initial stage of the evolution. This is mainly due to the fact that the initial numbers of population of the BA and WOAs (
= 30) were much larger than that of the CGA and ICGAs (
= 4). This means a relatively strong ability for searching the solution space. However, with the increase in evolutional iterations, the search ability of the BA and the WOA gradually deterioratesdand they fell into the local extremum in the 135th and 139th generations, respectively. Although the CGA should be good at fast search, the distribution of probability values in the probabilistic model all decreased with evolution, and thus and the search performance on the solution space decreased. The algorithm stopped evolving at the 87th generation, falling into the local extremum. On the other hand, the ICGA had the similar fast search performance as the CGA during the initial stage and encountered evolutionary stagnation at the 94th generation. But as evolution continues, the ICGA started the mapping operation to reactivate the algorithm’s evolutionary ability and found for the optimal solution in the 263th generation.
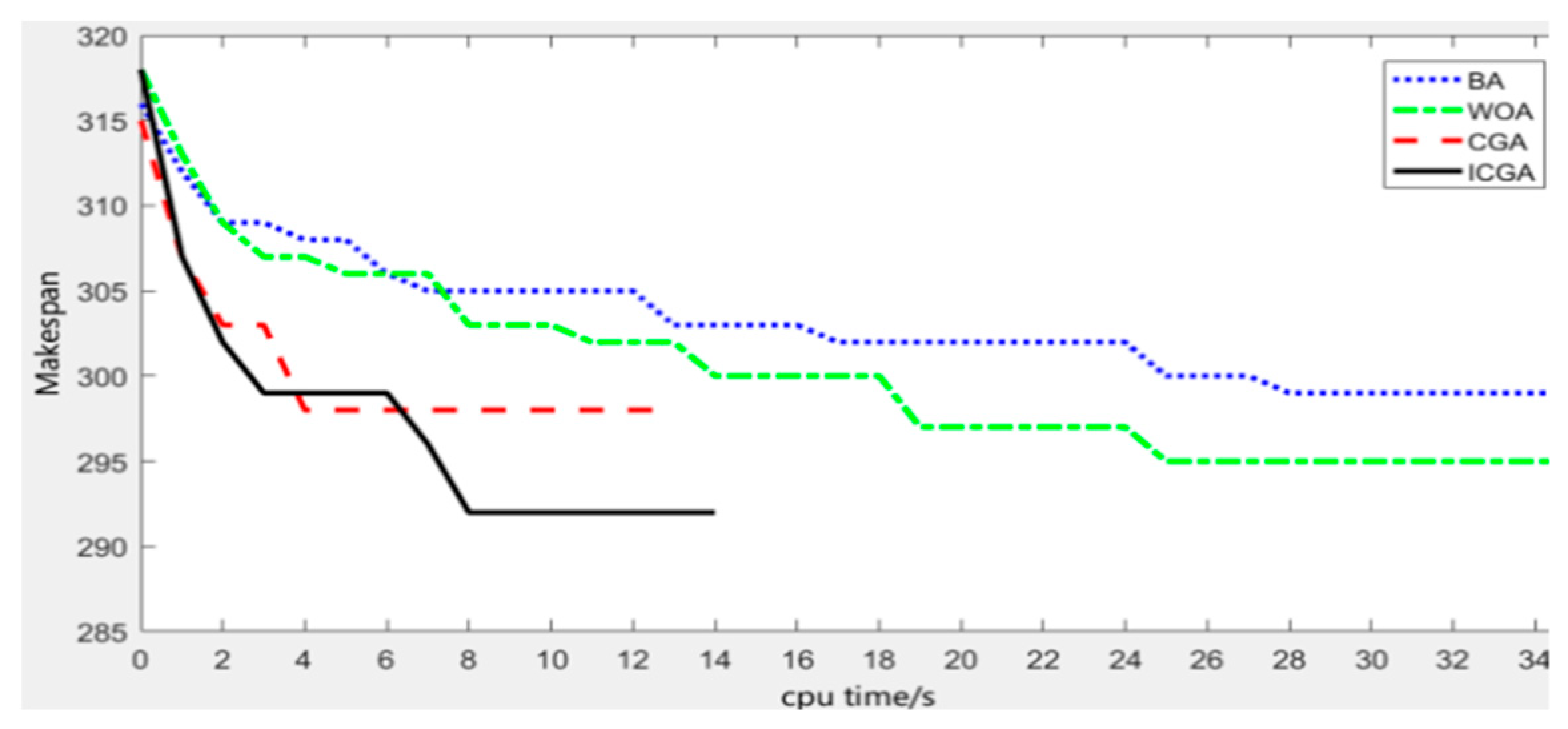
Figure 6 shows the relationship between fitness value and running time of schemes 5–8. As can be seen from the figure, the running speed of CGA and ICGA was very fast, but the CGA fell into the local extremum at 4 s. The optimization speed of the BA was the slowest among the four algorithms, and its optimal solution was 299 during the 35 s running time. From the figure, we can also see that the fitness value of the ICGA was the best among the four algorithms at the same CPU time. And the time used by the ICGA to get the same fitness value was the least among the four algorithms. The ICGA maintained the advantage that the CGA can converge quickly in the early stage of evolution. In the later stage of evolution, when falling into the local extremum, the ICGA improved the diversity of individuals in the population by mapping the original probabilistic model to a new probabilistic model, so that the algorithm could jump out of the local extremum and continue to evolve.
4. Statistical analysis of scheduling results
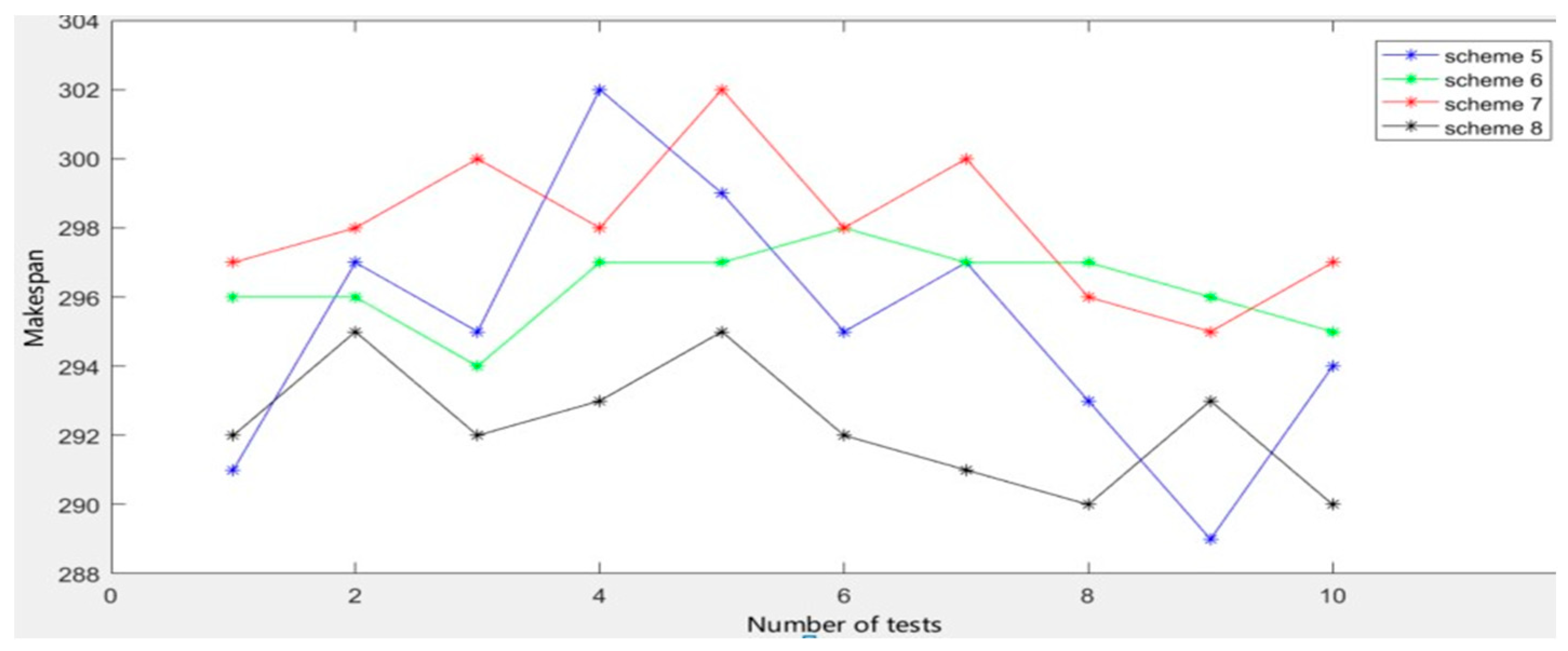
Figure 7 shows the makespan
of schemes 5–8 running 10 times separately. For scheme 7, the average value of makespan
in 10 tests was 298.1, which was the worst among the four schemes. Although scheme 5 could sometimes obtain better results, the results obtained in 10 tests were not stable enough and were with large fluctuations, easily falling into the local extremum sometimes. Its average value of 10 tests was 295.2. Compared with the other three schemes, the results obtained by the scheme 6 were relatively stable. However, its average result was poor, at 296.3. The average value of the test results of scheme 8 was 292.3, which was the best of all the schemes. The fluctuations of the curve indicate that the magnitude of the change in the results of scheme 8 in 10 tests is small. This shows that when solving multi-queue limited buffers scheduling problems in a flexible flow shop with setup times, compared with the CGA, the ICGA has not only greatly improved the optimization performance, but also improved the stability of the optimization results.