Empirical Bayes Prediction in a Sequential Sampling Plan Based on Loss Functions
Abstract
1. Introduction
2. Variables Sampling for Process Mean Testing
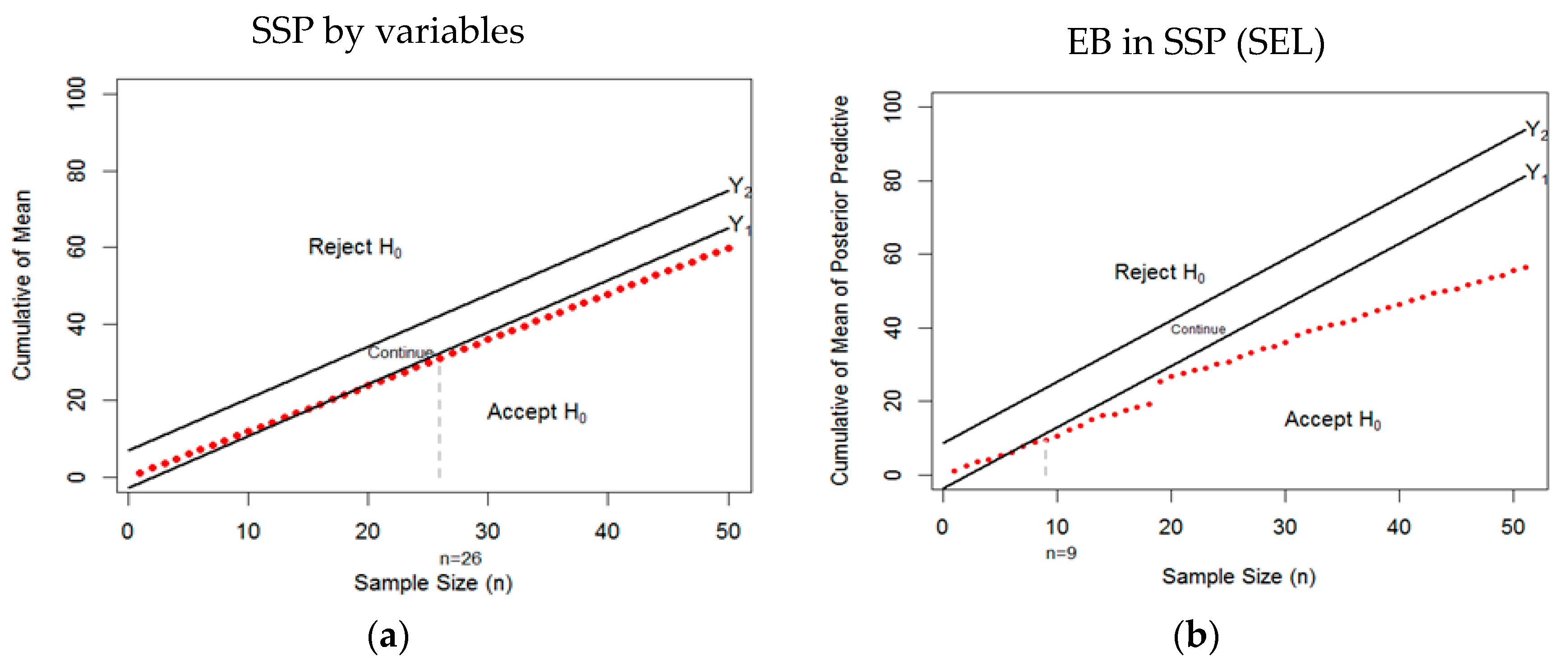
3. Sequential Sampling Plan by Variables
4. Empirical Bayes Prediction Approach
4.1. Determine the Marginal Likelihood Distribution Function
4.2. Calculate the Posterior Distribution Function of
4.3. Obtain the EB Estimator of with Respect to the SEL Function
4.4. Determine the EB Estimator of with Respect to the PL Function
4.5. Construct the Posterior Predictive Distribution Function of
5. Numerical and Results
6. An Application Example
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Montgomery, D.C. Statistical Quality Control: A Modern Introduction, 6th ed.; Jonh Wiley & Sons: New York, NY, USA, 2009. [Google Scholar]
- Balamurali, S.; Park, H.; Jun, C.-H.; Kim, K.-J.; Lee, J. Designing of Variables Repetitive Group Sampling Plan Involving Minimum Average Sample Number. Commun. Stat.-Simul. Comput. 2005, 34, 799–809. [Google Scholar] [CrossRef]
- Sankle, R.; Singh, J.R. Single Sampling Plans for Variables Indexed by AQL and AOQL with Measurement Error. J. Mod. Appl. Stat. Methods 2012, 11, 396–406. [Google Scholar] [CrossRef]
- Carlin, B.P.; Louis, T.A. Bayesian Methods for Data Analysis, 3rd ed.; Chapman & Hall/CRC: Boca Raton, FL, USA, 2009. [Google Scholar]
- Krutchkoff, R.G. Empirical Bayes Estimation. Am. Stat. Assoc. 1972, 26, 14–16. [Google Scholar]
- Casella, G. An Introduction to Empirical Bayes Data Analysis. Am. Stat. Assoc. 1985, 39, 83–87. [Google Scholar]
- Lu, W.-S. The efficiency of the method of moments estimates for hyperparameters in the empirical Bayes binomial model. Comput. Stat. 1999, 14, 263–276. [Google Scholar] [CrossRef]
- Cui, W.; George, E.I. Empirical Bayes vs. fully Bayes variable selection. J. Stat. Plan. Inference 2008, 138, 888–900. [Google Scholar] [CrossRef]
- Khaledi, M.J.; Rivaz, F. Empirical Bayes spatial prediction using a Monte Carlo EM algorithm. Stat. Methods Appl. 2009, 18, 35–47. [Google Scholar] [CrossRef]
- Maswadah, M. Empirical Bayes inference for the Weibull model. Comput. Stat. 2013, 28, 2849–2859. [Google Scholar] [CrossRef]
- Spiring, F.A. The Reflected Normal Loss Function. Can. J. Stat. 1993, 21, 321–330. [Google Scholar] [CrossRef]
- Moskowitz, H.; Tang, K. Bayesian Variables Acceptance-Sampling Plans: Quadratic Loss Function and Step-Loss Function. Technometrics 1992, 34, 340–347. [Google Scholar] [CrossRef]
- Jaheen, Z.F. Empirical Bayes analysis of record statistics based on linex and quadratic loss functions. Comput. Math. Appl. 2004, 47, 947–954. [Google Scholar] [CrossRef]
- Naji, L.F.; Rasheed, H.A. Bayesian Estimation for Two Parameters of Gamma Distribution under Precautionary Loss Function. Ibn AL-Haitham J. Pure Appl. Sci. 2019, 32, 187–196. [Google Scholar] [CrossRef]
- Rahman, H.; Roy, M.K.; Baizid, A. Bayes Estimation under Conjugate Prior for the Case of Power Function Distribution. Am. J. Math. Stat. 2012, 2, 44–48. [Google Scholar] [CrossRef]
- Zaka, A.; Akhter, A.S. Bayesian Analysis of Power Function Distribution Using Different Loss Functions. Int. J. Hybrid Inf. Technol. 2014, 7, 229–244. [Google Scholar] [CrossRef]
- Lavanya, A.; Alexander, T.L. Estimation of Parameters Using Lindley’s Method. Int. J. Adv. Res. 2016, 4, 1767–1778. [Google Scholar] [CrossRef]
- Gimlin, D.R.; Breipohl, A.M. Bayesian Acceptance Sampling. IEEE Trans. Reliab. 1972, R-21, 176–180. [Google Scholar] [CrossRef]
- Lam, Y.; Li, K.H.; Ip, W.-C.; Wong, H. Sequential variable sampling plan for normal distribution. Eur. J. Oper. Res. 2006, 172, 127–145. [Google Scholar] [CrossRef]
- Liang, T.; Chen, L.-S.; Yang, M.-C. Efficient Bayesian sampling plans for exponential distributions with random censoring. J. Stat. Plan. Inference 2012, 142, 537–551. [Google Scholar] [CrossRef]
- Dunsmore, I.R.; Wright, D.E. A Decisive Predictive Approach to the Construction of Sequential Acceptance Sampling Plans for Lifetimes. J. R. Stat. Soc. Ser. C 1985, 34, 1–13. [Google Scholar] [CrossRef]
- Ohta, H.; Ogawa, S. Design of Economic Sampling Plan Based on Empirical Bayesian Approach. Front. Stat. Qual. Control 4 1992, 4, 100–108. [Google Scholar]
- Shin, M.-W.; Shin, K.I. Empirical Bayes Estimation on Sampling Inspection by Variables. J. Korean Soc. Qual. Manag. 1995, 23, 45. [Google Scholar]
- Karunamuni, R.J. Empirical Bayes Sequential Estimation for Exponential Family: The Untruncated Component. Ann. Inst. Stat. Math. 1996, 48, 711–730. [Google Scholar] [CrossRef]
- Delgadillo, F.; Bremer, R. The development of a destructive sampling method designed for high quality production processes (DSM-HQ). Qual. Quant. 2010, 44, 595–605. [Google Scholar] [CrossRef]
- Taherian, T.; Asl, M.B. Capability Analysis and use of Acceptance and Control Charts in the 6-Sigma in Pharmaceutical Industries Case Study: Behestan Tolid Pharmaceutical Co. Int. J. Appl. Inf. Syst. 2016, 11, 127–135. [Google Scholar]
- Schilling, E.G.; Neubauer, D.V. Acceptance Sampling in Quality Control, 2nd ed.; Chapman & Hall/CRC: Boca Raton, FL, USA, 2009. [Google Scholar]
- Garthwaite, P.; Jolliffe, I.; Jones, B. Statistical Inference, 2nd ed.; Oxford University Press: New York, NY, USA, 2002. [Google Scholar]
- Ali, S.; Aslam, M.; Kazmi, S.M.A. A Study of the Effect of the loss function on Bayes Estimate, posterior risk and hazard function for Lindley distribution. Appl. Math. Model. 2013, 37, 6068–6078. [Google Scholar] [CrossRef]
- Rasheed, A.H.; Raghda, A. Reliability Estimation in Inverse Rayleigh Distribution Using Precautionary Loss Function. Math. Stat. J. 2016, 2, 9–15. [Google Scholar]
- Wu, C.-W.; Pearn, W.L. A variables sampling plan based on Cpmk for product acceptance determination. Eur. J. Oper. Res. 2008, 184, 549–560. [Google Scholar] [CrossRef]



| Pa | ASN | ||||
|---|---|---|---|---|---|
| SSP | EB in SSP (SEL) | EB in SSP (PL) | SSP | EB in SSP (SEL) | EB in SSP (PL) |
| 0.9662 | 0.9990 | 0.9977 | 21.1673 | 10.9694 | 12.4706 |
| 0.9598 | 0.9796 | 0.9998 * | 22.0605 | 18.8427 | 5.4135 |
| 0.9548 | 0.9976 | 0.9993 * | 22.7102 | 12.5077 | 10.5291 |
| 0.8883 | 0.9997 | 0.9980 | 28.5539 | 5.1358 | 3.4486 |
| 0.9568 | 0.9999 * | 0.9990 | 22.4496 | 8.5023 | 4.9671 |
| 0.9448 | 0.9996 | 0.9987 * | 23.8553 | 9.9511 | 8.4201 |
| 0.9645 | 0.1617 | 0.9599 | 21.4148 | 38.1324 | 22.0460 |
| 0.9703 | 0.9993 | 0.9989 * | 20.5323 | 10.3801 | 6.6090 |
| 0.9235 | 0.9999 * | 0.9995 * | 25.9091 | 4.7902 | 3.9721 |
| 0.9642 | 0.9963 | 0.9994 * | 21.4582 | 13.4647 | 9.9028 |
| 0.9407 | 0.8658 | 0.9762 | 24.2880 | 29.9258 | 19.5063 |
| 0.9651 | 0.9941 | 0.9995 * | 21.3328 | 14.6292 | 9.9395 |
| 0.9767 | 0.2157 | 0.9288 | 19.4190 | 33.5929 | 34.0495 |
| 0.8998 | 0.9998 * | 0.9987 * | 27.7680 | 8.7000 | 11.3738 |
| 0.9521 | 0.9997 * | 0.9997 * | 23.0272 | 4.1074 | 4.8513 |
| 0.9735 | 0.9996 | 0.9996 * | 19.9923 | 9.6105 | 6.4155 |
| 0.9586 | 0.9997 * | 0.9998 * | 22.2191 | 7.2359 | 6.0929 |
| 0.9691 | 0.9999 * | 0.9315 | 20.7170 | 8.0689 | 25.1862 |
| 0.9437 | 0.9785 | 0.9882 | 23.9723 | 15.8336 | 2.7129 |
| 0.9577 | 0.9775 | 0.9243 | 22.3429 | 19.2633 | 25.8429 |
| 0.9434 | 0.9998 * | 0.9991 | 24.0095 | 9.0979 | 7.4710 |
| 0.9544 | 0.9999 * | 0.9996 * | 22.7502 | 7.7668 | 7.5423 |
| 0.9586 | 0.9998 * | 0.9994 * | 22.2226 | 4.9286 | 5.1259 |
| 0.8849 | 0.9999 * | 0.9998 * | 28.7711 | 8.2136 | 6.7508 |
| 0.9463 | 0.9901 | 0.9990 * | 23.6941 | 6.5899 | 7.0308 |
| 0.9482 | 0.9932 | 0.9998 * | 23.4808 | 15.0636 | 8.8335 |
| 0.9386 | 0.9970 | 0.9994 * | 24.5044 | 12.9948 | 10.1527 |
| 0.9154 | 0.9998 * | 0.9993 * | 26.5839 | 8.9655 | 7.8158 |
| 0.9444 | 0.9904 | 0.9989 * | 23.8986 | 6.2963 | 6.8308 |
| 0.9748 | 0.9986 | 0.9999 * | 19.7757 | 11.5157 | 8.1897 |
| 0.9748 | 0.8417 | 0.9999 * | 21.7248 | 31.3442 | 15.1279 |
| 0.9623 | 0.9748 | 0.9930 | 25.2059 | 19.7683 | 17.1843 |
| 0.9313 | 0.9954 | 0.9867 | 21.5153 | 6.1856 | 6.4932 |
| 0.9638 | 0.9999 * | 0.9980 | 23.5936 | 8.3319 | 5.9042 |
| 0.9472 | 0.9999 * | 0.9974 | 25.5931 | 4.6231 | 5.1422 |
| 0.9271 | 0.9998 * | 0.9996 * | 21.5357 | 7.0424 | 6.6292 |
| 0.9637 | 0.8614 | 0.9894 | 26.0231 | 31.2110 | 9.7624 |
| 0.9222 | 0.9997 * | 0.9996 * | 23.5789 | 9.2951 | 6.9346 |
| 0.9463 | 0.9901 | 0.9997 * | 23.6941 | 6.5899 | 7.0308 |
| 0.9473 | 0.9999 * | 0.9983 | 23.2380 | 7.8688 | 11.2152 |
| 0.9503 | 0.9985 | 0.9988 | 22.7621 | 6.8328 | 7.9634 |
| 0.9543 | 0.9995 | 0.9999 * | 26.4014 | 10.1902 | 9.3346 |
| 0.9177 | 0.9999 * | 0.9997 * | 21.9923 | 8.2467 | 7.6790 |
| 0.9604 | 0.9999 * | 0.9999 * | 22.6079 | 8.3337 | 6.3901 |
| 0.9556 | 0.9967 | 0.9931 | 20.8212 | 6.0245 | 6.3629 |
| 0.9685 | 0.9997 * | 0.9935 | 23.2112 | 4.3715 | 4.7472 |
| 0.9506 | 0.9994 * | 0.9990 | 22.7027 | 10.3105 | 5.9873 |
| 0.9548 | 0.9999 * | 0.9969 | 22.9562 | 7.7538 | 7.1945 |
| 0.9527 | 0.9994 * | 0.9974 | 22.8379 | 10.2288 | 8.6005 |
| 0.9537 | 0.9968 | 0.9853 | 22.9239 | 6.0038 | 5.7879 |
| 0.9530 | 0.9690 | 0.9998 * | 27.7936 | 20.7371 | 9.7188 |
| - | 0.9998 * | 0.9959 | - | 6.9083 | 6.9956 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tinochai, K.; Jampachaisri, K.; Areepong, Y.; Sukparungsee, S. Empirical Bayes Prediction in a Sequential Sampling Plan Based on Loss Functions. Processes 2019, 7, 944. https://doi.org/10.3390/pr7120944
Tinochai K, Jampachaisri K, Areepong Y, Sukparungsee S. Empirical Bayes Prediction in a Sequential Sampling Plan Based on Loss Functions. Processes. 2019; 7(12):944. https://doi.org/10.3390/pr7120944
Chicago/Turabian StyleTinochai, Khanittha, Katechan Jampachaisri, Yupaporn Areepong, and Saowanit Sukparungsee. 2019. "Empirical Bayes Prediction in a Sequential Sampling Plan Based on Loss Functions" Processes 7, no. 12: 944. https://doi.org/10.3390/pr7120944
APA StyleTinochai, K., Jampachaisri, K., Areepong, Y., & Sukparungsee, S. (2019). Empirical Bayes Prediction in a Sequential Sampling Plan Based on Loss Functions. Processes, 7(12), 944. https://doi.org/10.3390/pr7120944





