1. Introduction
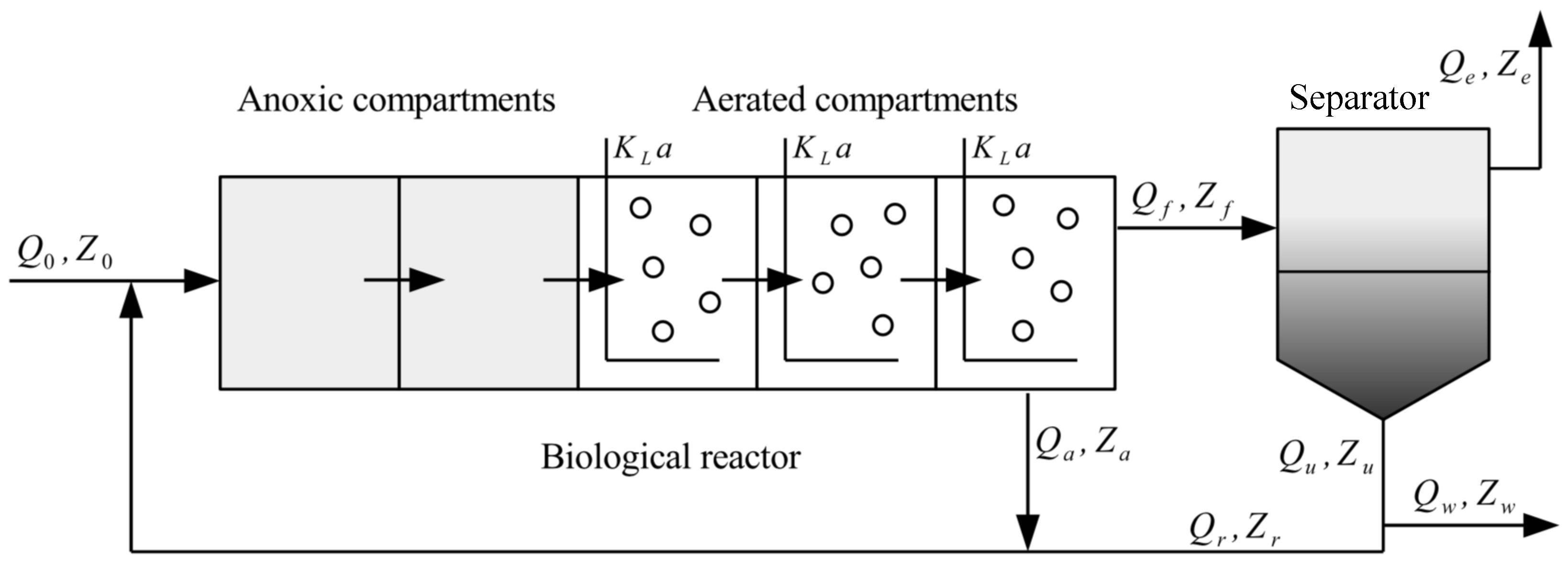
Wastewater treatment plants (WWTPs) have been widely used to recycle wastewater in order to minimize its adverse environmental impacts. A typical WWTP is a large-scale nonlinear process that consists of a series of interconnected biological reactors and a secondary settler. While meeting the strict requirements in environmental regulations, ensuring the process safety and minimizing the cost of operation, a wastewater treatment plant should be monitored and regulated [
1]. However, significant variability of inlet flow rates and wastewater compositions leads to the increased complexity in the design of advanced control and monitoring schemes for WWTPs [
2].
In the literature, there are many existing resutls on the control of WWTPs. For example, in [
3], proportional-integral (PI) was used to control a nutrient removal WWTP. In [
4], the tuning of proportional-integral-derivative control was considered in the control of the dissolved oxygen concentration in the activated sludge process. Advanced control methods such as model predictive control (MPC) have also attracted much research attention in the control of WWTPs. In [
5,
6,
7], simultaneous design and control of WWTPs were considered with MPC. In [
8], an MPC controller was developed for the Benchmark Simulation Model No.1 (BSM1). MPC was also used to in the control of oxygen concentration in [
9,
10]. In [
11,
12], MPC was applied to a WWTP to increase the plant efficiency, and in [
13] it was applied to reduce the power usage. In one of our previous works, we applied economic MPC (EMPC) to explicitly optimize the operating economics of WWTPs [
14]. While the EMPC can lead to improved effluent quality and improved overall operating cost, its high evaluation time renders the online implementation of this economic MPC intractable.
When considering economic MPC, it in general requires more time to evaluate the corresponding optimization problem compared with the traditional tracking MPC. One way to address the high evaluation time of economic MPC of nonlinear system is to use a distributed computing framework. Following this idea, in a recent work [
1], we developed distributed EMPC schemes for WWTPs to reduce the evaluation time of the centralized EMPC. In this work, we consider another approach to address the high evaluation time of economic MPC; that is, to design economic MPC based on approximated models. This is based on the consideration that when solving the nonlinear optimization problem of an economic MPC, the model of the system is evaluated many times. If we can use an approximated model that can be evaluated faster, then the economic MPC can be evaluated faster.
The objective of this work is to study how two model approximation methods can help speed up the evaluation of the optimization problem of economic MPC. Specifically, we propose to develop linear approximated models of the original nonlinear system and use the approximated models in EMPC design. A lot of achievements have been made on the use of approximated models in MPC. The work of [
15] applied feedback linearization to the plant and then used MPC in a cascade arrangement for the resulting linear system. The nonlinear programming problem was reduced to a quadratic optimization problem which can improve the computational efficiency. The implementation of MPC with a different linear model at each time step derived from a local (Jacobian) linearization of the nonlinear plant was first proposed in [
16]. An extended Kalman filter was proposed to be added to this approach to deal with unstable nonlinear process and ensure a better disturbance rejection in [
17,
18]. This idea was further developed in [
19], contraction constraints were applied and the explicit stability conditions were derived. In [
20], one technique was proposed to approximate the nonlinear system with a linear time varying (LTV) model, which is obtained from a linearization of the system along the predicted system trajectory. In [
21,
22], a novel MPC algorithm was proposed which can significantly reduce the online evaluation time. The approach is to only compute the first control move while approximating the rest of control moves by using a linear controller.
Pertaining to model approximation, model order reduction techniques are also popular and can significantly abate the complexity of the nonlinear system while conserving the dominant dynamics of the process [
23]. The proper orthogonal decomposition (POD) method is extensively used in data analysis for approximating the high-dimensional process by low-dimensional descriptions [
24]. The POD method has been widely applied in control in chemical engineering [
25,
26,
27,
28,
29]. In [
30], a state estimation scheme was established for WWTPs using POD-based model approximation. In [
31,
32], a reduced order model based on the POD-Galerkin projection method was constructed for economic MPC. With the reduced order model, the evaluation time of the economic MPC was significantly reduced. In [
33], a nonlinear system was represented by a piecewise-linear system and each of the pieces were reduced with a Krylov projections.
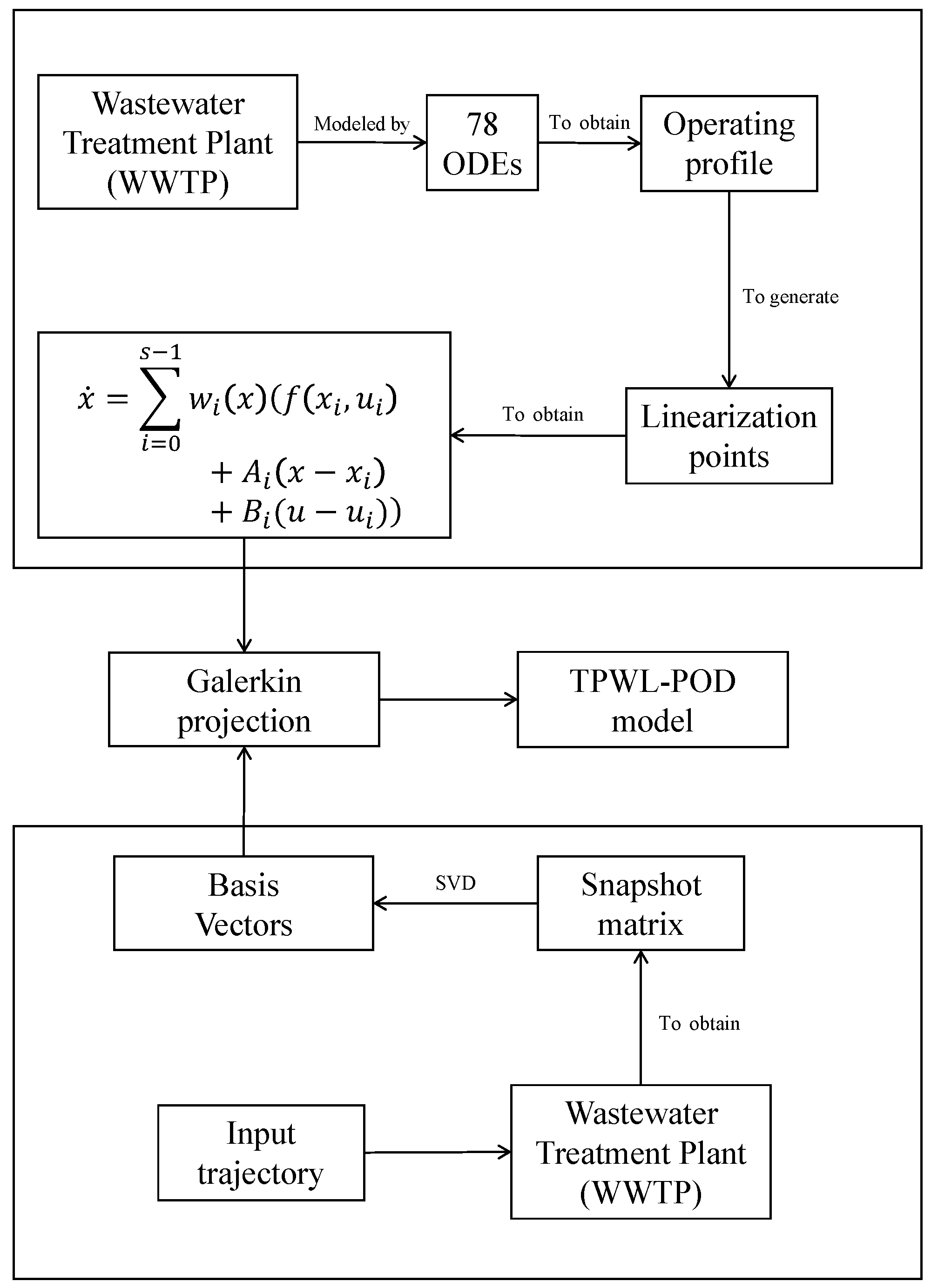
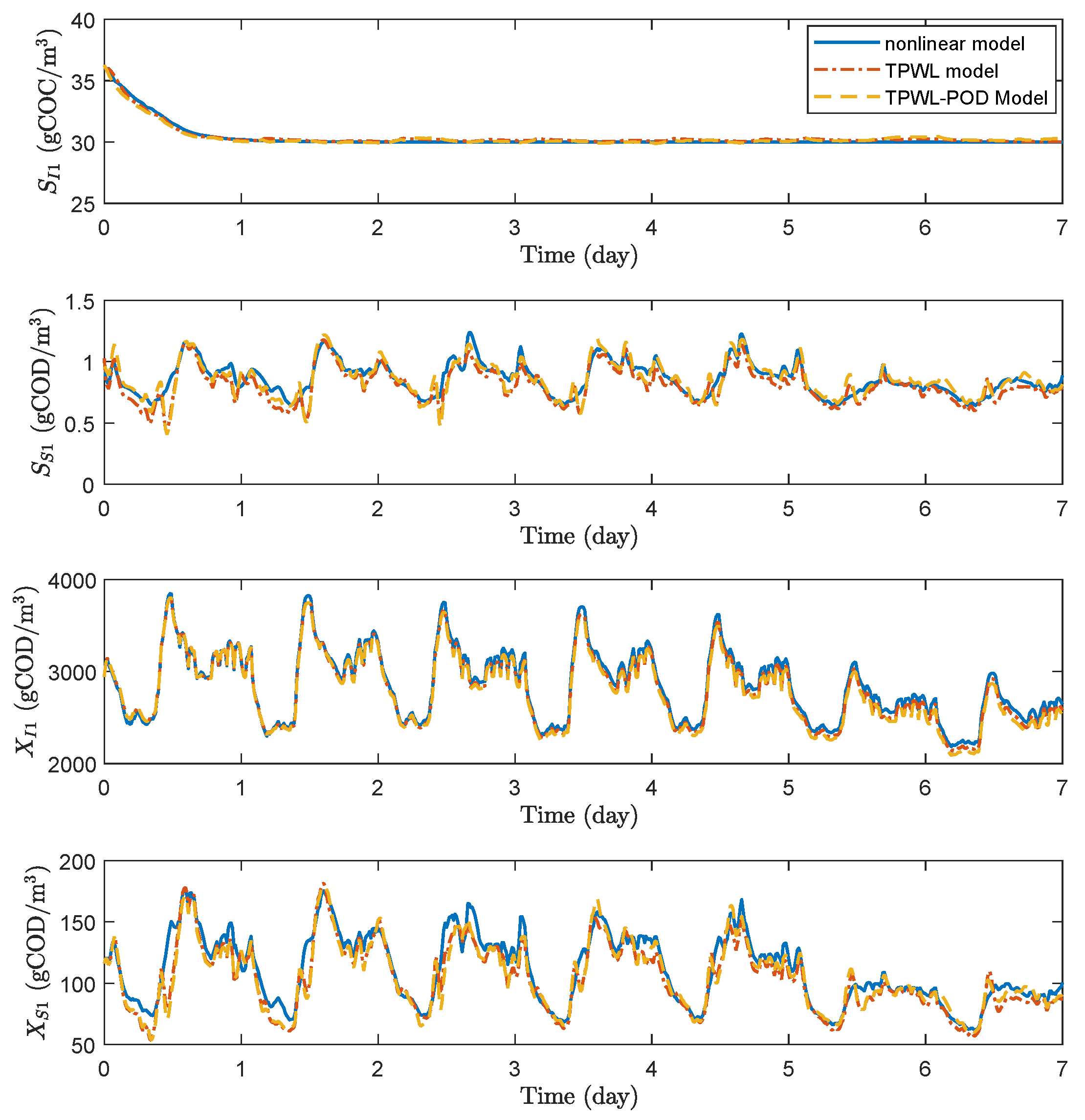
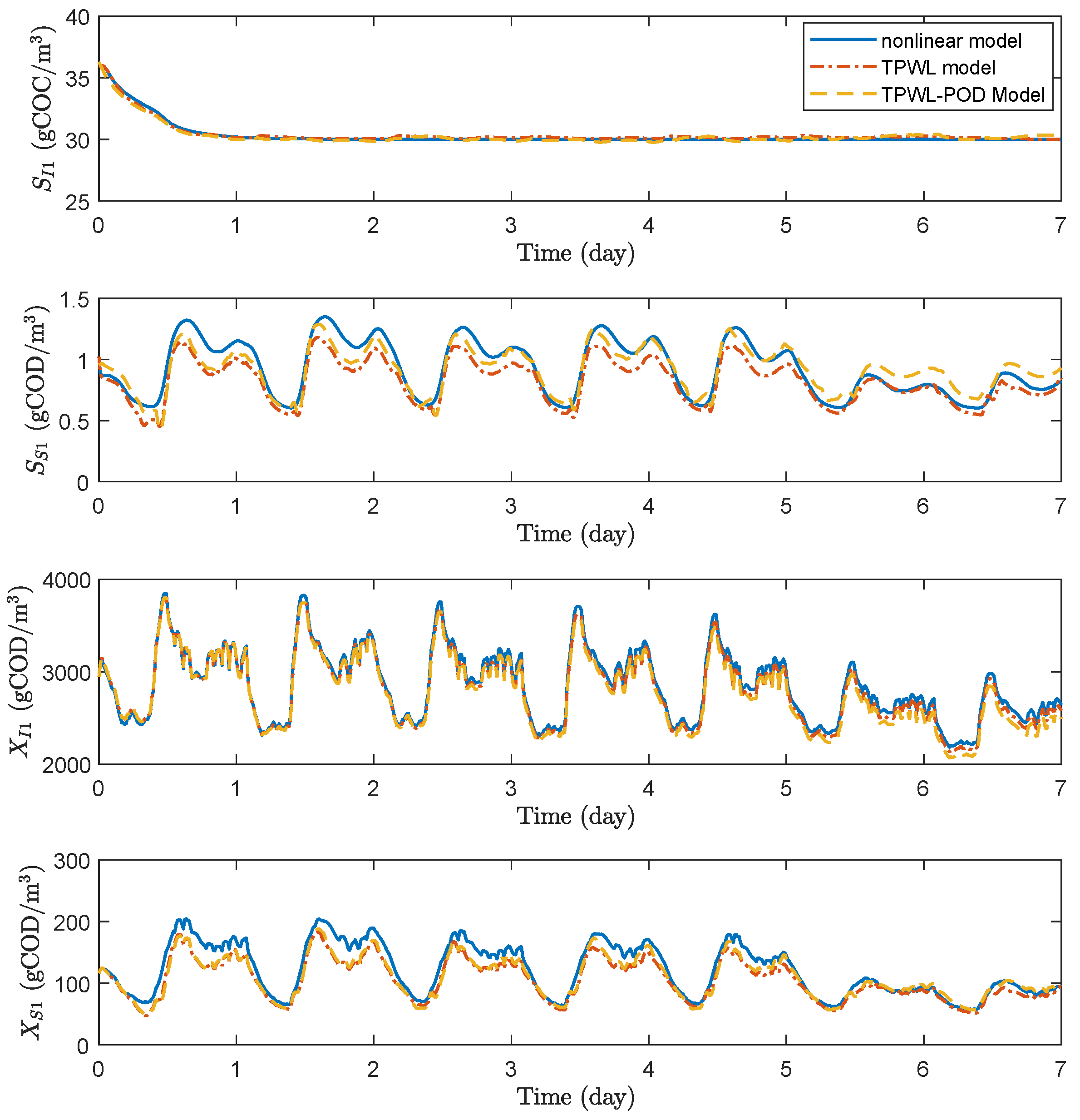
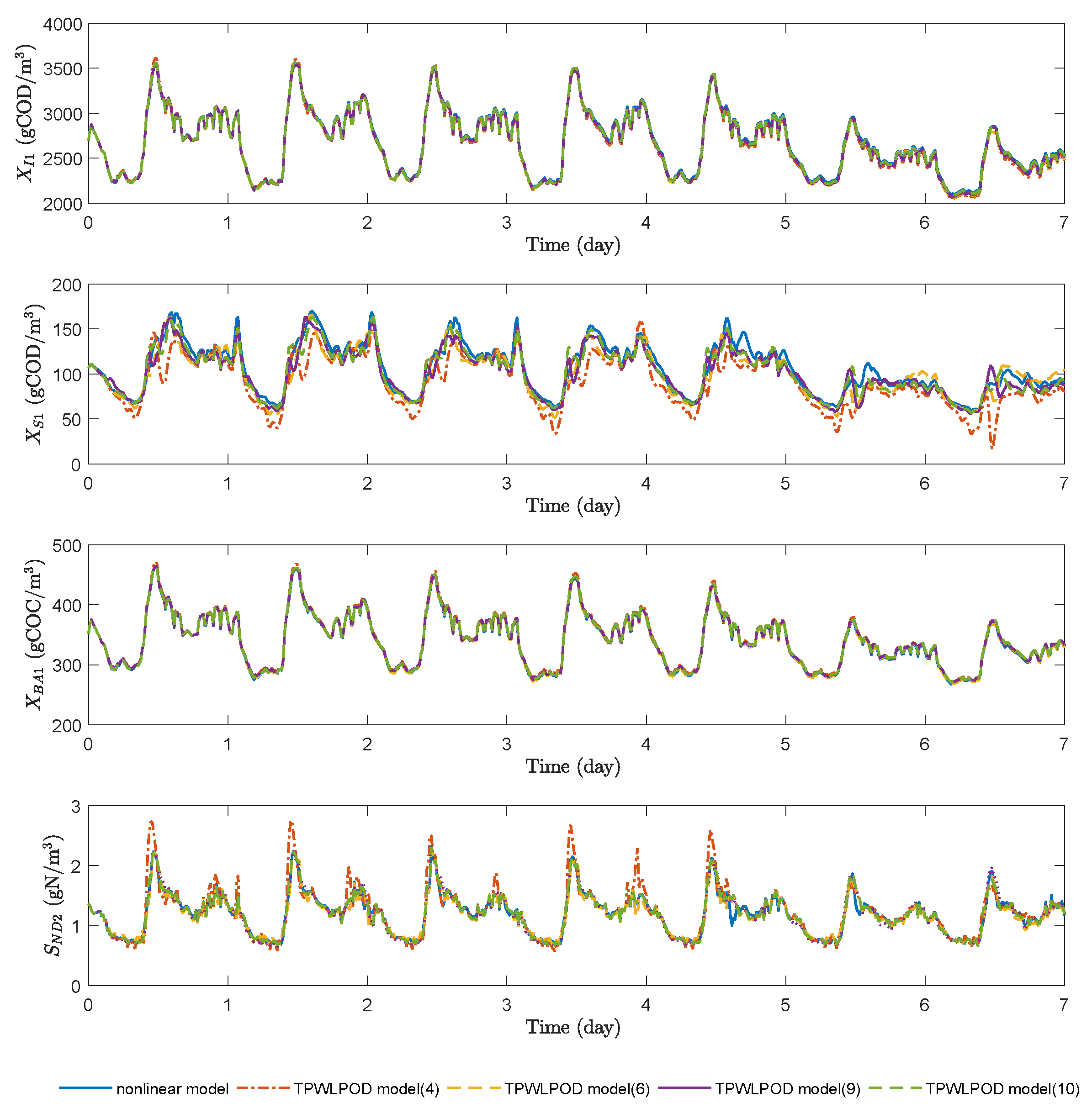
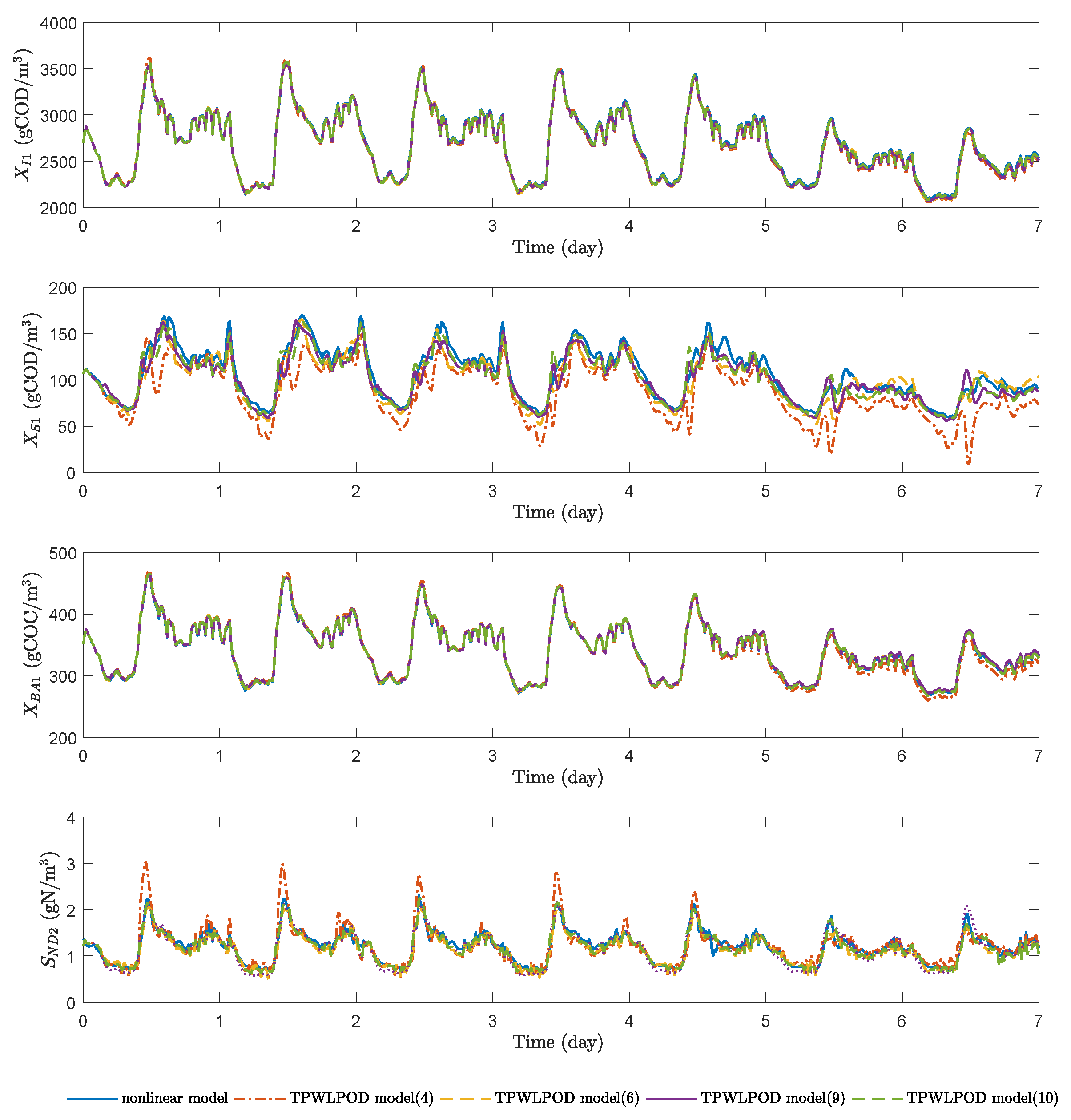
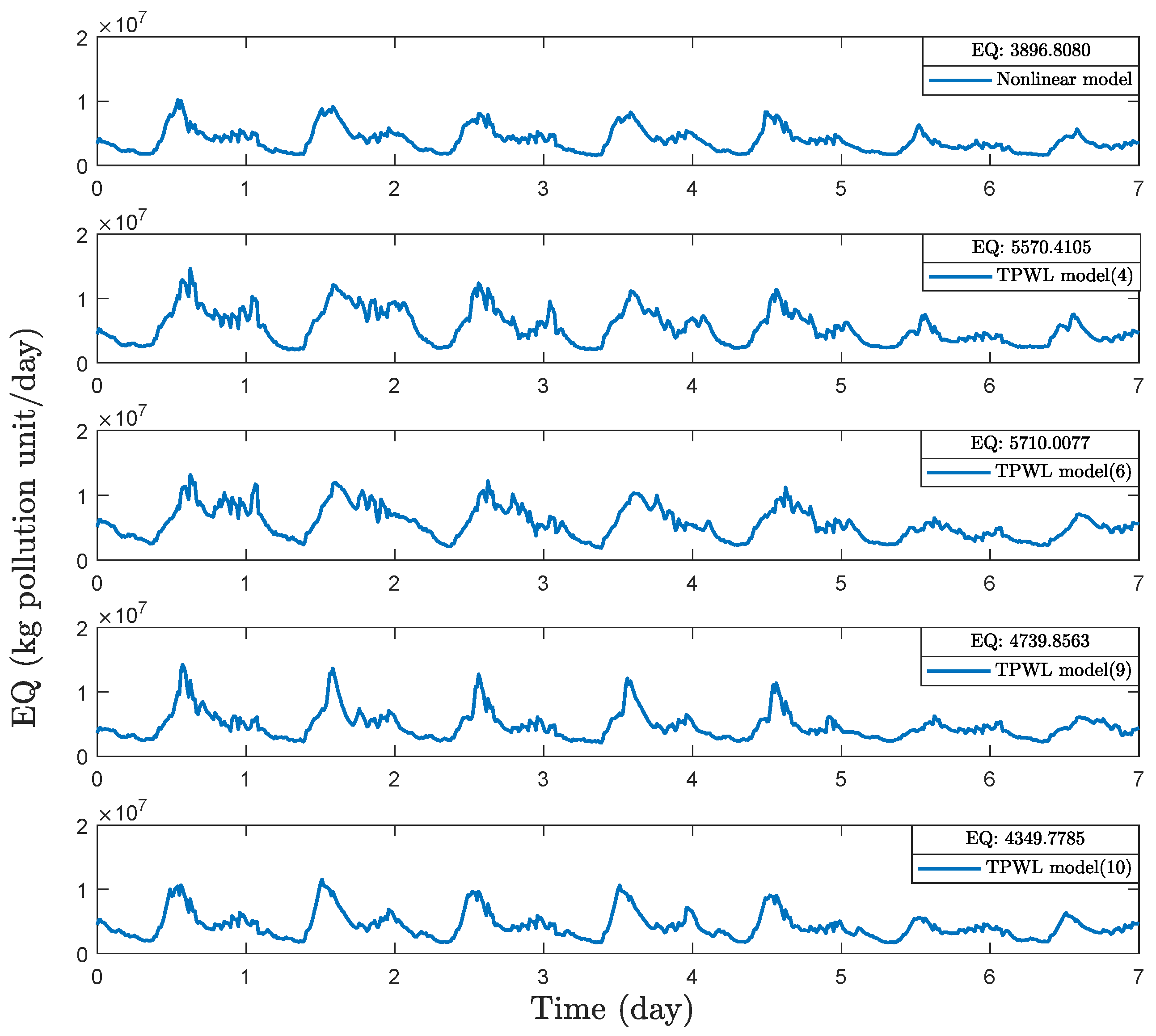
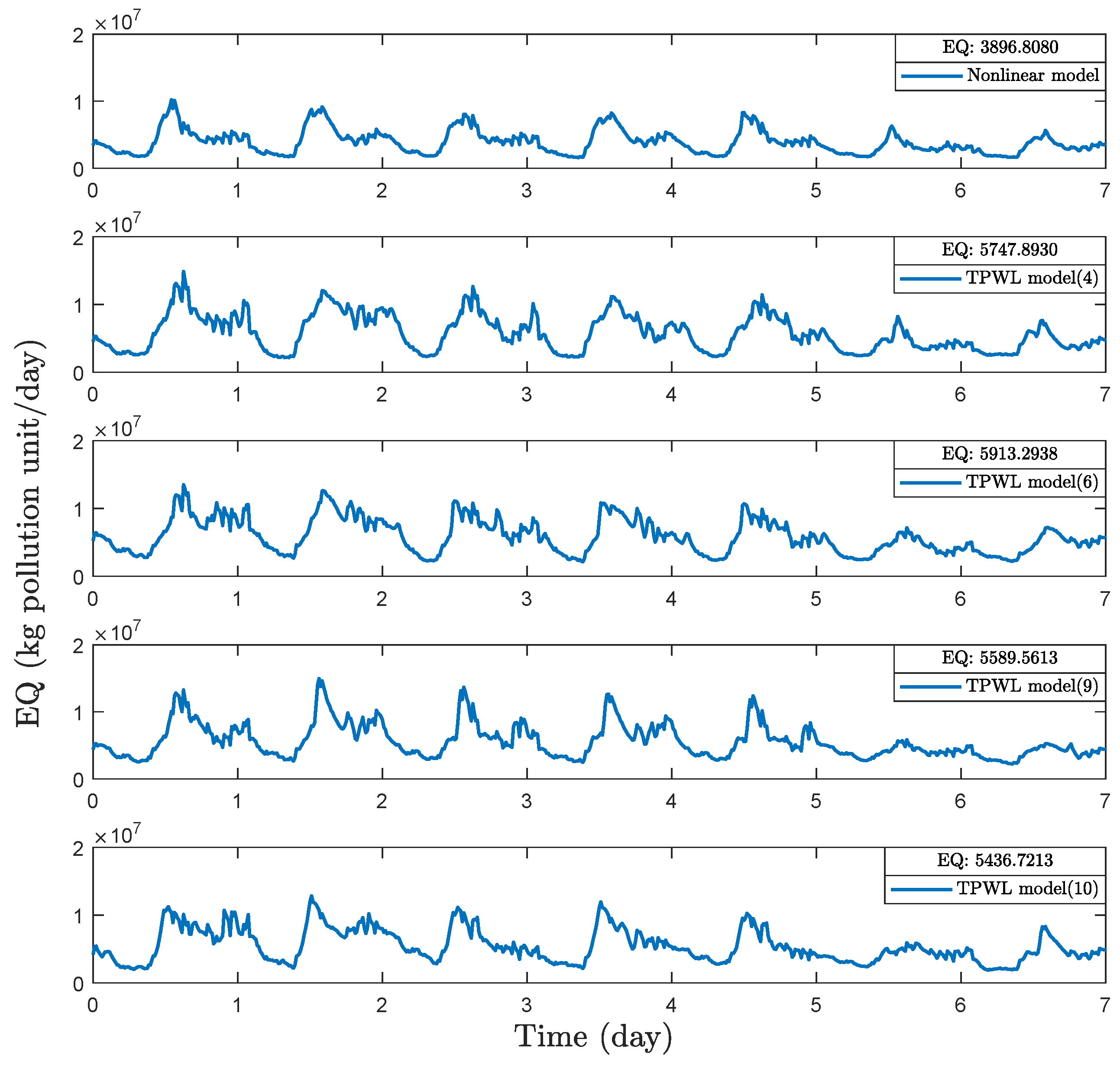
In this work, we apply the trajectory piecewise linearization and a combination of trajectory piecewise linearization and proper orthogonal decomposition method to WWTPs to derive low-order linear models, which are subsequently used for EMPC controller design. The model accuracy, economic MPC evaluation time, and economic control performance of the WWTP process under these EMPC controllers are compared. Note that we investigate the performance of these model approximation and reduction methods in a centralized control framework. These methods may also be used together with distributed control to further reduce the evaluation time of the centralized EMPC. The main contributions of this work include the folllowing:
The investigation of two model approximation methods in EMPC evaluation time reduction in the context of wastewater treatment control.
The detailed model reduction procedures for wastewater treatment processes and the design of EMPC based on the reduced models.
Extensive simulation results and analysis on the performance of EMPC based on reduced models in terms of economic performance and controller evaluation time.
3. Trajectory Piecewise Linear (TPWL) Model
In this section, the trajectory piecewise linear model approach is introduced and the trajectory piecewise linear model is presented. The steps to generate the piecewise linear model are also shown in this section.
3.1. Piecewise Linear Representation
A linearized model for the nonlinear system can be obtained at a steady-state point (
) as follows:
where
A is the Jacobian matrix of system
evaluated at the steady-state.
The simple linearized model can be used to approximate weakly nonlinear systems with less evaluation time [
33]. The approximated result of the linearized model usually depends on the range of inputs. If the system is a highly nonlinear system, the simple linearized model which is only linearized at one point would be less accurate. The main idea of the piecewise linear model approach is to generate a weighted combination of linear models which are linearized at appropriately selected states of the original nonlinear system. Compared with the system which is linearized at one single point, the system consisting of a combination of multiple linearizations would generate a better approximation result for a more complex nonlinear system.
Assuming that
s linearized models have been generated for the nonlinear system of Equation (
16) at points
,
:
A weighted combination of the linearized models in the form of Equation (25) of the nonlinear system leads to the following representation:
where the weight
is a state dependent variable and it can be computed from the distance between current state
x and the linearized point
[
33].
3.2. Generation of Piecewise Linear Model
The trajectory piecewise linear model is developed based on a fixed trajectory of the entire nonlinear system. The fixed trajectory is generated by simulating the nonlinear system based on a fixed training input u. Let us consider that we have generated a fixed trajectory of the nonlinear system, and the initial state is given. The selection of linearization points can be shown as in Algorithm 1.
| Algorithm 1: Algorithm for finding the linearization points of piecewise linear model |
Define and . Set and . If, then:
- 3.1.
Set as one of the linearization points. - 3.2.
For each ,
- 3.2.1
Calculate the distance between point and the linearization point , . - 3.2.2
If (), then: . Else, do: .
- 3.3.
Select such that . - 3.4.
Set , set . Go to Step 3.1.
Else, end. |
In Algorithm 1, the operator “\” denotes set subtraction such that . N is the number of sampled points on this fixed trajectory. is the set of the linearization points. The value is a pre-determined distance threshold, and it can be determined in Algorithm 2. In Algorithm 2, s is the number of models supposed to be generated.
| Algorithm 2: Determination of the pre-determined distance threshold value algorithm |
Find the maximum distance between any of the two points on the trajectory, , . Set .
|
The state dependent weight
shown in Equation (
26) can be computed as described in Algrithm 3 [
33].
| Algorithm 3: Computation algorithm for the state dependent weight parameter |
At each linearization point , compute the distance . Find the minimum value among , . For compute . Compute the summation of , . Compute the normalized parameter .
|
In Algorithm 3, is a positive constant value. The weighting parameter changes according to the position of current state x in state space. The exponential term in step 3 to determine the weighting parameter ensures that the distribution of the weight will change immediately close to one if current state x is sufficiently close to the linearization point .