Fine-Tuning Meta-Heuristic Algorithm for Global Optimization
Abstract
1. Introduction
- Genetic algorithms (GAs) [1], which simulate Darwin’s theory of evolution;
- Simulated annealing (SA) [2], which emerged from the thermodynamic argument;
- Ant colony optimization (ACO) algorithms [3], which mimic the behavior of an ant colony foraging for food;
- Particle swarm optimization (PSO) algorithms [4], which simulates the behavior of a flock of birds;
- Artificial bee colony (ABC) algorithms [5], which mimic the behavior of the honeybee colony; and
- Differential evolution algorithms (DEAs) [6], for solving global optimization problems.
2. Literature Review
3. Fine Tuning Meta-Heuristic Algorithm (FTMA)
4. Methodology
4.1. Well-Known Optimization Algorithms
- (1)
- Genetic algorithm (decimal form) (DGA): This is similar to a conventional GAs with the exception that the chromosomes are not converted to binary digits. It has the same steps as GAs, selection, crossover, and mutation. Here, the crossover or mutation procedures are performed upon the decimal digits as they are performed upon the bits in a binary GA. The entire procedure of the DGA is taken from [29].
- (2)
- Genetic algorithm (real form) (RGA): In this algorithm, the vectors are used in optimization as real values, without converting them to integers or binary numbers. As a binary GA, it performs the same procedures. The complete steps of DGA are taken from [30].
- (3)
- Particle swarm optimization (PSO) with optimizer: The success of this famous algorithm is down to its simplicity. It uses the velocity vector to update every solution, using the best solution of the vector along with the best global solution found so far. The core formula of PSO is taken from [4].
- (4)
- Differential evolution algorithm (DEAs): This algorithm chooses two (possibly three) solutions other than the current solution and searches stochastically, using selected constants to update the current solution. The whole algorithm is shown in [6].
- (5)
- Artificial bee colony (ABC): This algorithm gained use for its distributed behavior simulating the collaborative system of a honeybee colony. The system is divided into three parts, the employed bees which perform exploration, the onlooker which shows exploitation, and the scout which performs randomization. The algorithm is illustrated in [5].
| Algorithm 1: Fine-Tuning Meta-Heuristic Algorithm |
| Input: No. of solution population , Maximum number of iterations ; Tick; for to Initialize using Equation (1); Evaluate for every ; end for Search for and ; Initialize , set and ; while && ; for to Choose such that ; Compute using Exploration (Equation (2)); Evaluate for ; if && Compute using Exploitation (Equation (3)); Evaluate for ; if && Compute using Randomization (Equation (4)); Evaluate for ; end if end if if Update and using Equation (5); if Update and using Equation (6); end if end if end for end while Output:, , and the computation time. |
4.2. Benchmark Test Functions
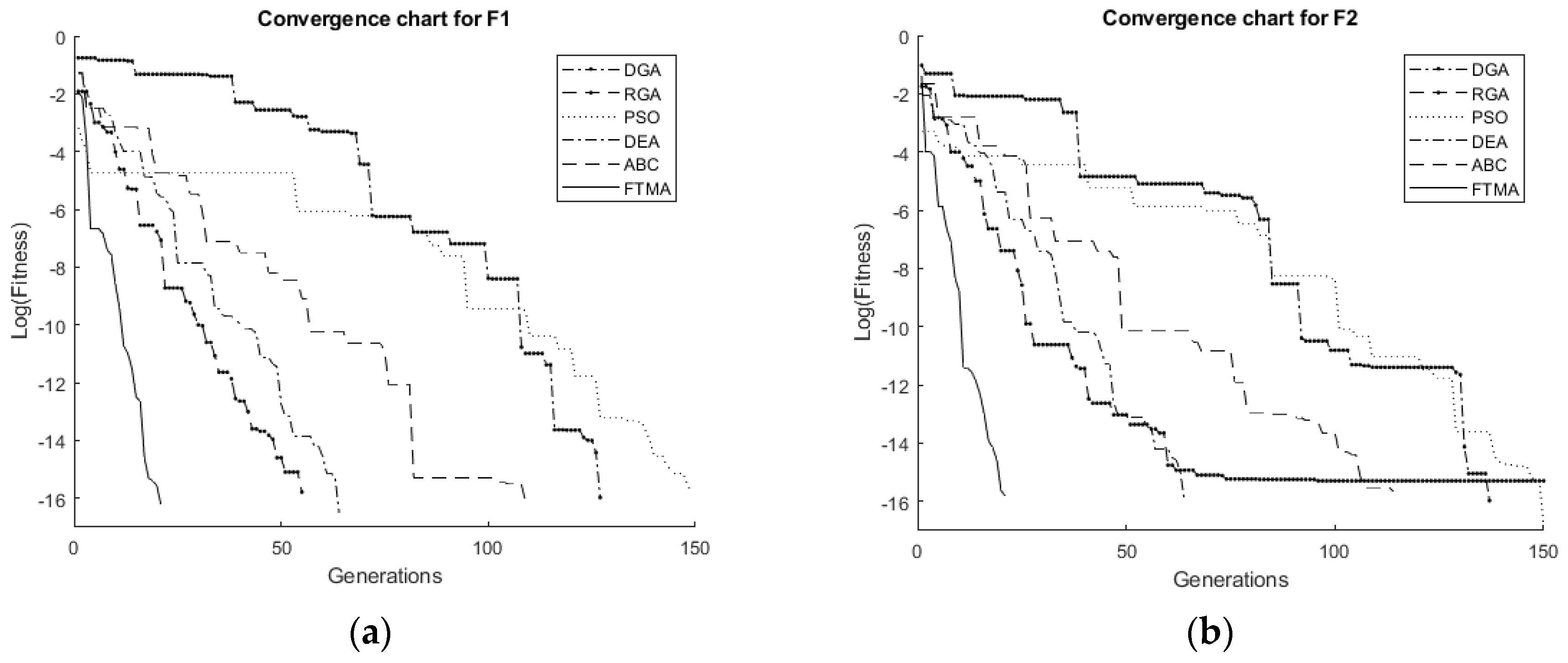
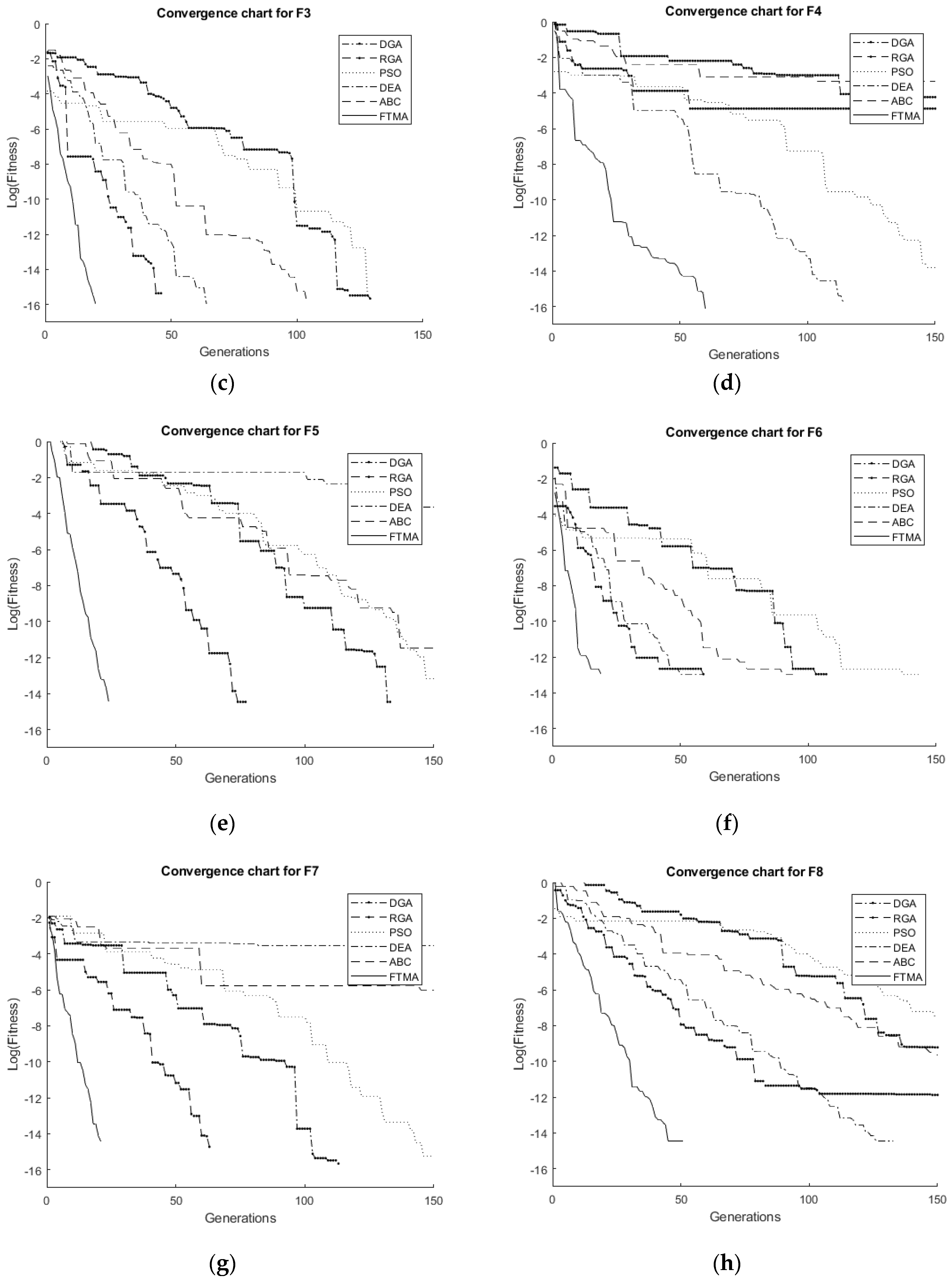
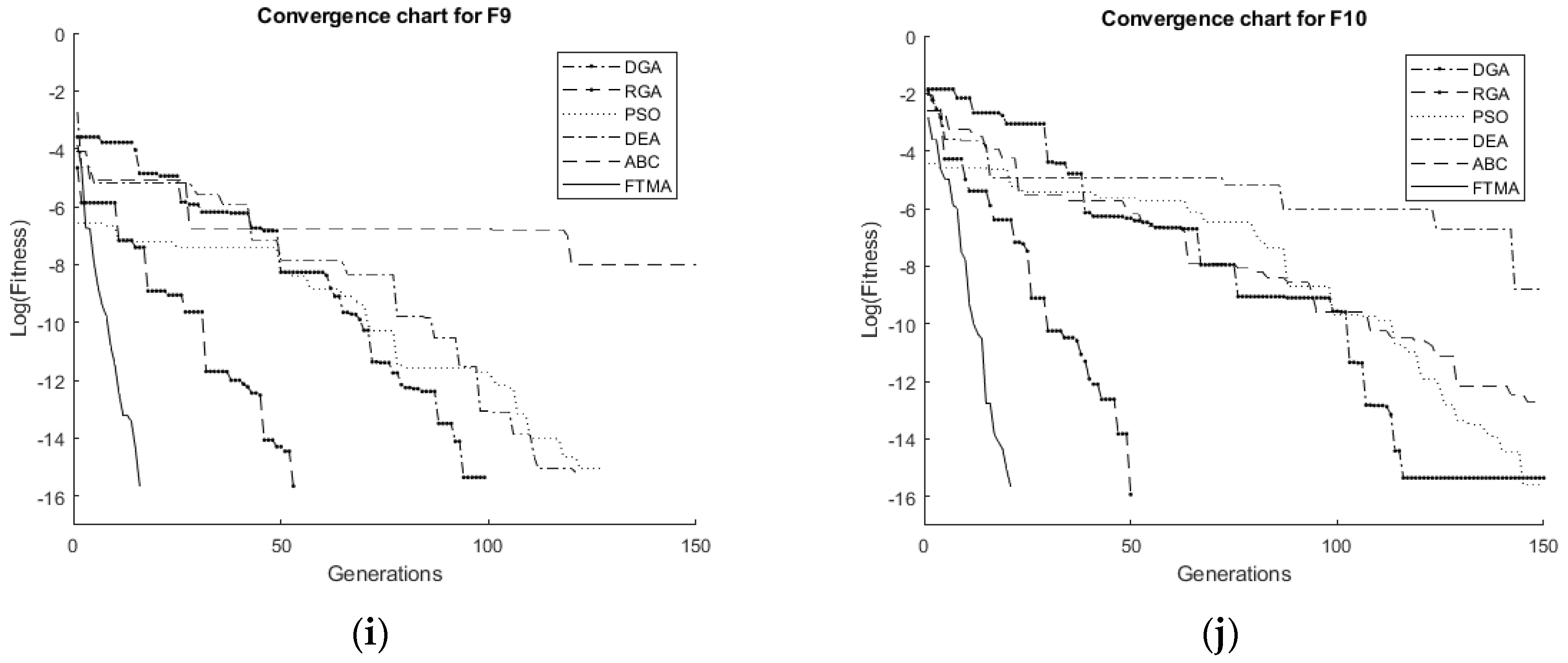
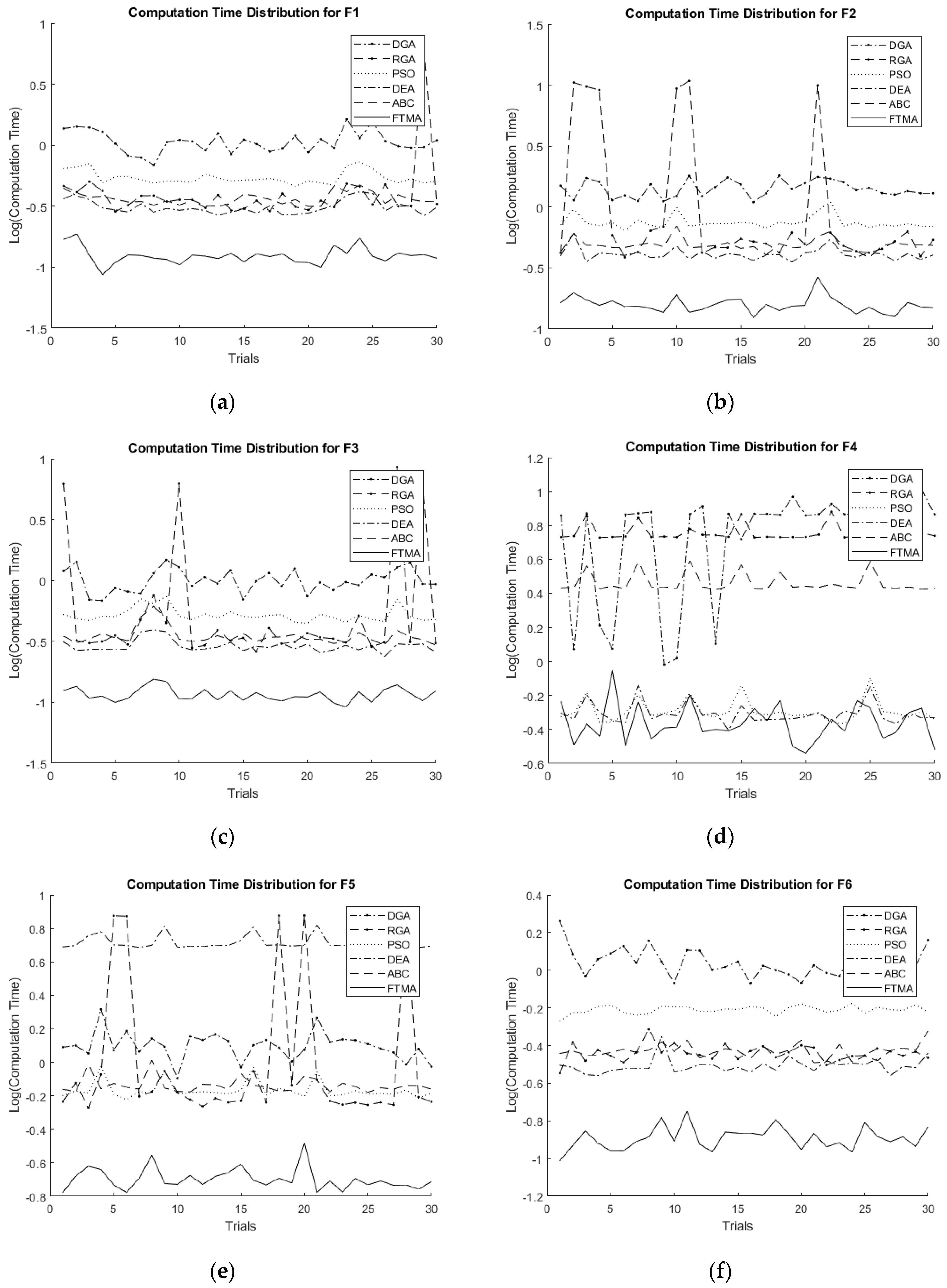
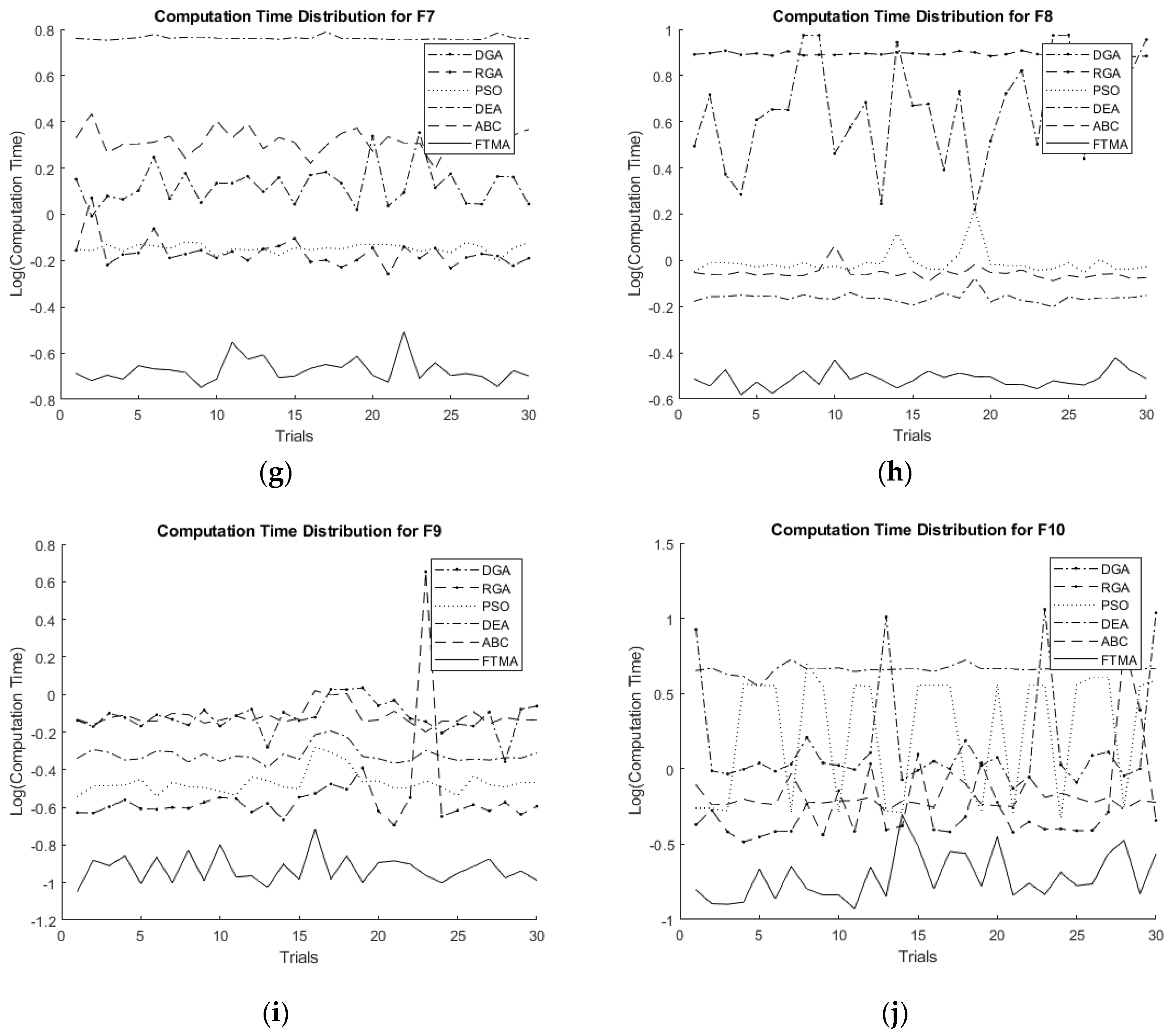
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Goldberg, D. Genetic Algorithms in Search, Optimization and Machine Learning, 1st ed.; Addison-Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 1989. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.; Vecchi, M. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 1996, 26, 29–41. [Google Scholar] [CrossRef] [PubMed]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, MHS’95, Nagoya, Japan, 4–6 October 1995; IEEE: Piscataway, NJ, USA, 1995; pp. 39–43. [Google Scholar]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Xing, B.; Gao, W. Innovative Computational Intelligence: A Rough Guide to 134 Clever Algorithms, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Ibraheem, I.K.; Ajeil, F.H. Path Planning of an autonomous Mobile Robot using Swarm Based Optimization Techniques Technique. Al-Khwarizmi Eng. J. 2016, 12, 12–25. [Google Scholar] [CrossRef]
- Ibraheem, I.K.; Al-hussainy, A.A. Design of a Double-objective QoS Routing in Dynamic Wireless Networks using Evolutionary Adaptive Genetic Algorithm. Int. J. Adv. Res. Comput. Commun. Eng. 2015, 4, 156–165. [Google Scholar]
- Ibraheem, I.K.; Ibraheem, G.A. Motion Control of an Autonomous Mobile Robot using Modified Particle Swarm Optimization Based Fractional Order PID Controller. Eng. Technol. J. 2016, 34, 2406–2419. [Google Scholar]
- Humaidi, A.J.; Ibraheem, I.K.; Ajel, A.R. A Novel Adaptive LMS Algorithm with Genetic Search Capabilities for System Identification of Adaptive FIR and IIR Filters. Information 2019, 10, 176. [Google Scholar] [CrossRef]
- Humaidi, A.; Hameed, M. Development of a New Adaptive Backstepping Control Design for a Non-Strict and Under-Actuated System Based on a PSO Tuner. Information 2019, 10, 38. [Google Scholar] [CrossRef]
- Allawi, Z.T.; Abdalla, T.Y. A PSO-Optimized Reciprocal Velocity Obstacles Algorithm for Navigation of Multiple Mobile Robots. Int. J. Robot. Autom. 2015, 4, 31–40. [Google Scholar] [CrossRef]
- Allawi, Z.T.; Abdalla, T.Y. An ABC-Optimized Type-2 Fuzzy Logic Controller for Navigation of Multiple Mobile Robots Ziyad. In Proceedings of the Second Engineering Conference of Control, Computers and Mechatronics Engineering, Baghdad, Iraq, February 2014; pp. 239–247. [Google Scholar]
- Tarasewich, P.; McMullen, P. Swarm intelligence: Power in numbers. Commun. ACM 2002, 45, 62–67. [Google Scholar] [CrossRef]
- Crepinsek, M.; Liu, S.; Mernik, M. Exploration and exploitation in evolutionary algorithms: A survey. ACM Comput. Surv. 2013, 45, 35. [Google Scholar] [CrossRef]
- Chen, J.; Xin, B.; Peng, Z.; Dou, L.; Zhang, J. Optimal contraction theorem for exploration and exploitation tradeoff in search and optimization. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2009, 39, 680–691. [Google Scholar] [CrossRef]
- Wolpert, D.; Macready, W. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Yang, X.S. Firefly algorithms for multimodal optimisation. In Proceedings of the Fifth Symposium on Stochastic Algorithms, Foundations and Applications, Sapporo, Japan, 26–28 October 2009; Watanabe, O., Zeugmann, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5792, pp. 169–178, Lecture notes in computer, science. [Google Scholar]
- Yang, X.S.; Deb, S. Cuckoo Search via Lévy flights. In Proceedings of the 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 210–214. [Google Scholar]
- Yang, X.S. A new Meta-heuristic bat-inspired algorithm. In Nature Inspired Cooperative Strategies for Optimization (NISCO 2010); Studies in computational intelligence; Springer: Berlin, Germany, 2010; pp. 65–74. [Google Scholar]
- Yang, X.S. Flower pollination algorithm for global optimization. In Unconventional Computation and Natural Computation; Lecture notes in computer science; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7445, pp. 240–249. [Google Scholar]
- Yang, X.S. Nature-Inspired Optimization Algorithms, 1st ed.; Elsevier: London, UK, 2014. [Google Scholar]
- Mirjalili, S.A.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mirjalili, S.A. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl. Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Mirjalili, S.A. The Ant Lion Optimizer. Adv. Eng. Softw. 2015, 83, 80–98. [Google Scholar] [CrossRef]
- Mirjalili, S.A. SCA: A Sine Cosine Algorithm for solving optimization problems. Knowl. Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Mirjalili, S.A.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Lee, Y.; Marvin, A.; Porter, S. Genetic algorithm using real parameters for array antenna design optimization. In MTT/ED/AP/LEO Societies Joint Chapter UK and Rep. of Ireland Section. 1999 High Frequency Postgraduate Student Colloquium; Cat. No.99TH840; IEEE: Piscataway, NJ, USA, 1999; pp. 8–13. [Google Scholar]
- Bessaou, M.; Siarry, P. A genetic algorithm with real-value coding to optimize multimodal continuous functions. Struct. Multidiscip. Optim. 2001, 23, 63–74. [Google Scholar] [CrossRef]

| Fn.Sym. | Function | Formula | Optimum | |
|---|---|---|---|---|
| F1 | SPHERE | 5 | ||
| F2 | ELLIPSOID | 5 | ||
| F3 | EXPONENTIAL | 5 | ||
| F4 | ROSENBROCK | 2 | ||
| F5 | RASTRIGIN | 5 | ||
| F6 | SCHWEFEL | 100 | ||
| F7 | GREIWANK | 600 | ||
| F8 | ACKLEY | 32 | ||
| F9 | SCHAFFER | 100 |
| Fn.Sym. | Function | Formula | Optimum | |
|---|---|---|---|---|
| F10 | ALLAWI | 2 |
| Fn. | DGA | RGA | PSO | DEA | ABC | FTMA | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fitness | Time | Fitness | Time | Fitness | Time | Fitness | Time | Fitness | Time | Fitness | Time | |
| F1 | 1.06 × 10−16 | 1.05 | 1.64 × 10−16 | 0.34 | 1.66 × 10−16 | 0.46 | 3.01 × 10−17 | 0.27 | 7.50 × 10−17 | 0.30 | 5.8 × 10−17 | 0.12 |
| F2 | 1.07 × 10−16 | 1.39 | 5.10 × 10−16 | 8.88 | 1.16 × 10−17 | 0.69 | 9.28 × 10−17 | 0.40 | 2.15 × 10−17 | 0.45 | 1.51 × 10−17 | 0.13 |
| F3 | 2.22 × 10−16 | 102 | 2.22 × 10−16 | 0.28 | 2.22 × 10−16 | 0.38 | 1.11 × 10−16 | 0.25 | 1.11 × 10−16 | 0.35 | 1.11 × 10−16 | 0.10 |
| F4 | 1.95 × 10−6 | 6.96 | 1.20 × 10−5 | 4.84 | 1.97 × 10−16 | 0.46 | 1.63 × 10−16 | 0.46 | 4.37 × 10−7 | 2.52 | 7.05 × 10−17 | 0.41 |
| F5 | 0 | 1.18 | 0 | 0.50 | 0 | 0.67 | 5.22 × 10−6 | 4.85 | 0 | 0.65 | 0 | 0.18 |
| F6 | 0 | 1.00 | 0 | 0.46 | 0 | 0.58 | 0 | 0.28 | 0 | 0.633 | 0 | 0.15 |
| F7 | 2.22 × 10−16 | 1.23 | 0 | 0.53 | 0 | 0.71 | 5.33 × 10−9 | 5.41 | 1.11 × 10−16 | 2.15 | 0 | 0.21 |
| F8 | 0 | 2.67 | 1.34 × 10−12 | 7.02 | 0 | 0.83 | 0 | 0.65 | 0 | 0.75 | 0 | 0.30 |
| F9 | 0 | 0.58 | 2.22 × 10−16 | 0.20 | 0 | 0.31 | 0 | 0.43 | 2.22 × 10−16 | 0.66 | 0 | 0.09 |
| F10 | 4.44 × 10−16 | 8.01 | 1.18 × 10−16 | 0.29 | 1.76 × 10−16 | 0.51 | 1.70 × 10−13 | 4.19 | 1.54 × 10−16 | 0.67 | 2.12 × 10−16 | 0.11 |
| Fn. | DGA | RGA | PSO | DEA | ABC | FTMA | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| m. | Std. | m. | Std. | m. | Std. | m. | Std. | m. | Std. | m. | Std. | |
| F1 | 5.94 × 10−17 | 5.84 × 10−17 | 5.10 × 10−15 | 2.43 × 10−14 | 1.03 × 10−16 | 6.23 × 10−17 | 9.13 × 10−17 | 5.75 × 10−17 | 1.00 × 10−16 | 6.80 × 10−17 | 7.84 × 10−17 | 5.35 × 10−17 |
| F2 | 6.29 × 10−17 | 5.46 × 10−17 | 2.20 × 10−16 | 7.04 × 10−16 | 7.74 × 10−17 | 5.98 × 10−17 | 1.05 × 10−16 | 6.76 × 10−17 | 8.78 × 10−17 | 6.24 × 10−17 | 9.95 × 10−17 | 6.52 × 10−17 |
| F3 | 1.29 × 1016 | 9.96 × 10−17 | 2.77 × 10−15 | 1.31 × 10−14 | 1.36 × 10−16 | 7.94 × 10−17 | 1.25 × 10−16 | 7.97 × 10−17 | 1.14 × 10−16 | 7.29 × 10−17 | 1.03 × 10−16 | 8.56 × 10−17 |
| F4 | 2.69 × 10−06 | 8.17 × 10−06 | 3.51 × 10−05 | 0.0001 | 1.07 × 10−16 | 6.38 × 10−17 | 1.09 × 10−16 | 6.92 × 10−17 | 1.05 × 10−06 | 1.85 × 10−06 | 1.25 × 10−16 | 6.43 × 10−17 |
| F5 | 0 | 0 | 8.52*10−15 | 4.52 × 10−14 | 0 | 0 | 3.99 × 10−07 | 4.84 × 10−07 | 0 | 0 | 0 | 0 |
| F6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| F7 | 1.18*10−16 | 1.03*10−16 | 1.33 × 10−16 | 8.78 × 10−17 | 1.03 × 10−16 | 8.56 × 10−17 | 1.50 × 10−07 | 1.96 × 10−07 | 1.11 × 10−16 | 9.50 × 10−17 | 1.03 × 10−16 | 8.56 × 10−17 |
| F8 | 2.36*10−16 | 8.86*10−16 | 1.59 × 10−08 | 4.54 × 10−08 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| F9 | 1.03*10−16 | 1.10*10−16 | 1.55 × 10−16 | 1.01 × 10−16 | 1.25 × 10−16 | 1.1 × 10−16 | 1.55 × 10−16 | 1.01 × 10−16 | 1.48 × 10−16 | 1.04 × 10−16 | 1.40 × 10−16 | 1.07 × 10−16 |
| F10 | 6.56*10−16 | 9.14*10−17 | 1.19 × 10−16 | 1.11 × 10−16 | 3.73 × 10−16 | 3.01 × 10−16 | 1.41 × 10−09 | 6.34 × 10−09 | 1.04 × 10−16 | 6.07 × 10−17 | 9.80 × 10−17 | 5.83 × 10−17 |
| Fn. | DGA | RGA | PSO | DEA | ABC | FTMA | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| m. | Std. | m. | Std. | m. | Std. | m. | Std. | m. | Std. | m. | Std. | |
| F1 | 1.085 | 0.221 | 0.566 | 1.091 | 0.546 | 0.072 | 0.315 | 0.047 | 0.364 | 0.040 | 0.125 | 0.021 |
| F2 | 1.423 | 0.221 | 2.389 | 3.780 | 0.754 | 0.103 | 0.413 | 0.052 | 0.490 | 0.063 | 0.159 | 0.026 |
| F3 | 1.021 | 0.219 | 1.215 | 2.224 | 0.525 | 0.075 | 0.291 | 0.034 | 0.353 | 0.067 | 0.166 | 0.015 |
| F4 | 6.299 | 2.660 | 5.747 | 0.658 | 0.518 | 0.087 | 0.500 | 0.076 | 2.920 | 0.410 | 0.449 | 0.126 |
| F5 | 1.275 | 0.247 | 1.788 | 2.561 | 0.687 | 0.091 | 5.200 | 0.500 | 0.733 | 0.084 | 0.203 | 0.033 |
| F6 | 1.122 | 0.202 | 0.365 | 0.037 | 0.617 | 0.030 | 0.312 | 0.032 | 0.372 | 0.032 | 0.129 | 0.018 |
| F7 | 1.361 | 0.290 | 0.686 | 0.110 | 0.714 | 0.030 | 5.783 | 0.111 | 2.100 | 0.241 | 0.213 | 0.028 |
| F8 | 5.055 | 2.518 | 7.832 | 0.124 | 0.984 | 0.147 | 0.691 | 0.035 | 0.811 | 0.059 | 0.307 | 0.026 |
| F9 | 0.773 | 0.139 | 0.404 | 0.761 | 0.343 | 0.054 | 0.478 | 0.051 | 0.765 | 0.092 | 0.119 | 0.022 |
| F10 | 2.288 | 3.154 | 0.785 | 1.188 | 2.460 | 1.585 | 4.583 | 0.300 | 0.643 | 0.110 | 0.124 | 0.055 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Allawi, Z.T.; Ibraheem, I.K.; Humaidi, A.J. Fine-Tuning Meta-Heuristic Algorithm for Global Optimization. Processes 2019, 7, 657. https://doi.org/10.3390/pr7100657
Allawi ZT, Ibraheem IK, Humaidi AJ. Fine-Tuning Meta-Heuristic Algorithm for Global Optimization. Processes. 2019; 7(10):657. https://doi.org/10.3390/pr7100657
Chicago/Turabian StyleAllawi, Ziyad T., Ibraheem Kasim Ibraheem, and Amjad J. Humaidi. 2019. "Fine-Tuning Meta-Heuristic Algorithm for Global Optimization" Processes 7, no. 10: 657. https://doi.org/10.3390/pr7100657
APA StyleAllawi, Z. T., Ibraheem, I. K., & Humaidi, A. J. (2019). Fine-Tuning Meta-Heuristic Algorithm for Global Optimization. Processes, 7(10), 657. https://doi.org/10.3390/pr7100657







