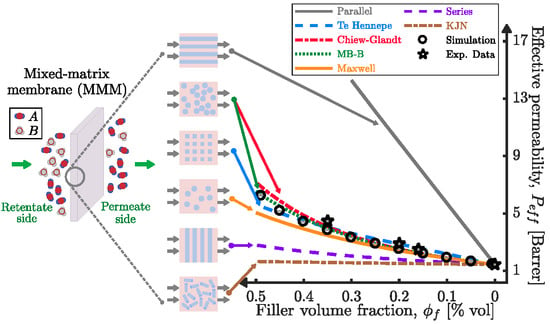
Modeling Permeation through Mixed-Matrix Membranes: A Review
Abstract
1. Introduction
2. Gas Transport through Mixed-Matrix Membranes
2.1. Permeability and Selectivity in MMMs
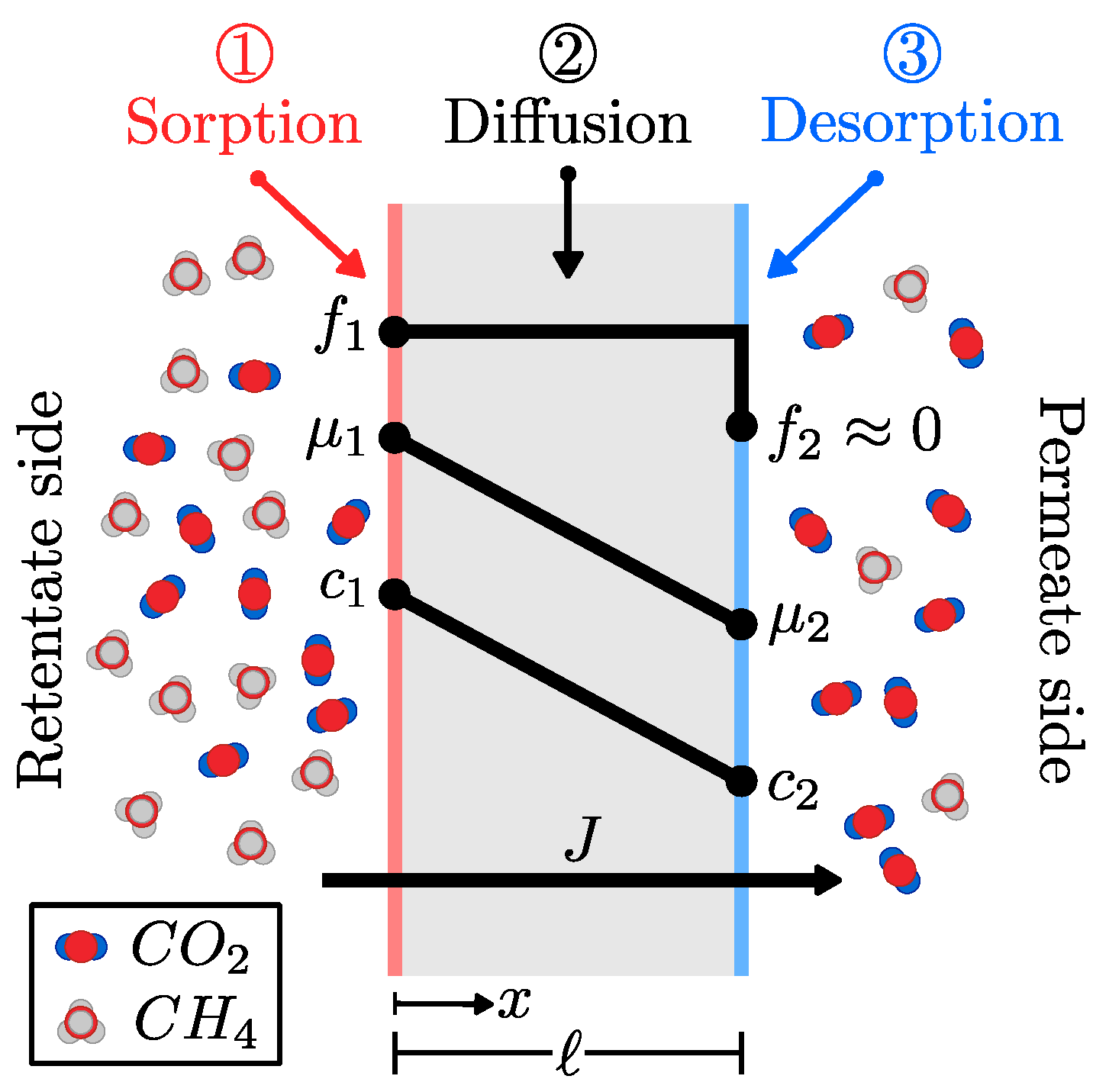
2.2. Diffusion and Sorption in MMMs
3. Models for Gas Permeation in Mixed-Matrix Membranes
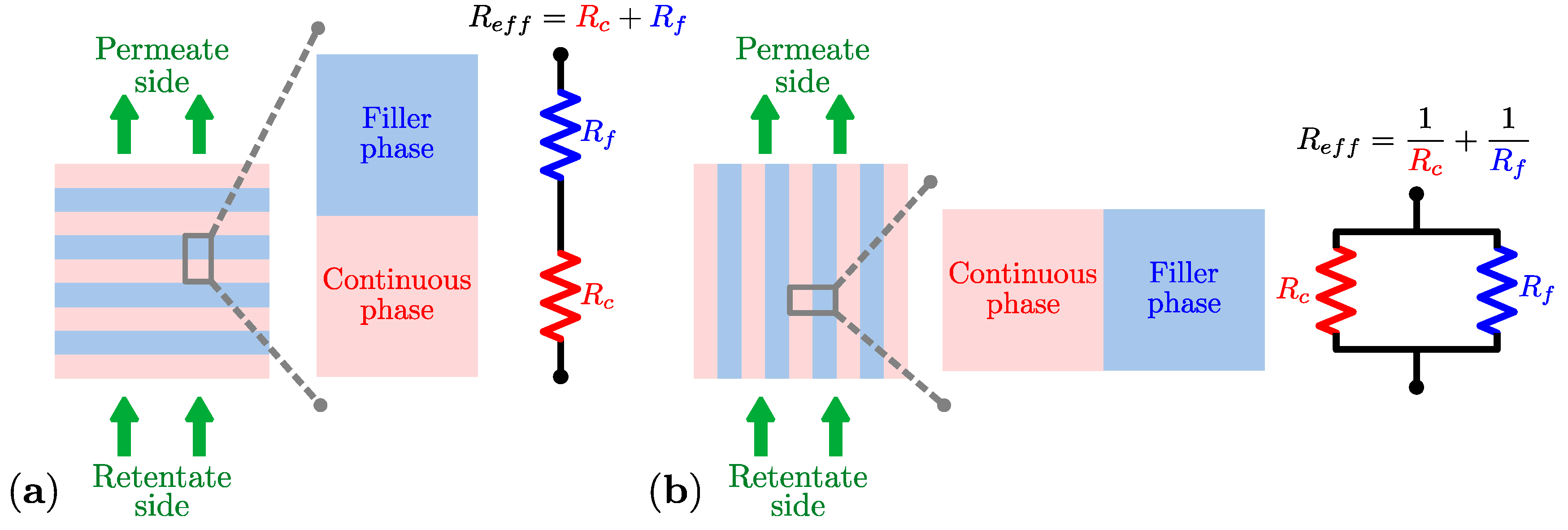
3.1. Resistance Model Approach
3.2. Effective Medium Approach
3.2.1. Maxwell Theory
3.2.2. Bruggeman’s Theory
3.3. Simulation-Based Rigorous Modeling Approach
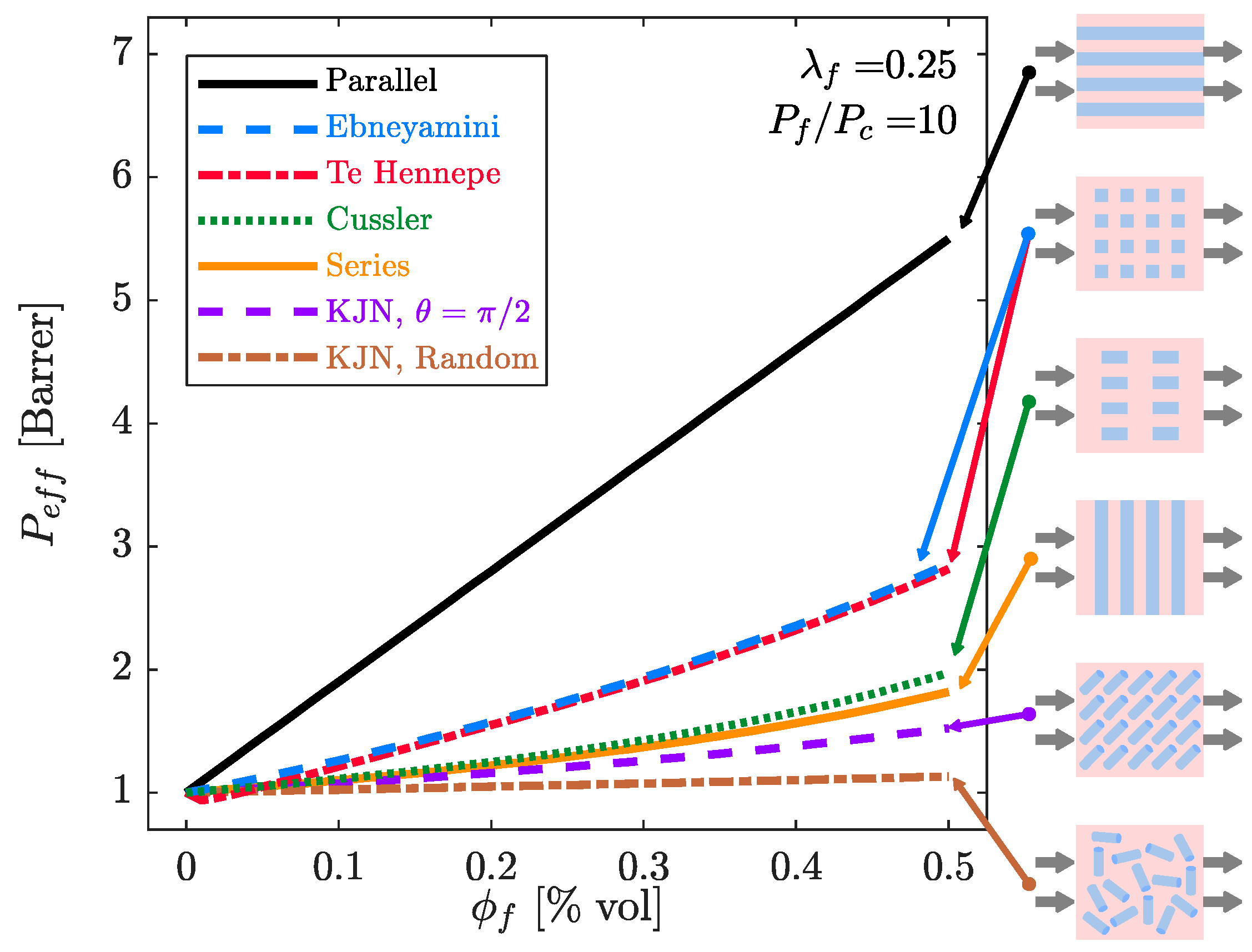
4. Predicting the Effective Permeability in Mixed-Matrix Membranes
4.1. Estimation of the Filler Phase Permeability through EMA and RMA Models
4.2. Prediction of the MMM Permeability through EMA and RMA Models
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sanders, D.F.; Smith, Z.P.; Guo, R.; Robeson, L.M.; McGrath, J.E.; Paul, D.R.; Freeman, B.D. Energy-efficient polymeric gas separation membranes for a sustainable future: A review. Polymer 2013, 54, 4729–4761. [Google Scholar] [CrossRef]
- Kosinov, N.; Gascon, J.; Kapteijn, F.; Hensen, E.J.M. Recent developments in zeolite membranes for gas separation. J. Membr. Sci. 2016, 499, 65–79. [Google Scholar] [CrossRef]
- Aroon, M.A.; Ismail, A.F.; Matsuura, T.; Montazer-Rahmati, M.M. Performance studies of mixed matrix membranes for gas separation: A review. Sep. Purif. Technol. 2010, 75, 229–242. [Google Scholar] [CrossRef]
- Werber, J.R.; Deshmukh, A.; Elimelech, M. The Critical Need for Increased Selectivity, Not Increased Water Permeability, for Desalination Membranes. Environ. Sci. Technol. Lett. 2016, 3, 112–120. [Google Scholar] [CrossRef]
- Han, Y.; Xu, Z.; Gao, C. Ultrathin Graphene Nanofiltration Membrane for Water Purification. Adv. Funct. Mater. 2013, 23, 3693–3700. [Google Scholar] [CrossRef]
- Lee, J.-Y.; Tan, W.S.; An, J.; Chua, C.K.; Tang, C.Y.; Fane, A.G.; Chong, T.H. The potential to enhance membrane module design with 3D printing technology. J. Membr. Sci. 2016, 499, 480–490. [Google Scholar] [CrossRef]
- Mohammad, A.W.; Ng, C.Y.; Lim, Y.P.; Ng, G.H. Ultrafiltration in Food Processing Industry: Review on Application, Membrane Fouling, and Fouling Control. Food Bioprocess Technol. 2012, 5, 1143–1156. [Google Scholar] [CrossRef]
- Ong, Y.K.; Shi, G.M.; Le, N.L.; Tang, Y.P.; Zuo, J.; Nunes, S.P.; Chung, T.-S. Recent membrane development for pervaporation processes. Prog. Polym. Sci. 2016, 57, 1–31. [Google Scholar] [CrossRef]
- Jia, Z.; Wu, G. Metal-organic frameworks based mixed matrix membranes for pervaporation. Microporous Mesoporous Mater. 2016, 235, 151–159. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, F.; Rezakazemi, M.; Zhang, W.; Lu, C.; Chang, H.; Quan, X. Modeling of a CO2-piperazine-membrane absorption system. Chem. Eng. Res. Des. 2018, 131, 375–384. [Google Scholar] [CrossRef]
- Asfand, F.; Bourouis, M. A review of membrane contactors applied in absorption refrigeration systems. Renew. Sustain. Energy Rev. 2015, 45, 173–191. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhang, W.; Tang, B.; Ding, J.; Zheng, Y.; Zhang, Z. Membrane fouling mechanism of biofilm-membrane bioreactor (BF-MBR): Pore blocking model and membrane cleaning. Bioresour. Technol. 2018, 250, 398–405. [Google Scholar] [CrossRef] [PubMed]
- Molinari, R.; Lavorato, C.; Argurio, P. Recent progress of photocatalytic membrane reactors in water treatment and in synthesis of organic compounds. A review. Catal. Today 2017, 281, 144–164. [Google Scholar] [CrossRef]
- Liu, C.; Kulprathipanja, S. Mixed-Matrix Membranes. In Zeolites in Industrial Separation and Catalysis; Wiley-VCH Verlag GmbH & CO. KGaA: Weinheim, Germany, 2010; pp. 329–353. ISBN 9783527629565. [Google Scholar]
- Zornoza, B.; Tellez, C.; Coronas, J.; Gascon, J.; Kapteijn, F. Metal organic framework based mixed matrix membranes: An increasingly important field of researCH with a large application potential. Microporous Mesoporous Mater. 2013, 166, 67–78. [Google Scholar] [CrossRef]
- Hua, D.; Ong, Y.K.; Wang, Y.; Yang, T.; Chung, T.-S. ZIF-90/P84 mixed matrix membranes for pervaporation dehydration of isopropanol. J. Membr. Sci. 2014, 453, 155–167. [Google Scholar] [CrossRef]
- Basu, S.; Cano-Odena, A.; Vankelecom, I.F.J. MOF-containing mixed-matrix membranes for CO2/CH4 and CO2/N2 binary gas mixture separations. Sep. Purif. Technol. 2011, 81, 31–40. [Google Scholar] [CrossRef]
- Rezakazemi, M.; Ebadi Amooghin, A.; Montazer-Rahmati, M.M.; Ismail, A.F.; Matsuura, T. State-of-the-art membrane based CO2 separation using mixed matrix membranes (MMMs): An overview on current status and future directions. Prog. Polym. Sci. 2014, 39, 817–861. [Google Scholar] [CrossRef]
- Goh, P.S.; Ismail, A.F.; Sanip, S.M.; Ng, B.C.; Aziz, M. Recent advances of inorganic fillers in mixed matrix membrane for gas separation. Sep. Purif. Technol. 2011, 81, 243–264. [Google Scholar] [CrossRef]
- Singh, T.; Kang, D.-Y.; Nair, S. Rigorous calculations of permeation in mixed-matrix membranes: Evaluation of interfacial equilibrium effects and permeability-based models. J. Membr. Sci. 2013, 448, 160–169. [Google Scholar] [CrossRef]
- Vinh-Thang, H.; Kaliaguine, S. Predictive Models for Mixed-Matrix Membrane Performance: A Review. Chem. Rev. 2013, 113, 4980–5028. [Google Scholar] [CrossRef] [PubMed]
- Vinh-Thang, H.; Kaliaguine, S. A comprehensive computational strategy for fitting experimental permeation data of mixed matrix membranes. J. Membr. Sci. 2014, 452, 271–276. [Google Scholar] [CrossRef]
- Park, H.B.; Kamcev, J.; Robeson, L.M.; Elimelech, M.; Freeman, B.D. Maximizing the right stuff: The trade-off between membrane permeability and selectivity. Science 2017, 356. [Google Scholar] [CrossRef] [PubMed]
- Fan, H.; Shi, Q.; Yan, H.; Ji, S.; Dong, J.; Zhang, G. Simultaneous Spray Self-Assembly of Highly Loaded ZIF-8–PDMS Nanohybrid Membranes Exhibiting Exceptionally High Biobutanol-Permselective Pervaporation. Angew. Chem. Int. Ed. 2014, 53, 5578–5582. [Google Scholar] [CrossRef] [PubMed]
- Robeson, L.M. The upper bound revisited. J. Membr. Sci. 2008, 320, 390–400. [Google Scholar] [CrossRef]
- Robeson, L.M. Correlation of separation factor versus permeability for polymeric membranes. J. Membr. Sci. 1991, 62, 165–185. [Google Scholar] [CrossRef]
- Burns, R.L.; Koros, W.J. Defining the challenges for C3H6/C3H8 separation using polymeric membranes. J. Membr. Sci. 2003, 211, 299–309. [Google Scholar] [CrossRef]
- Swaidan, R.J.; Ma, X.; Litwiller, E.; Pinnau, I. Enhanced propylene/propane separation by thermal annealing of an intrinsically microporous hydroxyl-functionalized polyimide membrane. J. Membr. Sci. 2015, 495, 235–241. [Google Scholar] [CrossRef]
- Jongok, W.; Ho, K.M.; Soo, K.Y.; Chae, P.H.; Young, K.U.; Chang, C.S.; Keun, K.S. Surface modification of polyimide and polysulfone membranes by ion beam for gas separation. J. Appl. Polym. Sci. 2000, 75, 1554–1560. [Google Scholar] [CrossRef]
- Koros, W.J.; Mahajan, R. Pushing the limits on possibilities for large scale gas separation: WhiCH strategies? J. Membr. Sci. 2000, 175, 181–196. [Google Scholar] [CrossRef]
- Zhao, S.; Wang, Z.; Qiao, Z.; Wei, X.; Zhang, C.; Wang, J.; Wang, S. Gas separation membrane with CO2-facilitated transport highway constructed from amino carrier containing nanorods and macromolecules. J. Mater. Chem. A 2013, 1, 246–249. [Google Scholar] [CrossRef]
- Mannan, H.A.; Mukhtar, H.; Murugesan, T.; Nasir, R.; Mohshim, D.F.; Mushtaq, A. Recent Applications of Polymer Blends in Gas Separation Membranes. Chem. Eng. Technol. 2013, 36, 1838–1846. [Google Scholar] [CrossRef]
- Zhang, C. Zeolitic Imidazolate Framework (Zif)-Based Membranes and Sorbents for Advanced Olefin/Paraffin Separations; Georgia Institute of Technology: Atlanta, GA, USA, 2014. [Google Scholar]
- Chung, T.-S.; Jiang, L.Y.; Li, Y.; Kulprathipanja, S. Mixed matrix membranes (MMMs) comprising organic polymers with dispersed inorganic fillers for gas separation. Prog. Polym. Sci. 2007, 32, 483–507. [Google Scholar] [CrossRef]
- Vinoba, M.; Bhagiyalakshmi, M.; Alqaheem, Y.; Alomair, A.A.; Pérez, A.; Rana, M.S. Recent progress of fillers in mixed matrix membranes for CO2 separation: A review. Sep. Purif. Technol. 2017, 188, 431–450. [Google Scholar] [CrossRef]
- Seoane, B.; Coronas, J.; Gascon, I.; Benavides, M.E.; Karvan, O.; Caro, J.; Kapteijn, F.; Gascon, J. Metal-organic framework based mixed matrix membranes: A solution for highly efficient CO2 capture? Chem. Soc. Rev. 2015, 44, 2421–2454. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Marand, E.; Ida, J.; Guliants, V. V Polysulfone and Mesoporous Molecular Sieve MCM-48 Mixed Matrix Membranes for Gas Separation. Chem. Mater. 2006, 18, 1149–1155. [Google Scholar] [CrossRef]
- Askari, M.; Chung, T.-S. Natural gas purification and olefin/paraffin separation using thermal cross-linkable CO-polyimide/ZIF-8 mixed matrix membranes. J. Membr. Sci. 2013, 444, 173–183. [Google Scholar] [CrossRef]
- Amedi, H.R.; Aghajani, M. Gas separation in mixed matrix membranes based on polyurethane containing SiO2, ZSM-5, and ZIF-8 nanoparticles. J. Nat. Gas Sci. Eng. 2016, 35, 695–702. [Google Scholar] [CrossRef]
- Galizia, M.; Chi, W.S.; Smith, Z.P.; Merkel, T.C.; Baker, R.W.; Freeman, B.D. 50th Anniversary Perspective: Polymers and Mixed Matrix Membranes for Gas and Vapor Separation: A Review and Prospective Opportunities. Macromolecules 2017. [Google Scholar] [CrossRef]
- Tanh Jeazet, H.B.; Staudt, C.; Janiak, C. Metal-organic frameworks in mixed-matrix membranes for gas separation. Dalton Trans. 2012, 41, 14003–14027. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Dai, Y.; Johnson, J.R.; Karvan, O.; Koros, W.J. High performance ZIF-8/6FDA-DAM mixed matrix membrane for propylene/propane separations. J. Membr. Sci. 2012, 389, 34–42. [Google Scholar] [CrossRef]
- Faiz, R.; Li, K. Olefin/paraffin separation using membrane based facilitated transport/chemical absorption techniques. Chem. Eng. Sci. 2012, 73, 261–284. [Google Scholar] [CrossRef]
- Liu, J.; Bae, T.-H.; Qiu, W.; Husain, S.; Nair, S.; Jones, C.W.; Chance, R.R.; Koros, W.J. Butane isomer transport properties of 6FDA–DAM and MFI–6FDA–DAM mixed matrix membranes. J. Membr. Sci. 2009, 343, 157–163. [Google Scholar] [CrossRef]
- Song, Q.; Nataraj, S.K.; Roussenova, M.V.; Tan, J.C.; Hughes, D.J.; Li, W.; Bourgoin, P.; Alam, M.A.; Cheetham, A.K.; Al-Muhtaseb, S.A.; et al. Zeolitic imidazolate framework (ZIF-8) based polymer nanocomposite membranes for gas separation. Energy Environ. Sci. 2012, 5, 8359–8369. [Google Scholar] [CrossRef]
- Vu, D.Q.; Koros, W.J.; Miller, S.J. Mixed matrix membranes using carbon molecular sieves: I. Preparation and experimental results. J. Membr. Sci. 2003, 211, 311–334. [Google Scholar] [CrossRef]
- Zimmerman, C.M.; Singh, A.; Koros, W.J. Tailoring mixed matrix composite membranes for gas separations. J. Membr. Sci. 1997, 137, 145–154. [Google Scholar] [CrossRef]
- Kiyono, M.; Williams, P.J.; Koros, W.J. Effect of polymer precursors on carbon molecular sieve structure and separation performance properties. Carbon N. Y. 2010, 48, 4432–4441. [Google Scholar] [CrossRef]
- Fernández-Barquín, A.; Casado-Coterillo, C.; Etxeberria-Benavides, M.; Zuñiga, J.; Irabien, A. Comparison of Flat and Hollow-Fiber Mixed-Matrix Composite Membranes for CO2 Separation with Temperature. Chem. Eng. Technol. 2017, 40, 997–1007. [Google Scholar] [CrossRef]
- Yun, Y.N.; Sohail, M.; Moon, J.; Tae, W.K.; Kyeng, M.P.; Dong, H.C.; Young, C.P.; Cho, C.; Kim, H. Defect-Free Mixed-Matrix Membranes with Hydrophilic Metal-Organic Polyhedra for Efficient Carbon Dioxide Separation. Chem. Asian J. 2018, 13, 631–635. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Swaidan, R.J.; Wang, Y.; Hsiung, C.; Han, Y.; Pinnau, I. Highly Compatible Hydroxyl-Functionalized Microporous Polyimide-ZIF-8 Mixed Matrix Membranes for Energy Efficient Propylene/Propane Separation. ACS Appl. Nano Mater. 2018, 1, 3541–3547. [Google Scholar] [CrossRef]
- Bushell, A.F.; Attfield, M.P.; Mason, C.R.; Budd, P.M.; Yampolskii, Y.; Starannikova, L.; Rebrov, A.; Bazzarelli, F.; Bernardo, P.; Carolus Jansen, J.; et al. Gas permeation parameters of mixed matrix membranes based on the polymer of intrinsic microporosity PIM-1 and the zeolitic imidazolate framework ZIF-8. J. Membr. Sci. 2013, 427, 48–62. [Google Scholar] [CrossRef]
- Adams, R.; Carson, C.; Ward, J.; Tannenbaum, R.; Koros, W. Metal organic framework mixed matrix membranes for gas separations. Microporous Mesoporous Mater. 2010, 131, 13–20. [Google Scholar] [CrossRef]
- Zhang, Y.; Feng, X.; Yuan, S.; Zhou, J.; Wang, B. Challenges and recent advances in MOF-polymer composite membranes for gas separation. Inorg. Chem. Front. 2016, 3, 896–909. [Google Scholar] [CrossRef]
- Nordin, N.A.H.M.; Ismail, A.F.; Mustafa, A.; Murali, R.S.; Matsuura, T. The impact of ZIF-8 particle size and heat treatment on CO2/CH4 separation using asymmetric mixed matrix membrane. RSC Adv. 2014, 4, 52530–52541. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, K.; Xu, L.; Labreche, Y.; Kraftschik, B.; Koros, W.J. Highly scalable ZIF-based mixed-matrix hollow fiber membranes for advanced hydrocarbon separations. AIChE J. 2014, 60, 2625–2635. [Google Scholar] [CrossRef]
- Carreon, M.; Dahe, G.; Feng, J.; Venna, S.R. Mixed Matrix Membranes for Gas Separation Applications. In Membranes for Gas Separations; World Scientific Series in Membrane Science and Technology: Biological and Biomimetic Applications, Energy and the Environment; World Scientific: Singapore, 2016; Volume 1, pp. 1–57. ISBN 978-981-320-770-7. [Google Scholar]
- Liu, L.; Nicholson, D.; Bhatia, S.K. Interfacial Resistance and Length-Dependent Transport Diffusivities in Carbon Nanotubes. J. Phys. Chem. C 2016, 120, 26363–26373. [Google Scholar] [CrossRef]
- Glavatskiy, K.S.; Bhatia, S.K. Effect of pore size on the interfacial resistance of a porous membrane. J. Membr. Sci. 2017, 524, 738–745. [Google Scholar] [CrossRef]
- Glavatskiy, K.S.; Bhatia, S.K. Thermodynamic Resistance to Matter Flow at The Interface of a Porous Membrane. Langmuir 2016, 32, 3400–3411. [Google Scholar] [CrossRef] [PubMed]
- Hinkle, K.R.; Jameson, C.J.; Murad, S. Transport of Vanadium and Oxovanadium Ions Across Zeolite Membranes: A Molecular Dynamics Study. J. Phys. Chem. C 2014, 118, 23803–23810. [Google Scholar] [CrossRef]
- Maxwell, J.C. A treatise on Electricity and Magnetism; Clarendon Press: Oxford, UK, 1873. [Google Scholar]
- Landauer, R. The Electrical Resistance of Binary Metallic Mixtures. J. Appl. Phys. 1952, 23, 779–784. [Google Scholar] [CrossRef]
- Bruggeman, D.A.G. Berechnung verschiedener physikalischer Konstanten von heterogenen Substanzen. Ann. Phys. 1935, 24, 636. [Google Scholar] [CrossRef]
- Pal, R. New models for thermal conductivity of particulate composites. J. Reinf. Plast. Compos. 2007, 26, 643–651. [Google Scholar] [CrossRef]
- Henis, J.M.S.; Tripodi, M.K. Composite hollow fiber membranes for gas separation: The resistance model approach. J. Membr. Sci. 1981, 8, 233–246. [Google Scholar] [CrossRef]
- Pinnau, I.; Wijmans, J.G.; Blume, I.; Kuroda, T.; Peinemann, K.V. Gas permeation through composite membranes. J. Membr. Sci. 1988, 37, 81–88. [Google Scholar] [CrossRef]
- Ebneyamini, A.; Azimi, H.; Tezel, F.H.; Thibault, J. Mixed matrix membranes applications: Development of a resistance-based model. J. Membr. Sci. 2017, 543, 351–360. [Google Scholar] [CrossRef]
- Kang, D.-Y.; Jones, C.W.; Nair, S. Modeling molecular transport in composite membranes with tubular fillers. J. Membr. Sci. 2011, 381, 50–63. [Google Scholar] [CrossRef]
- Shen, Y.; Lua, A.C. Theoretical and experimental studies on the gas transport properties of mixed matrix membranes based on polyvinylidene fluoride. AIChE J. 2013, 59, 4715–4726. [Google Scholar] [CrossRef]
- Shimekit, B.; Mukhtar, H.; Murugesan, T. Prediction of the relative permeability of gases in mixed matrix membranes. J. Membr. Sci. 2011, 373, 152–159. [Google Scholar] [CrossRef]
- Cussler, E.L. Membranes containing selective flakes. J. Membr. Sci. 1990, 52, 275–288. [Google Scholar] [CrossRef]
- Lewis, T.B.; Nielsen, L.E. Dynamic mechanical properties of particulate-filled Composites. J. Appl. Polym. Sci. 1970, 14, 1449–1471. [Google Scholar] [CrossRef]
- Higuchi, W.I.; Higuchi, T. Theoretical Analysis of Diffusional Movement Through Heterogeneous Barriers. J. Am. Pharm. Assoc. (Sci. Ed.) 1960, 49, 598–606. [Google Scholar] [CrossRef]
- Moore, T.T.; Koros, W.J. Gas sorption in polymers, molecular sieves, and mixed matrix membranes. J. Appl. Polym. Sci. 2007, 104, 4053–4059. [Google Scholar] [CrossRef]
- Chehrazi, E.; Sharif, A.; Omidkhah, M.; Karimi, M. Modeling the Effects of Interfacial Characteristics on Gas Permeation Behavior of Nanotube–Mixed Matrix Membranes. ACS Appl. Mater. Interfaces 2017, 9, 37321–37331. [Google Scholar] [CrossRef] [PubMed]
- Felske, J.D. Effective thermal conductivity of composite spheres in a continuous medium with contact resistance. Int. J. Heat Mass Transf. 2004, 47, 3453–3461. [Google Scholar] [CrossRef]
- Shariati, A.; Omidkhah, M.; Pedram, M.Z. New permeation models for nanocomposite polymeric membranes filled with nonporous particles. Chem. Eng. Res. Des. 2012, 90, 563–575. [Google Scholar] [CrossRef]
- Idris, A.; Man, Z.; Abdulhalim, S.M.; Uddin, F. Modified Bruggeman models for prediction of CO2 permeance in polycarbonate/silica nanocomposite membranes. Can. J. Chem. Eng. 2017, 95, 2398–2409. [Google Scholar] [CrossRef]
- Pal, R. On the Lewis–Nielsen model for thermal/electrical conductivity of composites. Compos. Part A Appl. Sci. Manuf. 2008, 39, 718–726. [Google Scholar] [CrossRef]
- Bouma, R.H.B.; Checchetti, A.; Chidichimo, G.; Drioli, E. Permeation through a heterogeneous membrane: The effect of the dispersed phase. J. Membr. Sci. 1997, 128, 141–149. [Google Scholar] [CrossRef]
- Funk, C.V.; Lloyd, D.R. Zeolite-filled microporous mixed matrix (ZeoTIPS) membranes: Prediction of gas separation performance. J. Membr. Sci. 2008, 313, 224–231. [Google Scholar] [CrossRef]
- Nan, C.-W.; Liu, G.; Lin, Y.; Li, M. Interface effect on thermal conductivity of carbon nanotube composites. Appl. Phys. Lett. 2004, 85, 3549–3551. [Google Scholar] [CrossRef]
- Li, Y.; Guan, H.-M.; Chung, T.-S.; Kulprathipanja, S. Effects of novel silane modification of zeolite surface on polymer chain rigidification and partial pore blockage in polyethersulfone (PES)–zeolite A mixed matrix membranes. J. Membr. Sci. 2006, 275, 17–28. [Google Scholar] [CrossRef]
- Mahajan, R.; Koros, W.J. Mixed matrix membrane materials with glassy polymers. Part 1. Polym. Eng. Sci. 2002, 42, 1420–1431. [Google Scholar] [CrossRef]
- Pal, R. Permeation models for mixed matrix membranes. J. Colloid Interface Sci. 2008, 317, 191–198. [Google Scholar] [CrossRef] [PubMed]
- Hashemifard, S.A.; Ismail, A.F.; Matsuura, T. A new theoretical gas permeability model using resistance modeling for mixed matrix membrane systems. J. Membr. Sci. 2010, 350, 259–268. [Google Scholar] [CrossRef]
- Higuchi, W.I. A New Relationship for the Dielectric Properties of Two Phase Mixtures. J. Phys. Chem. 1958, 62, 649–653. [Google Scholar] [CrossRef]
- Javaid, A. Membranes for solubility-based gas separation applications. Chem. Eng. J. 2005, 112, 219–226. [Google Scholar] [CrossRef]
- Ismail, A.F.; Khulbe, K.C.; Matsuura, T. Gas Separation Membranes: Polymeric and Inorganic; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Koros, W.J.; Fleming, G.K. Membrane-based gas separation. J. Membr. Sci. 1993, 83, 1–80. [Google Scholar] [CrossRef]
- Ghosh, A.; Mistri, E.A.; Banerjee, S. 3—Fluorinated Polyimides: Synthesis, Properties, and Applications. In Handbook of Specialty Fluorinated Polymers; William Andrew Publishing: Norwich, NY, USA, 2015; pp. 97–185. ISBN 978-0-323-35792-0. [Google Scholar]
- Zhang, C.; Lively, R.P.; Zhang, K.; Johnson, J.R.; Karvan, O.; Koros, W.J. Unexpected Molecular Sieving Properties of Zeolitic Imidazolate Framework-8. J. Phys. Chem. Lett. 2012, 3, 2130–2134. [Google Scholar] [CrossRef] [PubMed]
- Yujie, B.; Zhengjie, L.; Yanshuo, L.; Yuan, P.; Hua, J.; Wenmei, J.; Ang, G.; Po, W.; Qingyuan, Y.; Chongli, Z.; et al. Confinement of Ionic Liquids in Nanocages: Tailoring the Molecular Sieving Properties of ZIF-8 for Membrane-Based CO2 Capture. Angew. Chem. Int. Ed. 2015, 54, 15483–15487. [Google Scholar] [CrossRef]
- Li, W.; Zhang, Y.; Zhang, C.; Meng, Q.; Xu, Z.; Su, P.; Li, Q.; Shen, C.; Fan, Z.; Qin, L.; et al. Transformation of metal-organic frameworks for molecular sieving membranes. Nat. Commun. 2016, 7, 11315. [Google Scholar] [CrossRef] [PubMed]
- Budd, P.M.; Msayib, K.J.; Tattershall, C.E.; Ghanem, B.S.; Reynolds, K.J.; McKeown, N.B.; Fritsch, D. Gas separation membranes from polymers of intrinsic microporosity. J. Membr. Sci. 2005, 251, 263–269. [Google Scholar] [CrossRef]
- Thran, A.; Kroll, G.; Faupel, F. Correlation between fractional free volume and diffusivity of gas molecules in glassy polymers. J. Polym. Sci. Part B Polym. Phys. 1999, 37, 3344–3358. [Google Scholar] [CrossRef]
- Vrentas, J.S.; Vrentas, C.M. Evaluation of the free-volume theory of diffusion. J. Polym. Sci. Part B Polym. Phys. 2003, 41, 501–507. [Google Scholar] [CrossRef]
- Das, M.; Perry, J.D.; Koros, W.J. Gas-Transport-Property Performance of Hybrid Carbon Molecular Sieve−Polymer Materials. Ind. Eng. Chem. Res. 2010, 49, 9310–9321. [Google Scholar] [CrossRef]
- Wijmans, J.G.; Baker, R.W. The solution-diffusion model: A review. J. Membr. Sci. 1995, 107, 1–21. [Google Scholar] [CrossRef]
- Wijmans, J.G.; Baker, R.W. The Solution–Diffusion Model: A Unified Approach to Membrane Permeation. In Materials Science of Membranes for Gas and Vapor Separation; Freeman, B., Yampolskii, Y., Pinnau, I., Eds.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2006. [Google Scholar]
- Ghosal, K.; Freeman, B.D. Gas separation using polymer membranes: An overview. Polym. Adv. Technol. 1994, 5, 673–697. [Google Scholar] [CrossRef]
- O’Brien, K.C.; Koros, W.J.; Barbari, T.A.; Sanders, E.S. A new technique for the measurement of multicomponent gas transport through polymeric films. J. Membr. Sci. 1986, 29, 229–238. [Google Scholar] [CrossRef]
- Swaidan, R.J.; Ma, X.; Pinnau, I. Spirobisindane-based polyimide as efficient precursor of thermally-rearranged and carbon molecular sieve membranes for enhanced propylene/propane separation. J. Membr. Sci. 2016, 520, 983–989. [Google Scholar] [CrossRef]
- Stern, S.A. The “barrer” permeability unit. J. Polym. Sci. Part A-2 Polym. Phys. 1968, 6, 1933–1934. [Google Scholar] [CrossRef]
- An, H.; Park, S.; Kwon, H.T.; Jeong, H.-K.; Lee, J.S. A new superior competitor for exceptional propylene/propane separations: ZIF-67 containing mixed matrix membranes. J. Membr. Sci. 2017, 526, 367–376. [Google Scholar] [CrossRef]
- Liu, G.; Chernikova, V.; Liu, Y.; Zhang, K.; Belmabkhout, Y.; Shekhah, O.; Zhang, C.; Yi, S.; Eddaoudi, M.; Koros, W.J. Mixed matrix formulations with MOF molecular sieving for key energy-intensive separations. Nat. Mater. 2018, 17, 283–289. [Google Scholar] [CrossRef] [PubMed]
- Kamaruddin, D.H.; Koros, W.J. Some observations about the application of Fick’s first law for membrane separation of multicomponent mixtures. J. Membr. Sci. 1997, 135, 147–159. [Google Scholar] [CrossRef]
- Koros, W.J. Simplified analysis of gas/polymer selective solubility behavior. J. Polym. Sci. Polym. Phys. Ed. 1985, 23, 1611–1628. [Google Scholar] [CrossRef]
- Ruthven, D.M. Sorption kinetics for diffusion-controlled systems with a strongly concentration-dependent diffusivity. Chem. Eng. Sci. 2004, 59, 4531–4545. [Google Scholar] [CrossRef]
- Ruthven, D.M. Principles of Adsorption and Adsorption Processes; John Wiley & Sons: Hoboken, NJ, USA, 1984; ISBN 0471866067. [Google Scholar]
- Hashemifard, S.A.; Ismail, A.F.; Matsuura, T. Prediction of gas permeability in mixed matrix membranes using theoretical models. J. Membr. Sci. 2010, 347, 53–61. [Google Scholar] [CrossRef]
- Paul, D.R.; Koros, W.J. Effect of partially immobilizing sorption on permeability and the diffusion time lag. J. Polym. Sci. Polym. Phys. Ed. 1976, 14, 675–685. [Google Scholar] [CrossRef]
- Sheffel, J.A.; Tsapatsis, M. A semi-empirical approach for predicting the performance of mixed matrix membranes containing selective flakes. J. Membr. Sci. 2009, 326, 595–607. [Google Scholar] [CrossRef]
- Fu, S.; Sanders, E.S.; Kulkarni, S.S.; Koros, W.J. Carbon molecular sieve membrane structure–property relationships for four novel 6FDA based polyimide precursors. J. Membr. Sci. 2015, 487, 60–73. [Google Scholar] [CrossRef]
- Ning, X.; Koros, W.J. Carbon molecular sieve membranes derived from Matrimid® polyimide for nitrogen/methane separation. Carbon N. Y. 2014, 66, 511–522. [Google Scholar] [CrossRef]
- Barrer, R.M. Diffusivities in glassy polymers for the dual mode sorption model. J. Membr. Sci. 1984, 18, 25–35. [Google Scholar] [CrossRef]
- Barbari, T.A.; Koros, W.J.; Paul, D.R. Polymeric membranes based on bisphenol-A for gas separations. J. Membr. Sci. 1989, 42, 69–86. [Google Scholar] [CrossRef]
- Esekhile, O.; Qiu, W.; Koros, W.J. Permeation of butane isomers through 6FDA-DAM dense films. J. Polym. Sci. Part B Polym. Phys. 2011, 49, 1605–1620. [Google Scholar] [CrossRef]
- Vu, D.Q.; Koros, W.J.; Miller, S.J. Mixed matrix membranes using carbon molecular sieves II. Modeling permeation behavior. J. Membr. Sci. 2003, 211, 335–348. [Google Scholar] [CrossRef]
- Najari, S.; Hosseini, S.S.; Omidkhah, M.; Tan, N.R. Phenomenological modeling and analysis of gas transport in polyimide membranes for propylene/propane separation. RSC Adv. 2015, 5, 47199–47215. [Google Scholar] [CrossRef]
- Koros, W.J.; Chern, R.T.; Stannett, V.; Hopfenberg, H.B. A model for permeation of mixed gases and vapors in glassy polymers. J. Polym. Sci. Polym. Phys. Ed. 1981, 19, 1513–1530. [Google Scholar] [CrossRef]
- Sarra, Z.; Matthieu, Z.; Eliane, E. Modeling diffusion mass transport in multiphase polymer systems for gas barrier applications: A review. J. Polym. Sci. Part B Polym. Phys. 2018, 56, 621–639. [Google Scholar] [CrossRef]
- Nielsen, L.E. Thermal conductivity of particulate-filled polymers. J. Appl. Polym. Sci. 1973, 17, 3819–3820. [Google Scholar] [CrossRef]
- Henis, J.M.S.; Tripodi, M.K. A Novel ApproaCH to Gas Separations Using Composite Hollow Fiber Membranes. Sep. Sci. Technol. 1980, 15, 1059–1068. [Google Scholar] [CrossRef]
- Bánhegyi, G. Comparison of electrical mixture rules for Composites. Colloid Polym. Sci. 1986, 264, 1030–1050. [Google Scholar] [CrossRef]
- Karode, S.K.; Patwardhan, V.S.; Kulkarni, S.S. An improved model incorporating constriction resistance in transport through thin film composite membranes. J. Membr. Sci. 1996, 114, 157–170. [Google Scholar] [CrossRef]
- Erdem-Şenatalar, A.; Tatlier, M.; Tantekin-Ersolmaz, Ş.B. Questioning the validity of present models for estimating the performances of zeolite-polymer mixed matrix membranes. Chem. Eng. Commun. 2003, 190, 677–692. [Google Scholar] [CrossRef]
- Lopez, J.L.; Matson, S.L.; Marchese, J.; Quinn, J.A. Diffusion through composite membranes: A two-dimensional analysis. J. Membr. Sci. 1986, 27, 301–325. [Google Scholar] [CrossRef]
- Te Hennepe, H.J.C.; Smolders, C.A.; Bargeman, D.; Mulder, M.H.V. Exclusion and Tortuosity Effects for Alcohol/Water Separation by Zeolite-Filled PDMS Membranes. Sep. Sci. Technol. 1991, 26, 585–596. [Google Scholar] [CrossRef]
- Te Hennepe, H.J.C.; Boswerger, W.B.F.; Bargeman, D.; Mulder, M.H.V.; Smolders, C.A. Zeolite-filled silicone rubber membranes experimental determination of concentration profiles. J. Membr. Sci. 1994, 89, 185–196. [Google Scholar] [CrossRef]
- Fouda, A.; Chen, Y.; Bai, J.; Matsuura, T. Wheatstone bridge model for the laminated polydimethylsiloxane/polyethersulfone membrane for gas separation. J. Membr. Sci. 1991, 64, 263–271. [Google Scholar] [CrossRef]
- Nielsen, L.E. Models for the Permeability of Filled Polymer Systems. J. Macromol. Sci. Part A Chem. 1967, 1, 929–942. [Google Scholar] [CrossRef]
- Petropoulos, J.H. A Comparative study of approaches applied to the permeability of binary composite polymeric materials. J. Polym. Sci. Polym. Phys. Ed. 1985, 23, 1309–1324. [Google Scholar] [CrossRef]
- Carson, J.K.; Lovatt, S.J.; Tanner, D.J.; Cleland, A.C. Thermal conductivity bounds for isotropic, porous materials. Int. J. Heat Mass Transf. 2005, 48, 2150–2158. [Google Scholar] [CrossRef]
- Sheffel, J.A.; Tsapatsis, M. A model for the performance of microporous mixed matrix membranes with oriented selective flakes. J. Membr. Sci. 2007, 295, 50–70. [Google Scholar] [CrossRef]
- Myles, T.D.; Peracchio, A.A.; Chiu, W.K.S. Extension of anisotropic effective medium theory to account for an arbitrary number of inclusion types. J. Appl. Phys. 2015, 117, 25101. [Google Scholar] [CrossRef]
- Myles, T.D.; Peracchio, A.A.; Chiu, W.K.S. Effect of orientation anisotropy on calculating effective electrical conductivities. J. Appl. Phys. 2014, 115, 203503. [Google Scholar] [CrossRef]
- Ordóñez-Miranda, J.; Alvarado-Gil, J.J.; Medina-Ezquivel, R. Generalized Bruggeman Formula for the Effective Thermal Conductivity of Particulate Composites with an Interface Layer. Int. J. Thermophys. 2010, 31, 975–986. [Google Scholar] [CrossRef]
- Falla, W.R.; Mulski, M.; Cussler, E.L. Estimating diffusion through flake-filled membranes. J. Membr. Sci. 1996, 119, 129–138. [Google Scholar] [CrossRef]
- Chiew, Y.C.; Glandt, E.D. The effect of structure on the conductivity of a dispersion. J. Colloid Interface Sci. 1983, 94, 90–104. [Google Scholar] [CrossRef]
- Jeffrey, D.J. Conduction through a Random Suspension of Spheres. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1973, 335, 355–367. [Google Scholar] [CrossRef]
- Landauer, R.; Garland, J.C.; Tanner, D.B. Electrical Conductivity in inhomogeneous media. AIP Conf. Proc. 1978, 40, 2–45. [Google Scholar] [CrossRef]
- Hashin, Z. Assessment of the Self Consistent Scheme Approximation: Conductivity of Particulate Composites. J. Compos. Mater. 1968, 2, 284–300. [Google Scholar] [CrossRef]
- Gonzo, E.; Parentis, M.; Gottifredi, J. Estimating models for predicting effective permeability of mixed matrix membranes. J. Membr. Sci. 2006, 277, 46–54. [Google Scholar] [CrossRef]
- Rafiq, S.; Maulud, A.; Man, Z.; Mutalib, M.I.A.; Ahmad, F.; Khan, A.U.; Khan, A.L.; Ghauri, M.; Muhammad, N. Modelling in mixed matrix membranes for gas separation. Can. J. Chem. Eng. 2015, 93, 88–95. [Google Scholar] [CrossRef]
- Jeffrey, D.J. Group Expansions for the Bulk Properties of a Statistically Homogeneous, Random Suspension. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1974, 338, 503–516. [Google Scholar] [CrossRef]
- Lu, S.-Y.; Kim, S. Effective thermal conductivity of composites containing spheroidal inclusions. AIChE J. 1990, 36, 927–938. [Google Scholar] [CrossRef]
- Chiew, Y.C.; Glandt, E.D. Effective conductivity of dispersions: The effect of resistance at the particle surfaces. Chem. Eng. Sci. 1987, 42, 2677–2685. [Google Scholar] [CrossRef]
- Acrivos, A.; Chang, E. A model for estimating transport quantities in two-phase materials. Phys. Fluids 1986, 29. [Google Scholar] [CrossRef]
- Monsalve-Bravo, G.M.; Bhatia, S.K. Extending Effective Medium Theory to Finite Size Systems: Theory and Simulation for Permeation in Mixed-Matrix Membranes. J. Membr. Sci. 2017, 531, 148–159. [Google Scholar] [CrossRef]
- Monsalve-Bravo, G.M.; Bhatia, S.K. Comparison of Hollow Fiber and Flat Mixed-Matrix Membranes: Theory and Simulation. Chem. Eng. Sci. 2018, 187, 174–188. [Google Scholar] [CrossRef]
- Monsalve-Bravo, G.M.; Bhatia, S.K. Concentration-dependent transport in finite sized composites: Modified effective medium theory. J. Membr. Sci. 2018, 550, 110–125. [Google Scholar] [CrossRef]
- Bhatia, S.K. Transport in bidisperse adsorbents: Significance of the macroscopic adsorbate flux. Chem. Eng. Sci. 1997, 52, 1377–1386. [Google Scholar] [CrossRef]
- Ash, R.; Barrer, R.M. Mechanisms of surface flow. Surf. Sci. 1967, 8, 461–466. [Google Scholar] [CrossRef]
- Rayleigh, L. LVI. On the influence of obstacles arranged in rectangular order upon the properties of a medium. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1892, 34, 481–502. [Google Scholar] [CrossRef]
- Meredith, R.E.; Tobias, C.W. Resistance to Potential Flow through a Cubical Array of Spheres. J. Appl. Phys. 1960, 31, 1270–1273. [Google Scholar] [CrossRef]
- Petropoulos, J.H.; Papadokostaki, K.G.; Doghieri, F.; Minelli, M. A fundamental study of the extent of meaningful application of Maxwell’s and Wiener’s equations to the permeability of binary composite materials. Part III: Extension of the binary cubes model to 3-phase media. Chem. Eng. Sci. 2015, 131, 360–366. [Google Scholar] [CrossRef]
- Nielsen, L.E. The Thermal and Electrical Conductivity of Two-Phase Systems. Ind. Eng. Chem. Fundam. 1974, 13, 17–20. [Google Scholar] [CrossRef]
- Maghami, S.; Sadeghi, M.; Mehrabani-Zeinabad, A. Recognition of polymer-particle interfacial morphology in mixed matrix membranes through ideal permeation predictive models. Polym. Test. 2017, 63, 25–37. [Google Scholar] [CrossRef]
- Li, Y.; Chung, T.-S.; Cao, C.; Kulprathipanja, S. The effects of polymer chain rigidification, zeolite pore size and pore blockage on polyethersulfone (PES)-zeolite A mixed matrix membranes. J. Membr. Sci. 2005, 260, 45–55. [Google Scholar] [CrossRef]
- Erucar, I.; Keskin, S. Computational Methods for MOF/Polymer Membranes. Chem. Rec. 2016, 16, 703–718. [Google Scholar] [CrossRef] [PubMed]
- Moore, T.T.; Koros, W.J. Non-ideal effects in organic–inorganic materials for gas separation membranes. J. Mol. Struct. 2005, 739, 87–98. [Google Scholar] [CrossRef]
- Moore, T.T.; Mahajan, R.; Vu, D.Q.; Koros, W.J. Hybrid membrane materials comprising organic polymers with rigid dispersed phases. AIChE J. 2004, 50, 311–321. [Google Scholar] [CrossRef]
- Every, A.G.; Tzou, Y.; Hasselman, D.P.H.; Raj, R. The effect of particle size on the thermal conductivity of ZnS/diamond composites. Acta Metall. Mater. 1992, 40, 123–129. [Google Scholar] [CrossRef]
- Sadeghi, Z.; Omidkhah, M.; Masoumi, M.E.; Abedini, R. Modification of existing permeation models of mixed matrix membranes filled with porous particles for gas separation. Can. J. Chem. Eng. 2016, 94, 547–555. [Google Scholar] [CrossRef]
- Böttcher, C.J.F. The dielectric constant of crystalline powders. Recueil des Travaux Chimiques des Pays-Bas 1945, 64, 47–51. [Google Scholar] [CrossRef]
- Niklasson, G.A.; Granqvist, C.G.; Hunderi, O. Effective medium models for the optical properties of inhomogeneous materials. Appl. Opt. 1981, 20, 26–30. [Google Scholar] [CrossRef] [PubMed]
- Yang, A.-C.; Liu, C.-H.; Kang, D.-Y. Estimations of effective diffusivity of hollow fiber mixed matrix membranes. J. Membr. Sci. 2015, 495, 269–275. [Google Scholar] [CrossRef]
- Minelli, M.; Doghieri, F.; Papadokostaki, K.G.; Petropoulos, J.H. A fundamental study of the extent of meaningful application of Maxwell’s and Wiener’s equations to the permeability of binary composite materials. Part I: A numerical computation approach. Chem. Eng. Sci. 2013, 104, 630–637. [Google Scholar] [CrossRef]
- Wang, T.; Kang, D.-Y. Highly selective mixed-matrix membranes with layered fillers for molecular separation. J. Membr. Sci. 2015, 497, 394–401. [Google Scholar] [CrossRef]
- Wang, T.; Kang, D.-Y. Predictions of effective diffusivity of mixed matrix membranes with tubular fillers. J. Membr. Sci. 2015, 485, 123–131. [Google Scholar] [CrossRef]
- Andrady, A.L.; Merkel, T.C.; Toy, L.G. Effect of Particle Size on Gas Permeability of Filled Superglassy Polymers. Macromolecules 2004, 37, 4329–4331. [Google Scholar] [CrossRef]
- Petropoulos, J.H.; Papadokostaki, K.G.; Minelli, M.; Doghieri, F. On the role of diffusivity ratio and partition coefficient in diffusional molecular transport in binary composite materials, with special reference to the Maxwell equation. J. Membr. Sci. 2014, 456, 162–166. [Google Scholar] [CrossRef]
- Azimi, H.; Tezel, H.F.; Thibault, J. On the Effective Permeability of Mixed Matrix Membranes. J. Membr. Sci. Res. 2018, 4, 158–166. [Google Scholar] [CrossRef]
- Chen, X.Y.; Hoang, V.-T.; Rodrigue, D.; Kaliaguine, S. Optimization of continuous phase in amino-functionalized metal-organic framework (MIL-53) based co-polyimide mixed matrix membranes for CO2/CH4 separation. RSC Adv. 2013, 3, 24266–24279. [Google Scholar] [CrossRef]
- Vu, D.Q. Formation and Characterization of Asymmetric Carbon Molecular Sieve and Mixed-Matrix Membranes for Natural Gas Purification. Ph.D. Thesis, The University of Texas, Austin, TX, USA, 2001. [Google Scholar]
- Duval, J.-M.; Folkers, B.; Mulder, M.H.V.; Desgrandchamps, G.; Smolders, C.A. Adsorbent filled membranes for gas separation. Part 1. Improvement of the gas separation properties of polymeric membranes by incorporation of microporous adsorbents. J. Membr. Sci. 1993, 80, 189–198. [Google Scholar] [CrossRef]
- Mahajan, R.; Burns, R.; Schaeffer, M.; Koros, W.J. Challenges in forming successful mixed matrix membranes with rigid polymeric materials. J. Appl. Polym. Sci. 2002, 86, 881–890. [Google Scholar] [CrossRef]
- Dutta, R.C.; Bhatia, S.K. Structure and Gas Transport at the Polymer–Zeolite Interface: Insights from Molecular Dynamics Simulations. ACS Appl. Mater. Interfaces 2018, 10, 5992–6005. [Google Scholar] [CrossRef] [PubMed]
- Low, Z.-X.; Razmjou, A.; Wang, K.; Gray, S.; Duke, M.; Wang, H. Effect of addition of two-dimensional ZIF-L nanoflakes on the properties of polyethersulfone ultrafiltration membrane. J. Membr. Sci. 2014, 460, 9–17. [Google Scholar] [CrossRef]
- Galve, A.; Sieffert, D.; Staudt, C.; Ferrando, M.; Güell, C.; Téllez, C.; Coronas, J. Combination of ordered mesoporous silica MCM-41 and layered titanosilicate JDF-L1 fillers for 6FDA-based copolyimide mixed matrix membranes. J. Membr. Sci. 2013, 431, 163–170. [Google Scholar] [CrossRef]
- Zornoza, B.; Gorgojo, P.; Casado, C.; Téllez, C.; Coronas, J. Mixed matrix membranes for gas separation with special nanoporous fillers. Desalin. Water Treat. 2011, 27, 42–47. [Google Scholar] [CrossRef]
- Kim, S.; Pechar, T.W.; Marand, E. Poly(imide siloxane) and carbon nanotube mixed matrix membranes for gas separation. Desalination 2006, 192, 330–339. [Google Scholar] [CrossRef]
- Ismail, A.F.; Goh, P.S.; Sanip, S.M.; Aziz, M. Transport and separation properties of carbon nanotube-mixed matrix membrane. Sep. Purif. Technol. 2009, 70, 12–26. [Google Scholar] [CrossRef]
- Sedigheh, Z.; Mohammad, A. Improving O2/N2 Selective Filtration Using Carbon Nanotube-Modified Mixed-Matrix Membranes. Chem. Eng. Technol. 2015, 38, 2079–2086. [Google Scholar] [CrossRef]
- Galve, A.; Sieffert, D.; Vispe, E.; Téllez, C.; Coronas, J.; Staudt, C. Copolyimide mixed matrix membranes with oriented microporous titanosilicate JDF-L1 sheet particles. J. Membr. Sci. 2011, 370, 131–140. [Google Scholar] [CrossRef]
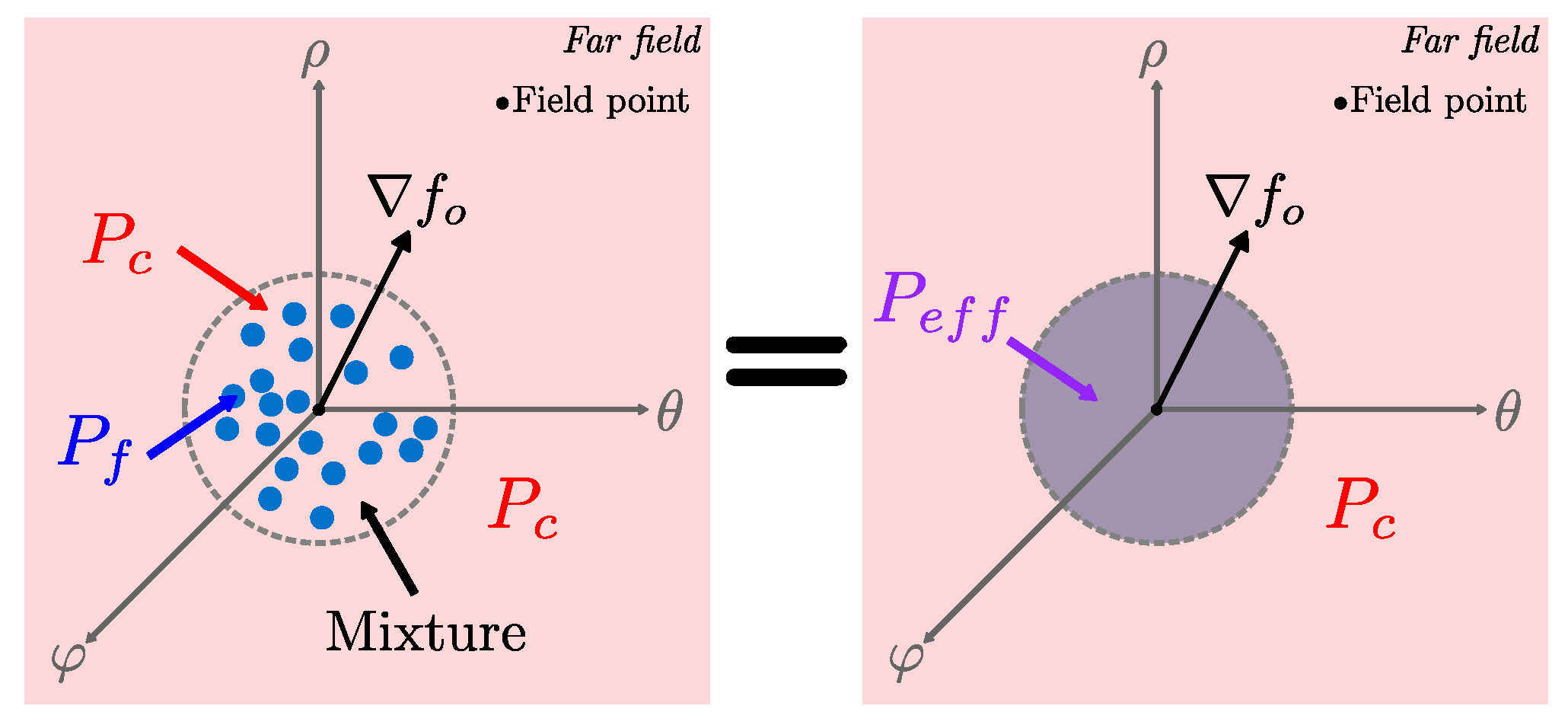
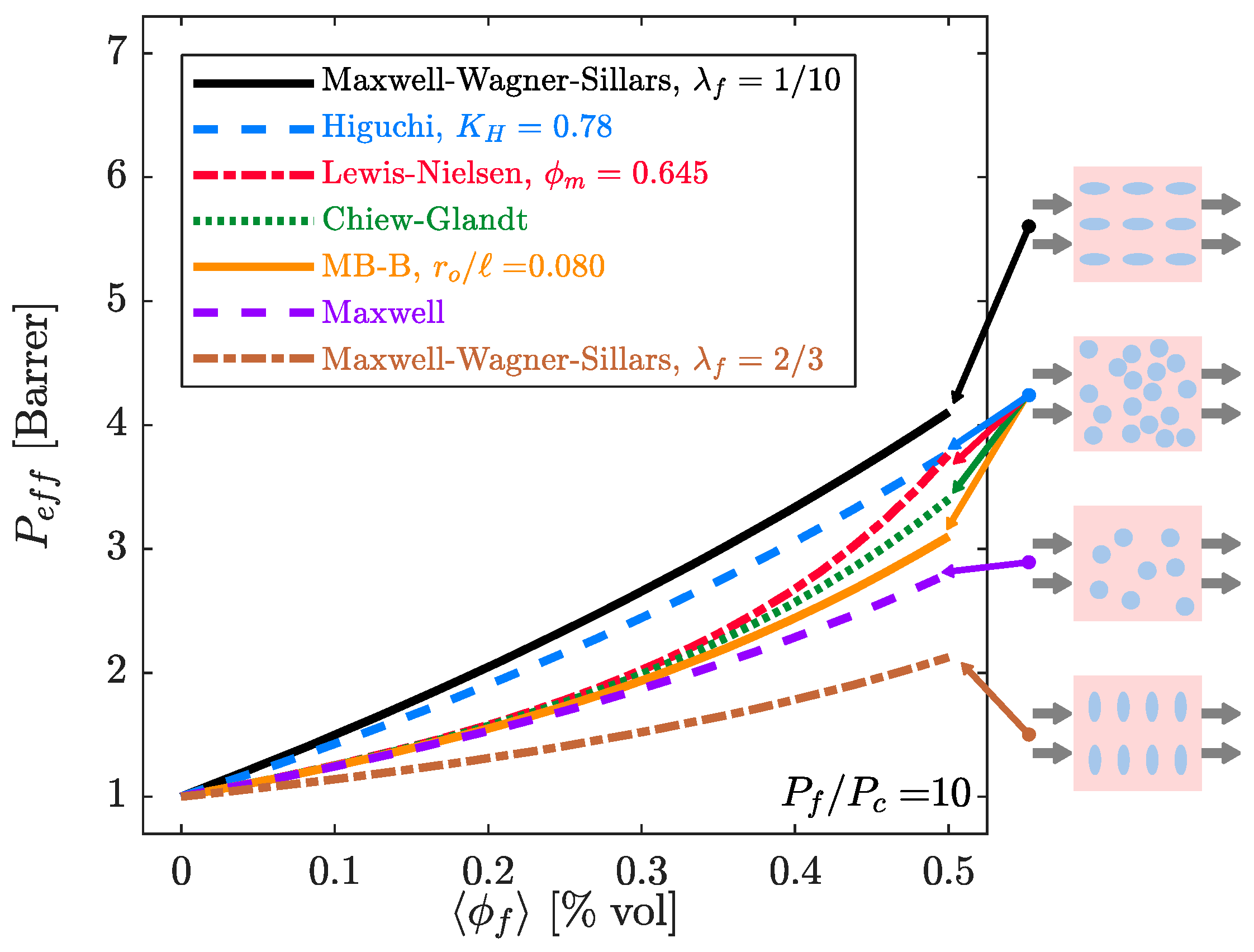
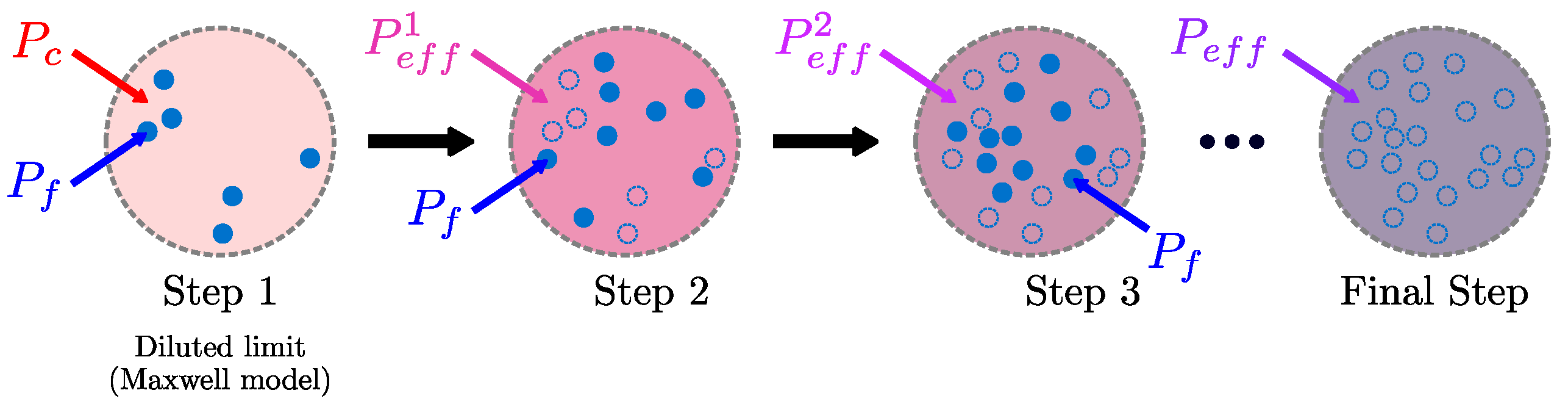
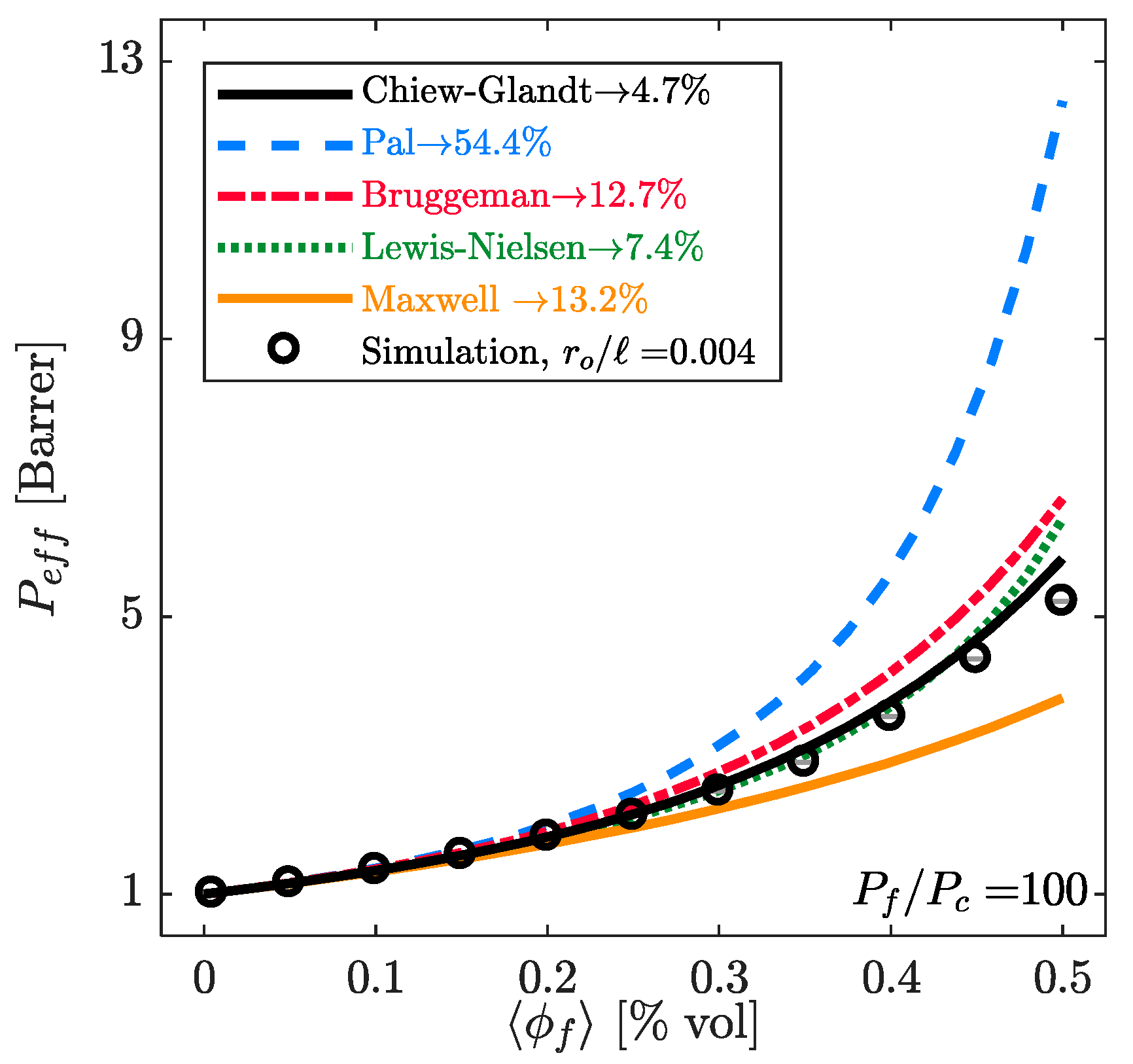
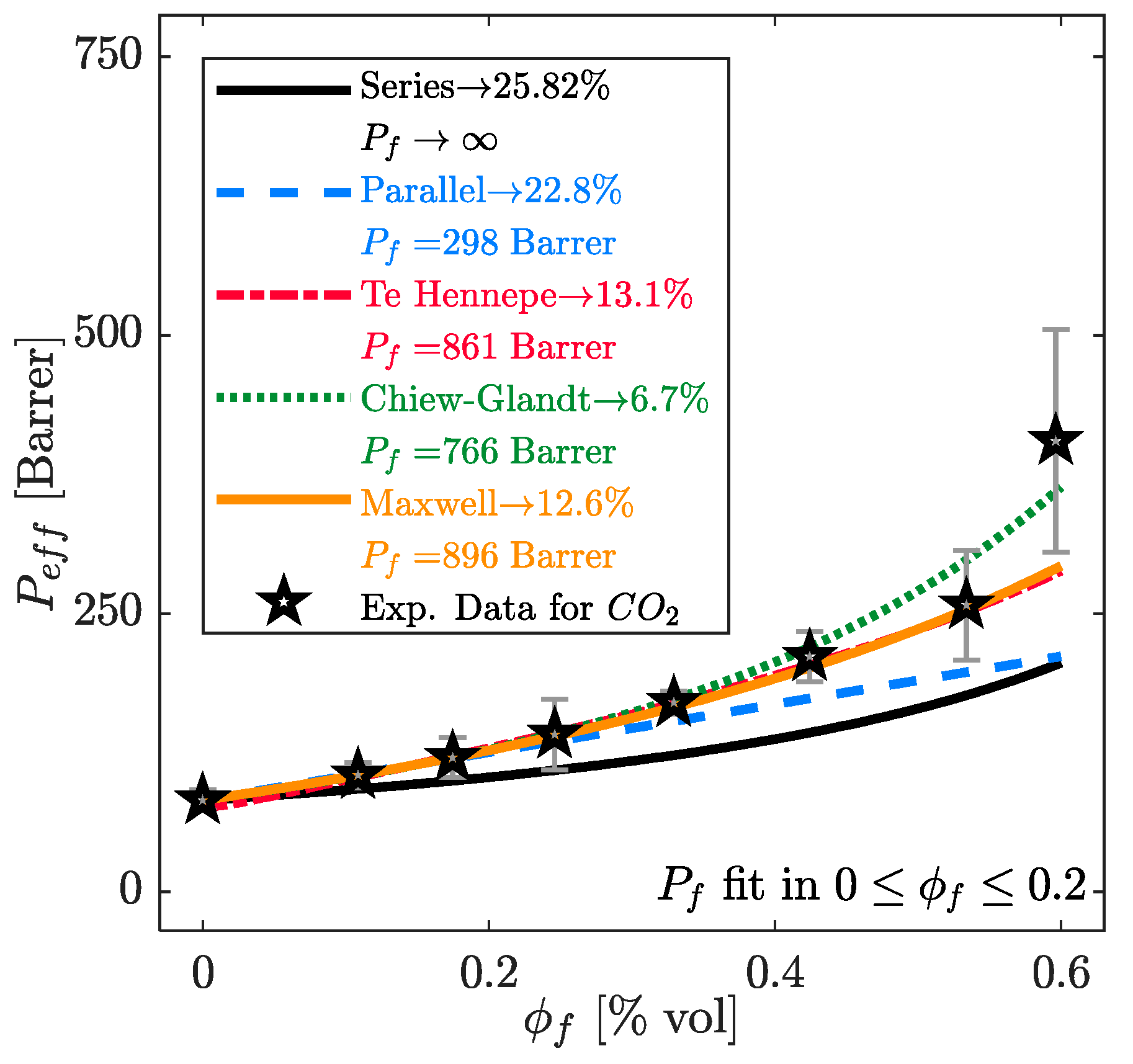
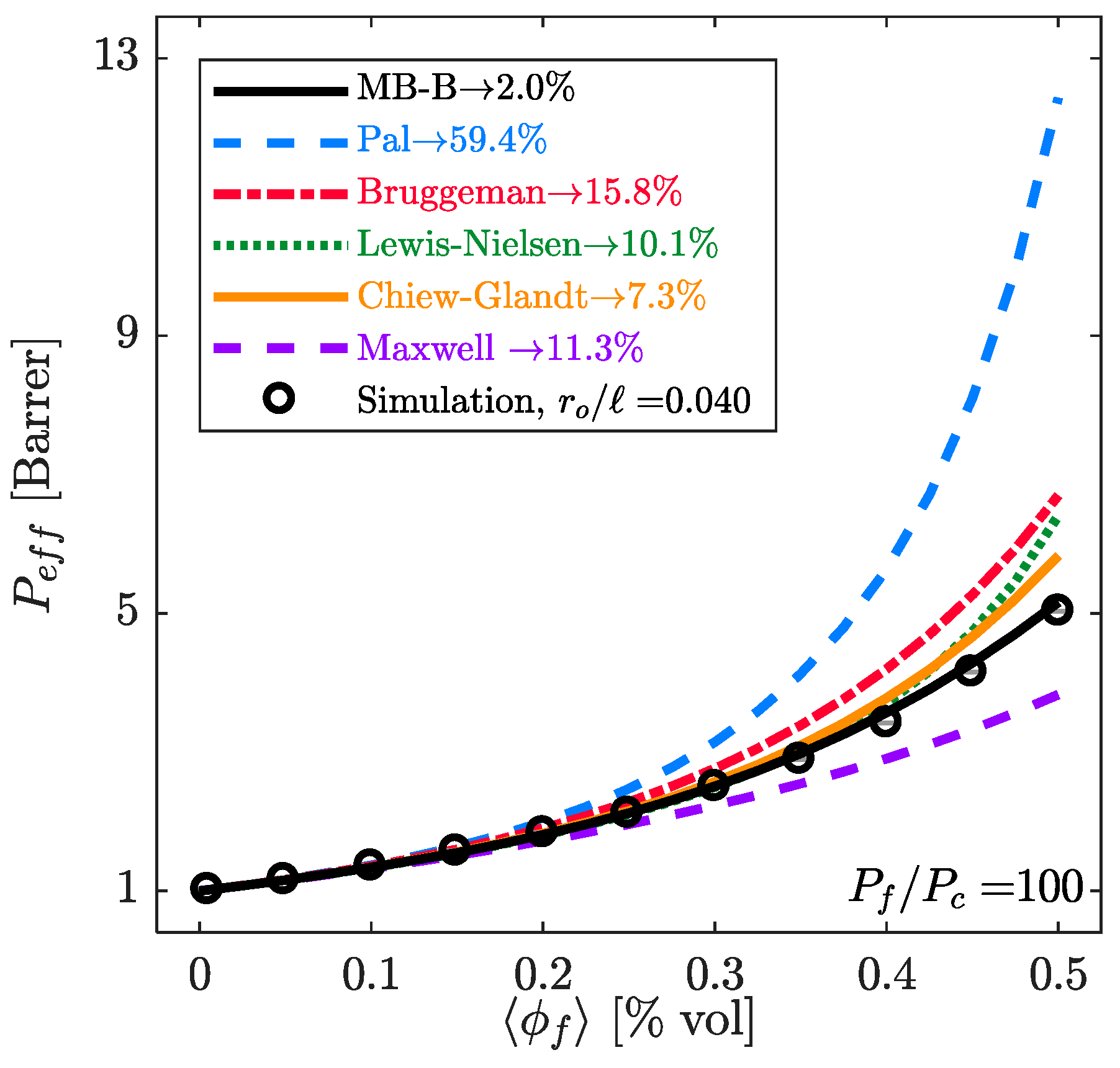
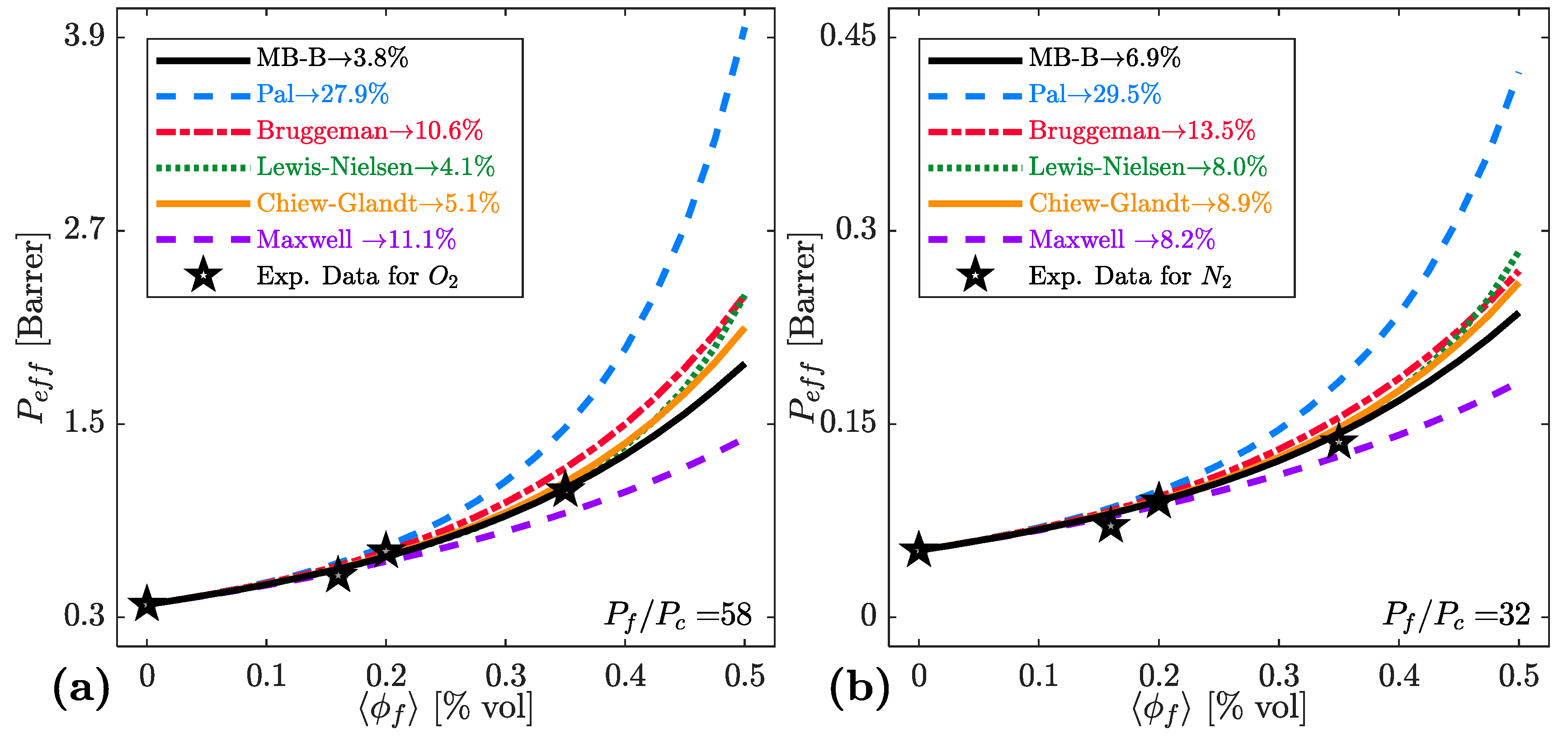
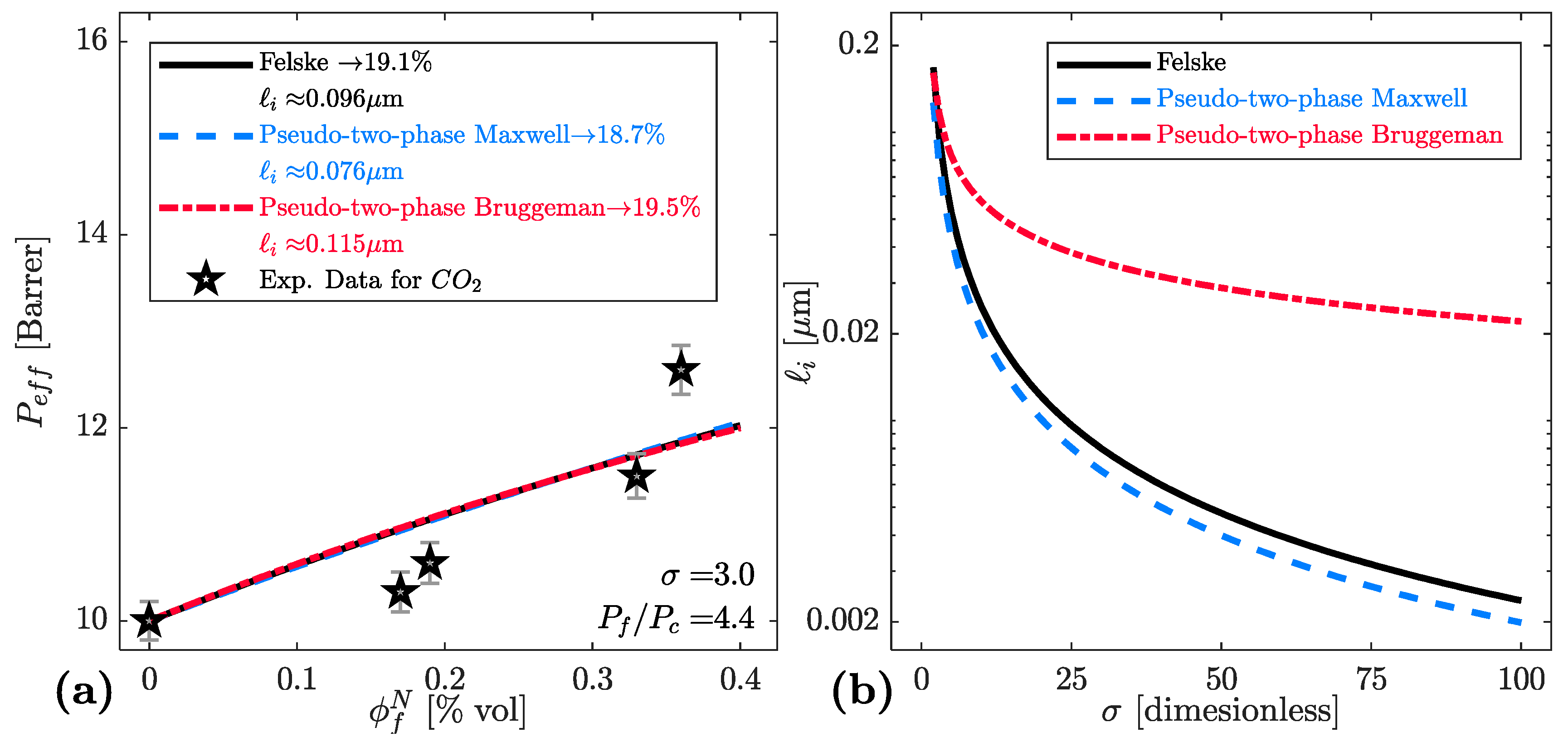
| Model | Key Equations | |
|---|---|---|
| Series [47] | (17) | |
| Parallel [47] | (18) | |
| Te Hennepe [130] | (19) | |
| Cussler [72] | (20) | |
| Ebneyamini [68] | (21) | |
| KJN [69] | (22) | |
| (23) | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Monsalve-Bravo, G.M.; Bhatia, S.K. Modeling Permeation through Mixed-Matrix Membranes: A Review. Processes 2018, 6, 172. https://doi.org/10.3390/pr6090172
Monsalve-Bravo GM, Bhatia SK. Modeling Permeation through Mixed-Matrix Membranes: A Review. Processes. 2018; 6(9):172. https://doi.org/10.3390/pr6090172
Chicago/Turabian StyleMonsalve-Bravo, Gloria M., and Suresh K. Bhatia. 2018. "Modeling Permeation through Mixed-Matrix Membranes: A Review" Processes 6, no. 9: 172. https://doi.org/10.3390/pr6090172
APA StyleMonsalve-Bravo, G. M., & Bhatia, S. K. (2018). Modeling Permeation through Mixed-Matrix Membranes: A Review. Processes, 6(9), 172. https://doi.org/10.3390/pr6090172