Basic Dye Removal with Sorption onto Low-Cost Natural Textile Fibers
Abstract
1. Introduction
2. Experimental Section
2.1. Materials
2.2. Characterization Techniques
2.3. Adsorption Experiments
2.3.1. Effect of pH
2.3.2. Effect of the Initial Dye Concentration and Temperature on Equilibrium (Isotherms)
2.3.3. Effect of the Adsorbent’s Mass
2.4. Desorption and Reuse Experiments
3. Results and Discussion
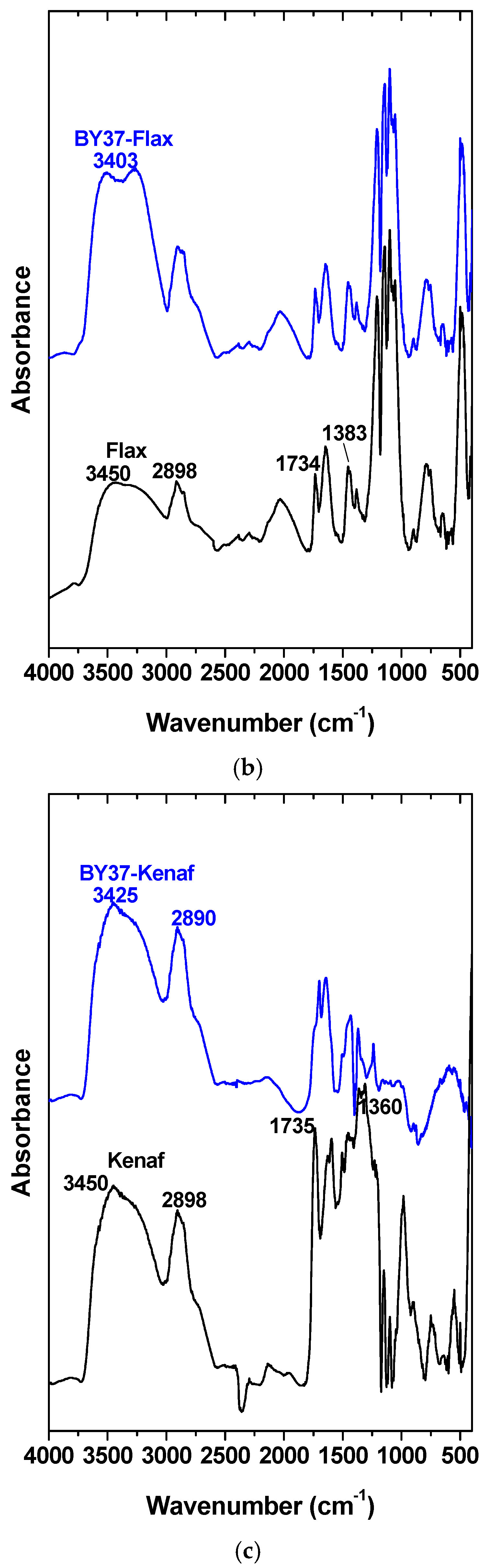
3.1. SEM, XRD, and Crystallinity
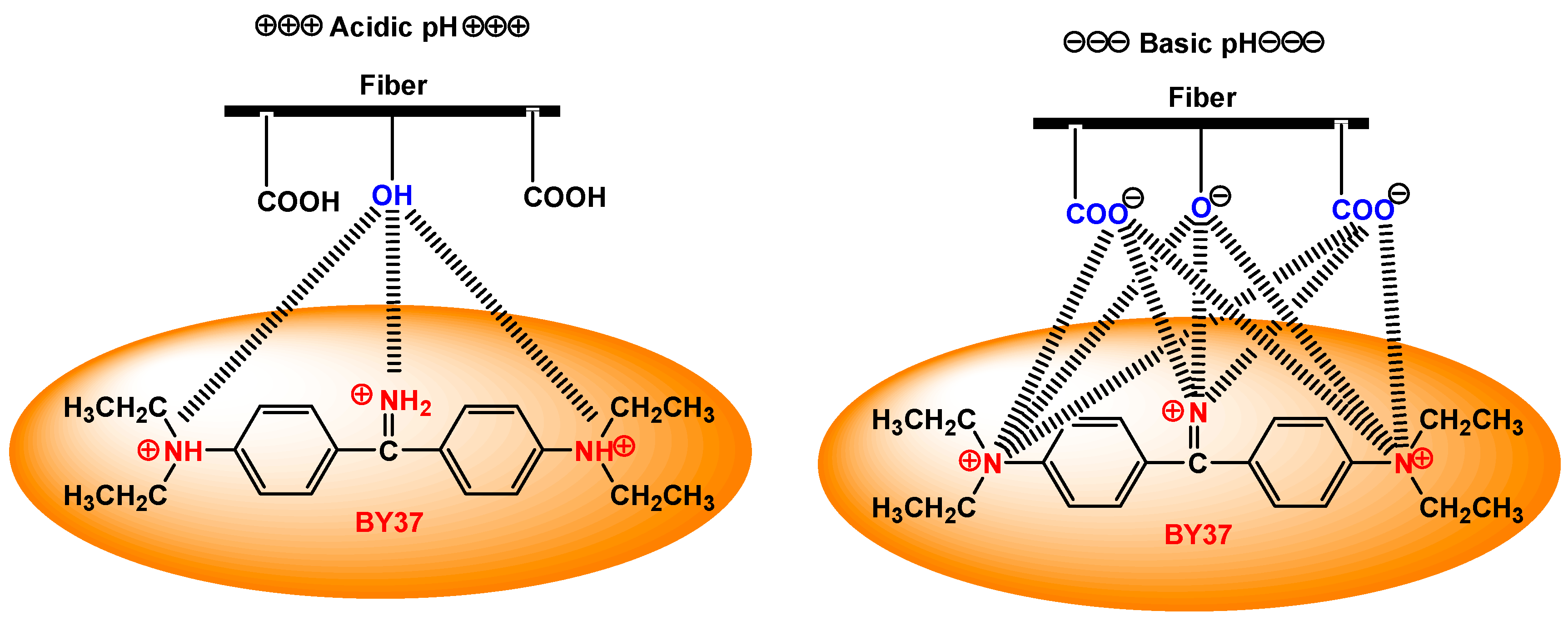
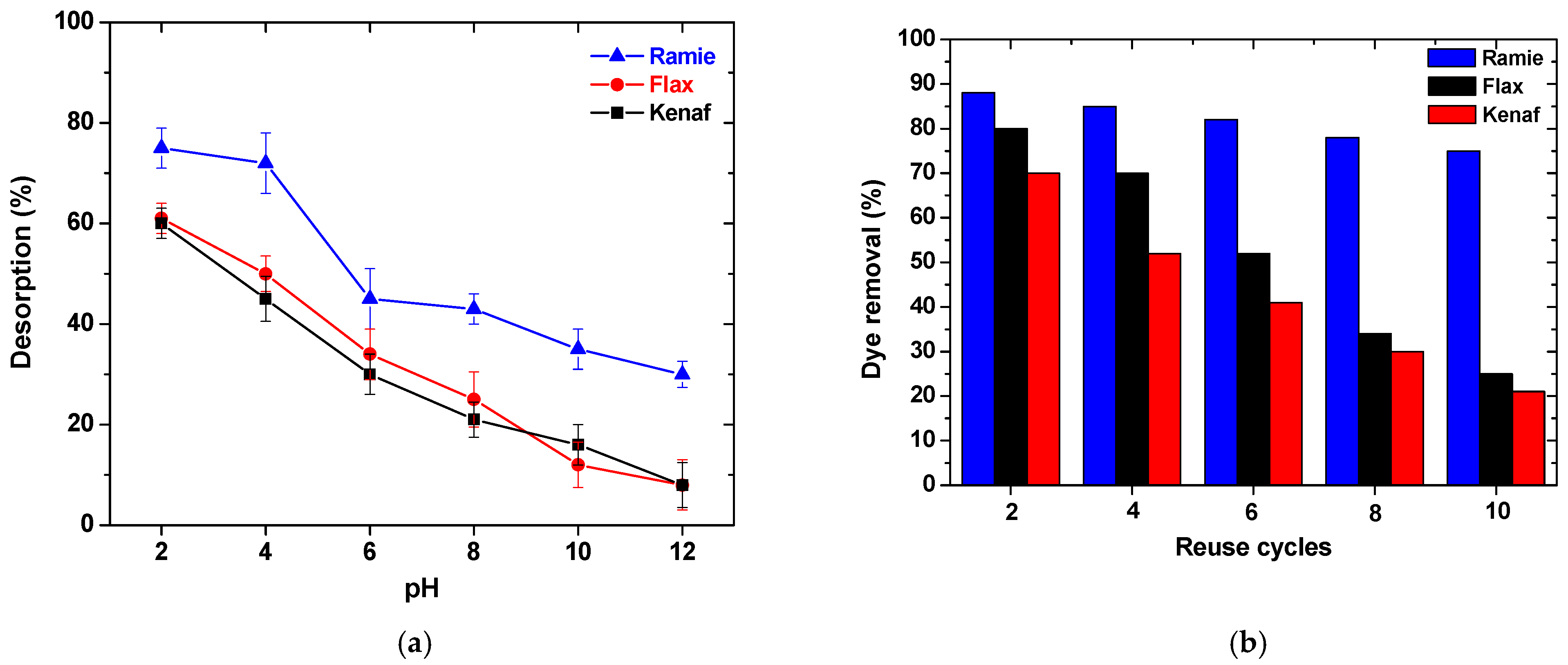
3.2. Effect of pH: Adsorption Mechanism
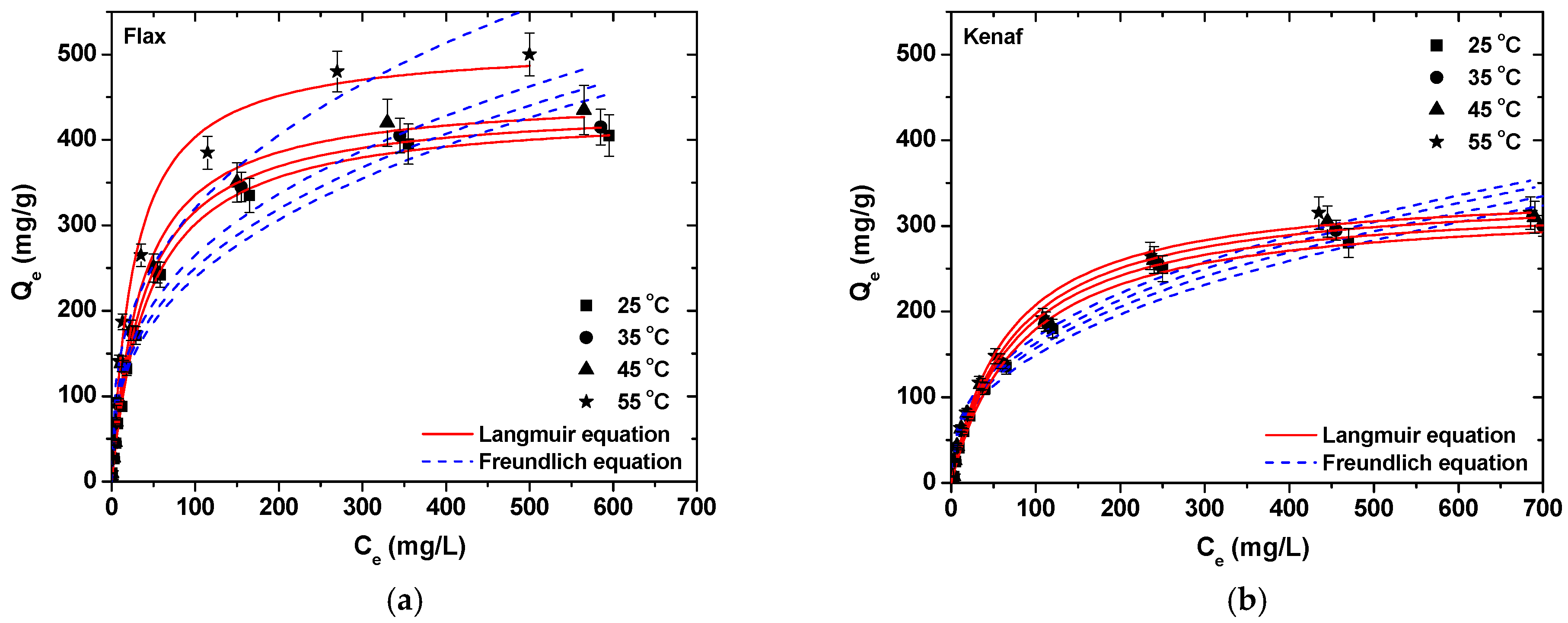
3.3. Isotherms and Thermodynamics
3.4. Effect of Adsorbent’s Dosage
3.5. Desorption and Reuse
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Reddy, N.; Yang, Y. Biofibers from agricultural byproducts for industrial applications. Trends Biotechnol. 2005, 23, 22–27. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Gao, B.; Wang, X.; Shi, R.; Rehman, R.U.; Gu, X. The influence of cation treatments on the pervaporation dehydration of naa zeolite membranes prepared on hollow fibers. Processes 2018, 6, 70. [Google Scholar] [CrossRef]
- Terzopoulou, Z.N.; Papageorgiou, G.Z.; Papadopoulou, E.; Athanassiadou, E.; Reinders, M.; Bikiaris, D.N. Development and study of fully biodegradable composite materials based on poly(butylene succinate) and hemp fibers or hemp shives. Polym. Compos. 2016, 37, 407–421. [Google Scholar] [CrossRef]
- Gamal, A.M.; Abo Farha, S.A.; Sallam, H.B.; Mahmoud, G.E.A.; Ismail, L.F.M. Kinetic study and equilibrium isotherm analysis of reactive dyes adsorption onto cotton fiber. Nat. Sci. 2010, 8, 95–110. [Google Scholar]
- Chetima, A.; Wahabou, A.; Zomegni, G.; Rahman, A.N.; Nde, D.B. Bleaching of neutral cotton seed oil using organic activated carbon in a batch system: Kinetics and adsorption isotherms. Processes 2018, 6, 22. [Google Scholar] [CrossRef]
- Di Marcoberardino, G.; Vitali, D.; Spinelli, F.; Binotti, M.; Manzolini, G. Green hydrogen production from raw biogas: A techno-economic investigation of conventional processes using pressure swing adsorption unit. Processes 2018, 6, 19. [Google Scholar] [CrossRef]
- Yang, F.; Chen, S.; Shi, C.; Xue, F.; Zhang, X.; Ju, S.; Xing, W. A facile synthesis of hexagonal spinel λ-MnO2 ion-sieves for highly selective Li+ adsorption. Processes 2018, 6, 59. [Google Scholar] [CrossRef]
- You, Z.; Zhang, L.; Zhang, S.; Sun, Y.; Shah, K. Treatment of oil-contaminated water by modified polysilicate aluminum ferric sulfate. Processes 2018, 6, 95. [Google Scholar] [CrossRef]
- Bian, Y.; Xiong, N.; Zhu, G. Technology for the remediation of water pollution: A review on the fabrication of metal organic frameworks. Processes 2018, 6, 122. [Google Scholar] [CrossRef]
- Bailey, S.E.; Olin, T.J.; Bricka, R.M.; Adrian, D.D. A review of potentially low-cost sorbents for heavy metals. Water Res. 1999, 33, 2469–2479. [Google Scholar] [CrossRef]
- Kyzas, G.; Bikiaris, D. Recent modifications of chitosan for adsorption applications: A critical and systematic review. Mar. Drugs 2015, 13, 312–337. [Google Scholar] [CrossRef] [PubMed]
- Boonamnuayvitaya, V.; Chaiya, C.; Tanthapanichakoon, W.; Jarudilokkul, S. Removal of heavy metals by adsorbent prepared from pyrolyzed coffee residues and clay. Sep. Purif. Technol. 2004, 35, 11–22. [Google Scholar] [CrossRef]
- Bharathi, K.S.; Ramesh, S.T. Removal of dyes using agricultural waste as low-cost adsorbents: A review. Appl. Water Sci. 2013, 3, 773–790. [Google Scholar] [CrossRef]
- Prashantha Kumar, T.K.M.; Mandlimath, T.R.; Sangeetha, P.; Revathi, S.K.; Ashok Kumar, S.K. Nanoscale materials as sorbents for nitrate and phosphate removal from water. Environ. Chem. Lett. 2018, 16, 389–400. [Google Scholar] [CrossRef]
- Vukelic, D.; Boskovic, N.; Agarski, B.; Radonic, J.; Budak, I.; Pap, S.; Turk Sekulic, M. Eco-design of a low-cost adsorbent produced from waste cherry kernels. J. Clean. Prod. 2018, 174, 1620–1628. [Google Scholar] [CrossRef]
- Monte Blanco, S.P.D.; Scheufele, F.B.; Módenes, A.N.; Espinoza-Quiñones, F.R.; Marin, P.; Kroumov, A.D.; Borba, C.E. Kinetic, equilibrium and thermodynamic phenomenological modeling of reactive dye adsorption onto polymeric adsorbent. Chem. Eng. J. 2017, 307, 466–475. [Google Scholar] [CrossRef]
- Ranjith, K.S.; Manivel, P.; Rajendrakumar, R.T.; Uyar, T. Multifunctional zno nanorod-reduced graphene oxide hybrids nanocomposites for effective water remediation: Effective sunlight driven degradation of organic dyes and rapid heavy metal adsorption. Chem. Eng. J. 2017, 325, 588–600. [Google Scholar] [CrossRef]
- Cai, K.; Shen, W.; Ren, B.; He, J.; Wu, S.; Wang, W. A phytic acid modified CoFe2O4 magnetic adsorbent with controllable morphology, excellent selective adsorption for dyes and ultra-strong adsorption ability for metal ions. Chem. Eng. J. 2017, 330, 936–946. [Google Scholar] [CrossRef]
- Abdi, J.; Vossoughi, M.; Mahmoodi, N.M.; Alemzadeh, I. Synthesis of metal-organic framework hybrid nanocomposites based on go and cnt with high adsorption capacity for dye removal. Chem. Eng. J. 2017, 326, 1145–1158. [Google Scholar] [CrossRef]
- Kim, J.; Kwak, S.Y. Efficient and selective removal of heavy metals using microporous layered silicate amh-3 as sorbent. Chem. Eng. J. 2017, 313, 975–982. [Google Scholar] [CrossRef]
- Li, Z.; Chen, J.; Ge, Y. Removal of lead ion and oil droplet from aqueous solution by lignin-grafted carbon nanotubes. Chem. Eng. J. 2017, 308, 809–817. [Google Scholar] [CrossRef]
- Lingamdinne, L.P.; Chang, Y.Y.; Yang, J.K.; Singh, J.; Choi, E.H.; Shiratani, M.; Koduru, J.R.; Attri, P. Biogenic reductive preparation of magnetic inverse spinel iron oxide nanoparticles for the adsorption removal of heavy metals. Chem. Eng. J. 2017, 307, 74–84. [Google Scholar] [CrossRef]
- Naushad, M.; Ahamad, T.; Al-Maswari, B.M.; Abdullah Alqadami, A.; Alshehri, S.M. Nickel ferrite bearing nitrogen-doped mesoporous carbon as efficient adsorbent for the removal of highly toxic metal ion from aqueous medium. Chem. Eng. J. 2017, 330, 1351–1360. [Google Scholar] [CrossRef]
- Yuan, G.; Tian, Y.; Liu, J.; Tu, H.; Liao, J.; Yang, J.; Yang, Y.; Wang, D.; Liu, N. Schiff base anchored on metal-organic framework for co(ii) removal from aqueous solution. Chem. Eng. J. 2017, 326, 691–699. [Google Scholar] [CrossRef]
- Zhou, Y.; Xia, S.; Zhang, J.; Nguyen, B.T.; Zhang, Z. Insight into the influences of ph value on pb(ii) removal by the biopolymer extracted from activated sludge. Chem. Eng. J. 2017, 308, 1098–1104. [Google Scholar] [CrossRef]
- Kyzas, G.Z.; Kostoglou, M. Green adsorbents for wastewaters: A critical review. Materials 2014, 7, 333–364. [Google Scholar] [CrossRef] [PubMed]
- Anastopoulos, I.; Kyzas, G.Z. Agricultural peels for dye adsorption: A review of recent literature. J. Mol. Liq. 2014, 200, 277–285. [Google Scholar] [CrossRef]
- Didaskalou, C.; Buyuktiryaki, S.; Kecili, R.; Fonte, C.P.; Szekely, G. Valorisation of agricultural waste with an adsorption/nanofiltration hybrid process: From materials to sustainable process design. Green Chem. 2017, 19, 3116–3125. [Google Scholar] [CrossRef]
- Kim, J.F.; Székely, G.; Valtcheva, I.B.; Livingston, A.G. Increasing the sustainability of membrane processes through cascade approach and solvent recovery—Pharmaceutical purification case study. Green Chem. 2014, 16, 133–145. [Google Scholar] [CrossRef]
- Razali, M.; Kim, J.F.; Attfield, M.; Budd, P.M.; Drioli, E.; Lee, Y.M.; Szekely, G. Sustainable wastewater treatment and recycling in membrane manufacturing. Green Chem. 2015, 17, 5196–5205. [Google Scholar] [CrossRef]
- Ko, D.; Siriwardane, R.; Biegler, L.T. Optimization of a pressure-swing adsorption process using zeolite 13x for CO2 sequestration. Ind. Eng. Chem. Res. 2003, 42, 339–348. [Google Scholar] [CrossRef]
- Agarwal, A.; Biegler, L.T.; Zitney, S.E. Superstructure-based optimal synthesis of pressure swing adsorption cycles for precombustion CO2 capture. Ind. Eng. Chem. Res. 2010, 49, 5066–5079. [Google Scholar] [CrossRef]
- Faruk, O.; Bledzki, A.K.; Fink, H.P.; Sain, M. Biocomposites reinforced with natural fibers: 2000–2010. Prog. Polym. Sci. 2012, 37, 1552–1596. [Google Scholar] [CrossRef]
- Yamaki, S.B.; Barros, D.S.; Garcia, C.M.; Socoloski, P.; Oliveira, O.N., Jr.; Atvars, T.D.Z. Spectroscopic studies of the intermolecular interactions of congo red and tinopal cbs with modified cellulose fibers. Langmuir 2005, 21, 5414–5420. [Google Scholar] [CrossRef] [PubMed]
- Ciovica, S.; Vlaic, M.; Stanciu, C.; Chiuaru, R.; Asandei, N. Some aspects concerning viscose fibres dyeing uniformity. I. Staple viscose dyeing uniformity. Cellul. Chem. Technol. 1990, 24, 251–261. [Google Scholar]
- Tsai, B.; Garcia-Valdez, O.; Champagne, P.; Cunningham, M.F. Poly(poly(ethylene glycol) methyl ether methacrylate) grafted chitosan for dye removal from water. Processes 2017, 5, 12. [Google Scholar] [CrossRef]
- Zhong, D.; Liu, Y.H.; Cheung, N.T.; Kan, C.W.; Chua, H. A parameter study of the effect of a plasma-induced ozone colour-fading process on sulphur-dyed cotton fabric. Processes 2018, 6, 81. [Google Scholar] [CrossRef]
- Zografi, G.; Kontny, M.J.; Yang, A.Y.S.; Brenner, G.S. Surface area and water vapor sorption of microcrystalline cellulose. Int. J. Pharm. 1984, 18, 99–116. [Google Scholar] [CrossRef]
- Demirbas, A. Heavy metal adsorption onto agro-based waste materials: A review. J. Hazard. Mater. 2008, 157, 220–229. [Google Scholar] [CrossRef] [PubMed]
- Mihranyan, A.; Llagostera, A.P.; Karmhag, R.; Strømme, M.; Eka, R. Moisture sorption by cellulose powders of varying crystallinity. Int. J. Pharm. 2004, 269, 433–442. [Google Scholar] [CrossRef] [PubMed]
- Tofan, L.; Teodosiu, C.; Paduraru, C.; Wenkert, R. Cobalt (ii) removal from aqueous solutions by natural hemp fibers: Batch and fixed-bed column studies. Appl. Surf. Sci. 2013, 285, 33–39. [Google Scholar] [CrossRef]
- Mahmoud, D.K.; Salleh, M.A.M.; Karim, W.A.W.A.; Idris, A.; Abidin, Z.Z. Batch adsorption of basic dye using acid treated kenaf fibre char: Equilibrium, kinetic and thermodynamic studies. Chem. Eng. J. 2012, 181–182, 449–457. [Google Scholar] [CrossRef]
- Park, S.; Baker, J.; Himmel, M.; Parilla, P.; Johnson, D. Cellulose crystallinity index: Measurement techniques and their impact on interpreting cellulase performance. Biotechnol. Biofuels 2010, 3, 10. [Google Scholar] [CrossRef] [PubMed]
- Jayaramudu, J.; Guduri, B.R.; Rajulu, A.V. Characterization of natural fabric sterculia urens. Int. J. Polym. Anal. Charact. 2009, 14, 115–125. [Google Scholar] [CrossRef]
- Langmuir, I. The adsorption of gases on plane surfaces of glass, mica and platinum. J. Am. Chem. Soc. 1918, 40, 1361–1403. [Google Scholar] [CrossRef]
- Freundlich, H. Over the adsorption in solution. Z. Phys. Chem. 1906, 57, 385–470. [Google Scholar]
- Tien, C. Adsorption Calculations and Modeling; Butterworth-Heinemann: Boston, MA, USA, 1994. [Google Scholar]
- Smith, J.M.; Van Ness, H.C. Introduction to Chemical Engineering Thermodynamics, 4th ed.; McGraw-Hill: New York, NY, USA, 1987. [Google Scholar]
- Bismarck, A.; Aranberri-Askargorta, I.; Springer, J.; Lampke, T.; Wielage, B.; Stamboulis, A.; Shenderovich, I.; Limbach, H.-H. Surface characterization of flax, hemp and cellulose fibers; surface properties and the water uptake behavior. Polym. Compos. 2002, 23, 872–894. [Google Scholar] [CrossRef]
- Razak, N.I.A.; Ibrahim, N.A.; Zainuddin, N.; Rayung, M.; Saad, W.Z. The influence of chemical surface modification of kenaf fiber using hydrogen peroxide on the mechanical properties of biodegradable kenaf fiber/poly(lactic acid). Compos. Mol. 2014, 19, 2957–2968. [Google Scholar] [CrossRef] [PubMed]
- Allègre, C.; Moulin, P.; Maisseu, M.; Charbit, F. Treatment and reuse of reactive dyeing effluents. J. Membr. Sci. 2006, 269, 15–34. [Google Scholar] [CrossRef]
- Alemdar, A.; Sain, M. Isolation and characterization of nanofibers from agricultural residues—Wheat straw and soy hulls. Bioresour. Technol. 2008, 99, 1664–1671. [Google Scholar] [CrossRef] [PubMed]
- Sgriccia, N.; Hawley, M.C.; Misra, M. Characterization of natural fiber surfaces and natural fiber composites. Compos. Part A Appl. Sci. Manuf. 2008, 39, 1632–1637. [Google Scholar] [CrossRef]
- Cao, Y.; Chan, F.; Chui, Y.-H.; Xiao, H. Characterization of flax fibres modified by alkaline, enzyme, and steam-heat treatments. BioResources 2012, 7, 4109–4121. [Google Scholar]
- Chatterjee, S.; Chatterjee, B.P.; Das, A.R.; Guha, A.K. Adsorption of a model anionic dye, eosin y, from aqueous solution by chitosan hydrobeads. J. Colloid Interface Sci. 2005, 288, 30–35. [Google Scholar] [CrossRef] [PubMed]
- Brunauer, S.; Deming, L.S.; Deming, W.E.; Teller, E. On a theory of the van der waals adsorption of gases. J. Am. Chem. Soc. 1940, 62, 1723–1732. [Google Scholar] [CrossRef]
- Kyzas, G.Z.; Kostoglou, M.; Lazaridis, N.K. Copper and chromium(vi) removal by chitosan derivatives-equilibrium and kinetic studies. Chem. Eng. J. 2009, 152, 440–448. [Google Scholar] [CrossRef]

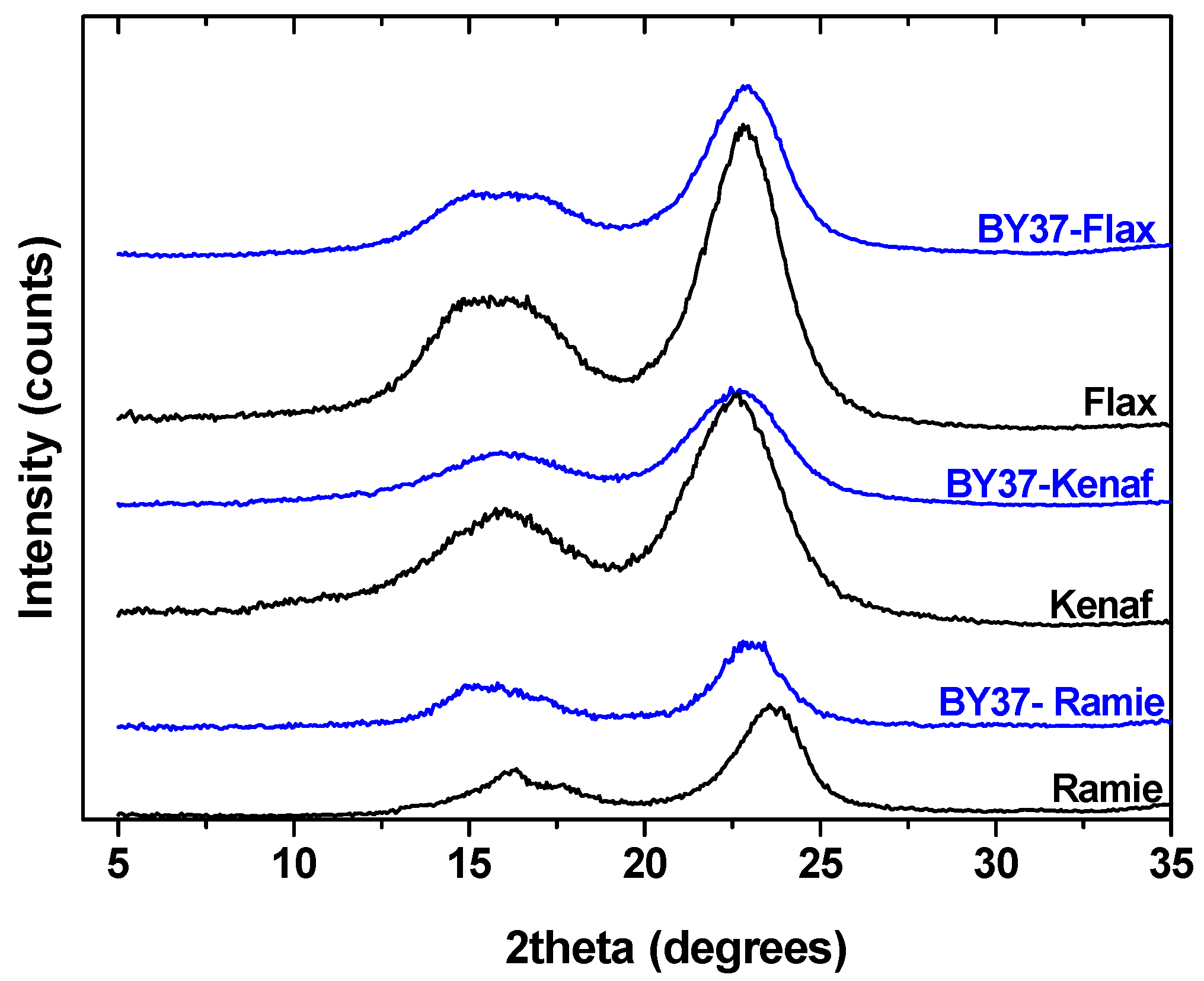


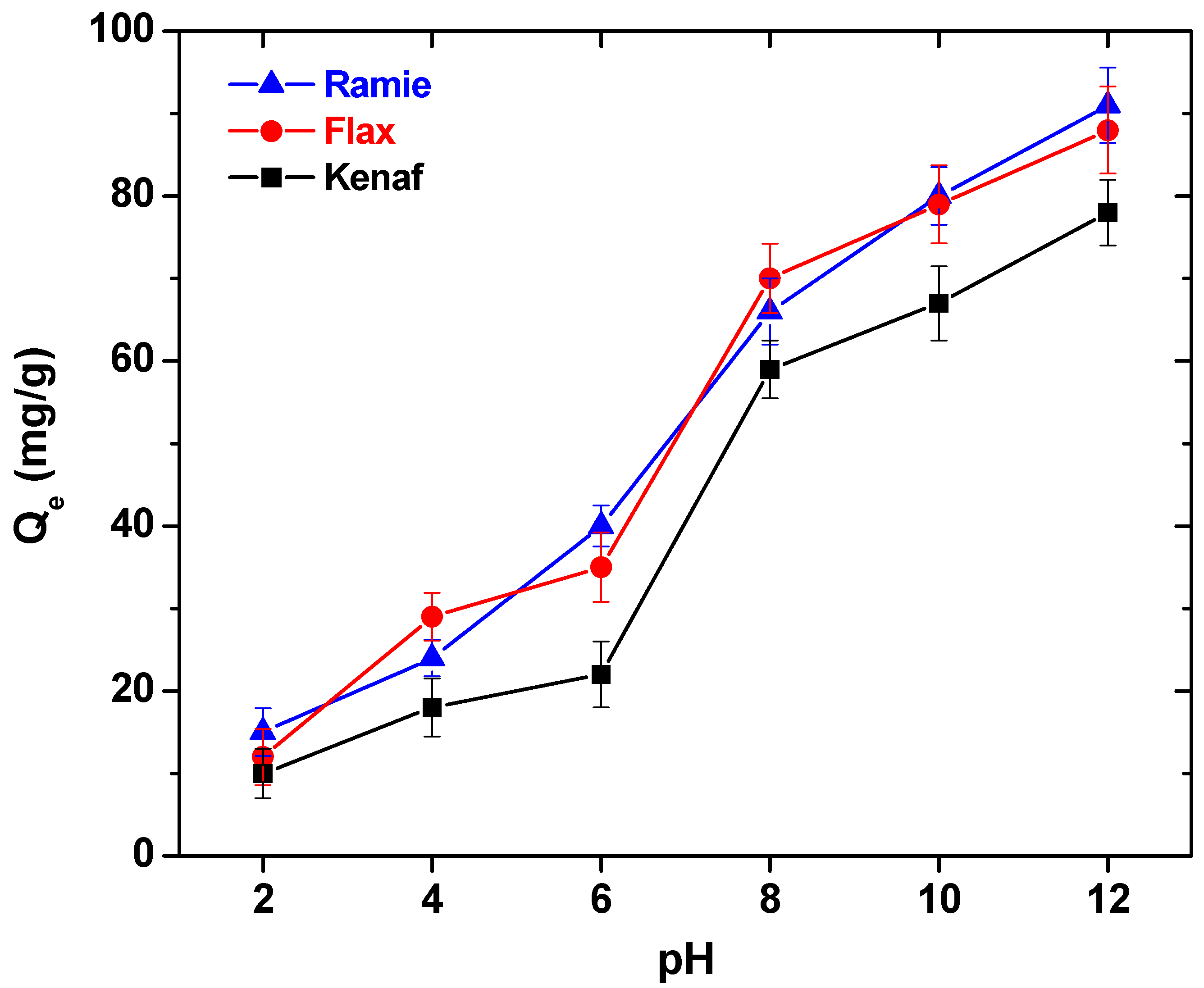
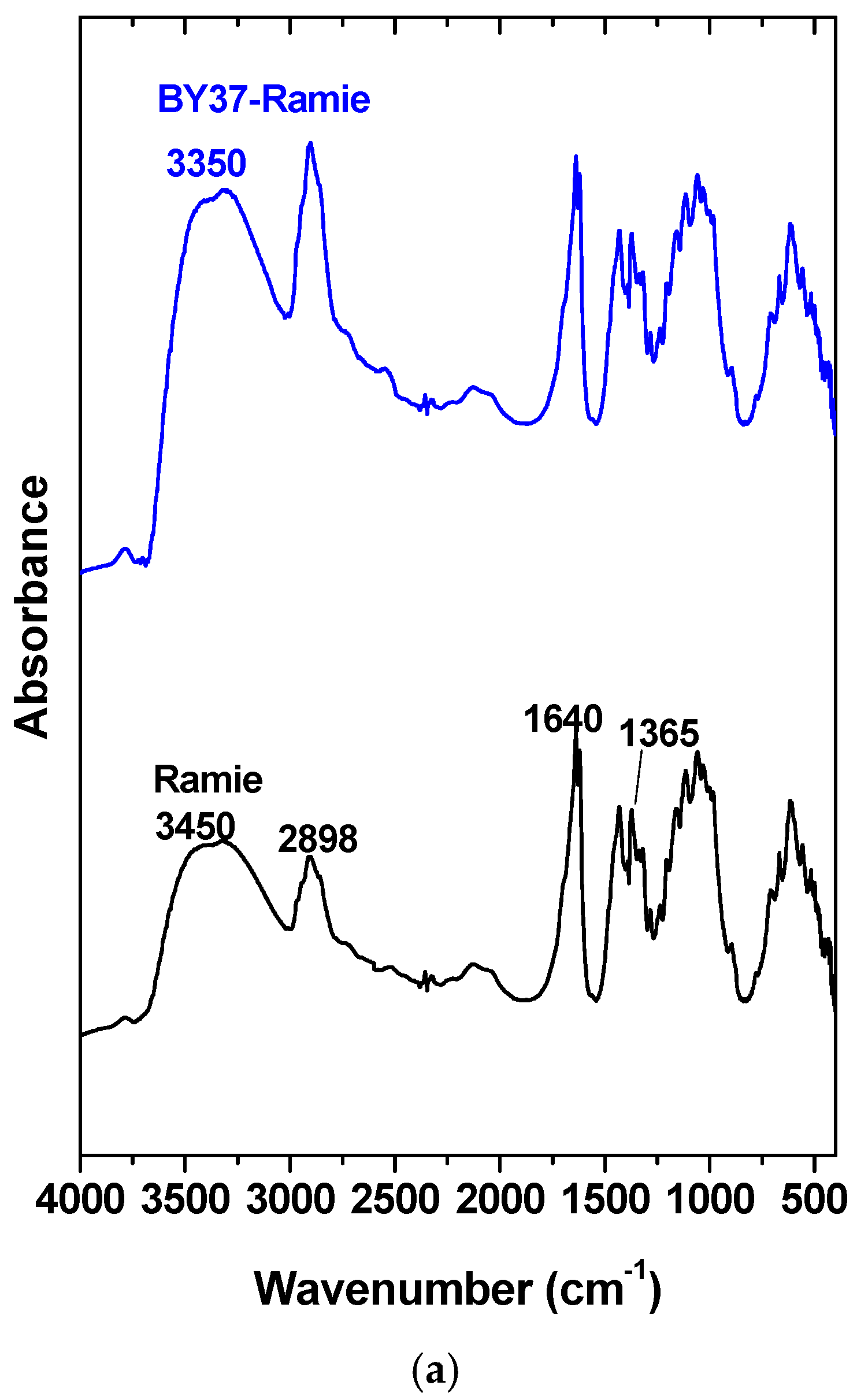


| Before Adsorption | After Adsorption | |||
|---|---|---|---|---|
| Fiber | CI | Xc (%) | CI | Xc (%) |
| Kenaf | 0.700 | 76.92 | 0.681 | 75.70 |
| Ramie | 0.885 | 89.70 | 0.872 | 88.60 |
| Flax | 0.820 | 84.09 | 0.795 | 83.01 |
| Langmuir Equation | Freundlich Equation | ||||||
|---|---|---|---|---|---|---|---|
| Fiber | T (°C) | Qm (mg·g−1) | KL (L·mg−1) | R2 | KF | n | R2 |
| Ramie | 25 | 460 | 0.025 | 0.997 | 51.74 | 2.84 | 0.951 |
| 35 | 475 | 0.028 | 0.995 | 56.72 | 2.89 | 0.953 | |
| 45 | 506 | 0.038 | 0.993 | 66.70 | 2.96 | 0.945 | |
| 55 | 507 | 0.043 | 0.992 | 71.61 | 3.06 | 0.947 | |
| Flax | 25 | 435 | 0.022 | 0.998 | 45.64 | 2.78 | 0.947 |
| 35 | 443 | 0.025 | 0.997 | 49.61 | 2.84 | 0.946 | |
| 45 | 453 | 0.028 | 0.993 | 53.68 | 2.89 | 0.954 | |
| 55 | 512 | 0.037 | 0.992 | 66.84 | 2.93 | 0.956 | |
| Kenaf | 25 | 327 | 0.012 | 0.994 | 23.87 | 2.51 | 0.962 |
| 35 | 333 | 0.013 | 0.993 | 26.24 | 2.57 | 0.961 | |
| 45 | 342 | 0.014 | 0.991 | 27.36 | 2.58 | 0.964 | |
| 55 | 346 | 0.015 | 0.989 | 29.82 | 2.84 | 0.962 | |
| Fiber | C0 (mg·L−1) | T (K) | Qe (mg·g−1) | Kc | ΔG0 (kJ·mol−1) | ΔH0 (kJ·mol−1) | ΔS0 (kJ·mol−1·K−1) |
|---|---|---|---|---|---|---|---|
| Ramie | 10 | 298 | 9.90 | 99.00 | −11.39 | +26.31 | +0.126 |
| 308 | 9.92 | 124.02 | −12.34 | ||||
| 318 | 9.95 | 199.07 | −14.00 | ||||
| 328 | 9.96 | 249.08 | −15.05 | ||||
| 100 | 298 | 91.04 | 10.11 | −5.73 | +11.79 | +0.052 | |
| 308 | 92.09 | 11.50 | −6.25 | ||||
| 318 | 93.41 | 13.29 | −6.84 | ||||
| 328 | 93.53 | 14.38 | −7.27 | ||||
| 500 | 298 | 350.24 | 2.33 | −2.10 | +10.51 | +0.042 | |
| 308 | 360.35 | 2.57 | −2.42 | ||||
| 318 | 380.41 | 3.17 | −3.05 | ||||
| 328 | 385.36 | 3.35 | −3.30 | ||||
| 1000 | 298 | 430.05 | 0.75 | 0.70 | +7.77 | +0.024 | |
| 308 | 448.09 | 0.81 | 0.53 | ||||
| 318 | 490.08 | 0.96 | 0.11 | ||||
| 328 | 495.87 | 0.98 | 0.05 | ||||
| Flax | 10 | 298 | 9.80 | 49.02 | −9.64 | +42.61 | +0.174 |
| 308 | 9.85 | 65.67 | −10.72 | ||||
| 318 | 9.91 | 99.10 | −12.15 | ||||
| 328 | 9.96 | 249.00 | −15.05 | ||||
| 100 | 298 | 88.04 | 7.33 | −4.94 | +20.13 | +0.083 | |
| 308 | 89.09 | 8.09 | −5.35 | ||||
| 318 | 91.07 | 10.11 | −6.12 | ||||
| 328 | 94.32 | 15.67 | −7.50 | ||||
| 500 | 298 | 335.44 | 2.03 | −1.75 | +12.43 | +0.047 | |
| 308 | 345.68 | 2.23 | −2.05 | ||||
| 318 | 350.71 | 2.33 | −2.24 | ||||
| 328 | 385.35 | 3.35 | −3.30 | ||||
| 1000 | 298 | 405.59 | 0.68 | 0.95 | +9.92 | +0.030 | |
| 308 | 415.31 | 0.71 | 0.88 | ||||
| 318 | 435.42 | 0.77 | 0.69 | ||||
| 328 | 500.24 | 1.00 | 0.00 | ||||
| Kenaf | 10 | 298 | 7.02 | 2.33 | −2.10 | +6.65 | +0.029 |
| 308 | 7.50 | 3.00 | −2.81 | ||||
| 318 | 7.51 | 3.02 | −2.90 | ||||
| 328 | 7.52 | 3.03 | −3.00 | ||||
| 100 | 298 | 78.04 | 3.55 | −3.14 | +6.25 | +0.033 | |
| 308 | 80.09 | 4.00 | −3.55 | ||||
| 318 | 81.12 | 4.26 | −3.83 | ||||
| 328 | 82.23 | 4.56 | −4.14 | ||||
| 500 | 298 | 250.34 | 1.00 | 0.00 | +3.25 | +0.011 | |
| 308 | 255.41 | 1.04 | −0.10 | ||||
| 318 | 260.35 | 1.08 | −0.21 | ||||
| 328 | 265.95 | 1.13 | −0.33 | ||||
| 1000 | 298 | 295.01 | 0.42 | 2.16 | +2.68 | +0.002 | |
| 308 | 300.34 | 0.43 | 2.17 | ||||
| 318 | 310.45 | 0.45 | 2.12 | ||||
| 328 | 315.55 | 0.46 | 2.12 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kyzas, G.Z.; Christodoulou, E.; Bikiaris, D.N. Basic Dye Removal with Sorption onto Low-Cost Natural Textile Fibers. Processes 2018, 6, 166. https://doi.org/10.3390/pr6090166
Kyzas GZ, Christodoulou E, Bikiaris DN. Basic Dye Removal with Sorption onto Low-Cost Natural Textile Fibers. Processes. 2018; 6(9):166. https://doi.org/10.3390/pr6090166
Chicago/Turabian StyleKyzas, George Z., Evi Christodoulou, and Dimitrios N. Bikiaris. 2018. "Basic Dye Removal with Sorption onto Low-Cost Natural Textile Fibers" Processes 6, no. 9: 166. https://doi.org/10.3390/pr6090166
APA StyleKyzas, G. Z., Christodoulou, E., & Bikiaris, D. N. (2018). Basic Dye Removal with Sorption onto Low-Cost Natural Textile Fibers. Processes, 6(9), 166. https://doi.org/10.3390/pr6090166







