Production Process Optimization of Metal Mines Considering Economic Benefit and Resource Efficiency Using an NSGA-II Model
Abstract
1. Introduction
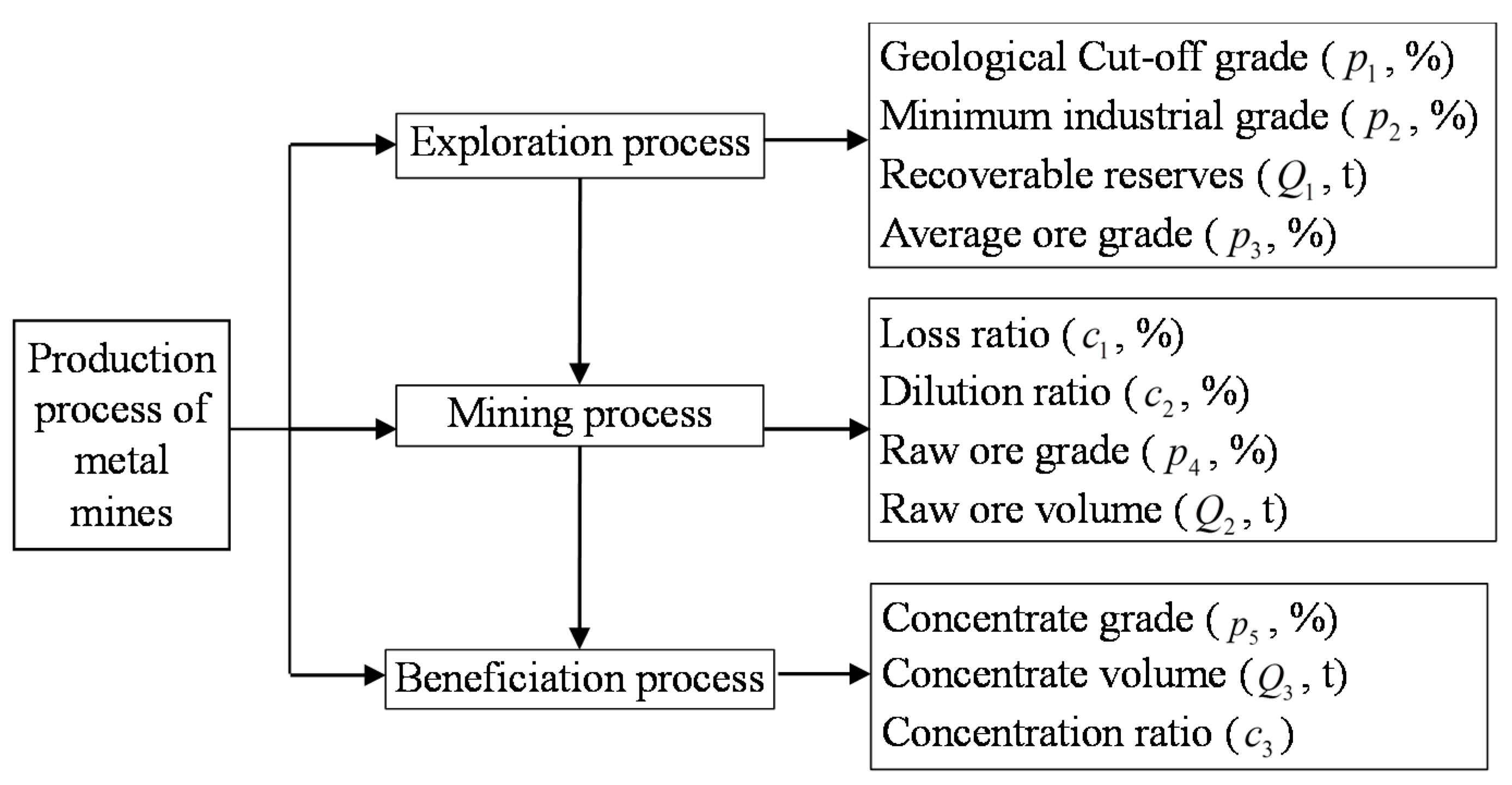
2. Production Process of Metal Mines
2.1. Exploration Process
2.2. Mining Process
2.3. Beneficiation Process
3. Multi-Objective Optimization Model Considering Economic Profit and Resource Efficiency
3.1. Decision Variables and Constraints
3.1.1. Decision Variables
3.1.2. Constraints
3.2. Objective Function
3.2.1. Economic Benefit Objective
3.2.2. Resource Efficiency Objective
3.3. Multi-Objective Optimization Model
3.4. Development of the NSGA-II Model to Solve the Established Model
- (a)
- Collect the data related to the production process of a specific metal mine, i.e., the value of each indicator, and the price of concentrate ores.
- (b)
- Determine the relationship between the indications, such as , , , , , , , .
- (c)
- Determine the decision variables according to the dependency analysis, and the upper and lower boundary values of the decision variables according to the production process of the mine.
- (d)
- The NSGA-II parameters, such as the population size, maximum number of iterations r, crossover probability, mutation probability, crossover index and mutation index, are initialized. Then, n possible individuals are randomly generated as the initial parent population.
- (e)
- The parent population generates a child population with n possible individuals by selection, mutation and crossover.
- (f)
- The parent and child populations are mixed to form a new population with 2n possible individuals.
- (g)
- The profit and resource utilization rate of each individual is calculated in the new population with the input data in (a) and the relationship in (b).
- (h)
- Based on the values of the objective functions, the mixed population is classified based on the non-dominated level, and the crowded distance is calculated.
- (i)
- Based on the non-dominated sorting and the crowding distance calculation results of step (h), the top n possible individuals are retained as a new parent population.
- (j)
- Check the termination condition. If satisfied, the optimization process is terminated and output the optimal decision variables, profit and resource utilization rate; otherwise, goes to step (e).
4. Multi-Objective Optimization of Process of the Huogeqi Copper Mine
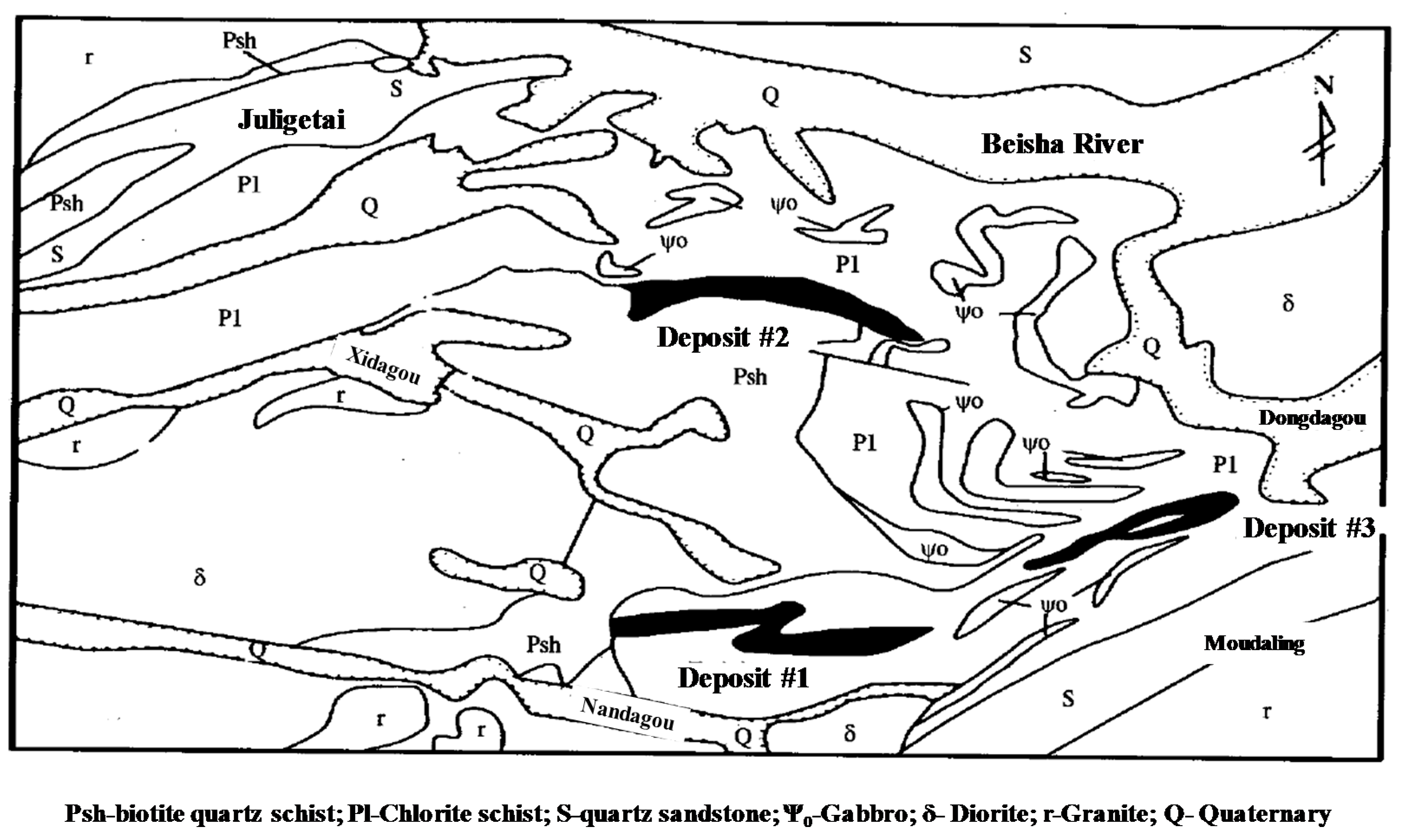
4.1. Brief Introduction of the Huogeqi Copper Mine
4.2. Production Indicators of the Huogeqi Copper Mine
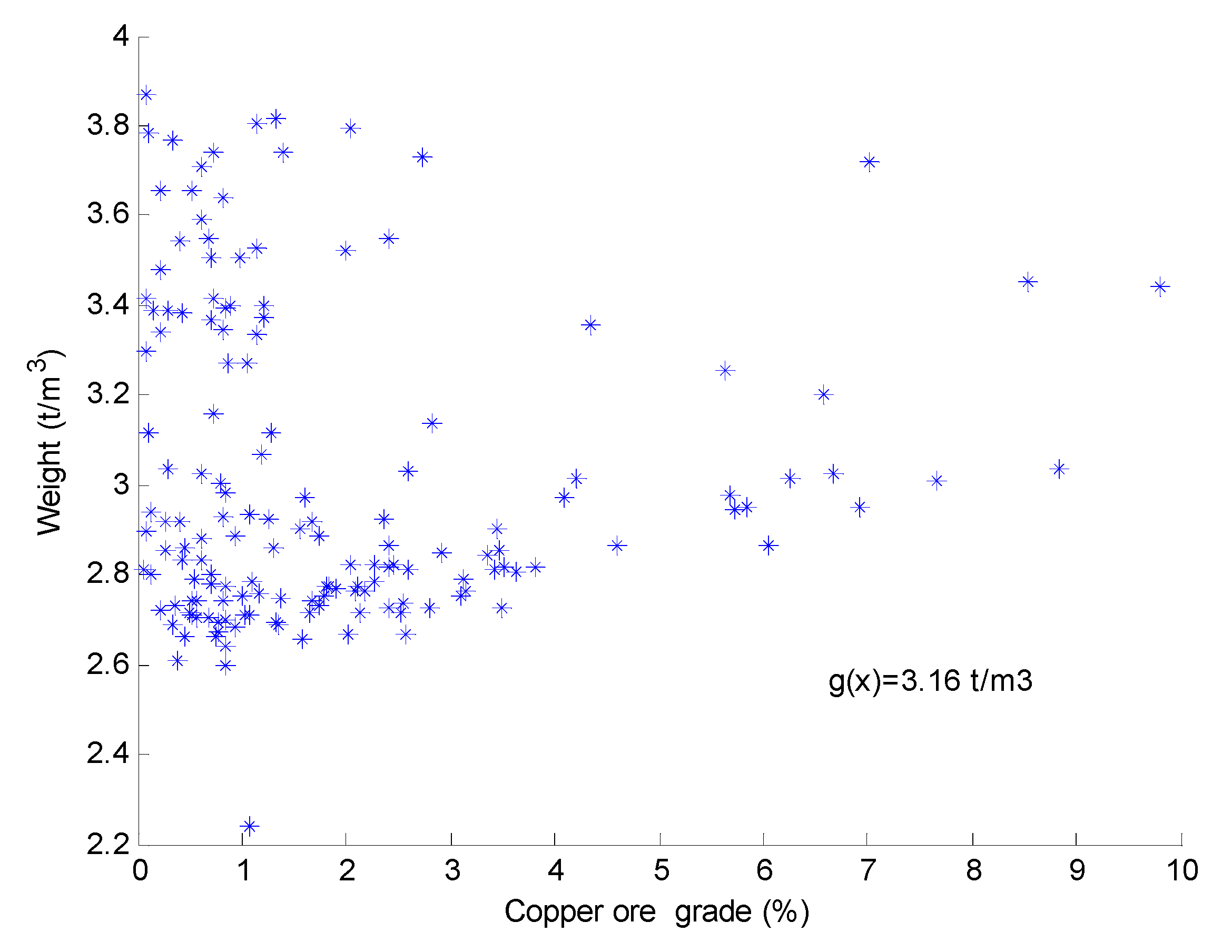
4.2.1. Relationship between Ore Weight and Grade
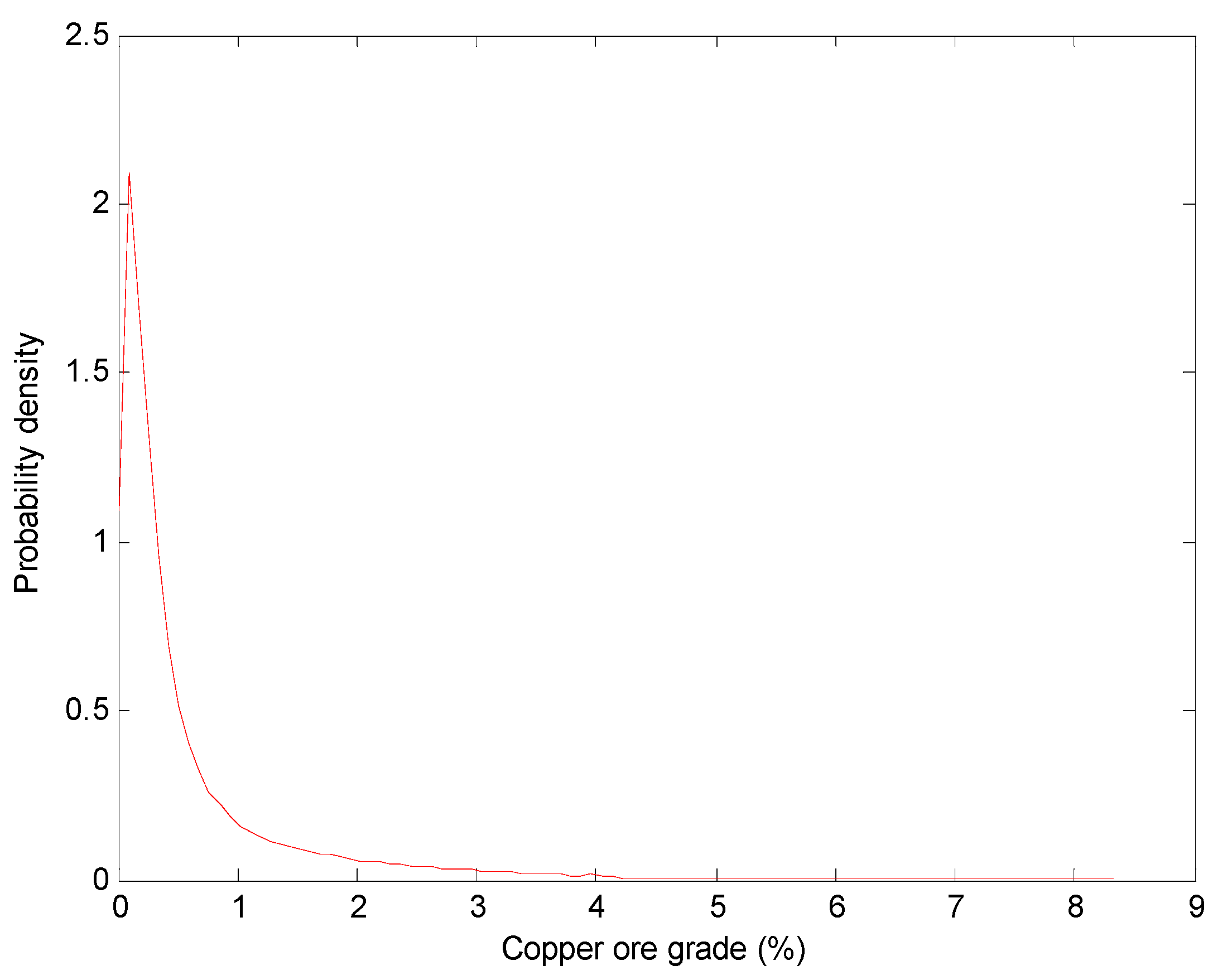
4.2.2. Probability Density of Ore Grade Distribution
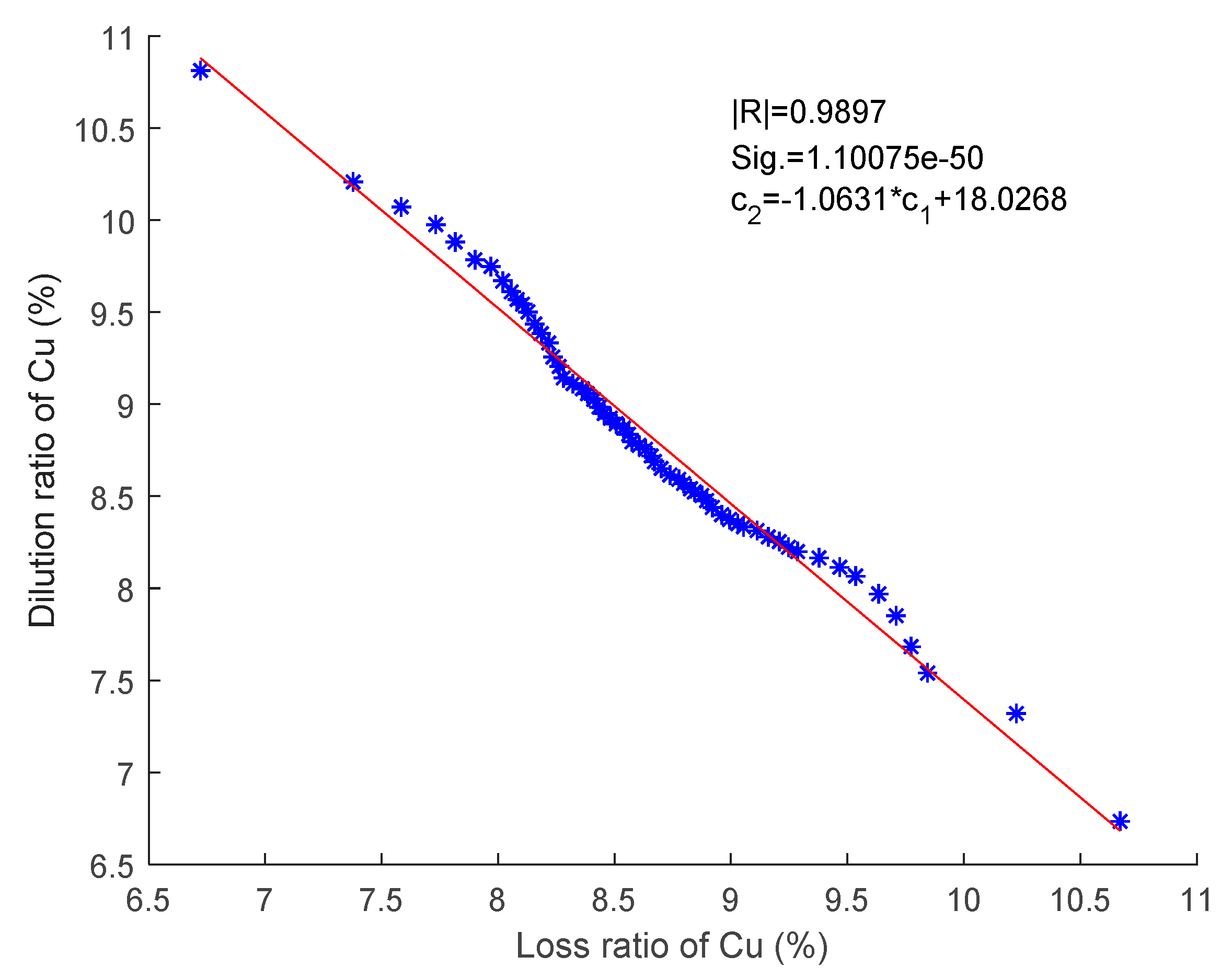
4.2.3. Relationship between Dilution Ratio and Loss Ratio
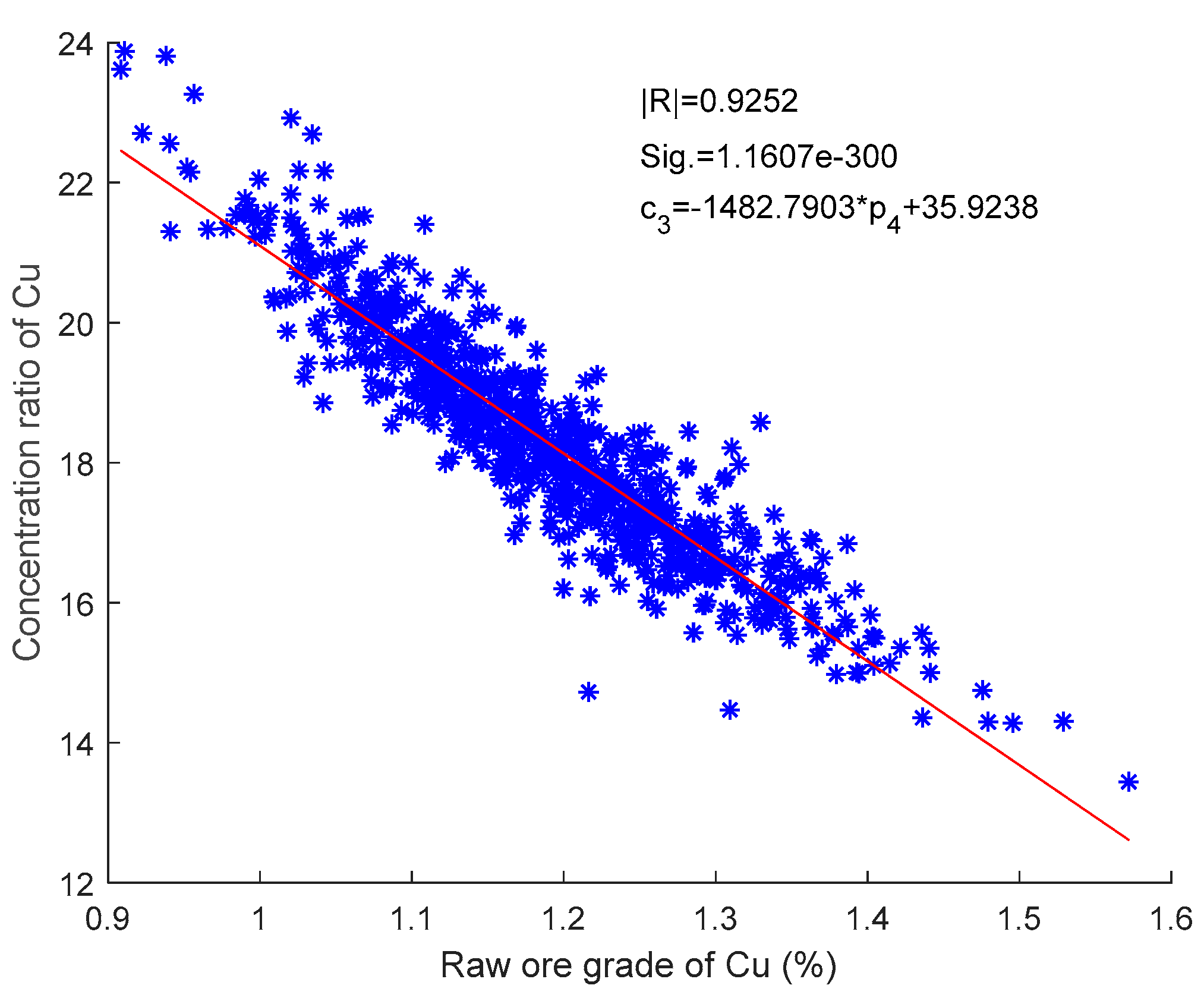
4.2.4. Relationship between Concentration Ratio and Raw Ore Grade
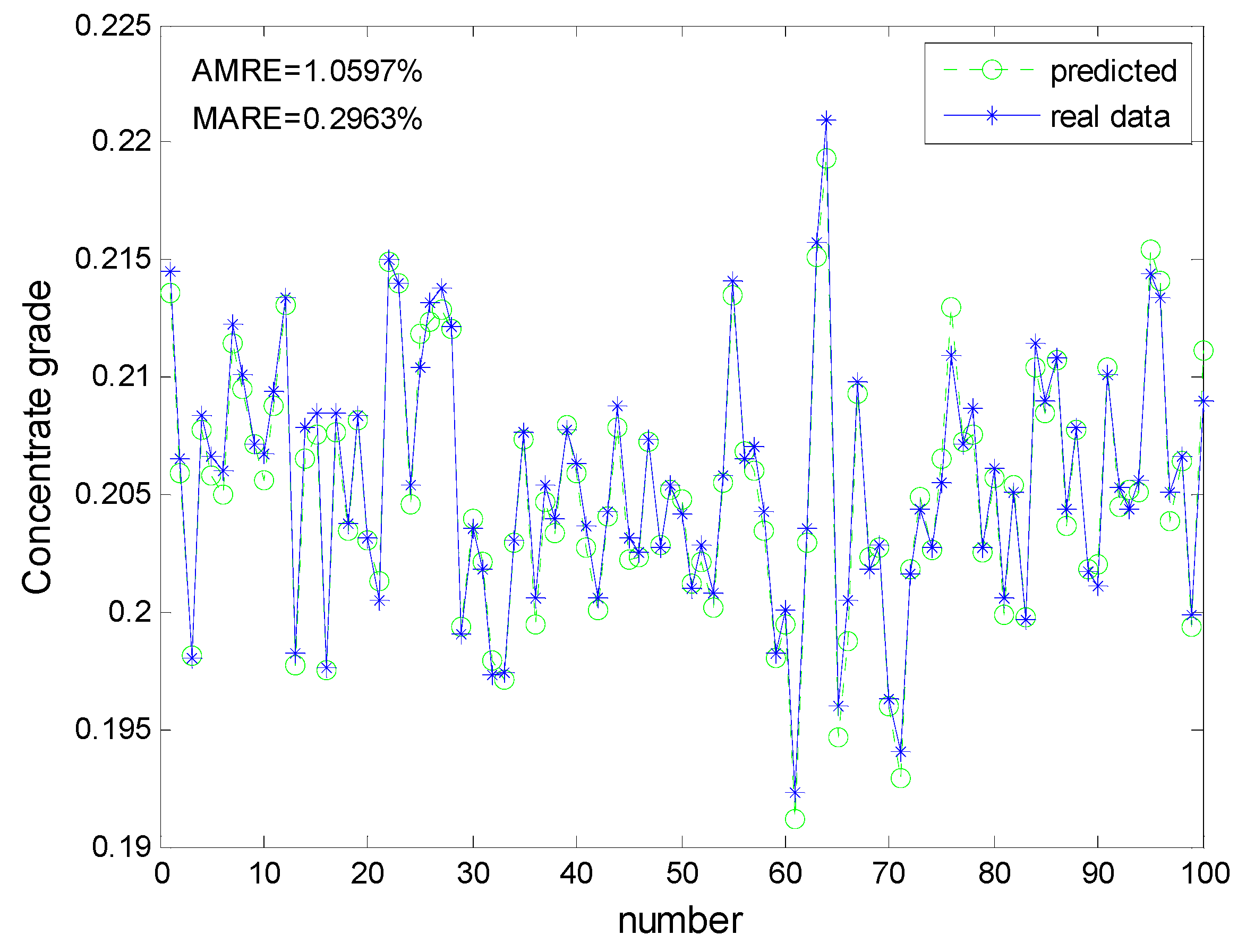
4.2.5. Concentrate Grade, Concentration Ratio and Raw Ore Grade
4.2.6. Copper Concentrate Transaction Price
4.3. Production Process of the Huogeqi Copper Mine Using the NSGA-II
4.3.1. Parameters of the Huogeqi Copper Mine and NSGA-II Model
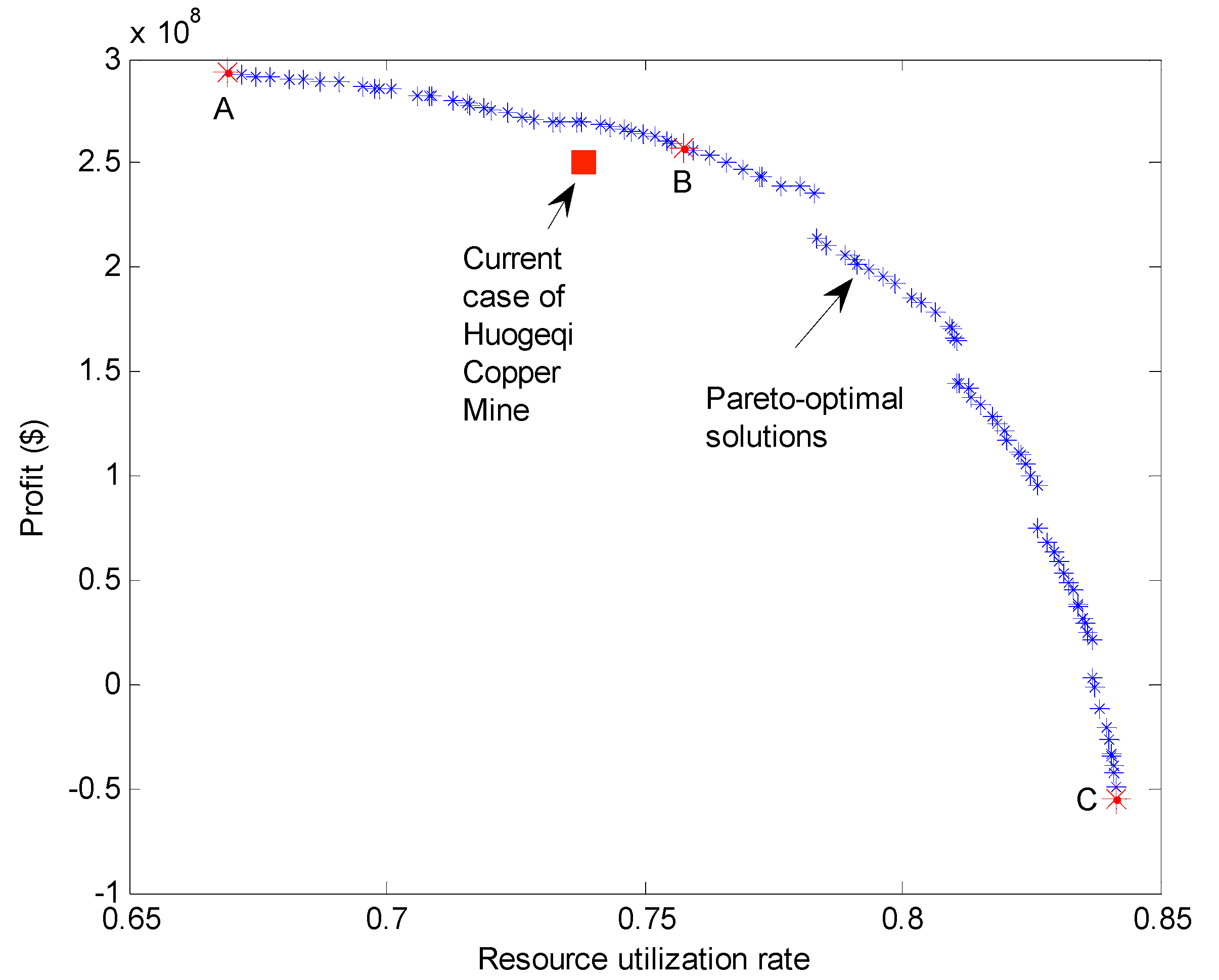
4.3.2. Optimization Results Using NSGA-II
5. Discussion
5.1. Comparison of Different Optimization Algorithms
5.2. Effect of Decision Variables on the Objective Function
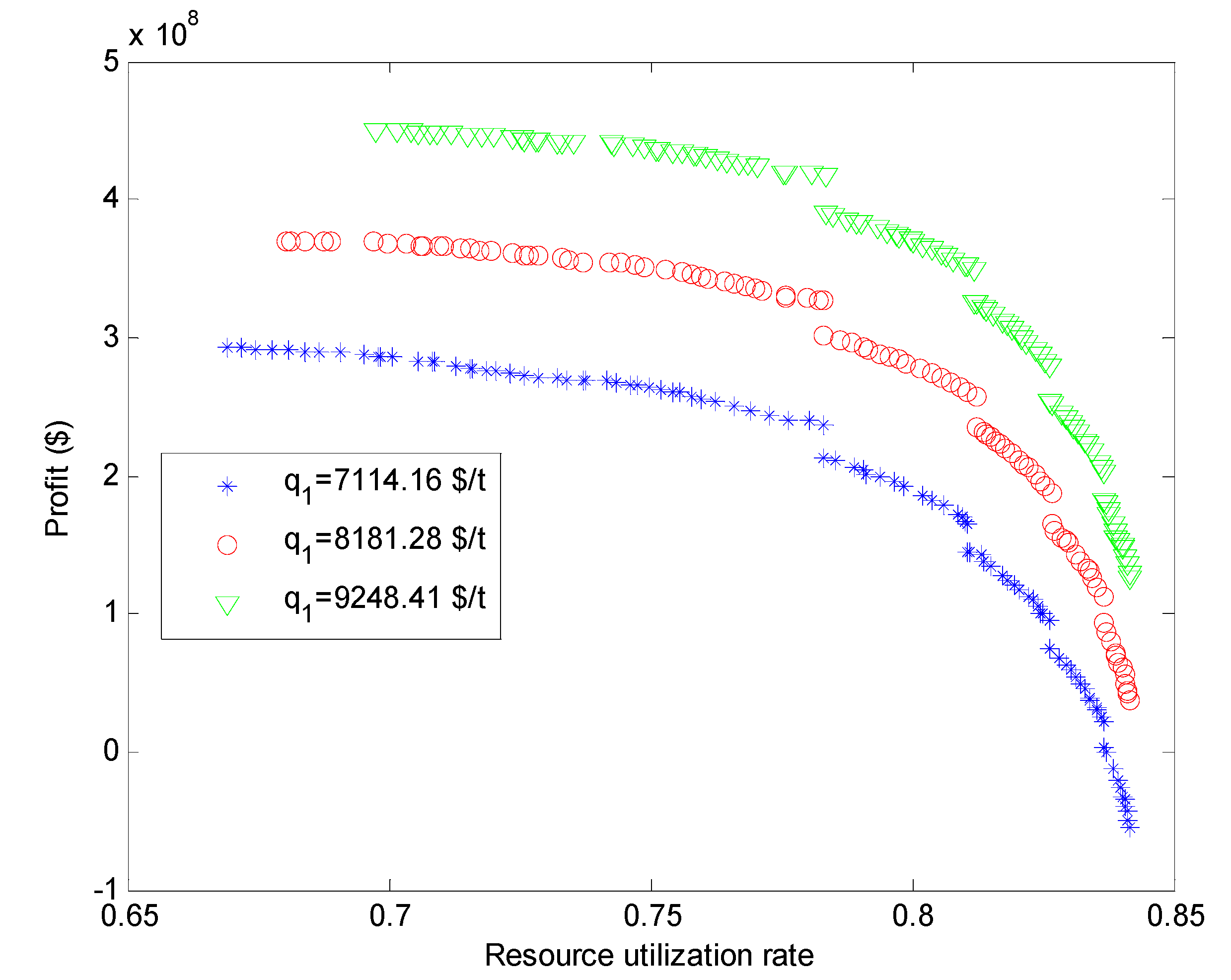
5.3. Sensitivity Analysis of Pareto-Optimal Solutions to Unit Copper Concentrate Price
6. Conclusions
- (1)
- The established NSGA-II method is an effective method to approach the multi-objective optimization of the production process of the Huogeqi Copper Mines. It outperforms the MOGA and SPEA2 with lower diversity in solution optimization of the whole production process of metal mines. The Pareto-optimal solutions produced by the NSGA-II method reflect the compromising relationship between the economic benefits and the resource efficiency. The optimization results suggest that the Huogeqi Copper Mine in its current state can be further optimized to obtain a better economic benefit and resource efficiency for sustainable development.
- (2)
- The contributions of decision variables on objective functions show that profit is mainly affected by the geological cut-off grade of Cu (with a contribution of 58.84%) and the minimum industrial grade of Cu (with a contribution of 39.45%), but barely affected by the loss ratio of Cu (with a contribution of 1.71%). With regard to the resource utilization rate, the geological cut-off grade of Cu is the most important decision variable (with a contribution of 54.19%).
- (3)
- The sensitivities of the Pareto-optimal solutions to the unit copper concentrate price show that the Pareto-optimal solutions shift upward towards higher profits with increasing unit copper concentrate prices. The variations of the Pareto-optimal solutions are more sensitive to the unit copper concentrate price at higher profits than those at lower profits.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lusty, P.A.J.; Gunn, A.G. Challenges to global mineral resource security and options for future supply. Geol. Soc. Lond. Spec. Publ. 2015, 393, 265–276. [Google Scholar] [CrossRef]
- Shishvan, M.; Benndorf, J. Operational Decision Support for Material Management in Continuous Mining Systems: From Simulation Concept to Practical Full-Scale Implementations. Minerals 2017, 7, 116. [Google Scholar] [CrossRef]
- Ding, J.; Chai, T.; Wang, H. Offline modeling for product quality prediction of mineral processing using modeling error PDF shaping and entropy minimization. IEEE Trans. Neural Netw. 2011, 22, 408–419. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Gao, S.; Liao, N.; Liu, H. A nonlinear goal-programming-based DE and ANN approach to grade optimization in iron mining. Neural Comput. Appl. 2016, 27, 2065–2081. [Google Scholar] [CrossRef]
- Ramazan, S. The new Fundamental Tree Algorithm for production scheduling of open pit mines. Eur. J. Oper. Res. 2007, 177, 1153–1166. [Google Scholar] [CrossRef]
- Xu, X.C.; Gu, X.W.; Wang, Q.; Gao, X.W.; Liu, J.P.; Wang, Z.K.; Wang, X.H. Production scheduling optimization considering ecological costs for open pit metal mines. J. Clean. Prod. 2018, 180, 210–221. [Google Scholar] [CrossRef]
- Yang, C.; Ding, J. Constrained dynamic multi-objective evolutionary optimization for operational indices of beneficiation process. J. Intell. Manuf. 2017. [Google Scholar] [CrossRef]
- Yu, G.; Chai, T.; Luo, X. Multiobjective Production Planning Optimization Using Hybrid Evolutionary Algorithms for Mineral Processing. IEEE Trans. Evolut. Comput. 2011, 15, 487–514. [Google Scholar] [CrossRef]
- Chai, T.; Ding, J.; Yu, G.; Wang, H. Integrated Optimization for the Automation Systems of Mineral Processing. IEEE Trans. Autom. Sci. Eng. 2014, 11, 965–982. [Google Scholar] [CrossRef]
- Yu, G.; Chai, T.; Luo, X. Two-Level Production Plan Decomposition Based on a Hybrid MOEA for Mineral Processing. IEEE Trans. Autom. Sci. Eng. 2013, 10, 1050–1071. [Google Scholar] [CrossRef]
- Wang, C.; Ding, J.; Cheng, R.; Liu, C.; Chai, T. Data-Driven Surrogate-Assisted Multi-Objective Optimization of Complex Beneficiation Operational Process. IFAC-PapersOnLine 2017, 50, 14982–14987. [Google Scholar] [CrossRef]
- Engell, S. Feedback control for optimal process operation. J. Process Control 2007, 17, 203–219. [Google Scholar] [CrossRef]
- Mercangöz, M.; Doyle, F.J., III. Real-time optimization of the pulp mill benchmark problem. Comput. Chem. Eng. 2008, 32, 789–804. [Google Scholar] [CrossRef]
- Bartusiak, R.D. NLMPC: A Platform for Optimal Control of Feed- or Product-Flexible Manufacturing. Lecture Notes Control Inf. Sci. 2007, 358, 367–381. [Google Scholar]
- Azimi, Y.; Osanloo, M. Determination of open pit mining cut-off grade strategy using combination of nonlinear programming and genetic algorithm. Arch. Min. Sci. 2011, 56, 189–212. [Google Scholar]
- Asad, M.W.A. Optimum cut-off grade policy for open pit mining operations through net present value algorithm considering metal price and cost escalation. Eng. Comput. 2007, 24, 723–736. [Google Scholar] [CrossRef]
- Zarshenas, Y.; Saeedi, G. Determination of optimum cutoff grade with considering dilution. Arab. J. Geosci. 2017, 10, 165. [Google Scholar] [CrossRef]
- Ahmadi, M.R. Cutoff grade optimization based on maximizing net present value using a computer model. J. Sustain. Min. 2018, 17, 68–75. [Google Scholar] [CrossRef]
- He, Y.; Zhu, K.; Gao, S.; Liu, T.; Li, Y. Theory and method of genetic-neural optimizing cut-off grade and grade of crude ore. Expert Syst. Appl. 2009, 36, 7617–7623. [Google Scholar] [CrossRef]
- Yu, S.; Zhu, K.; He, Y. A Hybrid Intelligent Optimization Method for Multiple Metal Grades Optimization; Springer: Berlin, Germany, 2012; pp. 1391–1402. [Google Scholar]
- He, Y.; Liao, N.; Bi, J. Intelligent integrated optimization of mining and ore-dressing grades in metal mines. Soft Comput. 2016, 22, 1–17. [Google Scholar] [CrossRef]
- Li, K.; Niu, J.; Yuan, H.; Liu, B. Optimization of the grade index of magnetite ore in Baiyunebo Iron Mine in China. J. Univ. Sci. Technol. Beijing 2007, 29, 334–337. [Google Scholar]
- He, Y. Multi-Objective Optimization of Grades Based on Soft Computing; Springer: Berlin/Heidelberg, Germany, 2010; pp. 144–151. [Google Scholar]
- Alkayem, N.F.; Parida, B.; Pal, S. Optimization of friction stir welding process using NSGA-II and DEMO. Neural Comput. Appl. 2017. [Google Scholar] [CrossRef]
- Alkayem, N.F.; Parida, B.; Pal, S. Optimization of friction stir welding process parameters using soft computing techniques. Soft Comput. 2016. [Google Scholar] [CrossRef]
- Liu, Z.; Shao, J.; Xu, W.; Wu, Q. Indirect estimation of unconfined compressive strength of carbonate rocks using extreme learning machine. Acta Geotech. 2015, 10, 651–663. [Google Scholar] [CrossRef]
- Liu, Z.B.; Shao, J.F.; Xu, W.Y.; Xu, F. Comprehensive Stability Evaluation of Rock Slope Using the Cloud Model-Based Approach. Rock Mech. Rock Eng. 2014, 47, 2239–2252. [Google Scholar] [CrossRef]
- Liu, Z.; Shao, J.; Xu, W.; Zhang, Y.; Chen, H. Prediction of elastic compressibility of rock material with soft computing techniques. Appl. Soft Comput. 2014, 22, 118–125. [Google Scholar] [CrossRef]
- Liu, Z.; Shao, J.; Xu, W.; Chen, H.; Zhang, Y. An extreme learning machine approach for slope stability evaluation and prediction. Nat. Hazards 2014, 73, 787–804. [Google Scholar] [CrossRef]
- Liu, Z.; Shao, J.; Xu, W.; Chen, H.; Shi, C. Comparison on landslide nonlinear displacement analysis and prediction with computational intelligence approaches. Landslides 2014, 11, 889–896. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Coello, C.A.C.; Pulido, G.T.; Lechuga, M.S. Handling multiple objectives with particle swarm optimization. IEEE Trans. Evol. Comput. 2004, 8, 256–279. [Google Scholar] [CrossRef]
- Xue, F.; Sanderson, A.C.; Graves, R.J. Pareto-based multi-objective differential evolution. In Proceedings of the 2003 Congress on Evolutionary Computation, Canberra, ACT, Australia, 8–12 December 2003; Volume 862, pp. 862–869. [Google Scholar]
- Sharifi, M.; Guilani, P.P.; Shahriari, M. Using NSGA II Algorithm for a Three-Objective Redundancy Allocation Problem with k-out-of-n Sub-Systems. J. Electrochem. Soc. 2015, 144, L23–L26. [Google Scholar]
- Aghbashlo, M.; Hosseinpour, S.; Tabatabaei, M.; Younesi, H.; Najafpour, G. On the exergetic optimization of continuous photobiological hydrogen production using hybrid ANFIS-NSGA-II. Energy 2016, 96, 507–520. [Google Scholar] [CrossRef]
- Huang, J.; Jin, L.; Zhang, C.; Huang, J.; Jin, L.; Zhang, C. Mathematical Modeling and a Hybrid NSGA-II Algorithm for Process Planning Problem Considering Machining Cost and Carbon Emission. Sustainability 2017, 9, 1769. [Google Scholar] [CrossRef]
- Shao, A. Innovation and practice of the“five grades ganged” engineering management mode. Eng. Sci. 2013, 15, 44–48. [Google Scholar]
- Wang, Q.; Ren, F. Mining Science; Metallurgical Industry Press: Beijing, China, 2011. [Google Scholar]
- Gu, X.-W.; Wang, Q.; Chu, D.-Z.; Zhang, B. Dynamic optimization of cutoff grade in underground metal mining. J. Cent. South Univ. Technol. 2010, 17, 492–497. [Google Scholar] [CrossRef]
- Liu, B.S.; Wang, X.Q. Integrated and dynamic optimization method on technological indexes for united enterprises of mining-dressing-smelting. China Min. Mag. 2013, 22, 104–107. [Google Scholar]
- Al-Momani, E.S.; Mayyas, A.T.; Alqudah, R. Modeling Blanking Process Using Multiple Regression Analysis and Artificial Neural Networks. J. Mater. Eng. Perform. 2012, 21, 1611–1619. [Google Scholar] [CrossRef]
- Srinivas, N.; Deb, K. Muiltiobjective optimization using nondominated sorting in genetic algorithms. Evol. Comput. 1994, 2, 221–248. [Google Scholar] [CrossRef]
- Liu, T.; Gao, X.; Wang, L. Multi-objective optimization method using an improved NSGA-II algorithm for oil–gas production process. J. Taiwan Inst. Chem. Eng. 2015, 57, 42–53. [Google Scholar] [CrossRef]
- Mandal, D.; Pal, S.K.; Saha, P. Modeling of electrical discharge machining process using back propagation neural network and multi-objective optimization using non-dominating sorting genetic algorithm-II. J. Mater. Process. Technol. 2007, 186, 154–162. [Google Scholar] [CrossRef]
- Yang, Y.; Cao, L.; Zhou, Q.; Wang, C.; Wu, Q.; Jiang, P. Multi-objective process parameters optimization of Laser-magnetic hybrid welding combining Kriging and NSGA-II. Robot. Comput.-Integr. Manuf. 2018, 49, 253–262. [Google Scholar] [CrossRef]
- Peng, F.; Dai, J.; Zhang, S. Characteristics and occurrence regularity of copper orebody in Huogeqi Copper Mine. Nonferrous Met. 2011, 2, 28–30. [Google Scholar]
- Wang, X.; Zhu, T. Application of backfilling method in Huogeqi Copper Mine. Nonferrous Met. 2012, 1, 4. [Google Scholar]
- Botev, Z.I.; Grotowski, J.F.; Kroese, D.P. Kernel density estimation via diffusion. Ann. Stat. 2010, 38, 2916–2957. [Google Scholar] [CrossRef]
- Murata, T.; Ishibuchi, H. MOGA: Multi-objective genetic algorithms. In Proceedings of the IEEE International Conference on Evolutionary Computation, Perth, WA, Australia, 29 November–1 December 1995; pp. 289–294. [Google Scholar]
- Adham, A.M.; Mohd-Ghazali, N.; Ahmad, R. Performance optimization of a microchannel heat sink using the Improved Strength Pareto Evolutionary Algorithm (SPEA2). J. Eng. Thermophys. 2015, 24, 86–100. [Google Scholar] [CrossRef]
- Tian, Y.; Cheng, R.; Zhang, X.; Jin, Y. PlatEMO: A MATLAB Platform for Evolutionary Multi-Objective Optimization [Educational Forum]. IEEE Comput. Intell. Mag. 2017, 12, 73–87. [Google Scholar] [CrossRef]
- Chaki, S.; Bathe, R.N.; Ghosal, S.; Padmanabham, G. Multi-objective optimisation of pulsed Nd:YAG laser cutting process using integrated ANN–NSGAII model. J. Intell. Manuf. 2015, 29, 175–190. [Google Scholar] [CrossRef]
- Chandra, S. Design and Analysis of Experiments. Springer Texts Stat. 2017, 404, 235–259. [Google Scholar]
- Leonzio, G. Methanol Synthesis: Optimal Solution for a Better Efficiency of the Process. Processes 2018, 6, 20. [Google Scholar] [CrossRef]





| Hidden Nodes | Concentrate Grade of Cu | |||
|---|---|---|---|---|
| Train MARE (%) | Test MARE (%) | Train AMRE (%) | Test AMRE (%) | |
| 1 | 0.8417 | 0.7491 | 7.3575 | 4.7698 |
| 2 | 0.3057 | 0.2979 | 1.4701 | 1.0916 |
| 3 | 0.3049 | 0.2963 | 1.4543 | 1.0597 |
| 4 | 0.3124 | 0.3019 | 1.6102 | 1.0677 |
| 5 | 0.3215 | 0.3025 | 1.8151 | 1.4596 |
| Grade of Cu (%) | Compensation Price ($·t−1) | Price Coefficient |
|---|---|---|
| ≥23 | 47.4 | 0.86 |
| 22.00~22.99 | 31.6 | 0.85 |
| 21.00~21.99 | 15.8 | 0.84 |
| 20.00~20.99 | 0 | 0.83 |
| 19.00~19.99 | −15.8 | 0.81 |
| 18.00~18.99 | −31.6 | 0.795 |
| 17.00~17.99 | −47.4 | 0.78 |
| 16.00~16.99 | −63.2 | 0.77 |
| Parameter of Huogeqi Copper Mine | Value | NSGA-II Parameter | Value |
|---|---|---|---|
| Initial value of the geological cut-off grade of Cu (%) | 0.30 | Number of decision variables | 3 |
| Initial value of the minimum industrial grade of Cu (%) | 0.50 | Number of objective functions | 2 |
| Recoverable reserve of the 1450–1570 stage of Cu (t) corresponding to and | 9 × 106 | Population size | 100 |
| Constant | 0.66 | Maximum number of iterations | 100 |
| Unit mining cost ($/t) | 15.8 | Crossover index (SBX) | 20 |
| Unit beneficiation cost ($/t) | 18.96 | Mutation index (polynomial mutation) | 20 |
| Unit #1 copper price ($/t) | 7114.16 | Crossover probabilities | 0.5 |
| Lower bound of geological cut-off grade of Cu (%) | 0.10 | Mutation probabilities | 1/3 |
| Upper bound of geological cut-off grade of Cu (%) | 0.90 | ||
| Lower bound of minimum industrial grade of Cu (%) | 0.10 | ||
| Upper bound of minimum industrial grade of Cu (%) | 0.90 | ||
| Lower bound of loss ratio of Cu (%) | 6 | ||
| Upper bound of loss ratio of Cu (%) | 12 | ||
| Lower bound of melted grade of Cu (%) | 16 |
| Parameters | Case A | Case B | Case C | Current Case |
|---|---|---|---|---|
| Profits ($) | 2.9317 × 108 | 2.5776 × 108 | −5.49 × 107 | 2.503 × 108 |
| Resource utilization rate | 0.6689 | 0.7578 | 0.8416 | 0.7383 |
| Geological cut-off grade of Cu (%) | 0.582 | 0.366 | 0.117 | 0.3 |
| Minimum industrial grade of Cu (%) | 0.647 | 0.410 | 0.135 | 0.5 |
| Loss ratio of Cu (%) | 6.018 | 6.006 | 6 | 8 |
| Factors | Degrees of Freedom | Sum of Squares | Mean Squares | F | P | Contribution (%) |
|---|---|---|---|---|---|---|
| Profit | ||||||
| Geological cut-off grade of Cu | 7 | 8.04912 × 1016 | 1.14987 × 1016 | 76.38 | 0 | 58.84 |
| Minimum industrial grade of Cu | 7 | 5.39543 × 1016 | 7.70776 × 1015 | 51.2 | 0 | 39.45 |
| Loss ratio of Cu | 10 | 3.33574 × 1015 | 3.33574 × 1014 | 2.22 | 0.0256 | 1.71 |
| Error | 75 | 1.12915 × 1016 | 1.50554 × 1014 | |||
| Total | 99 | 2.55872 × 1017 | ||||
| Resource utilization rate | ||||||
| Geological cut-off grade of Cu | 7 | 1.32481 × 109 | 189,258,746.7 | 2543.23 | 0 | 54.19 |
| Minimum industrial grade of Cu | 7 | 6.64489 × 108 | 94,926,983.4 | 1275.61 | 0 | 27.18 |
| Loss ratio of Cu | 10 | 6.50715 × 108 | 65,071,498.6 | 874.42 | 0 | 18.63 |
| Error | 75 | 5.58125 × 106 | 74,416.7 | |||
| Total | 99 | 5.35262 × 109 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Gu, X.; Liu, Z.; Wang, Q.; Xu, X.; Zheng, M. Production Process Optimization of Metal Mines Considering Economic Benefit and Resource Efficiency Using an NSGA-II Model. Processes 2018, 6, 228. https://doi.org/10.3390/pr6110228
Wang X, Gu X, Liu Z, Wang Q, Xu X, Zheng M. Production Process Optimization of Metal Mines Considering Economic Benefit and Resource Efficiency Using an NSGA-II Model. Processes. 2018; 6(11):228. https://doi.org/10.3390/pr6110228
Chicago/Turabian StyleWang, Xunhong, Xiaowei Gu, Zaobao Liu, Qing Wang, Xiaochuan Xu, and Minggui Zheng. 2018. "Production Process Optimization of Metal Mines Considering Economic Benefit and Resource Efficiency Using an NSGA-II Model" Processes 6, no. 11: 228. https://doi.org/10.3390/pr6110228
APA StyleWang, X., Gu, X., Liu, Z., Wang, Q., Xu, X., & Zheng, M. (2018). Production Process Optimization of Metal Mines Considering Economic Benefit and Resource Efficiency Using an NSGA-II Model. Processes, 6(11), 228. https://doi.org/10.3390/pr6110228





