This work investigates integration of scheduling and control with noncyclic scheduling and NMPC. The algorithm is allowed to select the number of products to manufacture during a prediction horizon, which products to manufacture, the production sequence, production durations, and optimal control moves. The mathematical formulation is presented in this section.
3.1. Decomposition
An objective of this work is feasibility for closed-loop online implementation. To accomplish this objective, the problem is decomposed into an MILP programming problem and multiple separable NLP dynamic optimization, or optimal control, problems without the need for alternating iterations. This formulation builds on previous work that demonstrates the separability of the integrated scheduling and control problem into subproblems without the need for iterations [
20] and builds on previous work which demonstrates the separation into MILP and dynamic optimization problems [
10,
46,
47]. This formulation also builds on previous work that demonstrates benefits from shifting separable computational burden into offline portions of the integrated problem [
11,
19,
22,
55].
The main decomposition employed in this work is a decomposition into an MILP problem that determines the production sequence and production amounts for each manufactured product, and a group of separable dynamic optimization NLP problems for optimal control during grade transitions. The formulation for the MILP problem is as follows:
where
is the makespan,
n is the number of products,
m is the number of slots (constrained to equal the number of products such that
),
is the binary variable that governs the assignment of product
i to a particular slot
s,
is the start time of the slot
s,
is the end time of slot
s,
is the per unit price of product
i,
is an optional weight on grade transition minimization,
is the transition time within slot
s,
is the per unit cost of storage for product
i, and
represents the amount of product
i manufactured,
Products are assigned to each slot using a set of binary variables,
that assign a product
i to be produced in a given slot
s. Constraints of the following form are added:
which limit the assignment of production within each slot, ensuring that one and only one product is assigned to each slot, and
which constrains the production of products. This constraint, unlike traditional continuous-time scheduling formulations, does not require each product to be produced once and only once during the schedule, but allows the optimization to select the number of products to produce during the horizon for scheduling provided each slot has a production assignment (Equation (
3)). Not every available product must be produced during each schedule.
The values of the vector
are determined by the optimization variables
.
represents the transition time between the product made in slot
s− 1 and product made in slot
s. Thus, the value of
is determined by the optimal values of
and
which determine which products are assigned to slots
and
s. For
and
,
would be equal to the calculated grade transition time from product
j to product
k. The possible values for
are the grade transition times calculated via NLP optimal grade transition problems (Equation (
9)). The time points must satisfy the precedence relations:
which require that a time slot be longer than the corresponding transition time, impose the coincidence of the end time of one time slot with the start time of the subsequent time slot, and define the relationship between the end time of the last time slot (
) and the total makespan or horizon duration (
).
The makespan is fixed to an arbitrary horizon for scheduling. Demand constraints restrict production from exceeding the maximum demand (
) for a given product, as follows:
The continuous-time scheduling optimization (or MILP problem) requires transition times between steady-state products () as well as transition times from the current state to each steady-state product if initial state is not at steady-state product conditions (). These grade transitions comprise the separable dynamic optimization problems or NLP portion of the overall problem decomposition.
Grade transition profiles are optimized using the following objective:
where
is the weight on the set point for meeting target product steady-state,
is the weight on restricting manipulated variable movement,
is the cost for the manipulated variables,
u is the vector of manipulated variables,
is the target product steady-state, and
is the start process state from which the transition time is being estimated. The transition time is taken as the time at which and after which
, where
is a tolerance for meeting product steady-state operating conditions. This formulation harnesses knowledge of nonlinear process dynamics in the system model to find an optimal trajectory and minimum time required to transition from an initial concentration to a desired concentration. The usage of NMPC for grade transitions in the integrated problem effectively captures the actual behavior of the controller used in the process, as the transition times are estimated by a simulation of actual controller implementation on a first-principles nonlinear model of the process.
Because product steady-state operating conditions can be known a priori, all grade transition times between production steady-state operating conditions can be calculated offline and stored in memory in a grade transition time table:
. The online portion of the NLP subproblem is comprised only of the calculation of
, the transition duration and corresponding optimal control profile from current measured state (
) and each steady-state operating condition, or, in other words, the vector of possible transitions for the first slot (
). For example, consider the case of three products as described in
Table 1. As product steady-state conditions are known a priori as shown in
Table 1, the transition times between product steady-states can be calculated through NLP problems (Equation (
9)) and stored in a grade transition time table prior to operation (
Table 2). However, before operation, process state measurements (
) cannot be known. For example, if in the three product case described in
Table 1 a process disturbance was measured at
mol/L during online operation, for an optimal rescheduling beginning from current state
to be calculated, transition durations from
to each operating steady-state would need to be estimated online by solving
n separable NLP optimal grade transition problems, where
n is the number of steady-state products considered. The results of these online optimal transition problems would be the vector
(
Table 3). These transitions would be the possible values for
for the first slot (
) in Equation (
1) for the MILP rescheduling problem.
With and grade transition information, the MILP problem is equipped to optimally select the production sequence and amounts for the prediction horizon based on product demands, prices, transition durations, raw material cost, storage cost, and other economic parameters. Even when a process disturbance is encountered and measured, the schedule can be optimally recalculated from the measured disturbance, , via the incorporation of transitions from to each production steady-state condition ().
3.2. Iterative Method
The cyclic continuous-time scheduling formulation is sub-optimal if the number of products on the wheel exceeds the optimal number of products to produce in a prediction horizon. The number of slots in the MILP problem is constrained to be equal to the number of products, causing the optimization to always create
n production slots and
n transitions even in cases in which <
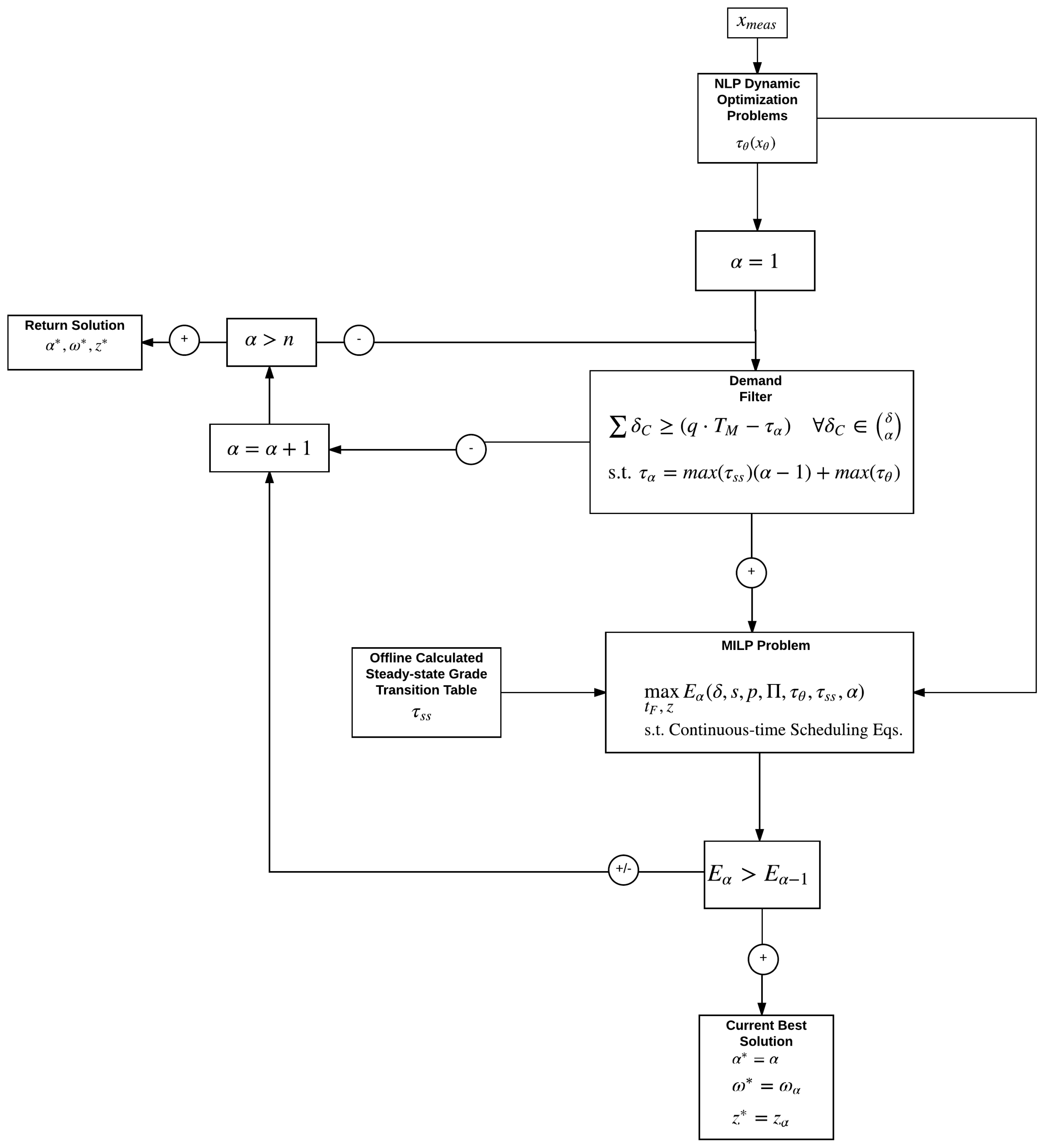
n slots would be most economical in the considered horizon for scheduling and control. To allow greater flexibility, an iterative method is introduced which leverages the computational lightness of the separated MILP subproblem. The number of slots in the continuous-time schedule is selected iteratively based on improvement to the objective function (profit), beginning from one slot, or only one product to produce during the horizon (
Figure 1). The iterations begin from one slot (
) due to the nature of grade transitions. Reducing the number of production slots reduces the number of necessary grade transitions, and reduces the corresponding amount of waste material produced. All grade transition NLP subproblems are calculated prior to slot iterations as grade transition information is independent of the number of production slots. This iterative method enables a noncyclic approach to combined scheduling and control and enables response to market fluctuations in product maximum demand and product price.
A heuristic demand filter is introduced to further reduce computational burden (
Figure 1). The filter checks for any combination of
products with summed demand sufficient to fill the prediction horizon for scheduling and control. This effectively filters each possible
for sufficient demand before the MILP problem is executed. In calculating the minimum summed demand which must be met for the given iteration for the MILP problem to be executed, the filter accounts for transition times calculated by NLP dynamic optimization problems both offline (all
stored in
) and online (all
stored in
). The demand must be sufficient to fill the production potential of the prediction horizon, which equates to (
), where
is the summed grade transition durations. To ensure each
which has potential for sufficient demand is tested in the MILP problem, the demand filter overestimates for transition times. In the case of underestimation of total transition times (
), the demand required to fill production during the prediction horizon (
) will be overestimated. In a such case, a combination
which would have had enough demand may inaccurately be deemed insufficient. Since often the optimal number of slots will be the smallest number of slots with sufficient demand (because the number of grade transitions and the corresponding amount of off-specification production increases with the number of slots), it is pertinent to not underestimate the durations of grade transitions. To eliminate such underestimation, the maximum transitions are used for estimations of the total transition time during the prediction horizon (
).