The design of controllers that optimize a cost function is an important objective in many control problems, in particular in scheduling problems that aim to allocate a limited number of resources within several users or servers according to the optimization of a given cost function. In the domains of flexible manufacturing, communication, computer science, transportation, and traffic, the makespan is commonly used as an effective cost function because it leads directly to minimal cycle times. However, due to multi-layer resource sharing and routing flexibility of the jobs, scheduling problems are often NP-hard problems. Many recent works in operations research, automatic control, and computer science communities have studied such problems. In operations research community, flow-shop, and job-shop problem have been investigated from a long time [
1,
2] and a lot of contributions have been proposed, based either on heuristic methods (like Nawaz, Enscore and Ham or Campbell, Dudek, and Smith heuristics) or artificial intelligence and evolutionary theory [
3,
4,
5]. In the automatic control community, automata, Petri nets (PNs), and max-plus algebra have been used to solve scheduling problems for discrete event systems (DESs) [
6,
7]. In particular, with PNs, the pioneer contributions for scheduling problems are based on the Dijkstra and A* algorithms [
8,
9]. Such algorithms explore the reachability graph of the net, in order to generate schedules. Numerous improvements have been proposed: pruning of non-promising branches [
10,
11], backtracking limitation [
12], determination of lower bounds for the makespan [
13], best first search with backtracking, and heuristic [
14] or dynamic programming [
15]. By combining scheduling and supervisory control in the same approach, one can also avoid deadlocks. Some approaches have been proposed: search in the partial reachability graph [
16], genetic algorithms [
17], and heuristic functions based on the firing vector [
13,
18]. The performance of operations research approaches are good, in general, compared to the automatic control approaches as long as static scheduling problems are considered. The advantage to solving scheduling problems with PNs or other tools issued from the control theory is to use a common formalism to describe a large class of problems and to facilitate the representation from one problem to another. In particular, PNs are suitable to represent many systems in various domains as flexible manufacturing, communication, computer science, transportation, and traffic [
6,
7]. This makes such approaches more suitable for dynamic and robust scheduling in uncertain environments. However, modularity and genericity usually suffer from a large computational effort that disqualifies the approaches for numerous large systems.
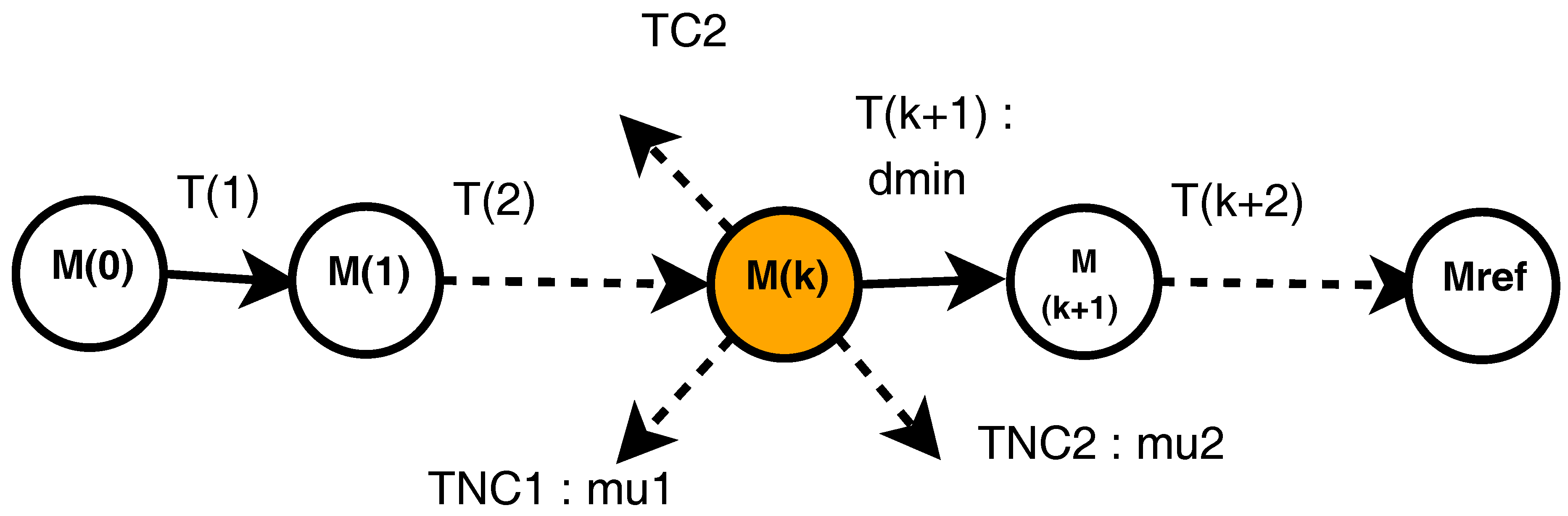
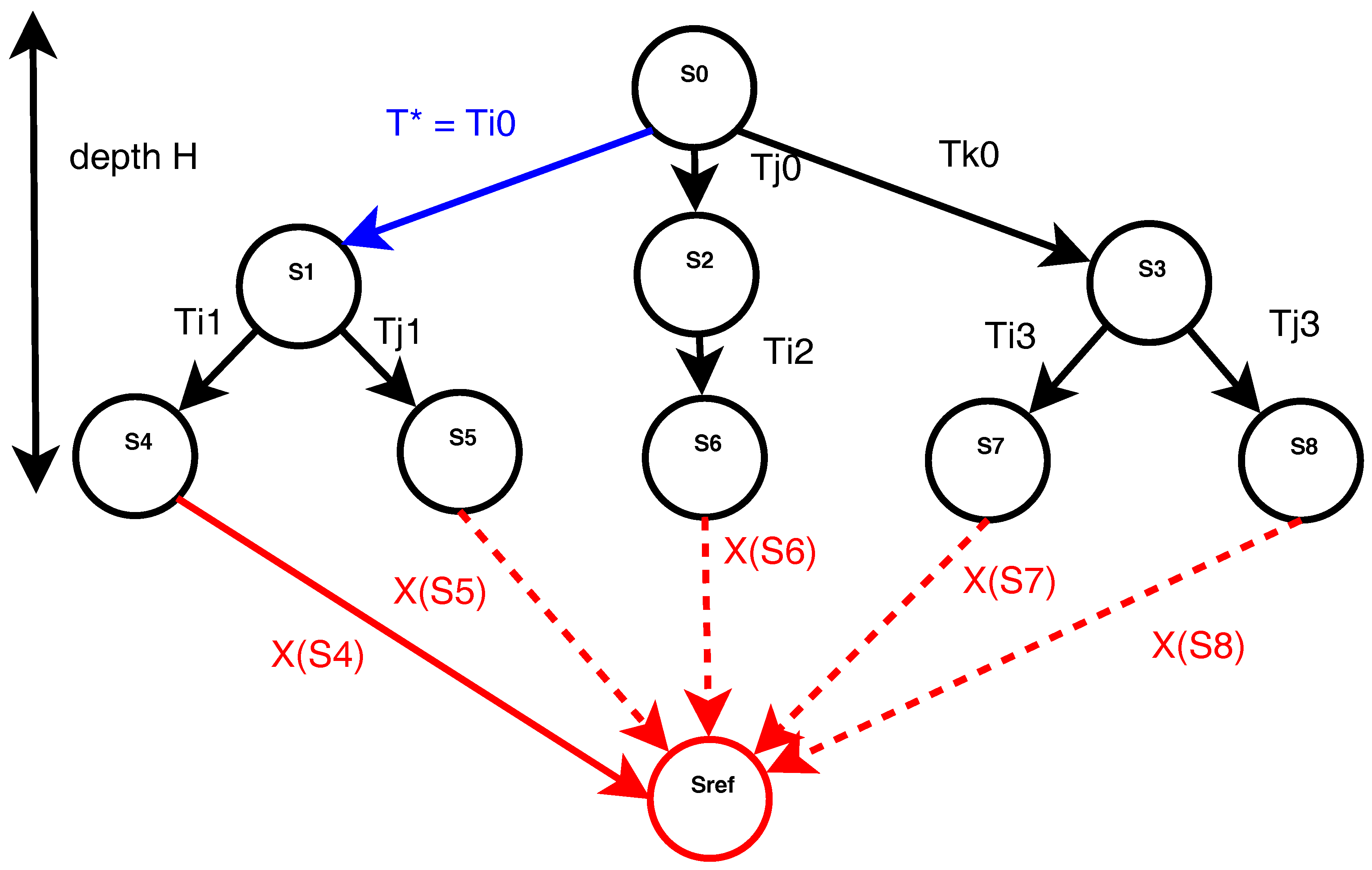
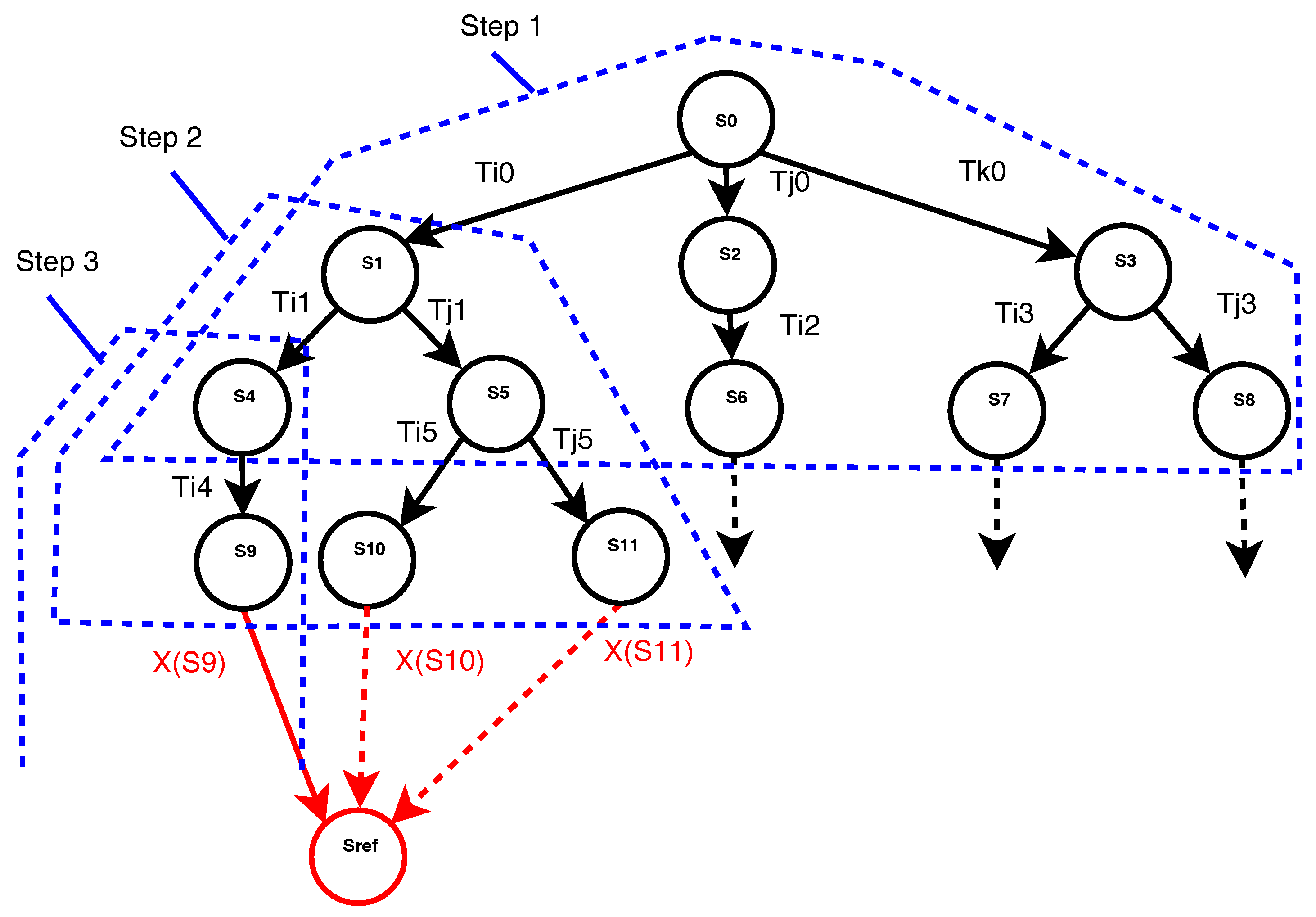
This work aims to propose a modular and generic approach of weak complexity. It details a method for timed PNs that incrementally computes control sequences in uncertain environments. Uncertainties are assumed to result from system failures or other unexpected events, and robustness with respect to such uncertainties is obtained thanks to a model predictive control (MPC) approach. The computed control sequences aim to reach a reference state from an initial one. The forbidden states, as deadlocks and dead-branches are avoided. The trajectory duration approaches its minimal value. Thanks to its robustness, the proposed approach generates dynamical and reconfigurable schedules. Consequently, it can be used in a real-time context. Resource allocation and operation scheduling for manufacturing systems are considered as the main applications. The robustness of the resulting trajectory is evaluated as a risk belief or probability. For that purpose structural and behavioral models of the uncertainties are considered. Finally, robust trajectories are computed. Compared to our previous works [
19,
20,
21,
22], the main contributions are: including, explicitly, uncertainties by means of uncontrollable stochastic transitions in the PNs model; evaluating the risk of the computed control sequences; proposing a sufficient condition for the existence of robust trajectories.
The paper is organized as follows. In
Section 2, the preliminary notions and the proposed method are developed: timed PNs with uncontrollable transitions are presented, non-robust and robust control sequences are introduced, and the approach to compute non-robust and robust control sequences with minimal duration is developed.
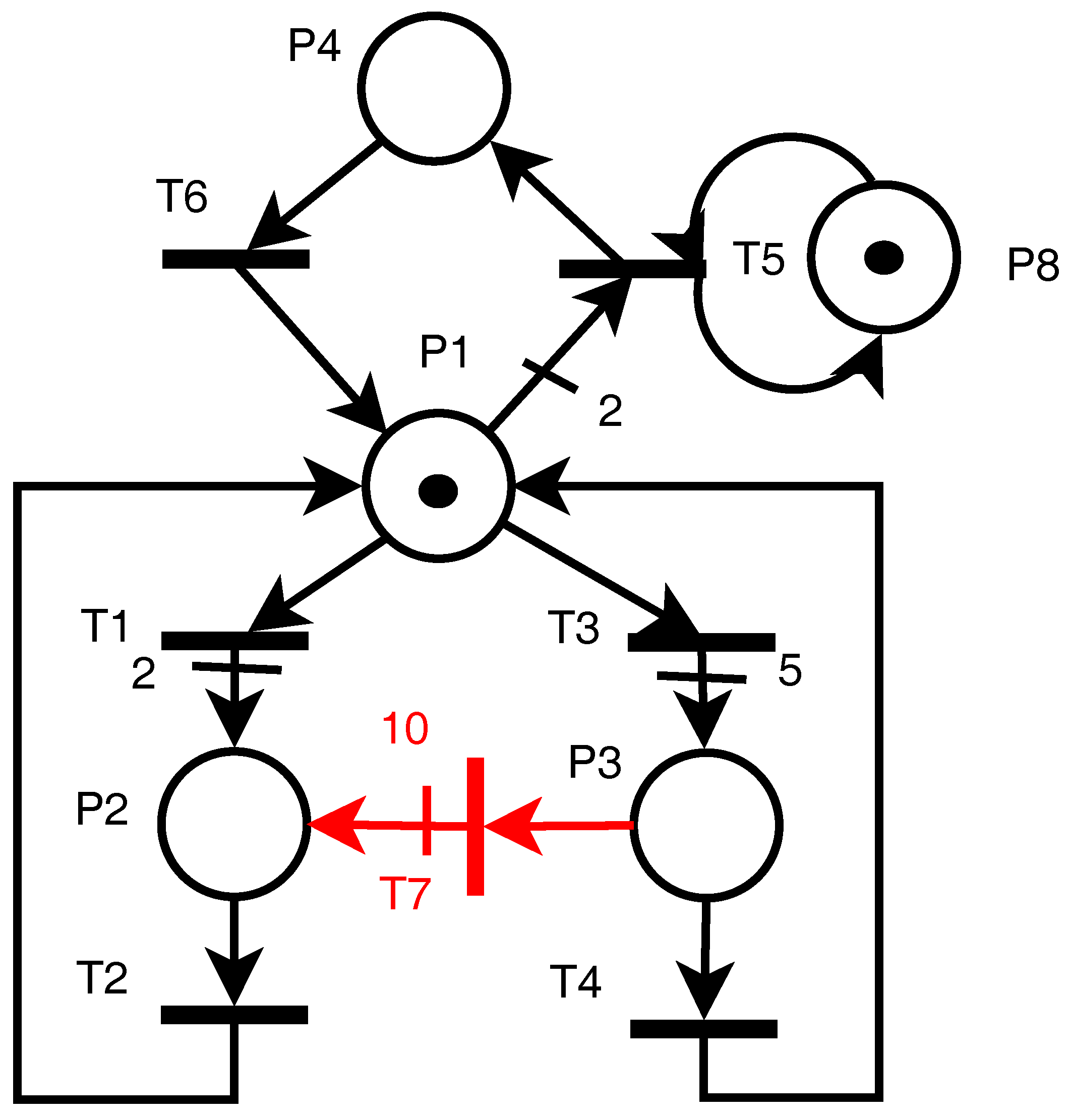
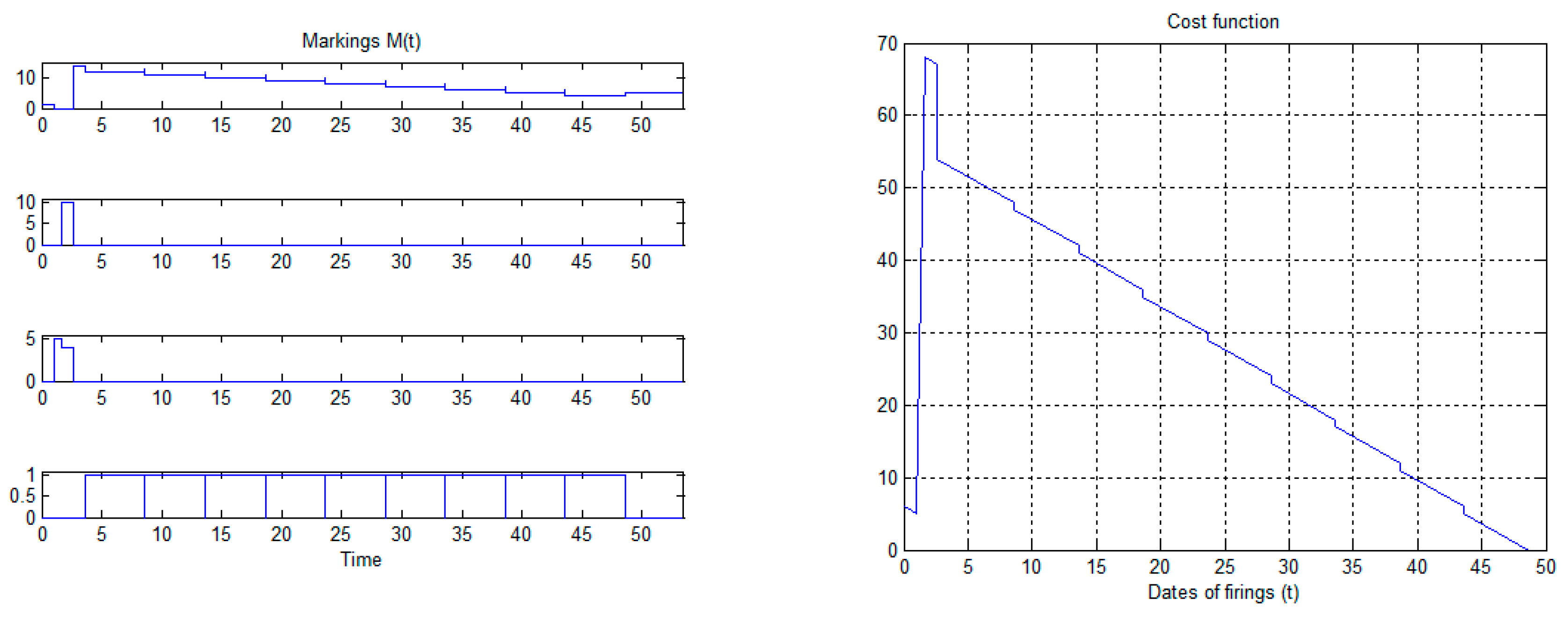
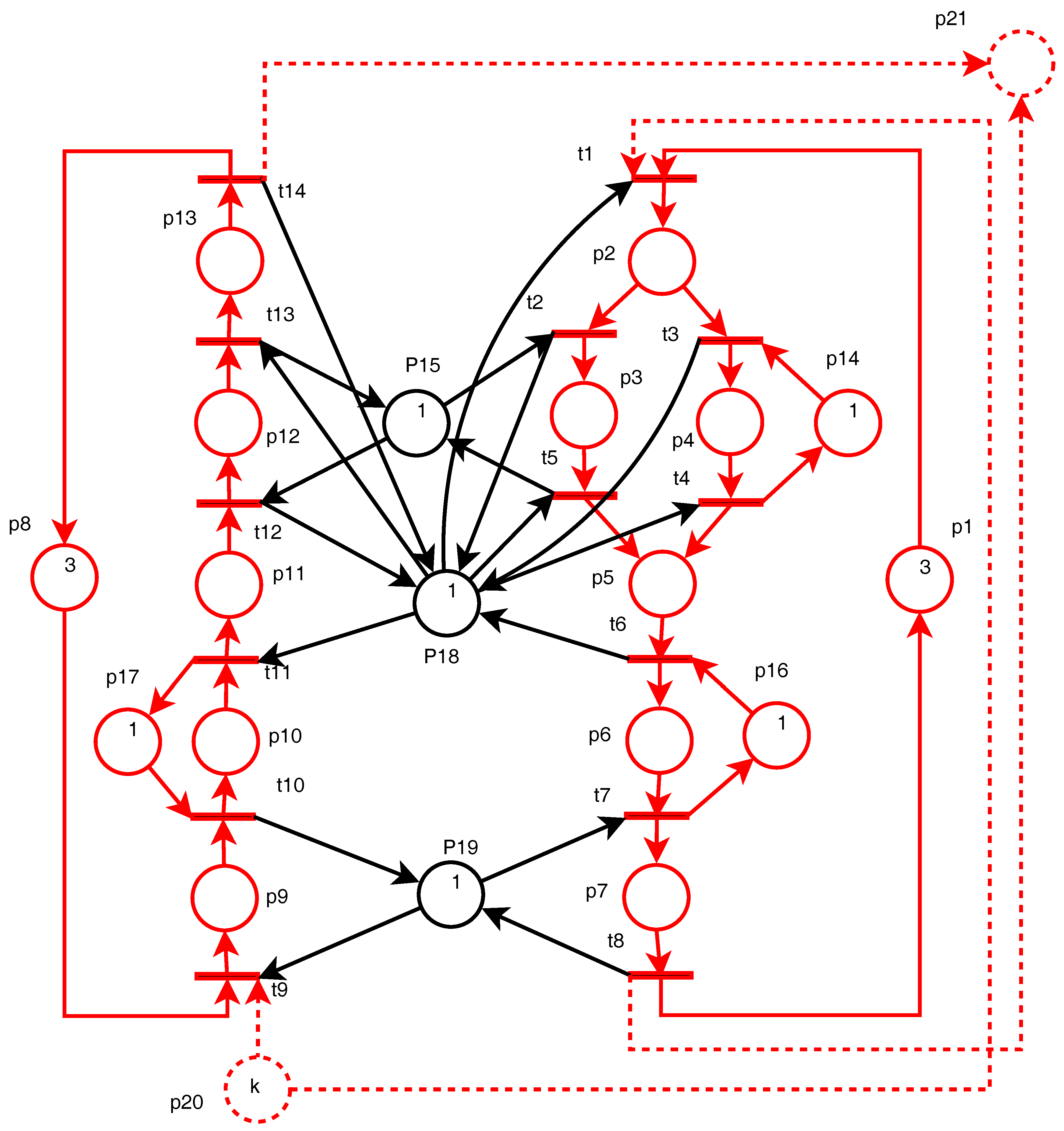
Section 3 illustrates the method on a simple example and then presents the performance for a case study.
Section 4 is a discussion about the method and the results.
Section 5 sums up the conclusions and perspectives.