Modifier Adaptation for Real-Time Optimization—Methods and Applications

Abstract

This paper presents an overview of the recent developments of modifier-adaptation schemes for real-time optimization of uncertain processes. These schemes have the ability to reach plant optimality upon convergence despite the presence of structural plant-model mismatch. Modifier Adaptation has its origins in the technique of Integrated System Optimization and Parameter Estimation, but differs in the definition of the modifiers and in the fact that no parameter estimation is required. This paper reviews the fundamentals of Modifier Adaptation and provides an overview of several variants and extensions. Furthermore, the paper discusses different methods for estimating the required gradients (or modifiers) from noisy measurements. We also give an overview of the application studies available in the literature. Finally, the paper briefly discusses open issues so as to promote future research in this area.

1. Introduction

This article presents a comprehensive overview of the modifier-adaptation strategy for real-time optimization. Real-time optimization (RTO) encompasses a family of optimization methods that incorporate process measurements in the optimization framework to drive a real process (or plant) to optimal performance, while guaranteeing constraint satisfaction. The typical sequence of steps for process optimization includes (i) process modeling; (ii) numerical optimization using the process model; and (iii) application of the model-based optimal inputs to the plant. In practice, this last step is quite hazardous—in the absence of additional safeguards—as the model-based inputs are indeed optimal for the model, but not for the plant unless the model is a perfect representation of the plant. This often results in suboptimal plant operation and in constraint violation, for instance when optimal operation implies operating close to a constraint and the model under- or overestimates the value of that particular constraint.

RTO has emerged over the past forty years to overcome the difficulties associated with plant-model mismatch. Uncertainty can have three main sources, namely, (i) parametric uncertainty when the values of the model parameters do not correspond to the reality of the process at hand; (ii) structural plant-model mismatch when the structure of the model is not perfect, for example in the case of unknown phenomena or neglected dynamics; and (iii) process disturbances. Of course these three sources are not mutually exclusive.

RTO incorporates process measurements in the optimization framework to combat the detrimental effect of uncertainty. RTO methods can be classified depending on how the available measurements are used. There are basically three possibilities, namely, at the level of the process model, at the level of the cost and constraint functions, and at the level of the inputs [1].

• The most intuitive strategy is to use process measurements to improve the model. This is the main idea behind the “two-step” approach [2,3,4,5]. Here, deviations between predicted and measured outputs are used to update the model parameters, and new inputs are computed on the basis of the updated model. The whole procedure is repeated until convergence is reached, whereby it is hoped that the computed model-based optimal inputs will be optimal for the plant. The requirements for this to happen are referred to as the model-adequacy conditions [6]. Unfortunately, the model-adequacy conditions are difficult to both achieve and verify.
• This difficulty of converging to the plant optimum motivated the development of a modified two-step approach, referred to as Integrated System Optimization and Parameter Estimation (ISOPE) [7,8,9,10]. ISOPE requires both output measurements and estimates of the gradients of the plant outputs with respect to the inputs. These gradients allow computing the plant cost gradient that is used to modify the cost function of the optimization problem. The use of gradients is justified by the nature of the necessary conditions of optimality (NCO) that include both constraints and sensitivity conditions [11]. By incorporating estimates of the plant gradients in the model, the goal is to enforce NCO matching between the model and the plant, thereby making the modified model a likely candidate to solve the plant optimization problem. With ISOPE, process measurements are incorporated at two levels, namely, the model parameters are updated on the basis of output measurements, and the cost function is modified by the addition of an input-affine term that is based on estimated plant gradients.
  Note that RTO can rely on a fixed process model if measurement-based adaptation of the cost and constraint functions is implemented. For instance, this is the philosophy of Constraint Adaptation (CA), wherein the measured plant constraints are used to shift the predicted constraints in the model-based optimization problem, without any modification of the model parameters [12,13]. This is also the main idea in Modifier Adaptation (MA) that uses measurements of the plant constraints and estimates of plant gradients to modify the cost and constraint functions in the model-based optimization problem without updating the model parameters [14,15]. Input-affine corrections allow matching the first-order NCO upon convergence. The advantage of MA, which is the focus of this article, lies in its proven ability to converge to the plant optimum despite structural plant-model mismatch.
• Finally, the third way of incorporating process measurements in the optimization framework consists in directly updating the inputs in a control-inspired manner. There are various ways of doing this. With Extremum-Seeking Control (ESC), dither signals are added to the inputs such that an estimate of the plant cost gradient is obtained online using output measurements [16]. In the unconstrained case, gradient control is directly applied to drive the plant cost gradient to zero. Similarly, NCO tracking uses output measurements to estimate the plant NCO, which are then enforced via dedicated control algorithms [17,18]. Furthermore, Neighboring-Extremal Control (NEC) combines a variational analysis of the model at hand with output measurements to enforce the plant NCO [19]. Finally, Self-Optimizing Control (SOC) uses the sensitivity between the uncertain model parameters and the measured outputs to generate linear combinations of the outputs that are locally insensitive to the model parameters, and which can thus be kept constant at their nominal values to reject the effect of uncertainty [20].

The choice of a specific RTO method will depend on the situation at hand. However, it is highly desirable for RTO approaches to have certain properties such as (i) guaranteed plant optimality upon convergence; (ii) fast convergence; and (iii) feasible-side convergence. MA satisfies the first requirement since the model-adequacy conditions for MA are much easier to satisfy than those of the two-step approach. These conditions are enforced quite easily if convex model approximations are used instead of the model at hand as shown in [21]. The rate of convergence and feasible-side convergence are also critical requirements, which however are highly case dependent. Note that these two requirements often oppose each other since fast convergence calls for large steps, while feasible-side convergence often requires small and cautious steps. It is the intrinsic capability of MA to converge to the plant optimum despite structural plant-model mismatch that makes it a very valuable tool for optimizing the operation of chemical processes in the absence of accurate models.

This overview article is structured as follows. Section 2 formulates the static real-time optimization problem. Section 3 briefly revisits ISOPE, while Section 4 discusses MA, its properties and several MA variants. Implementation aspects are investigated in Section 5, while Section 6 provides an overview of MA case studies. Finally, Section 7 concludes the paper with a discussion of open issues.

2. Problem Formulation

2.1. Steady-State Optimization Problem

The optimization of process operation consists in minimizing operating costs, or maximizing economic profit, in the presence of constraints. Mathematically, this problem can be formulated as follows:

$$\begin{array}{cc}\hfill {\mathbf{u}}_p^{★}=\underset{\mathbf{u}}{arg\; min}& {\mathsf{\Phi }}_p\left(\mathbf{u}\right):=\varphi (\mathbf{u},{\mathbf{y}}_p\left(\mathbf{u}\right))\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& G_{p,i}\left(\mathbf{u}\right):=g_i(\mathbf{u},{\mathbf{y}}_p\left(\mathbf{u}\right))\le 0,i=1,\dots ,n_g,\hfill \end{array}$$

(1)

where $\mathbf{u}\in \mathrm{I}{\mathrm{R}}^{n_u}$ denotes the decision (or input) variables; ${\mathbf{y}}_p\in \mathrm{I}{\mathrm{R}}^{n_y}$ are the measured output variables; $\varphi :\mathrm{I}{\mathrm{R}}^{n_u}\times \mathrm{I}{\mathrm{R}}^{n_y}\to \mathrm{I}\mathrm{R}$ is the cost function to be minimized; and $g_i:\mathrm{I}{\mathrm{R}}^{n_u}\times \mathrm{I}{\mathrm{R}}^{n_y}\to \mathrm{I}\mathrm{R}$, $i=1,\dots ,n_g$, is the set of inequality constraints on the input and output variables.

This formulation assumes that ϕ and $g_i$ are known functions of $\mathbf{u}$ and ${\mathbf{y}}_p$, i.e., they can be directly evaluated from the knowledge of $\mathbf{u}$ and the measurement of ${\mathbf{y}}_p$. However, in any practical application, the steady-state input-output mapping of the plant ${\mathbf{y}}_p\left(\mathbf{u}\right)$ is typically unknown, and only an approximate nonlinear steady-state model is available:

$$\begin{array}{c}\mathrm{F}(\mathbf{x},\mathbf{u})=0,\hfill \end{array}$$

(2a)

$$\begin{array}{c}\mathbf{y}=\mathrm{H}(\mathbf{x},\mathbf{u}),\hfill \end{array}$$

(2b)

where $\mathbf{x}\in \mathrm{I}{\mathrm{R}}^{n_x}$ are the state variables and $\mathbf{y}\in \mathrm{I}{\mathrm{R}}^{n_y}$ the output variables predicted by the model. For given $\mathbf{u}$, the solution to (2a) can be written as

$$\begin{array}{c}\mathbf{x}=\mathbf{\xi }\left(\mathbf{u}\right),\hfill \end{array}$$

(3)

where $\mathbf{\xi }$ is an operator expressing the steady-state mapping between $\mathbf{u}$ and $\mathbf{x}$. The input-output mapping predicted by the model can be expressed as

$$\begin{array}{c}\mathbf{y}\left(\mathbf{u}\right):=\mathrm{H}\left(\mathbf{\xi }\right(\mathbf{u}),\mathbf{u}).\hfill \end{array}$$

(4)

Using this notation, the model-based optimization problem becomes

$$\begin{array}{cc}\hfill {\mathbf{u}}^{★}=\underset{\mathbf{u}}{arg\; min}& \mathsf{\Phi }\left(\mathbf{u}\right):=\varphi (\mathbf{u},\mathbf{y}(\mathbf{u}\left)\right)\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& G_i\left(\mathbf{u}\right):=g_i(\mathbf{u},\mathbf{y}\left(\mathbf{u}\right))\le 0,i=1,\dots ,n_g.\hfill \end{array}$$

(5)

However, in the presence of plant-model mismatch, the model solution ${\mathbf{u}}^{★}$ does not generally coincide with the plant optimum ${\mathbf{u}}_p^{★}$.

2.2. Necessary Conditions of Optimality

Local minima of Problem (5) can be characterized via the NCO [11]. To this end, let us denote the set of active constraints at some point $\mathbf{u}$ by

$$\begin{array}{c}\mathcal{A}\left(\mathbf{u}\right)=\left\{i\in \{1,\dots ,n_g\}|G_i\left(\mathbf{u}\right)=0\right\}.\hfill \end{array}$$

(6)

The Linear Independence Constraint Qualification (LICQ) requires that the gradients of the active constraints, $\frac{\partial G_i}{\partial \mathbf{u}}\left(\mathbf{u}\right)$ for $i\in \mathcal{A}\left(\mathbf{u}\right)$, be linearly independent. Provided that a constraint qualification such as LICQ holds at the solution ${\mathbf{u}}^{★}$ and the functions Φ and $G_i$ are differentiable at ${\mathbf{u}}^{★}$, there exist unique Lagrange multipliers ${\mathbf{\mu }}^{★}\in \mathrm{I}{\mathrm{R}}^{n_g}$ such that the following Karush-Kuhn-Tucker (KKT) conditions hold at ${\mathbf{u}}^{★}$ [11]

$$\begin{array}{c}\mathbf{G}\le 0,{\mathbf{\mu }}^{\mathrm{T}}\mathbf{G}=0,\mathbf{\mu }\ge 0,\hfill \\ \frac{\partial \mathcal{L}}{\partial \mathbf{u}}=\frac{\partial \mathsf{\Phi }}{\partial \mathbf{u}}+{\mathbf{\mu }}^{\mathrm{T}}\frac{\partial \mathbf{G}}{\partial \mathbf{u}}=0,\hfill \end{array}$$

(7)

where $\mathbf{G}\in \mathrm{I}{\mathrm{R}}^{n_g}$ is the vector of constraint functions $G_i$, and $\mathcal{L}(\mathbf{u},\mathbf{\mu }):=\mathsf{\Phi }\left(\mathbf{u}\right)+{\mathbf{\mu }}^{\mathrm{T}}\mathbf{G}\left(\mathbf{u}\right)$ is the Lagrangian function. A solution ${\mathbf{u}}^{★}$ satisfying these conditions is called a KKT point.

The vector of active constraints at ${\mathbf{u}}^{★}$ is denoted by ${\mathbf{G}}^a\left({\mathbf{u}}^{★}\right)\in \mathrm{I}{\mathrm{R}}^{n_g^a}$, where $n_g^a$ is the cardinality of $A\left({\mathbf{u}}^{★}\right)$. Assuming that LICQ holds at ${\mathbf{u}}^{★}$, one can write:

$$\begin{array}{c}\frac{\partial {\mathbf{G}}^a}{\partial \mathbf{u}}\left({\mathbf{u}}^{★}\right)\mathrm{Z}=0,\hfill \end{array}$$

where $\mathrm{Z}\in \mathrm{I}{\mathrm{R}}^{n_u\times (n_u-n_g^a)}$ is a null-space matrix. The reduced Hessian of the Lagrangian on this null space, ${\nabla }_r^2\mathcal{L}\left({\mathbf{u}}^{★}\right)\in \mathrm{I}{\mathrm{R}}^{(n_u-n_g^a)\times (n_u-n_g^a)}$, is given by [22]

$$\begin{array}{c}{\nabla }_r^2\mathcal{L}\left({\mathbf{u}}^{★}\right):={\mathrm{Z}}^{\mathrm{T}}\left[\frac{{\partial }^2\mathcal{L}}{\partial {\mathbf{u}}^2}({\mathbf{u}}^{★},{\mathbf{\mu }}^{★})\right]\mathrm{Z}.\hfill \end{array}$$

In addition to the first-order KKT conditions, a second-order necessary condition for a local minimum is the requirement that ${\nabla }_r^2\mathcal{L}\left({\mathbf{u}}^{★}\right)$ be positive semi-definite at ${\mathbf{u}}^{★}$. On the other hand, ${\nabla }_r^2\mathcal{L}\left({\mathbf{u}}^{★}\right)$ being positive definite is sufficient for a strict local minimum [22].

3. ISOPE: Two Decades of New Ideas

In response to the inability of the classical two-step approach to enforce plant optimality, a modified two-step approach was proposed by Roberts [8] in 1979. The approach became known under the acronym ISOPE, which stands for Integrated System Optimization and Parameter Estimation [9,10]. Since then, several extensions and variants of ISOPE have been proposed, with the bulk of the research taking place between 1980 and 2002. ISOPE algorithms combine the use of a parameter estimation problem and the definition of a modified optimization problem in such a way that, upon convergence, the KKT conditions of the plant are enforced. The key idea in ISOPE is to incorporate plant gradient information into a gradient correction term that is added to the cost function. Throughout the ISOPE literature, an important distinction is made between optimization problems that include process-dependent constraints of the form $\mathbf{G}(\mathbf{u},\mathbf{y})\le 0$ and problems that do not include them [7,9]. Process-dependent constraints depend on the outputs $\mathbf{y}$, and not only on the inputs $\mathbf{u}$. In this section, we briefly describe the ISOPE formulations that we consider to be most relevant for contextualizing the MA schemes that will be presented in Section 4. Since ISOPE includes a parameter estimation problem, the steady-state outputs predicted by the model will be written in this section as $\mathbf{y}(\mathbf{u},\mathbf{\theta })$ in order to emphasize their dependency on the (adjustable) model parameters $\mathbf{\theta }\in \mathrm{I}\mathrm{R}$.

3.1. ISOPE Algorithm

The original ISOPE algorithm does not consider process-dependent constraints in the optimization problem, but only input bounds. At the kth RTO iteration, with the inputs ${\mathbf{u}}_k$ and the plant outputs ${\mathbf{y}}_p\left({\mathbf{u}}_k\right)$, a parameter estimation problem is solved, yielding the updated parameter values ${\mathbf{\theta }}_k$. This problem is solved under the output-matching condition

$$\begin{array}{c}\mathbf{y}({\mathbf{u}}_k,{\mathbf{\theta }}_k)={\mathbf{y}}_p\left({\mathbf{u}}_k\right).\hfill \end{array}$$

(8)

Then, assuming that the output plant gradient $\frac{\partial {\mathbf{y}}_p}{\partial \mathbf{u}}\left({\mathbf{u}}_k\right)$ is available, the ISOPE modifier ${\mathbf{\lambda }}_k\in \mathrm{I}{\mathrm{R}}^{n_u}$ for the gradient of the cost function is calculated as

$$\begin{array}{c}{\mathbf{\lambda }}_k^{\mathrm{T}}=\frac{\partial \varphi }{\partial \mathbf{y}}\left({\mathbf{u}}_k,\mathbf{y}({\mathbf{u}}_k,{\mathbf{\theta }}_k)\right)\left[\frac{\partial {\mathbf{y}}_p}{\partial \mathbf{u}}\left({\mathbf{u}}_k\right)-\frac{\partial \mathbf{y}}{\partial \mathbf{u}}({\mathbf{u}}_k,{\mathbf{\theta }}_k)\right].\hfill \end{array}$$

(9)

Based on the parameter estimates ${\mathbf{\theta }}_k$ and the updated modifier ${\mathbf{\lambda }}_k$, the next optimal RTO inputs are computed by solving the following modified optimization problem:

$$\begin{array}{cc}\hfill {\mathbf{u}}_{k+1}^{★}=\underset{\mathbf{u}}{arg\; min}& \varphi (\mathbf{u},\mathbf{y}(\mathbf{u},{\mathbf{\theta }}_k))+{\mathbf{\lambda }}_k^{\mathrm{T}}\mathbf{u}\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& {\mathbf{u}}^{\mathrm{L}}\le \mathbf{u}\le {\mathbf{u}}^{\mathrm{U}}.\hfill \end{array}$$

(10)

The new operating point is determined by filtering the inputs using a first-order exponential filter:

$$\begin{array}{c}{\mathbf{u}}_{k+1}={\mathbf{u}}_k+\mathrm{K}({\mathbf{u}}_{k+1}^{★}-{\mathbf{u}}_k).\hfill \end{array}$$

(11)

The output-matching condition (8) is required in order for the gradient of the modified cost function to match the plant gradient at ${\mathbf{u}}_k$. This condition represents a model-qualification condition that is present throughout the ISOPE literature [7,10,23,24].

3.2. Dealing with Process-Dependent Constraints

In order to deal with process-dependent constraints, Brdyś et al. [25] proposed to use a modifier for the gradient of the Lagrangian function. The parameter estimation problem is solved under the output-matching condition (8) and the updated parameters are used in the following modified optimization problem:

$$\begin{array}{cc}\hfill {\mathbf{u}}_{k+1}^{★}=\underset{\mathbf{u}}{arg\; min}& \varphi (\mathbf{u},\mathbf{y}(\mathbf{u},{\mathbf{\theta }}_k))+{\mathbf{\lambda }}_k^{\mathrm{T}}\mathbf{u}\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& g_i(\mathbf{u},\mathbf{y}(\mathbf{u},{\mathbf{\theta }}_k))\le 0,i=1,\dots ,n_g,\hfill \end{array}$$

(12)

where the gradient modifier is computed as follows:

$$\begin{array}{c}{\mathbf{\lambda }}_k^{\mathrm{T}}=\left[\frac{\partial \varphi }{\partial \mathbf{y}}\left({\mathbf{u}}_k,\mathbf{y}({\mathbf{u}}_k,{\mathbf{\theta }}_k)\right)+{\mathbf{\mu }}_k^{\mathrm{T}}\frac{\partial \mathbf{G}}{\partial \mathbf{y}}\left({\mathbf{u}}_k,\mathbf{y}({\mathbf{u}}_k,{\mathbf{\theta }}_k)\right)\right]\left[\frac{\partial {\mathbf{y}}_p}{\partial \mathbf{u}}\left({\mathbf{u}}_k\right)-\frac{\partial \mathbf{y}}{\partial \mathbf{u}}({\mathbf{u}}_k,{\mathbf{\theta }}_k)\right].\hfill \end{array}$$

(13)

The next inputs applied to the plant are obtained by applying the first-order filter (11), and the next values of the Lagrange multipliers to be used in (13) are adjusted as

$$\begin{array}{c}{\mu }_{i,k+1}=max\{0,{\mu }_{i,k}+b_i({\mu }_{i,k+1}^{★}-{\mu }_{i,k})\},i=1,\dots ,n_g,\hfill \end{array}$$

(14)

where ${\mathbf{\mu }}_{k+1}^{★}$ are the optimal values of the Lagrange multipliers of Problem (12) [7]. This particular ISOPE scheme is guaranteed to reach a KKT point of the plant upon convergence, and the process-dependent constraints are guaranteed to be respected upon convergence. However, the constraints might be violated during the RTO iterations leading to convergence, which calls for the inclusion of conservative constraint backoffs [7].

3.3. ISOPE with Model Shift

Later on, Tatjewski [26] argued that the output-matching condition (8) can be satisfied without the need to adjust the model parameters $\mathbf{\theta }$. This can be done by adding the bias correction term ${\mathbf{a}}_k$ to the outputs predicted by the model,

$$\begin{array}{c}{\mathbf{a}}_k:={\mathbf{y}}_p\left({\mathbf{u}}_k\right)-\mathbf{y}({\mathbf{u}}_k,\mathbf{\theta }).\hfill \end{array}$$

(15)

This way, the ISOPE Problem (10) becomes:

$$\begin{array}{cc}\hfill {\mathbf{u}}_{k+1}^{★}\in \underset{\mathbf{u}}{arg\; min}& \varphi (\mathbf{u},\mathbf{y}(\mathbf{u},\mathbf{\theta })+{\mathbf{a}}_k)+{\mathbf{\lambda }}_k^{\mathrm{T}}\mathbf{u}\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& {\mathbf{u}}^{\mathrm{L}}\le \mathbf{u}\le {\mathbf{u}}^{\mathrm{U}},\hfill \end{array}$$

(16)

with

$$\begin{array}{c}{\mathbf{\lambda }}_k^{\mathrm{T}}:=\frac{\partial \varphi }{\partial \mathbf{y}}({\mathbf{u}}_k,\mathbf{y}({\mathbf{u}}_k,\mathbf{\theta })+{\mathbf{a}}_k)\left[\frac{\partial {\mathbf{y}}_p}{\partial \mathbf{u}}\left({\mathbf{u}}_k\right)-\frac{\partial \mathbf{y}}{\partial \mathbf{u}}({\mathbf{u}}_k,\mathbf{\theta })\right].\hfill \end{array}$$

(17)

This approach can also be applied to the ISOPE scheme (12) and (13) and to all ISOPE algorithms that require meeting Condition (8). As noted in [26], the name ISOPE is no longer adequate since, in this variant, there is no need for estimating the model parameters. The name Modifier Adaptation becomes more appropriate. As will be seen in the next section, MA schemes re-interpret the role of the modifiers and the way they are defined.

4. Modifier Adaptation: Enforcing Plant Optimality

The idea behind MA is to introduce correction terms for the cost and constraint functions such that, upon convergence, the modified model-based optimization problem matches the plant NCO. In contrast to two-step RTO schemes such as the classical two-step approach and ISOPE, MA schemes do not rely on estimating the parameters of a first-principles model by solving a parameter estimation problem. Instead, the correction terms introduce a new parameterization that is specially tailored to matching the plant NCO. This parameterization consists of modifiers that are updated based on measurements collected at the successive RTO iterates.

4.1. Basic MA Scheme

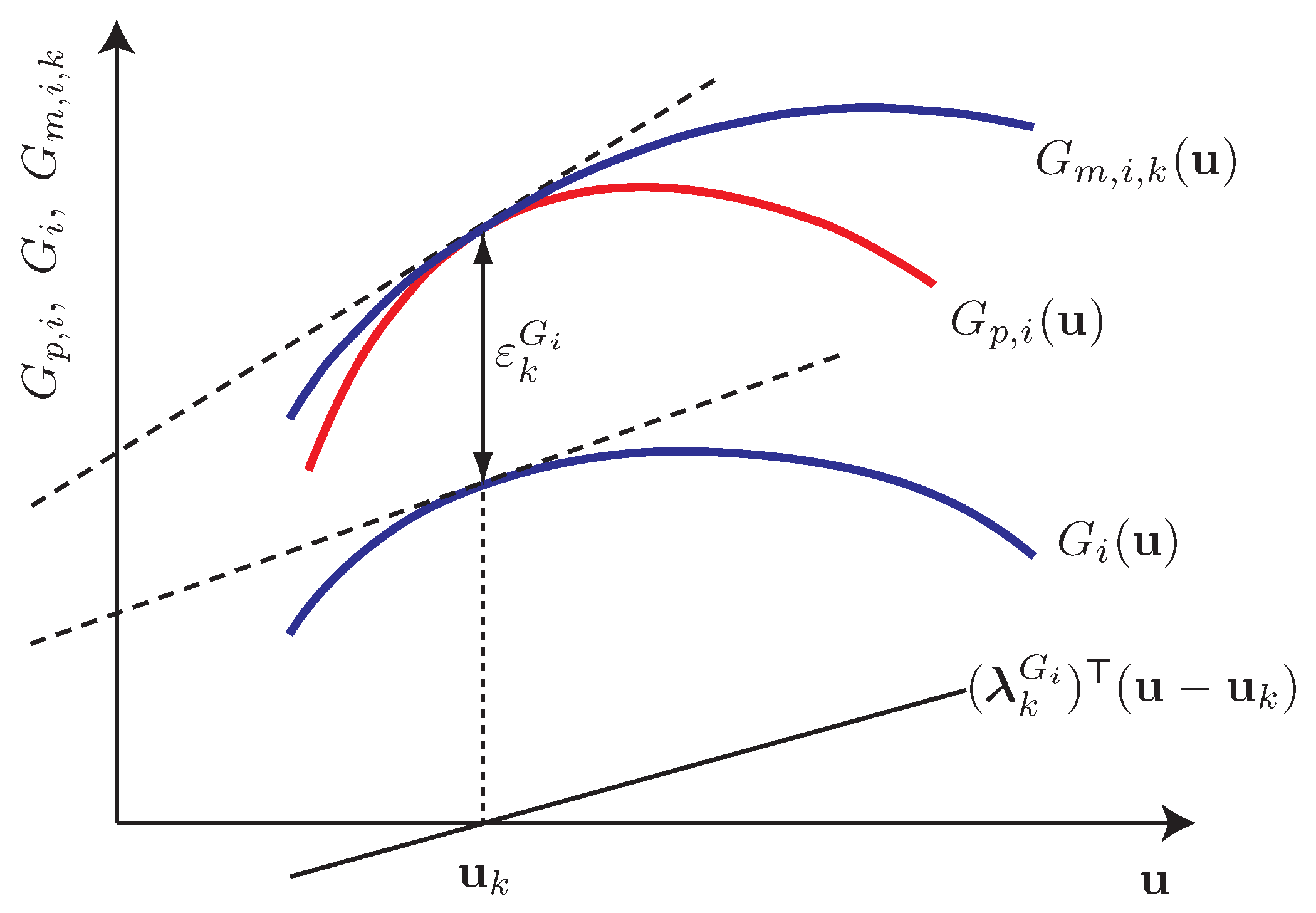
4.1.1. Modification of Cost and Constraint Functions

In basic MA, first-order correction terms are added to the cost and constraint functions of the optimization problem [14,15]. At the kth iteration with the inputs ${\mathbf{u}}_k$, the modified cost and constraint functions are constructed as follows:

$$\begin{array}{cc}\hfill {\mathsf{\Phi }}_{m,k}\left(\mathbf{u}\right)& :=\mathsf{\Phi }\left(\mathbf{u}\right)+{\epsilon }_k^{\mathsf{\Phi }}+{\left({\mathbf{\lambda }}_k^{\mathsf{\Phi }}\right)}^{\mathrm{T}}(\mathbf{u}-{\mathbf{u}}_k)\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill G_{m,i,k}\left(\mathbf{u}\right)& :=G_i\left(\mathbf{u}\right)+{\epsilon }_k^{G_i}+{\left({\mathbf{\lambda }}_k^{G_i}\right)}^{\mathrm{T}}(\mathbf{u}-{\mathbf{u}}_k)\le 0,i=1,\dots ,n_g,\hfill \end{array}$$

(19)

with the modifiers ${\epsilon }_k^{\mathsf{\Phi }}\in \mathrm{I}\mathrm{R}$, ${\epsilon }_k^{G_i}\in \mathrm{I}\mathrm{R}$, ${\mathbf{\lambda }}_k^{\mathsf{\Phi }}\in \mathrm{I}{\mathrm{R}}^{n_u}$, and ${\mathbf{\lambda }}_k^{G_i}\in \mathrm{I}{\mathrm{R}}^{n_u}$ given by

$$\begin{array}{cc}\hfill {\epsilon }_k^{\mathsf{\Phi }}& ={\mathsf{\Phi }}_p\left({\mathbf{u}}_k\right)-\mathsf{\Phi }\left({\mathbf{u}}_k\right),\hfill \end{array}$$

(20a)

$$\begin{array}{cc}\hfill {\epsilon }_k^{G_i}& =G_{p,i}\left({\mathbf{u}}_k\right)-G_i\left({\mathbf{u}}_k\right),i=1,\dots ,n_g,\hfill \end{array}$$

(20b)

$$\begin{array}{cc}\hfill {\left({\mathbf{\lambda }}_k^{\mathsf{\Phi }}\right)}^{\mathrm{T}}& =\frac{\partial {\mathsf{\Phi }}_p}{\partial \mathbf{u}}\left({\mathbf{u}}_k\right)-\frac{\partial \mathsf{\Phi }}{\partial \mathbf{u}}\left({\mathbf{u}}_k\right),\hfill \end{array}$$

(20c)

$$\begin{array}{cc}\hfill {\left({\mathbf{\lambda }}_k^{G_i}\right)}^{\mathrm{T}}& =\frac{\partial G_{p,i}}{\partial \mathbf{u}}\left({\mathbf{u}}_k\right)-\frac{\partial G_i}{\partial \mathbf{u}}\left({\mathbf{u}}_k\right),i=1,\dots ,n_g.\hfill \end{array}$$

(20d)

The zeroth-order modifiers ${\epsilon }_k^{\mathsf{\Phi }}$ and ${\epsilon }_k^{G_i}$ correspond to bias terms representing the differences between the plant values and the predicted values at ${\mathbf{u}}_k$, whereas the first-order modifiers ${\mathbf{\lambda }}_k^{\mathsf{\Phi }}$ and ${\mathbf{\lambda }}_k^{G_i}$ represent the differences between the plant gradients and the gradients predicted by the model at ${\mathbf{u}}_k$. The plant gradients $\frac{\partial {\mathsf{\Phi }}_p}{\partial \mathbf{u}}\left({\mathbf{u}}_k\right)$ and $\frac{\partial G_{p,i}}{\partial \mathbf{u}}\left({\mathbf{u}}_k\right)$ are assumed to be available at ${\mathbf{u}}_k$. A graphical interpretation of the first-order correction for the constraint $G_i$ is depicted in Figure 1. Note that, if the cost and/or constraints are perfectly known functions of the inputs $\mathbf{u}$, then the corresponding modifiers are equal to zero, and no model correction is necessary. For example, the upper and lower bounds on the input variables are constraints that are perfectly known, and thus do not require modification.

At the kth RTO iteration, the next optimal inputs ${\mathbf{u}}_{k+1}^{★}$ are computed by solving the following modified optimization problem:

$$\begin{array}{cc}\hfill {\mathbf{u}}_{k+1}^{★}=\underset{\mathbf{u}}{arg\; min}& {\mathsf{\Phi }}_{m,k}\left(\mathbf{u}\right):=\mathsf{\Phi }\left(\mathbf{u}\right)+{\left({\mathbf{\lambda }}_k^{\mathsf{\Phi }}\right)}^{\mathrm{T}}\mathbf{u}\hfill \end{array}$$

(21a)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& G_{m,i,k}\left(\mathbf{u}\right):=G_i\left(\mathbf{u}\right)+{\epsilon }_k^{G_i}+{\left({\mathbf{\lambda }}_k^{G_i}\right)}^{\mathrm{T}}(\mathbf{u}-{\mathbf{u}}_k)\le 0,i=1,\dots ,n_g.\hfill \end{array}$$

(21b)

Note that the addition of the constant term ${\epsilon }_k^{\mathsf{\Phi }}-{\left({\mathbf{\lambda }}_k^{\mathsf{\Phi }}\right)}^{\mathrm{T}}{\mathbf{u}}_k$ to the cost function does not affect the solution ${\mathbf{u}}_{k+1}^{★}$. Hence, the cost modification is often defined by including only the linear term in $\mathbf{u}$, that is, ${\mathsf{\Phi }}_{m,k}\left(\mathbf{u}\right):=\mathsf{\Phi }\left(\mathbf{u}\right)+{\left({\mathbf{\lambda }}_k^{\mathsf{\Phi }}\right)}^{\mathrm{T}}\mathbf{u}$.

The optimal inputs can then be applied directly to the plant:

$$\begin{array}{c}{\mathbf{u}}_{k+1}={\mathbf{u}}_{k+1}^{★}.\hfill \end{array}$$

(22)

However, such an adaptation strategy may result in excessive correction and, in addition, be sensitive to process noise. Both phenomena can compromise the convergence of the algorithm. Hence, one usually relies on first-order filters that are applied to either the modifiers or the inputs. In the former case, one updates the modifiers using the following first-order filter equations [15]:

$$\begin{array}{cc}\hfill {\mathbf{\epsilon }}_k^{\mathbf{G}}& =({\mathbf{I}}_{n_g}-{\mathbf{K}}^{\epsilon }){\mathbf{\epsilon }}_{k-1}^{\mathbf{G}}+{\mathbf{K}}^{\epsilon }\left({\mathbf{G}}_p\left({\mathbf{u}}_k\right)-\mathbf{G}\left({\mathbf{u}}_k\right)\right),\hfill \end{array}$$

(23a)

$$\begin{array}{cc}\hfill {\mathbf{\lambda }}_k^{\mathsf{\Phi }}& =({\mathbf{I}}_{n_u}-{\mathbf{K}}^{\mathsf{\Phi }}){\mathbf{\lambda }}_{k-1}^{\mathsf{\Phi }}+{\mathbf{K}}^{\mathsf{\Phi }}{\left(\frac{\partial {\mathsf{\Phi }}_p}{\partial \mathbf{u}}\left({\mathbf{u}}_k\right)-\frac{\partial \mathsf{\Phi }}{\partial \mathbf{u}}\left({\mathbf{u}}_k\right)\right)}^{\mathrm{T}},\hfill \end{array}$$

(23b)

$$\begin{array}{cc}\hfill {\mathbf{\lambda }}_k^{G_i}& =({\mathbf{I}}_{n_u}-{\mathbf{K}}^{G_i}){\mathbf{\lambda }}_{k-1}^{G_i}+{\mathbf{K}}^{G_i}{\left(\frac{\partial G_{p,i}}{\partial \mathbf{u}}\left({\mathbf{u}}_k\right)-\frac{\partial G_i}{\partial \mathbf{u}}\left({\mathbf{u}}_k\right)\right)}^{\mathrm{T}},i=1,\dots ,n_g,\hfill \end{array}$$

(23c)

where the filter matrices ${\mathbf{K}}^{\epsilon }$, ${\mathbf{K}}^{\mathsf{\Phi }}$, and ${\mathbf{K}}^{G_i}$ are typically selected as diagonal matrices with eigenvalues in the interval $(0,1]$. In the latter case, one filters the optimal RTO inputs ${\mathbf{u}}_{k+1}^{★}$ with $\mathbf{K}=diag(k_1,\dots ,k_{n_u}),k_i\in (0,1]$:

$$\begin{array}{c}{\mathbf{u}}_{k+1}={\mathbf{u}}_k+\mathbf{K}({\mathbf{u}}_{k+1}^{★}-{\mathbf{u}}_k).\hfill \end{array}$$

(24)

4.1.2. KKT Matching Upon Convergence

The appeal of MA lies in its ability to reach a KKT point of the plant upon convergence, as made explicit in the following theorem.

Theorem 1

(MA convergence ⇒ KKT matching [15]). Consider MA with filters on either the modifiers or the inputs. Let ${\mathbf{u}}_{\infty }={\displaystyle \underset{k\to \infty }{lim}}{\mathbf{u}}_k$ be a fixed point of the iterative scheme and a KKT point of the modified optimization Problem (21). Then, ${\mathbf{u}}_{\infty }$ is also a KKT point of the plant Problem (1).

4.1.3. Model Adequacy

The question of whether a model is adequate for use in an RTO scheme was addressed by Forbes and Marlin [27], who proposed the following model-adequacy criterion.

Definition 1

(Model-adequacy criterion [27]). A process model is said to be adequate for use in an RTO scheme if it is capable of producing a fixed point that is a local minimum for the RTO problem at the plant optimum ${\mathbf{u}}_p^{★}$.

In other words, ${\mathbf{u}}_p^{★}$ must be a local minimum when the RTO algorithm is applied at ${\mathbf{u}}_p^{★}$. The plant optimum ${\mathbf{u}}_p^{★}$ satisfies the first- and second-order NCO of the plant optimization Problem (1). The adequacy criterion requires that ${\mathbf{u}}_p^{★}$ must also satisfy the first- and second-order NCO for the modified optimization Problem (21), with the modifiers (20) evaluated at ${\mathbf{u}}_p^{★}$. As MA matches the first-order KKT elements of the plant, only the second-order NCO remain to be satisfied. That is, the reduced Hessian of the Lagrangian must be positive semi-definite at ${\mathbf{u}}_p^{★}$. The following proposition characterizes model adequacy based on second-order conditions. Again, it applies to MA with filters on either the modifiers or the inputs.

Proposition 1

(Model-adequacy conditions for MA [15]). Let ${\mathbf{u}}_p^{★}$ be a regular point for the constraints and the unique plant optimum. Let ${\nabla }_r^2\mathcal{L}\left({\mathbf{u}}_p^{★}\right)$ denote the reduced Hessian of the Lagrangian of Problem (21) at ${\mathbf{u}}_p^{★}$. Then, the following statements hold:

i 

If ${\nabla }_r^2\mathcal{L}\left({\mathbf{u}}_p^{★}\right)$ is positive definite, then the process model is adequate for use in the MA scheme.

ii 

If ${\nabla }_r^2\mathcal{L}\left({\mathbf{u}}_p^{★}\right)$ is not positive semi-definite, then the process model is inadequate for use in the MA scheme.

iii 

If ${\nabla }_r^2\mathcal{L}\left({\mathbf{u}}_p^{★}\right)$ is positive semi-definite and singular, then the second-order conditions are not conclusive with respect to model adequacy.

Example 1

(Model adequacy). Consider the problem ${\displaystyle \underset{u}{min}}{\mathsf{\Phi }}_p\left(u\right)=u_1^2+u_2^2$, for which ${\mathbf{u}}_p^{★}={[0,0]}^{\mathrm{T}}$. The models ${\mathsf{\Phi }}_1\left(\mathbf{u}\right)=u_1^2+u_2^4$ and ${\mathsf{\Phi }}_2\left(\mathbf{u}\right)=u_1^2-u_2^4$ both have their gradients equal to zero at ${\mathbf{u}}_p^{★}$, and their Hessian matrices both have eigenvalues $\{2,0\}$ at ${\mathbf{u}}_p^{★}$, that is, they are both positive semi-definite and singular. However, ${\mathsf{\Phi }}_1$ is adequate since ${\mathbf{u}}_p^{★}$ is a minimizer of ${\mathsf{\Phi }}_1$, while ${\mathsf{\Phi }}_2$ is inadequate since ${\mathbf{u}}_p^{★}$ is a saddle point of ${\mathsf{\Phi }}_2$.

4.1.4. Similarity with ISOPE

The key feature of MA schemes is that updating the parameters of a first-principles model is not required to match the plant NCO upon convergence. In addition, compared to ISOPE, the gradient modifiers have been redefined. The cost gradient modifier (20c) can be expressed in terms of the gradients of the output variables as follows:

$$\begin{array}{cc}\hfill {\left({\mathbf{\lambda }}_k^{\mathsf{\Phi }}\right)}^{\mathrm{T}}& =\frac{\partial {\mathsf{\Phi }}_p}{\partial \mathbf{u}}\left({\mathbf{u}}_k\right)-\frac{\partial \mathsf{\Phi }}{\partial \mathbf{u}}\left({\mathbf{u}}_k\right),\hfill \\ & =\frac{\partial \varphi }{\partial \mathbf{u}}({\mathbf{u}}_k,{\mathbf{y}}_p\left({\mathbf{u}}_k\right))+\frac{\partial \varphi }{\partial \mathbf{y}}({\mathbf{u}}_k,{\mathbf{y}}_p\left({\mathbf{u}}_k\right))\frac{\partial {\mathbf{y}}_p}{\partial \mathbf{u}}\left({\mathbf{u}}_k\right)\hfill \\ & -\frac{\partial \varphi }{\partial \mathbf{u}}({\mathbf{u}}_k,\mathbf{y}({\mathbf{u}}_k,\mathbf{\theta }))-\frac{\partial \varphi }{\partial \mathbf{y}}({\mathbf{u}}_k,\mathbf{y}({\mathbf{u}}_k,\mathbf{\theta }))\frac{\partial \mathbf{y}}{\partial \mathbf{u}}({\mathbf{u}}_k,\mathbf{\theta }).\hfill \end{array}$$

(25)

Notice that, if Condition (8) is satisfied, the gradient modifier ${\mathbf{\lambda }}_k^{\mathsf{\Phi }}$ in (25) reduces to the ISOPE modifier (9). In fact, Condition (8) is required in ISOPE in order for the gradient modifier (9) to represent the difference between the plant and model gradients. Put differently, output matching is a prerequisite for the gradient of the modified cost function to match the plant gradient. This requirement can be removed by directly defining the gradient modifiers as the differences between the plant and model gradients, as given in (25).

4.2. Alternative Modifications

4.2.1. Modification of Output Variables

Instead of modifying the cost and constraint functions as in (18) and (19), it is also possible to place the first-order correction terms directly on the output variables [15]. At the operating point ${\mathbf{u}}_k$, the modified outputs read:

$$\begin{array}{cc}\hfill {\mathbf{y}}_{m,k}\left(\mathbf{u}\right)& :=\mathbf{y}\left(\mathbf{u}\right)+{\mathbf{\epsilon }}_k^{\mathbf{y}}+{\left({\mathbf{\lambda }}_k^{\mathbf{y}}\right)}^{\mathrm{T}}(\mathbf{u}-{\mathbf{u}}_k),\hfill \end{array}$$

(26)

with the modifiers ${\mathbf{\epsilon }}_k^{\mathbf{y}}\in \mathrm{I}{\mathrm{R}}^{n_y}$ and ${\mathbf{\lambda }}_k^{\mathbf{y}}\in \mathrm{I}{\mathrm{R}}^{n_u\times n_y}$ given by:

$$\begin{array}{cc}\hfill {\mathbf{\epsilon }}_k^{\mathbf{y}}& ={\mathbf{y}}_p\left({\mathbf{u}}_k\right)-\mathbf{y}\left({\mathbf{u}}_k\right),\hfill \end{array}$$

(27a)

$$\begin{array}{cc}\hfill {\left({\mathbf{\lambda }}_k^{\mathbf{y}}\right)}^{\mathrm{T}}& =\frac{\partial {\mathbf{y}}_p}{\partial \mathbf{u}}\left({\mathbf{u}}_k\right)-\frac{\partial \mathbf{y}}{\partial \mathbf{u}}\left({\mathbf{u}}_k\right).\hfill \end{array}$$

(27b)

In this MA variant, the next RTO inputs are computed by solving

$$\begin{array}{cc}\hfill {\mathbf{u}}_{k+1}^{★}=\underset{\mathbf{u}}{arg\; min}& \varphi (\mathbf{u},{\mathbf{y}}_{m,k}\left(\mathbf{u}\right))\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& {\mathbf{y}}_{m,k}\left(\mathbf{u}\right)=\mathbf{y}\left(\mathbf{u}\right)+{\mathbf{\epsilon }}_k^{\mathbf{y}}+{\left({\mathbf{\lambda }}_k^{\mathbf{y}}\right)}^{\mathrm{T}}(\mathbf{u}-{\mathbf{u}}_k)\hfill \\ & g_i(\mathbf{u},{\mathbf{y}}_{m,k}\left(\mathbf{u}\right))\le 0,i=1,\dots ,n_g.\hfill \end{array}$$

(28)

Interestingly, the output bias ${\mathbf{\epsilon }}_k^{\mathbf{y}}$ is the same as the model shift term (15) introduced by Tatjewski [26] in the context of ISOPE. The MA scheme (28) also reaches a KKT point of the plant upon convergence and, again, one can choose to place a filter on either the modifiers or the inputs [15].

4.2.2. Modification of Lagrangian Gradients

Section 3.2 introduced the algorithmic approach used in ISOPE for dealing with process-dependent constraints, which consists in correcting the gradient of the Lagrangian function. An equivalent approach can be implemented in the context of MA by defining the modified optimization problem as follows:

$$\begin{array}{cc}\hfill {\mathbf{u}}_{k+1}^{★}=\underset{\mathbf{u}}{arg\; min}& {\mathsf{\Phi }}_{m,k}\left(\mathbf{u}\right):=\mathsf{\Phi }\left(\mathbf{u}\right)+{\left({\mathbf{\lambda }}_k^{\mathcal{L}}\right)}^{\mathrm{T}}\mathbf{u}\hfill \end{array}$$

(29a)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& G_{m,i,k}\left(\mathbf{u}\right):=G_i\left(\mathbf{u}\right)+{\epsilon }_k^{G_i}\le 0,i=1,\dots ,n_g,\hfill \end{array}$$

(29b)

where ${\epsilon }_k^{G_i}$ are the zeroth-order constraint modifiers, and the Lagrangian gradient modifier ${\mathbf{\lambda }}_k^{\mathcal{L}}$ represents the difference between the Lagrangian gradients of the plant and the model,

$$\begin{array}{cc}\hfill {\left({\mathbf{\lambda }}_k^{\mathcal{L}}\right)}^{\mathrm{T}}& =\frac{\partial {\mathcal{L}}_p}{\partial \mathbf{u}}({\mathbf{u}}_k,{\mathbf{\mu }}_k)-\frac{\partial \mathcal{L}}{\partial \mathbf{u}}({\mathbf{u}}_k,{\mathbf{\mu }}_k).\hfill \end{array}$$

(30)

This approach has the advantage of requiring a single gradient modifier ${\mathbf{\lambda }}_k^{\mathcal{L}}$, but the disadvantage that the modified cost and constraint functions do not provide first-order approximations to the plant cost and constraint functions at each RTO iteration. This increased plant-model mismatch may result in slower convergence to the plant optimum and larger constraint violations prior to convergence.

4.2.3. Directional MA

MA schemes require the plant gradients to be estimated at each RTO iteration. Gradient estimation is experimentally expensive and represents the main bottleneck for MA implementation (see Section 5 for an overview of gradient estimation methods). The number of experiments required to estimate the plant gradients increases linearly with the number of inputs, which tends to make MA intractable for processes with many inputs. Directional Modifier Adaptation (D-MA) overcomes this limitation by estimating the gradients only in $n_r<n_u$ privileged input directions [28,29]. This way, convergence can be accelerated since fewer experiments are required for gradient estimation at each RTO iteration. D-MA defines a $\left(n_u\times n_r\right)$-dimensional matrix of privileged directions, ${\mathbf{U}}_{\mathrm{r}}=\left[\delta {\mathbf{u}}_1\dots \delta {\mathbf{u}}_{\mathrm{r}}\right]$, the columns of which contain the $n_r$ privileged directions in the input space. Note that these directions are typically selected as orthonormal vectors that span a linear subspace of dimension $n_r$.

At the operating point ${\mathbf{u}}_k$, the directional derivatives of the plant cost and constraints that need to be estimated are defined as follows:

$$\begin{array}{cc}\hfill {\nabla }_{{\mathbf{U}}_{\mathrm{r}}}{j}_p& :={\left.\frac{\partial j_p({\mathbf{u}}_k+{\mathbf{U}}_{\mathrm{r}}\mathbf{r})}{\partial \mathbf{r}}\right|}_{\mathbf{r}=\mathbf{0}},j_p\in \{{\mathsf{\Phi }}_p,G_{p,1},G_{p,2},\dots ,G_{p,n_g}\},\hfill \end{array}$$

(31)

where $\mathbf{r}\in \mathrm{I}{\mathrm{R}}^{n_r}$. Approximations of the full plant gradients are given by

$$\begin{array}{cc}\hfill {\widehat{\nabla \mathsf{\Phi }}}_k& =\frac{\partial \mathsf{\Phi }}{\partial \mathbf{u}}\left({\mathbf{u}}_k\right)({\mathbf{I}}_{n_u}-{\mathbf{U}}_{\mathrm{r}}{\mathbf{U}}_{\mathrm{r}}^{+})+{\nabla }_{{\mathbf{U}}_{\mathrm{r}}}{\mathsf{\Phi }}_p{\mathbf{U}}_{\mathrm{r}}^{+},\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill {\widehat{\nabla G}}_{i,k}& =\frac{\partial G_i}{\partial \mathbf{u}}\left({\mathbf{u}}_k\right)({\mathbf{I}}_{n_u}-{\mathbf{U}}_{\mathrm{r}}{\mathbf{U}}_{\mathrm{r}}^{+})+{\nabla }_{{\mathbf{U}}_{\mathrm{r}}}{G}_{p,i}{\mathbf{U}}_{\mathrm{r}}^{+},i=1,\dots ,n_g,\hfill \end{array}$$

(33)

where the superscript ${(·)}^{+}$ denotes the Moore-Penrose pseudo-inverse, and ${\mathbf{I}}_{{\mathrm{n}}_{\mathrm{u}}}$ is the $n_u$-dimensional identity matrix. In D-MA, the gradients of the plant cost and constraints used in (20c) and (20d) are replaced by the estimates (32) and (33). Hence, the gradients of the modified cost and constraint functions match the estimated gradients at ${\mathbf{u}}_k$, that is, $\frac{\partial {\mathsf{\Phi }}_m}{\partial \mathbf{u}}\left({\mathbf{u}}_k\right)={\widehat{\nabla \mathsf{\Phi }}}_k$ and $\frac{\partial G_{m,i}}{\partial \mathbf{u}}\left({\mathbf{u}}_k\right)={\widehat{\nabla G}}_{i,k}$.

Figure 2 illustrates the fact that the gradient of the modified cost function $\frac{\partial {\mathsf{\Phi }}_m}{\partial \mathbf{u}}\left({\mathbf{u}}_k\right)$ and the plant cost gradient $\frac{\partial {\mathsf{\Phi }}_p}{\partial \mathbf{u}}\left({\mathbf{u}}_k\right)$ share the same projected gradient in the privileged direction $\delta \mathbf{u}$, while $\frac{\partial {\mathsf{\Phi }}_m}{\partial \mathbf{u}}\left({\mathbf{u}}_k\right)$ matches the projection of the model gradient $\frac{\partial \mathsf{\Phi }}{\partial \mathbf{u}}\left({\mathbf{u}}_k\right)$ in the direction orthogonal to $\delta \mathbf{u}$.

In general, D-MA does not converge to a KKT point of the plant. However, upon convergence, D-MA reaches a point for which the cost function cannot be improved in any of the privileged directions. This is formally stated in the following theorem.

Theorem 2

(Plant optimality in privileged directions [29]). Consider D-MA with the gradient estimates (32) and (33) in the absence of measurement noise and with perfect estimates of the directional derivatives (31). Let ${\mathbf{u}}_{\infty }={\displaystyle \underset{k\to \infty }{lim}}{\mathbf{u}}_k$ be a fixed point of that scheme and a KKT point of the modified optimization Problem (21). Then, ${\mathbf{u}}_{\infty }$ is optimal for the plant in the $n_r$ privileged directions.

The major advantage of D-MA is that, if the selected number of privileged directions is much lower than the number of inputs, the task of gradient estimation is greatly simplified. An important issue is the selection of the privileged directions.

Remark 1

(Choice of privileged directions). Costello et al. [29] addressed the selection of privileged input directions for the case of parametric plant-model mismatch. They proposed to perform a sensitivity analysis of the gradient of the Lagrangian function with respect to the uncertain model parameters θ. The underlying idea is that, if the likely parameter variations affect the Lagrangian gradient significantly only in a few input directions, it will be sufficient to estimate the plant gradients in these directions. The matrix of privileged directions ${\mathbf{U}}_{\mathrm{r}}$ is obtained by performing singular value decomposition of the normalized (by means of the expected largest variations of the uncertain model parameters θ) sensitivity matrix $\frac{\delta {\mathcal{L}}^2}{\delta \mathbf{u}\delta \theta }$ evaluated for the optimal inputs corresponding to the nominal parameter values. Only the directions in which the gradient of the Lagrangian is significantly affected by parameter variations are retained. Other choices of ${\mathbf{U}}_{\mathrm{r}}$ are currently under research. For example, it is proposed in [30] to adapt ${\mathbf{U}}_{\mathrm{r}}$ at each RTO iteration and considering large parametric perturbations.

D-MA is particularly well suited for the run-to-run optimization of repetitive dynamical systems, for which a piecewise-polynomial parameterization of the input profiles typically results in a large number of RTO inputs, thus making the estimation of full gradients prohibitive. For instance, Costello et al. [29] applied D-MA very successfully to a flying power-generating kite.

4.2.4. Second-Order MA

Faulwasser and Bonvin [31] proposed the use of second-order modifiers in the context of MA. The use of second-order correction terms allows assessing whether the scheme has converged to a point satisfying the plant second-order optimality conditions. Note that, already in 1989, Golden and Ydstie [32] investigated second-order modification terms for single-input problems.

Consider the second-order modifiers

$$\begin{array}{c}{\mathsf{\Theta }}_k^j:=\frac{{\partial }^2{j}_p}{\partial {\mathbf{u}}^2}\left({\mathbf{u}}_k\right)-\frac{{\partial }^{2}j}{\partial {\mathbf{u}}^2}\left({\mathbf{u}}_k\right),j\in \{\mathsf{\Phi },G_1,G_2,\dots ,G_{n_g}\},\hfill \end{array}$$

(34)

with ${\mathsf{\Theta }}_k^j\in \mathrm{I}{\mathrm{R}}^{n_u\times n_u}$. These modifiers describe the difference in the Hessians of the plant and model costs ($j=\mathsf{\Phi }$) and constraints ($j=G_i$), respectively. Second-order MA reads:

$$\begin{array}{cc}\hfill {\mathbf{u}}_{k+1}^{★}=\underset{\mathbf{u}}{arg\; min}& \underset{{\displaystyle =:{\mathsf{\Phi }}_{m,k}\left(\mathbf{u}\right)}}{\underbrace{\mathsf{\Phi }\left(\mathbf{u}\right)\phantom{{}_i}+{\epsilon }_k^{\mathsf{\Phi }}+{\left({\mathbf{\lambda }}_k^{\mathsf{\Phi }}\right)}^{\mathrm{T}}(\mathbf{u}-{\mathbf{u}}_k)+\frac{1}{2}{(\mathbf{u}-{\mathbf{u}}_k)}^T{\mathsf{\Theta }}_{k\phantom{,i}}^{\mathsf{\Phi }}(\mathbf{u}-{\mathbf{u}}_k)}}\hfill \end{array}$$

(35a)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& \underset{{\displaystyle =:G_{m,i,k}\left(\mathbf{u}\right)}}{\underbrace{G_i\left(\mathbf{u}\right)+{\epsilon }_k^{G_i}+{\left({\mathbf{\lambda }}_k^{G_i}\right)}^{\mathrm{T}}(\mathbf{u}-{\mathbf{u}}_k)+\frac{1}{2}{(\mathbf{u}-{\mathbf{u}}_k)}^T{\mathsf{\Theta }}_k^{G_i}(\mathbf{u}-{\mathbf{u}}_k)}}\le 0,\hfill \\ & i=1,\dots ,n_g,\hfill \end{array}$$

(35b)

$$\begin{array}{cc}& \mathbf{u}\in \mathcal{C},\hfill \end{array}$$

(35c)

with

$$\begin{array}{c}{\mathbf{u}}_{k+1}={\mathbf{u}}_k+K({\mathbf{u}}_{k+1}^{★}-{\mathbf{u}}_k).\hfill \end{array}$$

(36)

Note that, in contrast to the first-order formulation (21), we explicitly add the additional constraint $\mathbf{u}\in \mathcal{C}$ in (35c), where $\mathcal{C}$ denotes a known nonempty convex subset of $\mathrm{I}{\mathrm{R}}^{n_u}$. This additional constraint, which is not subject to plant-model mismatch, will simplify the convergence analysis.

Next, we present an extension to Theorem 1 that shows the potential advantages of second-order MA. To this end, we make the following assumptions:

A1 

Numerical feasibility: For all $k\in \mathbb{N}$, Problem (35) is feasible and has a unique minimizer.

A2 

Plant and model functions: The plant and model cost and constraint functions are all twice continuously differentiable on $\mathcal{C}\subset \mathrm{I}{\mathrm{R}}^{n_u}$.

Proposition 2

(Properties of second-order MA [31]). Assume that the second-order MA scheme (35 and 36) has converged with ${\mathbf{u}}_{\infty }={\displaystyle \underset{k\to \infty }{lim}}{\mathbf{u}}_k$. Let Assumptions A1 and A2 hold, and let a linear independence constraint qualification hold at ${\mathbf{u}}_{\infty }$. Then, the following properties hold:

i 

${\mathbf{u}}_{\infty }$ satisfies the KKT conditions of the plant, and

ii 

the cost and constraint gradients and Hessians of the modified Problem (35) match those of the plant at ${\mathbf{u}}_{\infty }$.

In addition, if (35) has a strict local minimum at ${\mathbf{u}}_{\infty }$ such that, for all $d\in {\mathbb{R}}^{n_d}$,

$$d^T{\nabla }_r^2\mathcal{L}\left({\mathbf{u}}_{\infty }\right)d>0,$$

(37)

then

iii 

${\mathsf{\Phi }}_p\left({\mathbf{u}}_{\infty }\right)$ is a strict local minimum of ${\mathsf{\Phi }}_p\left(\mathbf{u}\right)$.

Proposition 2 shows that, if second-order information can be reconstructed from measurements, then the RTO scheme (35 and 36) allows assessing, upon convergence, that a local minimum of the modified Problem (35) is also a local minimum of the plant.

Remark 2

(Hessian approximation). So far, we have tacitly assumed that the plant gradients and Hessians are known. However, these quantities are difficult to estimate accurately in practice. Various approaches to compute plant gradients from measurements will be described in Section 5.1. To obtain Hessian estimates, one can rely on well-known approximation formulas such as BFGS or SR1 update rules [33]. While BFGS-approximated Hessians can be enforced to be positive definite, the convergence of the SR1 Hessian estimates to the true Hessian can be guaranteed under certain conditions ([33] Chap. 6). However, the issue of computing Hessian approximations that can work in a RTO context (with a low number of data points and a fair amount of noise) is not solved yet!

Remark 3

(From MA to RTO based on surrogate models). It is fair to ask whether second-order corrections allow implementing model-free RTO schemes. Upon considering the trivial models $\mathsf{\Phi }\left(u\right)=0$ and $G_i\left(u\right)=0,i=1,\dots ,n_g$, that is, in the case of no model, the modifiers are

$$\begin{array}{c}{\epsilon }_k^j=j_p\left({\mathbf{u}}_k\right),{\left({\mathbf{\lambda }}_k^j\right)}^{\mathrm{T}}=\frac{\partial j_p}{\partial \mathbf{u}}\left({\mathbf{u}}_k\right),{\mathsf{\Theta }}_k^j=\frac{{\partial }^2{j}_p}{\partial {\mathbf{u}}^2}\left({\mathbf{u}}_k\right),j\in \{\mathsf{\Phi },G_1,G_2,\dots ,G_{n_g}\},\hfill \end{array}$$

and the second-order MA Problem (35) reduces to a Quadratically Constrained Quadratic Program:

$$\begin{array}{cc}\hfill {\mathbf{u}}_{k+1}^{★}=\underset{\mathbf{u}}{arg\; min}& {\mathsf{\Phi }}_p\left({\mathbf{u}}_k\right)+\frac{\partial {\mathsf{\Phi }}_p}{\partial \mathbf{u}}\left({\mathbf{u}}_k\right)(\mathbf{u}-{\mathbf{u}}_k)+\frac{1}{2}{(\mathbf{u}-{\mathbf{u}}_k)}^{\mathrm{T}}\frac{{\partial }^2{\mathsf{\Phi }}_p}{\partial {\mathbf{u}}^2}\left({\mathbf{u}}_k\right)(\mathbf{u}-{\mathbf{u}}_k)\hfill \\ \hfill s.t.& G_{p,i}\left({\mathbf{u}}_k\right)+\frac{\partial G_{p,i}}{\partial \mathbf{u}}\left({\mathbf{u}}_k\right)(\mathbf{u}-{\mathbf{u}}_k)+\frac{1}{2}{(\mathbf{u}-{\mathbf{u}}_k)}^{\mathrm{T}}\frac{{\partial }^2{G}_{p,i}}{\partial {\mathbf{u}}^2}\left({\mathbf{u}}_k\right)(\mathbf{u}-{\mathbf{u}}_k)\le 0,\hfill \\ & i=1,\dots ,n_g,\hfill \\ & \mathbf{u}\in \mathcal{C},\hfill \end{array}$$

(38)

where $\mathcal{C}$ is determined by lower and upper bounds on the input variables, $\mathcal{C}=\{\mathbf{u}\in \mathrm{I}{\mathrm{R}}^{n_u}:{\mathbf{u}}^{\mathrm{L}}\le \mathbf{u}\le {\mathbf{u}}^U\}$. Note that the results of Proposition 2 also hold for RTO Problem(38). Alternatively, the same information can be used to construct the QP approximations used in Successive Quadratic Programming (SQP) approaches for solving NLP problems [33]. The SQP approximation at the kth RTO iteration is given by,

$$\begin{array}{cc}\hfill {\mathbf{u}}_{k+1}^{★}=\underset{\mathbf{u}}{arg\; min}& {\mathsf{\Phi }}_p\left({\mathbf{u}}_k\right)+\frac{\partial {\mathsf{\Phi }}_p}{\partial \mathbf{u}}\left({\mathbf{u}}_k\right)(\mathbf{u}-{\mathbf{u}}_k)+\frac{1}{2}{(\mathbf{u}-{\mathbf{u}}_k)}^{\mathrm{T}}\frac{{\partial }^2{\mathcal{L}}_p}{\partial {\mathbf{u}}^2}\left({\mathbf{u}}_k\right)(\mathbf{u}-{\mathbf{u}}_k)\hfill \\ \hfill s.t.& G_{p,i}\left({\mathbf{u}}_k\right)+\frac{\partial G_{p,i}}{\partial \mathbf{u}}\left({\mathbf{u}}_k\right)(\mathbf{u}-{\mathbf{u}}_k)\le 0,i=1,\dots ,n_g,\hfill \\ & \mathbf{u}\in \mathcal{C},\hfill \end{array}$$

(39)

where the constraints are linearized at ${\mathbf{u}}_k$, and the Hessian of the Lagrangian function is used in the quadratic term of the cost function. Properties (i) and (iii) of Proposition 2 also hold for RTO Problem (39), and the Hessian of the Lagrangian function of Problem (39) matches the Hessian of the plant upon convergence. As the approximations of the cost and constraints are of local nature, a trust-region constraint may be added [33,34]. Obviously, such an approach leads to a SQP-like RTO scheme based on a surrogate model. A thorough investigation of RTO based on surrogate models is beyond the scope of this paper. Instead, we refer the reader to the recent progress made in this direction [35,36,37,38].

4.3. Convergence Conditions

Arguably, the biggest advantage of the MA schemes presented so far lies in the fact that any fixed point turns out to be a KKT point of the plant according to Theorem 1. Yet, Theorem 1 is somewhat limited in value, as it indicates properties upon convergence rather than stating sufficient conditions for convergence. Note that properties-upon-convergence results appear frequently in numerical optimization and nonlinear programming, see for example methods employing augmented Lagrangians with quadratic penalty on constraint violation ([39] Prop. 4.2.1). Hence, we now turn toward sufficient convergence conditions.

4.3.1. RTO Considered as Fixed-Point Iterations

In principle, one may regard any RTO scheme as a discrete-time dynamical system. In the case of MA, it is evident that the values of the modifiers at the kth RTO iteration implicitly determine the values of the inputs at iteration $k+1$.

We consider here the second-order MA scheme with input filtering from the previous section. Let $vec\left(\mathbf{a}\right)\in {\mathbb{R}}^{n(n+1)/2}$ be the vectorization of the symmetric matrix $\mathbf{A}\in {\mathbb{R}}^{n\times n}$. Using this short hand notation, we collect all modifiers in the vector $\mathsf{\Lambda }\in {\mathbb{R}}^{n_{\mathsf{\Lambda }}},n_{\mathsf{\Lambda }}=(n_g+1)\left(n_u+\frac{n_u(n_u+1)}{2}\right)+n_g+1$,

$${\mathsf{\Lambda }}_k:={\left({\epsilon }_k^{\mathsf{\Phi }},{\left({\mathbf{\lambda }}_k^{\mathsf{\Phi }}\right)}^{\mathrm{T}},vec\left({\mathsf{\Theta }}_k^{\mathsf{\Phi }}\right),{\epsilon }_k^{G_1},{\left({\mathbf{\lambda }}_k^{G_1}\right)}^{\mathrm{T}},vec\left({\mathsf{\Theta }}_k^{G_1}\right),\dots ,{\epsilon }_k^{G_{n_g}},{\left({\mathbf{\lambda }}_k^{G_{n_g}}\right)}^{\mathrm{T}},vec\left({\mathsf{\Theta }}_k^{G_{n_g}}\right)\right)}^{\mathrm{T}}.$$

(40)

As the minimizer in the optimization problem (35) depends on ${\mathsf{\Lambda }}_k$, we can formally state Algorithm (35 and 36) as

$${\mathbf{u}}_{k+1}=(1-\alpha ){\mathbf{u}}_k+\alpha {\mathbf{u}}^{★}({\mathbf{u}}_k,{\mathsf{\Lambda }}_k),$$

(41)

whereby ${\mathbf{u}}^{★}({\mathbf{u}}_k,{\mathsf{\Lambda }}_k)$ is the minimizer of (35), and, for sake of simplicity, the filter is chosen as the scalar $\alpha \in (0,1)$. Clearly, the above shorthand notation can be applied to any MA scheme with input filtering. Before stating the result, we recall the notion of a nonexpansive map.

Definition 2

(Nonexpansive map). The map $\mathsf{\Gamma }:\mathcal{C}\to \mathcal{C}$ is called nonexpansive, if

$$\forall x,y\in \mathcal{C}:\parallel \mathsf{\Gamma }\left(x\right)-\mathsf{\Gamma }\left(y\right)\parallel \le \phantom{k}\parallel x-y\parallel .$$

Theorem 3

(Convergence of MA [31]). Consider the RTO scheme (41). Let Assumptions A1 and A2 hold and let $\alpha \in (0,1)$. If the map $u^{★}:u\mapsto u^{★}(u,\mathsf{\Lambda }\left(u\right))$ is nonexpansive in the sense of Definition 2 and has at least one fixed point on $\mathcal{C}$, then the sequence ${\left(u_k\right)}_{k\in \mathbb{N}}$ of RTO iterates defined by (41) converges to a fixed point, that is,

$$\underset{k\to \infty }{lim}\parallel u^{★}(u_k,\mathsf{\Lambda }\left(u_k\right))-u_k\parallel =0.$$

Remark 4

(Reasons for filtering). Filtering can be understood as a way to increase the domain of attraction of MA schemes. This comes in addition to dealing with noisy measurements and the fact that large correction steps based on local information should be avoided.

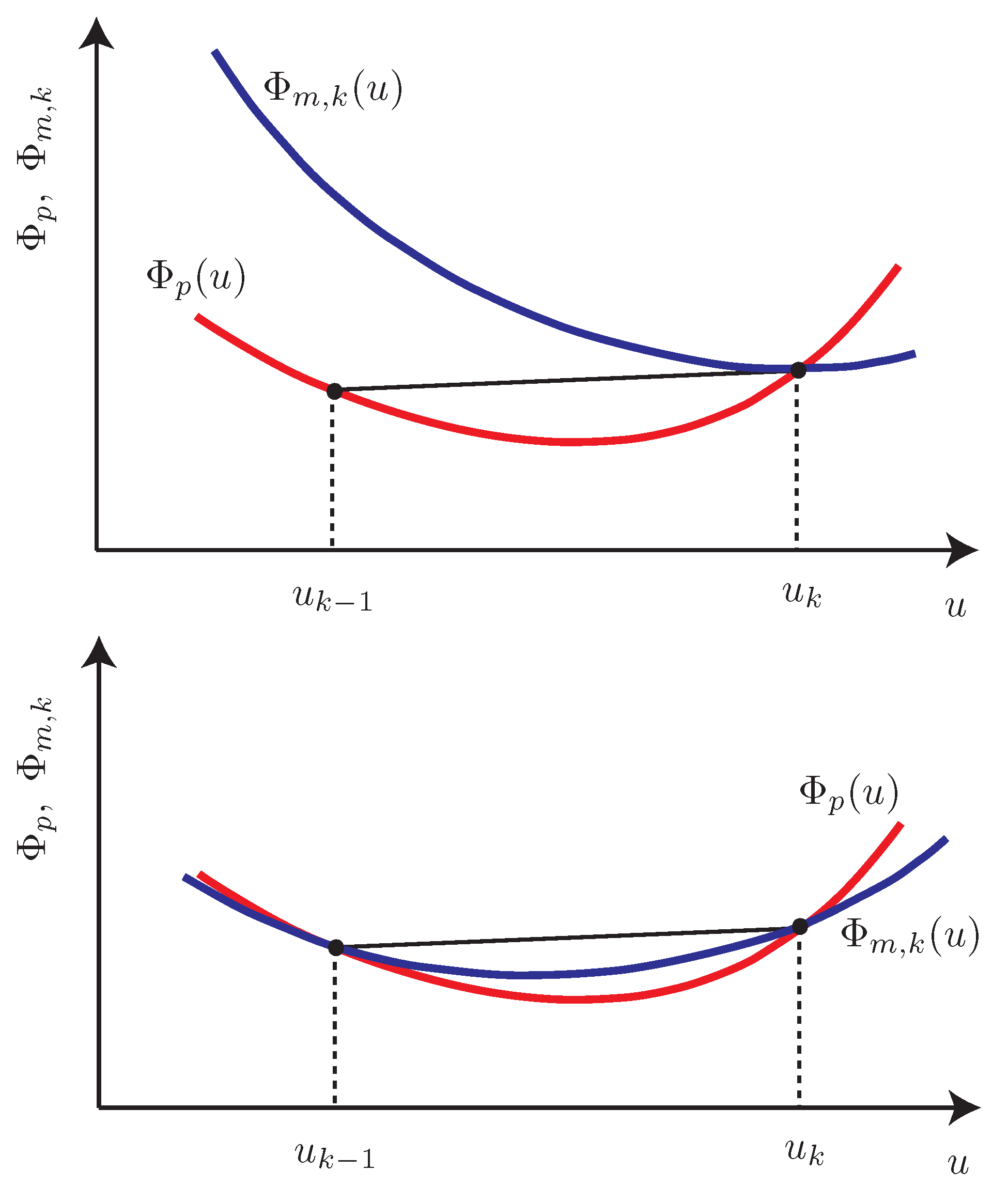
4.3.2. Similarity with Trust-Region Methods

The previous section has investigated global convergence of MA schemes. However, the analysis requires the characterization of properties of the $argmin$ operator of the modified optimization problem, which is in general challenging. Next, we recall a result given in [40] showing that one can exploit the similarity between MA and trust-region methods. This similarity has also been observed in [41].

To this end, we consider the following variant of (21)

$$\begin{array}{cc}\hfill {\mathbf{u}}_{k+1}^{★}=\underset{\mathbf{u}}{arg\; min}& {\mathsf{\Phi }}_{m,k}\left(\mathbf{u}\right):=\mathsf{\Phi }\left(\mathbf{u}\right)+{\left({\mathbf{\lambda }}_k^{\mathsf{\Phi }}\right)}^{\mathrm{T}}\mathbf{u}\hfill \end{array}$$

(42a)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& G_{m,i,k}\left(\mathbf{u}\right):=G_i\left(\mathbf{u}\right)+{\epsilon }_k^{G_i}+{\left({\mathbf{\lambda }}_k^{G_i}\right)}^{\mathrm{T}}(\mathbf{u}-{\mathbf{u}}_k)\le 0,i=1,\dots ,n_g,\hfill \end{array}$$

(42b)

$$\begin{array}{c}\mathbf{u}\in \mathcal{B}({\mathbf{u}}_k,{\rho }_k).\hfill \end{array}$$

(42c)

The only difference between this optimization problem and (21) is the trust-region constraint (42c), where $\mathcal{B}({\mathbf{u}}_k,{\rho }_k)$ denotes a closed ball in $\mathrm{I}{\mathrm{R}}^{n_u}$ with radius ${\rho }_k$ centered at ${\mathbf{u}}_k$.

Consider

$${\omega }_k:={\displaystyle \frac{{\mathsf{\Phi }}_p\left({\mathbf{u}}_k\right)-{\mathsf{\Phi }}_p\left({\mathbf{u}}_{k+1}^{★}\right)}{{\mathsf{\Phi }}_{m,k}\left({\mathbf{u}}_k\right)-{\mathsf{\Phi }}_{m,k}\left({\mathbf{u}}_{k+1}^{★}\right)}}$$

If ${\omega }_k\gg 1$, then, at ${\mathbf{u}}_{k+1}^{★}$, the plant performs significantly better than predicted by the modified model. Likewise, if ${\omega }_k\ll 1$, the plant performs significantly worse than predicted by the modified model. In other words, ${\omega }_k$ is a local criterion for the quality of the modified model. In trust-region methods, one replaces (input) filtering with acceptance rules for candidate points. In [40], it is suggested to apply the following rule:

$${\mathbf{u}}_{k+1}:=\left\{\begin{array}{c}{\mathbf{u}}_{k+1}^{★}\mathrm{if} {\omega }_k\ge {\eta }_1\\ {\mathbf{u}}_{k\phantom{+1}}\mathrm{otherwise}\end{array}\right.$$

(43)

Note that this acceptance rule requires application of ${\mathbf{u}}_{k+1}^{★}$ to the plant.

Another typical ingredient of trust-region methods is an update rule for the radius ${\rho }_k$. Consider the constant scalars $0<{\eta }_1\le {\eta }_2<1$, $0<{\gamma }_1\le {\gamma }_2<1$, and assume that the update satisfies the following conditions:

$${\rho }_{k+1}\in \left\{\begin{array}{c}[{\rho }_k,\infty )\mathrm{if} {\omega }_k\ge {\eta }_2\\ [{\gamma }_2{\rho }_k,{\rho }_k]\mathrm{if} {\omega }_k\in [{\eta }_1,{\eta }_2)\\ [{\gamma }_1{\rho }_k,{\gamma }_2{\rho }_k]\mathrm{if} {\omega }_k\le {\eta }_1\end{array}\right.$$

(44)

As in the previous section, we assume that Assumptions A1 and A2 hold. In addition, we require the following:

A3 

Plant boundedness: The plant objective ${\mathsf{\Phi }}_p$ is lower-bounded on $\mathrm{I}{\mathrm{R}}^{n_u}$. Furthermore, its Hessian is bounded from above on $\mathrm{I}{\mathrm{R}}^{n_u}$.

A4 

Model decrease: For all $k\in \mathbb{N}$, there exists a constant $\kappa \in (0,1]$ and a sequence ${\left({\beta }_k\right)}_{k\in \mathbb{N}}>1$ such that

$${\mathsf{\Phi }}_{m,k}\left({\mathbf{u}}_k^{★}\right)-{\mathsf{\Phi }}_{m,k}\left({\mathbf{u}}_{k+1}^{★}\right)\ge \kappa \parallel \nabla {\mathsf{\Phi }}_{m,k}\left({\mathbf{u}}_k\right)\parallel ·min\left\{{\rho }_k,\frac{\parallel \nabla {\mathsf{\Phi }}_{m,k}\left({\mathbf{u}}_k\right)\parallel }{{\beta }_k}\right\}.$$

Now, we are ready to state convergence conditions for the trust-region-inspired MA scheme given by (42)–(44).

Theorem 4

(Convergence with trust-region constraints [40]). Consider the RTO scheme (42)–(44) and let Assumptions A1–A4 hold, then

$$\underset{k\to \infty }{lim}\parallel \nabla {\mathsf{\Phi }}_p\left({\mathbf{u}}_k\right)\parallel =0.$$

The formal proof of this result is based on a result on convergence of trust-region methods given in [34]. For details, we refer to [40].

Remark 5

(Comparison of Theorems 3 and 4). A few remarks on the convergence results given by Theorems 3 and 4 are in order. While Theorem 3 is applicable to schemes with first- and second-order correction terms, the convergence result is based on the nonexpansiveness of the $argmin$ operator, which is difficult to verify in practice. However, Theorem 3 provides a good motivation for input filtering as the convergence result is based on averaged iterations of a nonexpansive operator. In contrast, Theorem 4 relies on Assumption A4, which ensures sufficient model decrease ([34] Thm. 6.3.4, p. 131). However, this assumption is in general not easy to verify.

There is another crucial difference between MA with and without trust-region constraints. The input update (43) is based on ${\omega }_k$, which requires application of ${\mathbf{u}}_{k+1}^{★}$ to the plant. Note that, if at the kth RTO iteration the trust region is chosen too large, then first ${\mathbf{u}}_{k+1}^{★}$ is applied to the plant, resulting in ${\omega }_k<{\eta }_1$ and thus to immediate (re-)application of ${\mathbf{u}}_k$. In other words, a trust region that is chosen too large can result in successive experiments that do not guarantee plant cost improvement. In a nominal setting with perfect gradient information, this is clearly a severe limitation. However, in any real world application, where plant gradients need to be estimated, the plant information obtained from rejected steps may be utilized for gradient estimation.

4.3.3. Use of Convex Models and Convex Upper Bounds

Next, we turn to the issue of convexity in MA. As already mentioned in Proposition 1, for a model to be adequate in MA, it needs to be able to admit, after the usual first-order correction, a strict local minimum at the generally unkown plant optimum ${\mathbf{u}}_p^{★}$. At the same time, it is worth noting that the model is simply a tool in the design of MA schemes. In Remark 3, for instance, we pointed toward second-order MA with no model functions. Yet, this is not the only possible choice. It has been observed in [21] that the adequacy issue is eliminated if one relies on strictly convex models and first-order correction terms. The next proposition summarizes these results.

Proposition 3

(Use of convex models in MA [21]). Consider the MA Problem (21). Let the model cost and constraint functions Φ and $G_i$, $i=1,\dots ,n_g$, be strictly convex functions. Then, (i) Problem (21) is a strictly convex program; and (ii) the model satisfies the adequacy condition of Definition 1.

Remark 6

(Advantages of convex models). The most important advantage of convex models in MA is that model adequacy is guaranteed without prior knowledge of the plant optimum. Furthermore, it is well known that convex programs are, in general, easier to solve than non-convex ones. Note that one can relax the strict convexity requirement to either the cost being strictly convex or at least one of the active constraints being strictly convex at the plant optimum [21].

4.4. Extensions

Several extensions and variants of MA have recently been developed to account for specific problem configurations and needs.

4.4.1. MA Applied to Controlled Plants

MA guarantees plant feasibility upon convergence, but the RTO iterates prior to convergence might violate the plant constraints. For continuous processes, it is possible to generate feasible steady-state operating points by implementing the RTO results via a feedback control layer that tracks the constrained variables that are active at the RTO solution [42]. This requires the constrained quantities in the optimization problem to be measured online at sufficiently high frequency. Navia et al. [43] recently proposed an approach to prevent infeasibilities in MA implementation by including PI controllers that become activated only when the measurements show violation of the constraints. In industry, model predictive control (MPC) is used widely due to its ability to handle large multivariable systems with constraints [44]. Recently, Marchetti et al.[45] proposed an approach for integrating MA with MPC, wherein MPC is used to enforce the equality and active inequality constraints of the modified optimization problem. The remaining degrees of freedom are controlled to their optimal values along selected input directions. In order to implement MA on a controlled plant, the gradients are corrected on the tangent space of the equality constraints.

The approach used in industry to combine RTO with MPC consists in including a target optimization stage at the MPC layer [44]. Since the nonlinear steady-state model used at the RTO layer is not in general consistent with the linear dynamic model used by the MPC regulator, the optimal setpoints given by the RTO solution are often not reachable by the MPC regulator. The target optimization problem uses a (linear) steady-state model that is consistent with the MPC dynamic model. Its purpose is to correct the RTO setpoints by computing steady-state targets that are reachable by the MPC regulator [46,47]. The target optimization problem executes at the same frequency as the MPC regulator and uses the same type of feedback. Three different designs of the target optimization problem have been analyzed in [48], each of which guarantees attaining only feasible points for the plant at steady state, and reaching the RTO optimal inputs upon convergence.

Another difficulty arises when the inputs of the model-based optimization problem are not the same as the plant inputs. This happens, for instance, when the plant is operated in closed loop, but only a model of the open-loop system is available [49]. In this case, the plant inputs are the controller setpoints $\mathbf{r}$, while the model inputs are the manipulated variables $\mathbf{u}$. Three alternative MA extensions have recently been proposed to optimize a controlled plant using a model of the open-loop plant [50]. The three extensions use the cost and constraint gradients of the plant with respect to the setpoints $\mathbf{r}$:

• The first approach, labeled “Method UR”, suggests solving the optimization problem for $\mathbf{u}$, but computes the modifiers in the space of the setpoints $\mathbf{r}$.
• The second approach, labelled “Method UU”, solves the optimization problem for $\mathbf{u}$, and computes the modifiers in the space of $\mathbf{u}$.
• The third approach, labelled “Method RR”, solves the optimization problem for $\mathbf{r}$, and computes the modifiers in the space of $\mathbf{r}$. It relies on the construction of model approximations for the controlled plant that are obtained from the model of the open-loop plant.

As shown in [50], the three extensions preserve the MA property of reaching a KKT point of the plant upon convergence.

4.4.2. MA Applied to Dynamic Optimization Problems

There have been some attempts to extend the applicability of MA to the dynamic run-to-run optimization of batch processes [51,52]. The idea therein is to build on the repetitive nature of batch processes and perform run-to-run iterations to progressively improve the performance of the batches.

The approach used in [51] takes advantage of the fact that dynamic optimization problems can be reformulated as static optimization problems upon discretization of the inputs, constraints and the dynamic model [17]. This allows the direct use of MA, the price to pay being that the number of decision variables increases linearly with the number of discretization points, as shown in [51]. Note that, if the active path constraints are known in the various intervals of the solution, a much more parsimonious input parameterization can be implemented, as illustrated in ([17] Appendix).

The approach proposed in [52] uses CA (that is, MA with only zeroth-order modifiers) for the run-to-run optimization of batch processes. Dynamic optimization problems are characterized by the presence of both path and terminal constraints. Because of uncertainty and plant-model mismatch, the measured values of both path and terminal constraints will differ from their model predictions. Hence, for each run, one can offset the values of the terminal constraints in the dynamic optimization problem with biases corresponding to the differences between the predicted and measured terminal constraints of the previous batch. Path constraints are modified similarly, by adding to the path constraints a time-dependent function corresponding to the differences between the measured and predicted path constraints during the previous batch. An additional difficulty arises when the final time of the batch is also a decision variable. Upon convergence, the CA approach [52] only guarantees constraint satisfaction, while the full MA approach [51] preserves the KKT matching property of standard MA.

4.4.3. Use of Transient Measurements for MA

MA is by nature a steady-state to steady-state RTO methodology for the optimization of uncertain processes. This means that several iterations to steady state are generally needed before convergence. However, there are cases where transient measurements can be used as well. Furthermore, it would be advantageous to be able to use transient measurements in a systematic way to speed up the steady-state optimization of dynamic processes.

The concept of fast RTO via CA was introduced and applied to an experimental solid oxide fuel-cell stack in the presence of operating constraints and plant-model mismatch [53]. Solid oxide fuel-cell stacks are, roughly speaking, electrochemical reactors embedded in a furnace. The electrochemical reaction between hydrogen and oxygen is almost instantaneous and results in the production of electrical power and water. On the other hand, thermal equilibration is much slower. The fast RTO approach in [53] is very simple and uses CA. The RTO period is set somewhere between the time scale of the electrochemical reaction and the time scale of the thermal process. This way, the chemical reaction has time to settle, and the thermal effects are treated as slow process drifts that are accounted for like any other source of plant-model mismatch. This shows that it is possible to use RTO before steady state has been reached, at least when a time-scale separation exists between fast optimization-relevant dynamics and slow dynamics that do not affect much the cost and constraints of the optimization problem.

In [54], a framework has been proposed to apply MA during transient operation to steady state for the case of parametric plant-model mismatch, thereby allowing the plant to converge to optimal operating conditions in a single transient operation to steady state. The basic idea is simply to implement standard MA during the transient “as if the process were at steady state”. Optimal inputs are computed and applied until the next RTO execution during transient. Hence, the time between two consecutive RTO executions becomes a tuning parameter just as the filter gains. Transient measurements obtained at the RTO sampling period are treated as if they were steady-state measurements and are therefore directly used for computing the zeroth-order modifiers and estimating the plant gradients at “steady state”. There are two main advantages of this approach: (i) standard MA can be applied; and (ii) the assumption that transient measurements can play the role of steady-state measurements becomes more and more valid as the system approaches steady state. Simulation results in [54] are very encouraging, but they also highlight some of the difficulties, in particular when the dynamics exhibit non-standard behaviors such as inverse response. A way to circumvent these difficulties consists in reducing the RTO frequency. Ultimately, this frequency could be reduced to the point that MA is only solved at steady state, when the process dynamics have disappeared. Research is ongoing to improve the use of transient measurements and characterize the types of dynamic systems for which this approach is likely to reduce the time needed for convergence [55].

4.4.4. MA when Part of the Plant is Perfectly Modeled

As mentioned above, MA is capable of driving a plant toward a KKT point even though the model is structurally incorrect. The only requirement for the model is that it satisfies the model-adequacy conditions, a property that can be enforced if convex model approximations are used [54]. In addition, plant measurements that allow good estimation of the plant constraints and gradients are required. The fact that MA can be efficient without an accurate model does not mean that it cannot benefit from the availability of a good model. For instance, in [56] the authors acknowledge that, for most energy systems, the model incorporates basic mass and energy balances that can often be very rigorously modeled and, thus, there is no need to include any structural or parametric plant-model mismatch. The authors suggest separating the process model equations into two sets of equations. The set of rigorous model equations is denoted the “process model”, while the second set of equations is referred to as the “approximate model” and describes performance and efficiency factors, which are much harder to model and therefore susceptible to carry plant-model mismatch. Hence, modifiers are used only for this second set of equations by directly modifying the corresponding model equations. Key to the approach in [56] is data reconciliation, which makes explicit use of the knowledge of the set of “perfect model equations”. One of the advantages of not modifying the well-known subparts of the model is that it may reduce the number of plant gradients that need to be estimated, without much loss in performance.

5. Implementation Aspects

The need to estimate plant gradients represents the main implementation difficulty. This is a challenging problem since the gradients cannot be measured directly and, in addition, measurement noise is almost invariably present. This section discusses different ways of estimating gradients, of computing modifiers, and of combining gradient estimation and optimization.

5.1. Gradient Estimation

Several methods are available for estimating plant gradients [57,58,59,60]. These methods can be classified as steady-state perturbation methods that use only steady-state data, and dynamic perturbation methods that use transient data.

5.1.1. Steady-State Perturbation Methods

Steady-state perturbation methods rely on steady-state data for gradient estimation. For each change in the input variables, one must wait until the plant has reached steady state before taking measurements, which can make these methods particularly slow. Furthermore, to obtain reliable gradient estimates, it is important to avoid (i) amplifying the noise present in experimental data [61,62]; and (ii) using past data that correspond to different conditions (for example, different qualities of raw materials, or different disturbance values).

Finite-difference approximation (FDA). The most common approach is to use FDA techniques that require at least $n_u+1$ steady-state operating points to estimate the gradients. Several alternatives can be envisioned for choosing these points:

• FDA by perturbing the current RTO point: A straightforward approach consists in perturbing each input individually around the current operating point to get an estimate of the corresponding gradient element. For example, in the forward-finite-differencing (FFD) approach, an estimator of the partial derivative $\frac{\partial {\mathsf{\Phi }}_p}{\partial u_j}\left({\mathbf{u}}_k\right)$, $j=1,\dots ,n_u$, at the kth RTO iteration is obtained as

  $${\left({\widehat{\nabla \mathsf{\Phi }}}_{p,k}\right)}_j=\left[{\tilde{\mathsf{\Phi }}}_p({\mathbf{u}}_k+h{\mathbf{e}}_j)-{\tilde{\mathsf{\Phi }}}_p\left({\mathbf{u}}_k\right)\right]/h,h>0,$$

  (45)

  where h is the step size, ${\mathbf{e}}_j$ is the jth unit vector, and the superscript $\widetilde{(·)}$ denotes a noisy measurement. This approach requires $n_u$ perturbations to be carried out at each RTO iteration, and for each perturbation a new steady state must be attained. Alternatively, the central-finite-differencing (CFD) approach can be used, which is more accurate but requires $2n_u$ perturbations at each RTO iteration [61]. Since perturbing each input individually may lead to constraint violations when the current operating point is close to a constraint, an approach has been proposed for generating $n_u$ perturbed points that take into account the constraints and avoid ill-conditioned points for gradient estimation [45].
• FDA using past RTO points: The gradients can be estimated by FDA based on the measurements obtained at the current and past RTO points $\{{\mathbf{u}}_k,{\mathbf{u}}_{k-1},\dots$, ${\mathbf{u}}_{k-n_u}\}$. This approach is used in dual ISOPE and dual MA methods [7,63,64,65]—the latter methods being discussed in Section 5.3. At the kth RTO iteration, the following matrix can be constructed:

  $$\begin{array}{c}{\mathrm{U}}_k:=\left[\begin{array}{cccc}{\mathbf{u}}_k-{\mathbf{u}}_{k-1},& {\mathbf{u}}_k-{\mathbf{u}}_{k-2},& \dots ,& {\mathbf{u}}_k-{\mathbf{u}}_{k-n_u}\end{array}\right]\in \mathrm{I}{\mathrm{R}}^{n_u\times n_u}.\hfill \end{array}$$

  (46)

  Assuming that measurements of the cost ${\mathsf{\Phi }}_p$ and constraints $G_{p,i}$ are available at each iteration, we construct the following vectors:

  $$\begin{array}{c}\mathbf{\delta }{\tilde{\mathsf{\Phi }}}_{p,k}:={\left[\begin{array}{cccc}{\tilde{\mathsf{\Phi }}}_{p,k}-{\tilde{\mathsf{\Phi }}}_{p,k-1},& {\tilde{\mathsf{\Phi }}}_{p,k}-{\tilde{\mathsf{\Phi }}}_{p,k-2},& \dots ,& {\tilde{\mathsf{\Phi }}}_{p,k}-{\tilde{\mathsf{\Phi }}}_{p,k-n_u}\end{array}\right]}^{\mathrm{T}}\in \mathrm{I}{\mathrm{R}}^{n_u},\hfill \end{array}$$

  (47)

  $$\begin{array}{c}\mathbf{\delta }{\tilde{G}}_{p,i,k}:={\left[\begin{array}{cccc}{\tilde{G}}_{p,i,k}-{\tilde{G}}_{p,i,k-1},& {\tilde{G}}_{p,i,k}-{\tilde{G}}_{p,i,k-2},& \dots ,& {\tilde{G}}_{p,i,k}-{\tilde{G}}_{p,i,k-n_u}\end{array}\right]}^{\mathrm{T}}\in \mathrm{I}{\mathrm{R}}^{n_u},\hfill \\ i=1,\dots ,n_g.\hfill \end{array}$$

  (48)

  The measured cost has measurement noise $v_k$:

  $$\begin{array}{c}{\tilde{\mathsf{\Phi }}}_{p,k}={\mathsf{\Phi }}_p\left({\mathbf{u}}_k\right)+v_k.\hfill \end{array}$$

  (49)

  If ${\mathrm{U}}_k$ is nonsingular, then the set of $n_u+1$ points ${\left\{{\mathbf{u}}_{k-j}\right\}}_{j=0}^{n_u}$ is said to be poised for linear interpolation in $\mathrm{I}{\mathrm{R}}^{n_u}$, and ${\mathrm{U}}_k$ is called a matrix of simplex directions [34]. The cost gradient at ${\mathbf{u}}_k$ can then be estimated by FDA as follows:

  $$\begin{array}{c}{\widehat{\nabla \mathsf{\Phi }}}_{p,k}={\left(\mathbf{\delta }{\tilde{\mathsf{\Phi }}}_{p,k}\right)}^{\mathrm{T}}{\left({\mathrm{U}}_k\right)}^{-1},\hfill \end{array}$$

  (50)

  which is known as the simplex gradient [34]. The constraint gradients can be computed in a similar way.

Broyden’s method. The gradients are estimated from the past RTO points using the following recursive updating scheme:

$$\begin{array}{c}{\widehat{\nabla \mathsf{\Phi }}}_{p,k}={\widehat{\nabla \mathsf{\Phi }}}_{p,k-1}+\frac{({\tilde{\mathsf{\Phi }}}_{p,k}-{\tilde{\mathsf{\Phi }}}_{p,k-1})-{\widehat{\nabla \mathsf{\Phi }}}_{p,k-1}({\mathbf{u}}_k-{\mathbf{u}}_{k-1})}{{({\mathbf{u}}_k-{\mathbf{u}}_{k-1})}^{\mathrm{T}}({\mathbf{u}}_k-{\mathbf{u}}_{k-1})}{({\mathbf{u}}_k-{\mathbf{u}}_{k-1})}^{\mathrm{T}}.\hfill \end{array}$$

(51)

The use of Broyden’s method was investigated for ISOPE in [66] and for MA in [67]. Comparative studies including this gradient estimation method can be found in [58,68].

Gradients from fitted surfaces. A widely used strategy for extracting gradient information from (noisy) experimental data consists in fitting polynomial or spline curves to the data and evaluating the gradients analytically by differentiating the fitted curves [69]. In the context of MA, Gao et al. [36] recently proposed to use least-square regression to obtain local quadratic approximations of the cost and constraint functions using selected data, and to evaluate the gradients by differentiating these quadratic approximations.

5.1.2. Dynamic Perturbation Methods

In dynamic perturbation methods, the steady-state gradients are estimated based on the transient response of the plant. Three classes of methods are described next.

Dynamic model identification. These methods rely on the online identification of simple dynamic input-output models based on the plant transient response. Once a dynamic model is identified, the steady-state gradients can be obtained by application of the final-value theorem. Indeed, the static gain of a transfer function represents the sensitivity (or gradient) of the output with respect to the input. McFarlane and Bacon [70] proposed to identify a linear ARX model and used the estimated static gradient for online optimizing control. A pseudo-random binary sequence (PRBS) was superimposed on each of the inputs to identify the ARX model. In the context of ISOPE, Becerra et al. [71] considered the identification of a linear ARMAX model using PRBS signals. Bamberger and Isermann [72] identified online a parametric second-order Hammerstein model by adding a pseudo-random ternary sequence to each input. The gradient estimates were used for online optimizing control. Garcia and Morari [73] used a similar approach, wherein the dynamic identification was performed in a decentralized fashion. The same approach was also used by Golden and Ydstie [32] for estimating the first- and second-order derivatives of a SISO plant. Zhang and Forbes [60] compared the optimizing controllers proposed in [70] and [32] with ISOPE and the two-step approach.

Extremum-seeking control. The plant gradients can also be obtained using data-driven methods as discussed in [74]. Among the most established techniques, ESC [16] suggests adding a dither signal (e.g., a sine wave) to each of the inputs during transient operation. High-pass filtering of the outputs removes the biases, while using low-pass filters together with correlation let you compute the gradients of the outputs with respect to the inputs. The main limitation of this approach is the speed of convergence as it requires two time-scale separations, the first one between the filters and the periodic excitation, and the second one between the periodic excitation and the controlled plant. Since all inputs have to be perturbed independently, convergence to the plant gradients can be prohibitively slow in the MIMO case. Recent efforts in the extremum-seeking community have led to a more efficient framework, referred to as “estimation-based ESC” (by opposition to the previously described perturbation-based ESC), which seems to be more efficient in terms of convergence speed [75].

Multiple units. Another dynamic perturbation approach relies on the availability of several identical units operated in parallel [76]. The minimal number of required units is $n_u+1$, since one unit operates with the inputs computed by the RTO algorithm, while a single input is perturbed in each of the remaining $n_u$ units in parallel. The gradients can be computed online by finite differences between units. Convergence time does not increase with the number of inputs. Obviously, this approach relies heavily on the availability of several identical units, which occurs for instance when several units, such as fuel-cell stacks, are arranged in parallel. Note that these units must be identical, although some progress has been made to encompass cases where this is not the case [77].

5.1.3. Bounds on Gradient Uncertainty

As discussed in [78], obtaining bounds on gradient estimates is often more challenging than obtaining the estimates themselves. The bounds on gradient estimates should be linked with the specific approach used to estimate the gradients. For the case of gradient estimates obtained by FFD, CFD, and two design-of-experiment schemes, Brekelmans et al. [61] proposed a deterministic quantification of the gradient error due to the finite-difference approximation (truncation error) and a stochastic characterization due to measurement noise. The expressions obtained for the total gradient error are convex functions of the step size, for which it is easy to compute for each scheme the step size that minimizes the total gradient error. Following a similar approach, the gradient error associated with the simplex gradient (50) was analyzed by Marchetti et al. [64].

The gradient estimation error is defined as the difference between the estimated gradient and the true plant gradient:

$$\begin{array}{c}{\mathbf{ϵ}}_k^{\mathrm{T}}={\widehat{\nabla \mathsf{\Phi }}}_{p,k}-\frac{\partial {\mathsf{\Phi }}_p}{\partial \mathbf{u}}\left({\mathbf{u}}_k\right).\hfill \end{array}$$

(52)

From (49) and (50), this error can be split into the truncation error ${\mathbf{ϵ}}^t$ and the measurement noise error ${\mathbf{ϵ}}^n$,

$$\begin{array}{c}{\mathbf{ϵ}}_k={\mathbf{ϵ}}_k^t+{\mathbf{ϵ}}_k^n,\hfill \end{array}$$

(53)

with

$$\begin{array}{c}{\left({\mathbf{ϵ}}_k^t\right)}^{\mathrm{T}}=[{\mathsf{\Phi }}_p\left({\mathbf{u}}_k\right)-{\mathsf{\Phi }}_p\left({\mathbf{u}}_{k-1}\right),\dots ,{\mathsf{\Phi }}_p\left({\mathbf{u}}_k\right)-{\mathsf{\Phi }}_p\left({\mathbf{u}}_{k-n_u}\right)]{\left({\mathrm{U}}_k\right)}^{-1}-\frac{\partial {\mathsf{\Phi }}_p}{\partial \mathbf{u}}\left({\mathbf{u}}_k\right),\hfill \end{array}$$

(54a)

$$\begin{array}{c}{\left({\mathbf{ϵ}}_k^n\right)}^{\mathrm{T}}=[v_k-v_{k-1},\dots ,v_k-v_{k-n_u}]{\left({\mathrm{U}}_k\right)}^{-1}.\hfill \end{array}$$

(54b)

Assuming that ${\mathsf{\Phi }}_p$ is twice continuously differentiable with respect to $\mathbf{u}$, the norm of the gradient error due to truncation can be bounded from above by

$$\begin{array}{c}\parallel {\mathbf{ϵ}}_k^t\parallel \le {\mathrm{d}}^{\mathsf{\Phi }}{r}_k,\hfill \end{array}$$

(55)

where ${\mathrm{d}}^{\mathsf{\Phi }}$ is an upper bound on the spectral radius of the Hessian of ${\mathsf{\Phi }}_p$ for $\mathbf{u}\in \mathcal{C}$, and $r_k$ is the radius of the unique n-sphere that can be generated from the points ${\mathbf{u}}_k,{\mathbf{u}}_{k-1},\dots ,{\mathbf{u}}_{k-n_u}$:

$$\begin{array}{c}{r}_k=r({\mathbf{u}}_k,{\mathbf{u}}_{k-1},\dots ,{\mathbf{u}}_{k-n_u})=\hfill \\ \frac{1}{2}∥\left[{({\mathbf{u}}_k-{\mathbf{u}}_{k-1})}^{\mathrm{T}}({\mathbf{u}}_k-{\mathbf{u}}_{k-1}),\dots ,{({\mathbf{u}}_k-{\mathbf{u}}_{k-n_u})}^{\mathrm{T}}({\mathbf{u}}_k-{\mathbf{u}}_{k-n_u})\right]{\left({\mathrm{U}}_k\right)}^{-1}∥.\hfill \end{array}$$

(56)

In turn, assuming that the noisy measurements ${\tilde{\mathsf{\Phi }}}_p$ remain within the interval ${\delta }^{\mathsf{\Phi }}$ at steady state, the norm of the gradient error due to measurement noise can be bounded from above:

$$\begin{array}{c}\parallel {\mathbf{ϵ}}_k^n\parallel \le \frac{{\delta }^{\mathsf{\Phi }}}{l_{\min ,k}},\hfill \\ l_{\min ,k}=l_{\min }({\mathbf{u}}_k,{\mathbf{u}}_{k-1},\dots ,{\mathbf{u}}_{k-n_u}),\hfill \end{array}$$

(57)

where $l_{\min ,k}$ is the minimal distance between all possible pairs of complement affine subspaces that can be generated from the set of points ${\mathcal{S}}_k=\{{\mathbf{u}}_k,{\mathbf{u}}_{k-1},\dots ,{\mathbf{u}}_{k-n_u}\}$. Using (55) and (57), the gradient-error norm can be bounded from above by

$$\begin{array}{c}\parallel {\mathbf{ϵ}}_k\parallel \le \parallel {\mathbf{ϵ}}_k^t\parallel +\parallel {\mathbf{ϵ}}_k^n\parallel \le E_k^{\mathsf{\Phi }}:={\mathrm{d}}^{\mathsf{\Phi }}{r}_k+\frac{{\delta }^{\mathsf{\Phi }}}{l_{\min ,k}}.\hfill \end{array}$$

(58)

5.2. Computation of Gradient Modifiers

5.2.1. Modifiers from Estimated Gradients

The most straightforward way of computing the gradient modifiers is to evaluate them directly from the estimated gradients, according to their definition (20):

$$\begin{array}{cc}\hfill {\left({\mathbf{\lambda }}_k^{\mathsf{\Phi }}\right)}^{\mathrm{T}}& ={\widehat{\nabla \mathsf{\Phi }}}_{p,k}-\frac{\partial \mathsf{\Phi }}{\partial \mathbf{u}}\left({\mathbf{u}}_k\right),\hfill \end{array}$$

(59a)

$$\begin{array}{cc}\hfill {\left({\mathbf{\lambda }}_k^{G_i}\right)}^{\mathrm{T}}& ={\widehat{\nabla G}}_{p,i,k}-\frac{\partial G_i}{\partial \mathbf{u}}\left({\mathbf{u}}_k\right),i=1,\dots ,n_g,\hfill \end{array}$$

(59b)

where, in principle, any of the methods described in Section 5.1 can be used to obtain the gradient estimates ${\widehat{\nabla \mathsf{\Phi }}}_{p,k}$ and ${\widehat{\nabla G}}_{p,i,k}$.

5.2.2. Modifiers from Linear Interpolation or Linear Regression

Instead of using a sample set of steady-state operating points to estimate the gradients, it is possible to use the same set to directly compute the gradient modifiers by linear interpolation or linear regression. For instance, Marchetti [65] proposed to estimate the gradient modifiers by linear interpolation using the set of $n_u+1$ RTO points ${\left\{{\mathbf{u}}_{k-j}\right\}}_{j=0}^{n_u}$. In addition to the plant vectors $\mathbf{\delta }{\tilde{\mathsf{\Phi }}}_{p,k}$ and $\mathbf{\delta }{\tilde{G}}_{p,i,k}$ given in (47) and (48), their model counterparts can be constructed at the kth RTO iteration:

$$\begin{array}{c}\mathbf{\delta }{\mathsf{\Phi }}_k:={\left[\begin{array}{ccc}\mathsf{\Phi }\left({\mathbf{u}}_k\right)-\mathsf{\Phi }\left({\mathbf{u}}_{k-1}\right),& \dots ,& \mathsf{\Phi }\left({\mathbf{u}}_k\right)-\mathsf{\Phi }\left({\mathbf{u}}_{k-n_u}\right)\end{array}\right]}^{\mathrm{T}}\in \mathrm{I}{\mathrm{R}}^{n_u},\hfill \end{array}$$

(60)

$$\begin{array}{c}\mathbf{\delta }{G}_{i,k}:={\left[\begin{array}{ccc}{G}_i\left({\mathbf{u}}_k\right)-G_i\left({\mathbf{u}}_{k-1}\right),& \dots ,& G_i\left({\mathbf{u}}_k\right)-G_i\left({\mathbf{u}}_{k-n_u}\right)\end{array}\right]}^{\mathrm{T}}\in \mathrm{I}{\mathrm{R}}^{n_u},i=1,\dots ,n_g.\hfill \end{array}$$

(61)

The interpolation conditions for the modified cost function read:

$$\begin{array}{c}\hfill {\mathsf{\Phi }}_{m,k}\left({\mathbf{u}}_{k-j}\right)=\mathsf{\Phi }\left({\mathbf{u}}_{k-j}\right)+{\epsilon }_k^{\mathsf{\Phi }}+{\left({\mathbf{\lambda }}_k^{\mathsf{\Phi }}\right)}^{\mathrm{T}}({\mathbf{u}}_{k-j}-{\mathbf{u}}_k)={\tilde{\mathsf{\Phi }}}_{p,k-j},j=1,\dots ,n_u,\end{array}$$

(62)

with ${\epsilon }_k^{\mathsf{\Phi }}={\tilde{\mathsf{\Phi }}}_{p,k}-\mathsf{\Phi }\left({\mathbf{u}}_k\right)$. Equation (62) forms a linear system in terms of the gradient modifier and can be written in matrix form as

$$\begin{array}{c}{\left({\mathrm{U}}_k\right)}^{\mathrm{T}}{\mathbf{\lambda }}_k^{\mathsf{\Phi }}=\mathbf{\delta }{\tilde{\mathsf{\Phi }}}_{p,k}-\mathbf{\delta }{\mathsf{\Phi }}_k,\hfill \end{array}$$

(63)

where ${\mathrm{U}}_k$ and $\mathbf{\delta }{\tilde{\mathsf{\Phi }}}_{p,k}$ are the quantities defined in (46) and (47), respectively. This system of equations has a unique solution if the matrix ${\mathrm{U}}_k$ is nonsingular. The constraint gradient modifiers can be computed in a similar way, which leads to the following expressions for the gradient modifiers [65]:

$$\begin{array}{cc}\hfill {\left({\mathbf{\lambda }}_k^{\mathsf{\Phi }}\right)}^{\mathrm{T}}& ={(\mathbf{\delta }{\tilde{\mathsf{\Phi }}}_{p,k}-\mathbf{\delta }{\mathsf{\Phi }}_k)}^{\mathrm{T}}{\left({\mathrm{U}}_k\right)}^{-1},\hfill \end{array}$$

(64a)

$$\begin{array}{cc}\hfill {\left({\mathbf{\lambda }}_k^{G_i}\right)}^{\mathrm{T}}& ={(\mathbf{\delta }{\tilde{G}}_{p,i,k}-\mathbf{\delta }{G}_{i,k})}^{\mathrm{T}}{\left({\mathrm{U}}_k\right)}^{-1},i=1,\dots ,n_g.\hfill \end{array}$$

(64b)

Here, the sample points consist of the current and $n_u$ most recent RTO points. However, it is also possible to include designed perturbations in the sample set.

Figure 3 shows how the modified cost function approximates the plant cost function using MA when (i) the points $\{u_k,u_{k-1}\}$ are used to obtain the simplex gradient estimate (50), which is then used in (59a) to compute the gradient modifier, and (ii) the same points are used to compute the linear interpolation gradient modifier (64a). It can be seen that the linear interpolation approach gives a better approximation of the plant cost function, especially if the points are distant from each other.

Remark 7

(Linear regression). If there are more than $n_u+1$ sample points, it might not be possible to interpolate all the points. In this case, it is possible to evaluate the gradient modifiers by linear least-square regression.

Remark 8

(Quadratic interpolation). In case of second-order MA, it is possible to compute the gradient and Hessian modifiers by quadratic interpolation or quadratic least-squares regression. In this case, the number of well-poised points required for complete quadratic interpolation is $(n_u+1)(n_u+2)/2$ (see [34] for different measures of well poisedness that can be used to select or design the points included in the sample set).

5.2.3. Nested MA

A radically different approach for determining the gradient modifiers has been proposed recently [79]. Rather than trying to estimate the plant gradients, it has been proposed to identify the gradient modifiers directly via derivative-free optimization. More specifically, the RTO problem is reformulated as two nested optimization problems, with the outer optimization computing the gradient modifiers at low frequency and the inner optimization computing the inputs more frequently. We shall use the indices j and k to denote the iterations of the outer and inner optimizations, respectively.

The inner optimization problem (for j fixed) is formulated as follows:

$$\begin{array}{cc}\hfill {\mathbf{u}}_{k+1}^{★}=\underset{\mathbf{u}}{arg\; min}& {\mathsf{\Phi }}_{m,k}\left(\mathbf{u}\right):=\mathsf{\Phi }\left(\mathbf{u}\right)+{\left({\mathbf{\lambda }}_j^{\mathsf{\Phi }}\right)}^{\mathrm{T}}\mathbf{u}\hfill \end{array}$$

(65a)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& G_{m,i,k}\left(\mathbf{u}\right):=G_i\left(\mathbf{u}\right)+{\epsilon }_k^{G_i}+{\left({\mathbf{\lambda }}_j^{G_i}\right)}^{\mathrm{T}}(\mathbf{u}-{\mathbf{u}}_k)\le 0i=1,\dots ,n_g.\hfill \end{array}$$

(65b)

Note the difference with (21a): for the inner optimization, the gradient modifiers are considered as constant parameters that are updated by the outer optimization. The values of the converged inputs, ${\mathbf{u}}_{\infty }^{★}$, and of the converged Lagrange multipliers associated with the constraints, ${\mathbf{\mu }}_{\infty }^{★}$, depend on the choice of the modifiers ${\mathbf{\lambda }}_j^{\mathsf{\Phi }}$ and ${\mathbf{\lambda }}_j^{G_i}$. For the sake of notation, let us group these modifiers in the matrix ${\mathbf{\Lambda }}_j:=\left[{\mathbf{\lambda }}_j^{\mathsf{\Phi }}{\mathbf{\lambda }}_j^{G_1}\dots {\mathbf{\lambda }}_j^{G_{n_g}}\right]$.

Once the inner optimization has converged, the following unconstrained outer optimization problem is solved:

$$\begin{array}{cc}\hfill {\mathbf{\Lambda }}_{j+1}^{★}=\underset{\mathbf{\Lambda }}{arg\; min}& \left\{{\mathsf{\Phi }}_p\left({\mathbf{u}}_{\infty }^{★}\left({\mathbf{\Lambda }}_j\right)\right)+{\left({\mathbf{\mu }}_{\infty }^{★}\left({\mathbf{\Lambda }}_j\right)\right)}^{\mathrm{T}}{\mathbf{G}}_p\left({\mathbf{u}}_{\infty }^{★}\right)\right\},\hfill \end{array}$$

(66)

and the inner optimization problem is repeated for the modifiers ${\mathbf{\Lambda }}_{j+1}$. Note that, since the functions ${\mathsf{\Phi }}_p$ and ${\mathbf{G}}_p$ are unknown, Problem (66) is conveniently solved using derivative-free optimization techniques such as the Nelder-Mead simplex method [79]. Furthermore, it has been shown that separating the MA problem into two nested optimization problems preserves the ability to reach a KKT point of the plant [79]. However, since Nested MA often requires many iterations (for both the j and k indices), it is characterized by potentially slow convergence.

5.3. Dual MA Schemes

Following the idea of the dual ISOPE algorithm [7,63], dual MA schemes estimate the gradients based on the measurements obtained at the current and past operating points by adding a duality constraint in the modified optimization problem. This constraint is used to ensure sufficient variability in the data for estimating the gradients reliably. Several dual MA schemes have been proposed that differ in the model modification introduced, the approach used for estimating the gradients, and the choice of the duality constraint.

The following duality constraint is used to position the next RTO point with respect to the $n_u$ most recent points $\{{\mathbf{u}}_k,{\mathbf{u}}_{k-1},\dots ,{\mathbf{u}}_{k-n_u+1}\}$:

$$\begin{array}{c}{\mathcal{D}}_k\left(\mathbf{u}\right):=\mathcal{D}(\mathbf{u},{\mathbf{u}}_k,{\mathbf{u}}_{k-1},\dots ,{\mathbf{u}}_{k-n_u+1})\le 0.\hfill \end{array}$$

(67)

To compute the simplex gradient (50), or the interpolation modifiers (64) at the next RTO point ${\mathbf{u}}_{k+1}$, we require the matrix ${\mathrm{U}}_{k+1}$ defined in (46) to be nonsingular. Assuming that the last $n_u-1$ columns of ${\mathrm{U}}_{k+1}$ are linearly independent, they constitute a basis for the unique hyperplane ${\mathcal{H}}_k=\{\mathbf{u}\in \mathrm{I}{\mathrm{R}}^{n_u}:{\mathrm{n}}_k^{\mathrm{T}}\mathbf{u}=b_k,\mathrm{with}{b}_k={\mathrm{n}}_k^{\mathrm{T}}{\mathbf{u}}_k\}$ that contains the points $\{{\mathbf{u}}_k,{\mathbf{u}}_{k-1},\dots ,{\mathbf{u}}_{k-n_u+1}\}$. Here, ${\mathrm{n}}_k$ is a vector that is orthogonal to the hyperplane. Hence, the matrix ${\mathrm{U}}_{k+1}$ will be nonsingular if ${\mathbf{u}}_{k+1}$ does not belong to ${\mathcal{H}}_k$ [65]. For this reason, duality constraints produce two disjoint feasible regions, one on each side of the hyperplane ${\mathcal{H}}_k$.

Dual MA schemes typically solve two modified optimization problems that include the duality constraint, one for each side of the hyperplane ${\mathcal{H}}_k$. For the half space ${\mathrm{n}}_k^{\mathrm{T}}\mathbf{u}>b_k$, we solve:

$$\begin{array}{cc}\hfill {\mathbf{u}}_{k+1}^{+}=\underset{\mathbf{u}}{arg\; min}& {\mathsf{\Phi }}_{m,k}\left(\mathbf{u}\right)=\mathsf{\Phi }\left(\mathbf{u}\right)+{\epsilon }_k^{\mathsf{\Phi }}+{\left({\mathbf{\lambda }}_k^{\mathsf{\Phi }}\right)}^{\mathrm{T}}(\mathbf{u}-{\mathbf{u}}_k)\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& G_{m,i,k}\left(\mathbf{u}\right)=G_i\left(\mathbf{u}\right)+{\epsilon }_k^{G_i}+{\left({\mathbf{\lambda }}_k^{G_i}\right)}^{\mathrm{T}}(\mathbf{u}-{\mathbf{u}}_k)\le 0,i=1,\dots ,n_g,\hfill \\ & {\mathcal{D}}_k\left(\mathbf{u}\right)\le 0,{\mathrm{n}}_k^{\mathrm{T}}\mathbf{u}\ge b_k,\hfill \end{array}$$

(68)

while for the half space ${\mathrm{n}}_k^{\mathrm{T}}\mathbf{u}<b_k$, we solve:

$$\begin{array}{cc}\hfill {\mathbf{u}}_{k+1}^{-}=\underset{\mathbf{u}}{arg\; min}& {\mathsf{\Phi }}_{m,k}\left(\mathbf{u}\right)=\mathsf{\Phi }\left(\mathbf{u}\right)+{\epsilon }_k^{\mathsf{\Phi }}+{\left({\mathbf{\lambda }}_k^{\mathsf{\Phi }}\right)}^{\mathrm{T}}(\mathbf{u}-{\mathbf{u}}_k)\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& G_{m,i,k}\left(\mathbf{u}\right)=G_i\left(\mathbf{u}\right)+{\epsilon }_k^{G_i}+{\left({\mathbf{\lambda }}_k^{G_i}\right)}^{\mathrm{T}}(\mathbf{u}-{\mathbf{u}}_k)\le 0,i=1,\dots ,n_g,\hfill \\ & {\mathcal{D}}_k\left(\mathbf{u}\right)\le 0,{\mathrm{n}}_k^{\mathrm{T}}\mathbf{u}\le b_k,\hfill \end{array}$$

(69)

The next operating point ${\mathbf{u}}_{k+1}$ is chosen as the solution that minimizes ${\mathsf{\Phi }}_{m,k}\left(\mathbf{u}\right)$:

$$\begin{array}{c}{\mathbf{u}}_{k+1}=\underset{\mathbf{u}}{arg\; min}{\mathsf{\Phi }}_{m,k}\left(\mathbf{u}\right),\mathrm{s}.\mathrm{t}.\mathbf{u}\in \{{\mathbf{u}}_{k+1}^{+},{\mathbf{u}}_{k+1}^{-}\}.\hfill \end{array}$$

Several alternative dual MA algorithms have been proposed in the literature, which we briefly describe next:

(a)

The original dual ISOPE algorithm [7,63] estimates the gradients by FDA according to (50) and introduces a constraint that prevents ill-conditioning in the gradient estimation. At the kth RTO iteration, the matrix

$$\begin{array}{c}{\overline{\mathrm{U}}}_k\left(\mathbf{u}\right):=\left[\begin{array}{cccc}\mathbf{u}-{\mathbf{u}}_k,& \mathbf{u}-{\mathbf{u}}_{k-1},& \dots ,& \mathbf{u}-{\mathbf{u}}_{k-n_u+1}\end{array}\right]\in \mathrm{I}{\mathrm{R}}^{n_u\times n_u}\hfill \end{array}$$

(70)

is constructed. Good conditioning is achieved by adding the lower bound φ on the inverse of the condition number of ${\overline{\mathrm{U}}}_k\left(\mathbf{u}\right)$:

$$\begin{array}{c}\frac{1}{{\kappa }_k\left(\mathbf{u}\right)}=\frac{{\sigma }_{\min }\left({\overline{\mathrm{U}}}_k\left(\mathbf{u}\right)\right)}{{\sigma }_{\max }\left({\overline{\mathrm{U}}}_k\left(\mathbf{u}\right)\right)}\ge \phi ,\hfill \end{array}$$

(71)

where ${\sigma }_{\min }$ and ${\sigma }_{\max }$ denote the smallest and largest singular values, respectively. This bound is enforced by defining the duality constraint

$$\begin{array}{c}{\mathcal{D}}_k\left(\mathbf{u}\right)=\phi {\kappa }_k\left(\mathbf{u}\right)-1\le 0,\hfill \end{array}$$

(72)

which is used in (68) and (69).

(b)

Gao and Engell [14] proposed a MA scheme that (i) estimates the gradients from the current and past operating points according to (50), and (ii) enforces the ill-conditioning duality constraint (72). However, instead of including the duality constraint in the optimization problem, it is used to decide whether an additional input perturbation is needed. This perturbation is obtained by minimizing the condition number ${\kappa }_k\left(\mathbf{u}\right)$ subject to the modified constraints. The approach was labeled Iterative Gradient-Modification Optimization (IGMO) [80].

(c)

Marchetti et al. [64] considered the dual MA scheme that estimates the gradients from the current and past operating points according to (50). The authors showed that the ill-conditioning bound (71) has no direct relationship with the accuracy of the gradient estimates, and proposed to upper bound the gradient-error norm of the Lagrangian function:

$$\begin{array}{c}\parallel {\mathbf{ϵ}}^L\left(\mathbf{u}\right)\parallel \le E^{\mathrm{U}},\hfill \end{array}$$

(73)

where ${\mathbf{ϵ}}^L$ is the Lagrangian gradient error. In order to compute the upper bound as a function of $\mathbf{u}$, we proceed as in (56)–(58) and define the radius $r_k\left(\mathbf{u}\right)=r(\mathbf{u},{\mathbf{u}}_k,\dots ,{\mathbf{u}}_{k-n_u+1})$ and the minimal distance $l_{\min ,k}\left(\mathbf{u}\right)=l_{\min }(\mathbf{u},{\mathbf{u}}_k,\dots ,{\mathbf{u}}_{k-n_u+1})$. This allows enforcing (73) by selecting $\mathbf{u}$ such that,

$$\begin{array}{c}{E}_k^L\left(\mathbf{u}\right):={\mathrm{d}}^L{r}_k\left(\mathbf{u}\right)+\frac{{\delta }^L}{l_{\min ,k}\left(\mathbf{u}\right)}\le E^{\mathrm{U}},\hfill \end{array}$$

(74)

where ${\mathrm{d}}^L$ is an upper bound on the spectral radius of the Hessian of the Lagrangian function, and ${\delta }^L$ is the range of measurement error in the Lagrangian function resulting from measurement noise in the cost and constraints [64]. This bound is enforced by defining the duality constraint used in (68) and (69) as

$$\begin{array}{cc}\hfill {\mathcal{D}}_k\left(\mathbf{u}\right)& =E_k^L\left(\mathbf{u}\right)-E^{\mathrm{U}}\le 0.\hfill \end{array}$$

(75)

(d)

Rodger and Chachuat [67] proposed a dual MA scheme based on modifying the output variables as in Section 4.2.1. The gradients of the output variables are estimated using Broyden’s formula (51). The authors show that, with Broyden’s approach, the MA scheme (28) may fail to reach a plant KKT point upon convergence due to inaccurate gradient estimates and measurement noise. This may happen if the gradient estimates are not updated repeatedly in all input directions and if the step $\parallel {\mathbf{u}}_{k+1}-{\mathbf{u}}_k\parallel$ is too small. A duality constraint is proposed for improving the gradient estimates obtained by Broyden’s approach.

(e)

Marchetti [65] proposed another dual MA scheme, wherein the gradient modifiers are obtained by linear interpolation according to (64). Using this approach, the modified cost and constraint functions approximate the plant in a larger region. In order to limit the approximation error in the presence of noisy measurements, a duality constraint was introduced that limits the Lagrangian gradient error for at least one point belonging to the simplex with the extreme points $\{\mathbf{u},{\mathbf{u}}_k,\dots ,{\mathbf{u}}_{k-n_u+1}\}$. This duality constraint produces larger feasible regions than (75) for the same upper bound $E^{\mathrm{U}}$, and therefore allows larger input moves and faster convergence.

6. Applications

As MA has many useful features, it is of interest to investigate its potential for application.

Table 1. Overview of MA case studies (FFD: forward finite difference with input perturbation; FDA: finite-difference approximation based on past and current operating points; NE: neighboring extremals; CA: Constraint Adaptation; MAWQA: MA with quadratic approximation; IGMO: iterative gradient-modification optimization, where gradients are estimated via FDA with added perturbation when necessary; in bold: experimental implementation).

Problems	MA Variant	Ref.	Gradient Est.	# of Inputs	Remarks
Williams-Otto CSTR (benchmark for MA)	MA	[64]	FFD	2	basic MA algorithm
	dual MA	[64,65]	FDA, lin. approx.	2	addition of a constraint on gradient accuracy
	2nd-order MA	[31]	FFD	2	addition of second-order correction terms
	MAWQA	[36,81]	quad. approx.	2	gradient computed via quadratic approximation
	nested MA	[82]	—	2	additional optimization to by-pass gradient calculation
	various MA	[80]	various	2	IGMO, dual MA, nested MA and MAWQA
CSTR (with pyrrole reaction)	convex MA	[21]	perfect	2	use of convex model
	transient MA	[54]	NE-based	2	use of transient measurements for static optimization
	MAWQA	[83]	quad. approx.	2	gradient computed via quadratic approximation
Semi-batch reactors	dual, nested MA	[79]	FDA, —	3	4 reactions, run-to-run scheme
	MA	[84]	FDA	11	1 reaction, run-to-run scheme
Distillation column	various MA	[85,86]	various	2	controlled column, dual, nested, transient measurements
Batch chromatography	various MA	[14,87]	various	2	IGMO, dual MA and MAWQA, run-to-run schemes
Electro-chromatography	dual MA	[88]	IGMO	2	Continuous process
Chromatographic separation	dual MA	[89]	IGMO	3	Continuous multi-column solvent gradient purification
Sugar and ethanol plant	MA	[56]	FDA	6	heat and power system
Leaching process	MA		FDA	4	4 CSTR in series, industrial implementation
Hydroformylation process	MAWQA	[91]	quad. approx.	4	reactor and decanter with recycle
Flotation column	various MA	[92]	FFD, FDA, —	3	implemented on lab-scale column
Three-tank system	MA	[15]; [79]	FFP; FDA, —	2	implemented on lab-scale setup
Solid-oxide fuel cell	CA	[93];[53]	—	3; 2	implemented on lab fuel-cell stack
Parallel compressors	MA	[94]	FFP	2 & 6	parallel structure exploited for gradient estimation
Path-following robot	CA	[95]	—	700	periodic operation, enforcing minimum-time motion
Power kite	D-MA	[28], [96]	FDA	40 → 2	periodic operation,implemented on small-scale kite

lists several case studies available in the literature and compares them in terms of the MA variant that is used, the way the gradients are estimated and the number of input variables. Although this list is not exhaustive, it provides an overview of the current situation and gives a glimpse of the potential ahead. From this table, several interesting conclusions can be drawn:

• About half of the available studies deal with chemical reactors, both continuous and discontinuous. In the case of discontinuous reactors, the decision variables are input profiles, that can be parameterized to generate a larger set of constant input parameters. The optimization is then performed on a run-to-run basis, with each iteration hopefully resulting in improved operation.
• One sees from the list of problems in Table 1 that the Williams-Otto reactor seems to be the benchmark problem for testing MA schemes. The problem is quite challenging due to the presence of significant structural plant model-mismatch. Indeed, the plant is simulated as a 3-reaction system, while the model includes only two reactions with adjustable kinetic parameters. Despite very good model fit (prediction of the simulated concentrations), the RTO techniques that cannot handle structural uncertainty, such as the two-step approach, fail to reach the plant optimum. In contrast, all 6 MA variants converge to the plant optimum. The differentiation factor is then the convergence rate, which is often related to the estimation of plant gradients.
• Most MA schemes use FDA to estimate gradients. In the case of FFD, one needs to perturb each input successively; this is a time-consuming operation since, at the current operating point, the system must be perturbed $n_u$ times, each time waiting for the plant to reach steady state. Hence, FDA based on past and current operating points is clearly the preferred option. However, to ensure that sufficient excitation is present to compute accurate gradients, the addition of a duality constraint is often necessary. Furthermore, both linear and nonlinear function approximations have been proposed with promising results. An alternative is to use the concept of neighboring extremals (NE), which works well when the uncertainty is of parametric nature (because the NE-based gradient law assumes that the variations are due to parametric uncertainties). Note that two approaches do not use an estimate of the plant gradient: CA uses only zeroth-order modifiers to drive the plant to the active constraints, while nested MA circumvents the computation of plant gradients by solving an additional optimization problem. Note also that IGMO can be classified as dual MA, with the peculiarity that the gradients are estimated via FDA with added perturbations when necessary.
• The typical number of input variables is small ($n_u<5$), which seems to be related to the difficulties of gradient estimation. When the number of inputs is much larger, it might be useful to investigate whether it is important to correct the model in all input directions, which is nicely solved using D-MA.
• Two applications, namely, the path-following robot and the power kite, deal with the optimization of dynamic periodic processes. Each period (or multiple periods) is considered as a run, the input profiles are parameterized, and the operation is optimized on a run-to-run basis.
• Five of these case studies have dealt with experimental implementation, four on lab-scale setups and one at the industrial level. There is clearly room for more experimental implementations and, hopefully, also significant potential for improvements ahead!

7. Conclusions

This section concludes the paper with a brief discussion of open issues and a few final words.

7.1. Open Issues

As illustrated in this paper, significant progress has been made recently on various aspects of MA. Yet, there are still unresolved issues with respect to both the methodology and applications. In particular, it is desirable for RTO schemes to exhibit the following features [38]:

  i

plant optimality and feasibility upon convergence,

 ii

acceptable number of RTO iterations, and

iii

plant feasibility throughout the optimization process.

These features and related properties are briefly discussed next.

Feasibility of all RTO iterates. By construction, MA satisfies Feature (i), cf. Theorem 1. However, Theorem 1 does not guarantee feasibility of the successive RTO iterates, nor does it imply anything regarding convergence speed. The Sufficient Conditions for Feasibility and Optimality (SCFO) presented in [35,97] can, in principle, be combined with any RTO scheme and enforce Feature (iii). However, SCFO often fails to enforce sufficiently fast convergence (cf. the examples provided in [35], Section 4.4) because of the necessity to upper bound uncertain plant constraints using Lipschitz constants. Hence, it is fair to search for other approaches that can ensure plant feasibility of the successive RTO iterates. One intuitive way is to replace the first-order (Lipschitz) upper bounds in [35] by second-order upper-bounding functions. For purely data-driven RTO, it has been shown numerically that this outperforms Lipschitz bounds [38]. Furthermore, the handling of plant infeasibility in dual MA has been discussed in [43]. New results given in [98] demonstrate that the combination of convex upper-bounding functions with the usual first-order MA corrections terms implies optimality upon convergence (Feature (i)) and feasibility for all iterates (Feature (iii)). However, a conclusive analysis of the trade-off between convergence speed and the issue of plant feasibility has not been conducted yet. Using the numerical optimization terminology, one could say that it remains open how one chooses the step length in RTO, when plant feasibility and fast convergence are both important.

Robustness to gradient uncertainty. The implementation of MA calls for the estimation of plant gradients. At the same time, as estimated gradients are prone to errors, it is not clear to which extent MA is robust to this kind of uncertainty. Simulation studies such as [15,64] indicate that MA is reasonably robust with respect to gradient uncertainty. For data-driven RTO schemes inspired by SCFO [35], robustness to multiplicative cost gradient uncertainty has been shown [37]. However, the assumption of purely multiplicative gradient uncertainty is hard to justify in practice, as this would imply exact gradient information at any unconstrained local optimum of the plant.

Realistically, one has to assume that gradient uncertainty is additive and bounded. First steps towards a strictly feasible MA scheme can be found in [99], wherein convex upper-bounding functions similar to [98] are combined with dual constraints from Section 5.3 [64].

Exploitation of plant structure for gradient estimation. In the presentation of the different MA variants, it is apparent that the physical structure of the plant (parallel or serial connections, recycles, weak and strong couplings) has not been the focus of investigation. At the same time, since many real-world RTO applications possess a specific structure, it is fair to ask whether one can exploit the physical interconnection structure to facilitate and possibly improve gradient estimation.

Parallel structures with identical units may be well suited for gradient estimation [76]. Recently, it has been observed that, under certain assumptions, parallel structures of heterogeneous units can also be exploited for gradient estimation [94]. A formal and general investigation of the interplay between plant structure and gradient estimation remains open.

RTO of interconnected processes. There is an evident similarity between many RTO schemes and numerical optimization algorithms. For example, one might regard MA adaptation in its simpliest form of Section 4.1 as an experimental gradient descent method, likewise the scheme of Section 4.3.2 is linked to trust-region algorithms, and Remark 3 has pointed toward a SQP-like scheme. Hence, one might wonder whether the exploitation of structures in the spirit of distributed NLP algorithms will yield benefits to RTO and MA schemes. The early works on distributed ISOPE methods [7,100,101] point into such a direction. Furthermore, a recent paper by Wenzel et al. [102] argues for distributed plant optimization for the sake of confidentiality. In the context of MA, it is interesting to note that different distributed MA algorithms have recently been proposed [103,104]. Yet, there is no common consensus on the pros and cons of distributed RTO schemes.

Integration with advanced process control. Section 4.4.1 discussed the application of MA to controlled plants, and highlighted that the implementation of RTO results by means of MPC can be used to prevent constraint violations. Section 4.4.3 reported on the use of transient data for the purpose of gradient estimation for static MA. In general, it seems that the use of transient measurements in RTO either requires specific dynamic properties of the underlying closed-loop system or a tight integration of RTO and advanced process control. As many industrial multivariable process control tasks are nowadays solved via MPC, this can be narrowed down to the integration of MA and MPC. Yet, there remain important questions: (i) How to exploit the properties of MPC for RTO or MA? (ii) Can one use the gradient information obtained for MA in the MPC layer? While there are answers to Question (i) [45,105]; Question (ii) remains largely unexplored. This also raises the research question of how to design (static) MA and (dynamic) process control in a combined fashion or, expressed differently, how to extend the MA framework toward dynamic RTO problems. The D-MA approach sketched in Section 4.2.3 represents a first promising step for periodic and batch dynamic processes. Yet, the close coupling between MA and economic MPC schemes might bring about interesting new research and implementation directions [106,107,108].

Model-based or data-driven RTO? The fact that all MA properties also hold for the trivial case of no model gives rise to the fundamental question regarding the role of models in RTO. As shown in Section 4, models are not needed in order to enforce plant optimality upon convergence in MA. Furthermore, models bring about the model-adequacy issue discussed in Section 4.1.3. At the same time, industrial practitioners often spend a considerable amount of time on model building, parameter estimation and model validation. Hence, from the industrial perspective, there is an evident expectation that the use of models should pay off in RTO. From the research perspective, this gives rise to the following question: How much should we rely on uncertain model and how much on available plant data? In other words, what is a good tuning knob between model-based and data-driven RTO?

7.2. Final Words

This overview paper has discussed real-time optimization of uncertain plants using Modifier Adaptation. It has attempted to present the main developments in a comprehensive and unified way that highlights the main differences between the schemes. Yet, as in any review, the present one is also a mere snapshot taken at a given time. As we tried to sketch it, there remain several open issues, some of which will be crucial for the success of modifier-adaptation schemes in industrial practice.