Species Coexistence in Nitrifying Chemostats: A Model of Microbial Interactions
Abstract
:1. Introduction
2. Materials and Methods
2.1. Nitrifying Chemostat Conditions
2.2. Microbial Community Measurements
2.3. Model Development
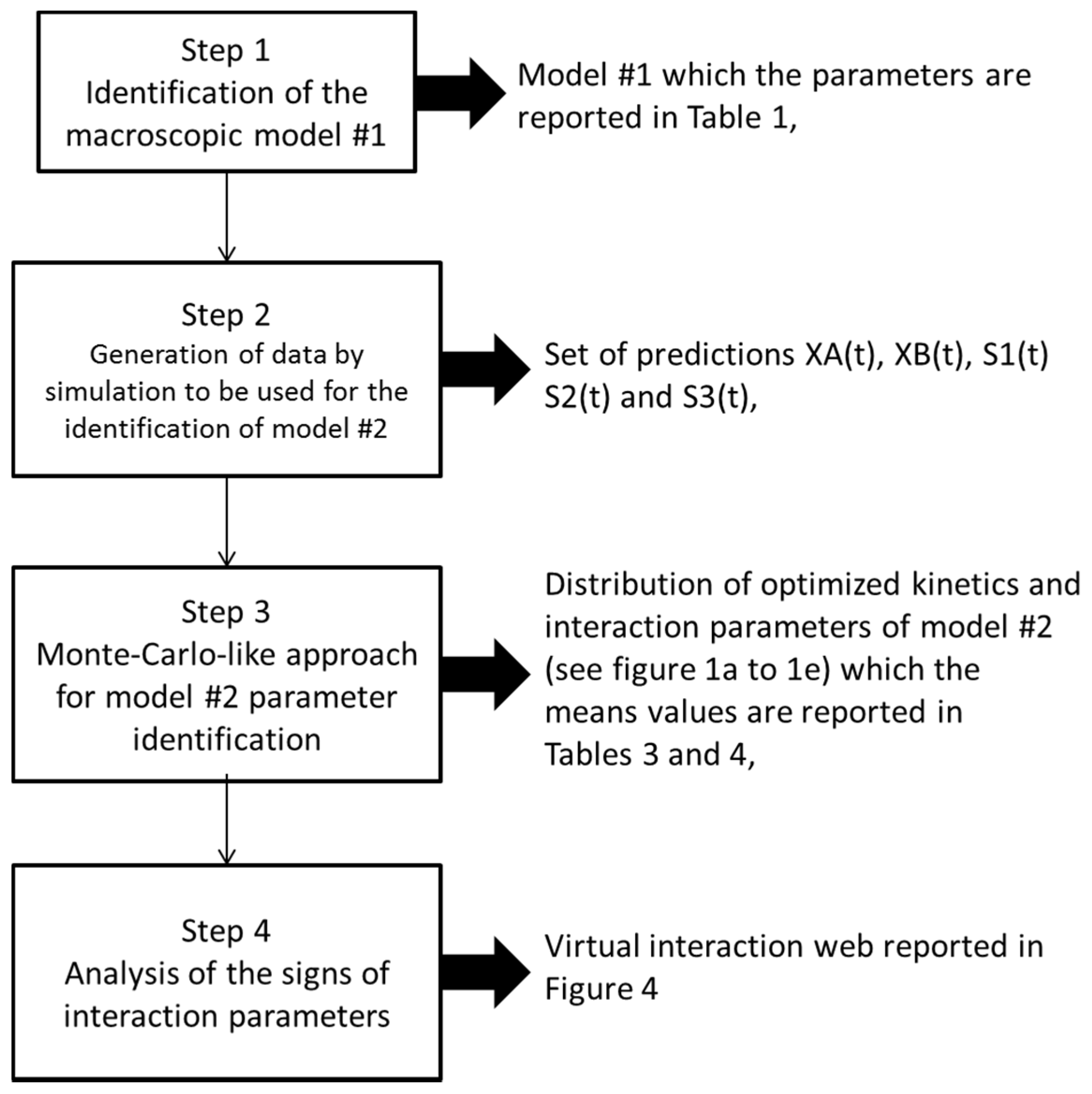
2.4. Identification of the Parameters of Microbial Interaction
- First, we randomly ran 2000 optimizations (using more did not improve the results (i.e., did not enable us to further decrease the final confidence intervals computed for each identified parameter) with different initial conditions for the parameters to be estimated (all unknown parameters in the right-hand terms of the above equations). In other terms, we identified all the parameters with different initial conditions 2000 times;
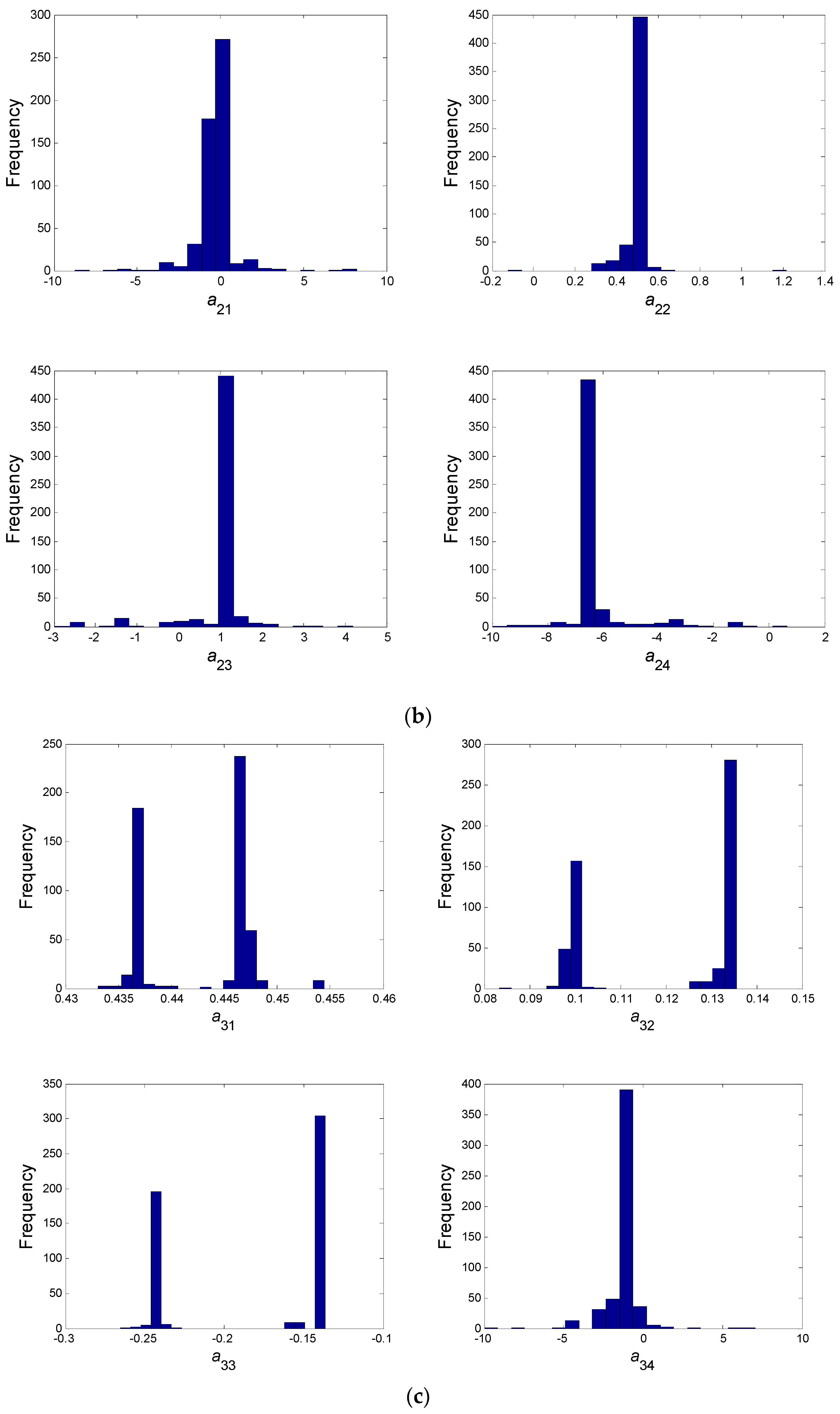
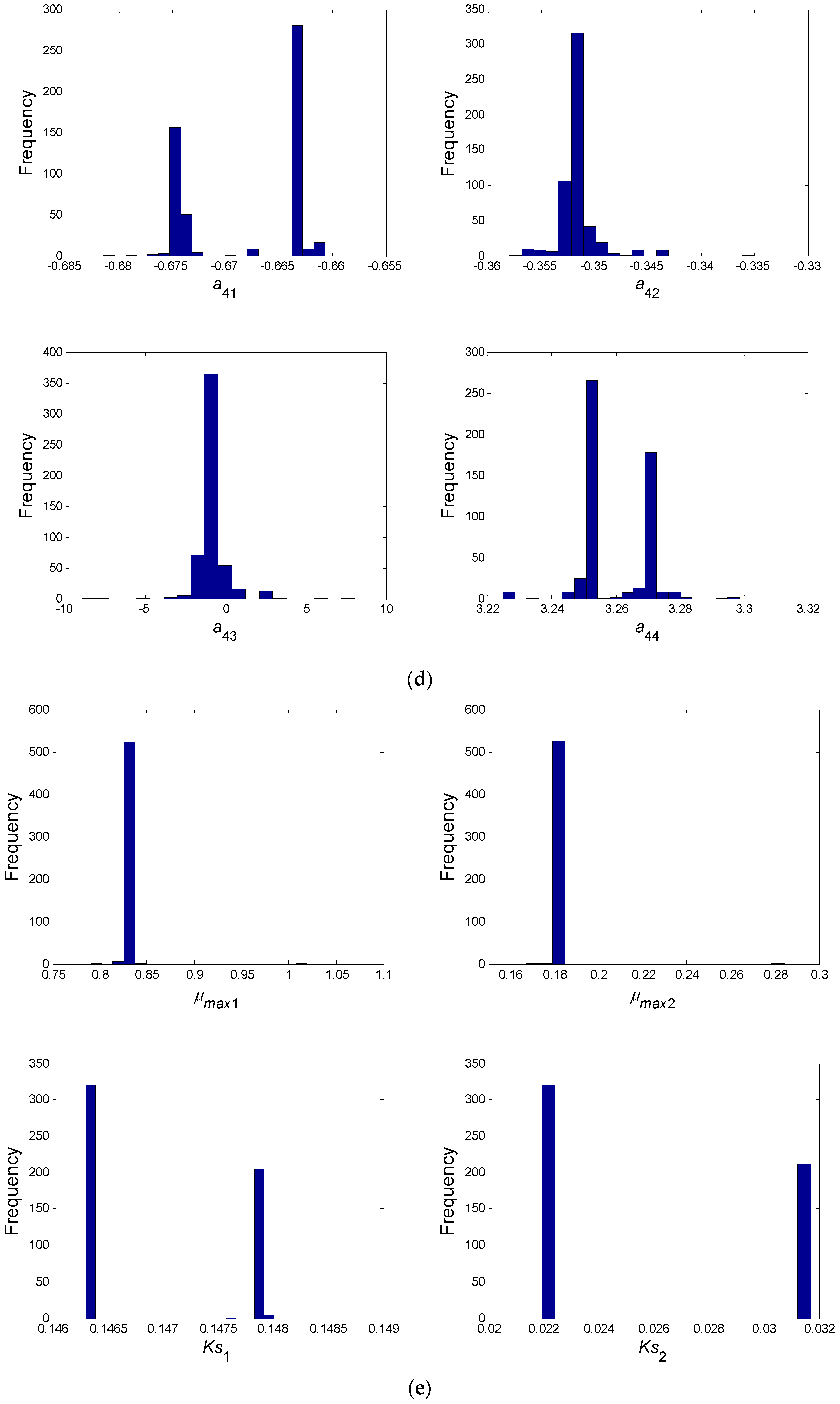
- In a second step, we have proceeded to a statistical analysis of the results, keeping only the best sets of optimized parameters that are the sets for which the SSR was, at most, 5% greater than the best solution over the 2000 optimizations. Instead of keeping only the best one, we proceeded in this way for two reasons: (i) The problem to be solved is complex, notably because the model is nonlinear and the number of unknowns is high. Thus, we did not necessarily obtain the same parameter values for each of the 2000 optimizations. In other words, the problem we consider here is said to be “non-identifiable”. It means that, given the structure of the model considered, a unique set of parameters cannot be found from the available data. In other words, there exist “hidden relationships” between parameters—possibly nonlinear—which prevent the optimization algorithm from converging towards a unique global minimum and, consequently, from delivering a unique set of optimized parameters (cf. for instance [35] or [36] for more information about this concept); (ii) in the results, either the parameters are centered around 0 with a large standard deviation (indicating either no interaction between the corresponding species or an undetermined interaction) or the signs of the identified interactions are always the same whatever the sets of optimized parameters considered and, thus, the proposed statistical analysis of the results to obtain qualitative insights about microbial interactions in the ecosystem is considered without considering precise parameter values. In the sequel, this procedure will be referred to as a “Monte-Carlo-like” approach;
- Finally, following the procedure described above, 520 sets of optimized parameters over the 2000 runs were kept and analyzed. The results are presented and discussed in the following sections.
2.5. Remarks
- An important question that may arise is the following: Why are outputs of the model #1 used in the optimization problem (in the evaluation of the left-hand terms of (5) and (6)) rather than experimental data available in [31]? The essential reason is that experimental data are corrupted by noise. It is well known in system identification that, by definition, noise is not informative. Since the problem posed here is very sensitive to data (recall, in particular, that the problem is non-identifiable), it is better to use noise-free data [35,36]. Here, completely noise-free data generated with the simulation of model #1 (itself optimized with respect to real data in Dumont’s work, cf. [31]) were used instead of using real data.
- As noted before, the sum of the four species considered within model #2 represented on average about 55% of the total biomass in the experiments published in [31]. For practical purposes, before proceeding to parameter identification, the relative abundances of these four species were re-normalized in such a way that their sum equaled the total biomass as measured in the experiments. In other words, considering that model #2 (which describes the dynamics of four species) is equivalent to saying that the two biological reactions involved are now only attributable to these four species and that the remaining detected species (41 − 4 = 37 in the data considered over the 525 days of experiments) are simply ignored.
- Finally, another question that may be posed is related to the parameter identification results. One may ask whether a solution to the optimization problem should be to fix all interaction parameters to zero or not. In fact, this solution cannot give a better fit than any other because there is no reason to have XA = X1 + X2 and XB = X3 + X4. In other terms, individual concentrations of the four AOBs and NOB species are taken explicitly into account in the criterion used to fit model #2 parameters while only the total biomass concentration was considered in the optimization criterion to optimize model #1 parameters. Since the criterions are different, model parameters (i.e., interaction terms) are tuned so that the differences between the two sides of Equations (5) and (6) are minimized.
3. Results
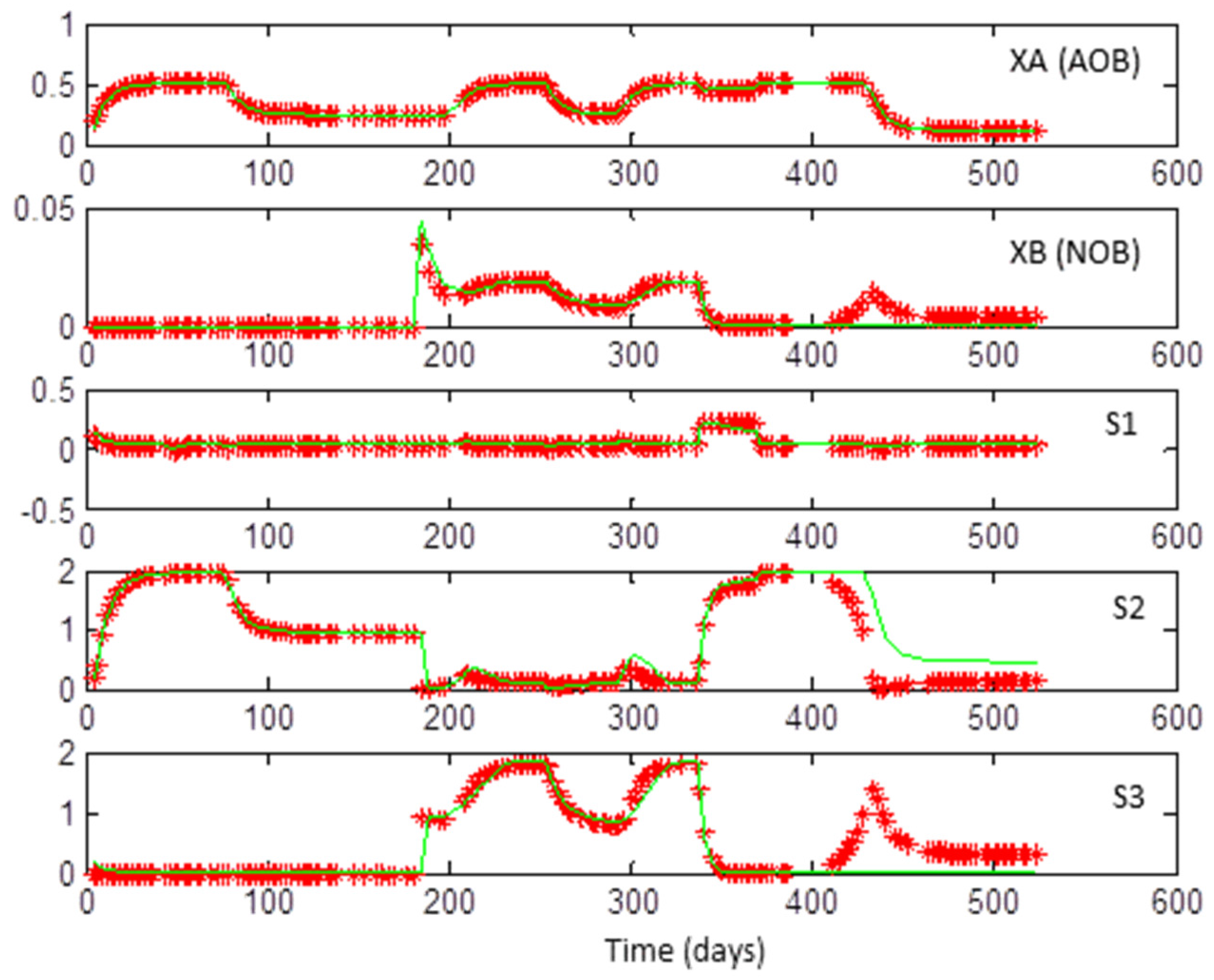
3.1. Coexistence of 2 + 2 Species on 1 + 1 Growth-Limiting Resources by Microbial Interaction
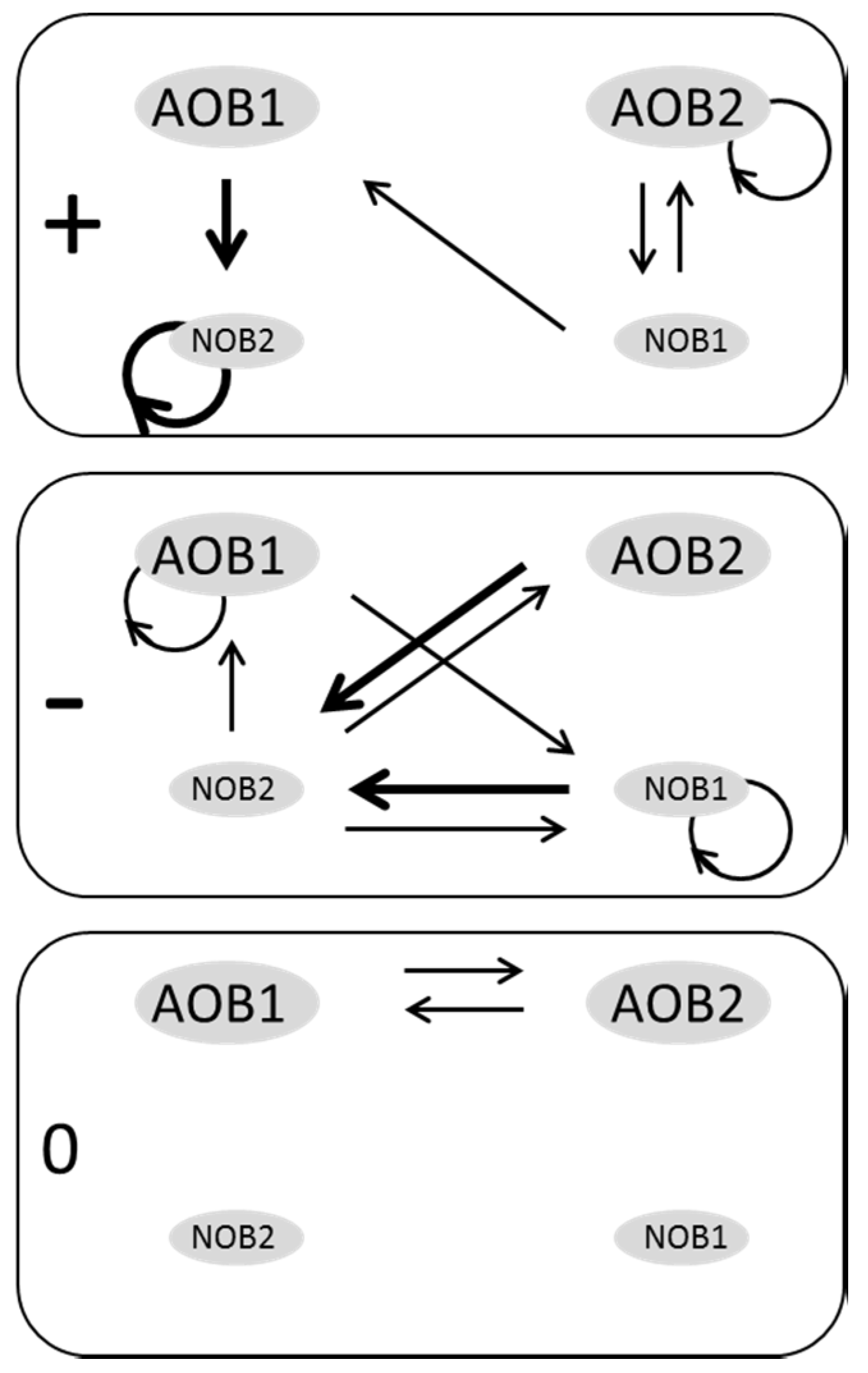
3.2. Web of Microbial Interactions
4. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Gause, G.F. Vérifications Expérimentales de la Théorie Mathématique de la Lutte pour la vie; Hermann et Cie: Paris, France, 1935. [Google Scholar]
- Hardin, G. The competitive exclusion principle. Science 1960, 131, 1292–1297. [Google Scholar] [CrossRef] [PubMed]
- Chesson, P. Mechanisms of maintenance of species diversity. Ann. Rev. Ecol. Syst. 2000, 31, 343–366. [Google Scholar] [CrossRef]
- Hutchinson, G.E. The paradox of the plankton. Am. Nat. 1961, 95, 137–145. [Google Scholar] [CrossRef]
- Hansen, S.R.; Hubbell, S.P. Single-nutrient microbial competition: qualitative agreement between experimental and theoretically forecast outcomes. Science 1980, 207, 1491–1493. [Google Scholar] [CrossRef] [PubMed]
- Aarssen, L.W. High productivity in grassland ecosystems: effected by species diversity or productive species? OIKOS 1997, 80, 183–184. [Google Scholar] [CrossRef]
- Schippers, P.; Verschoor, A.M.; Vos, M.; Mooij, W.M. Does “supersaturated coexistence” resolve the “paradox of the plankton”? Ecol. Lett. 2001, 4, 404–407. [Google Scholar] [CrossRef]
- Saikaly, P.E.; Oerther, D.B. Bacterial competition in activated sludge: Theoretical analysis of varying solids retention times on diversity. Microb. Ecol. 2003, 48, 274–284. [Google Scholar] [CrossRef] [PubMed]
- Sree Hari Rao, V.; Raja Sekhara Rao, P. Mathematical models of the microbial populations and issues concerning stability. Chaos Solitons Fractals 2005, 23, 657–670. [Google Scholar] [CrossRef]
- Hebeler, J.; Schmidt, J.K.; Reichl, U.; Flockerzi, D. Coexistence in the chemostat as a result of metabolic by-products. J. Math. Biol. 2006, 53, 556–584. [Google Scholar]
- Sommer, U. Comparison between steady state and non-steady state competition: experiments with natural phytoplankton. Limnol. Oceanogr. 1985, 30, 335–346. [Google Scholar] [CrossRef]
- Huisman, J.; Weissing, F.J. Coexistence and resource competition. Nature 2000, 4, 407–432. [Google Scholar]
- Schmidt, J.K.; Riedele, C.; Regestein, L.; Rausenberger, J.; Reichl, U. A novel concept combining experimental and mathematical analysis for the identification of unknown interspecies effects in a mixed culture. Biotechnol. Bioeng. 2011, 108, 1900–1911. [Google Scholar] [CrossRef] [PubMed]
- Marino, S.; Baxter, N.T.; Huffnagle, G.B.; Petrosino, J.F.; Schloss, P.D. Mathematical modeling of primary succession of murine intestinal microbiota. PNAS 2014, 111, 439–444. [Google Scholar] [CrossRef] [PubMed]
- Berlow, E.L.; Neutel, A.M.; Cohen, J.E.; De Ruiter, P.C.; Enbenman, B.O.; Emmerson, M.; Fox, J.W.; Jansen, V.A.A.; Jones, J.I.; Kokkoris, G.D.; et al. Interaction strengths in food webs: Issues and opportunities. J. Anim. Ecol. 2004, 73, 585–598. [Google Scholar] [CrossRef]
- Bascompte, J.; Jordano, P.; Olesen, J.M. Asymmetric coevolutionary networks facilitate biodiversity maintenance. Science 2006, 312, 431–433. [Google Scholar] [CrossRef] [PubMed]
- Michalet, R.; Brooker, R.W.; Cavieres, L.A.; Kikvidze, Z.; Lortie, C.J.; Pugnaire, F.I.; Valiente-Banuet, A.; Callaway, R.M. Do biotic interactions shape both sides of the humped-back model of species richness in plant communities? Ecol. Lett. 2006, 9, 767–773. [Google Scholar] [CrossRef] [PubMed]
- Brooker, R.W.; Maestre, F.T.; Callaway, R.M.; Lortie, C.L.; Cavieres, L.A.; Kunstler, G.; Liancourt, P.; Tielborger, K.; Travis, J.M.J.; Anthelme, F.; et al. Facilitation in plant communities: The past, the present, and the future. J. Ecol. 2008, 96, 18–34. [Google Scholar] [CrossRef]
- Gross, K. Positive interactions among competitors can produce species-rich communities. Ecol. Lett. 2008, 11, 929–936. [Google Scholar] [CrossRef] [PubMed]
- Haruta, S.; Kato, S.; Yamamoto, K.; Igarashi, Y. Intertwined interspecies relationships: Approaches to untangle the microbial network. Environ. Microbiol. 2009, 11, 2963–2969. [Google Scholar] [CrossRef] [PubMed]
- Faust, K.; Raes, J. Microbial interactions: From networks to models. Nat. Rev. 2012, 10, 538–550. [Google Scholar] [CrossRef] [PubMed]
- Ramirez, I.; Volcke, E.; Rajinikantha, R.; Steyer, J.P. Modeling microbial diversity in anaerobic digestion through an extended ADM1 model. Water Res. 2009, 43, 2787–2800. [Google Scholar] [CrossRef] [PubMed]
- Tapia, E.; Donoso, A.; Cabrol, L.; Alves, M.; Pereira, A.; Rapaport, A.; Ruiz, G. A methodology for coupling DGGE and mathematical modelling: Application in bio-hydrogen production. In Proceedings of the 13th IWA World Congress on Anaerobic Digestion, Santiago de Compostela, Spain, 25–28 June 2013.
- Sbarciog, M.; Vande Wouwer, A. Start-up of multispecies anaerobic digestion systems: Extrapolation of the single species approach. Math. Comput. Model. Dyn. Syst. 2014, 20, 87–104. [Google Scholar] [CrossRef]
- Rapaport, A.; Dochain, D.; Harmand, J. Long run coexistence in the chemostat with multiple species. J. Theor. Biol. 2009, 257, 252–259. [Google Scholar] [CrossRef] [PubMed]
- Lobry, C.; Harmand, J. A new hypothesis to explain the coexistence of n species in the presence of a single resource. C. R. Biol. 2006, 329, 40–46. [Google Scholar] [CrossRef] [PubMed]
- Saito, Y.; Miki, T. Species coexistence under resource competition with intraspecific and interspecific direct competition in a chemostat. Theor. Popul. Biol. 2010, 78, 173–182. [Google Scholar] [CrossRef] [PubMed]
- Bock, E.; Wagner, M. Oxidation of inorganic nitrogen compounds as an energy source. In The Prokaryotes: An Evolving Electronic Resource for the Microbiological Community; Dworkin, M., Ed.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2001. [Google Scholar]
- Koops, H.P.; Pommerening-Rôser, A. Distribution and ecophysiology of the nitrifying bacteria emphasizing cultured species. FEMS Microb. Ecol. 2001, 37, 1–9. [Google Scholar] [CrossRef]
- Dumont, M.; Rapaport, A.; Harmand, J.; Benyahia, B.; Godon, J.J. Observers for microbial ecology—How including molecular data into bioprocess modeling. In Proceeding of the 16th Mediterranean Conference on Control and Automation, Ajaccio, France, 25–27 June 2008.
- Dumont, M.; Harmand, J.; Rapaport, A.; Godon, J.J. Toward functional molecular fingerprints. Environ. Microbiol. 2009, 11, 1717–1727. [Google Scholar] [CrossRef] [PubMed]
- Monod, J. La technique de culture continue: Theorie et applications. Ann. Inst. Pasteur Lille 1950, 79, 390–410. [Google Scholar]
- Novick, A.; Szilard, L. Experiments with the chemostat on spontaneous mutations of bacteria. PNAS 1950, 36, 708–719. [Google Scholar] [CrossRef] [PubMed]
- Mounier, J.; Monnet, C.; Vallaeys, T.; Arditi, R.; Sarthou, A.S.; Hélias, A.; Irlinger, F. Microbial interactions within a cheese microbial community. Appl. Environ. Microbiol. 2008, 74, 172–180. [Google Scholar] [CrossRef] [PubMed]
- Walter, E.; Pronzato, L. Identification of Parametric Models from Experimental Data; Springer: Heidelberg, Germamy, 1997; p. 413. [Google Scholar]
- Ljung, L. System Identification: Theory for the User; Prentice Hall: Upper Saddle River, NJ, USA, 1987; p. 511. [Google Scholar]
- Bougard, D. Traitement Biologique D’effluents Azotés Avec Arrêt de la Nitrification au Stade Nitrite. Ph.D. Thesis, École Nationale Supérieure Agronomique, Montpellier, France, 2004. [Google Scholar]
- Williams, R.J.; Martinez, N.D. Simple rules yield complex food webs. Nature 2000, 404, 180–183. [Google Scholar] [CrossRef] [PubMed]
- Drossel, B.; MacKane, A.J. Modelling food webs. In Handbook of Graphs and Networks; Bornholdt, S., Schuster, H.G., Eds.; Wiley-VCH: Berlin, Germany, 2003; pp. 218–247. [Google Scholar]
- Chase, J.M.; Abram, P.A.; Grover, J.P.; Diehl, S.; Chesson, P.; Holt, R.D.; Richards, S.A.; Nisbet, R.M.; Case, T.J. The interaction between predation and competition: A review and synthesis. Ecol. Lett. 2002, 5, 302–315. [Google Scholar] [CrossRef]
- Fox, J.W.; MacGrady-Steed, J. Stability and complexity in microcosm communities. J. Anim. Ecol. 2002, 71, 749–756. [Google Scholar] [CrossRef]
- Ruan, S.; Ardito, A.; Ricciardi, P.; DeAngelis, D.L. Coexistence in competition models with density-dependent mortality. C. R. Biol. 2007, 330, 845–854. [Google Scholar] [CrossRef] [PubMed]


| μmax1 (1/day) | Ks1 (mg/L) | YA | μmax2 (1/day) | Ks2 (mg/L) | YB |
|---|---|---|---|---|---|
| 0.81 | 0.17 | 0.26 | 0.26 | 0.16 | 0.01 |
| μmax1 (1/day) | Ks1 (mg/L) | μmax2 (1/day) | Ks2 (mg/L) |
|---|---|---|---|
| 0.828 | 0.147 | 0.18 | 0.026 |
| a11 | a12 | a13 | a14 | a21 | a22 | a23 | a24 |
| −0.087 | ~0 | −0.697 | 4.815 | ~0 | 0.476 | 0.995 | −6.362 |
| a31 | a32 | a33 | a34 | a41 | a42 | a43 | a44 |
| B/+ | B/+ | B/− | −1.225 | B/− | −0.351 | −0.837 | B/+ |
| μmax1 (1/day) | Ks1 (mg/L) | μmax2 (1/day) | Ks2 (mg/L) |
|---|---|---|---|
| 0.81 | 0.17 | 0.26 | 0.016 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dumont, M.; Godon, J.-J.; Harmand, J. Species Coexistence in Nitrifying Chemostats: A Model of Microbial Interactions. Processes 2016, 4, 51. https://doi.org/10.3390/pr4040051
Dumont M, Godon J-J, Harmand J. Species Coexistence in Nitrifying Chemostats: A Model of Microbial Interactions. Processes. 2016; 4(4):51. https://doi.org/10.3390/pr4040051
Chicago/Turabian StyleDumont, Maxime, Jean-Jacques Godon, and Jérôme Harmand. 2016. "Species Coexistence in Nitrifying Chemostats: A Model of Microbial Interactions" Processes 4, no. 4: 51. https://doi.org/10.3390/pr4040051
APA StyleDumont, M., Godon, J.-J., & Harmand, J. (2016). Species Coexistence in Nitrifying Chemostats: A Model of Microbial Interactions. Processes, 4(4), 51. https://doi.org/10.3390/pr4040051






