Multi-Period Dynamic Optimization for Large-Scale Differential-Algebraic Process Models under Uncertainty
Abstract
:1. Introduction
2. Problem Statement
3. Proposed Solution Approach
3.1. Multi-Period Multiple-Shooting Discretization

3.2. First-Order Derivative Generation
3.3. Second-Order Derivative Generation
3.4. Implementation Details
| Algorithm 1 Multi-period gradient-based non-linear program (NLP) solution approach with embedded differential-algebraic equations (DAE). QP, quadratic programming. |
| Input: initial primal and dual variable guesses and tolerances |
| 1: generate scenario realizations: |
| 2: define initial guesses for primal, , and dual variables |
| 3: provide optimality (tol) and feasibility (tol) tolerances |
| Output: primal/dual solution , to a local minimum of the NLP satisfying tolerances |
| 4: procedure NLP_SOLVE(, , tol) |
| 5: |
| 6: initial eval of objective/constraints and 1st derivatives (gradient, Jacobian) |
| 7: ⊳explicit function eval |
| 8: DAE_SOLVE() ⊳implicit function eval |
| 9: ⊳explicit function eval |
| 10: initial Lagrangian Hessian approximately (or eval exactly via DSOA_SOLVE()) |
| 11: repeat until termination criteria satisfied |
| 12: check KKTconditions (and other termination criteria) |
| 13: compute search direction of primal/dual variables () via QP solver |
| 14: compute step size via a line search (requires objective/constraint eval) |
| 15: |
| 16: |
| 17: re-evaluate function derivatives (used to construct the next QP) |
| DAE_SOLVE() |
| 18: update Hessian approximately (or eval exactly via DSOA_SOLVE()) |
| 19: end |
| 20: end procedure |
| Algorithm 2 Parallel multi-period DAE and first-order sensitivity function evaluation. |
| Input: state initial conditions, control parameters and invariant model parameters |
| 1: specified scenario realizations |
| 2: NLP variables , d, |
| 3: provide relative (tol) and absolute (tol) integration tolerances for DAE solution |
| Output: differential state solution , |
| 4: procedure dae_solve(x, θ, tol) |
| 5: for i 1 to do ▹ in parallel using OpenMP for tasks |
| 6: for j 0 to do |
| 7: set initial differential and algebraic DAE variables:
|
| 8: set initial differential DAE sensitivity variables:
|
| 9: solve DAE and 1st order sensitivity system |
| {, } ← sundials_dae_solver |
| 10: end for |
| 11: end for |
| 12: end procedure |
4. Example Problems
4.1. Batch Reactor Problem
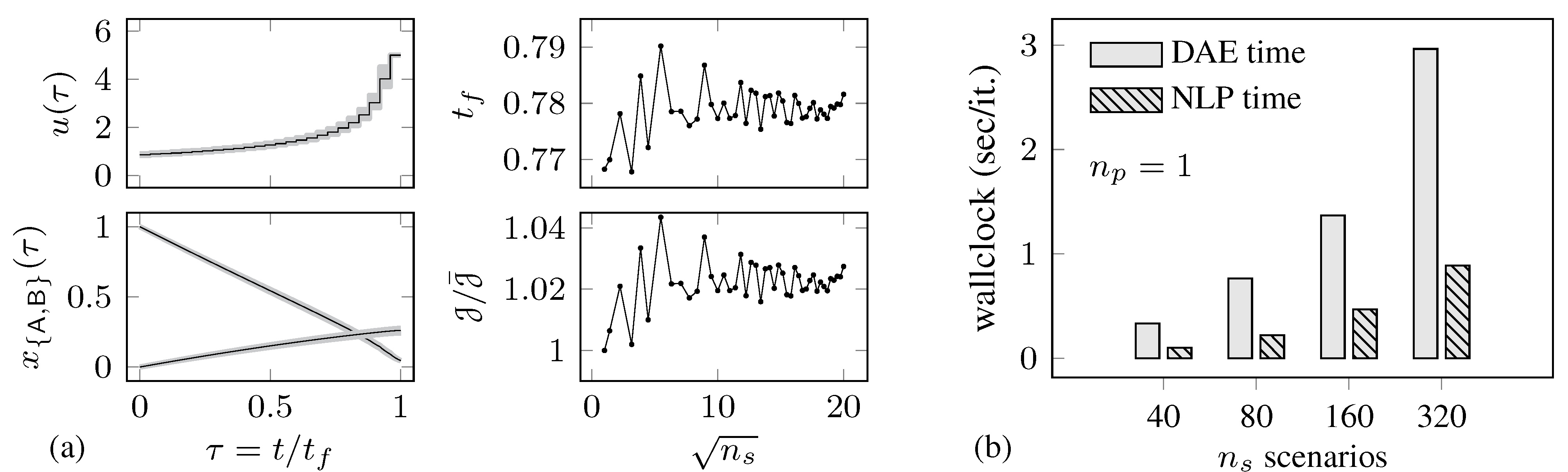
| Total Program Solution Time (s) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| m | vars | cons | iter | ||||||||
| 1 | 25 | 78 | 53 | 24 (60) | −1.4911 | 0.7683 | 0.389 | 0.251 | 0.235 | 0.201 | – |
| 40 | 1000 | 3081 | 2081 | 40 (1239) | −1.5235 | 0.7785 | 17.48 | 8.87 | 7.01 | 6.26 | 6.24 |
| 80 | 2000 | 6161 | 4161 | 46 (2244) | −1.5463 | 0.7868 | 45.41 | 21.61 | 16.88 | 15.20 | 14.87 |
| 160 | 4000 | 12,321 | 8321 | 49 (4395) | −1.5340 | 0.7823 | 90.00 | 42.37 | 34.74 | 30.87 | 30.35 |
| 320 | 8000 | 24,641 | 16,641 | 49 (8718) | −1.5200 | 0.7772 | 188.69 | 82.60 | 65.10 | 56.74 | 55.67 |
| iter | Total (s) | NLP (s) | FSA(s) | DSOA(s) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| qn | ex | qn | ex | qn | ex | qn | ex | ex | ||
| 1 | −1.4911 p | 52 | 48 | 0.793 | 22.96 | 0.311 | 0.111 | 0.482 | 0.297 | 22.56 |
| 40 | −1.5235 p | 70 | 66 | 27.81 | 632.42 | 2.277 | 0.591 | 25.54 | 12.27 | 619.56 |
| 80 | −1.5463 p | 65 | 64 | 48.61 | 1218.46 | 3.697 | 1.060 | 44.91 | 23.57 | 1193.82 |
| 160 | −1.5340 p | 71 | 65 | 107.3 | 2204.61 | 8.023 | 1.920 | 99.32 | 47.12 | 2155.57 |
| 320 | −1.5200 p | 49 | 44 | 151.2 | 4397.64 | 11.70 | 3.962 | 139.5 | 92.78 | 4300.90 |
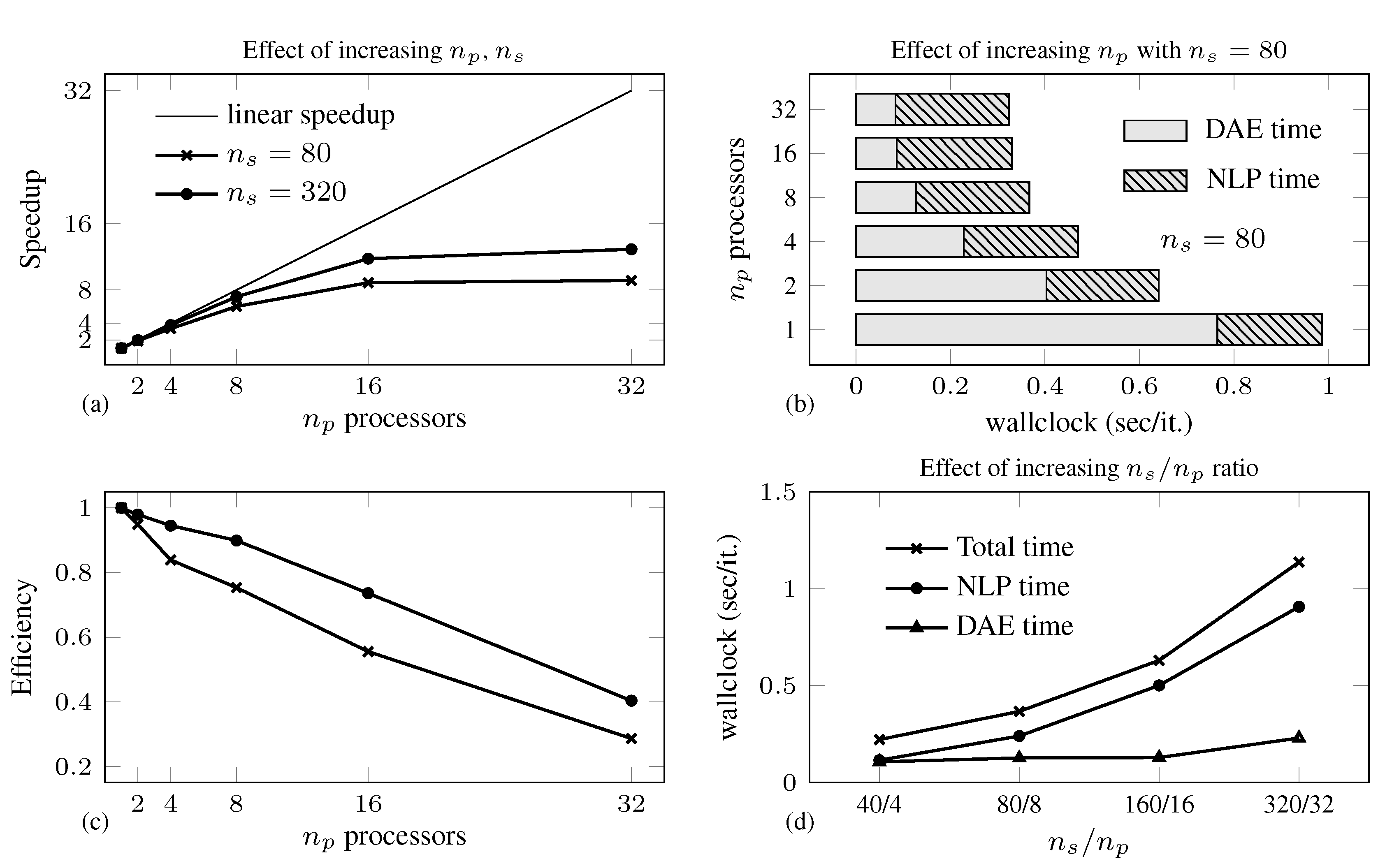
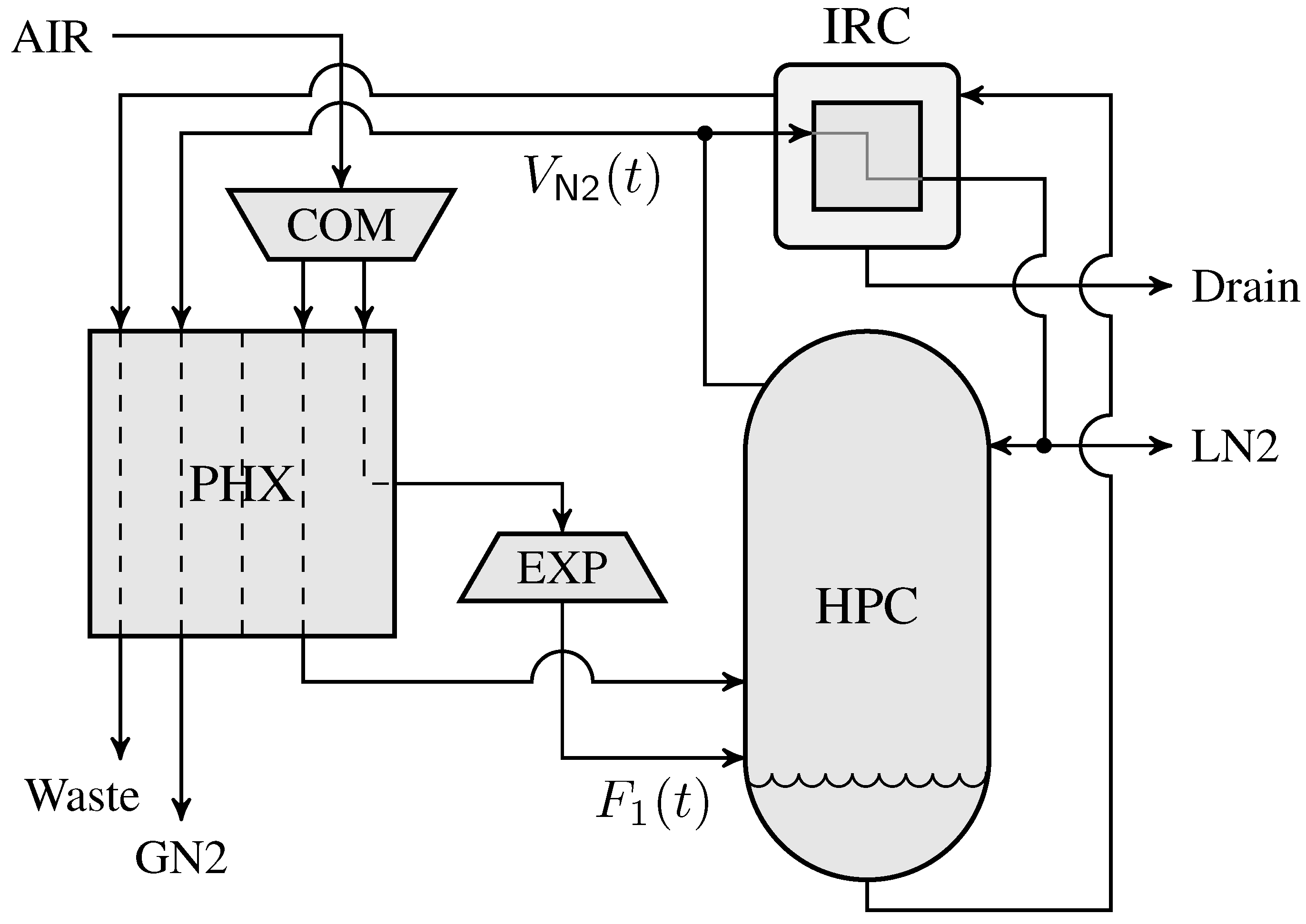
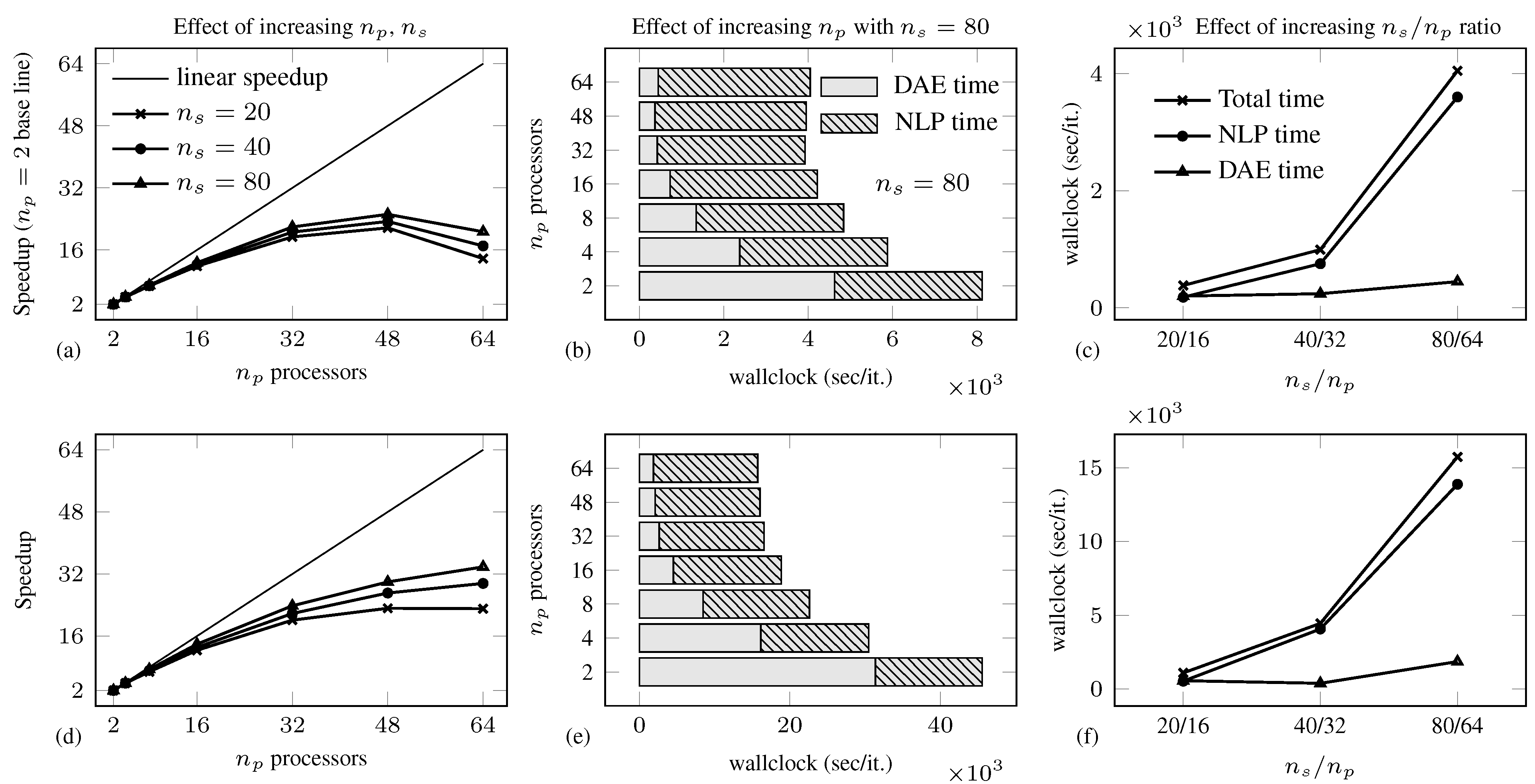
4.2. Air Separation Problem
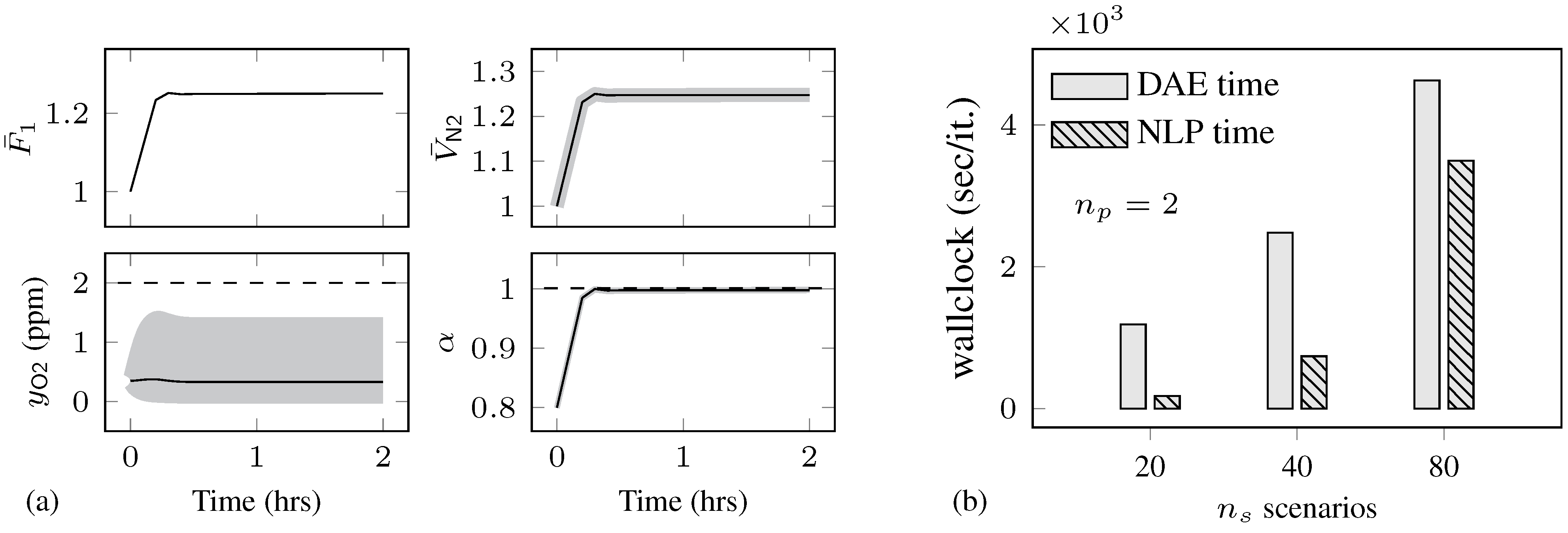
| Total solution time (s)/ | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| n | m | vars | cons | iter | |||||||
| 6 | 1 | 6 | 3184 | 3194 | 9 (1308) | 1.0159 | 0.0079 | – | – | – | – |
| 20 | 120 | 63,680 | 63,974 | 14 (42,704) | 1.0134 | 0.1908 | 0.0535 | 0.0420 | 0.0426 | 0.0501 | |
| 40 | 240 | 127,360 | 127,955 | 16 (85,672) | 1.0181 | 0.5146 | 0.1785 | 0.1589 | 0.1596 | 0.1688 | |
| 80 | 480 | 254,720 | 255,915 | 17 (170,391) | 1.0156 | 1.3808 | 0.7166 | 0.6669 | 0.6720 | 0.6882 | |
| 12 | 1 | 12 | 5914 | 5930 | 12 (3221) | 1.0141 | 0.0135 | – | – | – | – |
| 20 | 240 | 118,280 | 118,808 | 18 (81,273) | 1.0114 | 0.7163 | 0.1955 | 0.1558 | 0.1491 | 0.1474 | |
| 40 | 480 | 236,560 | 237,628 | 11 (162,037) | 1.0159 | 0.9167 | 0.5179 | 0.4891 | 0.4732 | 0.4714 | |
| 80 | 960 | 473,120 | 475,268 | 17 (322,952) | 1.0129 | 7.7468 | 3.2047 | 2.8156 | 2.7239 | 2.6748 | |
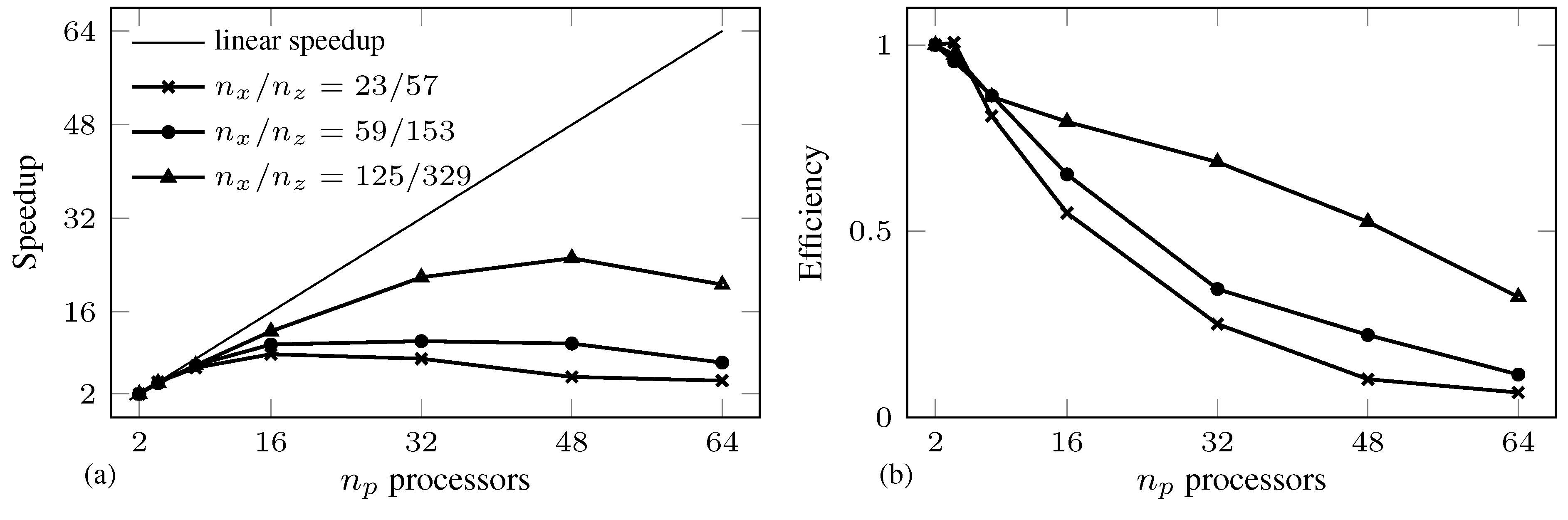
| Total Solution Time (s)/ | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| m | vars | cons | iter | |||||||
| 23/57 | 6 | 566 | 568 | 19 (184) | 0.8559 | 0.0006 | – | – | – | – |
| 480 | 45,280 | 45,915 | 22 (16,326) | 0.8560 | 0.0824 | 0.0230 | 0.0247 | 0.0368 | 0.0416 | |
| 59/153 | 6 | 1490 | 1492 | 12 (616) | 1.0111 | 0.0011 | – | – | – | – |
| 480 | 119,200 | 119,835 | 18 (38,928) | 1.0110 | 0.2185 | 0.0896 | 0.0870 | 0.0881 | 0.1052 | |
| 125/329 | 6 | 3184 | 3194 | 10 (1294) | 1.0159 | 0.0079 | – | – | – | – |
| 480 | 254,720 | 255,915 | 17 (170,391) | 1.0156 | 1.3808 | 0.7166 | 0.6669 | 0.6720 | 0.6882 | |
5. Concluding Remarks
Acknowledgements
Author Contributions
Conflicts of Interest
References
- Geletu, A.; Li, P. Recent Developments in Computational Approaches to Optimization under Uncertainty and Application in Process Systems Engineering. ChemBioEng Rev. 2014, 1, 170–190. [Google Scholar]
- Mohideen, M.J.; Perkins, J.D.; Pistikopoulos, E.N. Optimal design of dynamic systems under uncertainty. AIChE J. 1996, 42, 2251–2272. [Google Scholar] [CrossRef]
- Sakizlis, V.; Perkins, J.D.; Pistikopoulos, E.N. Recent advances in optimization-based simultaneous process and control design. Comput. Chem. Eng. 2004, 28, 2069–2086. [Google Scholar] [CrossRef]
- Wang, S.; Baldea, M. Identification-based optimization of dynamical systems under uncertainty. Comput. Chem. Eng. 2014, 64, 138–152. [Google Scholar] [CrossRef]
- Diwekar, U. Introduction to Applied Optimization; Springer: New York, NY, USA, 2008. [Google Scholar]
- Arellano-Garcia, H.; Wozny, G. Chance constrained optimization of process systems under uncertainty: I. Strict monotonicity. Comput. Chem. Eng. 2009, 33, 1568–1583. [Google Scholar] [CrossRef]
- Kloppel, M.; Geletu, A.; Hoffmann, A.; Li, P. Using Sparse-Grid Methods To Improve Computation Efficiency in Solving Dynamic Non-linear Chance-Constrained Optimization Problems. Ind. Eng. Chem. Res. 2011, 50, 5693–5704. [Google Scholar] [CrossRef]
- Diehl, M.; Gerhard, J.; Marquardt, W.; Monnigmann, M. Numerical solution approaches for robust non-linear optimal control problems. Comput. Chem. Eng. 2008, 32, 1279–1292. [Google Scholar] [CrossRef]
- Houska, B.; Logist, F.; Van Impe, J.; Diehl, M. Robust optimization of non-linear dynamic systems with application to a jacketed tubular reactor. J. Process Control 2012, 22, 1152–1160. [Google Scholar] [CrossRef]
- Huang, R.; Patwardhan, S.C.; Biegler, L.T. Multi-scenario-based robust non-linear model predictive control with first principle Models. In 10th International Symposium on Process Systems Engineering: Part A; de Brito Alves, R.M., do Nascimento, C.A.O., Biscaia, E.C., Eds.; Elsevier: Oxford, UK, 2009; Volume 27, pp. 1293–1298. [Google Scholar]
- Lucia, S.; Andersson, J.A.E.; Brandt, H.; Diehl, M.; Engell, S. Handling uncertainty in economic non-linear model predictive control: A comparative case study. J. Process Control 2014, 24, 1247–1259. [Google Scholar] [CrossRef]
- Washington, I.D.; Swartz, C.L.E. Design under uncertainty using parallel multi-period dynamic optimization. AIChE J. 2014, 60, 3151–3168. [Google Scholar] [CrossRef]
- Shapiro, A.; Dentcheva, D.; Ruszczynski, A. Lectures on Stochastic Programming; SIAM: Philadelphia, PA, USA, 2009. [Google Scholar]
- Brenan, K.E.; Campbell, S.L.; Petzold, L.R. Numerical Solution of Initial-Value Problems In Differential-Algebraic Equations; SIAM: Philadelphia, PA, USA, 1996. [Google Scholar]
- Varvarezos, D.K.; Biegler, L.T.; Grossmann, I.E. Multi-period design optimization with SQP decomposition. Comput. Chem. Eng. 1994, 18, 579–595. [Google Scholar] [CrossRef]
- Bhatia, T.K.; Biegler, L.T. Multi-period design and planning with interior point methods. Comput. Chem. Eng. 1999, 23, 919–932. [Google Scholar] [CrossRef]
- Albuquerque, J.; Gopal, V.; Staus, G.; Biegler, L.T.; Ydstie, B.E. Interior point SQP strategies for large-scale, structured process optimization problems. Comput. Chem. Eng. 1999, 23, 543–554. [Google Scholar] [CrossRef]
- Cervantes, A.M.; Wachter, A.; Tutuncu, R.H.; Biegler, L.T. A reduced space interior point strategy for optimization of differential algebraic systems. Comput. Chem. Eng. 2000, 24, 39–51. [Google Scholar] [CrossRef]
- Zavala, V.M.; Laird, C.D.; Biegler, L.T. Interior-point decomposition approaches for parallel solution of large-scale non-linear parameter estimation problems. Chem. Eng. Sci. 2008, 63, 4834–4845. [Google Scholar] [CrossRef]
- Word, D.P.; Kang, J.; Akesson, J.; Laird, C.D. Efficient parallel solution of large-scale non-linear dynamic optimization problems. Comput. Optim. Appl. 2014, 59, 667–688. [Google Scholar] [CrossRef]
- Kang, J.; Cao, Y.; Word, D.P.; Laird, C.D. An interior-point method for efficient solution of block-structured NLP problems using an implicit Schur-complement decomposition. Comput. Chem. Eng. 2014, 71, 563–573. [Google Scholar] [CrossRef]
- Leineweber, D.B.; Schafer, A.; Bock, H.G.; Schloder, J.P. An efficient multiple shooting based reduced SQP strategy for large-scale dynamic process optimization. Part II: Software aspects and applications. Comput. Chem. Eng. 2003, 27, 167–174. [Google Scholar] [CrossRef]
- Bachmann, B.; Ochel, L.; Ruge, V.; Gebremedhin, M.; Fritzson, P.; Nezhadali, V.; Eriksson, L.; Sivertsson, M. Parallel Multiple-Shooting and Collocation Optimization with OpenModelica. In Proceedings of the 9th International Modelica Conference, Munich, Germany, 3–5 September 2012; pp. 659–668.
- Andersson, J. A General-Purpose Software Framework for Dynamic Optimization. Ph.D. Thesis, Arenberg Doctoral School, KU Leuven, Department of Electrical Engineering (ESAT/SCD) and Optimization in Engineering Center, October 2013. [Google Scholar]
- Leineweber, D.B.; Bauer, I.; Bock, H.G.; Schloder, J.P. An efficient multiple shooting based reduced SQP strategy for large-scale dynamic process optimization. Part I: Theoretical aspects. Comput. Chem. Eng. 2003, 27, 157–166. [Google Scholar] [CrossRef]
- Houska, B.; Diehl, M. A quadratically convergent inexact SQP method for optimal control of differential algebraic equations. Optim. Control Appl. Methods 2013, 34, 396–414. [Google Scholar] [CrossRef]
- Maly, T.; Petzold, L.R. Numerical methods and software for sensitivity analysis of differential-algebraic systems. Appl. Numer. Math. 1996, 20, 57–79. [Google Scholar] [CrossRef]
- Feehery, W.F.; Tolsma, J.E.; Barton, P.I. Efficient sensitivity analysis of large-scale differential-algebraic systems. Appl. Numer. Math. 1997, 25, 41–54. [Google Scholar] [CrossRef]
- Schlegel, M.; Marquardt, W.; Ehrig, R.; Nowak, U. Sensitivity analysis of linearly-implicit differential-algebraic systems by one-step extrapolation. Appl. Numer. Math. 2004, 48, 83–102. [Google Scholar] [CrossRef]
- Kristensen, M.R.; Jorgensen, J.B.; Thomsen, P.G.; Michelsen, M.L.; Jorgensen, S.B. Sensitivity Analysis in Index-1 Differential Algebraic Equations by ESDIRK Methods; IFAC World Congress: Prague, Czech Republic, 2005; Volume 16, pp. 895–895. [Google Scholar]
- Ozyurt, D.B.; Barton, P.I. Cheap Second Order Directional Derivatives of Stiff ODE Embedded Functionals. SIAM J. Sci. Comput. 2005, 26, 1725–1743. [Google Scholar] [CrossRef]
- Cao, Y.; Li, S.; Petzold, L.; Serban, R. Adjoint sensitivity analysis for differential-algebraic equations: The adjoint DAE system and its numerical solution. SIAM J. Sci. Comput. 2003, 24, 1076–1089. [Google Scholar] [CrossRef]
- Hannemann-Tamas, R. Adjoint Sensitivity Analysis for Optimal Control of Non-Smooth Differential-Algebraic Equations. Ph.D. Thesis, RWTH-Aachen University, Aachen, Germany, February 2012. [Google Scholar]
- Albersmeyer, J. Adjoint-based algorithms and numerical methods for sensitivity generation and optimization of large scale dynamic systems. Ph.D. Thesis, University of Heidelberg, Interdisciplinary Center for Scientific Computing, Heidelberg, Germany, 23 December 2010. [Google Scholar]
- Davis, T. Direct Methods for Sparse Linear Systems; SIAM: Philadelphia, PA, USA, 2006. [Google Scholar]
- Hindmarsh, A.C.; Brown, P.N.; Grant, K.E.; Lee, S.L.; Serban, R.; Shumaker, D.E.; Woodward, C.S. SUNDIALS: Suite of non-linear and differential/algebraic equation solvers. ACM Trans. Math. Softw. 2005, 31, 363–396. [Google Scholar] [CrossRef]
- Gill, P.E.; Murray, W.; Saunders, M.A. SNOPT: An SQP algorithm for large-scale constrained optimization. SIAM Rev. 2005, 47, 99–131. [Google Scholar] [CrossRef]
- Wachter, A.; Biegler, L.T. On the implementation of an interior-point filter line-search algorithm for large-scale non-linear programming. Math. Program. 2006, 106, 25–57. [Google Scholar] [CrossRef]
- Walther, A.; Griewank, A. Getting started with ADOL-C. In Combinatorial Scientific Computing; Naumann, U., Schenk, O., Eds.; Chapman-Hall CRC Computational Science: London, UK, 2012; chapter 7; pp. 181–202. [Google Scholar]
- Albersmeyer, J.; Bock, H.G. Sensitivity Generation in an Adaptive BDF-Method. In Modeling, Simulation and Optimization of Complex Processes; Bock, H.G., Kostina, E., Phu, H.X., Rannacher, R., Eds.; Springer: New York, NY, USA, 2008; pp. 15–24. [Google Scholar]
- Quirynen, R.; Vukov, M.; Zanon, M.; Diehl, M. Autogenerating microsecond solvers for non-linear MPC: A tutorial using ACADO integrators. Optim. Control Appl. Methods 2014. [Google Scholar] [CrossRef]
- Hannemann-Tamas, R.; Imsland, L.S. Full algorithmic differentiation of a Rosenbrock-type method for direct single shooting. In Proceedings of the 2014 European Control Conference (ECC), Strasbourg, France, 24–27 June 2014; pp. 1242–1248.
- Nocedal, J.; Wright, S.J. Numerical Optimization, 2nd ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Pacheco, P.S. An Introduction to Parallel Programming; Morgan Kaufmann: New York, NY, USA, 2011. [Google Scholar]
- Hannemann, R.; Marquardt, W. Continuous and Discrete Composite Adjoints for the Hessian of the Lagrangian in Shooting Algorithms for Dynamic Optimization. SIAM J. Sci. Comput. 2010, 31, 4675–4695. [Google Scholar] [CrossRef]
- Cao, Y. Design for Dynamic Performance: Application to an Air Separation Unit. Master Thesis, McMaster University, June 2011. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Washington, I.D.; Swartz, C.L.E. Multi-Period Dynamic Optimization for Large-Scale Differential-Algebraic Process Models under Uncertainty. Processes 2015, 3, 541-567. https://doi.org/10.3390/pr3030541
Washington ID, Swartz CLE. Multi-Period Dynamic Optimization for Large-Scale Differential-Algebraic Process Models under Uncertainty. Processes. 2015; 3(3):541-567. https://doi.org/10.3390/pr3030541
Chicago/Turabian StyleWashington, Ian D., and Christopher L.E. Swartz. 2015. "Multi-Period Dynamic Optimization for Large-Scale Differential-Algebraic Process Models under Uncertainty" Processes 3, no. 3: 541-567. https://doi.org/10.3390/pr3030541
APA StyleWashington, I. D., & Swartz, C. L. E. (2015). Multi-Period Dynamic Optimization for Large-Scale Differential-Algebraic Process Models under Uncertainty. Processes, 3(3), 541-567. https://doi.org/10.3390/pr3030541





