A Multi-Scale Hybrid CFD-DEM-PBM Description of a Fluid-Bed Granulation Process
Abstract
:1. Introduction, Motivation and Objectives
1.1. Objectives
- Present a hybrid CFD-DEM-PBM framework using dynamic two-way coupling.
- Incorporate multi-scale information such that the model can be used to study the detailed process dynamics.
- Study the heterogenous particle velocity distribution and liquid binder distribution.
- Study the evolution of average particle diameter and particle liquid content with time.
2. Background
3. Multi-Scale Model Development
3.1. CFD Model for the Fluidizing Medium
- Flow near wall is laminar and the velocity varies linearly with the distance from wall.
- A no slip boundary condition has been set at the wall.
- A velocity inlet boundary condition has been used for the air entering the geometry.
- An outlet-vent boundary condition has been used at the geometry exit.
3.2. Discrete Element Model
| Particle properties | |
| Shear modulus | 1 × 10 Nm |
| Poisson’s ratio | |
| Density | 1030 kgm |
| Particle-particle interactions | |
| Coefficient of restitution | |
| Coefficient of static friction | |
| Coefficient of rolling friction | |
| Granulator walls | |
| Material | Steel |
| Shear modulus | 7.6 × 10 Nm |
| Poisson’s ratio | |
| Density | 7800 kgm |
| Particle-wall interactions | |
| Coefficient of restitution | |
| Coefficient of static friction | |
| Coefficient of rolling friction |
3.3. Population Balance Model for FBG
3.4. Information Exchange in the Coupling Framework
- The PBM considers aggregation only, breakage and consolidation has not been incorporated since FBG processes are low shear processes with reduced consolidation and breakage (similar approach has been followed by [48]).
- A simple aggregation kernel has been formulated based on collision frequency and collision efficiency (adapted from [46]).
- The collision efficiency in the aggregation kernel is size independent, non-mechanistic and conditional based on the liquid content of the powder particles (adapted from [47]).
- Liquid addition has been captured in EDEM by creating particles which get deleted from the system upon contact.
- A reasonable number of collisions occur among the particles between any two subsequent time steps.
- The PBM is solved a reasonable number of times such that there is a more consistent distribution of the particle size (as described in Section 4.3)
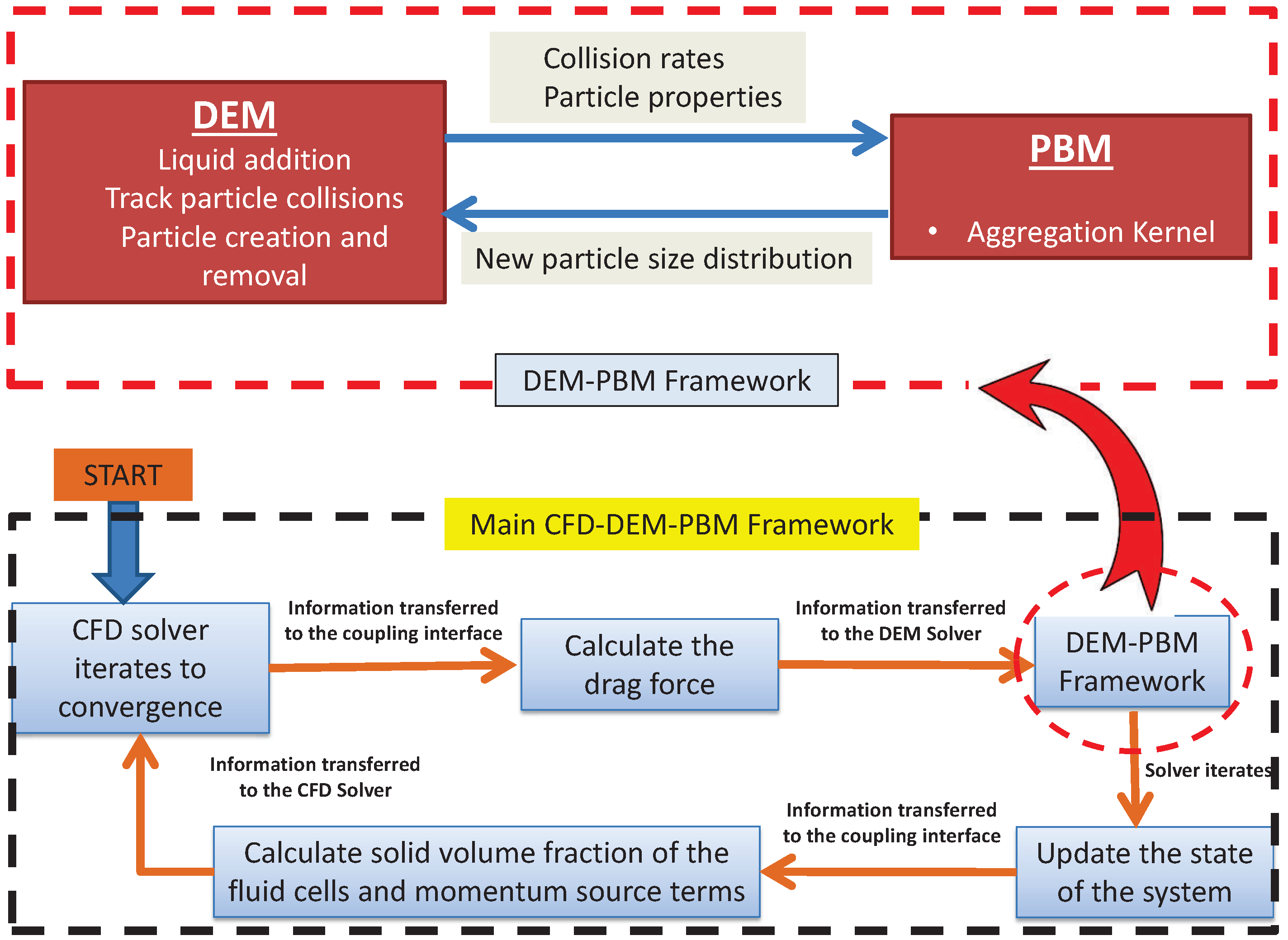
3.5. Model Outputs
4. Results and Discussion
4.1. Simulation Procedure
- The geometry has been made using ANSYS Design Modeler.
- The geometry has been meshed using ICEM-CFD.
- The mesh file has been imported within FLUENT.
- The mesh has been converted into Polyhedra domain.
- The gravity is defined in the correct direction and a transient simulation is selected.
- The flow model has been selected to be viscous laminar.
- The coupling server has been started.
- The FLUENT is coupled with EDEM for the desired fluid domain by selecting the Eulerian-Eulerian option.
- The coupling server will automatically import the geometry with the specified direction of gravity in EDEM and set the source terms in x-momentum, y-momentum and z-momentum calculation. The value of the simulation parameters of the coupling interface has been set as follows:
- Sample points: The number of points used by FLUENT to calculate the volume fraction of the fluid cell. This value has been set at 10, which means that a large particle can transfer its volume between 10 cells. This particular parameter decides the stability and speed of the simulation. A higher value of sample point may increase the stability but decrease the simulation speed.
- Relaxation factor: The relaxation factors again help with stability and convergence of the solution. Reducing the value helps to increase stability and achieve convergence. Both momentum-MTM-under-relaxation factor and volume under-relaxation factor have been set at 0.7.
- The inlet fluid velocity has been defined as 30 m/s.
- The custom contact model and custom factory (for PBM calculation) have been imported within EDEM.
- The material properties, particle-particle and particle-wall interaction parameters as given in Table 1 have been set in EDEM.
- The initial PSD has been created in EDEM.
- The liquid particles have been created in EDEM (the liquid addition starts at 0.2 s).
- Once the EDEM simulation is set up, initialize the solution in FLUENT.
- Run the calculation.
4.2. Model Geometry
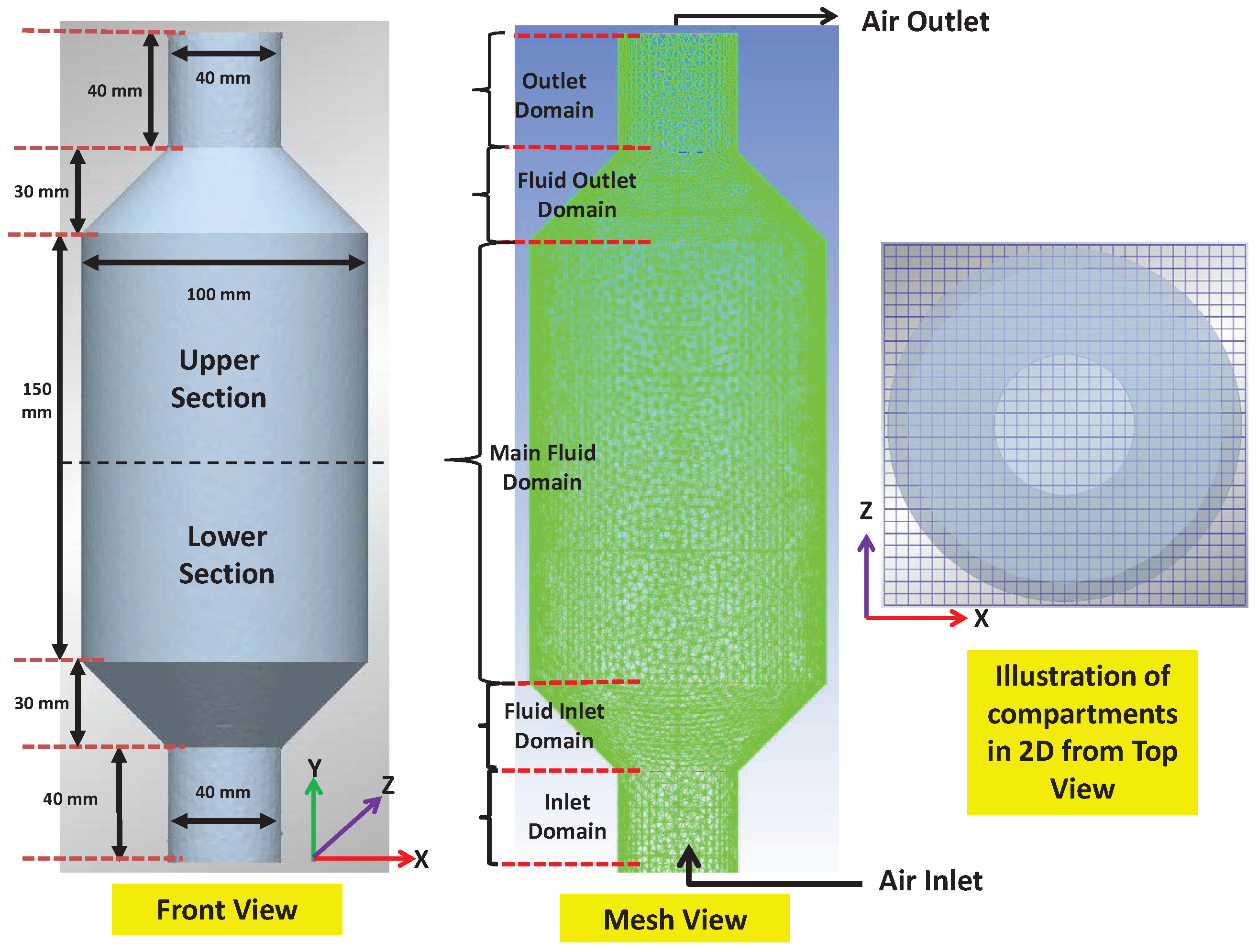
4.3. Multi-Scale Model Results
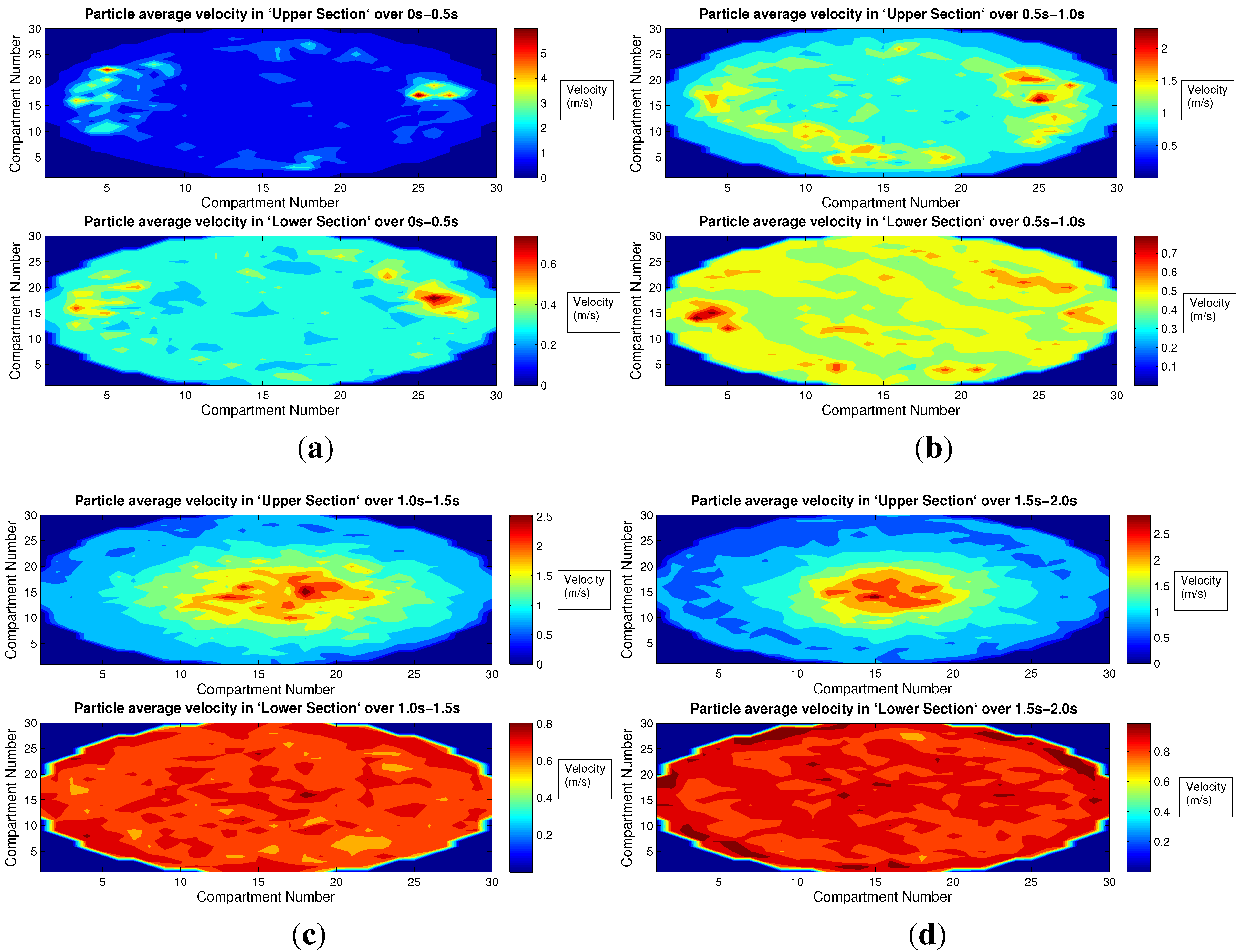
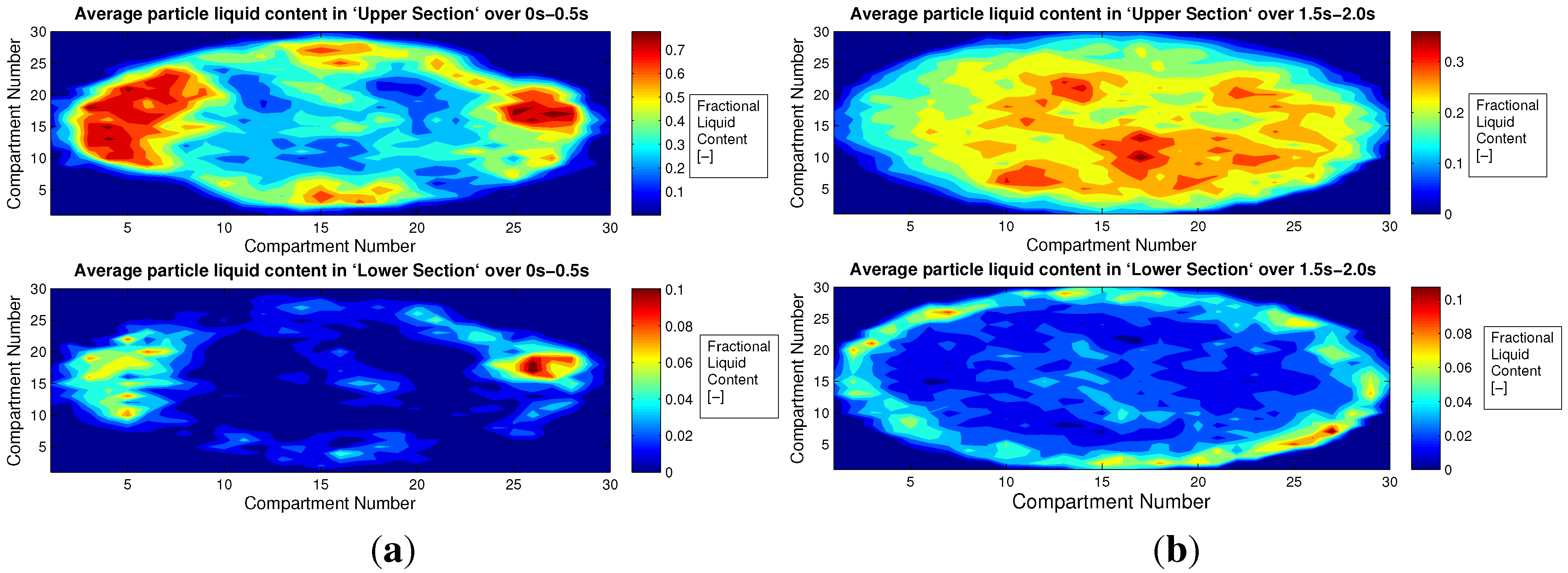
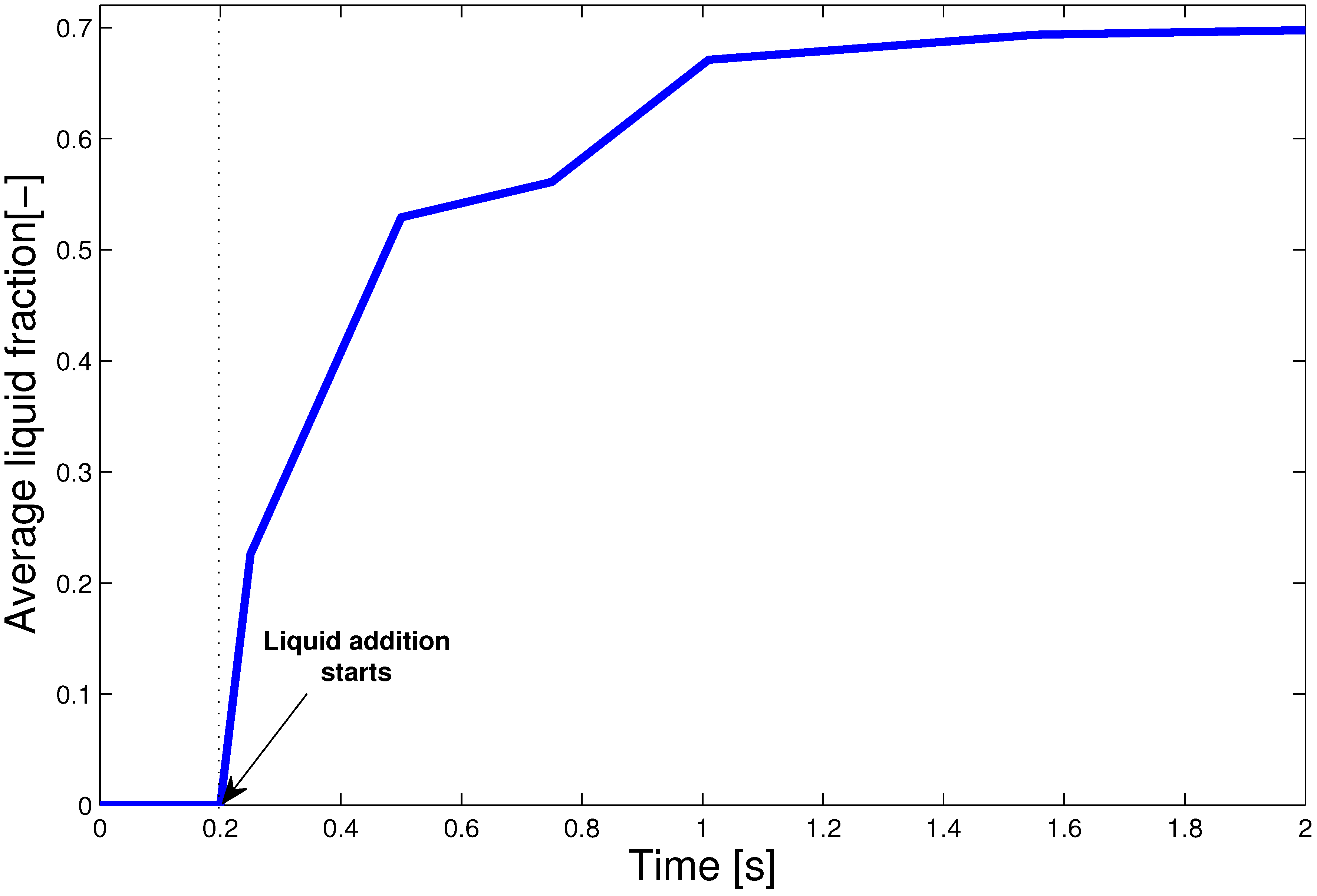
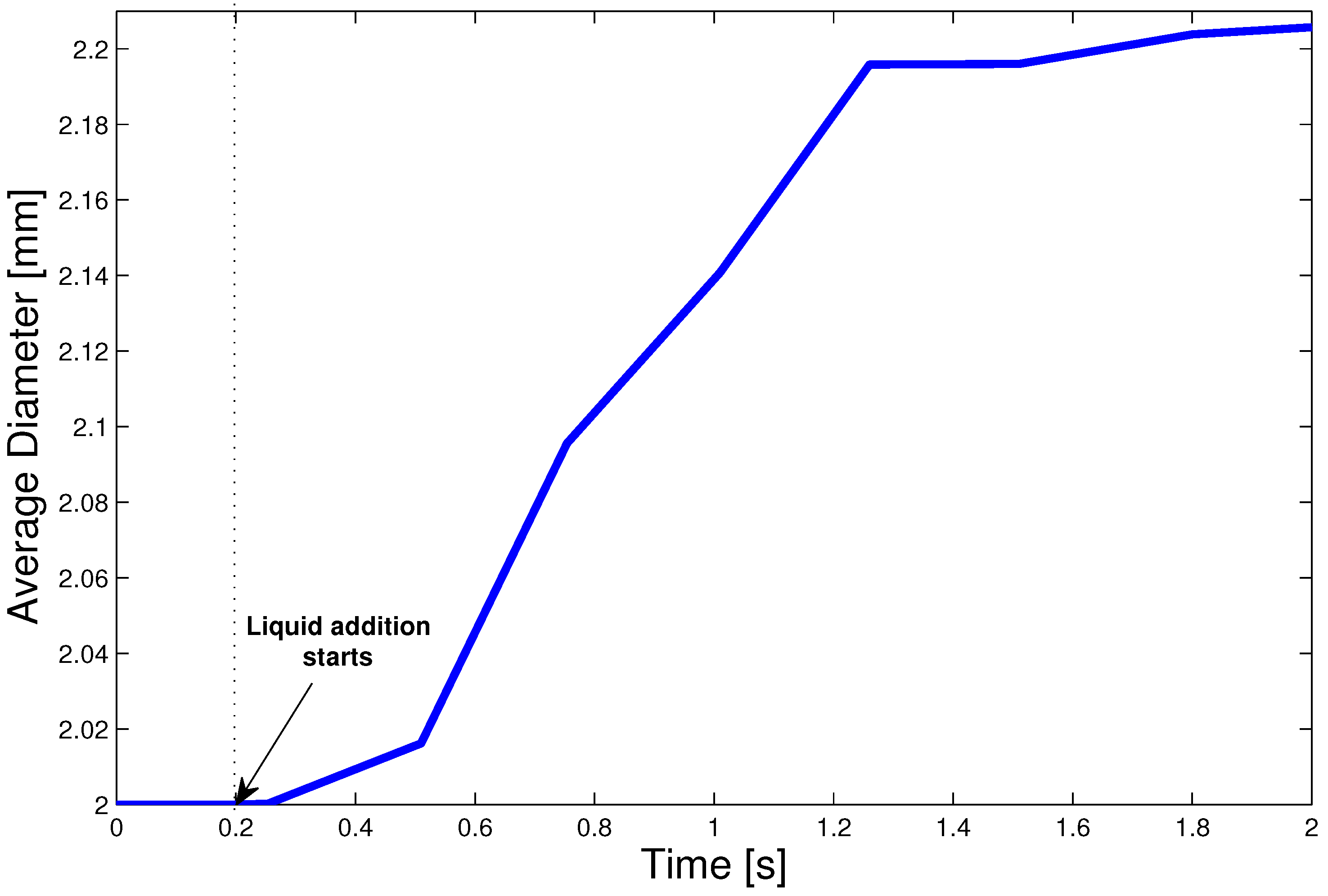
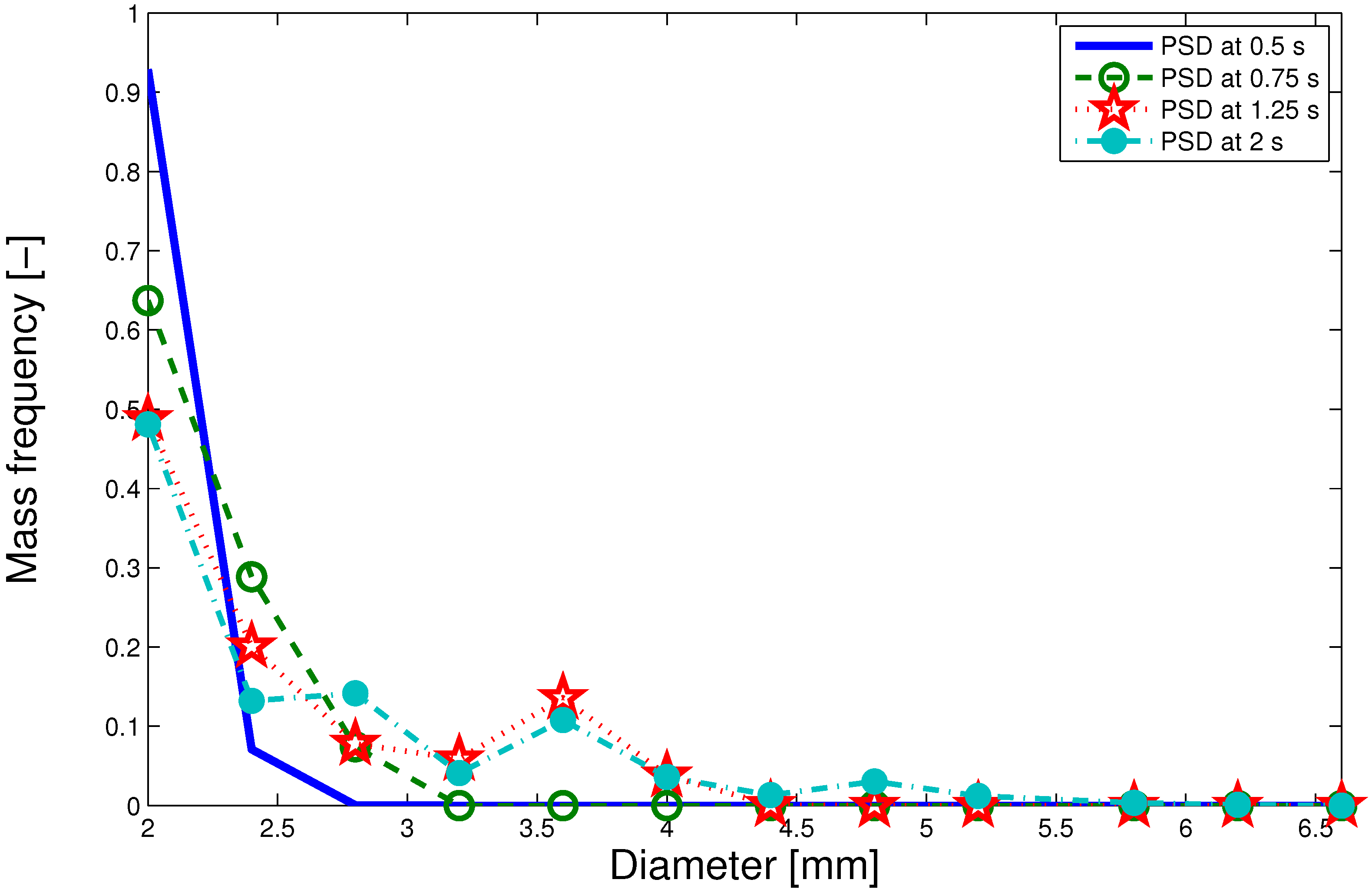
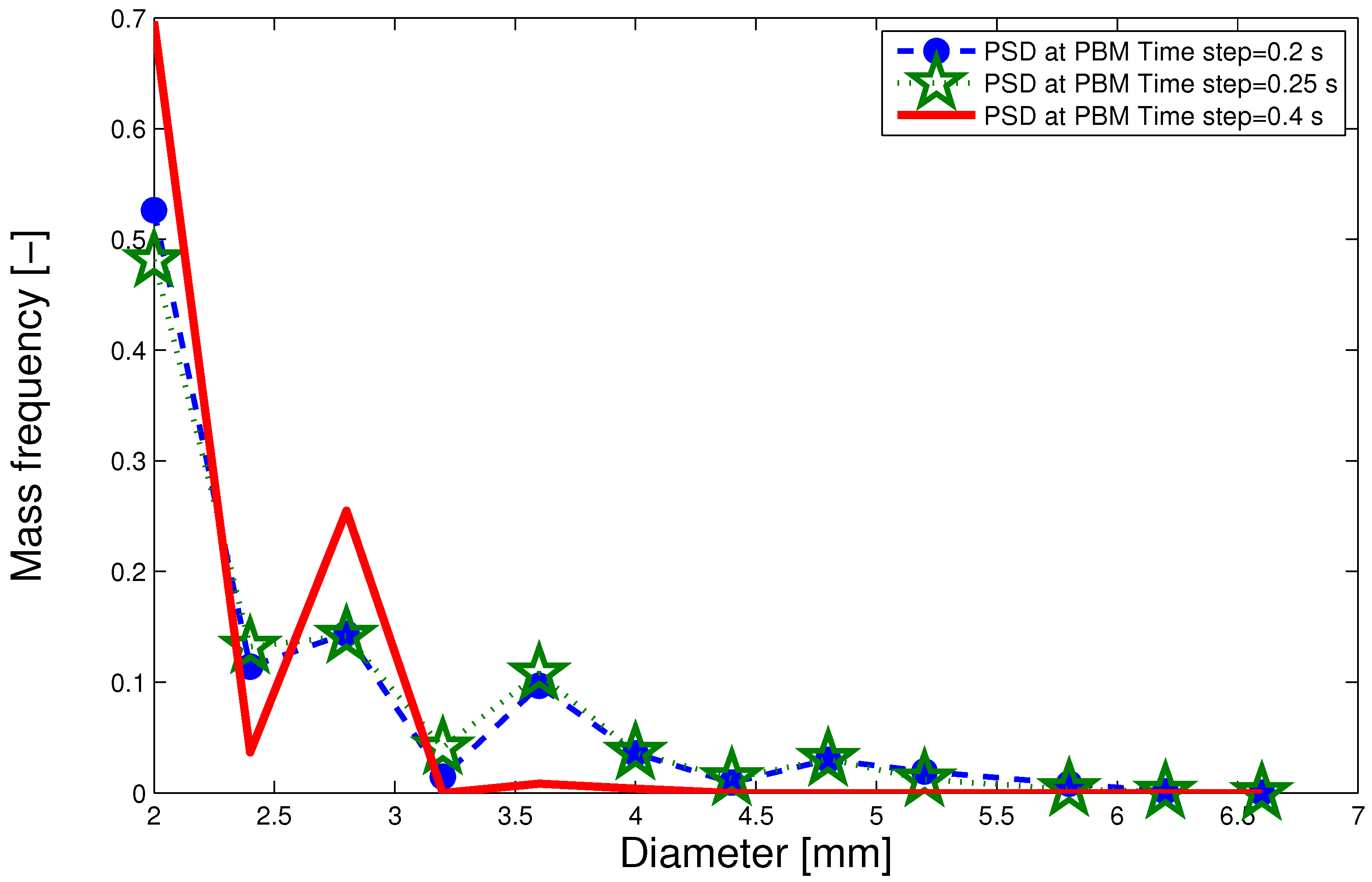
5. Conclusions
Acknowledgments
Conflicts of Interest
Appendix. Effect of PSD on Collision Frequency
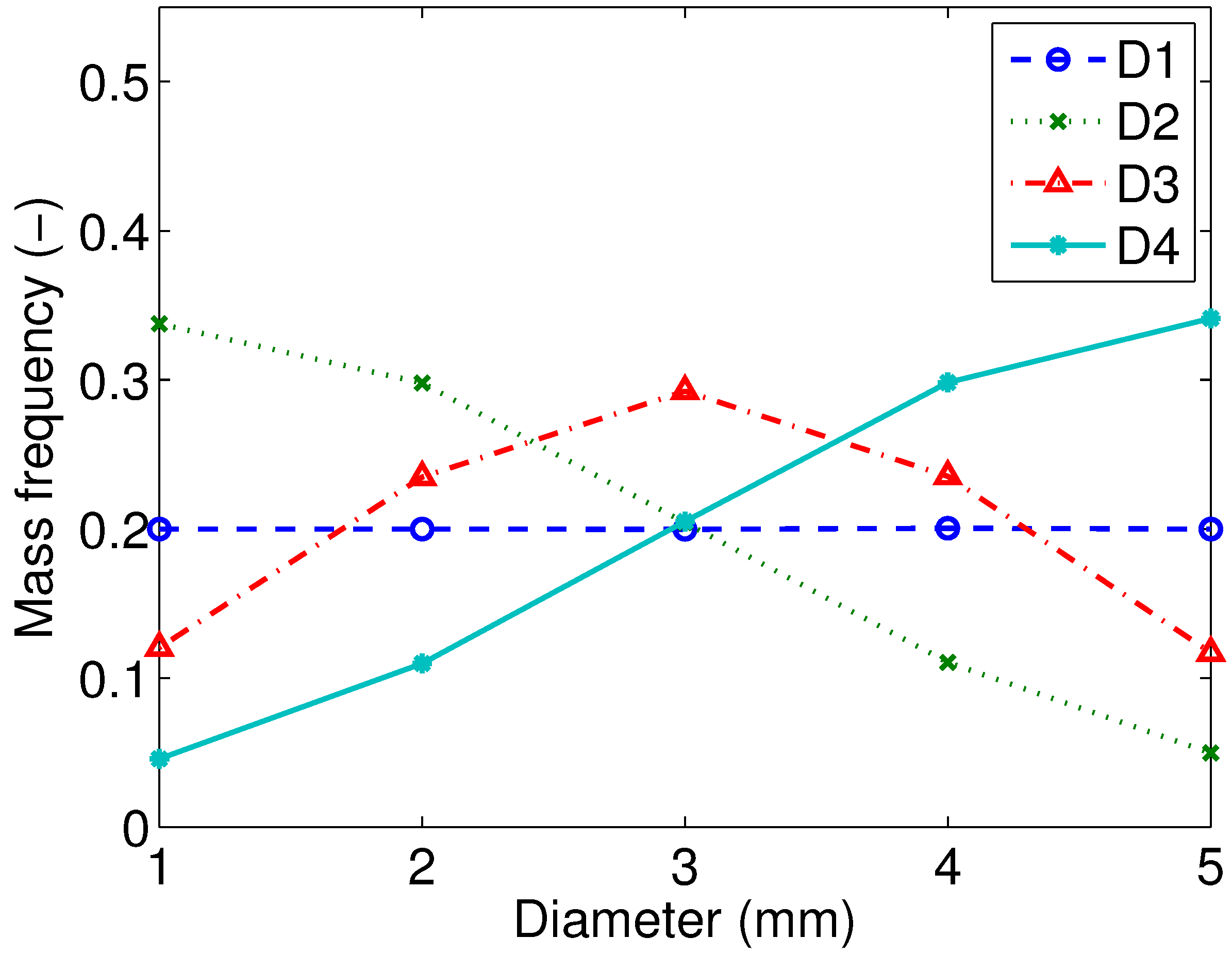
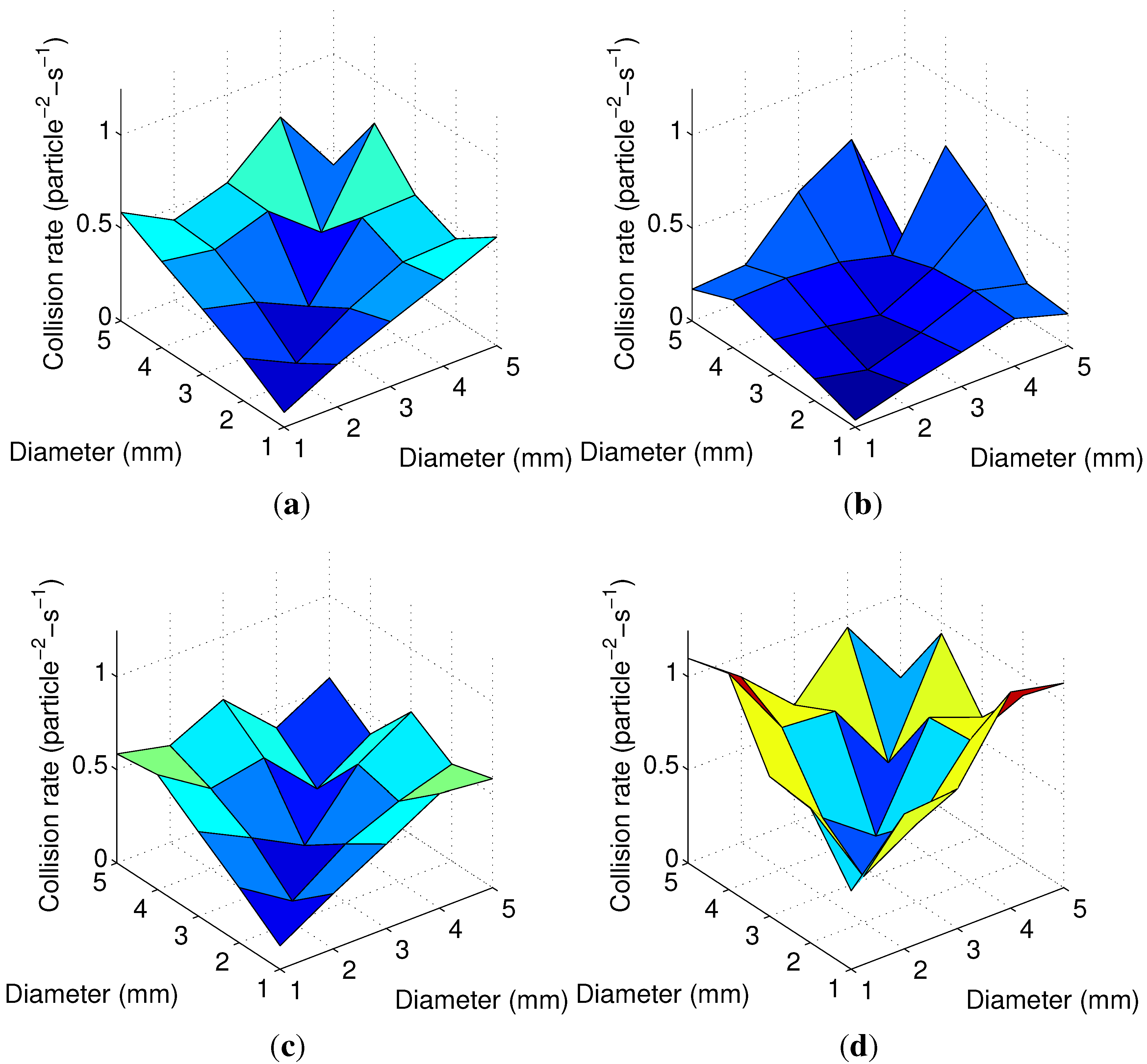
References
- Wang, F.Y.; Cameron, I.T. Review and future directions in the modelling and control of continuous drum granulation. Powder Technol. 2002, 124, 238–253. [Google Scholar] [CrossRef]
- Cameron, I.T.; Wang, F.Y.; Immanuel, C.D.; Stepanek, F. Process systems modeling and applications in granulation: A review. Chem. Eng. Sci. 2005, 60, 3723–3750. [Google Scholar] [CrossRef]
- Washino, K.; Tan, H.S.; Hounslow, M.J.; Salman, A.D. A new capillary force model implemented in micro-scale CFD-DEM coupling for wet granulation. Chem. Eng. Sci. 2013. [Google Scholar] [CrossRef]
- Iveson, S.M.; Litster, J.D.; Hapgood, K.; Ennis, B.J. Nucleation, growth and breakage phenomena in agitated wet granulation processes: A review. Powder Technol. 2001, 117, 3–39. [Google Scholar] [CrossRef]
- Fries, L.; Antonyuk, S.; Heinrich, S.; Palzer, S. DEM-CFD modeling of a fluidized bed spray granulator. Chem. Eng. Sci. 2011, 66, 2340–2355. [Google Scholar] [CrossRef]
- Ng, B.H.; Ding, Y.L.; Ghadiri, M. Modelling of dense and complex granular flow in high shear mixer granulator—A CFD approach. Chem. Eng. Sci. 2009, 64, 3622–3632. [Google Scholar] [CrossRef]
- Habib, Y.; Augsburger, L.L.; Shangraw, R.F. Production of inert cushioning beads: Effect of excipients on the physicomechanical properties of freeze-dried beads containing microcrystalline cellulose produced by extrusion-spheronization. Int. J. Pharm. 2002, 233, 67–83. [Google Scholar] [CrossRef]
- Cantor, S.L.; Kothari, S.; Koo, O.M.Y. Evaluation of the physical and mechanical properties of high drug load formulations: Wet granulation vs. novel foam granulation. Powder Technol. 2009, 195, 15–24. [Google Scholar] [CrossRef]
- Boukouvala, F.; Chaudhury, A.; Sen, M.; Zhou, R.; Mioduszewski, L.; Ierapetritou, M.G.; Ramachandran, R. Computer-aided flowsheet simulation of a pharmaceutical tablet manufacturing process incorporating wet granulation. J. Pharm. Innov. 2013, 8, 11–27. [Google Scholar] [CrossRef]
- Barrasso, D.; Walia, S.; Ramachandran, R. Multi-component population balance modeling of continuous granulation processes: A parametric study and comparison with experimental trends. Powder Technol. 2013, 241, 85–97. [Google Scholar] [CrossRef]
- Ramachandran, R.; Immanuel, C.D.; Stepanek, F.; Litster, J.D.; Doyle, F.J., III. A mechanistic model for breakage in population balances of granulation: Theoretical kernel development and experimental validation. Chem. Eng. Res. Des. 2009, 87, 598–614. [Google Scholar] [CrossRef]
- Reinhold, A.; Briesen, H. Numerical behavior of a multiscale aggregation model-coupling population balances and discrete element models. Chem. Eng. Sci. 2012, 70, 165–175. [Google Scholar] [CrossRef]
- Sen, M.; Dubey, A.; Singh, R.; Ramachandran, R. Mathematical development and comparison of a hybrid PBM-DEM description of a continuous powder mixing process. J. Powder Technol. 2013. [Google Scholar] [CrossRef]
- Sen, M.; Ramachandran, R. A multi-dimensional population balance model approach to continuous powder mixing processes. Adv. Powder Technol. 2013, 24, 51–59. [Google Scholar] [CrossRef]
- Chu, K.W.; Yu, A.B. Numerical simulation of the gas-solid flow in three dimensional pneumatic conveying bends. Ind. Eng. Chem. Res. 2008, 47, 7058–7071. [Google Scholar] [CrossRef]
- Ibsen, C.H.; Helland, E.; Hjertager, B.H. Comparison of multifluid and discrete particle modelling in numerical predictions of gas particle flow in circulating fluidised beds. Powder Technol. 2004, 149, 29–41. [Google Scholar] [CrossRef]
- Rong, D.G.; Horio, M. Behavior of particles and bubbles around immersed tubes fluidized bed at high temperature and pressure: A DEM simulation. Int. J. Multiph. Flow 2001, 27, 89–105. [Google Scholar] [CrossRef]
- Deen, N.G.; Annaland, M.S.; van der Hoef, M.A.; Kuipers, J.A.M. Review of discrete particle modelling of fluidized beds. Chem. Eng. Sci. 2007, 62, 28–44. [Google Scholar] [CrossRef]
- Tsuji, Y.; Tanaka, T.; Ishida, T. Lagrangian numerical-simulation of plug flow of cohesionless particles in a horizontal pipe. Powder Technol. 1992, 71, 239–250. [Google Scholar] [CrossRef]
- Helland, E.; Occelli, R.; Tadrist, L. Numerical study of cluster formation in a gas particle circulating fluidized bed. Powder Technol. 2000, 110, 210–221. [Google Scholar] [CrossRef]
- Hilton, J.E.; Ying, D.Y.; Cleary, P.W. Modelling spray coating using a combined CFD-DEM and spherical harmonic formulation. Chem. Eng. Sci. 2013, 99, 141–160. [Google Scholar] [CrossRef]
- Rhodes, M.J.; Wang, X.S.; Nguyen, M.; Stewart, P.; Liffman, K. Use of discrete element method simulation in studying fluidization characteristics: Influence of interparticle force. Chem. Eng. Sci. 2001, 56, 69–76. [Google Scholar] [CrossRef]
- Zhou, Z.Y.; Kuang, S.B.; Chu, K.W.; Yu, A.B. Assessments of CFD-DEM models in particle fluid flow modelling. J. Fluid Mech. 2010, 661, 482–510. [Google Scholar] [CrossRef]
- Chen, C.; Fan, L.-S. Discrete simulation of gas liquid bubble column and gas liquid solid fluidized beds. AIChE J. 2004, 50, 288–301. [Google Scholar] [CrossRef]
- Li, Y.; Yang, G.; Zhang, J.; Fan, L.-S. Numerical studies of bubble formation dynamics in gas liquid solid fluidization at high pressures. Powder Technol. 2001, 116, 246–260. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, J.; Fan, L.-S. Numerical simulation of gas-liquid-solid fluidization systems using a combined CFD-VOF-DPM method: bubble wake behavior. Chem. Eng. Sci. 1999, 54, 5101–5107. [Google Scholar] [CrossRef]
- Renzo, A.D.; Maio, F.P.D. Homogeneous and bubbling fluidization regimes in DEM-CFD simulations: Hydrodynamic stability of gas and liquid fluidized beds. Chem. Eng. Sci. 2007, 62, 116–130. [Google Scholar] [CrossRef]
- Tsuji, T.; Yabumoto, K.; Tanaka, T. Spontaneous structures in three-dimensional bubbling gas-fluidized bed by parallel DEM-CFD coupling simulation. Powder Technol. 2008, 185, 132–140. [Google Scholar] [CrossRef]
- Fernandez, X.R.; Nirschl, H. Simulation of particles and sediment behaviour in centrifugal field by coupling CFD and DEM. Chem. Eng. Sci. 2013. [Google Scholar] [CrossRef]
- Fries, L.; Antonyuk, S.; Heinrich, S.; Dopfer, D.; Palzer, S. Collision dynamics in fluidised bed granulators: A DEM-CFD study. Chem. Eng. Sci. 2013, 86, 108–123. [Google Scholar] [CrossRef]
- Drumm, C.; Attarakih, M.M.; Bart, H. Coupling of CFD with DPBM for an RDC extractor. Chem. Eng. Sci. 2009, 64, 721–732. [Google Scholar] [CrossRef]
- Yan, W.-C.; Luo, Z.-H.; Guo, A.-Y. Coupling of CFD with PBM for a pilot-plant tubular loop polymerization reactor. Chem. Eng. Sci. 2011, 66, 5148–5163. [Google Scholar] [CrossRef]
- Tan, H.S.; Goldschimdt, M.J.V.; Boerefijin, R.; Hounslow, M.J.; Salman, A.D.; Kuipers, J.A.M. Building population balance model for fluidized bed melt granulation: Lessons from kinetic theory of granular flow. Powder Technol. 2004, 142, 103–109. [Google Scholar] [CrossRef]
- Rajniak, P.; Stepanek, F.; Dhanasekharan, K.; Fan, R.; Mancinelli, C.; Chern, R.T. A combined experimental and computational study of wet granulation in a wurster fluid bed granulator. Powder Technol. 2009, 189, 190–201. [Google Scholar] [CrossRef]
- Dosta, M.; Antonyuk, S.; Heinrich, S. Multiscale simulation of agglomerate breakage in fluidized bed. Ind. Eng. Chem. Res. 2013, 70, 165–175. [Google Scholar] [CrossRef]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena; John Wiley & Sons (Asia) Pte. Ltd.: Singapore, 2007. [Google Scholar]
- Hirsch, C. Numerical Computation of Internal and External Flows; John Wiley & Sons: Hoboken, NJ, USA, 1990. [Google Scholar]
- Dubey, A.; Sarkar, A.; Ierapetritou, M.G.; Wassgren, C.R.; Muzzio, F.J. Computational approaches for studying the granular dynamics of continuous blending processes, 1 DEM based methods. Macromol. Mater. Eng. 2011, 296, 290–307. [Google Scholar] [CrossRef]
- El Hagrasy, A.S.; Cruise, P.; Jones, I.; Litster, J.D. In-line size monitoring of a twin screw granulation process using high-speed imaging. J. Pharm. Innov. 2013, 8, 90–98. [Google Scholar] [CrossRef]
- El Hagrasy, A.S.; Hennenkamp, J.R.; Burke, M.D.; Cartwright, J.J.; Litster, J.D. Twin screw wet granulation: Influence of formulation parameters on granule properties and growth behavior. Powder Technol. 2013, 238, 108–115. [Google Scholar] [CrossRef]
- EDEM CFD Coupling Interface, 2013. EDEM 2.5.1 Documentation. DEM Solutions. Available online: http://www.dem-solutions.com/ (accessed on 17 July 2013).
- Meade, E.A.; Smith, W.L.; Dewitt, D.L. Differential inhibition of prostaglandin endoperoxide synthase (cyclooxygenase) isozymes by aspirin and other non-steroidal anti-inflammatory drugs. J. Biol. Chem. 1993, 9, 6610–6614. [Google Scholar]
- Mehvar, R.; Jamali, F. Pharmacokinetic analysis of the enantiomeric inversion of chiral nonsteroidal antiinflammatory drugs. Pharm. Res. 1988, 5, 76–79. [Google Scholar] [CrossRef] [PubMed]
- Mangwandi, C.; Cheong, Y.S.; Adams, M.J.; Hounslow, M.J.; Salman, A.D. The coefficient of restitution of different representative types of granules. Chem. Eng. Sci. 2007, 62, 437–450. [Google Scholar] [CrossRef]
- Ramakrishna, D. Population Balances; Academic Press: San Diego, CA, USA, 2000. [Google Scholar]
- Gantt, J.A.; Cameron, I.T.; Litster, J.D.; Gatzke, E.P. Determination of coalescence kernels for high-shear granulation using DEM simulations. Powder Technol. 2006, 170, 53–63. [Google Scholar] [CrossRef]
- Biggs, C.; Sanders, C.; Scott, A.; Willemse, A.; Hoffman, A.; Instone, T.; Salman, A.; Hounslow, M. Coupling granule properties and granulation rates in high-shear granulation. Powder Technol. 2003, 130, 162–168. [Google Scholar] [CrossRef]
- Madec, L.; Falk, L.; Plasari, E. Modelling of the agglomeration in suspension process with multidimensional kernels. Powder Technol. 2003, 130, 147–153. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Sen, M.; Barrasso, D.; Singh, R.; Ramachandran, R. A Multi-Scale Hybrid CFD-DEM-PBM Description of a Fluid-Bed Granulation Process. Processes 2014, 2, 89-111. https://doi.org/10.3390/pr2010089
Sen M, Barrasso D, Singh R, Ramachandran R. A Multi-Scale Hybrid CFD-DEM-PBM Description of a Fluid-Bed Granulation Process. Processes. 2014; 2(1):89-111. https://doi.org/10.3390/pr2010089
Chicago/Turabian StyleSen, Maitraye, Dana Barrasso, Ravendra Singh, and Rohit Ramachandran. 2014. "A Multi-Scale Hybrid CFD-DEM-PBM Description of a Fluid-Bed Granulation Process" Processes 2, no. 1: 89-111. https://doi.org/10.3390/pr2010089
APA StyleSen, M., Barrasso, D., Singh, R., & Ramachandran, R. (2014). A Multi-Scale Hybrid CFD-DEM-PBM Description of a Fluid-Bed Granulation Process. Processes, 2(1), 89-111. https://doi.org/10.3390/pr2010089





