Internal Flow Characteristics in a Prototype Spray Tower Based on CFD
Abstract
1. Introduction
2. Physical Model and Computational Methods
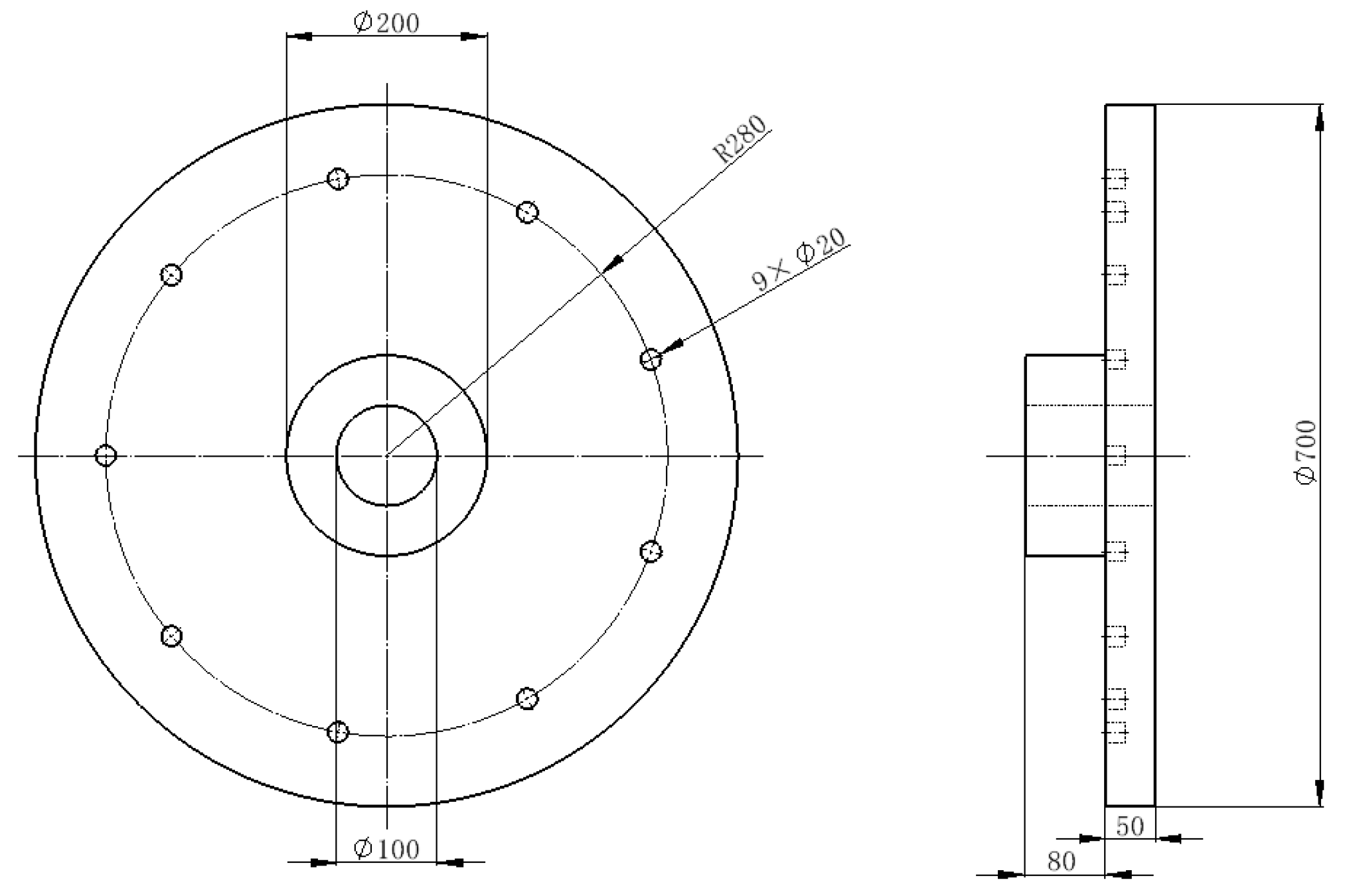
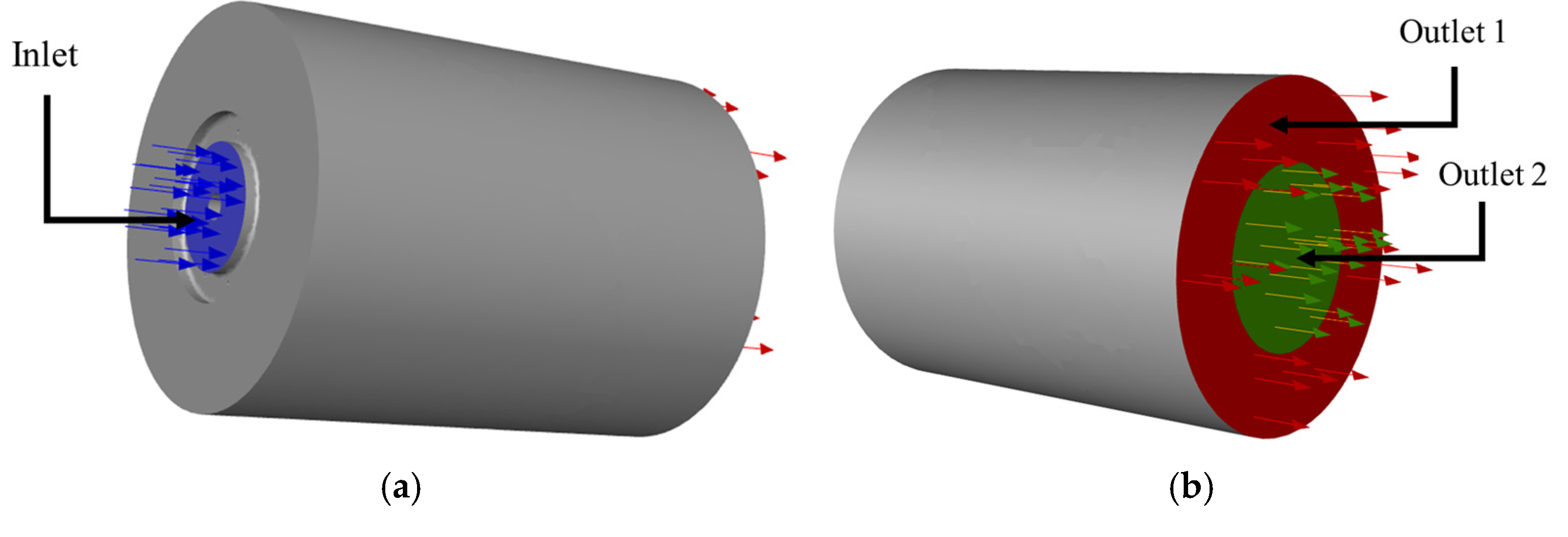
2.1. Spray Tower Model
2.2. Governing Equations
2.3. Mesh Generation
2.4. Boundary Conditions and Computational Methods
3. Results Analysis
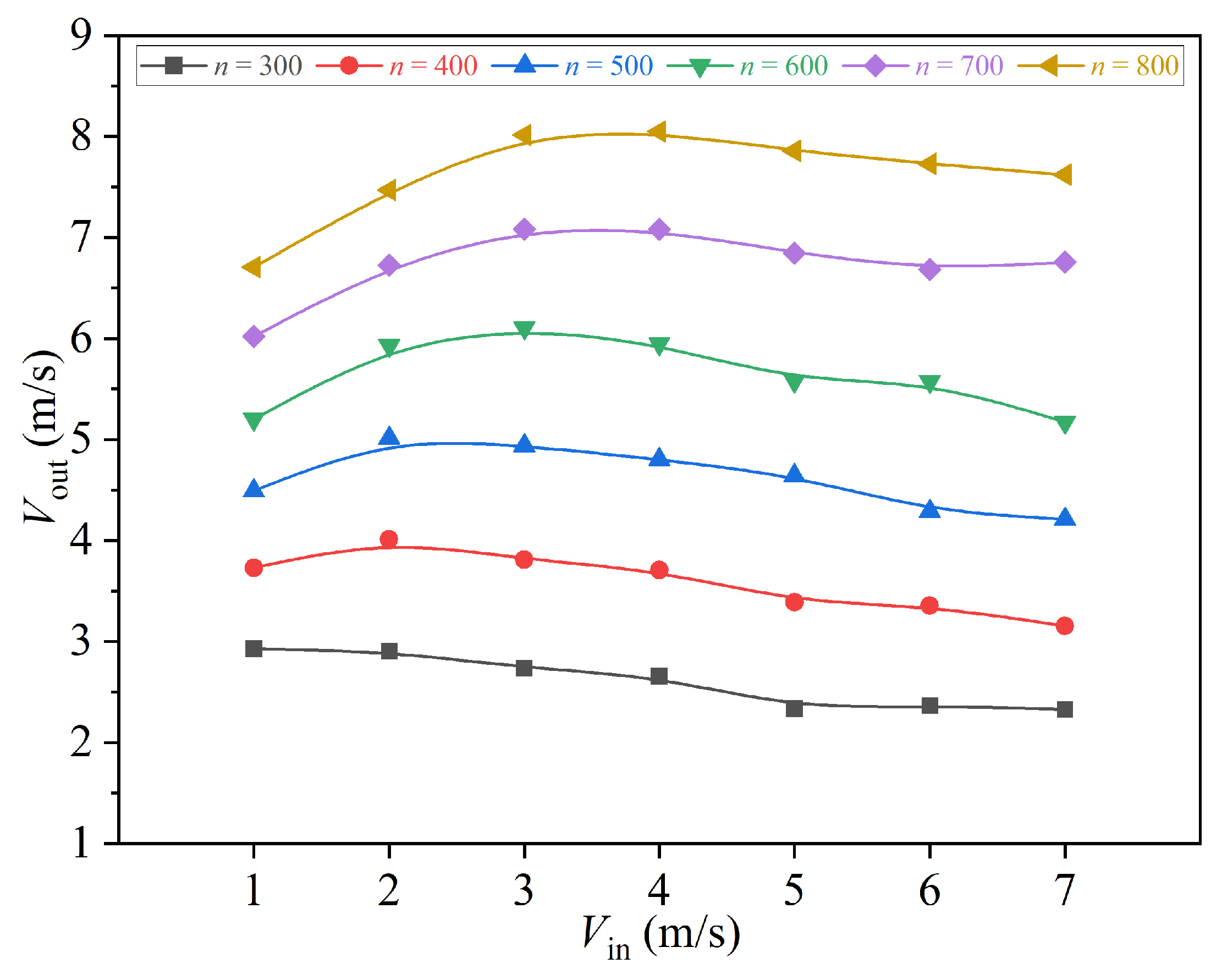
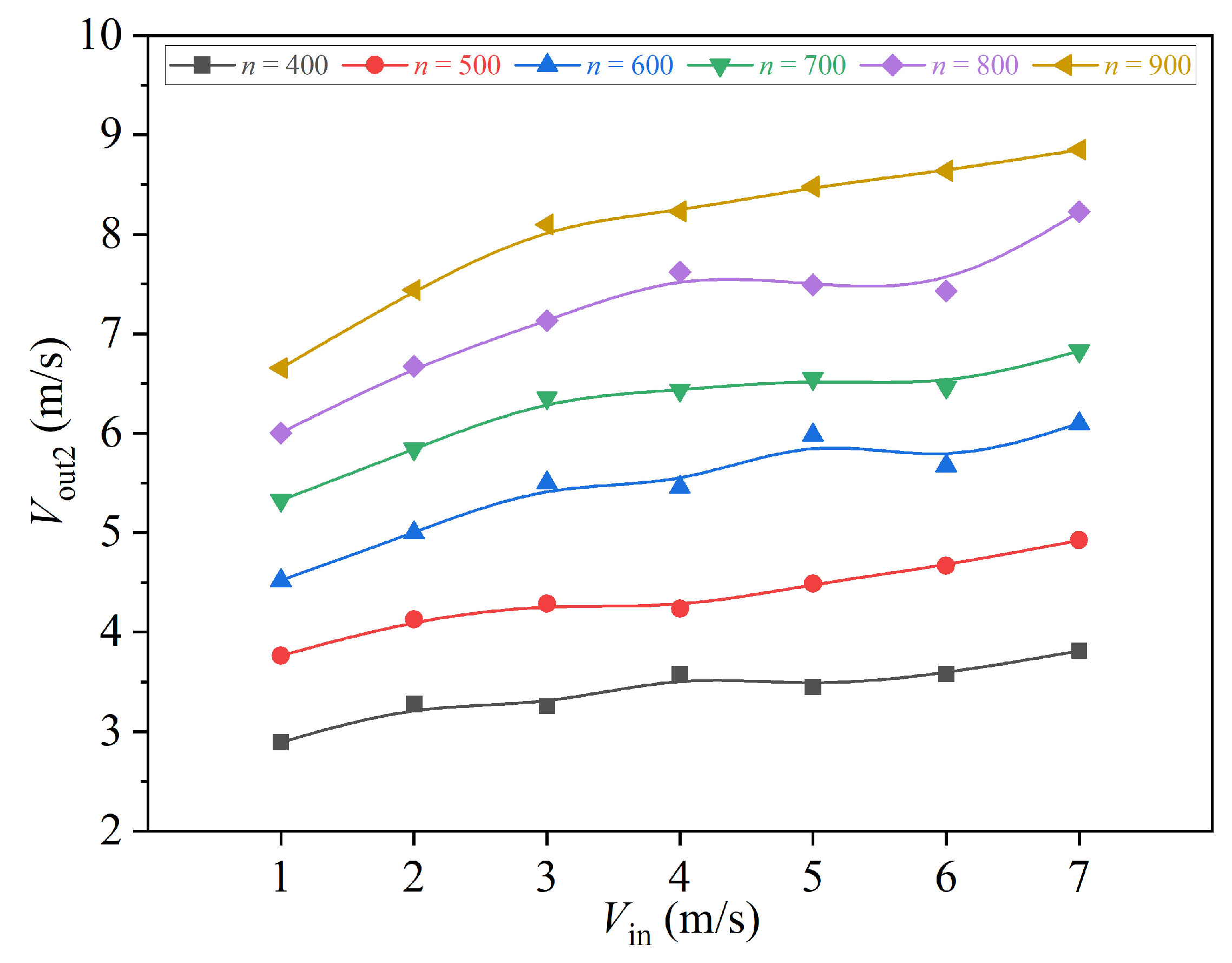
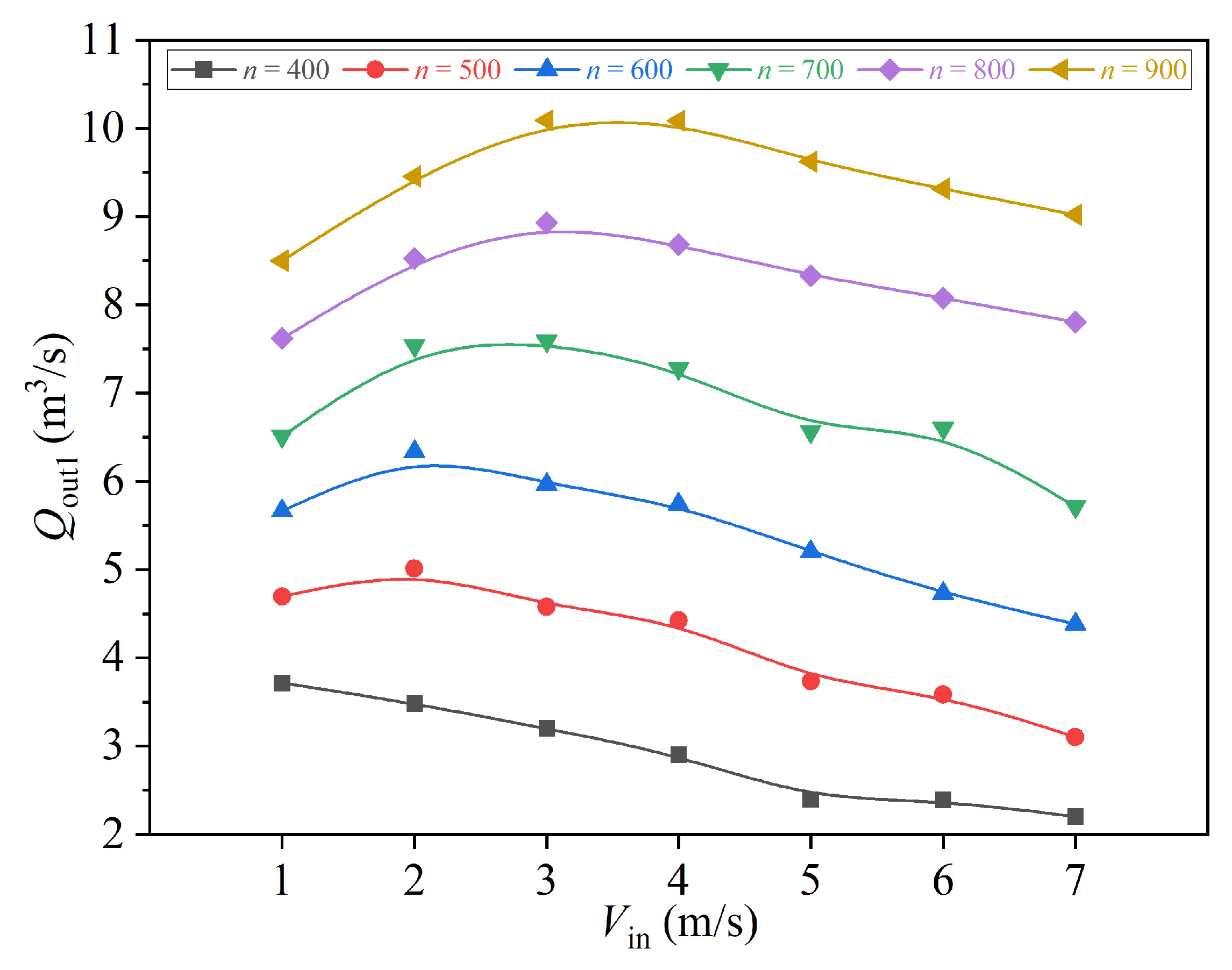
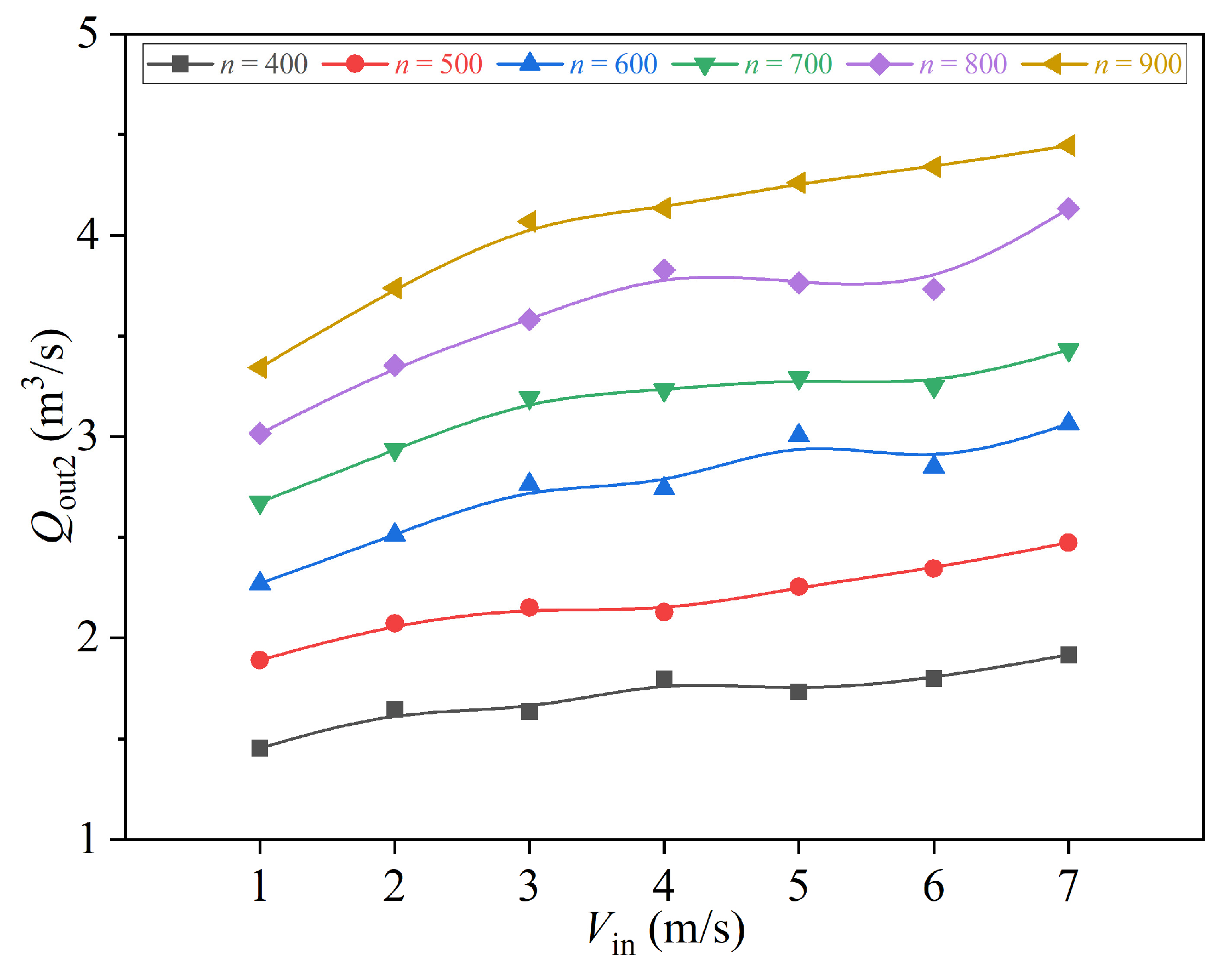
3.1. Operational Condition Effects
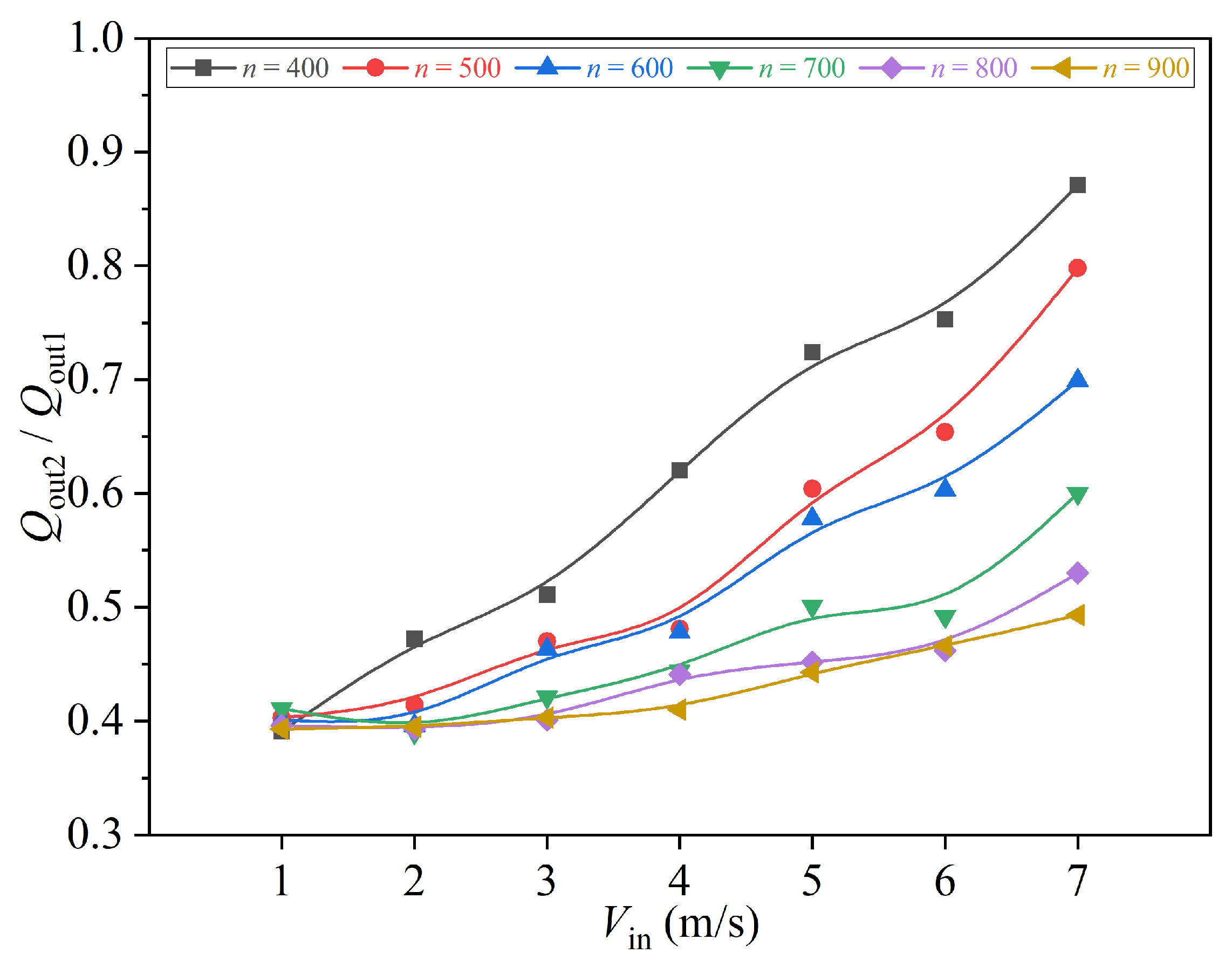
3.2. Correlation Analysis
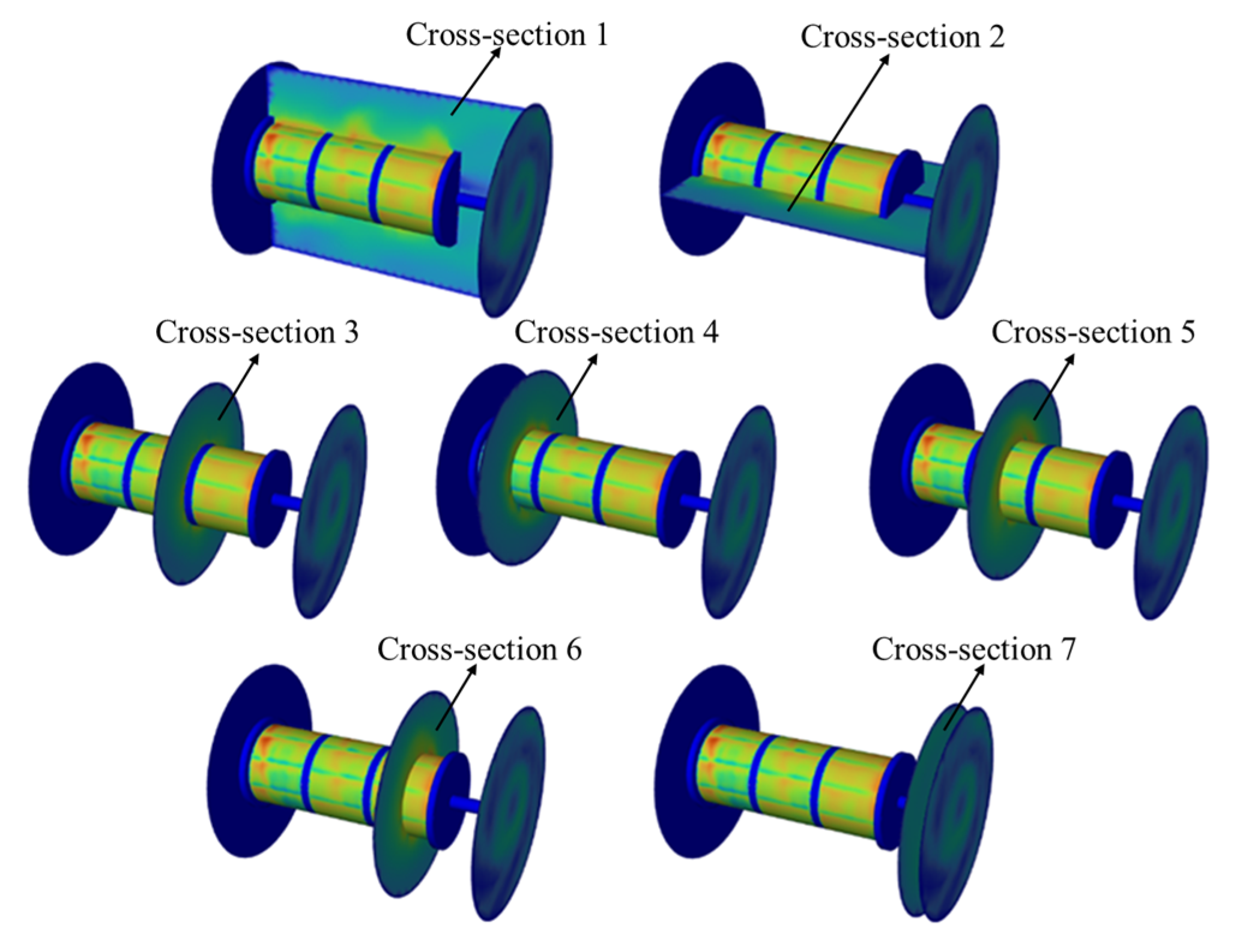
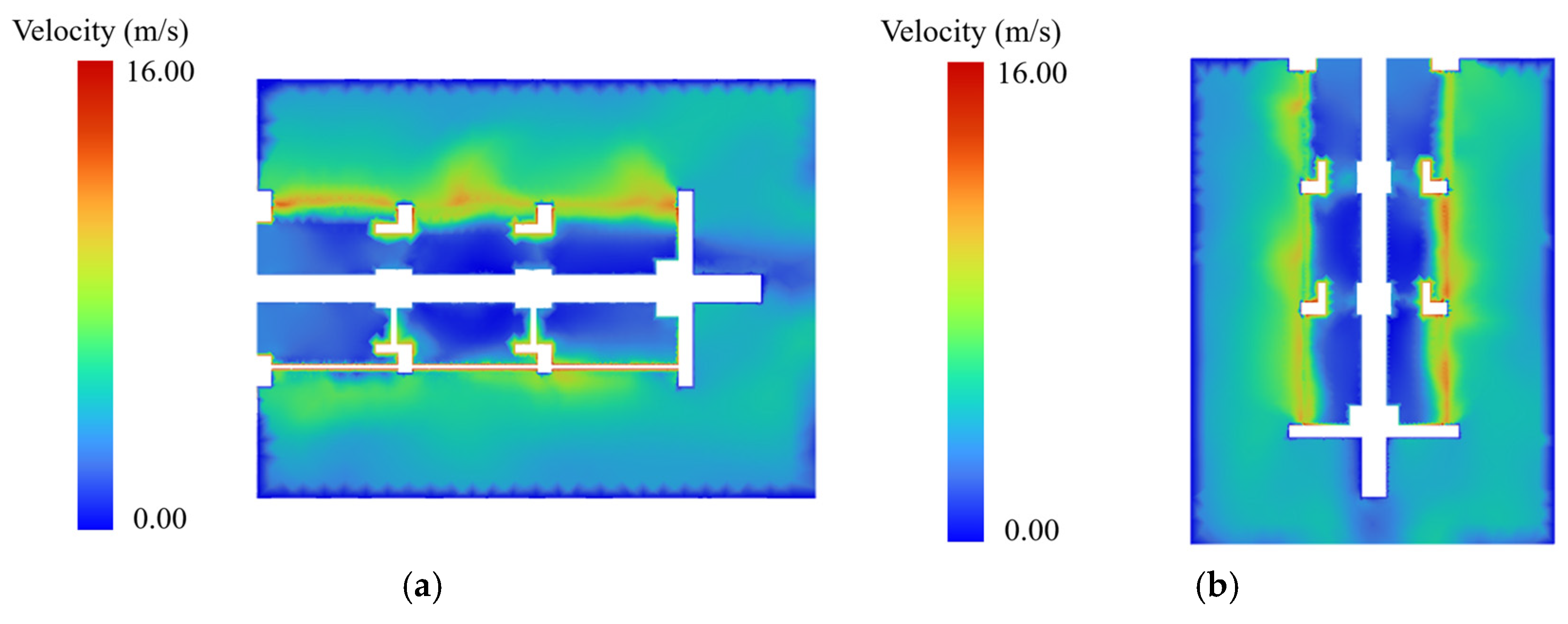
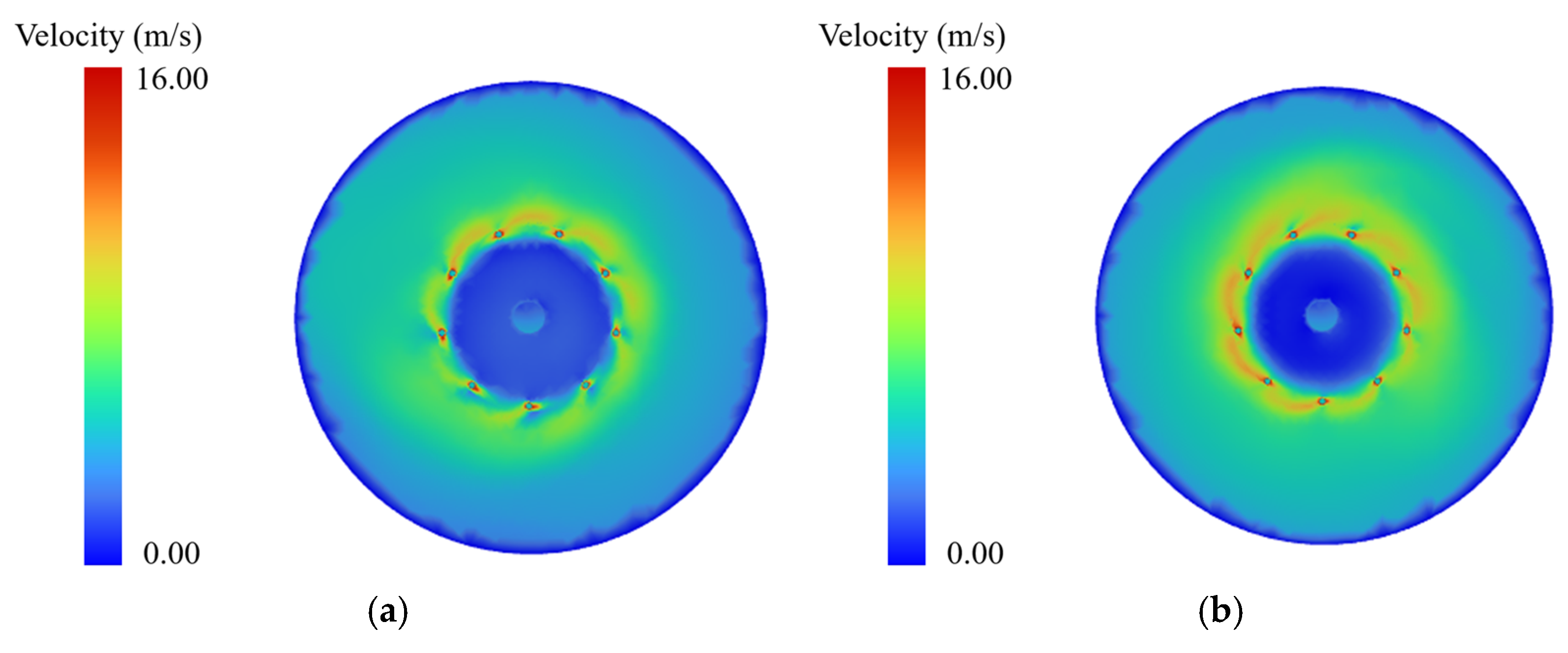
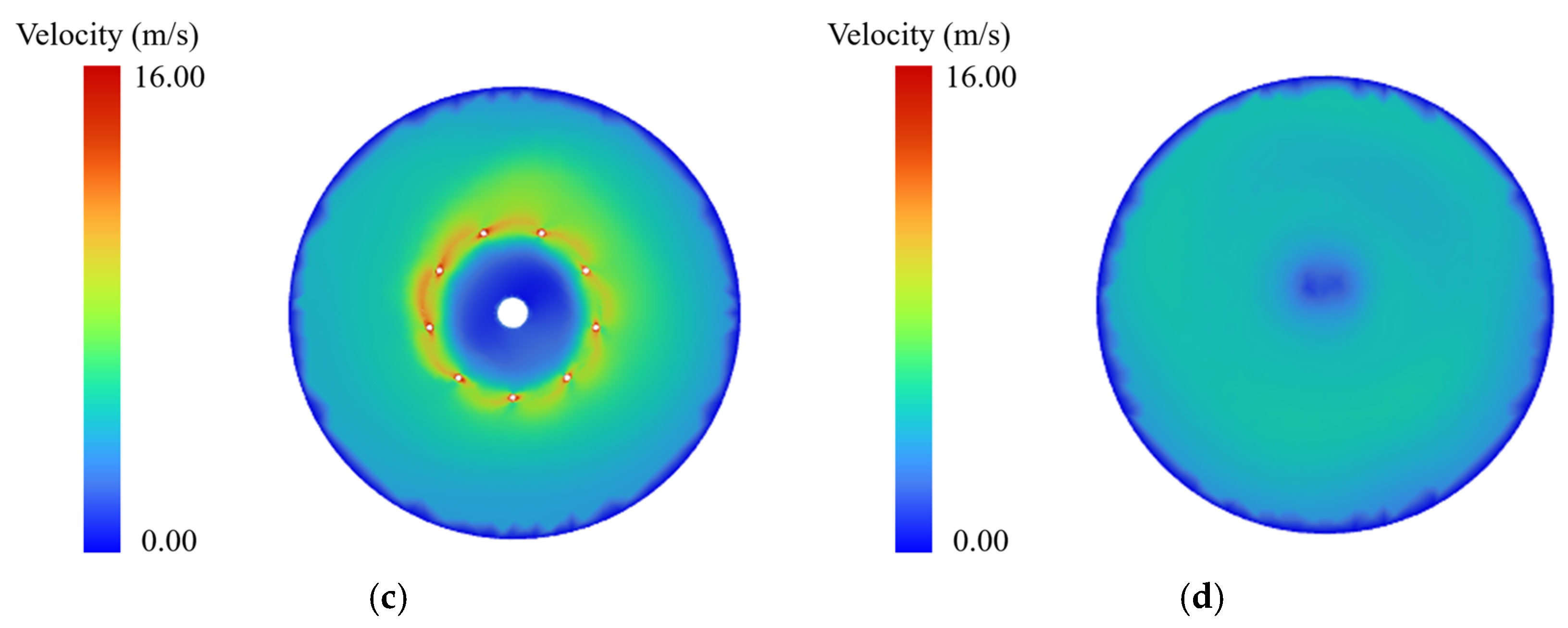
3.3. Flow Field Characteristics
3.4. Prediction Model
- (1)
- Gray Prediction Model
- (2)
- The Partial Least Squares Regression Prediction Model
- (3)
- Prediction Results
4. Conclusions
- (1)
- Increased rotational speed (300–800 r/min) significantly enhances outlet flow rate (outlet 2 increases from 1.453 m3/s to 4.446 m3/s) and velocity, particularly in higher rotational speed ranges (600–800 r/min). Inlet water velocity exhibits nonlinear effects: it suppresses flow velocity at low speeds while initially promoting but later reducing flow due to resistance at medium-high speeds. Synergistic control of rotational speed and water volume is required to optimize separation efficiency.
- (2)
- The correlation between inlet water velocity and outlet velocity varies with rotational speed (negative correlation at low speeds, R = −0.9831; weak positive correlation at high speeds, R = 0.5229). The ratio of outlet 2 to outlet 1 flow rate shows a strong negative correlation with rotational speed (R = −0.9918). When rotational speed exceeds 500 r/min, turbulent disturbances weaken centrifugal effects, stabilizing flow distribution and highlighting rotational speed’s dominant role in liquid phase allocation.
- (3)
- The gray model demonstrates high accuracy (minimum MRE of 1.88%), stability, and efficiency in flow velocity and rate predictions, outperforming the partial least squares model. It is particularly suitable for high real-time requirement scenarios. Future work will integrate more precise computational methods or machine learning algorithms to enhance transient flow velocity capture and improve parameter optimization design.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Danzomo, B.A.; Umar, S.A.; Salami, M.J.E. Wet Scrubber Design. In Control Engineering in Robotics and Industrial Automation: Malaysian Society for Automatic Control Engineers (MACE) Technical Series 2018; Springer International Publishing: Cham, Switzerland, 2021; pp. 19–62. [Google Scholar] [CrossRef]
- Bozorgi, Y.; Keshavarz, P.; Taheri, M.; Fathikaljahi, J. Simulation of a spray scrubber performance with Eulerian/Lagrangian approach in the aerosol removing process. J. Hazard. Mater. 2006, 137, 509–517. [Google Scholar] [CrossRef] [PubMed]
- Mohan, B.R.; Jain, R.; Meikap, B. Comprehensive analysis for prediction of dust removal efficiency using twin-fluid atomization in a spray scrubber. Sep. Purif. Technol. 2008, 63, 269–277. [Google Scholar] [CrossRef]
- Yao, J.; Tanaka, K.; Kawahara, A.; Sadatomi, M. Geometrical Effects on Spray Performance of a Special Twin-fluid Atomizer without Water Power and its CO2 Absorption Capacity. Jpn. J. Multiph. FLOW 2014, 27, 511–520. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, S.; Zhu, P.; Wang, Z.; Zhang, G. Full-scale simulation of flow field in ammonia-based wet flue gas desulfurization double tower. J. Energy Inst. 2018, 91, 619–629. [Google Scholar] [CrossRef]
- Zeng, F.; Yin, L.; Chen, L. Numerical simulation and optimized design of the wet flue gas desulphurization spray tower. In Challenges of Power Engineering and Environment: Proceedings of the International Conference on Power Engineering 2007; Springer: Berlin/Heidelberg, Germany, 2007; pp. 783–787. [Google Scholar] [CrossRef]
- Kallinikos, L.; Farsari, E.; Spartinos, D.; Papayannakos, N. Simulation of the operation of an industrial wet flue gas desulfurization system. Fuel Process. Technol. 2010, 91, 1794–1802. [Google Scholar] [CrossRef]
- Leng, Y.; Hu, R.; Cui, L.; Dong, Y. Study on energy efficiency characteristics of wet flue gas desulfurization tower. Power Gener. Technol. 2020, 41, 543. [Google Scholar] [CrossRef]
- Schwarz, A.D.; König, L.; Meyer, J.; Dittler, A. Impact of water droplet and humidity interaction with soluble particles on the operational performance of surface filters in gas cleaning applications. J. Aerosol Sci. 2020, 142, 105523. [Google Scholar] [CrossRef]
- Wang, S.; Zhu, P.; Zhang, G.; Zhang, Q.; Wang, Z.; Zhao, L. Numerical simulation research of flow field in ammonia-based wet flue gas desulfurization tower. J. Energy Inst. 2015, 88, 284–291. [Google Scholar] [CrossRef]
- Kaltenbach, C.; Laurien, E. CFD simulation of spray cooling in the model containment THAI. Nucl. Eng. Des. 2018, 328, 359–371. [Google Scholar] [CrossRef]
- Wang, B.; Huang, Y.; Yuan, Y.C. Modeling Spray Formed by Spring Nozzle Using Volume-of-Fluid Method. Adv. Mater. Res. 2011, 354–355, 499–503. [Google Scholar] [CrossRef]
- Zhang, Z.; Lei, F.; Ma, L.; Du, J.; Zhao, H.; Zhao, Y.; Yuan, J. Research on parameter optimisation of closed wet cooling tower for oil and gas fields. Int. J. Ambient. Energy 2025, 46, 2508344. [Google Scholar] [CrossRef]
- Xu, M.; Cao, L.; Luo, H.; Hu, P.; Wang, Y. Effect of water spray in exhaust passage of steam turbine on flow field of the last stage during windage. Int. J. Heat Mass. Transf. 2020, 161, 120296. [Google Scholar] [CrossRef]
- Javed, K.; Mahmud, T.; Purba, E. Enhancement of Mass Transfer in a Spray Tower Using Swirling Gas Flow. Chem. Eng. Res. Des. 2006, 84, 465–477. [Google Scholar] [CrossRef]
- Jafari, M.J.; Matin, A.H.; Rahmati, A.; Azari, M.R.; Omidi, L.; Hosseini, S.S.; Panahi, D. Experimental optimization of a spray tower for ammonia removal. Atmos. Pollut. Res. 2018, 9, 783–790. [Google Scholar] [CrossRef]
- Licht, W.; Conway, J.B. Mechanism of Solute Transfer in Spray Towers. Ind. Eng. Chem. 1950, 42, 1151–1157. [Google Scholar] [CrossRef]
- Darake, S.; Hatamipour, M.; Rahimi, A.; Hamzeloui, P. SO2 removal by seawater in a spray tower: Experimental study and mathematical modeling. Chem. Eng. Res. Des. 2016, 109, 180–189. [Google Scholar] [CrossRef]
- Dimiccoli, A.; Di Serio, M.; Santacesaria, E. Mass Transfer and Kinetics in Spray-Tower-Loop Absorbers and Reactors. Ind. Eng. Chem. Res. 2000, 39, 4082–4093. [Google Scholar] [CrossRef]
- Ochowiak, M.; Włodarczak, S.; Pavlenko, I.; Janecki, D.; Krupińska, A.; Markowska, M. Study on Interfacial Surface in Modified Spray Tower. Processes 2019, 7, 532. [Google Scholar] [CrossRef]
- Ma, S.; Zang, B.; Song, H.; Chen, G.; Yang, J. Research on mass transfer of CO2 absorption using ammonia solution in spray tower. Int. J. Heat Mass. Transf. 2013, 67, 696–703. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, H.; Zhuo, J.; You, C. Experimental and numerical study on effects of deflectors on flow field distribution and desulfurization efficiency in spray towers. Fuel Process. Technol. 2017, 162, 1–12. [Google Scholar] [CrossRef]
- Bandyopadhyay, A.; Biswas, M.N. Modeling of SO2 scrubbing in spray towers. Sci. Total. Environ. 2007, 383, 25–40. [Google Scholar] [CrossRef] [PubMed]
- Cui, H.; Li, N.; Wang, X.; Peng, J.; Li, Y.; Wu, Z. Optimization of reversibly used cooling tower with downward spraying. Energy 2017, 127, 30–43. [Google Scholar] [CrossRef]
- Wu, X.; Sharif, M.; Yu, Y.; Chen, L.; Zhang, Z.; Wang, G. Hydrodynamic mechanism study of the diameter-varying spray tower with atomization impinging spray. Sep. Purif. Technol. 2021, 268, 118608. [Google Scholar] [CrossRef]
- Hou, B.; Chen, O.; Wang, Y.; Wang, F.; Lu, G. Structural optimization and flow field simulation of gas distribution device in desulfurization tower. Asia-Pacific J. Chem. Eng. 2023, 19, e2988. [Google Scholar] [CrossRef]
- Zhong, Y.; Gao, X.; Huo, W.; Luo, Z.-Y.; Ni, M.-J.; Cen, K.-F. A model for performance optimization of wet flue gas desulfurization systems of power plants. Fuel Process. Technol. 2008, 89, 1025–1032. [Google Scholar] [CrossRef]
- Hong, M.; Xu, G.; Lu, P.; Huang, Z.; Miao, H.; Zhang, Y.; Ma, C.; Zhang, Q. CFD analysis of the spray droplet parameters effect on gas-droplet flow and evaporation characteristics in circulating fluidized bed desulfurization tower. Chem. Eng. Res. Des. 2023, 196, 184–203. [Google Scholar] [CrossRef]
- Chen, S.; Zhao, X.; Xiao, Z.; Cheng, M.; Zou, R.; Luo, G. Enhancement of fine particle removal through flue gas cooling in a spray tower with packing materials. J. Hazard. Mater. 2024, 478, 135390. [Google Scholar] [CrossRef] [PubMed]
- Salins, S.S.; Kumar, S.; Chouhan, J.; Tejero-González, A.; Nair, P.S. Experimental performance of a spray tower system for water desalination and indoor thermal comfort. Process. Saf. Environ. Prot. 2023, 180, 122–135. [Google Scholar] [CrossRef]
- Huang, J.; Zeng, Z.; Hong, F.; Yang, Q.; Wu, F.; Peng, S. Sustainable Operation Strategy for Wet Flue Gas Desulfurization at a Coal-Fired Power Plant via an Improved Many-Objective Optimization. Sustainability 2024, 16, 8521. [Google Scholar] [CrossRef]
- Zhevzhyk, O.; Potapchuk, I.; Pertsevyi, V.; Bosyi, D.; Biriukov, D.; Shevchenko, S. Numerical modeling of the thermal characteristics of a fan spray cooling tower. Proc. IOP Conf. Ser. Earth Environ. Sci. 2024, 1348, 012090. [Google Scholar] [CrossRef]
- Valera, V.Y.; Martins, T.D.; Codolo, M.C. Experimental evaluation and neural networks modeling of removal efficiency and volumetric mass transfer coefficient for gas desulfurization in spray tower. Chem. Eng. Sci. 2023, 285, 119568. [Google Scholar] [CrossRef]
- Ghosh, D.; Biswas, D.; Datta, A. Absorption height in spray tower for wet-limestone process in flue gas desulphurization. Mater. Today Proc. 2024. [Google Scholar] [CrossRef]
- Zhu, S.; Zhu, Q. Numerical study on the heat transfer performance of a novel spray tower. J. Phys. Conf. Ser. 2020, 1600, 012023. [Google Scholar] [CrossRef]
- Zhang, T.; Tang, Q.; Pu, C.; Zhang, L. Numerical simulation of gas-droplets mixing and spray evaporation in rotary spray desulfurization tower. Adv. Powder Technol. 2022, 33, 103420. [Google Scholar] [CrossRef]
- Reuter, H.C.R.; Viljoen, D.J.; Kröger, D.G. A method to determine the performance characteristics of cooling tower spray zones. In Proceedings of the 2010 14th International Heat Transfer Conference, Washington, DC, USA, 8–13 August 2010; Volume 49392, pp. 619–628. [Google Scholar] [CrossRef]
- Ye, J.-G.; Xu, S.-S.; Huang, H.-F.; Zhao, Y.-J.; Zhou, W.; Zhang, Y.-L. Optimization Design of Nozzle Structure Inside Boiler Based on Orthogonal Design. Processes 2023, 11, 2923. [Google Scholar] [CrossRef]
- Baker, N.; Kelly, G.; O’SUllivan, P.D. A grid convergence index study of mesh style effect on the accuracy of the numerical results for an indoor airflow profile. Int. J. Vent. 2019, 19, 300–314. [Google Scholar] [CrossRef]
- Ma, X.; Wu, W.; Zhang, Y. Application of a novel quadratic polynomial discrete grey model to forecast energy consumption of China. Sci. Iran. 2024, 31, 469–480. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, H.; Hou, P.; Jia, X. A novel prediction model of desulfurization efficiency based on improved FCM-PLS-LSSVM. Multimed. Tools Appl. 2022, 82, 5685–5708. [Google Scholar] [CrossRef]
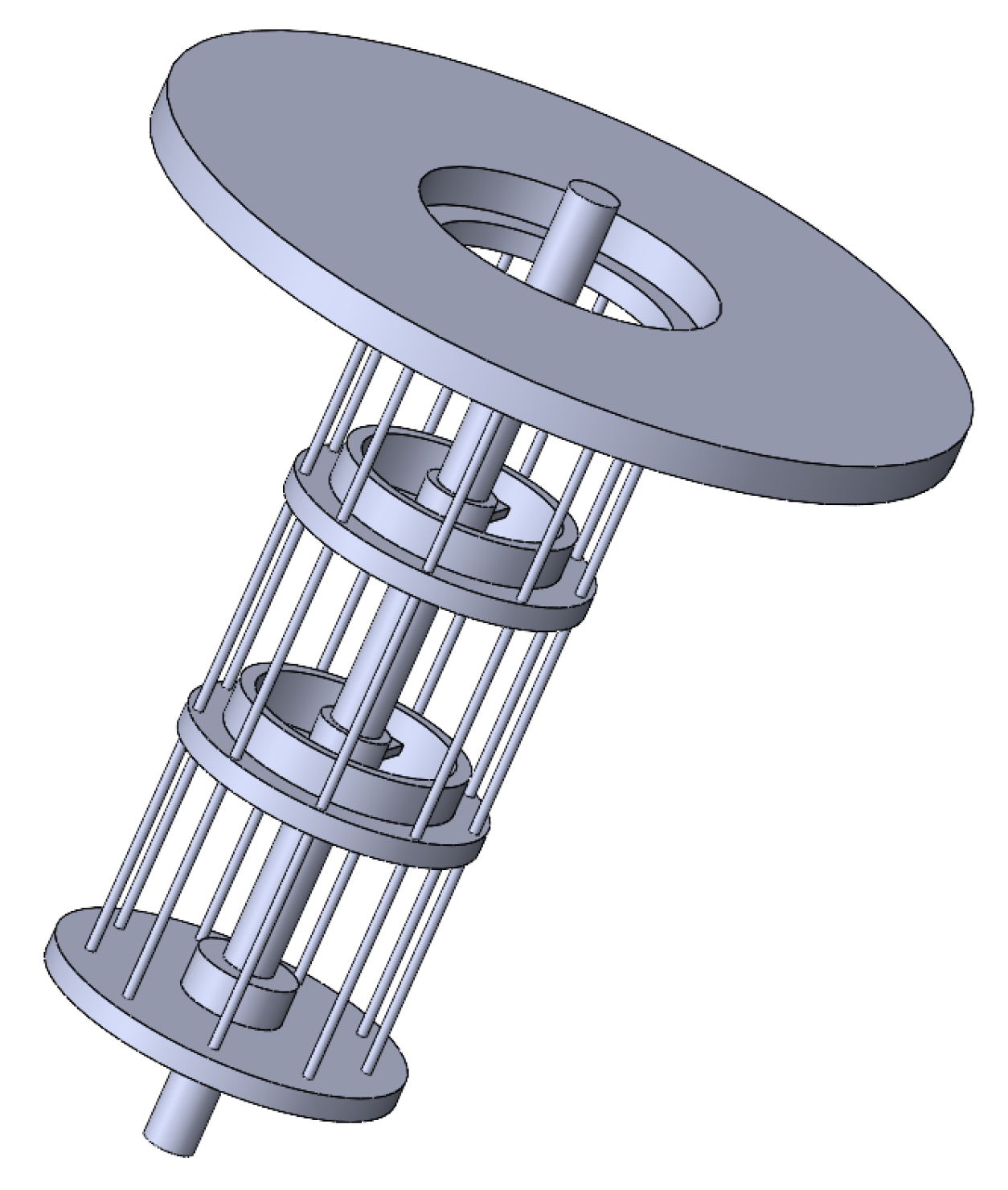
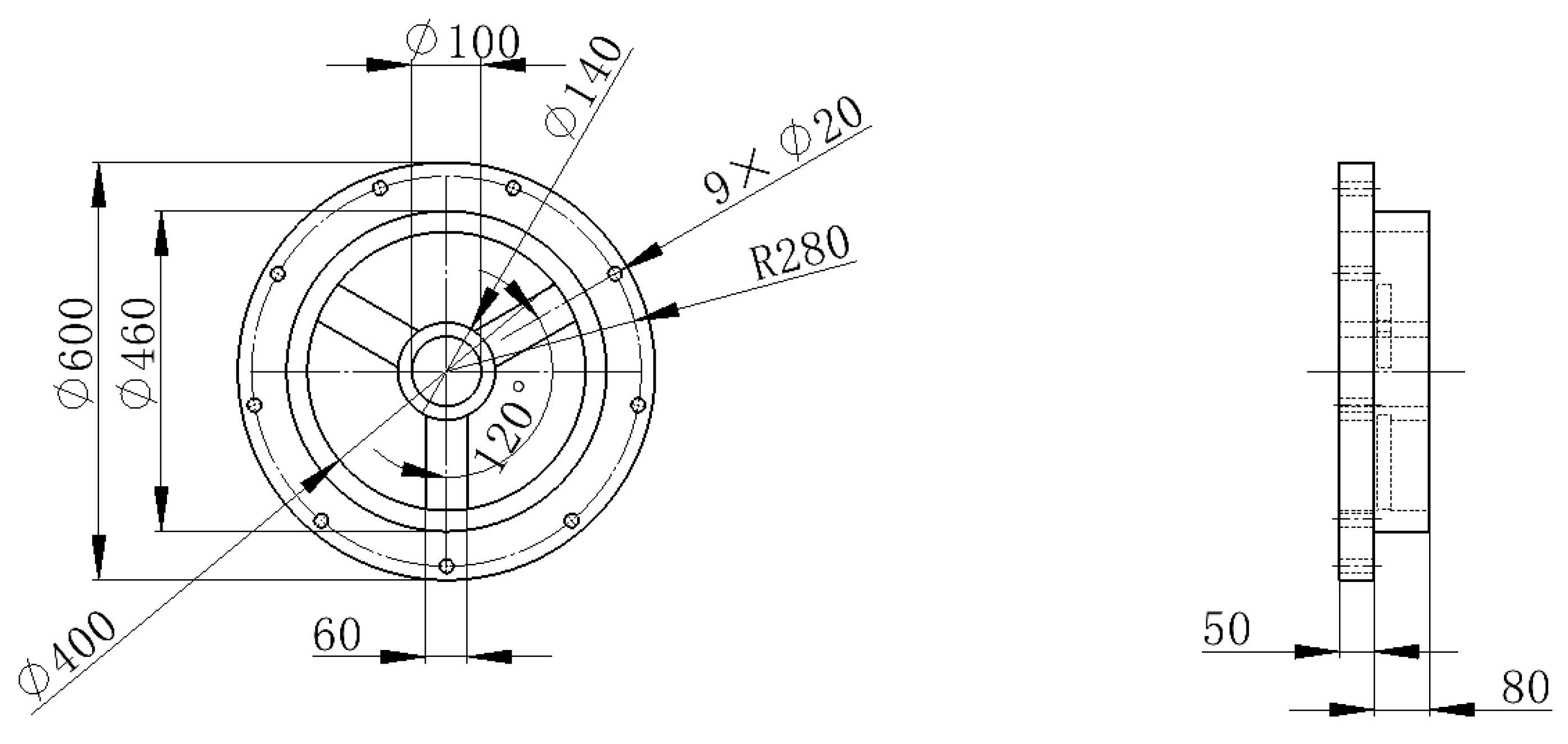

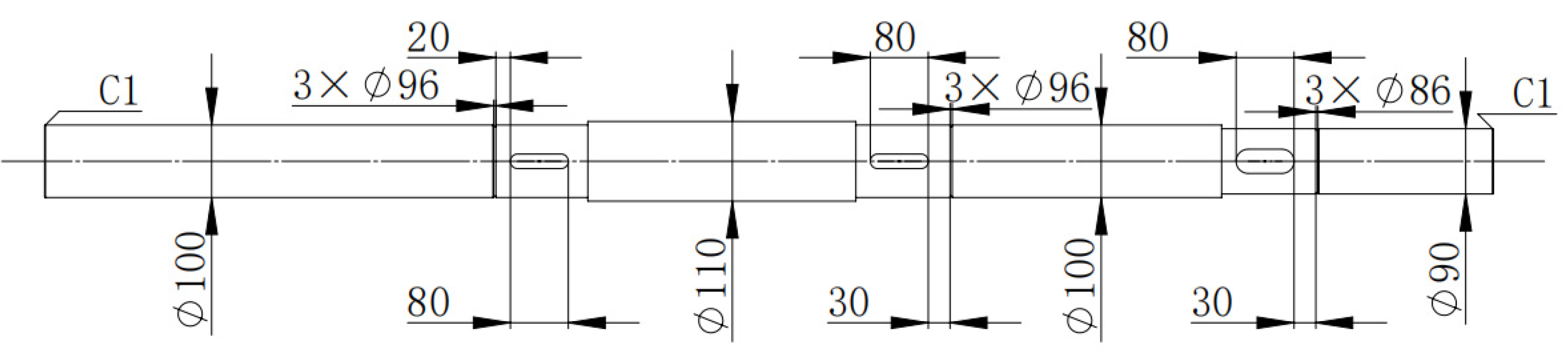
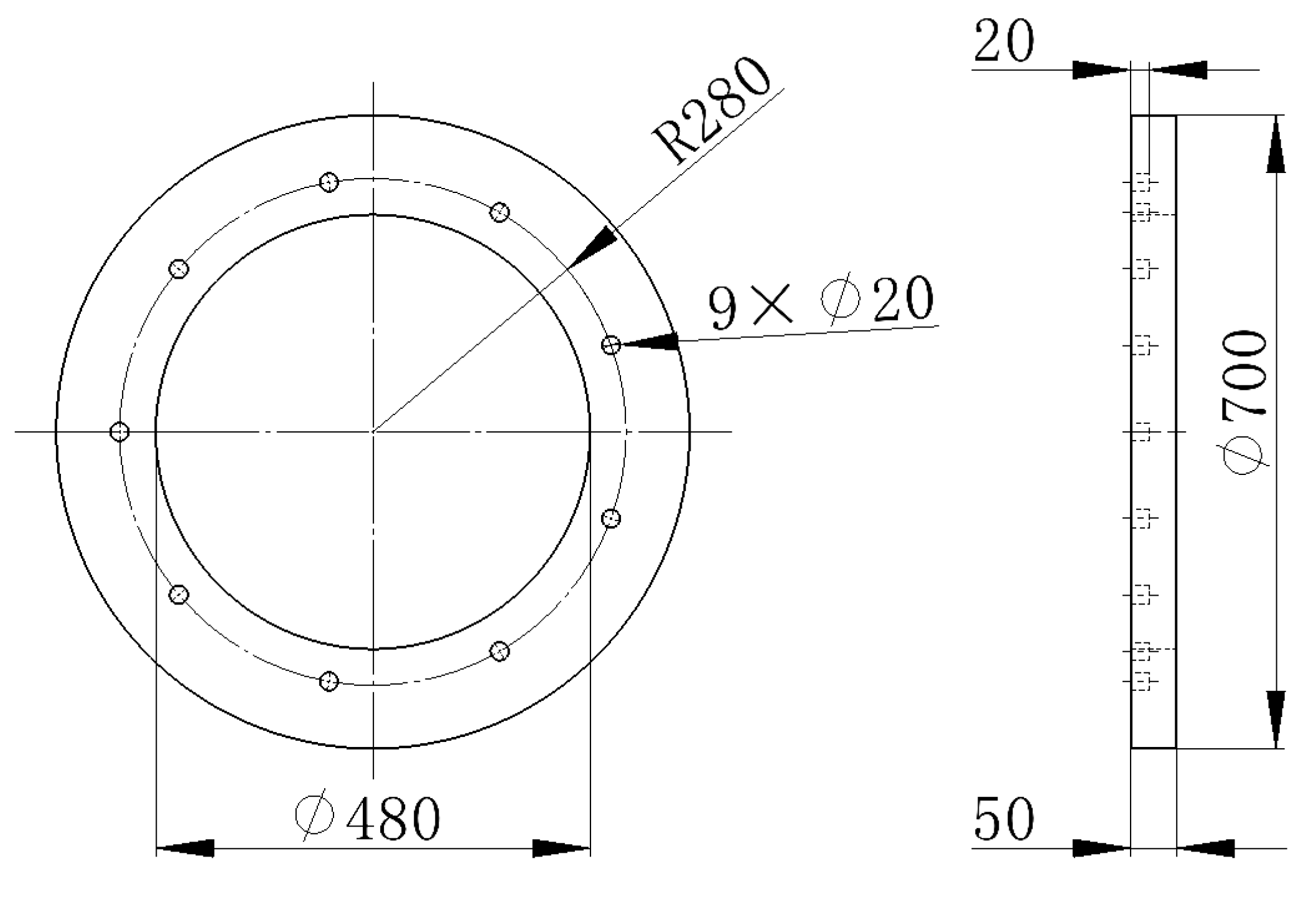




| Serial Number | Rotational Speed of Spray Tower (r/min) | Inlet Water Velocity (m/s) | Serial Number | Rotational Speed of Spray Tower (r/min) | Inlet Water Velocity (m/s) |
|---|---|---|---|---|---|
| 01 | 300 | 1 | 22 | 600 | 1 |
| 02 | 300 | 2 | 23 | 600 | 2 |
| 03 | 300 | 3 | 24 | 600 | 3 |
| 04 | 300 | 4 | 25 | 600 | 4 |
| 05 | 300 | 5 | 26 | 600 | 5 |
| 06 | 300 | 6 | 27 | 600 | 6 |
| 07 | 300 | 7 | 28 | 600 | 7 |
| 08 | 400 | 1 | 29 | 700 | 1 |
| 09 | 400 | 2 | 30 | 700 | 2 |
| 10 | 400 | 3 | 31 | 700 | 3 |
| 11 | 400 | 4 | 32 | 700 | 4 |
| 12 | 400 | 5 | 33 | 700 | 5 |
| 13 | 400 | 6 | 34 | 700 | 6 |
| 14 | 400 | 7 | 35 | 700 | 7 |
| 15 | 500 | 1 | 36 | 800 | 1 |
| 16 | 500 | 2 | 37 | 800 | 2 |
| 17 | 500 | 3 | 38 | 800 | 3 |
| 18 | 500 | 4 | 39 | 800 | 4 |
| 19 | 500 | 5 | 40 | 800 | 5 |
| 20 | 500 | 6 | 41 | 800 | 6 |
| 21 | 500 | 7 | 42 | 800 | 7 |
| Value of |R| | Correlation Level |
|---|---|
| |R| = 0 | No correlation |
| 0 ≤ |R| ≤ 0.3 | Weak correlation |
| 0.3 ≤ |R| ≤ 0.5 | Low correlation |
| 0.5 ≤ |R| ≤ 0.8 | Moderate correlation |
| 0.8 ≤ |R| ≤ 1 | Strong correlation |
| |R| = 1 | Totally relevant |
| Variable | vout | vout1 | vout2 | Qout1 | Qout2 | Qout2/Qout1 |
|---|---|---|---|---|---|---|
| Inlet water velocity at 300 r/min | −0.9551 | −0.9831 | 0.9253 | −0.9831 | 0.9253 | 0.993 |
| Inlet water velocity at 400 r/min | −0.8855 | −0.9427 | 0.9712 | −0.9427 | 0.9712 | 0.9564 |
| Inlet water velocity at 500 r/min | −0.6395 | −0.8676 | 0.9185 | −0.8676 | 0.9185 | 0.9703 |
| Inlet water velocity at 600 r/min | −0.2754 | −0.6021 | 0.9064 | −0.6021 | 0.9064 | 0.9106 |
| Inlet water velocity at 700 r/min | 0.4071 | −0.1533 | 0.9203 | −0.1533 | 0.9203 | 0.932 |
| Inlet water velocity at 800 r/min | 0.5229 | 0.111 | 0.9427 | 0.111 | 0.9427 | 0.9515 |
| Variable | vout | vout1 | vout2 | Qout1 | Qout2 | Qout2/Qout1 |
|---|---|---|---|---|---|---|
| Rotational speed at 1 m/s | 0.9998 | 0.9996 | 0.9987 | 0.9996 | 0.9987 | 0.0014 |
| Rotational speed at 2 m/s | 0.9972 | 0.9954 | 0.9998 | 0.9954 | 0.9998 | −0.765 |
| Rotational speed at 3 m/s | 0.9992 | 0.9991 | 0.9974 | 0.9991 | 0.9974 | −0.9626 |
| Rotational speed at 4 m/s | 0.9998 | 0.9999 | 0.9961 | 0.9999 | 0.9961 | −0.8703 |
| Rotational speed at 5 m/s | 0.9994 | 0.9993 | 0.9941 | 0.9993 | 0.9941 | −0.9667 |
| Rotational speed at 6 m/s | 0.999 | 0.9974 | 0.9985 | 0.9974 | 0.9985 | −0.9574 |
| Rotational speed at 7 m/s | 0.9959 | 0.9933 | 0.9964 | 0.9933 | 0.9964 | −0.9918 |
| Parameter | Model Type | Mean Relative Error Absolute (MRE) | Mean Absolute Error, m/s (MAE) | Proportion of Relative Error Absolute ≤ 10% | Proportion of Relative Error Absolute ≤ 5% |
|---|---|---|---|---|---|
| Average outlet velocity | Gray prediction model | 1.879607 | 0.092669 | 0.988095 | 0.928571 |
| Average outlet velocity | Partial least squares regression model | 5.109452 | 0.248564 | 0.904762 | 0.47619 |
| Average velocity at outlet 1 | Gray prediction model | 2.401143 | 0.108914 | 0.964286 | 0.892857 |
| Average velocity at outlet 1 | Partial least squares regression model | 8.836238 | 0.3549 | 0.666667 | 0.333333 |
| Average velocity at outlet 2 | Gray prediction model | 2.13869 | 0.129914 | 0.97619 | 0.904762 |
| Average velocity at outlet 2 | Partial least squares regression model | 8.36869 | 0.465669 | 0.738095 | 0.404762 |
| Parameter | Model Type | Mean Relative Error Absolute (MRE) | Mean Absolute Error, m3/s (MAE) | Proportion of Relative Error Absolute ≤ 10% | Proportion of Relative Error Absolute ≤ 5% |
|---|---|---|---|---|---|
| Flow rate at outlet 1 | Gray prediction model | 2.401143 | 0.13767 | 0.964286 | 0.892857 |
| Flow rate at outlet 1 | Partial least squares regression model | 8.836238 | 0.448543 | 0.666667 | 0.333333 |
| Flow rate at outlet 2 | Gray prediction model | 2.13869 | 0.065267 | 0.97619 | 0.904762 |
| Flow rate at outlet 2 | Partial least squares regression model | 8.36869 | 0.233945 | 0.738095 | 0.404762 |
| Ratio of flow rate at outlet 2 to outlet 1 | Gray prediction model | 3.34369 | 0.018844 | 0.952381 | 0.880952 |
| Ratio of flow rate at outlet 2 to outlet 1 | Partial least squares regression model | 15.20321 | 0.07819 | 0.380952 | 0.238095 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Huang, H.-F.; Xu, X.-W.; Zhang, Y.-L. Internal Flow Characteristics in a Prototype Spray Tower Based on CFD. Processes 2025, 13, 2308. https://doi.org/10.3390/pr13072308
Li X, Huang H-F, Xu X-W, Zhang Y-L. Internal Flow Characteristics in a Prototype Spray Tower Based on CFD. Processes. 2025; 13(7):2308. https://doi.org/10.3390/pr13072308
Chicago/Turabian StyleLi, Xin, Hui-Fan Huang, Xiao-Wei Xu, and Yu-Liang Zhang. 2025. "Internal Flow Characteristics in a Prototype Spray Tower Based on CFD" Processes 13, no. 7: 2308. https://doi.org/10.3390/pr13072308
APA StyleLi, X., Huang, H.-F., Xu, X.-W., & Zhang, Y.-L. (2025). Internal Flow Characteristics in a Prototype Spray Tower Based on CFD. Processes, 13(7), 2308. https://doi.org/10.3390/pr13072308






